Generation time and effective population size in Polar Eskimos

Abstract

North Greenland Polar Eskimos are the only hunter–gatherer population, to our knowledge, who can offer precise genealogical records spanning several generations. This is the first report from Eskimos on two key parameters in population genetics, namely, generation time (T) and effective population size (N_e). The average mother–daughter and father–son intervals were 27 and 32 years, respectively, roughly similar to the previously published generation times obtained from recent agricultural societies across the world. To gain an insight for the generation time in our distant ancestors, we calculated maternal generation time for two wild chimpanzee populations. We also provide the first comparison among three distinct approaches (genealogy, variance and life table methods) for calculating N_e, which resulted in slightly differing values for the Eskimos. The ratio of the effective to the census population size is estimated as 0.6–0.7 for autosomal and X-chromosomal DNA, 0.7–0.9 for mitochondrial DNA and 0.5 for Y-chromosomal DNA. A simulation of alleles along the genealogy suggested that Y-chromosomal DNA may drift a little faster than mitochondrial DNA in this population, in contrast to agricultural Icelanders. Our values will be useful not only in prehistoric population inference but also in understanding the shaping of our genome today.

1. Introduction

The human species has existed for at least 150 000 years (White et al. 2003; McDougall et al. 2005), and for most of this time has led a Palaeolithic hunter–gatherer lifestyle until the start of agriculture in the Neolithic Age within the last 10 000 years. Many questions that prehistorians ask refer to events at Palaeolithic time depths, such as the initial settling of the continents by hunter–gatherers or the demographic effects of the Last Ice Age. When using genetic variation in living humans to reconstruct these prehistoric events, it is therefore crucial to apply demographic parameters (such as generation time and differences between the sexes in reproductive success) which are realistic for ancient hunter–gatherers. Our best proxies for ancient hunter–gatherers are the few remaining hunter–gatherer groups who have retained their lifestyle into modern times. Here, however, a difficulty arises because hunter–gatherers do not usually keep accessible genealogical records. It is only in very rare cases that outside observers have written down genealogical information for such groups, but fortunately this does apply to the Polar Eskimo population in Greenland where a Danish medical family compiled extensive genealogical records between 1805 and 1974 (Gilberg et al. 1978).

To our knowledge, this is the first report from Eskimos on two key parameters in population research and in genome analyses, namely, generation time (T) and effective population size (N_e). These parameter values from hunter–gatherers are increasingly valuable because during the last 20 years, the study of human prehistory has been accelerated by the accumulation of genetic data in living humans and by the introduction of new statistical methods (Harpending & Rogers 2000; Beaumont 2004). The age of the most recent common ancestor for non-recombining loci (e.g. Vigilant et al. 1991) or that of the peopling of a particular region (e.g. Forster et al. 1996) is estimated from the number of mutations found in a DNA sample. The past population size is inferred from the variation found in a sample (e.g. Murray-McIntosh et al. 1998). Some kinds of population genetic models are needed when such inference is carried out. The accuracy of inference depends on the values of the two parameters used in the models.

Generation time (T), or the intergeneration interval, is one of the most important parameters in human population genetics. Since genetic dating methods give us answers primarily in the form of the number of generations, we need the generation time to translate generations to years. In many applications, it has been assumed to be 20–25 years for prehistoric humans (Fenner 2005). However, recent studies on pre-industrial Europeans suggested that the generation time is longer than previously considered (Denmark/Germany: Forster 1996; Canada: Tremblay & Vézina 2000; Iceland: Helgason et al. 2003). Moreover, we have to pay attention to the variation among peoples living in different locations. Some demographic factors such as high mortality at young ages shorten the interval.

The effective population size N_e is another important parameter in population genetics. Genetic variation in a population is lost more quickly by stochastic processes when the size of the population is smaller. However, the speed of the loss is not determined by its census size N (including individuals of both sexes and all ages) but by its effective size N_e (where factors such as unequal family sizes are involved). Genetic variation is lost quickly (and hence its N_e is small) when there is a large variance in the offspring number (family size) and/or a biased operational sex ratio. The relationship between the census size N and the effective size N_e is critical when we apply population genetic models to real populations. For example, when we infer past population size from present genetic data, most models provide us with answers expressed as effective sizes. We need to translate them into actual sizes. In a review of the ratio of effective to actual population size (N_e/N) in wildlife (Frankham 1995), most estimates of N_e/N in humans fall in a range between 0.3 and 0.9 for autosomal loci. The variation may result from differences in demographic and social conditions.

The objective of this study is to estimate the values of these two important parameters, generation time and the ratio of the effective population size to census size, in one of the few extensively documented hunter–gatherer populations, the Polar Eskimos in North Greenland. Eskimos and previously studied Europeans differ considerably in their environment, physical characteristics and culture. If any of these factors made a great impact on generation time or the effective population size then we should see it in our Eskimo samples. On the other hand, if T and N_e/N were similar between Eskimos and Europeans, we are more justified in using modern T and N_e/N estimates for prehistoric peoples. Polar Eskimo genealogies have been recorded remarkably well since the mid-nineteenth century (Gilberg et al. 1978). They provide us with an extremely rare opportunity to measure these two parameters in a hunter–gatherer population.

2. Material and methods

(a) Polar Eskimo database

The subjects of this study are the Polar Eskimos in the Thule District of North Greenland. A good summary of their demography based on censuses became available in 1976 (Gilberg 1976). Europeans came into contact with the Thule Eskimos in 1818, and since 1909 there has been continuous contact. The population size in the early nineteenth century was estimated to be approximately 150 or less. It was approximately 200–300 in the late nineteenth and the early twentieth century, and increased to 400 in 1959.

Genealogical information on the Polar Eskimos was collected and published by a Danish resident physician and his family (Gilberg et al. 1978). The database includes 1614 individuals who were born between ca 1805 and 1974. Edwards (1992a) studied the basic structure of their genealogy from a population genetic viewpoint. Following his definition, we regard 225 individuals whose parents do not appear in the database as founders. For generation time, we restrict the analysis to those who finished their reproduction (females: 49 years and above and males: 68 years and above), that is, parents born in or after 1926 (female) or 1907 (male) are disregarded. For lifetime offspring number, we analyse the data from the cohorts born between 1820 and 1906 (inclusive). We include all the individuals whose birth year is known in the compilation of life tables that summarize the mortality and reproduction rates at each age class.

(b) Comparison with ape generation times

Although it is impossible to know the generation time in our distant ancestors, it may be helpful to compare the generation time of wild chimpanzees with ours. Therefore, we carried out a rough calculation of generation time using the mortality and fertility data published from long-term research sites (Boesch & Boesch-Achermann 2000; Nishida et al. 2003).

(c) Estimation of effective population size

Effective population size has been traditionally defined in terms of either inbreeding or loss of genetic variation (Crow & Kimura 1970). We calculated the effective sizes for autosomal loci (N_eA), for mitochondrial loci (N_eMit), for Y-linked loci (N_eY) and for X-linked loci (N_eX). If we assume an ideal population where the offspring number follows a Poisson distribution and the sex ratio N_m/N_f=1 apply, the expected value of N_eA is equal to the census size N. N_eMit and N_eY are expected to be one-quarter of N_eA, while N_eX is expected to be three-quarters of N_eA (Storz et al. 2001).

The strength of this study lies in the fact that we know the actual genealogy of the population in addition to the birth records. This enables us to calculate N_e directly by simulating changes in the allele frequency through the genealogy (gene-flow simulation: Edwards 1968, 1992b; allele-dropping simulation: Heyer 1999). Two common alleles were assigned to the founders (50 : 50) and the frequency of the alleles was traced over time. This simulation was repeated 100 000 times, and the variance of the allele frequency among iterations was calculated. N_e was estimated from the increase of the variance between 1850 and 1940. We restricted the analysis to this period when the genealogical data were considered reliable enough. The increase during the period was then adjusted to the increase per generation time.

For comparison, we calculated N_e using two other methods that are commonly applied when only limited demographic information is available. First, we estimated N_e from the actual mean and variance of the number of offspring (family size). We counted the number of offspring for every individual born between 1820 and 1906. We then calculated the effective number for autosomal loci N_eA and X-chromosomal DNA N_eX from the variance of their offspring number (Hill 1972, 1979; Pollak 1990)

$$\frac{1}{N_{\text{eA}}}=\frac{1}{16ML}\left[2+{\sigma }_{\text{mm}}^2+2(M/F)\text{cov}(mm,mf)+{(M/F)}^2{\sigma }_{\text{mf}}^2\right]+\frac{1}{16FL}\left[2+{(F/M)}^2{\sigma }_{\text{fm}}^{\text{2}}+2(F/M)\text{cov}(fm,ff)+{\sigma }_{\text{ff}}^2\right],$$

$$\frac{1}{N_{\text{eX}}}=\frac{1}{9ML}\left[1+2{(M/F)}^2{\sigma }_{\text{mf}}^2\right]+\frac{1}{9FL}\left[1+{(F/M)}^2{\sigma }_{\text{fm}}^2+2(F/M)\text{cov}(fm,ff)+{\sigma }_{\text{ff}}^2\right],$$

where M and F are the male and female cohort sizes, respectively. The mean intergeneration interval L is calculated as L=(L_mm+L_mf+L_fm+L_ff)/4 for autosomal loci or L=(L_mf+L_fm+L_ff)/3 for X-chromosomal loci, where L_mm, L_mf, L_fm and L_ff are the father–son, father–daughter, mother–son and mother–daughter intervals, respectively. ${\sigma }_{\text{mm}}^2$ and ${\sigma }_{\text{mf}}^2$ represent the variance of the number of male and female offspring from each male parent, respectively, and cov(mm, mf) the covariance between the number of male and female offspring from each male parent. For haploids, Hill (1979) gave

$$N_{\text{e}}=BL/{\sigma }_n^2,$$

where B is the cohort size; L is the intergeneration interval; and ${\sigma }_n^2$ is the variance of the number of offspring. As the haploid effective size is twice the diploid effective size

$$N_{\text{eMit}}=F{L}_{\text{ff}}/\left(2{\sigma }_{\text{ff}}^2\right),$$

$$N_{\text{eY}}=M{L}_{\text{mm}}/\left(2{\sigma }_{\text{mm}}^2\right).$$

Although Hill's formulae for the estimation of N_e are convenient, they rely on the critical assumption of a constant population size. We conducted a discrete-generation forward simulation to quantify the deviations from the true values when the assumption is violated, and to suggest an adjustment method. Basically, we used an adjusted variance, which represents the variance when the average number of offspring is two (or one for haploid loci), suggested by Crow & Morton (1955). The details of the results are shown in the appendix A.

Next, we estimated N_e of sex-linked loci from the life table which summarizes the age-specific mortality and fertility in the population. Age-specific mortality rate (p_x), cumulative survival rate (l_x) and fertility rate (m_x) are calculated for each sex at age x. In the present study, female m_x represents the average number of daughters produced at that age and male m_x represents the average number of sons. We applied Felsenstein's (1971) formula that calculates N_e of populations with overlapping generations from life tables.

3. Results

(a) Intergeneration intervals

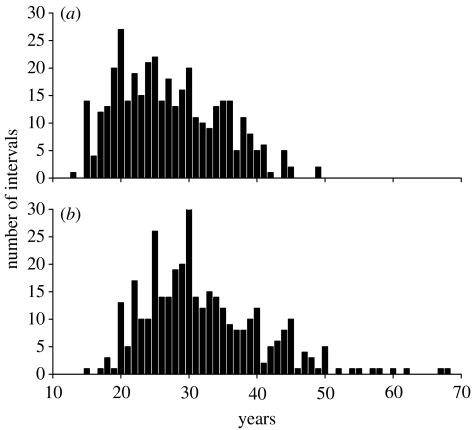
In the genealogies, the oldest female who gave birth to a child was 49 years old, while the oldest male at the birth of his child was 68. The average intergeneration intervals could be underestimated if those who have not finished their reproduction yet were included into the analysis. Therefore, we considered only the cohorts born before 1926 (female) or 1907 (male) as parental generations. The intergeneration intervals were defined as the parent's age when each child was born. A total of 1549 intervals were recorded. The mean intergeneration interval was 29.3 years. The simple mean mother–daughter interval is 27.0 years (N=379, s.e.=0.38), and the mean father–son interval is 32.1 years (N=352, s.e.=0.46; figure 1). We also calculated, for every individual alive at the end of the study period, the mean maternal/paternal intervals of her/his ancestors, and then averaged them. This alternative is designed to double-count those parts of genealogy shared by two or more descendants and yields an interval length that weighs successful parents. We obtained similar values by this genealogy-based method (maternal, 27.2 years and paternal, 32.0 years).

Figure 1.

(a) Mother–daughter intervals (N=379, mean=27.0, s.e.=0.38) and (b) father–son intervals (N=352, mean=32.1, s.e.=0.46).

Next, we constructed the life tables for two wild chimpanzee populations and calculated the generation time. The maternal generation time is estimated to be 24 years in the Mahale population and 19 years in the Taï population. The lower value for Taï results from the higher mortality rate among adults. We were unable to calculate the paternal generation time because their paternity relationships were hardly confirmed.

(b) Effective population size

The effective size of the Polar Eskimo was estimated by the genealogy (gene-flow or allele-dropping) method. The estimated N_eA, N_eX, N_eMit and N_eY values during the period between 1850 and 1940 were 179.2, 139.3, 53.8 and 39.7, respectively. If we use the actual population size at the end of the study period (N=299), the estimate for N_eA/N was 0.60. Similarly, we obtained N_eX/N=0.47, N_eMit/N=0.18 and N_eY/N=0.13. If we use the harmonic mean of the population size during the period as a representative of the actual population size (N=271.9), the estimates for N_eA/N, N_eX/N, N_eMit/N and N_eY/N were 0.66, 0.51, 0.20 and 0.15, respectively. The increase in genetic variation during the whole period (90 years) was greater in Y-chromosomal DNA than in mtDNA. This means that the evolutionary rate by genetic drift is higher in Y-chromosomal DNA than that in mtDNA.

Next, the effective population size was calculated from the variance in the offspring number (table 1). For females, the mean and variance of the number of daughters were 1.51 and 2.54, respectively. The adjusted variance, which represents the variance when the average number of daughters is one, was 1.45. The equivalent procedure was repeated for males and we obtained the adjusted variance equal to 1.89 (the mean number of sons, 1.26 and variance, 2.66). Using Hill's formula and the adjustment procedure of variances in a growing population (see appendix A), we obtained

$$N_{\text{eMit}}=0.35N_{\text{f}}=0.16N$$

and

$$N_{\text{eY}}=0.26N_{\text{m}}=0.14N.$$

These values are overestimates if there is a positive correlation in the number of offspring between parents and offspring. However, we found no statistically significant correlations (between mothers and daughters: Kendall's τ=0.009, n=150; between fathers and sons: τ=0.025, n=202). We also calculated the effective size for autosomal and X-chromosomal DNA and obtained

$$N_{\text{eA}}=0.58N$$

and

$$N_{\text{eX}}=0.42N.$$

Table 1.

The mean, variance and covariance of the number of offspring. (The minimum and maximum numbers of offspring per parent are also shown.)

parent	mother			father
offspring	all	daughter	son	all	daughter	son
mean	2.95a	1.51	1.28	2.46a	1.06	1.26
variance	6.89	2.54	1.98	7.99	2.08	2.66
covariance	—	0.99		—	1.30
minimum	0	0	0	0	0	0
maximum	11	7	6	11	7	7

^aThe values exceed the sums of daughters and sons because the sex of some offspring who died during their first year was not recorded.

Finally, the effective population sizes for sex-linked loci were calculated using the life table method. A life table that shows age-specific mortality (p_x) and fertility (m_x) for x=0–100 years old was made for each sex. Using the life table data, we obtained

$$N_{\text{eMit}}=9.9B_{\text{f}}$$

and

$$N_{\text{eY}}=10.3B_{\text{m}},$$

where B_f and B_m are the cohort sizes of females and males, respectively. The expected length of life of a newborn female was estimated to be 42.5 years, while that of a male was 39.9 years. If we consider the annual intrinsic rate of increase, which was calculated here as λ=1.01, we have

$$N_{\text{eMit}}=0.34N_{\text{f}}$$

and

$$N_{\text{eY}}=0.35N_{\text{m}},$$

where N_f and N_m are the census numbers.

It must be noted that the ratio of the effective size to the census size considered in the two approaches is a short-term value. In a population varying in size, the long-term effective size is close to a harmonic mean of the sizes during the period. Therefore, if a population experienced a bottleneck or a rapid expansion from a small population, the effective size could be quite small in relation to the current census size.

4. Discussion

(a) Generation time

The generation time in the Polar Eskimos is similar to those from recent studies, which investigated long-term genealogical records (table 2). All these studies suggested that the human generation time is longer than that previously assumed in population genetic models. There are several other studies which reported less precise estimates of the generation time on the basis of demographic data or short-term genealogical data. Felsenstein (1971) obtained 26.3 years as the mean generation time (mother–offspring) when he calculated the effective population size on the basis of the US white female population for 1967. Based on the relatively short-term but maternity-tested records, Forster et al. (2002) described that the mother–daughter generation interval in two sampled areas of South India is 29.7 and 31.6 years, respectively (based on dead mothers and postmenopausal mothers of age more than 55 years). Storz et al. (2001) referred to a longer generation time for the Gainj population (Papua New Guinea). More recently, Fenner (2005) suggested 25–28 years as the maternal generation interval on the basis of his analysis of a wide range of demographic data including 40 less-developed nations and eight societies of hunter-gatherers. The generation time looks rather consistent regardless of the cultural and environmental differences among human societies.

Table 2.

Average intergeneration intervals.

intervals	locus	Greenlanda	Canadab	Icelandc	Germanyd
maternal	mitochondrial	27.0 (years)	28.7 (years)	28.1 (years)	30.0 (years)
paternal	Y-chromosomal	32.1	35.0	31.1	—
all	autosomal	29.3	32*	—	—
	X-chromosomal	28.9	31*	—	—

^aTraditional Eskimos, this study. The value for X-chromosomal locus is calculated as the average of mother–daughter, mother–son and father–daughter intervals.

^bRural French Canadian, 1842–1971, Tremblay & Vézina (2000; ^*, values are taken from their table 2).

^cIcelanders, 1848–1972, Helgason et al. (2003).

^dRural Germans, 1644–1880, Forster (1996).

Dating from DNA data is strongly influenced by the value of the generation time applied in the models. Time estimates are obtained usually in generations, and then translated into years. It is easy to see that a longer generation time yields a longer age estimate in years. This effect is serious when the mutation rate of the locus of interest is estimated from genealogical studies (e.g. Howell et al. 2003). The generation time may not have an effect if the mutation rate is calibrated at some past event (e.g. chimpanzee–human divergence: Horai et al. 1995; demographic expansion after a climate change: Forster et al. 1996), because the mutation rate per generation changes accordingly. The generation time may have a different kind of effect on demographic inference; a shorter generation time means more generations in a particular time period.

The majority of the previous studies assumed that the generation time for mitochondrial DNA and Y-chromosomal DNA is 20 and 25 years, respectively (e.g. Harpending & Rogers 2000). We suggest that a higher value, 25–30 for mtDNA and 30–35 years for Y-chromosomal DNA, should be used in genetic inference.

It may be argued that our distant ancestors might have had a shorter generation time because they must have suffered from a higher mortality rate or had smaller body sizes. In several studies estimating the age of the most recent common ancestors of humans and great apes, the generation time of great apes was assumed to be 7–15 years (Takahata & Satta 1997; Excoffier & Yang 1999) with the notable exception of Ruvolo (1997) who obtained information from a primatologist and used a generation time of 15–25 years. Unfortunately, there have been no published values for the generation time among apes. Our estimates of the maternal generation time for two wild chimpanzee populations are 19 and 24 years. Although we need more data on great apes, values of less than 15 years are clearly underestimates. This suggests that the hominin generation times in the past few million years may also have been longer than generally assumed.

(b) Effective population size

Our estimated ratios of the effective to the census population size in the present study agree with those reported in other human populations (Frankham 1995; Storz et al. 2001). Humans generally exhibit higher values (0.3–0.9) than other animals (Frankham 1995).

Interestingly, there are slight differences between the values of the effective population size calculated by the different methods (table 3). This is partly because they measure different quantities by definition and are based on different assumptions that may be unfulfilled in reality. The estimates obtained from the genealogy method would be the most realistic if we had a perfect genealogical record. Unfortunately, the Eskimo genealogy contains some uncertain records even in the period between 1850 and 1940. The life table method might provide overestimates, in particular for males, because the variance in the offspring number reflects merely a stochastic variation resulting from the average age–sex mortality/fertility of each age–sex class. In other words, the method does not take into account skewed offspring numbers, for example in situations where some higher status males have many more children than others.

Table 3.

Diploid effective population size of the Polar Eskimos estimated using different methods. (The harmonic means of the population sizes (male and/or female) between 1850 and 1940 were used for the calculation of the ratios by the genealogy method.)

	genealogy	variance	life table
NeMit/Nf	0.46	0.35	0.34
NeY/Nm	0.26	0.26	0.35
NeX/N	0.51	0.42	—
NeA/N	0.66	0.58	—

When we infer the population size of past human populations from the present genetic data, we need a ratio of the effective to the census population size (N_e/N) as we usually obtain results as effective sizes. A ratio of N_eMit(h)/N_f or N_eY(h)/N_m should be used instead of N_eA/N if such an inference is carried out using a haploid model on the basis of mitochondrial or Y-chromosomal data. The haploid effective population sizes N_eMit(h) and N_eY(h) are twice as large as the diploid ones N_eMit and N_eY, respectively. Considering the fact that table 2 shows the diploid effective sizes, we suggest using a ratio of 0.7–0.9 for females or mitochondrial DNA, 0.5 for males or Y-chromosomal DNA, and 0.6–0.7 for autosomal and X-chromosomal DNA. The difference between sexes reflects the variance of the offspring number. It is important to remember that reported paternity, and possibly maternity (Forster et al. 2002), may be incorrect. The actual effective sizes are smaller if the variances of the number of offspring are larger than those reported.

Helgason et al. (2003) suggested that mtDNA drifts faster than Y-chromosomal DNA in Iceland owing to a shorter generation time as well as to stronger intergenerational correlations in maternal than paternal lineages concerning the offspring number and generation time. In contrast, our gene flow simulation suggests that Y DNA may evolve a little faster than mtDNA in the Polar Eskimo population. The shorter maternal generation time (84%) does not cancel out the smaller effective population size of males (71%), and a clear sign of intergenerational correlations is not detected. It is a promising research subject to study whether the slightly faster drift of Y-chromosomal DNA observed in the Polar Eskimos is typical of other hunter-gatherer populations.

Overall, our hunter-gatherer genealogies show that the basic population genetic parameters are similar between humans across a wide range of cultures and geographical locations. It is therefore a reasonable working hypothesis to assume that these demographic values were also similar through time in human prehistory. Therefore, our results give some justification for the widespread use of modern human demographic values for prehistoric population inference in the human species.

Appendix A. Test of the variance method (Hill's formulae) in simulated populations

Hill's (1972, 1979) formulae were commonly used for the estimation of N_e, for example, in conservation biology, because they require relatively simple demographic information. However, they rely on the critical assumption of a constant population size. It is necessary to make some assumptions on the ways of reproduction and survival, and adjust the variance of the offspring number and the covariance between the number of sons and daughters. We decided to follow the logic of Crow & Morton (1955). They suggested using the following equation to adjust the variance in a growing population to a constant-size population.

$$\frac{\left({\sigma }_1^2/{\mu }_1\right)-1}{{\mu }_1}=\frac{\left({\sigma }_2^2/{\mu }_2\right)-1}{{\mu }_2}.$$

The variance ${\sigma }_2^2$ in a growing population where the mean number of offspring is greater than two (μ₂>2) is equivalent to the variance ${\sigma }_1^2$ in a constant-size population (μ₁=2). We applied a similar logic to the covariance, for example

$$\frac{(\mathrm{cov}{(mm,mf)}_1/{\mu }_1)}{{\mu }_1}=\frac{(\mathrm{cov}{(mm,mf)}_2/{\mu }_2)}{{\mu }_2}.$$

These adjusted values are then used in Hill's formulae.

We conducted a simple discrete-generation forward simulation to quantify the deviations from the true values when the assumption is violated. The duration of the simulation was two generations. The population size changed from N₁ to N₂ (i.e. the mean number of offspring is 2N₂/N₁) in the first generation and from N₂ to N₃ in the second. In each demographic scenario, iterations were repeated for a thousand times. Five Poisson scenarios and seven non-Poisson ones were tested. Every female was assumed to form a pair with a male, and to produce an (infinitely) large number of offspring. When the number of the surviving offspring was assumed to follow the Poisson distribution, survivors were chosen randomly from their offspring (the variance of the offspring number equals to the mean). In non-Poisson cases, either some of the pairs were programmed to produce more surviving offspring than the others (larger variances) or the maximum number of surviving offspring per pair was limited (smaller variances). The changes in the allele frequency between generations, as well as the mean, variance and covariance of the offspring number, were recorded in each simulation run. Using the data on the allele frequency and the number of offspring, effective population sizes N_e were calculated based on the genealogy (gene-flow or allele-dropping) method and the variance (Hill's) method.

We expected that the genealogy method would provide us with reliable estimates of N_e because it counts the actual change in the allele frequency through the perfectly known genealogies. The effective size for autosomal loci N_eA is equal to the actual size when the offspring number follows a Poisson distribution where the variance of the offspring number is equal to its mean. If the population size changes, the effective population size is equal to the harmonic mean of the generations N₂ and N₃. The effective size is smaller than the actual size when the variance of offspring number is larger than its mean, and vice versa. These results agree with the expectations from population genetic theories (e.g. Crow & Kimura 1970).

The variance method provided the same values as the genealogy method did when the population size was constant (table A1). If it was applied to a growing population, however, the effective size was underestimated because the variance in the offspring number exceeds one even if it follows a Poisson distribution. The greater the population growth rate was, the smaller the estimate we obtained. If we used adjusted variances and covariances and entered harmonic means (see above) for N_m and N_f, we obtained values similar to those from the genealogy method (table A1).

Table A1.

Estimates of the effective population size for autosomal and mitochondrial DNA (mtDNA) in simulated populations. (The results for the period of two generations were summarized here. In each case, the population size changed from N₁ to N₂ and then to N₃. μ and σ² represent the mean and variance of the number of offspring (daughters in the case of mtDNA), respectively.)

	population growth			number of offspring			effective population size (NeA)
	N1	N2	N3	μ	σ2	σ2/μ	genealogy	variance	adjusted variance
autosomal DNA
offspring number follows a Poisson distribution
1	200	120	72	1.20	1.20	1.00	90.9	250.0	90.2
2	200	160	128	1.60	1.60	1.00	143.1	222.4	142.5
3	200	200	200	2.00	2.00	1.00	202.0	200.3	200.3
4	200	240	288	2.40	2.41	1.00	263.3	181.9	261.8
5	200	280	392	2.80	2.80	1.00	329.4	166.9	326.8
offspring number follows a non-Poisson distribution
1	200	200	200	2.00	1.21	0.60	250.6	249.3	249.3
2	200	200	200	2.00	1.79	0.90	212.2	211.1	211.1
3	200	200	200	2.00	3.51	1.76	146.6	145.5	145.5
4	200	200	200	2.00	5.39	2.70	111.0	108.5	108.5
5	200	160	160	1.78	1.14	0.64	196.3	254.9	203.9
6	200	160	128	1.60	2.56	1.60	110.7	175.8	103.8
7	200	240	240	2.18	1.22	0.56	309.0	247.9	297.5
8	200	240	288	2.40	4.55	1.89	182.7	122.5	191.1

	population growth			number of daughter			effective population size (NeMt)
	Nf1	Nf2	Nf3	μ	σ2	σ2/μ	genealogy	variance	adjusted variance
mitochondrial DNA
daughter number follows a Poisson distribution
1	100	60	36	0.60	0.60	1.00	23.4	84.0	23.1
2	100	80	64	0.80	0.80	1.00	36.6	63.1	36.1
3	100	100	100	1.00	1.00	1.00	51.6	50.5	50.5
4	100	120	144	1.20	1.20	1.00	67.0	41.9	65.7
5	100	140	196	1.40	1.39	1.00	84.6	36.1	82.2
daughter number follows a non-Poisson distribution
1	100	100	100	1.00	0.80	0.80	63.7	62.8	62.8
2	100	100	100	1.00	0.94	0.94	54.8	53.8	53.8
3	100	100	100	1.00	1.38	1.38	37.3	36.5	36.5
4	100	100	100	1.00	1.99	1.99	26.4	25.2	25.2
5	100	80	80	0.89	0.73	0.82	50.2	69.4	55.5
6	100	80	64	0.80	1.04	1.30	28.3	48.4	26.2
7	100	120	120	1.09	0.86	0.78	78.6	58.9	70.6
8	100	120	144	1.20	1.73	1.44	46.9	29.1	48.0

We also examined mitochondrial DNA (table A1) as well as Y- and X-chromosomal loci (results not shown) and reached similar conclusions concerning the genealogy and variance methods.