Geometry explains the benefits of division of labour in a leafcutter ant

Abstract

Many ant species have morphologically distinct worker sub-castes. This presumably increases colony efficiency and is thought to be optimized by natural selection. Optimality arguments are, however, often lacking in detail. In ants, the benefits of having workers in a range of sizes have rarely been explained mechanistically. In Atta leafcutter ants, large workers specialize in defence and also cut fruit. Fruit is soft and can be cut by smaller workers. Why, therefore, are large workers involved? According to the geometry hypothesis, cutting large pieces from three-dimensional objects like fruit is enhanced by longer mandibles. By contrast, long mandibles are not needed to cut leaves that are effectively two-dimensional. Our results from Atta laevigata support three predictions from the geometry hypothesis. First, larger workers cut larger fruit pieces. Second, the effect of large size is greater in cutting fruit than leaves. Third, the size of fruit pieces cut increases approximately in proportion to the cube of mandible length. Our results are a novel mechanistic example of how size variation among worker ants enhances division of labour.

1. Introduction

The role of natural selection in optimization forms a long-standing controversy in evolutionary biology (Gould & Lewontin 1979; Queller 1995; Pigliucci & Kaplan 2006). On one hand, optimality arguments have provided a valuable tool in understanding why organisms have specific structures and behaviours, and have contributed to major advances in evolutionary biology and especially behavioural ecology (e.g. sex ratio (Herre et al. 2001) and foraging theory (Stephens & Krebs 1986)). On the other hand, optimality arguments often do not consider mechanisms and factors such as phylogenetic and developmental constraints that form part of the wider picture in understanding evolution in the light of optimality. Incorporating mechanisms underlying adaptation into analyses of optimality can lead to greater insights into the precision of adaptation, as for example shown in recent sex ratio studies (Boomsma et al. 2003; Shuker & West 2004).

The castes of worker insects were the subject of a highly influential book by Oster & Wilson (1978) in which optimality arguments were given a comprehensive mathematical treatment. Oster & Wilson hypothesized that within-colony worker size diversity, or ‘caste distribution function’, is optimized by natural selection because it increases colony ergonomic efficiency by allowing workers of appropriate sizes or shapes to specialize in different tasks. In support, many studies have shown that workers of different sizes specialize in different tasks that appear qualitatively suitable to their size (Oster & Wilson 1978). For example, large workers are often soldiers. However, as in many other areas of research on optimality, studies of caste distributions are often lacking in detail. Few studies have demonstrated how worker polymorphism is actually beneficial to the colony (Hasegawa 1993) or that colonies rear more workers of a particular size when needed (Passera et al. 1996). Particularly, mechanistic explanations of why a certain caste is more efficient at performing a particular task are lacking.

Atta leafcutter ants are ecologically and economically important Neotropical herbivores. They are considered a pinnacle of social evolution and have arguably the most sophisticated system of work organization in ants, both in terms of task partitioning and division of labour (Hölldobler & Wilson 1990; Hart et al. 2002). Division of labour is built upon substantial polymorphism within the worker caste. Workers vary more than 300-fold in body mass. In general, the largest specialize in colony defence, the medium sized in cutting and carrying leaves and the smallest in processing leaves and tending the fungus garden (Wilson 1980a). The medium-sized workers that normally cut the leaves are energetically the most efficient in this task (Wilson 1980b). But even this rare quantification of the benefits of division of labour offers little mechanistic explanation of the observed efficiency difference.

In addition to leaves, leafcutter ants also forage on fallen fruit (Leal & Oliveira 1998, 2000; Evison & Ratnieks 2007). Fallen ripe fruit can be an abundant food resource and is used by many types of animal. Worker Atta that cut fallen mango fruit are on average larger than those cutting leaves, although the distributions overlap considerably (Evison & Ratnieks 2007). Task partitioning with indirect transfer occurs (Ratnieks & Anderson 1999), as the fruit pieces are carried back to the nest not by the cutters but by medium-sized workers. The cutting of fruit by large workers raises a puzzle. Why are larger workers disproportionately involved in fruit cutting given that they rarely cut leaves? Medium-sized workers do cut fruit (Evison & Ratnieks 2007), which shows that their mandibles are strong enough to do this. Furthermore, fallen fruit is soft and thus should be easier to cut than leaves.

The hypothesized reason is geometry (Evison & Ratnieks 2007). When cutting up an essentially two-dimensional leaf, mandible length does not limit the size of the piece that can be cut since even short mandibles can cut through the leaf and cut out a large area. By contrast, when cutting up fruit, a worker thrusts its mandibles into the fruit and uses the whole length of the mandible to cut three-dimensional pieces (figure 1). Longer mandibles can cut deeper and hence can cut out a larger piece. Thus, the geometry hypothesis is based on the idea that the size of a piece cut from a three-dimensional object is more limited by the worker size (i.e. mandible length) than a piece cut from a two-dimensional object. The underlying logic also requires that a fruit piece cut by a large worker is still small enough for a medium-sized worker to transport back to the nest. In cutting a leaf, a worker moves its head in an arc using its legs to anchor its body to the leaf and normally cuts a piece that approximates to an arc of a circle. As a result of using the body and legs as a pair of compasses, there is a weak and variable positive correlation between the body length and the size of the leaf piece cut (e.g. Wetterer 1991; Burd 1995). This may also serve a role in ensuring that the pieces cut are of a suitable size to carry.

Figure 1.

(a) Large workers of Atta laevigata cutting mango. (b) Heads of a small and a large worker, showing the difference in head size and shape. The arrow in the right panel shows the distance between apical tooth tip and basal angle, which was used as the measure of mandible length.

Geometry hypothesis provides a mechanistic explanation for the size-based division of labour and gives a rare opportunity to test both qualitative and quantitative predictions relating to division of labour. Using data from field study of Atta laevigata, we test three predictions of the geometry hypothesis. First and the most general prediction is that larger workers should cut larger pieces of fruit. Second, the geometry hypothesis predicts that the effect of worker size on the size of the pieces cut should be greater for cutting fruit (three-dimensional) than leaves (two-dimensional). Finally, it also makes the quantitative prediction that the mass of the fruit pieces cut by individual workers should scale to the cube of mandible length, and that this relationship should not occur for leaf pieces.

2. Material and methods

The study was carried out at Fazenda Aretuzina, near São Simão, São Paulo state, Brazil, during January–February 2007. Fazenda Aretuzina is a farm owned by Dr Paulo Nogueira-Neto, and is dedicated to the study and conservation of Brazilian wildlife. We studied four mature natural colonies of A. laevigata Smith, which were foraging during daylight hours. The mature status of the colonies was confirmed by the presence of large worker ants (soldiers) and well-defined trunk trails.

The colonies were simultaneously offered slices of ripe mango and whole leaves of a tree of the family Rubiaceae on an active foraging trail within 1 m of the nest entrance. Sampling of leaf-cutting and mango-cutting workers began 20 min later. Individuals were observed as they cut a piece of leaf or mango, and all those that cut out a complete piece during the observation period were collected along with the item cut. The fresh weights of the cut piece and the worker were determined using a portable electronic balance (Tanita, 2 mg sensitivity). Each colony was sampled on at least four separate occasions. To obtain an overall estimate of worker sizes on foraging trails, we took a haphazard sample of workers on three different occasions from the trails of two colonies (in total n=120 for colony 2; n=256 for colony 3). The colonies were foraging naturally during sampling, without added leaves or fruit.

After weighing, the workers were killed by freezing at −20°C. The head was removed from the body and one mandible was removed from the head. The pieces were then laid onto a 1 mm graph paper and photographed using a Fuji 7000FinePix digital camera, using 6 megapixel resolution in super macro. Enlarging the images to 30× natural size on a computer screen allowed measurements of body parts to ±0.033 mm. The measurements taken were maximum head width excluding eyes and mandible length from the basal angle to the tip of the apical tooth (figure 1).

(a) Statistical analyses

All mass and length measurements were log transformed for the analyses and corresponded to a normal distribution (all Wilk–Shapiro statistics>0.93). Using log-transformed values in the regression analyses facilitated assessment of whether the relationships between variables are isometric or allometric. This is because the slope b of the regression log (y)=log (a)+b log (x) equals the power term from the geometric relationship of the untransformed data y=ax^b. The exponent term from the geometric relationship y=ax^b encompasses both allometry (b≠1) and isometry (b=1). All analyses were carried out in S-Plus v. 6.1. Instead of pooling the data across the colonies, all analyses were carried out for each colony separately, and the consistency of results across colonies was compared using meta-analytical techniques (Rosenthal 1991).

The masses of workers cutting leaves or fruit and workers on the trail were compared using Kruskal–Wallis ANOVAs. Heterogeneity of effect sizes for the difference of leaf and mango cutters among colonies was tested using z-transformed values of the effect size r (Rosenthal 1991). We also tested whether the size difference of leaf and mango cutters among colonies was consistent with that previously found at the same study site (Evison & Ratnieks 2007).

The predictions from the geometry hypothesis were tested using linear regressions of log item mass against log worker size. First, to test whether larger workers cut larger pieces of fruit, we determined whether the 95% CIs for the worker mass versus mango mass regression slopes overlapped with 0. Second, to test whether the effect of worker size on the size of the pieces cut is greater for workers cutting fruit than those cutting leaves, we compared the slope of worker mass versus leaf mass against slope of worker mass versus mango mass within each colony. The heterogeneity of the r values of the slopes was tested both within colonies (slope of log worker mass versus log leaf mass and slope of log worker mass versus log mango mass) and among colonies (slopes of worker mass versus leaf mass among colonies and slopes of worker mass versus mango mass among colonies). Third, to determine how mandible length affects the size of the mango piece cut, we again used linear regression within each colony. The 95% CIs of the regression slope of log mango piece size versus log mandible length were compared to 3, the quantitative prediction from the geometry hypothesis, and compared to each other among colonies.

3. Results

In confirmation of previous research at this study site (Evison & Ratnieks 2007), in each of the four colonies the workers cutting ripe mango fruit were considerably and significantly larger than the workers cutting leaves (figure 2, range of colony means 28.5–30.3 mg versus 18.7–23.6 mg, respectively; Kruskal–Wallis results in figure 2). The mass differences between fruit and leaf cutters were similar among the study colonies and not significantly different from those observed previously (Evison & Ratnieks 2007; Χ²-test for heterogeneity of effect sizes, Χ₄²=3.2, p=0.52). Both fruit and leaf cutters were larger than the average size of all workers on the trail in the two colonies where random workers on the trail were also sampled (colony means 10.0–12.3 mg, figure 1). In none of the four study colonies were leaf pieces (colony means 21.1–28.9 mg) significantly lighter than mango pieces (colony means 13.1–24.4 mg; colony 1: one-tailed t-test, t=1.7, d.f.=150, p=0.08; colony 2: t=1.1, d.f.=138, p=0.87; colony 3: t=6.1, d.f.=199, p=1; colony 4, t=0.45, d.f.=199, p=0.68). In fact, the trend was for the leaf pieces to be heavier. This confirms an important assumption underlying our test of the geometry hypothesis, namely that carrying ability does not set an upper limit to the size of the fruit pieces that can be cut.

Figure 2.

Size distributions of workers cutting mango (white bars), cutting leaf (black bars) and workers on a trail (hatched bars). First Kruskal–Wallis ANOVA's are between mango and leaf cutters and second among all three classes for the two colonies where a trail sample was obtained. (a) Colony 1: KW=8.1, d.f.=1, p=0.004; (b) colony 2: KW=19.7, d.f.=1, p<0.001; KW=71.7, d.f.=2, p<0.001; (c) colony 3: KW=20.3, d.f.=1, p<0.001; KW=161.3, d.f.=2, p<0.001; (d) colony 4: KW=17.4, d.f.=1, p<0.001.

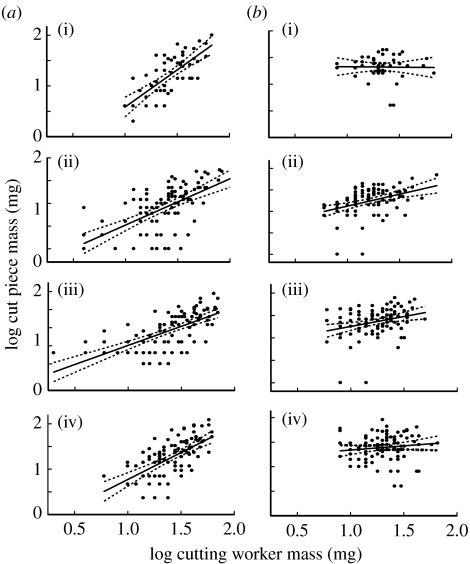
As predicted by the geometry hypothesis, larger workers cut larger fruit pieces. The slopes of the regressions of log-transformed fruit piece mass on log-transformed worker mass were significantly larger than 0 (range of lower 95% confidence limits 0.75–1.06) for all the four colonies and overlapping with 1 for all the colonies except colony 1 (figure 2). This shows that the relationship between the masses of workers and the pieces of fruit that they have cut is consistent with isometry. Also in keeping with the second prediction of the geometry hypothesis, the log-transformed sizes of the fruit pieces scale with log-transformed worker mass with a higher allometry gradient (range of slopes 1.02–1.47; figure 3) than the size of the leaf pieces (range of slopes−0.02 to 0.56, F-tests within each colony all F>5.2, p<0.02). Two of the four slopes of leaf mass on worker mass were not significantly larger than zero (lower 95% confidence limits of colonies 1 and 4 are −0.36 and −0.09, respectively; figure 2). The slope of the combined data did not overlap with zero but was smaller than those for mango weight (0.37, 95% CI 0.24–0.51). Furthermore, the explanatory power of worker size was higher for mango piece size (r² values 0.36–0.52) than leaf size (r² values 0.0–0.16) in each colony (Χ₁²>2.0, p<0.023) except colony 2 (Χ₁²=1.0, p=0.16), and for the combined data (Χ₁²=4.6, p<0.001). Overall, these results show that ant size has a large effect on the size of the fruit pieces cut but only a small effect on the sizes of leaf pieces cut. Effect sizes of worker mass on the masses of both mango and leaf pieces were homogenous across colonies (Χ₃²<2.4, p>0.50).

Figure 3.

Regressions of mass (log transformed) of the item cut against mass of the cutting worker (log transformed). Slopes are given with 95% CI. (a) Mango pieces: (i) colony 1: slope=1.46 (1.06–1.87); (ii) colony 2: slope=1.02 (0.75–1.28); (iii) colony 3: slope=1.06 (0.83–1.29); (iv) colony 4: slope=1.18 (0.87–1.50). (b) Leaf pieces: (i) colony 1: slope=−0.02 (−0.36 to 0.33); (ii) colony 2: slope=0.56 (0.30–0.81); (iii) colony 3: slope=0.38 (0.24–0.51); (iv) colony 4: slope=0.17 (−0.09 to 0.42).

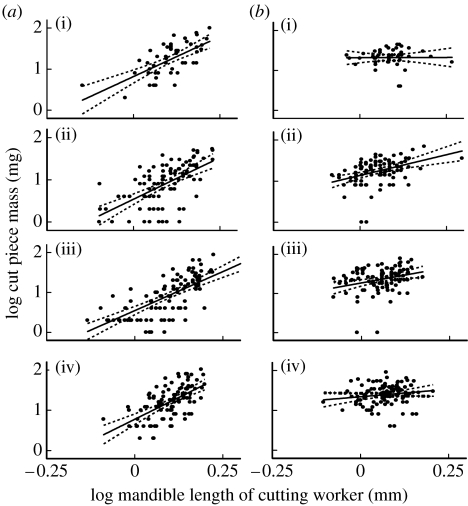
The third, quantitative, prediction of the geometry hypothesis is supported in two of the four colonies. For each colony, the slope of the allometric relationship between the mass of the fruit piece cut and the length of the worker's mandibles was slightly larger than 3 (range of slopes 3.89–4.33, figure 4), the cubic prediction from the geometry hypothesis, but for colonies 3 and 4 the 95% CIs did not overlap with 3 (lower 95% CI 3.1 and 3.2, respectively). For the combined data, the slope was 4.1 (95% CI 3.6–4.7). The explanatory power of the regressions (r² values 0.34–0.48) was again consistent among colonies (Χ₃²=1.46, p=0.69).

Figure 4.

Regressions of mass of the mango piece cut (log transformed) against mandible length (log transformed) of the cutting worker. Slopes are given with 95% CI. (a) Mango pieces: (i) colony 1: slope=3.91 (3.10–4.72); (ii) colony 2: slope=4.33 (3.17–5.49); (iii) colony 3: slope=3.95 (2.87–5.03); (iv) colony 4: slope=3.89 (2.64–5.14). (b) Leaf pieces: (i) colony 1: slope=−0.02 (−1.18 to 1.23); (ii) colony 2: slope=2.02 (1.10–2.94); (iii) colony 3: slope=1.63 (0.54–2.69); (iv) colony 4: slope=0.74 (−0.21 to 1.72).

4. Discussion

Our results support the geometry hypothesis and are a novel example of how division of labour among castes can enhance colony foraging efficiency. Owing to their longer mandibles, larger workers are able to cut larger pieces of fruit. Because a carrier ant only transports a single piece of forage, the cutting of larger pieces of fruit can increase the efficiency of the carrying sub-task of the overall foraging task, which is partitioned between cutters and carriers (Ratnieks & Anderson 1999; Hart et al. 2002; Evison & Ratnieks 2007). The benefit of carrying heavier pieces per foraging trip is confirmed by data from Atta cephalotes and Atta vollenweideri (Burd 2000; Röschard & Roces 2002) showing that the total transport rate is increased when the mass of individual loads is experimentally increased.

The two qualitative predictions of the geometry hypothesis were strongly supported. However, support for the quantitative prediction was variable. In two of the four colonies, the exponents of the allometric relationships of mango mass on mandible length were greater than cubic meaning that larger ants tended to cut fruit pieces that were slightly larger than predicted. Thus, even though geometry is an important determinant of foraging efficiency (r² values 0.36–0.52 for mass of mango piece), more details need to be incorporated into the geometry hypothesis. As is common in tests of optimality models (Alcock 2005), a single factor is not enough for a precise fit between prediction and observation. We can only speculate on the cause of the discrepancy between prediction and observation. Possibly, larger ants can use their greater body strength to pull pieces of fruit away even if these have not been fully cut out or can thrust their mandibles into the fruit more effectively. In any event, this discrepancy is an additional reason why larger ants should specialize on fruit cutting given that even the largest pieces cut are not too large to be carried back to the nest by a single carrier worker.

The involvement of large workers, whose primary role is colony defence, in foraging has implications for testing optimality hypotheses with caste distribution functions. In our study colonies, the larger workers were only a small proportion (figure 2) of those present on foraging trails and were disproportionately involved in cutting fruit. However, much of the fruit was actually cut by the more numerous medium-sized workers. Transportation of fruit back to the nest by carrier ants would have been more efficient if there had been more large workers to cut more large fruit pieces. Presumably, the reason why there are not more large workers is because they are expensive to rear and maintain (Oster & Wilson 1978) and their actual numbers primarily reflect the requirements of colony defence. In other words, several tasks and their relative importance to the colony need to be considered when caste distributions are analysed.

In addition, morphological data show that it is not only the proportion of large workers but also their head shape that is sub-optimal for fruit cutting. Smaller workers, such as the medium-sized workers that do most of the leaf cutting, have heads that are approximately oval (figure 1, electronic supplementary material and Wilson 1953). In larger workers, the head is notably heart shaped with the lobes housing the muscles that power the mandibles (Wilson 1953). Reflecting this, the allometric relationships of head width on the cube root of body mass (a linear measure of volume) in medium-sized and large workers have slopes of 1.19–1.54 (figure S1 in the electronic supplementary material). This is significantly greater than the allometric relationship of mandible length on body size (0.88–1.04, F-test within each colony, all F>45.8, p<0.0001). Thus, in larger workers, the muscles powering the mandibles are proportionately larger while the mandibles, if anything, are proportionately shorter. This reinforces the idea that large Atta workers are actually designed more for defence, which requires larger muscles to give a powerful bite, than to cut large pieces of fruit, which requires longer mandibles.

Large Atta workers enhance colony foraging efficiency by helping to cut fruit with their long mandibles. But their head shape and the fact that few of them are actually reared show that their primary function is defence, not fruit cutting. However, the large workers that are available are put to good use by being over-represented in fruit cutting. This highlights an important distinction in testing optimality arguments. Even if the tools available are not optimal, what is available can be used in an optimal way within the constraints of more primary tasks. Co-option of structures into new uses is a common feature in evolution from genes and developmental pathways to physical structures, and co-opted features are constrained by their other uses. Our results show that this also applies to worker castes in insect societies.

Supplementary Material

Electronic supplementary information

Allometry analyses of worker head shapes

Supplementary results

Figure S1