The Initial Development of Object Knowledge by a Learning Robot

Abstract

We describe how a robot can develop knowledge of the objects in its environment directly from unsupervised sensorimotor experience. The object knowledge consists of multiple integrated representations: trackers that form spatio-temporal clusters of sensory experience, percepts that represent properties for the tracked objects, classes that support efficient generalization from past experience, and actions that reliably change object percepts. We evaluate how well this intrinsically acquired object knowledge can be used to solve externally specified tasks including object recognition and achieving goals that require both planning and continuous control.

1 Introduction

One reason why people function well in a changing environment is their ability to learn from experience. Moreover, learning from experience produces knowledge with semantics that are grounded in the sensorimotor experience. Replicating this human capability in robots is one of the goals of the robotics community. This paper describes how a robot can acquire knowledge of objects directly from its experience in the world.

This experiential knowledge has some significant advantages over knowledge directly encoded by programmers as it intrinsically captures the capabilities and limitations of a robot platform. The advantage of experiential knowledge has been demonstrated in the field of robot mapping where robot generated maps are more effective than human generated maps for robot navigation [31]. A similar situation arises when reasoning about objects, namely the robot's perception of the environment can differ greatly from that of a person. Hence, a robot should autonomously develop models for the objects in its environment, and then use these models to perform human specified tasks.

An important capability for a robot is to solve a current problem with knowledge acquired from past experience. Much research effort is spent on generalizing from past experience across individual objects (“a chair”), however a more pressing problem for a robot is to generalize across experiences of individual objects (“the red lab chair”) so as to reliably reason and interact with the individual objects encountered in the environment over extended periods of time. This approach has the advantage that broader object classes can potentially be formed by weakening the restrictions on recognizing individual objects.

We describe how a physical robot can learn about objects from its own autonomous experience in the continuous world. The robot develops an integrated system for tracking, perceiving, recognizing, and acting on objects. This is a key step in the larger agenda of developmental robotics, which aims to show how a robot can start with the “blooming, buzzing confusion” of low-level sensorimotor interaction, and can learn higher-level symbolic structures of common-sense knowledge. We assume here that the robot has already learned the basic structure of its sensorimotor system [24] and the ability to construct and use local maps of the static environment [31].

The robot represents its knowledge of the individual objects in its environment with trackers, percepts, classes and actions. Trackers separate the spatio-temporal sensory experience of an individual object from the background. This sensory experience is filtered though perceptual functions to generate informative percepts such as the distance to the object and the object's shape. The robot uses the observed shape of a tracked object to generate shape classes, which the robot uses to efficiently generalize from past experiences. Finally, the robot is able to interact with an individual object using learned actions that modify the object's percepts.

In the following sections, we describe the motivations for this work, the representations for the objects and actions, the algorithm for learning this knowledge from experience, the evaluation with a physical robot, future directions and related work.

2 Motivation

Objects play a central role in the way that people reason about the world, so it is natural to want robots to share this capability. However, the manner in which people think of objects is often different from the needs of a robot. People rarely have difficulty with object tracking, recognition, or interaction. However, it is difficult for a robot to acquire these capabilities even individually and a robot must be able to integrate these capabilities to solve tasks.

The semantic dictionary Wordnet [6] treats objects primarily as physical entities that belong somewhere on a classification tree. Wordnet attempts to bridge the gap between the representation of a word as a sequence of characters and its human-defined meaning by forming hierarchical relationships between words. For example, Wordnet states that a can is a container, while spoons and forks are cutlery. The Open Mind Indoor Common Sense project [9] goes further by defining multiple relationships between the names for common household entities. This style of knowledge is of little direct use to a robot without a connection between these words and the robot's experience in the world.

There is a broader role for object semantics, which is to support the formation of object representations that are defined from the robot's sensorimotor experience. It is tempting to think of objects as physical entities in the world that are derived from abstract classes, i.e. that the experience of seeing a fork is coming from a physical fork, which in turn is an instantiation of an abstract fork model that is shared by all people. The reality is the reverse, people start from sensorimotor experience, and classes are formed from individual experiences.

Instead of considering an object to be a physical entity, we consider an object to be an explanation for some subset of an agent's experience. With this approach, the semantics of an object are intrinsically defined from the agent's sensorimotor experience. When the robot uses its internal representations to solve externally specified tasks, the internal object representations may acquire a societally shared meaning.

Our approach to learning object models is inspired by theories in child development, in particular the assumption that coherent motion is one of the primary mechanisms for the initial perception of objects [28]. As modern techniques in robotics can effectively model the local static structure of the environment, any dynamic changes in the environment must come from some dynamic entity. By relying on a static environmental model, the robot can still perceive objects that are not moving. We use this as a basis for focusing our attention on learning about dynamic objects. The focus on dynamic objects provides a tractable way to make progress on an otherwise difficult problem—to perceive objects that have never been previously observed.

The focus of this work is to demonstrate how a robot can acquire an integrated set of object representations that can be used solve externally specified tasks although the representations are internally formed directly from the robot's experience in the world. If a human and a robot are to share similar meanings for objects, then the robot must be able to perceive previously unseen physical objects, reason about the perceived objects, and take actions to achieve goals. The efficacy of the robot's internal object representations can be measured by how well they enable the robot to accomplish externally specified tasks such as recognizing a yoga ball or moving the recycling-bin to a goal location.

3 Representing the Object

The robot's description of physical objects is a symbolic abstraction of the low level continuous experience of the robot.

3.1 Continuous System

From an experimenter's perspective, a robot and its environment can be modeled as a dynamical system:

$$\begin{array}{cc}\hfill x_{t+1}& =F(x_t,u_t)\hfill \\ \hfill z_t& =G\left(x_t\right)\hfill \\ \hfill u_t& =H_i(z_0,\dots ,z_t)\hfill \end{array}$$ (1)

where x_t represents the robot's state vector at time t, z_t is the raw sense vector, and u_t is the motor vector. The function F encodes state transitions while the function G encodes the observation from each state. The functions F and G represent relationships among the environment, the robot's physical state, and the information returned by its sensors, but these functions are not known to the robot itself [12].

The robot acts by selecting a control law H_i such that the dynamical system (Equation 1) moves the robot's state x closer to its goal, in the context of the current local environment. When this control law terminates, the robot selects a new control law H_j and continues onward.

The raw sensorimotor trace is a sequence of sense and motor vectors.

$$\langle z_0,u_0\rangle ,\langle z_1,u_1\rangle ,\cdots \langle z_t,u_t\rangle ,\cdots$$ (2)

3.2 Symbolic Abstraction

The components of the object knowledge are represented by a tuple,

$$𝒪\equiv \langle 𝒯,𝒫,𝒞,𝒜\rangle$$ (3)

consisting of trackers (𝒯), perceptual functions (𝒫), classes (𝒞), and actions (𝒜).

An object, considered as part of the agent's knowledge representation, is a hypothesized entity that accounts for a spatio-temporally coherent cluster of sensory experience. Note that the word “object”, when used in this sense, does not refer to a physical thing in the external world, but to something within the agent's knowledge representation that helps it make sense of its experiences.

A tracker τ ∈ 𝒯 names two corresponding things:

• (1) the active process that tracks a cluster of sensory experience as it evolves over time, and

• (2) the symbol in the agent's knowledge representation that represents the object (i.e., the hypothesized entity that accounts for the tracked cluster).

A perceptual function f ∈ 𝒫 is used to generate the percept f_t(τ) which represents a property of τ at time t. The percept is formed from the sensory experience by the tracker τ. Examples of simple percepts include the distance or location of a particular object at a particular time. A more complex percept is the shape of an object, which can be assembled from multiple observations over time.

For a particular perceptual function f, a class σ_f ∈ 𝒞 is an implicitly defined set of percepts similar to an exemplar percept q̄ = f_t′(τ′),

$${\sigma }_f\left[\stackrel{-}{q}\right]=\{q\mid d(q,\stackrel{-}{q})\approx 0\},$$ (4)

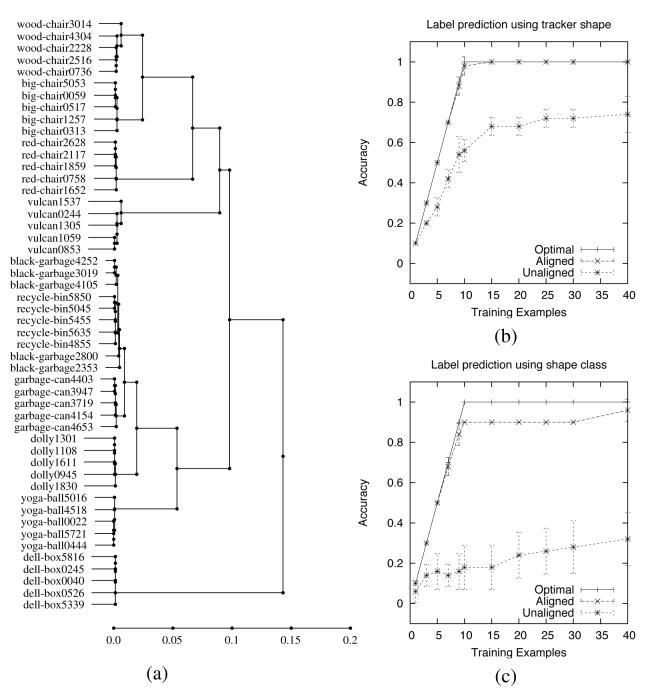
where d is a distance function (an example is given in Equation 13). For example, a shape class is a set of shape percepts that are similar to a prototype shape percept. Figure 5 shows ten shape models, which are percepts obtained from the robot's sensory experience with the ten depicted objects. These individual percepts belong to ten classes, each corresponding to percepts obtained from the same real-world object on different occasions.

Fig. 5.

A set of physical objects with their learned shapes.

An action α ∈ 𝒜 is specified by a description D of its effects on the object's percepts, the context C for the action to be reliable, and an associated control law H.

$$\alpha =\langle D,C,H\rangle$$ (5)

The description is a tuple that provides both a qualitative and a quantitative characterization of the action's effects. The context is represented as a conjunction of boolean constraints on the percepts. The control law is a function that maps percepts to motor vectors. An action encapsulates a reliable sensorimotor interaction between the robot and the object: when the object percepts satisfy the constraints in the context C then the execution by the robot of the control law H will result in changes to percepts as described by D. The description is used to predict the effects of an action. The context defines the preconditions for the action, and so facilitates planning. The control law provides the executable component of the action. These components are described in more detail when the action learning algorithm is introduced.

The tuple in Equation 3 represents not just the information about one object, but rather it represents all the object information that the robot has collected. There is information about each tracked object, the known perceptual functions, the known classes, and the known actions. As the robot gathers experience and applies inference algorithms, the robot can create new knowledge of the objects in the environment. While this representation has limitations, we show in the subsequent sections how this knowledge can be created and then used to solve externally specified tasks.

4 Learning Object Representations

One goal of developmental robotics is for robots to be capable of learning both incrementally and without extrinsic rewards. Incremental acquisition allows the robot to learn from novel experience throughout its lifetime. An autonomous, internal process is used to generate knowledge without extrinsic rewards. The following sections describe how components of the object knowledge can be learned by a robot while satisfying these constraints from developmental robotics.

4.1 Formation of Trackers

Using the method from [17], a mobile robot can create trackers for movable objects. The robot senses the environment with a laser range finder. Each observation from the sensor is an array of distances to obstacles

$$z_t:ϴ\to \Re$$

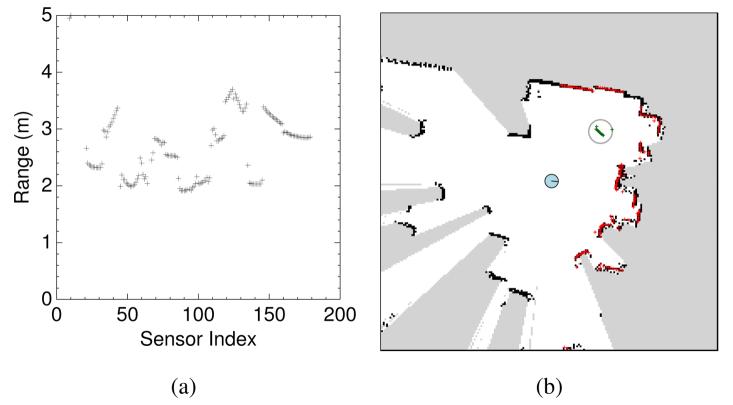
where Θ are the array indices, as shown in Figure 1(a).

Fig. 1.

(a) The sensor measures distances to obstacles, with readings taken at every degree. (b) By projecting the readings into an occupancy grid, the robot is able to identify readings from dynamic obstacles. A snapshot is formed by spatially clustering these readings, and forming a bounding circle.

The robot uses these observations to construct an occupancy grid map of space as shown in Figure 1(b). The occupancy grid is constructed with the assumption that the world is static. In the occupancy grid, local space is divided into grid cells, each of which has some probability of being occupied or clear, and a SLAM algorithm updates these probabilities using sensor observations. The robot needs a SLAM algorithm to simultaneously localize itself within the current map, and to extend the map into previously unseen areas. In addition to the standard SLAM process, at each time step the algorithm marks each grid cell that is currently clear with high confidence. This is used to identify cells that are not part of the static world. SLAM with occupancy grids is a robust way to build a static world model in spite of significant amounts of noise, some of which is random sensor noise, but other parts of which are due to unmodeled dynamics such as pedestrians and other moving objects.

When a physical object moves into a previously clear region in the map, the sensor readings that fall on the object violate the map's static world explanation. These readings are clustered spatially to define snapshots. A snapshot S of an object is a cluster of these dynamic range sensor readings in the map. An example of a snapshot is shown in Figure 1(b). A snapshot is characterized by a circle that encompasses all the sensor readings.

Finally, a tracker τ is created by forming associations between snapshots over time. The support of a tracker, supp_t(τ), is given by the sensor indices of the points in the snapshots, and is represented as a subset of the sensor indices Θ. The tracker associates snapshots using their bounding circles. The tracker is terminated when clear successor snapshots do not exist.

4.1.1 Tracking implementation and limitations

In our implementation, agglomerative clustering is used to place every pair of dynamic sensor readings that fall within 0.5 meters of each other into the same snapshot. The bounding circles are used to define the distance between snapshots as the distance between centers plus the absolute value of the difference between the radii. For snapshots in subsequent timesteps to be associated with the same tracker, the distance between the snapshots must be less than one meter with no other snapshots within a distance of 0.01 m. Similar tracking performance is observed when the thresholds are varied by twenty percent.

Part of an agent's development are early failures in the perceptual system. One commonly discussed phenomenon in child development is the lack of object permanence, where the child fails to maintain a representation for an object when it is not perceived in the observation stream. Another type of failure is the failure to correctly track objects. The following example demonstrates both kinds of failure.

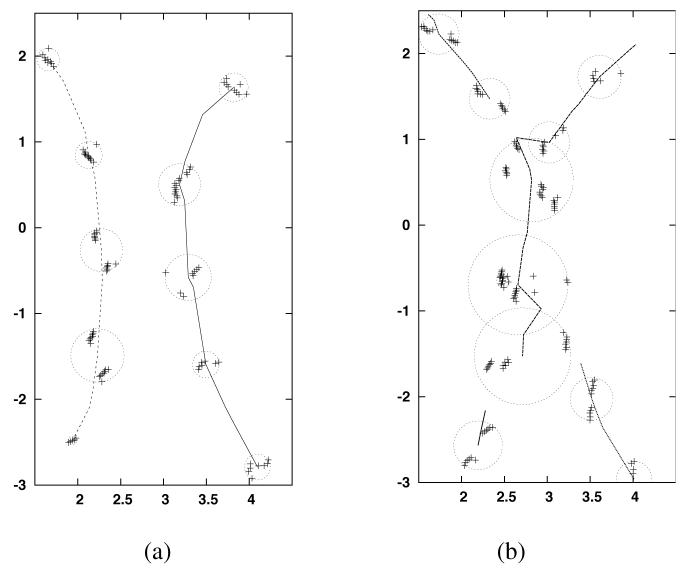
Figure 2 shows two examples of a scenario where two people are walking. The people start at the bottom of the figures and walk towards the top, first approaching one another and then separating. The people are observed using a SICK LMS-200 sensor at a height of 40cm above the ground plane. In the first example, the people remain sufficiently far apart so tracking keeps the two people separate. In the second example, as the people move close together, the spatial clustering into snapshots fails to separate them. This failure causes a new tracker to be created. When the two people separate, the tracker for the pair follows the person on the right, and a new tracker is created for the other person.

Fig. 2.

Two examples of tracking. In both examples, two people are walking, starting at the bottom of the figure and moving to the top. The plus signs show laser readings taken at one second intervals, shown in the coordinates of the local map. These readings are shown in the bounding circles of their associated snapshots. The lines indicate the path of the trackers. The units on the axes are in meters. (a) The people first approach each other and then move apart. Since the people do not come too close together, the tracking system generates exactly two trackers, one for each person. The two paths show the trajectory of the center of each tracker. (b) This example demonstrates two methods by which tracking can fail. One is the failure to track a single object in the presence of distractions. The second is the failure to notice when a tracked cluster separates into multiple distinct entities. Initially at the bottom of the figure, each person has a separate tracker. As they approach, the spatial clustering process returns a single snapshot for both people. Since the snapshot at the merger has no clear successor (as each of the original trackers can explain the merged snapshot), the existing trackers are terminated and a new tracker is created. A similar inference occurs when the two people move apart. Spatial clustering creates two snapshots that must be explained. The tracking algorithm finds that one snapshot (on the right) is the only clear successor for the merged tracker and a new tracker is formed for the second snapshot.

This example shows that the robot is able to track multiple objects when they are well separated, but can make errors when objects are in close proximity. Hence, the robot and the human experimenter agree on the semantics of which objects exist in a scene when the objects are well separated, but differ when the objects are in close proximity. The difference is largely due to the human's superior visual senses, and background knowledge about the structure of humans and their activities.

4.2 Formation of Percepts

For each tracker τ, We manually define a small set of perceptual functions f ∈ P. Each perceptual function gives rise to the percept f_t(τ) for a given tracker τ at a time t. The simplest percept is the object's support (supp_t(τ)).

Some percepts can be defined as functions of the object support. For this work we consider two such functions.

$${\text{angle}}_t\left(\tau \right)=\mathrm{mean}\{i\mid i\in {\mathrm{supp}}_t\left(\tau \right)\}$$ (6)

$${\text{distance}}_t\left(\tau \right)=\min \{z_t\left(i\right)\mid i\in {\mathrm{supp}}_t\left(\tau \right)\}$$ (7)

A larger set of perceptual functions could be generated autonomously using a constructive induction process [27,24]. In constructive induction, new functions are generated from old functions by applying functional transformations. For example, a new scalar perceptual function can be the sum, product or difference of two original scalar perceptual functions, while for a vector perceptual function, the mean, minimum, or argument of the minimum can form new perceptual functions.

Another percept is the object's shape. A shape is represented with a set of situated views of the object, where each situated view is a tuple with the robot location, the robot heading, the object support and the sensor observation from a set of previous time steps I. The location and heading of the robot (robot-location_t and robot-heading_t) are non-object percepts that are generated from localization in the occupancy grid.

$${\text{shape}}_t\left(\tau \right)=\{\langle {\text{robot-location}}_{t^{\prime }},{\text{robot-heading}}_{t^{\prime }},{\mathrm{supp}}_{t^{\prime }}\left(\tau \right),z_{t^{\prime }}\rangle \mid t^{\prime }\in I\}$$ (8)

When a tracker's shape matches a known shape (described in the next section), the robot is also able to generate percepts for the object's location and heading (location_t(τ) and heading_t(τ)) in the map.

4.3 Formation of Classes

Given a temporal sequence of percept values,

$$\dots ,f_{t-1}\left(\tau \right),f_t\left(\tau \right),f_{t+1}\left(\tau \right),\dots$$

with a distance function d, a percept is a candidate for defining a class if

$$\forall k>0,d(f_t\left(\tau \right),f_{t+k}\left(\tau \right))\approx 0.$$ (9)

Thus, classes are formed by creating clusters from object percepts that are stable in time. Shape is a good class-defining percept, but angle and distance are not. Classes facilitate generalization from past experience.

Using a particular perceptual function f ∈ P, a class σ_f is defined by Equation 4 to be a set of percepts that are near the prototype percept q̄ = f_t′ (τ′) (within the threshold η).

$${\sigma }_f\left[\stackrel{-}{q}\right]=\{q\mid d(q,\stackrel{-}{q})\le \eta \}$$ (10)

When the robot observes a stable potentially class-defining percept f_t(τ), the robot first checks to see if it is a member of a known class by measuring the distance between the observed percept and all prototypes associated with the perceptual function f. When the percept does not belong to a known class, a new class is generated from the percept.

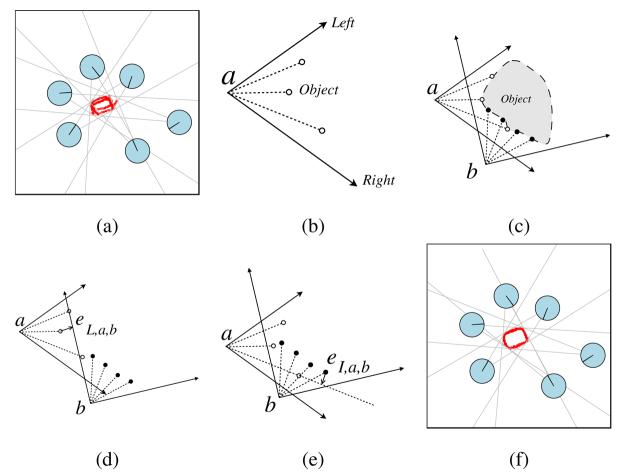
We now describe how a class is formed from a shape percept. First, structurally consistent shapes are created by minimizing violations of geometric constraints between the situated views in the shape percept. Figure 4 shows how error vectors are defined between situated views. Using three error vectors defined in the figure, we define an inconsistency measure for an object shape A,

$$\mu \left(A\right)=\underset{a\in A}{\Sigma }\underset{b\in A}{\Sigma }\Vert e_{L,a,b}{\Vert }^2+\Vert e_{R,a,b}{\Vert }^2+\Vert e_{I,a,b}{\Vert }^2.$$ (11)

Fig. 4.

(a) The shape percept is a set of situated views of the physical object. A single situated view consists of the robot's pose, the tracker's support and the sensory observation. (b) The object is bounded by rays on the left and right. (c) The sensor readings from one situated view must fall within the bounding rays from all other situated views. (d) Exterior error vectors are defined from violations of this geometric constraint. A left error vector (e_L,a,b) is shown here and a right error vector (e_R,a,b) is defined similarly [18]. (e) An interior error vector (e_I,a,b) is defined from sensor readings that come from the inside of an object. (f) A consistent shape description is created by minimizing the lengths of these error vectors.

Minimizing this error generates consistent shapes, as shown in Figure 5. In our implementation, this minimization is performed by numerical optimization with the Nelder-Mead simplex algorithm where the minimization is initialized with the robot's poses in the local map.

We denote the rigid transformation of a shape B (defined as a set of tuples in Equation 8) by offset vectors for the location and heading (λ and γ respectively) by

$$T_{\lambda ,\gamma }\left(B\right)=\{\langle l+\lambda ,h+\gamma ,S,z\rangle \mid \langle l,h,S,z\rangle \in B\}.$$ (12)

The distance between two shapes is then defined to be the minimum error over all rigid transformations.

$$d(A,B)=\underset{\lambda ,\gamma }{\min }\mu (A\cup T_{\lambda ,\gamma }\left(B\right))$$ (13)

This distance function is used by the robot to create the shape classes shown in Figure 5. We use the threshold η = .02 in Equation 10 which is twice the sensor resolution. In our implementation, optimizing over rigid transformations is performed by aligning the geometric centers of the shapes and taking the minimum after performing numerical optimization starting from eighteen initial orientations spaced twenty degrees apart.

New percepts for the object location and heading are also defined using this distance function. Given an object shape A, the robot estimates its pose in the object frame of reference, by searching for a robot location and heading that are consistent with the tracker τ,

$${\lambda }^{\prime },{\gamma }^{\prime }=\arg \underset{\lambda ,\gamma }{\min }d(A,\{\langle \lambda ,\gamma ,{\mathrm{supp}}_t\left(\tau \right),z_t\rangle \}).$$ (14)

Given the robot location and heading in both the reference frame of the map and the reference frame of the object, the robot can estimate the location and orientation (location_t(τ) and heading_t(τ)) of the object in the map. These values are computed by the object tracker in real-time using numerical optimization.

4.4 Formation of Actions

Thus far, the robot does not have any knowledge of its interactions with the object. To address this need, we now describe how the robot learns actions that reliably change individual object properties. Our definition of an action differs from STRIPS actions (with complete declarative preconditions and postconditions), and reinforcement learning actions (with no declarative description). Our definition of an action (Equation 5) includes a partial description of an action's postconditions, along with complete declarative preconditions. The partial description of postconditions simplifies learning, but it can limit the reliability of plans.

Actions facilitate planning by characterizing the behavior of a control law. To sequence actions, the planner must know the preconditions of a control law and its postconditions. We form actions by learning control laws whose postconditions and preconditions have simple descriptions.

The robot learns actions by observing the effects of performing random motor babbling in the presence of the object. Motor babbling is a process of repeatedly performing a random motor command for a short duration. One strength of the action learning approach we present here is that the robot is able to use this goal-free experience to form actions that can be later used for goal directed planning. The robot performs self-supervised learning, where the observations in the training data are labeled using the qualitative changes that occur to an individual percept. Once learned, actions are used to achieve goals by reducing the difference between the robot's current perception and the desired goal, as demonstrated in the evaluation (Section 5.2). Thus goals are not required while the actions are being learned but they are required for planning and execution.

4.4.1 Action Definition

An action is defined in Equation 5 as a tuple with a description, a context and a control law. These components are now formally defined.

Our action learning algorithm is restricted to perceptual functions f_j which are either vector-valued or not perceived.

$$f_{j,t}\left(\tau \right)\in {\Re }^{n_j}\cup \{\perp \}.$$ (15)

In particular, the robot does not learn an action to change the shape of an object, as a shape percept is represented by a set. The change in a perceptual function is denoted by δ_j,t = f_j,t+1 − f_j,t (the indices j and t are sometimes elided for clarity).

The description of an action, D = 〈j, b, q_b〉, consists of the name j of the perceptual function to be controlled, the qualitative behavior b,

$$b\in \{\mathit{inc},\mathit{dec}\}\cup \{\mathit{dir}\left[f_k\right]\mid f_k\in 𝒫\},$$ (16)

and the quantitative effect q_b. Two qualitative behaviors are defined for a scalar perceptual function: increasing and decreasing. The qualitative behavior dir[f_k] is defined for a vector function f_j and means that f_j changes in the direction of f_k. The quantitative effect for scalars is bounded by ∊ > 0,

$$q_{\mathit{inc}}\left({\delta }_t\right)\equiv {\delta }_t>∊,q_{dec}\left({\delta }_t\right)\equiv -{\delta }_t>∊.$$ (17)

The quantitative effect for vectors is bounded by ∊ > 0 and ∊′ > 0,

$$q_{\mathit{dir}\left[f_k\right]}\left({\delta }_t\right)\equiv \Vert {\delta }_t\Vert >∊\wedge \frac{\langle {\delta }_t,f_{k,t}\rangle }{\Vert {\delta }_t\Vert \cdot \Vert f_{k,t}\Vert }>1-{∊}^{\prime }.$$ (18)

The context of an action is represented as a conjunction of inequality constraints on scalar perceptual functions:

$$\left(\mathit{xRc}\right)\text{where}x\in \left\{f_k\right\},R\in \{\le ,\ge \},c\in \Re .$$ (19)

Finally, the control law of an action is a function H from a percept to a motor output. In this work we restrict our attention to constant functions H.

4.4.2 Learning Algorithm

Learning an action that satisfies a qualitative description requires specifying the components of the action given Equation 5. First, to complete the description, a threshold ∊ is selected from the observed values of δ. Next, the quantitative effect is used to search for constraints on the perceptual context and motor output that reliably induce the desired behavior. Finally, the constraints are used to define a perceptual context and a control law.

For each perceptual function, a threshold ∊ > 0 is chosen by running a Parzen window [5] with a Gaussian kernel over the observations of δ (or ∥δ∥ for vector percepts). The threshold ∊ is set to the first local minimum above zero if it exists, otherwise it is set to a value one standard deviation from the mean. The value of ∊′ for vector percepts is set along with the perceptual constraints while optimizing the utility function defined below.

The threshold ∊ is used to define q_b via Equations 17-18, and q_b is used to label the examples in the training data. The learning algorithm uses the labeled examples to search for constraints on the percepts and motor outputs that generate the desired behavior. The constraints are represented by axis aligned half-spaces, specified as inequalities over the variables of the scalar perceptual functions (f_k) and the components of the motor vector (π_k(u)).

To find the perceptual constraints C and motor constraints M, we define a set of measures for the precision (μ₀), recall (μ₁), and repeatability (μ₂). The utility function U is their geometric mean. These functions are defined using the empirical probability (Pr) as measured in the training data.

$$\begin{array}{cc}\hfill {\mu }_0& =\mathit{Pr}(q_b\left({\delta }_t\right)\mid z_t\in C\wedge u_t\in M)\hfill \\ \hfill {\mu }_1& =\mathit{Pr}(z_t\in C\wedge u_t\in M\mid q_b\left({\delta }_t\right))\hfill \\ \hfill {\mu }_2& =\mathit{Pr}(z_{t+1}\in C\mid z_t\in C\wedge u_t\in M)\hfill \\ \hfill U& ={\left({\mu }_0{\mu }_1{\mu }_2\right)}^{\frac{1}{3}}\hfill \end{array}$$ (20)

Constraints are added incrementally to greedily optimize the utility function. The process terminates when adding a constraint provides no significant improvement to utility. The newly generated action is discarded if the final utility measure is low (less than 50%). Otherwise, the learned context C becomes part of the action.

A constant control law is defined from M.

$$H\left(z_t\right)=m=\arg \underset{u\in M}{\min }\Vert u\Vert$$ (21)

The constant control law is enhanced during execution in two ways. The first is to account for perceptual latencies by predicting the current value of the percept. The second is to scale down the motor output for fine control, when the robot wants to change a percept to a goal value g.

$$s(g,\tau )=\min (1,\Vert E\left[f_{k,t}\left(\tau \right)\right]-g\Vert ∕∊)$$ (22)

$$H\left(z_t\right)=s(g,\tau )\cdot m$$ (23)

The learned components define the new action α = 〈D, C, H〉.

4.4.3 Training Scenario

Several perceptual functions were used for learning and they are listed in Table 1. Perceptual functions for the robot's location and heading come from the robot's ontology of space. The robot's heading is represented as a unit vector. The remaining perceptual functions are computed for each tracker. Object localization, described in the previous section, provides the position and heading of the object.

Table 1.

Perceptual functions used by the learning robot. The robot has previously learned actions that change its location and heading in the map. The robot learns to control the properties of the object image on its sensor array (the angle and distance to the object). The robot also learns an action to control the object position in the environment (Figure 2). The headings are represented by unit vectors.

Name	Definition	Dim
robot-location	robot's location in the map	2
robot-heading	robot's heading in the map	2
distance(τ)	distance from sensor to object τ	1
angle(τ)	angle from sensor to object τ	1
location(τ)	location in map of object τ	2
heading(τ)	heading in map of object τ	2

The robot was physically modified for this experiment by the addition of a small foam bumper to the front of the robot. The bumper reduced the impact of the object collisions on the robot's body. The bumper also kept the objects further away from the range sensor which limited the amount of the static environment obscured by the object. This was necessary as the localization algorithm requires an adequate view of the static environment to keep the robot localized in the map.

The robot created a log of observations for training data. The robot gathered observations by randomly selecting a motor command and executing it for a fixed duration. The motor commands for drive and turn (linear and angular velocities) were selected from the following set.

$$\{-0.2,0.0,0.2\}m∕s\times \{-0.4,0.0,0.4\}\mathit{rad}∕s$$

The data was gathered in different environmental configurations, where the experimenter changed the environment between trials. The experimenter ensured that the robot could see the training object (the recycle-bin) at the start of every trial. The experimenter varied the configurations observed by the robot to ensure that the robot gathered experience from multiple configurations of the robot and the object. For example, the robot experienced some situations when the object was far away and and others when it was nearby. The robot also experienced situations where the object was on the left, directly ahead, and on the right. The training session included periods of time where the robot was pushing the object, and the object would fall away to the left or to the right if the object was significantly off-center. Approximately ten minutes of training data were gathered, with one observation per second.

Running the learning algorithm generated several useful actions that are shown in Table 2. These actions can be thought of as simple affordances of the object; actions which the robot assumes will always work. However, the action for pushing an object will fail for heavy objects that the robot can not move. This was not tested to avoid damaging the robot. As an extension to the current work, a more robust robot could use this action to create new perceptual functions that predict which objects are pushable and which are not.

Table 2.

The above actions were learned by the robot from its observations of the effects of motor babbling by optimizing the utility function defined in Equation 20. These actions cause changes in the angle to the object (by turning), (III,IV) the distance to the object (by driving), and (V) the location of the object in the map (by pushing). The context of an action represents the precondition for the action to be successfully executed for a single time step.

Action I	{ Move the sensor image of the object to the left }
Description	〈 angle(τ), inc , δ > 12 〉
Context	∅
Control Law	( 0.0 m/s , −0.4 rad/s)
Utility	73%
Action II	{ Move the sensor image of the object to the right }
Description	〈 angle(τ), dec, −δ > 12 〉
Context	∅
Control Law	( 0.0 m/s , 0.4 rad/s)
Utility	74%
Action III	{ Move away from the object }
Description	〈 distance(τ), inc , δ > .19 〉
Context	∅
Control Law	( −0.2 m/s , 0.0 rad/s)
Utility	69%
Action IV	{ Approach the object }
Description	〈 distance(τ), dec, −δ > .19 〉
Context	(distance(τ) ≥ 0.43) ∧ (angle(τ) ≥ 69 ∧ (angle(τ) ≤ 132))
Control Law	( 0.2 m/s , 0.0 rad/s)
Utility	61 %
Action V	{ Move the object }
Description	〈 location(τ), dir[robot-heading], ∥δ∥ > .21 ∧ ∊′ = .13 〉
Context	(distance(τ) ≤ 0.22) ∧ (angle(τ) ≥ 68) ∧ (angle(τ) ≤ 103)
Control Law	( 0.2 m/s , 0.0 rad/s)
Utility	65%

The learning algorithm was not able to learn an action to control every object property. In particular, it was not able to learn an action for changing the heading of the object. The robot's physical configuration makes it difficult for the robot to continuously push and turn the object. When the robot pushes the object off-center, the object tends to slide off the bumper. Without examples of successfully turning an object, the learning algorithm was unable to find a reliable action for changing the object's heading.

4.4.4 Representing Goals and Planning to Achieve Them

Part of the value of the object representation is that it provides a formalism for representing and achieving goals. The high-level task specified in natural language as “Place the recycle bin in the center of the room” can be formally represented as a goal state with a tracker whose shape corresponds to the recycle bin and whose location is in the center of the room. The robot can describe goals and measure its progress towards achieving them. A goal is formally expressed either with an inequality bound (distance(τ) < 1) or with a tolerance from a setpoint (|angle(τ)−90| < 10).

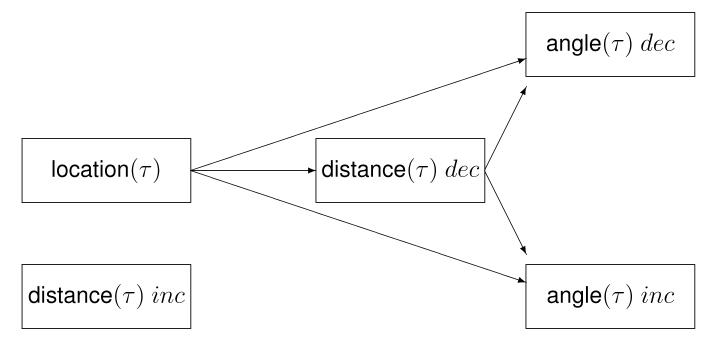
The learned actions are used by a planner to achieve goals by sequentially reducing differences between the robot's current percepts and the goal. First, a dependency graph is formed among the actions by linking constraints in the context of one action with the description of the effects of other actions (Figure 6). For example, the constraint angle(τ) ≥ 68 in the action that changes location(τ), can be satisfied by the action that increases angle(τ). Planning relies on this duality between the constraints in the context and the described effects, which is essentially means-ends analysis [13]. To achieve goals, the constraints provided in an action's context are used with backchaining to create reactive plans that change a percept to a goal value.

Fig. 6.

Dependency graph between actions used for planning

Attempting to satisfy the preconditions sequentially can fail when more than one precondition is not satisfied. For example, to push an object to a goal position when the robot, object, and goal do not lie in a line, the robot must first move to a position near the object which is opposite from the goal. In this situation, the robot simulates observations from possible robot poses to find a pose from which the perceptual context is satisfied. The simulation based planning algorithm first creates an error vector, with one dimension per constraint. The value of each component of the vector is the amount by which the corresponding constraint is violated. The algorithm hill-climbs on the error vector length in the space of robot poses to find a pose with a zero length error vector. A procedure for simulating observations from different poses was provided externally to the robot. The process of simulating observations relies on the shape percept for the object. Hence, even though an action may not explicitly reference an object's shape, planning with simulated observations may require knowledge of an object's shape in order to find a pose for the robot from which the context is satisfied. If a satisfying pose is found, the robot moves to this pose and then attempts to execute the desired action.

5 Evaluation

We have described algorithms that generate object representations for robots. Now we demonstrate the utility of these representations on our mobile robot. Our experimental platform is a Magellan Pro robot with a laser rangefinder running with Player drivers [7]. The mapping and localization code is implemented in C++, and the object-based code is implemented in Python. The laser rangefinder provides a planar perspective of the world, from approximately 40cm above the ground. We evaluated the learned object representation on two tasks. The first is a classification task that tests the robot's object recognition capability. The second task tests the robot's ability to achieve goals.

5.1 Classification

We evaluated the robot's ability to perform an object recognition task. The robot modeled the shape of each of the ten objects in Figure 5 on five separate occasions. The classification task was to predict the object's label as provided by the experimenter. The first graph shows prediction accuracy using the shape percept of each tracked object. The second graph shows prediction accuracy using the shape class for each tracked object. We compared the performance using nearest neighbor learning with unaligned shapes (before minimization of Equation 11), nearest neighbor learning with aligned shapes (after minimization of Equation 11), and a theoretical optimal learner. A perfect learner would achieve 100 percent accuracy after ten examples (one example for each class), while random guessing would only achieve 10 percent accuracy.

The results from a five fold stratified cross validation experiment are shown in Figure 7(b,c). The results show that using aligned shapes performs significantly better than using unaligned shapes. Also, while learning with the shape class performs well, learning with the raw percepts will perform better. However, using the raw percepts has a disadvantage that is not shown in these graphs, namely greater runtime computation and space requirements from comparisons with all of the percepts instead of a few class prototypes.

Fig. 7.

(a) Shape hierarchies are created from multiple observations of the objects in Figure 5. The identifiers for the objects are included here for clarity, but they are not used for clustering. The graph depicts the minimum spanning tree formed using the distances between the observed shapes. The horizontal axis shows the distance at which a branch is connected to its neighbors. Note that all observations of the same physical object are grouped near zero. (b) Accuracy of label prediction using the tracker's shape percept. (c) Accuracy of label prediction using the shape class.

To better understand the shape classes formed by clustering with the shape distance function, we can create a hierarchy of the shape percepts as shown in Figure 7(a). This hierarchy is formed by taking the minimum spanning tree of a fully connected graph where the shape percepts are the nodes and the edge weights are given by the shape distance function. The horizontal axis indicates the link length at which a set of percepts is connected to its neighbors. Setting the class threshold η to a value near zero in Equation 10 will create classes that are in close correspondence with the physical objects.

Although the number of examples is limited, this figure provides some evidence that distance between object shapes can suggest similarity in function. The recycle bin and black garbage bin are the closest two objects, and the garbage can is linked to these before any others. All three of the physical objects share the function of being waste receptacles. The three chairs are also linked together into a cluster. This “chair” cluster is joined to another cluster with a variant of a chair (Vulcan the wheelchair) but excludes other large objects (including the yoga ball and the box).

5.2 Interaction Tasks

To evaluate the learned actions, we measured the ability of the robot to perform three tasks: facing the object, approaching the object and moving the object to a location. These tasks were represented by setting goal values for the angle(τ), distance(τ) and location(τ) percepts respectively. The starting state for the three tasks was approximately the same (the object was placed at different orientations), and is shown in Figure 8. The desired final states for the tasks were to have the object in front of the robot (|angle(τ) − 90| < 10), to have the robot near the object (distance(τ) ≤ 1.0), and to have the object at the goal location in the figure (∥location(τ) − (3,2)∥ < .15 m). Ten runs were performed for each task, and the experimenter physically verified task completion for each run. The results in Table 3 show that the robot is able to achieve these goals reliably and accurately. Figure 8 shows an example of the robot pushing the object to a goal.

Fig. 8.

(a) The robot pushes a recycling bin towards a goal location. (b) The shaded shapes show the robot's percepts for itself and the object. The starting poses of the robot and the object are shown unshaded, and the goal location for the object is indicated by ×.

Table 3.

The robot used the learned actions to perform three tasks: facing the object, approaching the object and moving the object. The columns indicate the initial distance to the goal, the final distance from the goal and elapsed time. Each task was performed ten times, and the results are shown with the standard deviations. The goal was achieved on every trial.

Behavior	Goal	Distance	Accuracy	Time (s)
Face	|angle(τ) − 90| < 10	45 °	7.4° (σ=3)	4.38 (σ=.51)
Approach	distance(τ) < 1	1.8 m	.04 m (σ=.02)	21.1 (σ=5.7)
Move	∥location(τ) − (3,2)∥ < .15	2.0 m	.09 m (σ=.04)	258 (σ=138)

6 Related Work

Work in psychology has explored the development of object representations in children. Work by Spelke [28] has studied how children develop from using motion as an indicator of object unity to using other cues. Work by Mandler [16] has explored how classes might form in more general conditions. Work by Bloom [3] has studied how objects and classes are used to quickly learn a language. Our work builds upon these ideas to implement a computationally tractable method for learning about objects on a mobile robot.

Previous work in developmental robotics [24,23,4] has shown how the structure of an agent's sensory and motor systems can be learned. A key method in this process is the projection of high-dimensional observations into a low-dimensional space. Further advances include Isomap [30] which identifies manifolds in the data, the use of information distance for sensor organization [21], and the use of intrinsically learned spatial representations to accelerate learning externally specified tasks [25]. Our work in this paper conceptually builds upon a foundation of spatial knowledge to learn about objects.

There is also work studying how a robot can learn object representations with actions. Kemp and Edsinger [11] showed how mutual information connects proprioception in an arm joint with visual patches associated with the hand. Work by Stoytchev [29] has a robot learning the affordances of simple tools. Related work [10] demonstrates how a robot can learn the preconditions for actions. Natale [20] has shown how motor babbling with a robot arm can be used to learn how to move objects. The work in these papers use stationary perception, whereas our work demonstrates the use of mobile perception.

Related work has also explored object recognition and action but not in conjunction. Work on object recognition has used laser-based mapping techniques [2], and image-based models [15]. Object-based actions have been learned in simulated symbolic domains [8,1,33,14]. These approaches provide methods for learning object interactions when a symbolic abstraction is already available, but do not address how continuous actions can be learned on a mobile robot.

Some studies have attempted to more directly connect the robot's intrinsic experience of objects with their extrinsic shared meaning. Work by Yu and colleagues [32] has explored how internal visual object representations can be associated with object names represented as phoneme sequences. Work on the Open Mind Indoor Common Sense project [9] has explored ways of directly specifying relationships between between the names of objects. Combining these approaches with the work presented here would yield a system that would have access to both a rich intrinsic object representation and a shared extrinsic object representation.

7 Future Directions

We have described an approach by which a robot can learn an integrated representation of objects that is grounded in experience, However, the completed work has several limitations which are fertile areas for further research. Some of the most important are sensor generalization, active exploration, extending the learning process, and real-world applicability.

The use of a planar laser rangefinder as the sensor for this work has both benefits and drawbacks. As a benefit, it shows that many critical tasks for working with objects can be accomplished with a limited sensor. These tasks include tracking objects, building structural models, and learning actions. Moreover, these representations can support object classification and goal-directed planning. As a drawback, a richer data stream could provide more information for distinguishing objects. As the planar laser rangefinder is a range sensor, similar methods could be applied to building object representations from three dimensional range sensors including 3D scanners and stereo vision. Tracking would generalize directly using SLAM techniques to separate the dynamic sensor readings from the static background. The geometric constraints used to determine an object's shape could be generalized from rays to planes, though some algorithmic modifications may be required for handling higher volume data streams. Generalizing to other sensors such as monocular vision requires more research, since real-time background subtraction with a moving camera is still a challenging research problem. Alternatively, local image features may prove to be effective as a basis for image-based object representations [26].

Another area that requires further research is the use of active exploration to discover object actions. The current work required a person for the data gathering process to ensure that data samples were collected from different parts of the feature space. Ideally, the robot would be able to engage in active exploration, perhaps driven by an intrinsic reward [22] for acquiring new actions. This is challenging to perform on physical robots due to the fact that the not all robot actions are invertible: while our robot can push an object against a wall, the robot can not pull the object back from the wall. The inability to restore the environment in such circumstances limits the use of completely human-free exploration strategies.

The learning process could be extended to find actions that are object contingent, to generate new perceptual functions, and to discover relations between objects. On a less fragile robot platform (without the risk of motor burnout) the robot could attempt to learn a constraint that large objects can not be moved. This constraint in an action's context is an example of how learned actions can be contingent on an object's properties such as its size or mass. Automatically generating new perceptual functions by constructive induction would relieve the burden of relying on hand-generated perceptual functions. However, a perceptual function that yields an efficient structural model would be challenging to discover automatically. Learning relationships between objects could help the robot generalize across the relative ways objects are positioned, used, or shaped. Relations between objects may also support learning from demonstration by observing natural interactions between people and objects.

This work is based on ideas from human development, and several more learning stages may be required before this approach performs well on real-world problems. However, the robot could use its current knowledge for self-supervision to bootstrap more capabilities. For example, the robot could use the experience gathered from dynamic objects to improve its ability to track dynamic objects and to find stationary objects. The robot could learn more efficient control laws for the individual actions, and also learn the side effects of actions. Adding these extensions should allow this developmental approach to tackle more significant real-world tasks.

8 Conclusions

The above work shows how a robot that starts with an understanding of its sensors and space can construct object representations. Multiple representations are acquired, which form perceptual, structural and functional object representations. The object snapshots and trackers form perceptual representations. The shape percept provides a structural representation. The learned actions provide a functional representation. By integrating these different aspects of objects, the learned representations support perception, geometric inference, and goal-directed planning. The robot can effectively learn and use knowledge about objects. The learned knowledge is adequate for generalizing from past experience both for object recognition tasks and for acting to achieve goals.

The learned object representations are grounded in the robot's sensorimotor experience. The robot creates object trackers for individual objects, forms percepts from observations, forms classes to generalize from past experience, and learns actions to change the perceived features of an object. Using this knowledge, the physical robot is able to recognize objects and plan with learned actions to achieve goals. The learned representation is simple and lays the foundation for learning more complex object models in the future.

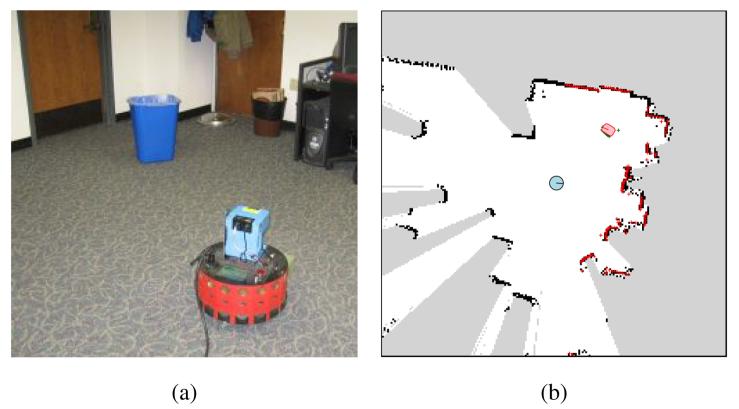
Fig. 3.

(a) A scene with the learning robot observing a physical object. (b) The robot builds a structured description of its local environment consisting of a static map, the learning robot, and the recognized object.

Biographies

Joseph Modayil is a postdoctoral researcher at the University of Rochester. He earned his Ph. D. from the University of Texas at Austin in 2007. His research interests include intelligent robotics,developmental learning and activity recognition.

Benjamin Kuipers holds an endowed Professorship in Computer Sciences at the University of Texas at Austin. He received his B.A. from Swarthmore College, and his Ph.D. from MIT. He has held research or faculty appointments at MIT, Tufts University, and the University of Texas at Austin, where he served as Department Chairman. He is a Fellow of AAAI and IEEE. His research interests span computational models of cognitive maps, robot exploration and mapping methods, the qualitative simulation algorithm QSIM, and foundational learning methods.