Abstract
Herbivorous top-down forces and bottom-up competition for nutrients determine the coexistence and relative biomass patterns of producer species. Combining models of predator–prey and producer–nutrient interactions with a structural model of complex food webs, I investigated these two aspects in a dynamic food-web model. While competitive exclusion leads to persistence of only one producer species in 99.7% of the simulated simple producer communities without consumers, embedding the same producer communities in complex food webs generally yields producer coexistence. In simple producer communities, the producers with the most efficient nutrient-intake rates increase in biomass until they competitively exclude inferior producers. In food webs, herbivory predominantly reduces the biomass density of those producers that dominated in producer communities, which yields a more even biomass distribution. In contrast to prior analyses of simple modules, this facilitation of producer coexistence by herbivory does not require a trade-off between the nutrient-intake efficiency and the resistance to herbivory. The local network structure of food webs (top-down effects of the number of herbivores and the herbivores' maximum consumption rates) and the nutrient supply (bottom-up effect) interactively determine the relative biomass densities of the producer species. A strong negative feedback loop emerges in food webs: factors that increase producer biomasses also increase herbivory, which reduces producer biomasses. This negative feedback loop regulates the coexistence and biomass patterns of the producers by balancing biomass increases of producers and biomass fluxes to herbivores, which prevents competitive exclusion.
Keywords: bottom-up, top-down, predator–prey, competition theory, biodiversity
1. Introduction
A classic debate in ecology addresses how producer species can coexist in the face of interspecific competition for nutrients that should reduce biodiversity via competitive exclusion (Gurevitch et al. 2000; Chase et al. 2002). Here, the term nutrient is used instead of the more general term resource to avoid potential confusion of abiotic and biotic resources. Classic competition theory predicts that the dominant producer species with the most efficient nutrient intake will obtain the highest biomass and eventually competitively exclude all the other producer species (Tilman 1982). Thus, the number of coexisting producer species cannot exceed the number of limiting nutrients (Tilman 1982) unless factors such as predation or chaotic population dynamics counteract competitive exclusion (Armstrong & McGehee 1980; Huisman & Weissing 1999; Chesson 2000).
Predation of the dominant producer species has long been considered an important factor maintaining producer coexistence (Paine 1980; Menge 1992; Leibold 1996; Gurevitch et al. 2000; Chase et al. 2002; Brose et al. 2005b; Hulot & Loreau 2006). Specialist predators can facilitate the coexistence of a diverse guild of competitors when they suppress the density of each competitor independently (Janzen 1970). Generalist predators impose apparent competition on a guild of competitors: the least vulnerable prey sustains the highest predator densities, which eventually leads to the exclusion of all other prey species (Holt et al. 1994). In modules of few species, the combination of exploitative and apparent competition can facilitate the coexistence of competing producer species only if there is a strict trade-off between nutrient-intake efficiency and resistance to predation (Holt et al. 1994; Leibold 1996; Grover & Holt 1998; Chase et al. 2000). However, it is unclear whether this trade-off is strictly necessary when the producer guild is embedded in a complex food web.
Traditionally, the chronic instability of complex food webs has hindered theoretical advances in understanding their dynamical behaviour. Recently, it was shown that (i) natural food webs exhibit a body-mass structure of predators being on average one to two orders of magnitude larger than their prey (Brose et al. 2006a), and (ii) this body-mass structure promotes the dynamic persistence of complex food webs (Emmerson & Raffaelli 2004; Brose et al. 2006b; Otto et al. 2007; Rall et al. 2008). In persistent food webs, biomass increases of a population are directly balanced by increasing biomass fluxes to upper trophic levels (De Ruiter et al. 1995), which prevents biomass overshooting of populations at low trophic levels (Neutel et al. 2007). Interestingly, this balance of biomasses and biomass fluxes could prevent competitive exclusion that is driven by biomass overshooting of producers with superior nutrient-intake efficiencies. This suggests that persistent food webs may enable producer coexistence despite a competitive hierarchy in nutrient-intake efficiencies.
Here, I use a dynamic model that synthesizes the structure of complex food webs, predator–prey interactions and nutrient-dependent growth of the producer species (Brose et al. 2005a) to study the effects of complex food webs on guilds of five producer species with random nutrient-intake hierarchies. The producer guilds are embedded in complex food webs without assuming a trade-off between nutrient-intake efficiency and resistance to herbivory. First, I address the question of whether complex food webs promote producer coexistence without such a trade-off. Second, I analyse which food-web and population parameters determine the producer biomass densities, their nutrient-intake rates and their losses to herbivory to gain a mechanistic understanding of how competitive exclusion is prevented.
2. Material and methods
The model studied here describes the interactions between heterotrophic consumer and autotrophic producer populations by coupling models of producer–nutrient (Tilman 1982; Huisman & Weissing 1999) and predator–prey interactions (Yodzis & Innes 1992). The simulated communities include five producer species with random nutrient-intake efficiencies whose growth depends on two limiting nutrients (see §2c). The probability of producer coexistence in simulations of the simple producer communities comprising only these five producers is compared with simulations of multitrophic food webs that include the same producer guild. The dynamic food-web models are built in a three-step process: (i) the link structure is created by a structural model, (ii) the trophic levels of the populations are calculated, and (iii) the parameters of the allometrically scaled predator–prey model are calculated based on randomly sampled predator–prey body-mass ratios constrained by their respective trophic levels.
(a) Food-web structure
The network structure (‘who eats whom’) of the food webs follows the niche model (Williams & Martinez 2000). This stochastic model is based on algorithms that arrange trophic links, L, among species based on species richness, S, and connectance, C=L/S2, as input parameters. The food-web structures predicted by the niche model have been successfully tested against empirical data (Williams & Martinez 2008). To allow comparisons with the producer communities, I selected the particular subset of the niche-model food webs, which contains five producer species. S and C were sampled from normal distributions (table 1). The feeding matrix created by the niche model was used to calculate the trophic levels of the species in the food webs as prey-averaged trophic levels (Williams & Martinez 2004a).
Table 1.
Model parameters that were randomly sampled from different distributions for each simulation run independently. (Note: the range of body-mass ratios, Z, is consistent with empirical data (Brose et al. 2006a).)
| variable | distribution | normal distribution | equation | description | |
|---|---|---|---|---|---|
|
| |||||
| mean | s.d. | ||||
| y | normal | 10 | 2 | (2.1a) and (2.1b) | maximum consumption rate |
| h | normal | 1.5 | 0.25 | (2.2) | Hill exponent |
| c | normal | 0.5 | 0.25 | (2.2) | predator interference coefficient |
| Z | normal | 101 | 102 | (2.5) | consumer–resource body-mass ratio |
| S l | normal | 4 | 2 | (2.7) | supply concentration of nutrient l |
| S | normal | 25 | 5 | species richness | |
| C | normal | 0.15 | 0.025 | connectance | |
| K li | uniform | (range 0.1–0.2) | (2.6) | producer i's half-saturation for nutrient l | |
(b) Predator–prey model
The population dynamics within these food webs follow a multi-species predator–prey model (Brose et al. 2005b, 2006b), where
| (2.1a) |
and
| (2.1b) |
describe changes in relative, dimensionless biomass densities of primary producer (equation (2.1a)) and consumer species (equation (2.1b)). In these equations, Bi is the biomass density of population i; ri is i's mass-specific maximum growth rate; Gi is i's nutrient-dependent growth rate (see §2c); xi is i's mass-specific metabolic rate; y is the maximum consumption rate of the consumers relative to their metabolic rate; and eji is j's assimilation efficiency when consuming population i. The functional response, Fij, describes the realized fraction of i's maximum rate of consumption achieved when consuming species j,
| (2.2) |
where ωij is the proportion (0–1) of i's maximum consumption rate targeted to consuming j (hereafter preference); B0 is the half-saturation density of i (B0=0.5); h is the Hill exponent that regulates the shape of the curve from Holling type II to Holling type III (Williams & Martinez 2004b; Rall et al. 2008); and c quantifies predator interference (Rall et al. 2008). The predator interference term in the denominator quantifies the degree to which individuals within population i interfere with one another's consumption activities, which reduces i's per capita consumption if c>0 (Beddington 1975; De Angelis et al. 1975). The functional response Fij can continuously vary between type II (h=1, c=0), type III (h=2, c=0), type II with predator interference (h=1, c=1) and type III with predator interference (h=2, c=1). I used two different types of preferences: (i) uniform preferences of consumers with n resources (ωij=1/n); that is, consumers do not have an active prey preference, but rather feed according to the relative biomasses of their prey species, or (ii) random preferences (randomly sampled from a uniform distribution for every consumer independently), where consumers have random preferences for their prey. Note that in both the cases, preferences sum to unity. The per unit biomass biological rates of production, R, metabolism, X, and maximum consumption, Y, follow negative-quarter power-law relationships with the species' body masses (Enquist et al. 1999; Brown et al. 2004),
| (2.3a) |
| (2.3b) |
| (2.3c) |
where ar, ax and ay are allometric constants; M is the average body mass of individuals within the population; and the subscripts C and P indicate consumer and producer parameters, respectively (Yodzis & Innes 1992). The time scale of the system is defined by normalizing the biological rates (2.3a)–(2.3c) to the mass-specific growth rate of the basal population. Then, the maximum consumption rates are normalized by the metabolic rates
| (2.4a) |
| (2.4b) |
| (2.4c) |
Inserting equations (2.4a)–(2.4c) into equations (2.1a) and (2.1b) yields a population dynamic model with allometrically scaled parameters. In food webs with constant predator–prey body-mass ratios, Z, the body masses of predators depend on trophic levels, T,
| (2.5) |
Knowledge of the trophic levels of the species from the binary feeding matrix predicted by the niche model (see §2a) allows the calculation of their body masses relative to the body mass of the producer species (equation (2.5)), which parametrizes the biological rates (equations (2.4a)–(2.4c)) of the consumer–resource model (equations (2.1a)–(2.1b)). I used the simplifying assumption that all the producer species are equally sized and the following constant model parameters: eij=0.85 for carnivores and eij=0.45 for herbivores; ax/ar=0.314 for invertebrates; and ax/ar=0.138 for producers (Brown et al. 2004; Savage et al. 2004; Brose et al. 2006b). For every simulation run, the Hill exponent, h, the predator-interference coefficient, c, the maximum ingestion rate, y, and the body-mass ratio, Z, were sampled from normal distributions (table 1).
(c) Producer–nutrient model
Consistent with previous studies (Brose et al. 2005a,b), the growth rate of the producer species follows a well-established nutrient-intake model,
| (2.6) |
that depends on the concentrations of two limiting nutrients Nl. This model has been widely used in theoretical plant ecology (Tilman 1982; Huisman & Weissing 1999) and successfully evaluated in experiments (Passarge et al. 2006). In equation (2.6), MIN is the minimum operator and Kli is species i's half-saturation density for nutrient l. Lower half-saturation densities define higher nutrient-intake efficiencies. Therefore, Gi(N) follows a Monod equation and is determined by the nutrient that is most limiting. The variation in the density of nutrient l is given by
| (2.7) |
where cli is the content of nutrient l in the biomass of species i. Nutrients are exchanged at a turnover rate D—i.e. expressed relative to time scale of the growth rate of the producer species—with a supply concentration of Sl, and removal depends on the current nutrient concentration in the system, Nl. Throughout all simulations, the turnover rate was kept constant (D=0.25), and the first nutrient is the one most needed by all the producer species as it has the highest content in their biomasses (c1i=1 and c2i=0.5). Since all the producer species have similar ri and xi, the half-saturation densities (K1i) for the first nutrient define the competitive hierarchy among the producers: the nutrient-intake efficiency decreases with the half-saturation density. The half-saturation densities of the producer species' growth, K1i, and the supply concentration of nutrient l, Sl, were varied randomly as independent simulation parameters (table 1).
(d) Simulations and analyses
The independent parameters of the model were randomly sampled from the normal or uniform distributions for each simulation run independently (table 1). Every individual simulation started with uniformly random biomass densities (0.05<Bi<1) and recorded the numbers of the persistent consumer and producer species (Bi>10−30) at the end of the time series (t=2000). The producer and consumer persistence equals the ratio between the final and initial producer species and the ratio between the final and initial consumer species, respectively. I characterized the initial food webs by the mean prey-averaged trophic level (Williams & Martinez 2004a) and omnivory (Williams & Martinez 2000). I omitted analyses of other structural food-web variables that are highly correlated with these two parameters (Dunne et al. 2004, 2005). Together with the independent simulation parameters (table 1), omnivory and the prey-averaged trophic level were entered in two independent classification and regression tree (CART) analyses (De'Ath & Fabricius 2000) to explain the variance in (i) producer persistence and (ii) consumer persistence. Regression trees explained variation in the dependent variables by repeatedly splitting the data into more homogeneous groups until additional splits did not increase the coefficient of variation by more than 1%. Unlike multiple linear regressions, regression trees are flexible analytical methods that are robust to non-normally distributed data, nonlinear relationships and high-order interactions (De'Ath & Fabricius 2000).
At the producer population level, I quantified the time averages (averaged over the second half of the time series) of the biomass, the nutrient intake (i.e. the amount of the first, most limiting nutrient that is on average consumed per time step) and the herbivory (i.e. the amount of the producer biomass that is on average consumed by all of its herbivores per time step) for each individual producer in the food-web simulations. To determine the effects of the local network structure (Brose et al. 2005b) on these dependent variables, I quantified the number of herbivores, their average vulnerability, their average generality, their average biomass, their average maximum consumption rate, y, and their average body mass for each producer species independently. These variables of the local network structure and the independent simulation parameters (table 1) were entered as explanatory variables in three independent CART analyses to explain the variance in (i) producer biomass, (ii) herbivory, and (iii) nutrient intake.
3. Results
(a) Producer coexistence and food-web persistence
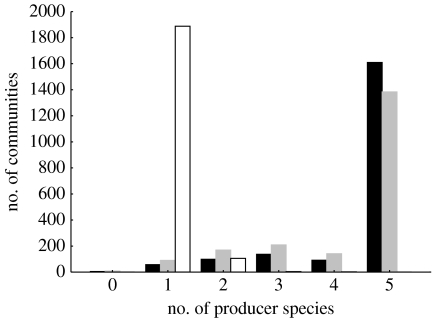
In 94.4% of the simulations of the five producer species communities, only one of the producer species was persistent, whereas the other four producer species were competitively excluded (figure 1). The coexistence of two (5.3% of the simulations), three (0.02%) or four (0.01%) producer species was rare, and coexistence of all the five producer species occurred in none of the simulated producer communities.
Figure 1.
Frequency distribution of the number of persistent producer species in simple producer communities (white bars) and complex food webs with random (black bars) or uniform (grey bars) preferences. Each of the three histograms is based on 2000 simulated communities that each initially contained five producer species.
By contrast, the coexistence of the five producer species was found in 69.2 and 80.5% of the food webs with uniform and random preferences, respectively (figure 1). Overall, the number of persistent producer species was significantly higher in the food webs with uniform or random preferences than in the producer communities (Mann–Whitney U-tests, p<0.001; figure 1). Some of the food webs simulated were unstable with low producer and consumer persistence. In the CART analyses, consumer persistence was the most important predictor variable of producer persistence (figure 2a). Consumer persistence was negatively influenced by the initial number of species in the food web and positively affected by the average predator–prey body-mass ratio across all consumers in the food web (figure 2b).
Figure 2.
CART analyses (see §2) identifying the main effects on (a) producer persistence and (b) consumer persistence. Bars indicate the proportional contribution of independent variables (see the y-axes) to the overall explained variance. Additional information is given by the signs of the effects and the number of splits that an independent variable contributed. Note that the signs of the effects were unambiguous for independent variables affecting multiple splits. The analyses were based on models with uniform preferences and similar results were obtained under random preferences (data not shown).
(b) Relative biomass densities of the producer species
In producer communities, the relative biomass densities of the producer species decrease significantly with their relative half-saturation densities for the most limiting nutrient (figure 3a). Here, efficient nutrient intake—indicated by low relative half-saturation densities—leads to dominance in producer biomass. In complex food webs, however, the relative biomass densities of the same producer species do not decrease with their relative half-saturation densities (figure 3b), indicating that nutrient-intake efficiencies do not determine producer biomass densities. Moreover, the relative biomass densities of producers in producer communities and complex food webs are not correlated (figure 3c). Given that food-web simulations were carried out with exactly the same producer species as the simulations of the producer communities, this shows that herbivory in complex food webs predominantly reduces the biomass densities of those producer species that dominated the biomass density in producer communities (figure 3d), which yields a more even biomass distribution across the producer species in complex food webs (figure 3c).
Figure 3.
Producer biomass in producer communities (without herbivores) and complex food webs: relationship between producer biomass and nutrient-intake inefficiency in (a) producer communities and (b) food webs; (c) relationship between producer biomasses in food webs and producer communities; (d) biomass difference depending on the biomass density in producer communities. The nutrient-intake inefficiency of a producer is the ratio between its nutrient half-saturation density and the average nutrient half-saturation density across all producers in the community. The biomass difference expresses the difference between the biomass densities in the food webs and the producer communities.
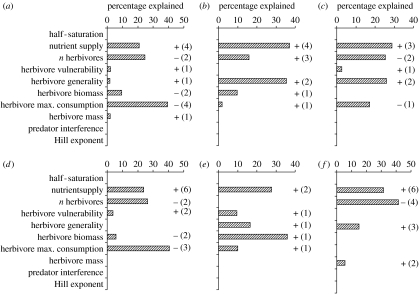
The subsequent CART analyses show which parameters influence producer biomasses in complex food webs. In food webs with uniform preferences, there is a strong positive effect of the nutrient supply on the producer biomass densities, whereas the number of herbivores and their maximum consumption rate exhibit strong negative effects (figure 4a). The strength of herbivory is mainly driven by the strong positive effects of the nutrient supply, the number of herbivores and their generality (figure 4b). The nutrient intake by the producer species increases with the nutrient supply and the herbivore generality, and it decreases with the number of herbivores and their maximum consumption rate (figure 4c). The analyses of food webs with random preferences yield qualitatively similar results (figure 4d–f). The relative half-saturation densities of the producer species that define their competitive hierarchy and the functional response parameters of the herbivores (i.e. the Hill exponent and the amount of predator interference) do not explain any variance in the nutrient intake or the relative biomass densities of the producer species (figure 4).
Figure 4.
CART analyses (see §2) identifying the main effects of various independent variables (see the y-axes) on (a,d) producer biomass, (b,e) the amount of herbivory and (c,f) the nutrient intake. Results are shown for models with (a–c) uniform or (d–f) random preferences. Bars indicate the proportional contribution of independent variables (see the y-axes) to the overall explained variance. Additional information is given by the signs of the effects and the number of splits that an independent variable contributed. Note that the signs of the effects were unambiguous for independent variables affecting multiple splits.
4. Discussion
Consistent with classic competition theory predictions that the producer species that is most efficient at acquiring a limiting nutrient should competitively exclude all the competing producer species (Tilman 1982), only one producer species persisted in 99.7% of the non-equilibrium simulations of the simple producer communities. Only in 0.03% of all simulated producer communities with two limiting resources, more than two producer species coexisted. In models of homogeneous, well-mixed communities such as those modelled here, the number of coexisting producer species can exceed the number of limiting resources if chaotic population dynamics prevent competitive exclusion (Armstrong & McGehee 1980; Huisman & Weissing 1999). Consistent with previous model results (Huisman et al. 2001), I found that this rarely occurred when the nutrient-intake efficiencies are randomly distributed among the producer species even though most producer communities initially exhibited chaotic dynamics before reduced by competitive exclusion. In the same vein, recent experiments have demonstrated that random mixtures of phytoplankton species generally lead to competitive exclusion and survival of the best competitor (Passarge et al. 2006). Together, these theoretical and empirical findings provide compelling evidence that competitive exclusion prevents coexistence in simple, spatially and temporally well-mixed producer communities.
Subsequently, I addressed the question of whether the top-down effects can mediate coexistence when the producer species are embedded in complex food webs. Interestingly, the number of coexisting producer species exceeded the number of limiting nutrients in 86.7 and 91.9% of all food webs with uniform and random preferences, respectively. These food-web simulations were carried out with exactly the same producer species as the analyses of the simple producer communities, suggesting that only herbivory can account for the differences in the number of persistent producer species. In simple producer communities, the nutrient half-saturation densities of the producers determine their nutrient-intake rates, and the producer with the lowest half-saturation density increases in biomass until it competitively excludes all other producers. In complex food webs, however, herbivory prevents increasing biomass dominance of the dominant over the inferior producer species and competitive exclusion in most food webs. A comparison of biomasses illustrates that herbivory has a disproportionally strong effect on producers that are competitively dominant in producer communities. Consistent with the empirical data from dune succession series (Neutel et al. 2007), increasing biomass densities at low trophic levels are balanced by increasing biomass fluxes to upper trophic levels to provide coexistence of producers.
In contrast to most prior studies of simple herbivore–producer–nutrient modules (Holt et al. 1994; Leibold 1996; Grover & Holt 1998), coexistence of the producer species in the more complex webs modelled here does not require a trade-off among the producer species between nutrient-intake efficiency (here, the nutrient half-saturation densities of the producers) and any a priori established resistance to herbivory (e.g. inverse of the number of herbivores or inverse of herbivores' maximum consumption rates). Moreover, these indicators of a priori resistance to herbivory are uncorrelated with the nutrient-intake efficiencies in the final persistent food webs (Pearson's product-moment correlations: r<0.009, p>0.28), which show that no trade-offs randomly emerged. Instead, producer coexistence depends on consumer persistence in complex food webs. These analyses of a model with explicit nutrient dynamics support prior studies of food webs with logistically growing producer species (Brose et al. 2006b; Otto et al. 2007; Rall et al. 2008), showing that food-web persistence is promoted by high predator–prey body-mass ratios that are consistent with those found in empirical food webs (Brose et al. 2006a). Surprisingly, consumer and producer coexistence emerges here in models with a competitive hierarchy among the producers that lead to competitive exclusion in simple producer communities. Despite the lack of trade-off between nutrient-intake efficiency and a priori resistance to herbivory, this suggests that the balance between herbivory and producer biomass in complex food webs prevents competitive exclusion.
Subsequently, I studied which model parameters are responsible for this balance between herbivory and producer biomass. The Monte Carlo approach I used generated random variation in the local network structure (e.g. the number and generality of a producer's herbivores) as well as in herbivore consumption and nutrient-intake parameters. The results corroborate empirical work (Menge 1992; Gurevitch et al. 2000; Chase et al. 2002), showing that both top-down (i.e. the number of herbivores and the sum of their per capita consumption rates) and bottom-up (i.e. the nutrient supply rate) forces work together to regulate basal species biomasses. Surprisingly, the nutrient half-saturation densities of the producers—that define their competitive hierarchy and determine their relative biomasses in producer communities—do not affect their relative biomasses in food webs. Similarly, herbivory traits (e.g. functional response parameters) do not influence producer biomass.
Consistent with empirical work (Menge et al. 1997, 2003, 2004), the intensity of herbivory increases with bottom-up supply (here, nutrient supply), suggesting a strong feedback mechanism regulating producer biomass. Such strong negative feedback loops stabilize ecological communities, because the producer species depress their own per capita growth via herbivory more than they depress the per capita growth of other producer species via competition (Chesson 2000). Here, these negative feedback loops mediate the coexistence of multiple producer species on two limiting nutrients without requiring keystone predators that preferentially or exclusively feed on the competitive dominant producer species (Brose et al. 2005b). The strength of this interaction between nutrient supply and herbivory intensity also increases with the average generality of the herbivores. Generalist herbivores have higher time-averaged biomass consumption rates than specialist herbivores, which increase the biomass flow from producers to herbivores, but also enable producer coexistence. This is mechanistically similar to a subsidy effect to the generalist consumers that can maintain high biomass densities and high consumption rates even if one of their prey becomes rare—as long as alternative prey are sufficiently abundant (Polis & Strong 1996).
Generally, one would expect that factors increasing the herbivorous top-down pressure reduce the producer biomasses and the nutrient intake, whereas factors that increase the nutrient intake should have positive bottom-up effects on the producer biomass and the herbivory. The effects of the number of herbivores, their maximum consumption rates, their biomass densities and the nutrient supply are consistent with this expectation. However, the generality of herbivores increases both herbivory and nutrient intake. This counter-intuitive finding is due to the fact that herbivore generality decreases the per capita effects of the herbivores (per capita effects∼1/the number of producer consumed), which primarily yields higher producer biomasses. Subsequently, these increased producer biomasses cause higher rates of nutrient intake and total herbivory.
The model presented here assumes consumers with saturating, nonlinear functional responses that dominate among empirical herbivore–plant interactions (Jeschke et al. 2004). Interestingly, the results of models with uniform or random prey preferences were consistent, suggesting the broad generality of the pattern documented here. However, adaptive herbivore functional responses (Beckerman 2005) were not included in the present study. Most likely, the adaptive evolution of preferences towards the most abundant prey would increase food-web stability (Kondoh 2006), maintain the network structure (Uchida et al. 2007) and yield even stronger responses of the biomass fluxes to biomass increases of plants. Together, these effects should strengthen the stabilizing effects of herbivory on the coexistence of producer guilds that are embedded in complex food webs.
The model presented here helps elucidate how the interplay between top-down characteristics of complex food webs and bottom-up nutrient supply determines the coexistence and biomasses of the producer species with a competitive hierarchy. The negative feedback effects of herbivory in response to increasing the nutrient intake prevent biomass dominance among producers and maintain their coexistence. Moreover, by linking food-web structure, predator–prey dynamics and producer–nutrient interactions, the model presented here can be used as a bridge between competition (Tilman 1982) and food-web theory (Brose et al. 2006b). In addition to providing an insight to how producer guilds may overcome competitive exclusion, integration of these previously disparate fields allows research on how complex communities respond to enrichment (Rall et al. 2008) and determine ecosystem processes (Thebault & Loreau 2003).
Acknowledgments
I thank Eric Berlow for his statistical advice and many helpful suggestions, Neo Martinez for his stimulating discussions, Rich Williams for his contributions to simulation programs, and Stefan Scheu and Björn Rall for their comments. Financial support has been provided by the German Research Foundation (Emmy-Noether program, BR 2315/1-1,2,3; BR 2315/4-1).
References
- Armstrong R.A, McGehee R. Competitive exclusion. Am. Nat. 1980;115:151–170. doi: 10.1086/283553. [DOI] [Google Scholar]
- Beckerman A.P. The shape of things eaten: the functional response of herbivores foraging adaptively. Oikos. 2005;110:591–601. doi: 10.1111/j.0030-1299.2005.13546.x. [DOI] [Google Scholar]
- Beddington J.R. Mutual interference between parasites or predators and its effect on searching efficiency. J. Anim. Ecol. 1975;44:331–340. doi: 10.2307/3866. [DOI] [Google Scholar]
- Brose U, Berlow E.L, Martinez N.D. From food webs to ecological networks: linking non-linear trophic interactions with nutrient competition. In: De Ruiter P, Moore J.C, Wolters V, editors. Dynamic food webs: multispecies assemblages, ecosystem development, and environmental change. Elsevier/Academic Press; San Diego, CA: 2005a. pp. 27–36. [Google Scholar]
- Brose U, Berlow E.L, Martinez N.D. Scaling up keystone effects from simple to complex ecological networks. Ecol. Lett. 2005b;8:1317–1325. doi: 10.1111/j.1461-0248.2005.00838.x. [DOI] [Google Scholar]
- Brose U, et al. Consumer–resource body-size relationships in natural food webs. Ecology. 2006a;87:2411–2417. doi: 10.1890/0012-9658(2006)87[2411:CBRINF]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- Brose U, Williams R.J, Martinez N.D. Allometric scaling enhances stability in complex food webs. Ecol. Lett. 2006b;9:1228–1236. doi: 10.1111/j.1461-0248.2006.00978.x. [DOI] [PubMed] [Google Scholar]
- Brown J.H, Gillooly J.F, Allen A.P, Savage V.M, West G.B. Toward a metabolic theory of ecology. Ecology. 2004;85:1771–1789. doi: 10.1890/03-9000. [DOI] [Google Scholar]
- Chase J.M, Leibold M.A, Simms E. Plant tolerance and resistance in food webs: community-level predictions and evolutionary implications. Evol. Ecol. 2000;14:289–314. doi: 10.1023/A:1010983611618. [DOI] [Google Scholar]
- Chase J.M, Abrams P.A, Grover J.P, Diehl S, Chesson P, Holt R.D, Richards S.A, Nisbet R.M, Case T.J. The interaction between predation and competition: a review and synthesis. Ecol. Lett. 2002;5:302–315. doi: 10.1046/j.1461-0248.2002.00315.x. [DOI] [Google Scholar]
- Chesson P. Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 2000;31:343–366. doi: 10.1146/annurev.ecolsys.31.1.343. [DOI] [Google Scholar]
- De'Ath G, Fabricius K.E. Classification and regression trees: a powerful yet simple technique for ecological data analysis. Ecology. 2000;81:3178–3192. doi: 10.2307/177409. [DOI] [Google Scholar]
- De Angelis D.L, Goldstein R.A, O'Neill R.V. A model for trophic interactions. Ecology. 1975;56:881–892. doi: 10.2307/1936298. [DOI] [Google Scholar]
- De Ruiter P, Neutel A.-M, Moore J.C. Energetics, patterns of interaction strengths, and stability in real ecosystems. Science. 1995;269:1257–1260. doi: 10.1126/science.269.5228.1257. [DOI] [PubMed] [Google Scholar]
- Dunne J.A, Williams R.J, Martinez N.D. Network structure and robustness of marine food webs. Mar. Ecol. Prog. Ser. 2004;273:291–302. doi: 10.3354/meps273291. [DOI] [Google Scholar]
- Dunne J.A, Brose U, Williams R.J, Martinez N.D. Modeling food web dynamics: complexity–stability implications. In: Belgrano A, Scharler U.M, Dunne J.A, Ulanowicz R.E, editors. Aquatic food webs. Oxford University Press; New York, NY: 2005. pp. 117–129. [Google Scholar]
- Emmerson M.C, Raffaelli D. Predator–prey body size, interaction strength and the stability of a real food web. J. Anim. Ecol. 2004;73:399–409. doi: 10.1111/j.0021-8790.2004.00818.x. [DOI] [Google Scholar]
- Enquist B.J, West G.B, Charnov E.L, Brown J.H. Allometric scaling of production and life-history variation in vascular plants. Nature. 1999;401:907–911. doi: 10.1038/44819. [DOI] [Google Scholar]
- Grover J.P, Holt R.D. Disentangling resource and apparent competition: realistic models for plant–herbivore communities. J. Theor. Biol. 1998;191:353–376. doi: 10.1006/jtbi.1997.0562. [DOI] [Google Scholar]
- Gurevitch J, Morrison J.A, Hedges L.V. The interaction between competition and predation: a meta-analysis of field experiments. Am. Nat. 2000;155:435–453. doi: 10.1086/303337. [DOI] [PubMed] [Google Scholar]
- Holt R.D, Grover H, Tilman D. Simple rules for interspecific dominance in systems with exploitative and apparent competition. Am. Nat. 1994;144:741–771. doi: 10.1086/285705. [DOI] [Google Scholar]
- Huisman J, Weissing F.J. Biodiversity of plankton by species oscillations and chaos. Nature. 1999;402:407–410. doi: 10.1038/46540. [DOI] [Google Scholar]
- Huisman J, Johansson A.M, Folmer E.O, Weissing F.J. Towards a solution of the plankton paradox: the importance of physiology and life history. Ecol. Lett. 2001;4:408–411. doi: 10.1046/j.1461-0248.2001.00256.x. [DOI] [Google Scholar]
- Hulot F.D, Loreau M. Nutrient-limited food webs with up to three trophic levels: feasibility, stability, assembly rules, and effects of nutrient enrichment. Theor. Popul. Biol. 2006;69:48–66. doi: 10.1016/j.tpb.2005.08.005. [DOI] [PubMed] [Google Scholar]
- Janzen D.H. Herbivores and number of tree species in tropical forests. Am. Nat. 1970;104:501–529. doi: 10.1086/282687. [DOI] [Google Scholar]
- Jeschke J.M, Kopp M, Tollrian R. Consumer-food systems: why type I functional responses are exclusive to filter feeders. Biol. Rev. 2004;79:337–349. doi: 10.1017/S1464793103006286. [DOI] [PubMed] [Google Scholar]
- Kondoh M. Does foraging adaptation create the positive complexity–stability relationship in realistic food-web structure? J. Theor. Biol. 2006;238:646–651. doi: 10.1016/j.jtbi.2005.06.028. [DOI] [PubMed] [Google Scholar]
- Leibold M.A. A graphical model of keystone predators in food webs: trophic regulation of abundance, incidence, and diversity patterns in communities. Am. Nat. 1996;147:784–812. doi: 10.1086/285879. [DOI] [Google Scholar]
- Menge B.A. Community regulation: under what conditions are bottom-up factors important on rocky shores? Ecology. 1992;73:755–765. doi: 10.2307/1940155. [DOI] [Google Scholar]
- Menge B.A, Daley B.A, Wheeler P.A, Dahlhoff E.P, Sanford E, Strub P.T. Benthic-pelagic links and rocky intertidal communities: bottom-up effects on top-down control? Proc. Natl Acad. Sci. USA. 1997;94:14 530–14 535. doi: 10.1073/pnas.94.26.14530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menge B.A, et al. Coastal oceanography sets the pace of rocky intertidal community dynamics. Proc. Natl Acad. Sci. USA. 2003;100:12 229–12 234. doi: 10.1073/pnas.1534875100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menge B.A, et al. Species interaction strength: testing model predictions along an upwelling gradient. Ecol. Monogr. 2004;74:663–684. doi: 10.1890/03-4060. [DOI] [Google Scholar]
- Neutel A.M, Heesterbeek J.A.P, van de Koppel J, Hoenderboom G, Vos A, Kaldeway C, Berendse F, de Ruiter P.C. Reconciling complexity with stability in naturally assembling food webs. Nature. 2007;449:599–602. doi: 10.1038/nature06154. [DOI] [PubMed] [Google Scholar]
- Otto S.B, Rall B.C, Brose U. Allometric degree distributions facilitate food-web stability. Nature. 2007;450:1226–1229. doi: 10.1038/nature06359. [DOI] [PubMed] [Google Scholar]
- Paine R.T. Food webs, linkage interaction strength, and community infrastructure. J. Anim. Ecol. 1980;49:667–685. [Google Scholar]
- Passarge J, Hol S, Escher M, Huisman J. Competition for nutrients and light: stable coexistence, alternative stable states, or competitive exclusion? Ecol. Monogr. 2006;76:57–72. doi: 10.1890/04-1824. [DOI] [Google Scholar]
- Polis G.A, Strong D.R. Food web complexity and community dynamics. Am. Nat. 1996;147:813–846. doi: 10.1086/285880. [DOI] [Google Scholar]
- Rall B.C, Guill C, Brose U. Food-web connectance and predator interference dampen the paradox of enrichment. Oikos. 2008;117:202–213. doi: 10.1111/j.2007.0030-1299.15491.x. [DOI] [Google Scholar]
- Savage V.M, Gillooly J.F, Woodruff W.H, West G.B, Allen A.P, Enquist B.J, Brown J.H. The predominance of quarter-power scaling in biology. Funct. Ecol. 2004;18:257–282. doi: 10.1111/j.0269-8463.2004.00856.x. [DOI] [Google Scholar]
- Thebault E, Loreau M. Food-web constraints on biodiversity–ecosystem functioning relationships. Proc. Natl Acad. Sci. USA. 2003;100:14 949–14 954. doi: 10.1073/pnas.2434847100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilman D. Princeton University Press; Princeton, NJ: 1982. Resource competition and community structure. [PubMed] [Google Scholar]
- Uchida S, Drossel B, Brose U. The structure of food webs with adaptive behaviour. Ecol. Model. 2007;206:263–276. doi: 10.1016/j.ecolmodel.2007.03.035. [DOI] [Google Scholar]
- Williams R.J, Martinez N.D. Simple rules yield complex food webs. Nature. 2000;404:180–183. doi: 10.1038/35006555. [DOI] [PubMed] [Google Scholar]
- Williams R.J, Martinez N.D. Limits to trophic levels and omnivory in complex food webs: theory and data. Am. Nat. 2004a;163:458–468. doi: 10.1086/381964. [DOI] [PubMed] [Google Scholar]
- Williams R.J, Martinez N.D. Stabilization of chaotic and non-permanent food web dynamics. Eur. Phys. J. B. 2004b;38:297–303. doi: 10.1140/epjb/e2004-00122-1. [DOI] [Google Scholar]
- Williams R.J, Martinez N.D. Success and its limits among structural models of complex food webs. J. Anim. Ecol. 2008;77:512–519. doi: 10.1111/j.1365-2656.2008.01362.x. [DOI] [PubMed] [Google Scholar]
- Yodzis P, Innes S. Body size and consumer–resource dynamics. Am. Nat. 1992;139:1151–1175. doi: 10.1086/285380. [DOI] [Google Scholar]