Does face image statistics predict a preferred spatial frequency for human face processing?

Abstract

Psychophysical experiments suggested a relative importance of a narrow band of spatial frequencies for recognition of face identity in humans. There exists, however, no conclusive evidence of why it is that such frequencies are preferred. To address this question, I examined the amplitude spectra of a large number of face images and observed that face spectra generally fall off more steeply with spatial frequency compared with ordinary natural images. When external face features (such as hair) are suppressed, then whitening of the corresponding mean amplitude spectra revealed higher response amplitudes at those spatial frequencies which are deemed important for processing face identity. The results presented here therefore provide support for that face processing characteristics match corresponding stimulus properties.

1. Introduction

It has been suggested that the processing of sensory information in the brain has adapted to the specific signal statistics of stimuli (Barlow 1989). Such stimulus-specific adaptation is tantamount to taking advantage of statistical regularities in order to encode the highest possible amount of information about the signal (Attneave 1954; Linsker 1988; Baddeley et al. 1998; Nadal et al. 1998; Wainwright 1999) under various constraints. The constraints include, for example, minimizing energy expenditure (Levy & Baxter 1996; Laughlin et al. 1998; Lenny 2003), minimizing wiring costs between processing units (Laughlin & Sejnowski 2003) or reducing spatial and temporal redundancies in the input signal (Attneave 1954; Barlow 1961; Srinivasan et al. 1982; Atick & Redlich 1992; Hosoya et al. 2005).

In the case of visual stimuli, natural images reveal a statistical regularity that corresponds to an approximately linear decrease of their amplitude spectra as a function of spatial frequency when scaling both coordinate axes logarithmically (Burton & Moorhead 1987; Field 1987). This property is equivalent to strong pairwise correlations between pairs of luminance values (Wiener 1964). It has been proposed that visual neurons use this statistical property in a way that cells tuned to different spatial frequencies have equal sensitivities (Field 1987). Thus, neurons tuned to high spatial frequencies should increase their response gain such that they achieve the same response levels as low frequency neurons. This is the response equalization hypothesis (which should be distinguished from the decorrelation hypothesis; Srinivasan et al. 1982; Atick & Redlich 1992; Graham et al. 2006). Response equalization (‘whitening’) may enhance the information throughput from one neuronal stage to another by adjusting the output of one stage such that it matches the limited dynamic range of the successive stage (Graham et al. 2006).

The present article unveils a link between statistical properties of face images and psychophysical data for the processing of face identity. The processing of face identity was found to preferably depend on a narrow spatial frequency band (approx. 2 octaves) from 8 to 16 cycles per face (Tieger & Ganz 1979; Fiorentini et al. 1983; Hayes et al. 1986; Costen et al. 1994, 1996; Peli et al. 1994; Näsänen 1999; Ojanpää & Näsänen 2003). However, to the best of my knowledge, no explanation has yet been offered of why it is that face processing mechanisms in the human brain reveal such a preference.

Here I analysed the amplitude spectra of a large number of face images. Different types of amplitude spectra were considered—with and without suppression of external face features (hair, shoulders, etc.). The spectra were whitened (i.e. ‘response’-equalized) according to three different procedures. In this way, it is demonstrated that the main results are largely independent of the specific method that was used for whitening: amplitudes were higher at spatial frequencies at approximately 10 cycles per face—but only in those spectra where external face features were suppressed. Therefore, the effect must have been produced by internal face features (eyes, mouth and nose).

2. Material and methods

(a) Face images

We used 868 female and 868 male face images from the face recognition grand challenge database (FRGC, http://www.frvt.org/frgc or www.bee-biometrics.org; see electronic supplementary material, figure 5). Original images (1704×2272 pixels, 24-bit true colour) were adjusted for horizontal alignment of the eyes, before they were downsampled to 256×256 pixels and converted into 8-bit greyscale. Subsequently, the positions of the left eye, the right eye and the mouth ((x_le, y_le), (x_re, y_re) and (x_mouth, y_mouth), respectively) were manually marked by two persons (M.S.K. and E.C.) with an ad hoc programmed graphical interface. The position of each face centre (approx. the nose) was approximated as x_nose=rnd((x_le+x_re)/4+x_mouth/2) and y_nose=rnd[0.95×rnd(y_le+(y_mouth−(y_le+y_re)/2)/2), where rnd(·) denotes rounding to the nearest integer value.

(b) Dimension of spatial frequency

For conversion of spatial frequency units, face dimensions were manually marked with an ad hoc programmed graphical interface. The factors for multiplying cycles per image to obtain cycles per face width were 0.41±0.013 (females, n=868) and 0.43±0.012 (males, n=868). Corresponding factors for obtaining ‘cycles per face height’ were 0.46±0.021 (females) and 0.47±0.018 (males). Conversion factors at oblique orientations were calculated under the assumption that horizontal and vertical conversion factors define the two main axes of an ellipse. Pooling of results over gender also implied a corresponding averaging of conversion factors and the factors for width and height were averaged in the isotropic case.

(c) Amplitude spectra

Let the features that are not part of the actual face be denoted by external features (e.g. shoulder region or hair). On the other hand, internal features refer to the eyes, the mouth and the nose. The presence of external features in our face images influences in their amplitude spectra, and may cause truncation artefacts. It is thus desirable to compare results with and without the presence of external features. A good suppression of external features could be achieved by centring a minimum four-term Blackman–Harris (B.H.) window (Harris 1978) at (x_nose, y_nose) (see electronic supplementary material, figures 8 and 9). Nevertheless, application of the window leaves a characteristic fingerprint in each spectrum (see electronic supplementary material, figure 6a). This artificial fingerprint, as well as the spurious lines caused by truncation, could be attenuated with a correction procedure based on a spatially varying diffusion mechanism (outlined below). Thus, for each face image, originally four types of amplitude spectra were considered: the original raw spectrum, the B.H. spectrum, and their respective corrected versions (i.e. corr. raw and corr. B.H.).

(d) Correction of amplitude spectra

Let P∈{0,1}^n×n be a binary n×n matrix of the same size as the two-dimensional amplitude spectra $\mathcal{A}$. In P, artefacts are represented by ones, while all other positions are set to zero. Thus, P is set to the image for correcting the B.H. spectrum and the raw spectrum as shown in figure 6b,c, respectively, in the electronic supplementary material. The idea of the correction algorithm consists in simply averaging out the positions with artefacts. To this end, information from neighbouring positions flows into artefact positions. This process is called inward diffusion. Let $\mathcal{X}$(t) be a sequence of corrected amplitude spectra parametrized over time t, with the initial condition $\mathcal{X}$(0)≡$\mathcal{A}$. Inward diffusion is defined by $\mathrm{\partial }{\mathcal{X}}_{ij}/\mathrm{\partial }t=P_{ij}{\nabla }^2{\mathcal{X}}_{ij}$, where (i, j) denotes matrix positions. The diffusion process was terminated at the moment when the correlation difference c(t)−c(t+Δt) was smaller than 0.001 or when a maximum of 100 iterations was reached.

(e) Slopes of amplitude spectra

(i) Isotropic slopes α

Amplitudes associated with a given spatial frequency lie on a circle. This is to say that when representing the spectrum with polar coordinates, then spatial frequencies vary along the radial coordinate, but stay constant while varying orientation. An isotropic amplitude spectra is obtained by averaging all amplitudes with a fixed spatial frequency across orientations (i.e. for each circle, the mean value of all amplitudes of the circle was computed). Because the logarithmized amplitude spectra of face images fall approximately linear as a function of log frequency, a line with slope α could be fitted to the isotropic spectra. Although, in principle, amplitude data were available from k=1 to 127 cycles per image, only the interval from k_min=8 to k_max=100 was used for line fitting. I used the function ‘robustfit’ (linear regression with low sensitivity to outliers) provided with Matlab's statistical toolbox (Matlab v. 7.1.0.183 R14 SP3, Statistical Toolbox v. 5.1, see www.mathworks.com).

(ii) Oriented spectral slopes α(Θ)

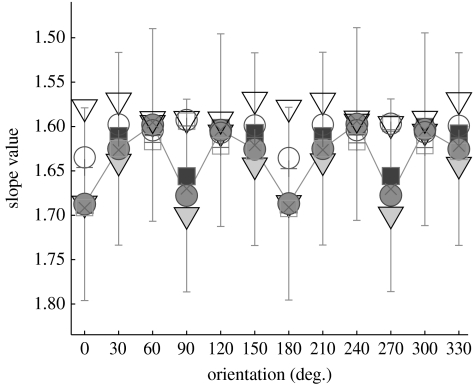
Each two-dimensional amplitude spectrum was subdivided into 12 ‘pie slices’ (each with ΔΘ=30°). For each pie slice with orientation Θ, an (oriented) isotropic one-dimensional spectrum was analogously computed as just described (with amplitudes being averaged across arcs) and subsequently a line with slope α(Θ) was fitted (figure 2).

Figure 2.

Oriented spectral slopes. The curves juxtapose oriented spectral slopes from corrected raw (‘corr. raw’) spectra and corrected B.H.-windowed (‘corr. B.H.’) spectra (robust fit). Slopes were computed from the respective averaged spectra, with angular increments of 30° (van der Schaaf & van Hateren 1996). Error bars denote ±1 s.d. (estimated using robust statistics). Uncorrected spectra show similar dependencies of slopes from orientation. Note that the slope values are defined modulus 180°. Solid lines, s.d. corr. B.H. (m+f); filled squares, mean corr. B.H. (m); filled triangles, mean corr. B.H. (f); filled circles, mean corr. B.H. (m+f); open squares, mean corr. raw (m); open triangles, mean corr. raw (f); open circles, mean corr. raw (m+f); pluses, median corr. raw (m+f); crosses, median corr. B.H. (m+f).

(f) Slope whitening of amplitude spectra

This algorithm proceeds in straight analogy to whitening of the isotropic spectra. Let α be the isotropic slope value corresponding to a two-dimensional amplitude spectrum $\mathcal{A}$(k_x, k_y) with spatial frequency coordinates k_x, k_y∈[1,127] cycles per image. Let $k=\sqrt{k_x^2+k_y^2}$ (radial spatial frequency). Then, the corresponding whitened spectrum $\mathcal{W}$ is defined as $\mathcal{W}$(k_x, k_y)=$\mathcal{A}$(k_x, k_y)·k^|α|. Qualitatively, the $\mathcal{W}$ were not different from a more advanced procedure that consisted in subdividing $\mathcal{A}$ into oriented pie slices and whitening each with its corresponding oriented slope value α(Θ). Therefore, only those results are presented where $\mathcal{A}$ was whitened with an isotropic slope value (the term ‘isotropic’ in the headline of the spectra in figure 4 and electronic supplementary material, figure 15 indicates just this).

Figure 4.

Two-dimensional whitening. (a) Slope whitening of the mean corrected B.H. spectra unveiled clear maxima at horizontal feature orientations (marked by a white box). Here, the female data are shown (for male data see electronic supplementary material, figure 15). (b) The curves show the amplitudes at the location demarcated by the white box in the spectrum: green circles are the logarithmized amplitudes without whitening; amplitudes whitened ‘by slope’ are shown in light grey, ‘by variance’ in mid grey and ‘by diffusion’ in dark grey (see §2 for further details on the three whitening procedures). The important result here is that whitened amplitudes reveal distinct maxima irrespective of the specific whitening method at approximately 10–15 cycles per face height. The variance-whitened spectra are shown in electronic supplementary material, figure 16.

(g) Whitening by variance

Amplitudes in the spectrum $\mathcal{A}$(k_x, k_y) with equal spatial frequencies lie on a circle with radius $k=\sqrt{k_x^2+k_y^2}$. Let n_k be the number of points on this circle (n_k monotonically increases as a function of k). Let $\mathcal{A}$(k, Θ) be the spectrum in polar coordinates. Then, we first average, for each k, all amplitudes across orientations according to $\mu (k)={\sum }_{\Theta }\mathcal{A}(k,\Theta )/n_k$. The variance is subsequently computed as ${\sigma }^2(k)={\sum }_{\Theta }{(\mathcal{A}(k,\Theta )-\mu )}^2/(n_k-1)$. Finally, the variance-whitened spectrum is defined as $\mathcal{V}$=$\mathcal{A}$/(σ²(k)+ϵ) with a small positive constant ϵ≪1. Examples of $\mathcal{V}$ are shown in electronic supplementary material, figure 16.

(h) Whitening by diffusion

Let $\mathcal{X}$(k_x, k_y, t) a sequence of amplitude spectra parametrized over time t, with the initial condition $\mathcal{X}$(k_x, k_y, 0)≡$\mathcal{A}$(k_x, k_y). For t>0, the $\mathcal{X}$ are defined according to the diffusion equation $\mathrm{\partial }\mathcal{X}/\mathrm{\partial }t={\nabla }^2\mathcal{X}$. The whitened spectrum then is $\mathcal{D}$≡$\mathcal{A}$/(1+$\mathcal{X}$(t_max)) at precisely the instant t_max when the Shannon entropy of $\mathcal{D}$ is maximal.

3. Results

(a) Amplitude spectra

Amplitude spectra are best conceived in polar coordinates, where the spatial frequency k varies proportional to radius. Thus, spectral amplitudes that have the same spatial frequency lie on a circle. The two-dimensional spectrum can be collapsed into a one-dimensional isotropic spectrum for each k by averaging all amplitudes on that circle. This means that in an isotropic spectrum any orientation dependence on the amplitudes is lost.

The amplitude spectra of natural images were found to depend on spatial frequency as ∝k^α, with an average (isotropic) spectral slope α≈−1 (Burton & Moorhead 1987; Field 1987).

How do the amplitude spectra of face images compare to this finding? To answer, I computed slopes of the amplitude spectra of 868 female and 868 male face images (size 256×256, samples are shown in electronic supplementary material, figure 5). In a double-logarithmic representation, these spectra also decreased approximately linear as a function of spatial frequency (figure 1). Therefore, a line with (spectral) slope α could be fitted to each spectrum. Four different types of amplitude spectra were considered for each face image (with different α; see table 1 and §2).

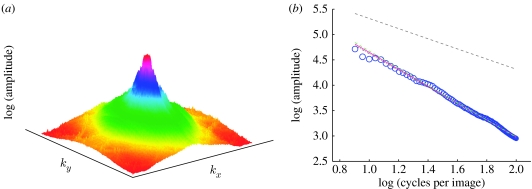
Figure 1.

Corrected B.H. spectrum (females). (a) Logarithmized, mean amplitude spectrum of all female face images. Prior to computing individual spectra, a B.H. window was applied to each face image in order to suppress external face features (see electronic supplementary material, figure 8d). The application of the B.H. window, however, leaves an undesired spectral ‘fingerprint’ in each of the spectra (see electronic supplementary material, figure 6a), which was attenuated before averaging (see electronic supplementary material, figure 7). (b) The two-dimensional spectrum shown in (a) is transformed into a one-dimensional isotropic spectrum by averaging all amplitudes with different orientations at a fixed frequency k (blue circles, female data). The size of each circle is proportional to the standard deviation (s.d.). The maximum s.d. (biggest circle) was 9186.75 (39.3%) and the minimum s.d. (smallest circle) was 252.67 (28.08%). Notice that in the supplementary material (e≡α). For comparison, the typical slope of natural images (α=−1) is also shown as a grey dashed line. The grey dot-dashed line shows the result of an ordinary linear regression (least-square fit) for computing slopes (α=1.63; notice that this line is practically hidden behind the pink line. Since linear regression is sensitive to outliers, slope values were additionally computed with an outlier-insensitive (robust; pink line, α=−1.67) algorithm. Finally, the slope for the uncorrected amplitude spectrum is also indicated (green line, α=1.7). Further spectra are shown in electronic supplementary material, figures 12–14.

Table 1.

For each gender, the table shows the average slope values for the four types of amplitude spectra. (Two possibilities for computing these values were considered: slopes means that individual slope values were averaged (each gender n=868, cf. electronic supplementary material, figures 10 and 11), and spectra refers to the slope of the average spectrum as illustrated with figure 1a (as well as in electronic supplementary material, figures 12–14).)

gender	averaging of	raw	corrected raw	B.H.	corrected B.H.
female	slopes	−1.608±0.0858	−1.604±0.0870	−1.686±0.0698	−1.654±0.0731
	spectra	−1.584	−1.579	−1.701	−1.668
male	slopes	−1.649±0.0738	−1.645±0.0757	−1.673±0.0785	−1.642±0.0895
	spectra	−1.644	−1.637	−1.689	−1.658

At first the spectra of the original images were computed (‘raw’). The second type of spectrum is defined by attenuating in each spectrum the truncation artefacts (‘corr. raw’; see electronic supplementary material, figures 6c and 7). These artefacts are a consequence of the cropped shoulder region being displayed in each image besides the actual face (see electronic supplementary material, figure 5). To smoothly strip off external face features (like the hair, i.e. anything but the actual face), a B.H. window was applied to each image prior to computing its spectrum (‘B.H.’; see electronic supplementary material, figure 8d). Because application of the B.H. window leaves a faint but characteristic spectral fingerprint (see electronic supplementary material, figure 6a), a further spectrum type (‘corr. B.H.’) was considered, with the artificial fingerprint being attenuated.

The mean isotropic slope values were computed in two ways. First, the spectral slope of each face image was computed, and individual slope values were averaged (label ‘slopes’ in table 1). Second, an average spectrum is computed at first, which is composed of all individual spectra (figure 1). The second slope value corresponds then to the slope of the average spectrum (label ‘spectra’ in table 1). Isotropic slope values are situated approximately at −1.6, with minima and maxima of −2.014 and −1.180 (females), respectively, and −1.994 and −1.007 (males).

Note that the standard deviations associated with the slopes of arbitrary natural images are usually bigger (Tolhurst et al. 1992; van der Schaaf & van Hateren 1996), as there is no restriction on displayed content and scale, respectively (Torralba & Oliva 2003).

Usually, α varies also as a function of orientation Θ (Switkes et al. 1978; van der Schaaf & van Hateren 1996). The orientation dependence is illustrated by means of the averaged corrected spectra (figure 2). Minimum slope values are located at 0° (wavevector pointing to east) and 90° (north), respectively, whereas maxima tend to be at oblique orientations. Slope values of the B.H. spectra vary more than with the raw spectra. As external features are widely suppressed in the B.H. spectra, minimum slopes are associated with the orientations of the internal face features (0°, 180°: nose; 90°, 270°: eyes, mouth and the bottom termination of the nose).

Summarizing so far, the majority of the individual α for face images is more negative than the theoretically predicted lower bound of −1.5 for natural images (Balboa & Grzywacz 2001; table 1; see electronic supplementary material, figures 10 and 11). Similar observations also hold for spectral slopes of the mean amplitude spectra (figure 1; see electronic supplementary material, figures 12–14). This should not come as a surprise since the structure of face images is different from natural images: face images are not composed of self-occluding, constant intensity surface patches (Ruderman 1997; Balboa & Grzywacz 2001), and lack the self-similar distribution of spectral energy as was reported for natural images (Field 1987).

(b) Whitening the amplitude spectra

Here I ask whether by amplitude equalization of amplitude spectra (whitening) one could explain psychophysical data on face perception. The results that are presented below were obtained with the mean spectra.

Consider first the isotropic (one-dimensional) spectra. Because the spectra fall, as a function of spatial frequency k, as ∝k^−|α|, we can multiply amplitudes by k^|α| to obtain a ‘flat’ spectrum (in the sense that its Shannon entropy is maximal). The slopes that were used to this end are the spectra ones from table 1. Whitened one-dimensional spectra are shown in figure 3. They are not completely flat, but instead have a global maximum at approximately 10 cycles per face, and a second but local maximum at approximately 30 cycles per face.

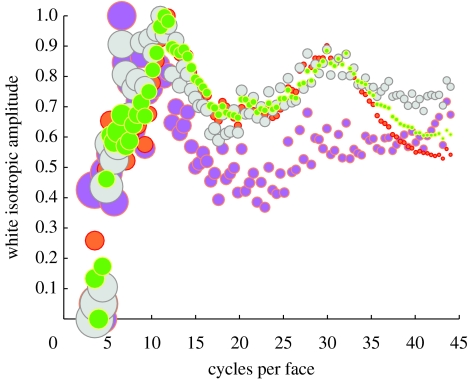
Figure 3.

One-dimensional whitening. Whitening of the corrected mean isotropic one-dimensional spectra reveals a global amplitude maximum at approximately 10 cycles per face with all four spectra. Symbol size is proportional to standard deviation (ranging from 12% to 45%). The slopes that were used for whitening are (cf. table 1): pink, female corr. raw α=−1.58; orange, female corr. B.H. α=−1.67; grey, male corr. raw α=−1.64; green, male corr. raw B.H. α=−1.66.

Consider now the two-dimensional spectra, where whitening was carried out according to three different procedures: whitening by slopes (analogous to the one-dimensional case), by variance and by diffusion (see §2). Results are shown in figure 4 for females and in electronic supplementary material, figure 15 for males. For both genders, the whitened B.H. spectra reveal amplitude maxima only within a narrow band of low spatial frequencies. Furthermore, frequency maxima appear only at a specific orientation in the spectra which corresponds to horizontally oriented face features (‘horizontal amplitudes’, i.e. eyes and mouth). These results are obtained independently from the specific whitening procedure that was used (slope whitening: figure 4a and electronic supplementary material, figure 15a; variance whitening: electronic supplementary material, figure 16; diffusion whitening: not shown).

Plotting of only these horizontal amplitudes (indicated by a white box in figure 4a) for all three whitening procedures allows the identification of the spatial frequencies of the maxima with higher precision. The curves now show clearly that the maxima occur in the range from 10 to 15 cycles per face height. Nevertheless, maxima are revealed only by whitening of the B.H.-windowed spectra, but not by whitening of any raw spectra. This means that amplitude enhancement due to internal face features is annihilated by the presence of external face features (such as hair or shoulder).

4. Discussion

Here, I studied amplitude spectra of face images in the context of response equalization (whitening). When external face features (hair and shoulder) are suppressed by windowing the face images with a B.H. window, then amplitude maxima are observed in the whitened spectra at low spatial frequencies. For the isotropic one-dimensional spectra, maxima are situated approximately 10 cycles per face, and for the two-dimensional spectra at approximately 10–15 cycles per face height. In the two-dimensional case, three different whitening methods yielded consistent results.

Several psychophysical studies suggest that recognition of face identity works best in a narrow band (bandwidth approx. 2 octaves) of spatial frequencies from approximately 8 to approximately 16 cycles per face (Ginsburg 1978; Tieger & Ganz 1979; Fiorentini et al. 1983; Hayes et al. 1986; Costen et al. 1994; Peli et al. 1994; Näsänen 1999). Note that this does not mean that face recognition exclusively depends on this frequency band, as faces can still be recognized when corresponding frequency information is suppressed (Näsänen 1999; Ojanpää & Näsänen 2003).

Because the amplitude maxima appear in the whitened spectra exclusively at horizontal feature orientations, the results suggest that the psychophysical frequency preference might have been caused by an adaptation of corresponding neuronal mechanisms to the eyes and the mouth.

Interestingly, in the earlier cited psychophysical studies the spatial frequencies are often measured in ‘cycles per face width’ (i.e. along vertically oriented face features), whereas the results presented here were rather brought about by horizontally oriented face features. The factors to convert spatial frequencies from ‘cycles per image’ to ‘cycles per face’ (see §2) are statistically different for width and height (as suggested by a one-way ANOVA and a Kruskal–Wallis test). However, they are not so different in absolute terms. The aforementioned frequency interval of 10–15 cycles per face height transforms into approximately 9–13.5 cycles per face width for females and approximately 9–13.6 cycles per face width for males, respectively, which is still in good agreement with the psychophysical data.

Psychophysical thresholds for face recognition are not significantly affected by the structure of the background in which a face is embedded (Collin et al. 2006). Therefore, although the faces used in this study are shown against a uniform background, the validity of results should extend to arbitrary backgrounds. However, note that amplitude spectra consider the complete frequency content of an image, whereas humans have attentional mechanisms that allow them to process only a region of interest, and ignore background effects. Windowing the face images with a B.H. window achieves the same computational purpose: anything but the internal face features are suppressed. A follow-up paper examines in more detail the properties of internal face features by means of a model of simple and complex cells.

The statistical prediction of a preferred band of spatial frequencies may also have implications for artificial face recognition systems. Future experiments should systematically address the question whether the recognition performance of artificial systems is optimal at spatial frequencies similar to those used by humans.