Abstract
Vitevitch and Luce (1998) showed that the probability with which phonemes co-occur in the language (phonotactic probability) affects the speed with which words and nonwords are named. Words with high phonotactic probabilities between phonemes were named more slowly than words with low probabilities, whereas with nonwords, just the opposite was found. To reproduce this reversal in performance, a model would seem to require not merely sublexical representations, but sublexical representations that are relatively independent of lexical representations. ARTphone (Grossberg, Boardman, & Cohen, 1997) is designed to meet these requirements. In this study, we used a technique called parameter space partitioning to analyze ARTphone’s behavior and to learn if it can mimic human behavior and, if so, to understand how. To perform best, differences in sublexical node probabilities must be amplified relative to lexical node probabilities to offset the additional source of inhibition from top-down masking) that is found at the sublexical level.
Research in spoken word recognition focuses on delineating how the acoustics of a spoken word are mapped onto a listener’s memory representation of that word. One dimension in which models of word recognition differ is the issue of whether smaller, sublexical representations, such as phonemes, biphones, or syllables, are also formed during recognition. In models such as the dynamic cohort model (Gaskell & Marslen-Wilson, 2002), the neighborhood activation model (Luce & Pisoni, 1998), and the lexical access from spectra model (Klatt, 1980), sublexical representations are absent and considered to be unnecessary and potentially disruptive to successful recognition. In contrast, models such as TRACE (McClelland & Elman, 1986), Merge (Norris, McQueen, & Cutler, 2000), Shortlist (Norris, 1994), PARSYN (Luce, Goldinger, Auer, & Vitevitch, 2000), and Adaptive Resonance Theory (ART; Grossberg, 1986) postulate at least one sublexical level of representation. Among other things, these models help to explain how nonwords and subword segments are perceived.
Evidence in support of the existence of sublexical representations has been accumulating, most recently in perceptual learning studies (Eisner & McQueen, 2005; Norris, McQueen, & Cutler, 2003). Participants in these experiments first performed a brief lexical decision task in which a subset of the words had the same final segment (e.g., /∫/), but the segment had been replaced with one that was perceptually ambiguous (e.g., a segment midway between /s/ and /∫/). In a subsequent phoneme identification task using an /s/–/∫/ continuum, listeners displayed a bias toward labeling ambiguous segments as /∫/, suggesting that their /∫/ category was altered due to their exposure to it in the initial lexical decision task. These data are parsimoniously accounted for by positing a sublexical representation, in which perceptual learning is specific to a sublexical (e.g., phonemic) representation. How such segment-specific learning could be accounted for lexically (i.e., across words) is not clear.
Additional support for sublexical representations comes from a series of studies by Vitevitch and Luce (1998, 1999, 2005). Listeners heard consonant–vowel–consonant (CVC) words and nonwords that varied in phonotactic probability (the frequency with which segments co-occur in the language), which correlates strongly with neighborhood density (the number of words in the language that are phonologically similar to a specific word). Across sets of stimuli and multiple tasks (e.g., naming, same–different judgment), facilitatory effects of phonotactic probability were found when listeners responded to nonwords, but inhibitory effects were found when they responded to words. Nonword naming times were fastest when phonotactic probability was high versus low (see Lipinski & Gupta, 2005, for constraining conditions). Just the opposite was found with words—naming times were slowest for words with high phonotactic probabilities between segments.
Vitevitch and Luce (1998, 1999, 2005) explained their findings by suggesting that the negative effect of phonotactic probability for words was due to lexical inhibition. Words in dense neighborhoods would receive much more inhibition than those in sparse neighborhoods. Nonwords, whether low or high in phonotactic probability, were likely to generate little lexical activity. Thus any inhibition should be weak, enabling facilitatory effects of phonotactic probability to emerge, presumably from a sublexical level, since nonwords do not have lexical representations.
Vitevitch and Luce (1999) also noted that the reversal of probability and density effects as a function of lexical status would seem to require that sublexical processing be relatively independent of lexical processing. Such independence is found in the ARTphone model (Grossberg, Boardman, & Cohen, 1997), and Vitevitch and Luce used the ARTphone framework to explain how this model could generate their results. Support for ARTphone’s suitability, and for the necessity of a sublexical representation, could be strengthened by demonstrating that the model can in fact reproduce the Vitevitch and Luce data. The purpose of the present study is to perform such a test of ARTphone, not only to determine whether it can mimic human behavior, but also to examine the extent to which the mechanisms hypothesized to be responsible for the empirical pattern (probability dominant sublexically and inhibition dominant lexically) operate in the way suggested by Vitevitch and Luce.
The ARTphone Model
ARTphone (Grossberg et al., 1997) is an interactive activation model that has two main stages of processing. The first processing stage is working memory, which encodes the phonetic features of speech into phonemes. The second stage is short-term memory, which stores representations of chunks of speech of varying sizes, from phonemes to words (referred to generically as list chunks). In contrast to models like TRACE and Merge, list chunks are not hierarchically arranged according to size to form sequentially ordered stages of processing. Rather, chunks of all sizes coexist together in short-term memory, although they are differentiated by how they are wired. Items in working memory are connected to list chunks in short-term memory via bidirectional excitatory links, which are the source of the resonance that, if sufficiently strong, can lead to perception. Inhibitory links interconnect chunks of the same size. Larger chunks (e.g., words) mask (i.e., inhibit) smaller chunks (e.g., biphones and phonemes).
The network is depicted in Figure 1. Only the parts of short-term memory of most relevance for this investigation are shown in detail. Four word nodes and eight biphone nodes are shown in detail; the seven phoneme nodes are not. For clarity, only the masking and a few of the lateral inhibition links are drawn, but the total number of such inhibitory links (masking + lateral) impinging on each node is indicated by the numeral inside the node. The word nodes were interconnected to represent two levels of lexical density: low (i.e., zero neighbors: the word bin) and high (i.e., two neighbors: the words can, ran, tan). The corresponding biphones that make up the words are represented sublexically. Two additional sublexical chunks, ba and at, were included for the purpose of simulating nonword processing. Note that each word masks the two biphones that comprise it and that an receives the most masking whereas ba and at receive none. Chunks of the same size inhibit each other if they overlap. For words, overlap was defined in terms of biphones. For biphones, it was defined in terms of phonemes.1
Figure 1.
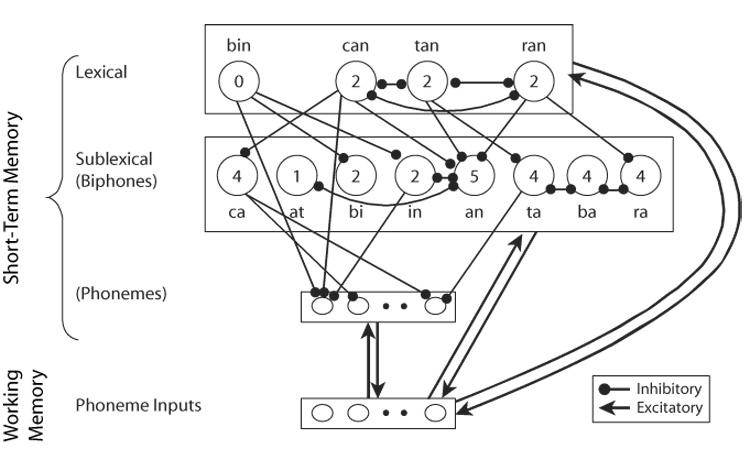
Schematic illustration of ARTphone with details of the connectivity in short-term memory. The most relevant inhibition and masking links between nodes are shown. Numerals inside the nodes denote the number of impinging inhibitory links.
Phonotactic probabilities were encoded in the network by multiplying the biphone and word bottom-up activation functions by a constant, whose value corresponded to the list chunk’s probability in a corpus of English. Biphone probabilities were obtained from the Phonotactic Probability Calculator (Vitevitch & Luce, 2004). Following Vitevitch and Luce (1999), phonotactic probabilities for words were computed by averaging the two biphone probabilities that make up a word. Pilot simulations showed ARTphone to be highly sensitive to probability differences, so interval relations between item (word and biphone) probabilities could not be preserved, but ordinal relations were. The node with the highest probability was assigned a constant of 1.0, and the remaining nodes were scaled downward by a function of their phonotactic probability. Item probability was not held constant throughout the investigation. Rather, we varied the range over which the probabilities extended (close together or farther apart). The purpose of this procedure was twofold. One purpose was to identify an appropriate scaling of probability in which the empirical pattern was most robust; this is necessary when new factors are introduced into a model because the level of granularity at which probability should be represented is not known beforehand. The second purpose was to learn how changes in probability affected model performance lexically and sublexically. The ranges and a description of this calculation can be found in the Appendix.
Vitevitch and Luce (1998) calculated neighborhood density by summing the log frequencies of a word’s neighbors. To increase the similarity of the simulations to their experiment, bottom-up activation of word nodes was also modulated by word frequency, in addition to phonotactic probability. The correlation between the two measures is very low (r < .10; M. S. Vitevitch, personal communication), so information about word frequency is not redundant. Frequency counts were taken from Kučera and Francis (1967) and were converted to proportions using the same formula as that used with phonotactic probabilities (see the Appendix). Each value was multiplied by the word’s phonotactic probability prior to being integrated with the bottom-up activation function for that word.
Input to ARTphone was a CVC, with the phonemes sequentially presented, each over three time units. To simulate coarticulation, the vowel and the final consonant overlapped their preceding phoneme by one time unit. The word inputs were tan and bin. Both have the same frequency, but tan is from a higher density neighborhood (i.e., has greater phonotactic probability) than bin. Although ban and bat are words, they served as nonword inputs for the simulations (note that they have no corresponding lexical nodes). These items differ in the probability of their second biphones, with an having greater probability than at. There is currently no mechanism in ARTphone for combining biphone chunks to yield a nonword node on the fly, so resonance functions of the second biphone (an and at) were used as the measure of nonword perception. The first biphone, ba, was held constant to ensure network behavior remained the same prior to presentation of the final phoneme.
We first coded the network described in Grossberg et al. (1997), validated the implementation by replicating the simulations described in their article (see, e.g., their Figures 10 and 11), and then scaled up the model to the design described above. Parameters were held constant at the values listed in Figure 10 of Grossberg et al., except that μ was set to equal 2.2 (this affects connection dynamics), and two parameters were added to the network—masking (described more fully below) and kappa, a constant that modulates the strength of top-down excitation (list chunk to input), which was set to 0.2 based on pilot simulations.
Analysis Methodology
We studied ARTphone’s performance using a model analysis method called parameter space partitioning (PSP; Pitt, Kim, Navarro, & Myung, 2006). In PSP, the range of data patterns a model can produce (i.e., the empirical pattern plus any others) in an experimental design is identified by repeating a simulation across the ranges of the model’s parameters. Two of ARTphone’s nine parameters were of interest, inhibition (between chunks of the same size) and masking (from large chunks to smaller chunks), so only these two were varied. Pilot testing of various parameter values showed that the model generated sensible patterns (i.e., functions with a single, identifiable resonance peak and no further resonance oscillations) when inhibition was restricted to the range 0–.15 and masking to the range 0–.30. Because only two parameters were varied, a simple grid search procedure (Johansen & Palmeri, 2002) was used to map the parameter space instead of the more sophisticated algorithm described in Pitt et al.
To perform a PSP analysis, the results of Vitevitch and Luce (1998) must be defined quantitatively in terms of ARTphone performance. Resonance refers to the strength of the interaction between phoneme inputs and a list chunk; the greater the match between the two, the greater the resonance. Peak resonance is therefore a reasonable quantitative measure of the strength of evidence in favor of a particular list chunk, biphone, or word. It is important to point out that predictions with behavioral measures such as reaction time (RT) correlate negatively with resonance strength: Longer RTs (i.e., less efficient or slower processing) are equivalent to weaker resonance. To transform the results of Vitevitch and Luce into ARTphone performance, the predictions across word and nonword conditions must be reversed, so that faster RTs correspond to greater resonance.
For ARTphone to reproduce the Vitevitch and Luce (1998) data, low-density words (bin) should achieve a higher peak resonance than high-density words (tan), and high-probability nonwords (ban) should achieve higher resonance than low-probability nonwords (bat). This empirical data pattern is one of nine possible in the 2 × 2 design of Vitevitch and Luce if equalities and inequalities between conditions are considered (node resonances were classified as equal if their peak activations differed by less than .02 units). All nine patterns are shown in the table in Figure 2. To qualify as one of these patterns, all four inputs had to exceed a minimum level of activation for a given set of parameter values. For word nodes, this value was 0.2. For biphones, it was 0.1. Simulations in which activation failed to reach this level were labeled as invalid (Pattern 10). Note that Pattern 3 is the empirical pattern, and Pattern 7 is the opposite pattern. MATLAB code for the simulations and analyses is available from the authors; included with these files is a document that describes the model in more detail and includes equations.
Figure 2.
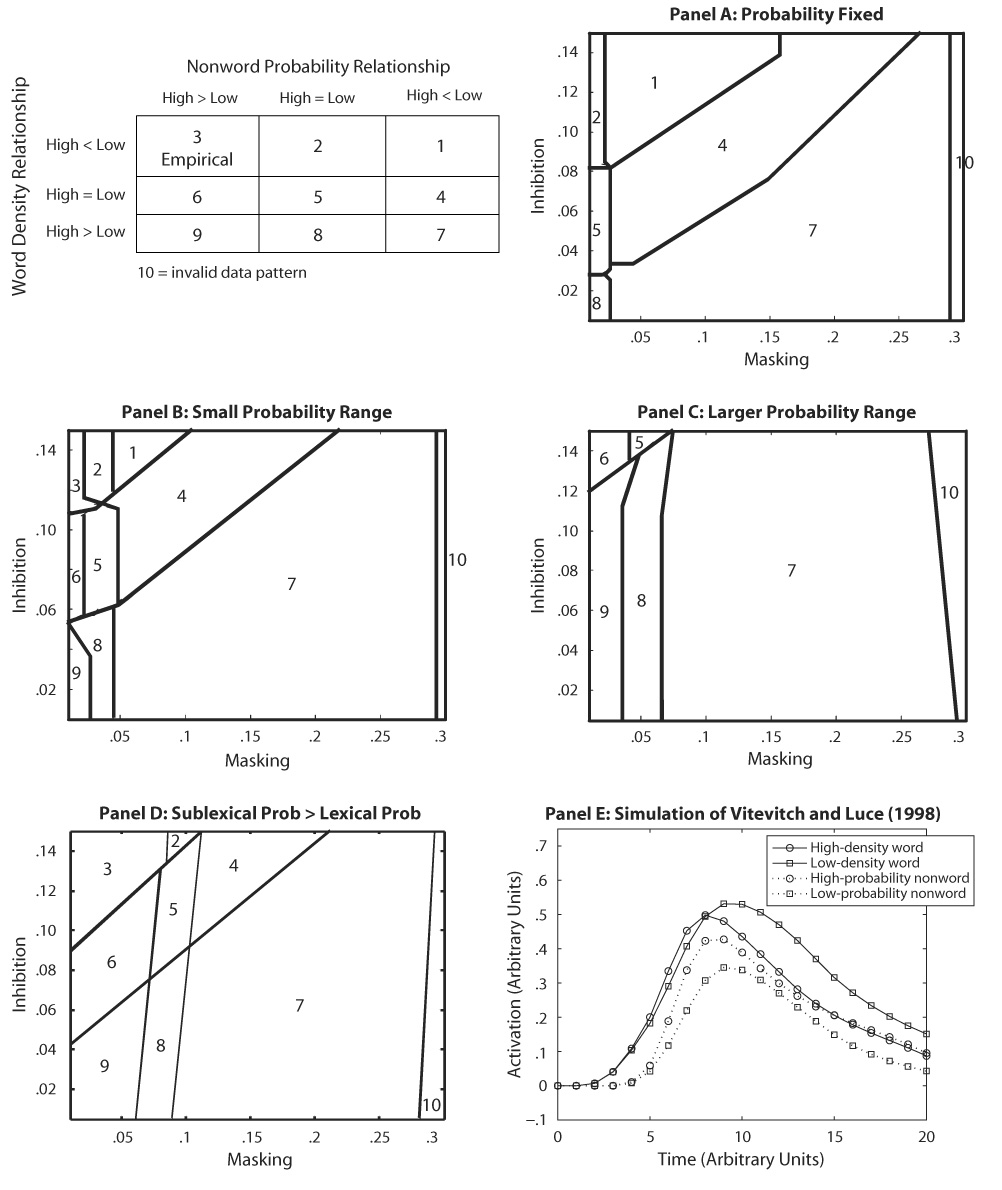
The table contains the nine data patterns that are possible in the 2 × 2 design of Vitevitch and Luce (1998). The relationship between high- and low-probability nonwords (sublexical items) is represented across columns. The relationship between high- and low-probability words is represented across rows. Each pattern is identified with a numeral, which is referenced in the text. Regions labeled 10 indicate an invalid data pattern. Starting with Pattern 7 (opposite of the empirical pattern) and moving upward and to the left, the patterns begin to more closely resemble human patterns, with Pattern 3 being the most humanlike. Panels A–D show the range and extent of the data patterns that ARTphone generates when simulations are run over the specified range of inhibition and masking settings. These four graphs differ in their ranges of nonword and word probabilities. Panel E contains output from ARTphone using parameter and probability settings that generate the empirical pattern.
A PSP analysis is ideal for studying model behavior because it can reveal how many of the nine patterns the model can produce. The analysis also provides information about the centrality of each data pattern in the model, in the form of the size of the area occupied by that pattern in the model’s parameter space. Data patterns that occupy a large region are more representative of model behavior than those that occupy a small region. This analysis assumes a uniform distribution of prior probabilities of parameter values in the specified ranges.
Results and Discussion
The goal of this investigation was to learn not just whether ARTphone could generate the empirical pattern, but how. Vitevitch and Luce (1999) suggest that it arises because probability dominates sublexically and inhibition dominates lexically. Inspection of the model’s design in Figure 1 suggests that this data pattern might be difficult to produce. Because there are more direct sources of inhibition sublexically (lateral and masking) than lexically (lateral only), one might think that inhibition should dominate sublexically. However, this prediction ignores potential influences of phonotactic probability, which could reverse this built-in bias and thus generate the empirical pattern. Can it? To answer this question, as well as to examine how these multiple forces would interact in the model, we ran the PSP analysis several times while varying the range of phonotactic probabilities.
In the first analysis, all sublexical and lexical nodes were fixed at the same phonotactic probability and frequency (1.0, the maximum). If differences in phonotactic probability are necessary to produce the empirical pattern, then the empirical pattern should not have been found in the analysis, which was indeed the case. Panel A of Figure 2 shows a plot of the regions in ARTphone’s parameter space (i.e., each combination of inhibition and masking settings) occupied by each of the nine possible data patterns in the experimental design. The lines separating the regions had to be hand edited, so their positions should be considered approximate.
With no differences in probability, only masking and inhibition drive processing. Sublexically, this means that a node with fewer inhibitory links (at) achieves greater resonance than a node with more links (an), exactly opposite what is found with humans. This result (Patterns 1, 4, and 7) occupies most of the parameter space. Only at very low levels of masking does an achieve enough resonance to be considered equivalent to at (Patterns 2, 5, and 8). For the lexical items (tan and bin), all three outcomes (high < low, high = low, high > low) are possible, depending on the combination of inhibition and masking. Under some parameter settings, the effects of masking can percolate back up to alter lexical node activation.
In the next two analyses, probability differences between nodes (sublexical and lexical) were introduced by a small amount (Figure 2, panel B) and a larger amount (panel C; see the Appendix for ranges). In panel B, the empirical pattern is present in the upper left corner. In this rather small region of parameter space, differences in probability at the sublexical level are large enough to offset weak masking effects (combined with strong inhibitory effects) and yield greater resonance for high- than for low-probability chunks. At the same time, at the lexical level, inhibition is great enough in this region to achieve just the reverse effect: Inhibition in a high-density neighborhood overwhelms any advantage of greater phonotactic probability so that the word in the low-density neighborhood achieves the highest resonance. Nevertheless, the empirical data pattern is rather fragile with these probability settings, disappearing quickly if masking is increased. As in panel A, ARTphone generates the other lexical patterns (high = low, high > low) depending on inhibition and masking level.
Further comparison of panels A and B shows ARTphone to be extremely sensitive to the phonotactic probability of the words. After the introduction of small differences in probability, Patterns 7–9 occupied even larger portions of the parameter space. The higher density word (tan) easily overcomes the inhibition from its somewhat small neighborhood, leading to an increase in area occupied by the high > low lexical pattern.
In panel C, where the range of probabilities was greater, three patterns dominated (7, 8, and 9). Relative to panel B, what happened was that these patterns occupied even more of the parameter space, further extending their reach upward into regions of greater inhibition. Again, when phonotactic probability differences were introduced, the higher density word quickly dominated, which is why only the high > low pattern is found. Sublexically, as masking decreases, the pattern again shifts from high < low (7) to high > low (9), reaffirming the need for small amounts of masking to generate the empirical nonword pattern.
Two observations emerge from these first three analyses. One is that ARTphone is highly sensitive to differences in phonotactic probability. Perhaps because of this, simply introducing such differences is not enough to generate the empirical pattern robustly. The other observation is that differences in phonotactic probability appear to be much more potent lexically than sublexically. One reason for this was alluded to earlier: There is only one type of lexical inhibition (lateral), but there are two types of sublexical inhibition (lateral and masking). ARTphone’s rather weak ability to generate the empirical pattern thus far could be a result of failing to compensate adequately for the strength of this difference.
One way to offset the difference is to vary phonotactic probability more widely across sublexical items than lexical items. Such a configuration of the model is in keeping with what Vitevitch and Luce (1999) suggest is necessary to generate the empirical pattern, in which inhibition should dominate lexically (because phonotactic effects are weak), and probability should be strongest sublexically (to offset two sources of inhibition).
Accordingly, a final PSP analysis was run in which sublexical probability varied much more widely than lexical probability. panel D of Figure 2 shows the results. This change had the intended effect of substantially increasing Region 3, the area occupied by the empirical pattern. Additional analyses using other combinations of probability ranges did not increase this area substantially. The graph on the right (panel E) shows ARTphone’s simulation of the empirical pattern using masking and inhibition values from the center of Region 3 (masking =.04, inhibition = .13).
Although it is reassuring that ARTphone can generate the empirical pattern, it is somewhat disconcerting that this configuration of ARTphone can also produce all of the other data patterns in the experimental design except Pattern 1. In particular, that Pattern 7, which is the opposite of the empirical pattern, is still the most stable suggests that the proclivities of ARTphone have to be counteracted in order for it to perform as listeners do. Together, these findings can cast doubt on ARTphone’s suitability.
This conclusion holds only if the parameterization of the model remains as is, with much of it unused. At the start of this study, we purposefully chose ranges of the inhibition and masking parameters that generated reasonable resonance functions (e.g., panel E). The knowledge gained from the current simulations suggests that the range of both parameters could be restricted even further, perhaps keeping masking below 0.15 and inhibition above 0.06. This would have the benefit of decreasing the number of data patterns produced as well as increasing the area of the empirical pattern. Such a change would be particularly justifiable if ARTphone used parameter values in this range when simulating other data sets.
ARTphone’s ability to produce a wide range of data patterns is not unexpected given its architecture. The virtual independence of lexical and sublexical chunks (they are connected only via one-way masking links) gives the network flexibility in producing a range of data patterns. Pitt et al. (2006) observed similar flexibility in the Merge model of phoneme perception (Norris et al., 2000), which shares structural similarities with ARTphone. In Merge, phoneme input is fed simultaneously to a lexical stage and a phoneme decision stage. Excitatory links connect the lexical stage to the decision stage. As with ARTphone, the independence of these two higher level stages enables the model to produce a range of data patterns. A downside of this flexibility, which is visible in Figure 2, is that less of the parameter space will be occupied by the empirical pattern.
In the introduction, we mentioned that the independence of the sublexical and lexical list chunks might allow ARTphone to simulate the Vitevitch and Luce (1998) data. The results of this study suggest that masking performs a key role in simulating the empirical pattern. Masking must be present but only at low levels. Between-level masking is a unique feature of ARTphone that distinguishes it from other models. For example, in a model such as TRACE, connections between lexical and sublexical levels are excitatory in both directions, making processing of shared phonemes mutually reinforcing. Unless TRACE can mimic masking in another way, simulating the Vitevitch and Luce data could pose a challenge.
Future work should focus on the fact that the empirical pattern was found only when there were minimal differences in phonotactic probability across words. In fact, the area occupied by the empirical pattern actually increased slightly (expanding into Region 6) when the final analysis (panel D) was rerun with word probabilities equated. Ideally, this should not happen. ARTphone’s small lexicon might be to blame. In a larger network, more and longer words would be present. Longer list chunks would mask smaller ones. This additional source of inhibition could be offset by increasing probability differences between words.
The results of Vitevitch and Luce (1998) have been around for almost a decade, yet we know of no model that has simulated this challenging pattern of data. ARTphone can do so, and the means by which it succeeds correspond nicely with what appears to drive the effect in listeners. Finally, the PSP analyses bring to light the inner workings of ARTphone so that we understand how ARTphone succeeds.
AUTHOR NOTE
This work was supported by Research Grant R01-MH57472 from the National Institute of Mental Health, National Institutes of Health. N.A. was also supported by an Undergraduate Research Scholarship from Ohio State University. MATLAB code plus additional documentation of the model can be found at lpl.psy.ohio-state.edu/software.html. Correspondence concerning this article should be addressed to M. A. Pitt, Department of Psychology, Ohio State University, 1835 Neil Avenue, Columbus, OH 43210 (e-mail: pitt.2@osu.edu).
APPENDIX
Values used to Represent Biphone and Word Probabilities in the Simulation
| Simulation Probability Values |
|||||
|---|---|---|---|---|---|
| Phonotactic Probability | Fixed | Small Range | Larger Range | Sublexical > Lexical | |
| Biphones | (a = 0) | (a = .08) | (a = .15) | (a = .3) | |
| an | .0144 | 1 | 1 | 1 | 1 |
| ca | .0144 | 1 | .9942 | .9892 | .9784 |
| in | .0095 | 1 | .9855 | .9729 | .9458 |
| ba | .0059 | 1 | .9690 | .9419 | .8837 |
| at | .0059 | 1 | .9690 | .9419 | .8837 |
| ra | .0050 | 1 | .9632 | .9311 | .8622 |
| bi | .0041 | 1 | .9564 | .9182 | .8363 |
| ta | .0039 | 1 | .9546 | .9149 | .8298 |
| Words | (a = 0) | (a = .23) | (a = .60) | (a = .017) | |
| can (1.00) | .0133 | 1 | 1 | 1 | 1 |
| ran (.943932) | .0097 | 1 | .9685 | .9178 | .9977 |
| tan (.885289) | .0092 | 1 | .9626 | .9025 | .9972 |
| bin (.885289) | .0068 | 1 | .9330 | .8252 | .9950 |
Note—Rather than choose sets of values arbitrarily, the values were generated using the equation a × log(prob) + 1 − a × log(b), where a was the slope of the logarithmic function, prob was the phonotactic probability of the biphone or word, and b was set to the highest value in each category (.0144 for biphones and .0133 for words) to ensure that the intercept was equal to 1. Biphone probabilities were taken from the Phonotactic Probability Calculator (Vitevitch & Luce, 2004). Following Vitevitch and Luce (1999), phonotactic probabilities for words were computed from the same source by averaging the two biphone probabilities of each word.2 Word frequency values (in parentheses) were rescaled from the values in Kučera and Francis (1967) and then plugged into the above equation with a = .05 and b = .01772.
Readers familiar with Vitevitch and Luce (1999, Experiment 1) might notice that the word probabilities for tan and bin (.0092 vs. .0068) are more similar to one another than were the mean biphone probabilities from the high- and low-probability conditions in Vitevitch and Luce’s experiment, which were .0143 and .0006, respectively. Had we used these means instead, only those values of a associated with words (and not biphones) in the Appendix would have changed, not the simulation results. Recall that multiple ranges of probability values were used for the purpose of determining the granularity at which word and biphone probability should be represented in ARTphone in order to generate the empirical pattern. When the Vitevitch and Luce means are substituted [and appropriate probabilities are assigned to can (.015) and ran (.0147)], a graph very similar to the one shown in panel D is produced, with a = .00347 and b = .015.
Footnotes
The pragmatics of trying to create a small but realistic network in which neighborhood density is manipulated prompted us to define overlap differently for lexical representations than for sublexical representations. The connectivity of this network would not have to change if overlap were defined solely in terms of phonemes; instead, different words could be substituted. Also, although a much larger network could yield more realistic results, all links in ARTphone must be wired by hand, which makes it tricky to scale up the model further. Over 100 data vectors were required for this implementation.
REFERENCES
- Eisner F, McQueen JM. The specificity of perceptual learning in speech processing. Perception & Psychophysics. 2005;67:224–238. doi: 10.3758/bf03206487. [DOI] [PubMed] [Google Scholar]
- Gaskell MG, Marslen-Wilson WD. Representation and competition in the perception of spoken words. Cognitive Psychology. 2002;45:220–266. doi: 10.1016/s0010-0285(02)00003-8. [DOI] [PubMed] [Google Scholar]
- Grossberg S. The adaptive self-organization of serial order in behavior: Speech, language, and motor control. In: Schwab EC, Nusbaum HC, editors. Pattern recognition by humans and machines: Vol. 1. Speech perception. Orlando, FL: Academic Press; 1986. pp. 187–294. [Google Scholar]
- Grossberg S, Boardman I, Cohen M. Neural dynamics of variable-rate speech categorization. Journal of Experimental Psychology: Human Perception & Performance. 1997;23:481–503. doi: 10.1037//0096-1523.23.2.481. [DOI] [PubMed] [Google Scholar]
- Johansen MK, Palmeri TJ. Are there representational shifts during category learning? Cognitive Psychology. 2002;45:482–553. doi: 10.1016/s0010-0285(02)00505-4. [DOI] [PubMed] [Google Scholar]
- Klatt DH. Speech perception: A model of acoustic–phonetic analysis and lexical access. In: Cole RA, editor. Perception and production of fluent speech. Hillsdale, NJ: Erlbaum; 1980. pp. 243–288. [Google Scholar]
- Kučera H, Francis WN. Computational analysis of present-day American English. Providence, RI: Brown University Press; 1967. [Google Scholar]
- Lipinski J, Gupta P. Does neighborhood density influence repetition latency for nonwords? Separating the effects of density and duration. Journal of Memory & Language. 2005;52:171–192. [Google Scholar]
- Luce PA, Goldinger SD, Auer ET, Jr, Vitevitch MS. Phonetic priming, neighborhood activation, and PARSYN. Perception & Psychophysics. 2000;62:615–625. doi: 10.3758/bf03212113. [DOI] [PubMed] [Google Scholar]
- Luce PA, Pisoni DB. Recognizing spoken words: The neighborhood activation model. Ear & Hearing. 1998;19:1–36. doi: 10.1097/00003446-199802000-00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland JL, Elman JL. The TRACE model of speech perception. Cognitive Psychology. 1986;18:1–86. doi: 10.1016/0010-0285(86)90015-0. [DOI] [PubMed] [Google Scholar]
- Norris D. Shortlist: A connectionist model of continuous speech recognition. Cognition. 1994;52:189–234. [Google Scholar]
- Norris D, McQueen JM, Cutler A. Merging information in speech recognition: Feedback is never necessary. Behavioral & Brain Sciences. 2000;23:299–325. doi: 10.1017/s0140525x00003241. [DOI] [PubMed] [Google Scholar]
- Norris D, McQueen JM, Cutler A. Perceptual learning in speech. Cognitive Psychology. 2003;47:204–238. doi: 10.1016/s0010-0285(03)00006-9. [DOI] [PubMed] [Google Scholar]
- Pitt MA, Kim W, Navarro DJ, Myung JI. Global model analysis by parameter space partitioning. Psychological Review. 2006;113:57–83. doi: 10.1037/0033-295X.113.1.57. [DOI] [PubMed] [Google Scholar]
- Vitevitch MS, Luce PA. When words compete: Levels of processing in perception of spoken words. Psychological Science. 1998;9:325–329. [Google Scholar]
- Vitevitch MS, Luce PA. Probabilistic phonotactics and neighborhood activation in spoken word recognition. Journal of Memory & Language. 1999;40:374–408. [Google Scholar]
- Vitevitch MS, Luce PA. A Web-based interface to calculate phonotactic probability for words and nonwords in English. Behavior Research Methods, Instruments, & Computers. 2004;36:481–487. doi: 10.3758/bf03195594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vitevitch MS, Luce PA. Increases in phonotactic probability facilitate spoken nonword repetition. Journal of Memory & Language. 2005;52:193–204. [Google Scholar]


