More Accurate Talairach Coordinates for NeuroImaging using Nonlinear Registration

Abstract

While the Talairach atlas remains the most commonly used system for reporting coordinates in neuroimaging studies, the absence of an actual 3D image of the original brain used in its construction has severely limited the ability of researchers to automatically map locations from 3D anatomical MRI images to the atlas. Previous work in this area attempted to circumvent this problem by constructing approximate linear and piecewise linear mappings between standard brain templates (e.g. the MNI template) and Talairach space. These methods are limited in that they can only account for differences in overall brain size and orientation but cannot correct for the actual shape differences between the MNI template and the Talairach brain. In this paper we describe our work to digitize the Talairach atlas and generate a non-linear mapping between the Talairach atlas and the MNI template that attempts to compensate for the actual differences in shape between the two, resulting in more accurate coordinate transformations. We present examples in this paper and note that the method is available freely online as a Java applet.

1 Introduction

The Talairach atlas (Talairach and Tournoux (1988)) is the most commonly used system for reporting coordinates in neuroimaging and is used in both BrainMap (Fox et al. (1994)) and the Talairach Daemon (Lancaster et al. (1997)). However, the absence of an actual “Talairach”-brain image means that modern non-linear registration methods can not be used to map any individual subject brain to “Talairach”-space directly. Instead, the two most common methods currently used are: (1) a direct piecewise-linear scaling of each individual subject into Talairach space such as that which is applied in, for example, the AFNI software package (Cox (1996)) or (2) mapping each individual subject into a common reference space (the most common reference space is the Montreal Neurological Institute (MNI) space) (Evans et al. (1993)) and then applying a piecewise-linear conversion for mapping MNI coordinates to Talairach coordinates. Neither of these methods is particularly accurate as both of them can only account for the overall size and orientation of the brain as opposed to any differences in brain shape. It has been shown that the overall shape of the MNI template is taller, longer and has larger temporal lobes than the Talairach brain. Brett et al. (Brett et al. (2001)) created the mni2tal transform which maps MNI space into Talairach space using two linear transformation matrices, but notes that the technique is merely an approximation. To improve on the above mentioned techniques, researchers have studied the disparity between Talairach coordinates derived from different methods and have applied various affine transforms to optimize the coordinates between MNI space and Talairach space (Carmack et al. (2004); Chau and McIntosh (2005); Lancaster et al. (2007)). While affine transformations contain more information than the piecewise-linear transformations, they still do not account for differences in brain shape. Non-linear registrations employ thousands of parameters instead of the 12 parameters used typically for affine registrations and therefore can account for these regional shape differences.

In this work, we generated a 3-D image of the Talairach brain by digitally scanning and aligning the axial slices of the Talairach atlas. This 3-D version of the Talairach brain surface was used to create a more accurate nonlinear mapping between MNI space, as represented by the “Colin” brain (Holmes et al. (1998)), and Talairach space. (Colin 27).

We note that this work was motivated in part by the observation that standard piecewise mapping of MNI space to Talairach space resulted in points that are on, or close, to the surface of the brain in MNI space having corresponding Talairach coordinates outside the brain as a result of inaccurate MNI to Talairach coordinate conversion.

2 Methods

Constructing a Digital Talairach Atlas

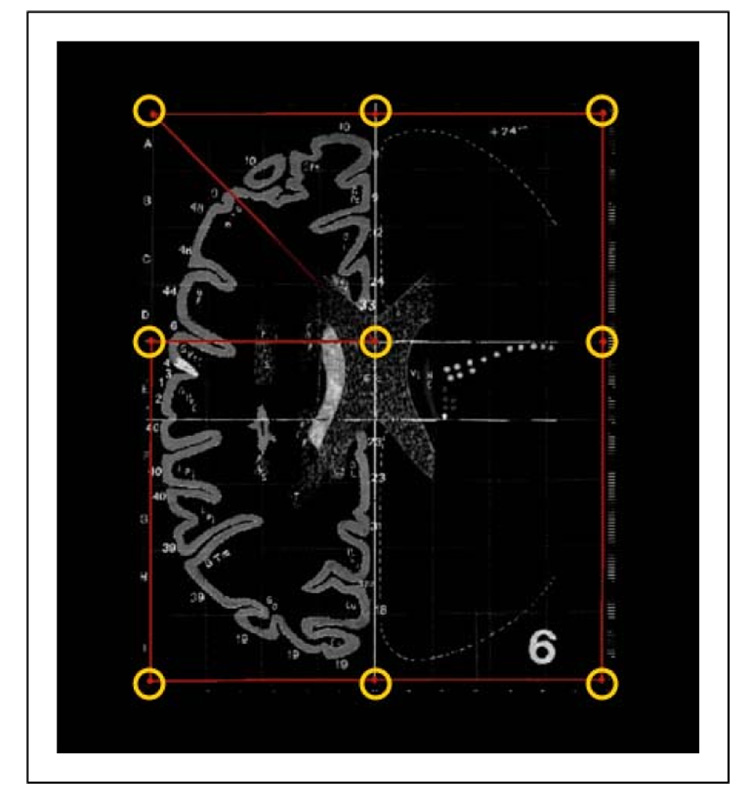
All 27 axial slices of the Talairach atlas (ranging from z=+65 to z=−40) were digitally scanned using an HP OfficeJet 7210 scanner. Since some of the grid lines in the atlas do not have 90 degree angles, the individual slice images were distortion-corrected using the following procedure. First the slice images were aligned using 9 points per slice: the four corners of the grid, the AC position, and the two points where the AC met the right and left gridlines, and the two points where the midline met the anterior and posterior gridlines. This is illustrated in Figure 1. Next a 2-D thin-plate spline transformation (Bookstein (1989, 1991)) was applied to each slice to map these 9 points to their theoretically true locations. Finally, all the individual distortion-corrected and aligned slice images were stacked to form a three-dimensional image.

Fig. 1. Scanning and Distortion Correction.

The digital “Talairach” atlas was constructed by first scanning in the atlas and performing distortion correction on the scanned images to correct for distortions in both the original printed atlas and any distortions introduced by the scanning process. (Distortions result in the underlying graph paper used in the atlas not having orthogonal, equispaced lines). We semi-automatically located nine landmarks in each slice and then used these to map each scanned slice to the true orthogonal coordinate system using a thin-plate spline transformation.

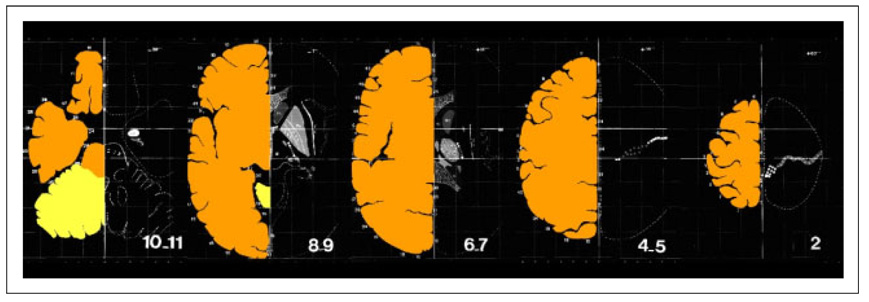
The left side, or right hemisphere, of this 3-D image was manually segmented maintaining gyral patterns. Since, the gyral patterns of the Talairach atlas are incomplete for the right side or left hemisphere, the image was assumed to be left-right symmetric. (Figure 2). Given this segmentation we proceed to extract the outer surface of this “Talairach brain” to use it as an input to our registration method, described next.

Fig. 2. Digitized, Aligned and Segmented Axial Slices of the Talairach Atlas.

The figure above shows selected slices from the digitized atlas with superimposed manual segmentations of the brain.

Non-linear Point-Based Registration

The Robust Point Matching Framework

The transformation from MNI space to Talairach space is constructed using a non-linear point-based registration using as inputs the outer surface of a manually stripped version of the MNI-T1 template (the “Colin” brain) and our digitized atlas.

This non-linear registration method is based on the robust point matching framework (see Chui et al. (2003); Papademetris et al. (2003); Duncan et al. (2004)). The robust point matching framework enables correspondence estimation in the case of outliers. This approach consists of two alternating steps: (i) the correspondence estimation step and (ii) the transformation estimation step. In the following discussion, we will label the reference point set as X and the transform point set as Y . We aim to estimate the transformation G : X ↦ Y . G_k is the estimate of G at the end of iteration k, and G⁰ is the starting transformation which can be set to the identity transformation.

Correspondence Estimation

Given the point sets X and Y, we estimate the match matrix M, where M_ij is the distance metric between points G(X_i) and Y_j. The standard distance metric is defined as:

$$M_{\mathit{\text{ij}}}=\frac{1}{\sqrt{2\pi T^2}}{e}^{\frac{-|G(X_i)-Y_j{|}^2}{2T^2}},\forall i{\displaystyle \sum _j{M}_{\mathit{\text{ij}}}+C_i=1,\forall j{\displaystyle \sum _i{M}_{\mathit{\text{ij}}}+R_j=1}}$$ (1)

where |X_i − Y_j| is the Euclidean distance between points X_i and Y_j and T is the temperature that controls the fuzziness of the correspondence. The correspondence is posed as a linear assignment problem and the rows and columns of M must sum to 1. The framework is further extended to handle outlier points by introducing an outlier column C and an outlier row R. C_i is a measure of the degree of ‘outlierness’ of a point in the reference point set X_i and R_j is the same for a point in the transform point set Y_j. C and R are initialized with constant values. The ability to model outliers allows this method to robustly match features of high variability (e.g. sulci) and manually outlined structures where the ends of the structures are user defined and potentially arbitrary.

Once the normalization is completed, we can then compute the correspondence. Let V_i be the corresponding point to X_i and w_i be the confidence in the match. Then, V_i is defined as a normalized weighted sum of the points Y_j where the weights are the elements of the match matrix M, i.e. V_i = (Σ_j M_ijY_j)/(Σ_j M_ij), and w_i = (Σ_j M_ij) = 1 − C_i. Note that a point that has a high value in the outlier column C will have low confidence.

Transformation Estimation

The transformation is estimated by a regularized weighted least squares fit between X_i and V_i:

$$G^k=\stackrel{\text{arg min}}{G}{\displaystyle \sum _i{w}_i(G(X_i)-V_i){)}^2+f(T)S(G)}$$ (2)

where S(G) is a regularization functional (e.g. bending energy function) weighted by a decreasing function of the temperature f(T). f(T) is used to decrease the regularization as we approach convergence.

Deterministic Annealing Framework

The alternating estimation of M and G is performed in a deterministic annealing framework. Starting with a high value of T, corresponding to a rough estimate of the maximum mis-alignment distance, we first estimate M, and then G. Then, T is decreased by multiplying it with an annealing factor and the process is repeated until T becomes sufficiently small.

In this specific case, the robustness of the method enables the accurate registration of what essentially is an “open surface” (the surface extracted from the digital atlas does not extend all the way to the top/bottom of the brain) and a “closed surface” (the MNI brain surface) with no geometric distortions in those regions that would commonly be generated by non-linear registration methods in such cases of missing structures.

Registration Results

The RPM-framework was used to map the MNI/Colin (CB) outer brain surface to the Talairach surface. Example registrations are shown in Figure 3 and 4. The nonlinear registration was applied to the Colin Brain to create a “Talairached” Colin brain (TalCB). The TalCB was examined by a Radiologist for defined Talairach parameters such as the Anterior Commissure to Posterior Commissure (AC-AP) line, the Verticofrontal (VCA) line and the Posterior Commissure (VCP) line. The AC-AP line is defined as the plane that passes through the superior edge of the anterior commissure and the inferior edge of the posterior commissure. The VCA line is defined as the vertical line traversing the posterior margin of the anterior commmissure and the VCP line is defined as the vertical line parallel to the VCA, but traversing the anterior margin of the posterior commissure. The radiologist examined the TalCB and determined that a rotation of 2 degrees was needed in order to orient the top of the Anterior Commissure (AC) and the bottom of the Posterior Commissure (PC) on the same axial plane. Therefore, a rotation of 2 degrees was added to the nonlinear mapping and applied to the CB to create a new TalCB (this is similar to what is noted by Brett ¹ – this webpage contains a helpful overview of the whole Talairach to MNI mapping problem.)

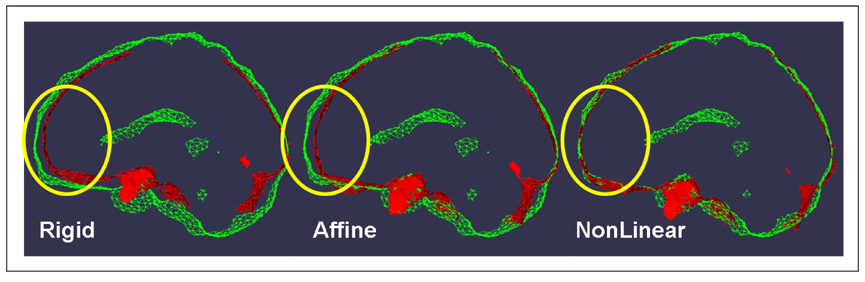
Fig. 3. MNI to Talairach Point-Based Registration.

In this figure the results of progressively more complex registrations between the MNI brain surface and the Talairach brain surface are shown. In particular we show a thick section of outer brain surface of (i) Talairach Brain Mask (red) (ii) Colin Brain Mask (green) following rigid (left), affine (middle) and non-linear (right) point-based registration using RPM. Note especially the improved alignment in the frontal region (highlighted by a yellow ellipse.) We note that the affine registration is roughly equivalent to current piecewise linear methods (Brett et al. (2001)).

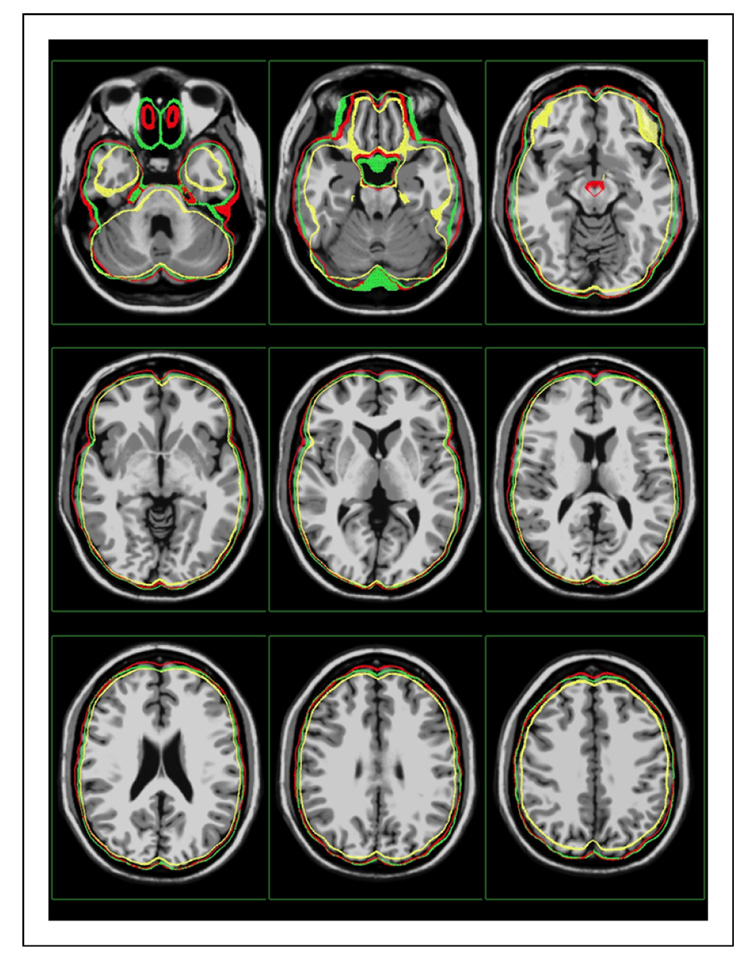
Fig. 4. MNI to Talairach Point-Based Registration, Image Overlay II.

Another view of the result from Figure 3, where the surface from the Talairach atlas is overlaid on the Colin 27 brain. The result from the rigid transformation is shown in yellow, the affine transformation in green and the nonlinear transformation in red.

Estimating the Talairach Transformation

In addition to the non-rigid registration an expert radiologist identified the following landmarks in both the MNI (CB) brain and the Talairach (TalCB) brain: AC, PC, two mid-sagittal points and the bounding box of the brain which consisted of six boundary points: superior, inferior, anterior, posterior, right lateral and left lateral. These points were then used to create a piecewise-linear mapping into Talairach space, for comparisons.

The end result of our method is a lookup table (this available as part of BioImage Suite – see www.bioimagesuite.org) that given any coordinate in MNI space returns the equivalent coordinate in Talairach space. This is pre-computed using (i) the nonlinear map from the MNI brain to the Talairach brain estimated above and (ii) the piecewise mapping (really rigid in this case) of the Talairached-Colin Brain (TalCB) to Talairach coordinates (essentially subtracting the location of the AC).

3 Results

In this section we report results of the application of our method. First we use the nonlinear mapping to visualize the Talairach brain and to quantify the regional morphometric (volume) differences between this and the MNI template. Then we examine a number of different locations in the brain and illustrate that our new mapping yields more accurate estimates of Talairach transformations than standard methods.

3.1 Global Differences

In addition to establishing a more accurate coordinate system conversion between MNI and Talairach coordinates, the non-rigid registration also enables us to (i) generate a “Talairach Brain” and more usefully (ii) to quantify the shape differences between the Talairach brain and the MNI template.

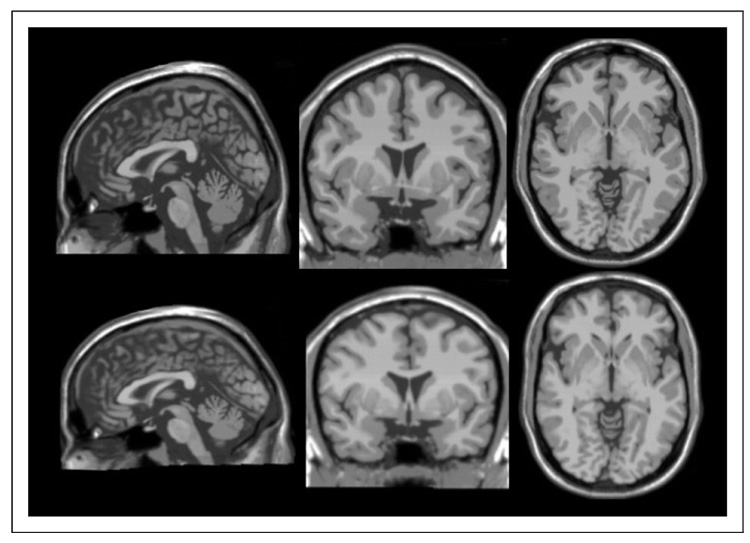
A comparison between the Talairach brain (TalCB) and the MNI template (CB) is shown in Figure 5. While this might have been useful in its own right as a template for non-rigid registrations, the emergence of more sophisticated templates (e.g. MNI 152) makes this of little use. However, it enables us to get a summary view of what the Talairach brain might have looked like had an MRI been available.

Fig. 5. A Direct Look at the Differences Between the MNI template and the Talairach Brain.

Top, AC centered slices of MNI Template (Colin) Brain. Bottom: AC-centered slices of Colin Brain inversely mapped to Talairach space using the non-linear registration above. Note that the Talairach brain is, (i) Wider left to right, (ii) Shorter anterior to posterior and (iii) Appears to have no obvious distortions – demonstrating the smoothness of the overall nonlinear registration.

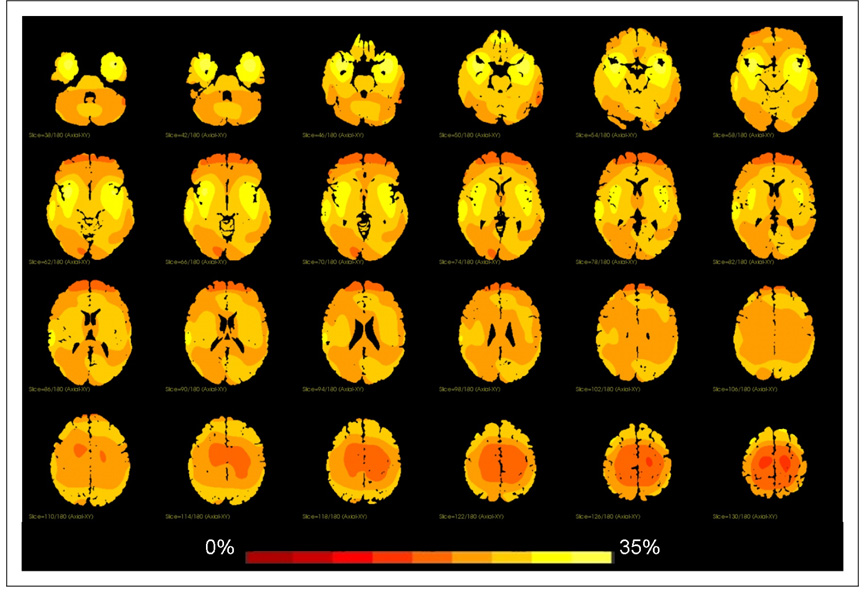
We quantified the shape difference between the MNI template and the Talairach brain by using the determinant of the Jacobian of the non-linear transformation, as is commonly done in brain morphometric studies. The determinant of the Jacobian, in this case, is effectively a measure of local volume changes. For example, if the determinant of the Jacobian has value 1.1 at a specific location in the brain, it implies that the target brain at that location is 10% larger than the template. Similarly a value of 0.9 indicates that the target brain is 10% smaller than the template. An overlay of this measure on the MNI template is shown in Figure 6. The local percent volume difference ranges from 0 (red) to 35 (yellow); the biggest differences between the two brains are found in the temporal lobes, as was again noted by Brett.

Fig. 6. Regional Volume Differences Between the MNI template and the Talairach Brain.

In this figure we plot the magnitude of the Jacobian of the nonlinear mapping of the Talairach Brain to the MNI template. This is a measure of volume change which shows where the MNI template is substantially bigger (locally) than the Talairach brain. Note the relatively large difference in the temporal lobes.

3.2 Local Coordinate Differences

We demonstrate the improvement in estimating the mapping from MNI to Talairach coordinates using several examples from different locations in the brain. In particular we will compare (as a proxy) the localizations (Talairach coordinates) using a piecewise linear mapping applied to the original MNI template brain (CB) to the same piecewise linear mapping applied to the Talairached Colin Bran (TalCB).

In Figure 7, Figure 8, Figure 9 and Figure 10 we present results from eight different locations in the brain to demonstrate the improvement resulting from using the nonlinear mapping – through the shortcut of creating the Talairached MNI brain.

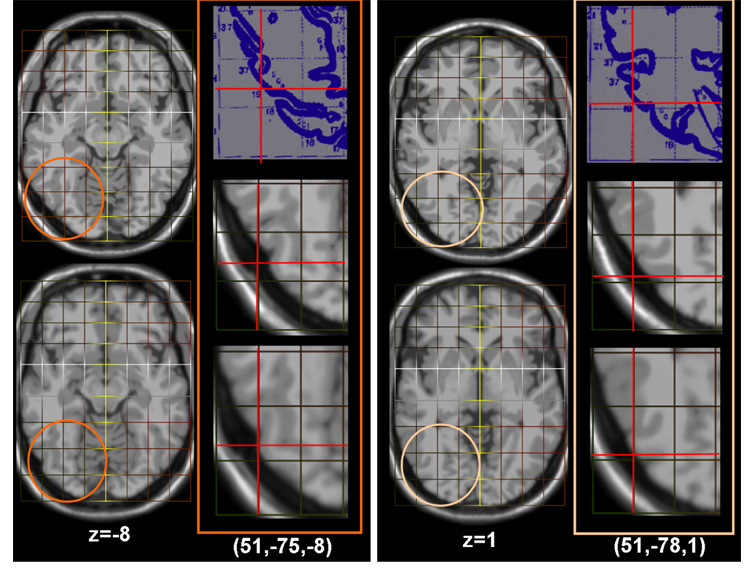
Fig. 7. Improved Talairach Coordinates I: Axial Slices of Inferior Occipital Regions.

Result from two locations (51,−75,8) and (51,−78,1). First Column: Slice z=−8 from the MNI template (top) and the Talairached Brain (bottom). Second Column: Top: The Talairach atlas slices for these locations. Middle: The location of this point on the original MNI template using a piecewise mapping (red cross-hairs). Bottom: The location of the same point on the Talairached-MNI brain. The third and fourth columns are repeats for location (51,−78,1). Note that in both cases these points are on the brain surface in the Talairached brain (as they should be, see the original atlas) whereas in the MNI brain they are located outside the brain.

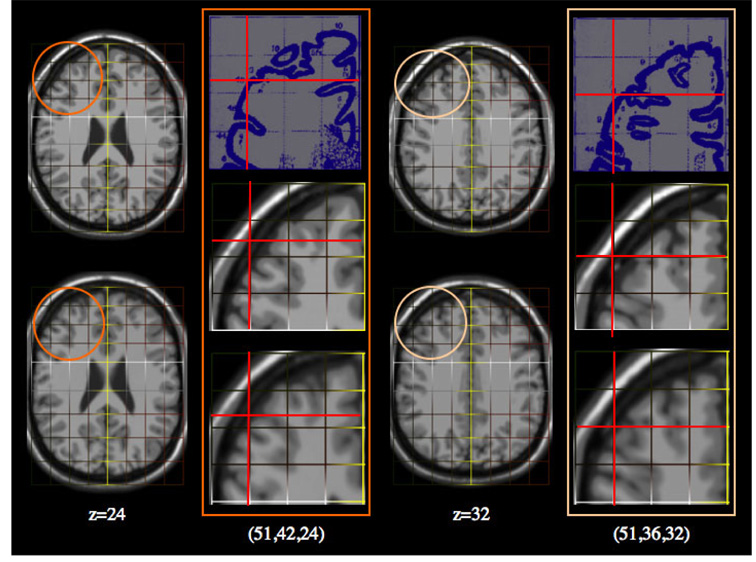
Fig. 8. Improved Talairach Coordinates II: Axial Slices of Frontal Regions.

Result from two locations (51,42,24) and (51,36,32). First Column: Slice z=24 from the MNI template (top) and the Talairached Brain (bottom). Second Column: Top: The Talairach atlas slices for these locations. Middle: The location of this point on the original MNI template using a piecewise mapping (red cross-hairs). Bottom: The location of the same point on the Talairached-MNI brain. The third and fourth columns are repeats for location (51,36,32).

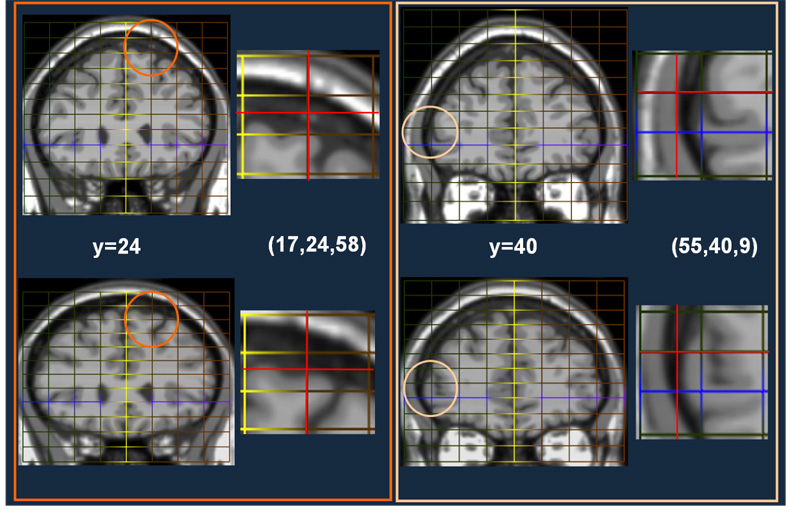
Fig. 9. Improved Talairach Coordinates III: Coronal Slices of Frontal Regions.

Result from two locations (−17,24,58) and (55,40,9). First Column: Slice y=24 from the MNI template (top) and the Talairached Brain (bottom). Second Column: Top: The location of this point on the original MNI template using a piecewise mapping (red cross-hairs). Bottom: The location of the same point on the Talairached-MNI brain. The third and fourth columns are repeats for location (55,40,9).

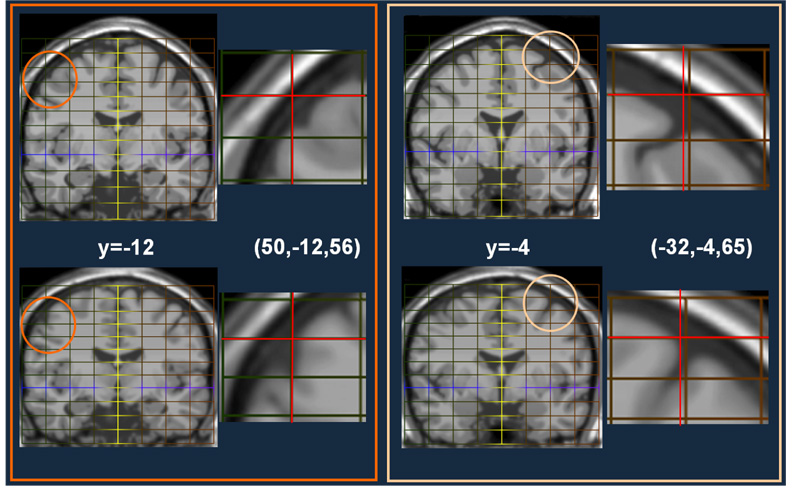
Fig. 10. Improved Talairach Coordinates IV: Coronal Slices of Superior Frontal/Premotor Regions.

Result from two locations (50,−12,56) and (−32,−4,65). First Column: Slice y=−12 from the MNI template (top) and the Talairached Brain (bottom). Second Column: Top: The location of this point on the original MNI template using a piecewise mapping (red cross-hairs). Bottom: The location of the same point on the Talairached-MNI brain. The third and fourth columns are repeats for location (51,−78,1).

4 Discussion & Conclusions

Using a non-linear registration lookup table as opposed to a piecewise linear mapping yields more accurate mapping of Talairach coordinates. In the piecewise mapping, coordinates can appear outside the brain, whereas using the new method, the coordinates localize accurately to the edge of the brain as in the Talairach atlas. The overall difference between piecewise mapping and non-linear registration ranges from as much as 4–5 mm in cortical regions to practically zero in subcortical regions. Hence our new method can be used to improve on the accuracy of reporting Talairach coordinates.

The existing methods (Lancaster et al. (2007); Brett et al. (2001)) are limited by the relative inflexibility of the transformation model chosen. The first reference (icbm2tal Lancaster et al. (2007)), uses an optimal linear affine mapping. While this is optimized to be the best possible mapping over a large number of brains given the mapping accuracy of a number of key landmarks selected in all these brains, it still results in a linear transformation and is unable to account for shape differences between the individual brains (or the MNI template) and the Talairach brain. Some of the issues of points that lie on the brain surface in Talairach space mapping to points well outside the brain in the MNI template can be observed using this model.

The mni2tal method (Brett et al. (2001)) while in name nonlinear, is only nonlinear in the most technical sense. It essentially is a piecewise linear method where there are two linear transformations one for the top half and one for the bottom half of the brain. It has a maximum of 24 parameters. Our method is fully non-linear in the sense usually used for non-linear registration methods (or spatial normalization). It has about 3,000 degrees of freedom. This allows for a registration that accounts for the differences in shape, as opposed to simply position, orientation and scale between the two brains. On a secondary note, the mni2tal method is also not-invertible in the region close to the boundary between the upper part of the brain and the lower part of the brain. As a result, two different points in MNI space can potentially be mapped to the same point in Talairach space.

Each method, naturally, has its own limitations. Our mapping is based on the outer surface of the brain alone; a smoothness constraint is used to propagate the estimate correspondences there to yield a smooth whole brain transformation map, as illustrated in Figure 6. The mapping will thus be more accurate on or close to the brain surface and less accurate elsewhere. In future work we will add outlines of interior brain structures to augment this. However, given the limited accuracy possible (the original atlas only has 27 axial slices) we are now entering into the problem of diminishing returns. In addition, we note that the cerebellum in the Talairach atlas is fairly crude and used a smooth version of this as part of the outer brain surface to ensure algorithmic stability. Clearly the accuracy of any method of this form is highly limited in the area of the cerebellum given the lack of atlas information there.

While our method is a mapping from the Colin27 brain (which is in MNI space) to Talairach space, it can be also used from any brain, by first non-linearly registering (using any one of several available methods) to the Colin27 brain first, and then using our mapping to convert from the space of the Colin27 brain to Talairach brain. The Colin27 brain was chosen because it is both widely used as a reference (e.g. SPM) and because unlike many templates (e.g. MNI 305) it is a high contrast (i.e. not blurry) brain and can be easily used with powerful non-rigid registration methods.

Availability

The methodology is available as part of the BioImage Suite software (www.bioimagesuite.org) (Papademetris et al. (2006)), it is also available online in a custom Java applet – this is shown in Figure 11.

Fig. 11. The MNI to Talairach Conversion Applet.

We would happy to see this methodology incorporated into other software packages if researchers find it useful. The actual implementation is a lookup table image which has the same dimensions as the MNI T1 1mm template (181×217×181) and 3 components (frames). At each voxel of the image (which is in MNI space) the 3 components represent the Talairach coordinates of the voxel (multiplied by 10). Since, BioImage Suite is open source (GPL) and has a fairly liberal redistribution policy, any other user/software wishing to use this lookup table setup internally or incorporate this into other software, can simply use/redistribute this lookup table with proper attribution.