Causal Vaccine Effects on Binary Postinfection Outcomes

Abstract

The effects of vaccine on postinfection outcomes, such as disease, death, and secondary transmission to others, are important scientific and public health aspects of prophylactic vaccination. As a result, evaluation of many vaccine effects condition on being infected. Conditioning on an event that occurs posttreatment (in our case, infection subsequent to assignment to vaccine or control) can result in selection bias. Moreover, because the set of individuals who would become infected if vaccinated is likely not identical to the set of those who would become infected if given control, comparisons that condition on infection do not have a causal interpretation. In this article we consider identifiability and estimation of causal vaccine effects on binary postinfection outcomes. Using the principal stratification framework, we define a postinfection causal vaccine efficacy estimand in individuals who would be infected regardless of treatment assignment. The estimand is shown to be not identifiable under the standard assumptions of the stable unit treatment value, monotonicity, and independence of treatment assignment. Thus selection models are proposed that identify the causal estimand. Closed-form maximum likelihood estimators (MLEs) are then derived under these models, including those assuming maximum possible levels of positive and negative selection bias. These results show the relations between the MLE of the causal estimand and two commonly used estimators for vaccine effects on postinfection outcomes. For example, the usual intent-to-treat estimator is shown to be an upper bound on the postinfection causal vaccine effect provided that the magnitude of protection against infection is not too large. The methods are used to evaluate postinfection vaccine effects in a clinical trial of a rotavirus vaccine candidate and in a field study of a pertussis vaccine. Our results show that pertussis vaccination has a significant causal effect in reducing disease severity.

1. INTRODUCTION

The success of vaccines in reducing the burden of infectious diseases is one of the great achievements in public health. The goal of vaccination is often not to prevent infection, but rather to prevent or to ameliorate disease (Clements-Mann 1998). Therefore, many questions of interest in understanding the effects of prophylactic vaccines concern postinfection outcomes, such as severe disease, death, or transmission to others. As early as 1939, Kendrick and Eldering described less severe disease in children inoculated with pertussis vaccine. More recently, Préziosi and Halloran (2003a) estimated the beneficial effects of pertussis vaccination on reducing transmission to others (see also Halloran, Préziosi, and Chu 2003) and preventing severe disease (Préziosi and Halloran 2003b) in breakthrough cases. Individuals with varicella (chickenpox) vaccination also develop less severe disease (Vazquez et al. 2001). Assessing candidate human immunodeficiency virus (HIV) vaccine effects on progression to AIDS through both clinical and surrogate postinfection endpoints (Gilbert, Bosch, and Hudgens 2003a) as well as on transmission (Longini, Datta, and Halloran 1996) is crucial for evaluating their potential public health benefit.

Two main approaches are currently used for estimating postinfection effects of vaccines. The first approach includes all individuals under study, whether they become infected or not; the second includes only the individuals who become infected. The first approach enjoys the statistical validity associated with an intent-to-treat (ITT) analysis and provides an assessment of the overall benefit of vaccination. However, such an approach does not distinguish vaccine effects on susceptibility to infection from effects on the postinfection endpoints of interest. Also, it may be less sensitive in detecting postinfection vaccine effects than an analysis that conditions on infection. The second approach conditions on infection to estimate a net effect of the vaccine on the postinfection endpoint in just those people who become infected. However, conditioning on an event, such as infection, that occurs subsequent to receipt of vaccine or control may result in selection bias (Halloran and Struchiner 1995). Because the set of individuals who would become infected if vaccinated is likely not identical to the set of those who would become infected if given control, comparisons that condition on infection do not have a causal interpretation (Frangakis and Rubin 2002). For example, a vaccine might protect only people with strong immune systems, so that infected vaccinees tend to have weaker immune systems on average compared with infected controls. As a result, infected vaccinees could have worse postinfection outcomes on average than the infected controls due solely to selection bias. The resulting false conclusion that vaccination is harmful with respect to postinfection outcomes could result in the discarding of a potentially useful vaccine candidate (Hudgens, Hoering, and Self 2003; Gilbert et al. 2003a).

As a first motivating example, Préziosi and Halloran (2003b) analyzed data from a pertussis vaccine field study in Niakhar, Senegal from January 1 to December 31, 1993, in children age 6 months through 8 years. During that one calendar year, there were 3,845 and 1,020 person-years at risk in the vaccinated and unvaccinated children (M.-P. Préziosi, personal communication). Of 548 cases in the vaccinated group, 176 were severe, and of 206 cases in the unvaccinated group, 129 were severe. Préziosi and Halloran (2003b) defined an estimator of vaccine efficacy against severe disease conditional on being infected and having disease as

$${\widehat{\mathrm{VE}}}_P=1-\frac{\frac{\text{no. severe vaccinated cases}}{\text{no. vaccinated cases}}}{\frac{\text{no. severe unvaccinated cases}}{\text{no. unvaccinated cases}}}.$$ (1)

The analysis yields ${\widehat{\mathrm{VE}}}_P=.49$, 95% confidence interval (CI) = (.40, .56).

Vesikari, Rautanen, Varis, Beards, and Kapikian (1990) provided a second motivating example in their analysis of a randomized, double-blinded, placebo-controlled trial of a Rhesus rotavirus candidate vaccine. The trial was conducted in children age 2–5 months in 1985–1987 in Finland, with 100 children randomized to each arm. The effect of the vaccine on the clinical course of infection was considered by comparing severity (mild, moderate, or severe) between vaccinees and placebotreated individuals with confirmed Rotavirus diarrhea using Fisher’s exact test. If severe and moderately severe cases were combined, then the foregoing approach of Préziosi and Halloran could also be used. In particular, of 10 cases in the vaccinated group, 5 were severe or moderately severe, and of 16 cases in the placebo group, 13 were severe or moderately severe, such that, using (1), we have ${\widehat{\mathrm{VE}}}_P=.38$, 95% CI=(-.11,.74).

At first glance, both vaccines seem to be protective against severe disease. However, due to the possibility of selection bias, we cannot be sure of this without further investigation. Different methods are used to adjust analyses for posttreatment variables, such as infection (Robins and Greenland 1992, 1994; Rosenbaum 1984). Our approach is based on an extension of the potential outcomes framework for estimating causal effects (Rubin 1978; Holland 1986). In particular, Frangakis and Rubin (2002) and Rubin (2000) proposed a method to adjust for posttreatment variables, called principal stratification, that stratifies on the joint potential posttreatment variables (e.g., infection) under each treatment being considered. The causal effects of one treatment compared with the other on a main outcome of interest (e.g., disease severity) are defined within these principal strata and are called principal effects. In studying HIV vaccines, Hudgens et al. (2003) and Gilbert et al. (2003b) adopted the principal stratification approach to assess HIV vaccine effects on the continuous postinfection outcome viral load in the principal stratum of individuals who would be infected under vaccine and placebo. However, they focused on testing, and did not consider binary postinfection endpoints.

In this article we use a similar approach, but in contrast to the previous work, here we use principal stratification to define causal vaccine effects on binary postinfection endpoints and focus on estimation and identifiability. We also analyze data from two actual vaccine studies. In Section 2 we formally define the estimands, particularly the causal estimand of interest and two currently used estimands for vaccine effects on postinfection outcomes, and state our three main assumptions of stable unit treatment value (SUTVA), independence, and monotonicity. In Section 3 we show the causal estimand to be not identifiable without further assumptions regarding the selective mechanism of the vaccine. In Section 4 we developed a variety of selection models that identify the causal estimand. We then derive closedform maximum likelihood estimators (MLEs) under several of these models, including the models that assume maximum possible levels of positive and negative selection bias. Using these approaches, we analyze the rotavirus vaccine candidate and the pertussis vaccine studies.

2. DEFINING VACCINE EFFECTS

Consider a group of individuals, i = 1,…,n, each of whom potentially receives either vaccine or placebo. Following the notation of Rubin (1990a) and similar to the development of Gilbert et al. (2003b), let the vector Z = (Z₁,…,Z_n) denote the vector of treatment assignments for n individuals with Z_i = v if the ith individual is assigned vaccine and Z_i = p if the ith individual is assigned placebo or control. In this article assignment is assumed to be equivalent to receipt. Denote the potential infection outcome of the ith individual if the study group were assigned Z as S_i(Z), where S_i(Z) = 0 if uninfected and S_i(Z) 1 if infected. Then S(Z) is the n-vector of potential infection outcomes if the assignment vector were Z. For simplicity, we suppress the dependence on Z by letting S = S(Z). The focus of this work is on evaluating the causal effect of vaccine on a binary outcome Y that occurs after an individual becomes infected, such as transmission to another individual, severe disease, or death. Formally, if S_i(Z) = 1, then we define the potential postinfection outcome Y_i(Z, S) 1 if the ith individual would have the worse (i.e., more severe) postinfection outcome of interest given (Z, S), and Y_i(Z, S) = 0 otherwise. If an individual’s potential infection outcome for an assignment is uninfected [i.e., S_i(Z) = 0], then Y_i(Z, S) is undefined and denoted by *.

We assume that the potential outcomes for each individual i are independent of the treatment assignment of other individuals. This assumption, known also as the assumption of no interference between units (Cox 1958), is obviously violated in many infectious disease settings (Rubin 1978, 1990a; Halloran and Struchiner 1995); however, we make it to clarify the problem in its simplest form. We also assume there are only two possible infection outcomes and, at most, two possible postinfection outcomes. These two assumptions are expressed formally as follows.

Assumption 1

Stable unit treatment value assumption (SUTVA) (Rubin 1978; Angrist, Imbens, and Rubin 1996). For any two treatment assignments, Z = (Z₁,…,Z_n) and ${\mathrm{Z}}^{\prime }=(Z_1^{\prime },\dots ,Z_n^{\prime })$, the following hold:

1. If $Z_i=Z_i^{\prime }$, then S_i(Z) = S_i(Z′).

2. If $Z_i=Z_i^{\prime }$ and $S_i=S_i^{\prime }$, then Y_i(Z,S) = Y_i(Z′, S′).

The SUTVA assumption allows us to write S_i(Z_i) and Y_i(Z_i, S_i(Z_i)) rather than S_i(Z) and Y_i(Z, S). Under SUTVA, $S_i\left(Z_i\right)=S_i\left(Z_i^{\prime }\right)$ whenever $Z_i=Z_i^{\prime }$, so we can write Y_i(Z_i) instead of Y_i(Z_i, S_i(Z_i)). Finally, we let $S_i^{\mathrm{obs}}$ denote the observed infection outcome S_i(v) or S_i(p), depending on treatment assignment, and analogously, $Y_i^{\mathrm{obs}}$ for the observed postinfection outcome.

We define a basic principal stratification, P₀, according to the joint potential infection outcomes S^P₀ = (S(v), S(p)) (Frangakis and Rubin 2002). Table 1 summarizes the four basic principal strata defined by the joint potential infection outcomes, (S(v), S(p)), and the strata defined by the joint potential postinfection outcomes, (Y(v), Y(p)), within each principal stratum. The four basic principal strata are composed of immune (not infected under both vaccine and placebo), harmed (infected under vaccine but not placebo), protected (infected under placebo but not vaccine), and doomed individuals (infected under both vaccine and placebo). Because membership in a basic principal stratum is not affected by whether an individual is actually assigned to vaccine or placebo, the strata can be used in the same way as pretreatment covariates, with causal postinfection vaccine effects defined within a basic principal stratum S^P₀.

Table 1.

Basic Principal Stratification P₀ Based on the Potential Infection Outcomes (S(v), S(p)) With Potential Postinfection Strata Based on (Y(v), Y(p))

Potential infection strata		Potential postinfection strata
Basic principal stratum, SP0	Potential infection outcomes (S(v), S(p))	Potential postinfection outcomes (Y(v), Y(p))	Postinfection interpretation
Immune	(0, 0)	(*, *)	Always undefined
Harmed	(1, 0)	(0, *)	Not severe vaccine, undefined placebo
		(1, *)	Severe vaccine, undefined placebo
Protected	(0, 1)	(*, 0)	Undefined vaccine, not severe placebo
		(*, 1)	Undefined vaccine, severe placebo
Doomed	(1, 1)	(0, 0)	Never severe
		(1, 0)	Harmed by vaccine
		(0, 1)	Helped by vaccine
		(1, 1)	Always severe

In general, causal effects are defined in terms of potential outcomes. Table 1 shows that the doomed basic principal stratum, S^P₀ = (1, 1), is the only stratum in which both potential postinfection endpoints, and thus their joint distribution, are defined. For this reason, in our setting, defining individual postinfection causal vaccine effects makes sense only in the doomed basic principal stratum, S^P₀ = (1, 1). In other words, we can speak of a vaccine causing an improvement or worsening of a postinfection outcome only for an individual who would become infected whether vaccinated or not. Thus, following Rubin (2000), two population-level causal estimands can be validly defined: (1) the effect of vaccine on infection (S) for all participants, and (2) the effect of vaccine on the binary postinfection outcome (Y) for those participants who would be infected under both treatment assignments.

To define the first causal estimand, the individual causal effect of vaccination on infection in individual i might be expressed as a difference or ratio (Rubin 1990b),

$$S_i\left(p\right)-S_i\left(v\right)\text{or}\frac{S_i\left(v\right)}{S_i\left(p\right)}.$$ (2)

Vaccine efficacy is typically expressed in terms of a relative risk difference, so that, similar to Struchiner and Halloran (1996), we define the individual causal effect of vaccination on infection as

$${\mathrm{VE}}_{Si}=\frac{S_i\left(p\right)-S_i\left(v\right)}{S_i\left(p\right)}=1-\frac{S_i\left(v\right)}{S_i\left(p\right)},$$ (3)

with the convention VE_Si = 0 when S_i(v) = S_i(p) = 0. Recall that we assume there is perfect compliance; that is, assignment to vaccine (control) is equivalent to receipt of vaccine (control). Without this assumption, (2) and (3) would be causal effects of assignment to vaccine. The ramifications of noncompliance on the assessment of causal vaccine effects are not considered here.

Because for any individual at least one potential outcome is always unobserved, the individual causal effect of vaccine on infection cannot be observed. Therefore, one must rely on contrasts between different individuals to estimate average or population-level causal effects (Holland 1986). Given the individual causal effect (3), similar to Struchiner and Halloran (1996) and Gilbert et al. (2003b), we define the corresponding population causal vaccine effect by

$${\mathrm{VE}}_S=\frac{E\{S\left(p\right)-S\left(v\right)\}}{E\left\{S\right(p\left)\right\}}=\frac{E\left\{S\left(p\right)\right\}-E\left\{S\left(v\right)\right\}}{E\left\{S\left(p\right)\right\}}=1-\frac{E\left\{S\left(v\right)\right\}}{E\left\{S\left(p\right)\right\}}.$$

We call this the relative average causal effect (RACE) of vaccination on infection. Because S(v) and S(p) are binary, the expectations can be replaced by probabilities, and VE_S can be interpreted as the relative reduction in the probability of infection given vaccine compared with control.

Estimation of population average causal effects requires specification of the assignment mechanism (Rubin 1990b), that is, how the individuals were assigned to vaccine or placebo. We assume that treatment assignment is independent of the potential outcomes.

Assumption 2

Z is independent of {Y(v), Y(p), S(v), S(p)}.

Here and in the sequel, Y(z) = * if S(z) = 0 for z = v, p. Randomization is one assignment mechanism where the treatment assignment is independent of the potential outcomes. It now follows

$${\mathrm{VE}}_S=1-\frac{E\{S\left(v\right)\mid Z=v\}}{E\{S\left(p\right)\mid Z=p\}}=1-\frac{E\{S^{\mathrm{obs}}\mid Z=v\}}{E\{S^{\mathrm{obs}}\mid Z=p\}}.$$

Next we define three estimands regarding the effect of vaccination on the postinfection outcome Y. Usually, the notation VE_I is used specifically for vaccine efficacy for infectiousness, that is, the effect of vaccination on transmission to others (Halloran, Struchiner, and Longini 1997), and VE_P is used for vaccine efficacy for progression or severity as in (1). Here we use VE_I throughout the development to refer to vaccine efficacy for any binary postinfection outcome. This enables us to use standard notation for the secondary attack rate (SAR), the probability of transmission from an infected to a susceptible individual. In the development that follows, SAR is defined more generally as the proportion of infected individuals with the worse postinfection outcome.

One current approach to assessing vaccine effects on postinfection endpoints defines a net vaccine effect estimand that conditions on infection, that is,

$$\begin{array}{cc}\hfill {\mathrm{VE}}_I^{\text{net}}& =1-\frac{E\{Y^{\mathrm{obs}}\mid S^{\mathrm{obs}}=1,Z=v\}}{E\{Y^{\mathrm{obs}}\mid S^{\mathrm{obs}}=1,Z=p\}}\hfill \\ \hfill & =1-\frac{E\{Y\left(v\right)\mid S\left(v\right)=1\}}{E\{Y\left(p\right)\mid S\left(p\right)=1\}},\hfill \end{array}$$

with the second equality following from Assumption 2. However, in general ${\mathrm{VE}}_I^{\text{net}}$ does not have a causal interpretation, because the set of individuals with S(v) = 1 is not necessarily identical to the set of individuals with S(p) = 1 (Rosenbaum 1984; Frangakis and Rubin 2002).

Another current approach defines an estimand for the effect of vaccination on different levels of severity of disease or mortality without conditioning on being infected. Such an estimand might be considered ITT, because it does not condition on the posttreatment variable S^obs; that is, it incorporates all individuals according to their treatment assignment. An example of an ITT estimand is

$${\mathrm{VE}}_I^{\mathrm{ITT}}=1-\frac{E\{Y\left(v\right)\times S\left(v\right)\}}{E\{Y\left(p\right)\times S\left(p\right)\}},$$

where we adopt the convention Y(z) × S(z) = 0 if S(z) = 0, z = v, p. This is a general form for what Préziosi and Halloran (2003b) called “VE_S for severity.” Although ${\mathrm{VE}}_I^{\mathrm{ITT}}$ does have a causal interpretation, it combines vaccine effects on susceptibility and postinfection outcome as shown by the following relation:

$${\mathrm{VE}}_I^{\mathrm{ITT}}=1-(1-{\mathrm{VE}}_S)(1-{\mathrm{VE}}_I^{\text{net}}).$$

We propose a third estimand for the effect of vaccination on a binary postinfection outcome that has a causal interpretation and is separate from vaccine effects on susceptibility. To define the causal VE_I, we use the basic principal stratification shown in Table 1. In particular, the individual causal vaccine effect on the postinfection outcomes is defined as

$${\mathrm{VE}}_{\mathit{Ii}}=1-\frac{Y_i\left(v\right)}{Y_i\left(p\right)},$$

for individuals within the doomed principal stratum only. Following the development of VE_S earlier, we define the population postinfection causal vaccine effect VE_I within the doomed principal stratum as

$${\mathrm{VE}}_I=1-\frac{E\{Y\left(v\right)\mid S^{P_0}=(1,1)\}}{E\{Y\left(p\right)\mid S^{P_0}=(1,1)\}}.$$ (4)

Like VE_S, (4) could equivalently be given in terms of probabilities, because the postinfection random variables Y(v) and Y(p) are assumed to be binary, such that VE_I can be interpreted as the causal estimand measuring the relative reduction in the probability of the worse postinfection outcome given vaccine compared with placebo in those individuals who would be infected under either treatment assignment. The challenge in estimating principal effects such as (4) lies in identifying those individuals in the doomed basic principal stratum, because at most one potential infection outcome is ever observed for a particular individual. To help overcome this obstacle, we make the following monotonicity assumption.

Assumption 3

Monotonicity. The individual causal effect of vaccination on infection is nonnegative; that is, VE_Si ≥ 0 for all i.

Under this assumption, an individual who would become infected under vaccine also would become infected under placebo, so the harmed principal stratum S^P₀ = (1, 0) is empty. In the context of possible noncompliance with treatment assignment, Angrist et al. (1996) and Imbens and Rubin (1997) made a monotonicity assumption akin to Assumption 3, which immediately eliminates the basic principal stratum of defiers (persons who would always take the opposite of their treatment assignment). By Assumption 3, we are not assuming that the individual postinfection causal effect of vaccination is nonnegative; rather, we allow that vaccination could have a negative (i.e., harmful) causal effect on the postinfection outcome. Indeed, one of our goals is to identify the conditions under which it could be determined the postinfection causal effect is negative.

Under Assumption 3, for each possible observed combination of $(Z_i,S_i^{\mathrm{obs}})$, we can deduce to which basic principal stratum an individual must belong:

$$\begin{array}{cc}\hfill & (Z_i=p,S_i^{\mathrm{obs}}=0)\to S^{P_0}=(0,0)(\text{because}{\mathrm{VE}}_{Si}\ge 0),\hfill \\ \hfill & (Z_i=p,S_i^{\mathrm{obs}}=1)\to S^{P_0}=(0,1)\text{or}{S}^{P_0}=(1,1),\hfill \\ \hfill & (Z_i=v,S_i^{\mathrm{obs}}=0)\to S^{P_0}=(0,1)\text{or}{S}^{P_0}=(0,0),\hfill \\ \hfill & (Z_i=v,S_i^{\mathrm{obs}}=1)\to S^{P_0}=(1,1)(\text{because}{\mathrm{VE}}_{Si}\ge 0).\hfill \end{array}$$

Thus the infected vaccine recipients will immediately provide information about the distribution of the postinfection outcome Y(v) in the doomed principal stratum. However, getting a handle on Y(p) in S^P₀ = (1, 1) is still problematic, because infected placebo recipients may be members of either the protected or the doomed principal stratum. In Section 4 we derive models that allow us to identify the distribution of Y(p) in the doomed principal stratum and, in turn, the postinfection causal vaccine effect VE_I given in (4).

3. IDENTIFIABILITY AND ESTIMATION OF VACCINE EFFECTS

In this section we investigate identifiability and estimation of the estimands defined in the previous section under Assumptions 1–3 only.

3.1 Parameterization

Let the parameters θ govern the probabilities associated with the basic principal stratum. In our case the stratum S^P₀ is empty, so let θ = (θ₀₀, θ₀₁, θ₁₁), where

$$\mathrm{Pr}\{S^{P_0}=(i,j,);\theta \}={\theta }_{ij}\text{for}i,j=0,1;i\le j.$$ (5)

Next, let the parameters ϕ = (ϕ₀₀, ϕ₀₁, ϕ₁₀, ϕ₁₁) govern the probabilities associated with the joint potential postinfection outcomes in the doomed basic principal stratum S^P₀ = (1, 1), where

$$\mathrm{Pr}\{\left(Y\right(v),Y\left(p\right))=(k,m)\mid S^{P_0}=(1,1);\varphi \}={\varphi }_{\mathit{km}}\text{for}k,m=0,1.$$ (6)

Let the parameters γ = (γ₀, γ₁) govern the probabilities associated with the two possible potential postinfection outcomes under placebo in the protected basic principal stratum, S^P₀ = (0, 1), where

$$\mathrm{Pr}\{Y\left(p\right)=i\mid S^{P_0}=(0,1);\gamma \}={\gamma }_l\text{for}l=0,1.$$ (7)

Finally, let the law of Z be given by Pr{Z=z; ψ}=ψ_z for z = v, p.

Under this parameterization, the causal estimand of vaccine efficacy for susceptibility is

$${\mathrm{VE}}_S=1-\frac{{\theta }_{11}}{{\theta }_{01}+{\theta }_{11}}.$$

Based on the definition of the causal estimand VE_I given in (4), we are interested not in the joint probabilities ϕ_km(k,m=0,1), but rather in just two of the marginal probabilities. In particular, under the foregoing parameterization,

$${\mathrm{VE}}_I=1-\frac{{\varphi }_1.}{{\varphi }_{.1}},$$ (8)

where

$$\mathrm{Pr}\{Y\left(v\right)=1\mid S^{P_0}=(1,1)\}={\varphi }_{10}+{\varphi }_{11}={\varphi }_1.$$

and

$$\mathrm{Pr}\{Y\left(p\right)=1\mid S^{P_0}=(1,1)\}={\varphi }_{01}+{\varphi }_{11}={\varphi }_{.1}.$$

We also have

$${\mathrm{VE}}_I^{\text{net}}=1-\frac{{\varphi }_1.}{{\gamma }_1{\mathrm{VE}}_S+{\varphi }_{.1}(1-{\mathrm{VE}}_S)}$$

and

$${\mathrm{VE}}_I^{\mathrm{ITT}}=1-\frac{{\varphi }_1.(1-{\mathrm{VE}}_S)}{{\gamma }_1{\mathrm{VE}}_S+{\varphi }_{.1}(1-{\mathrm{VE}}_S)}.$$

3.2 Identifiability

Without further assumptions, VE_I is not identifiable from the observable random variables (Y^obs, S^obs, Z). To see this, first write the probability function for the observable random variables Pr[Z=z,S^obs=s,Y^obs=y; θ, γ, ϕ ψ] as

$$\begin{array}{c}{\theta }_{00}{\psi }_{p}I(z=p,s=0,y=\ast )\hfill \\ \hfill +\{{\theta }_{01}+{\theta }_{11}-({\theta }_{01}{\gamma }_1+{\theta }_{11}{\varphi }_{.1})\}{\psi }_{p}I(z=p,s=1,y=0)\hfill \\ \hfill +({\theta }_{01}{\gamma }_1+{\theta }_{11}{\varphi }_{.1}){\psi }_{p}I(z=p,s=1,y=1)\hfill \\ \hfill +({\theta }_{00}+{\theta }_{01}){\psi }_{v}I(z=v,s=0,y=\ast )\hfill \\ \hfill +{\theta }_{11}(1-{\varphi }_1.){\psi }_{v}I(z=v,s=1,y=0)\hfill \\ \hfill +{\theta }_{11}{\varphi }_1.{\psi }_{v}I(z=v,s=1,y=1),\end{array}$$ (9)

where I(·) is the usual indicator function. Next, suppose that we have θ₀₁ = θ₁₁, ϕ_.1=∊, and γ₁=1-∊ for ∊ ε ∈ (0,1). Then the probability function given in (9) is constant for different values of ∊. Moreover, VE_I =1-ϕ_1./∊ depends on the choice of ∊, indicating that VE_I is not identifiable. In contrast, the estimands VE_S, ${\mathrm{VE}}_I^{\mathrm{ITT}}$, and ${\mathrm{VE}}_I^{\text{net}}$ are identifiable without further assumptions.

3.3 Estimation

Suppose that we observe n independent and identically distributed realizations of (Z, S^obs, Y^obs), where Y^obs is undefined or does not exist if S^obs = 0. There are six possible observed combinations of (Z, S^obs, Y^obs). Let n_sy(z) be the number of each combination observed in the study population, where s = 0, 1 is the observed infection outcome S^obs; y = 0, 1, * is the observed postinfection outcome Y^obs; and z = v, p. That is,

$$\begin{array}{cc}\hfill & n_{0\ast }\left(p\right)=\sum _{i}I(Z_i=p,S_i^{\mathrm{obs}}=0,Y_i^{\mathrm{obs}}\text{does not exist}),\hfill \\ \hfill & n_{10}\left(p\right)=\sum _{i}I(Z_i=p,S_i^{\mathrm{obs}}=1,Y_i^{\mathrm{obs}}=0),\hfill \\ \hfill & n_{11}\left(p\right)=\sum _{i}I(Z_i=p,S_i^{\mathrm{obs}}=1,Y_i^{\mathrm{obs}}=1)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & n_{0\ast }\left(v\right)=\sum _{i}I(Z_i=v,S_i^{\mathrm{obs}}=0,Y_i^{\mathrm{obs}}\text{does not exist}),\hfill \\ \hfill & n_{10}\left(v\right)=\sum _{i}I(Z_i=v,S_i^{\mathrm{obs}}=1,Y_i^{\mathrm{obs}}=0),\hfill \\ \hfill & n_{11}\left(v\right)=\sum _{i}I(Z_i=v,S_i^{\mathrm{obs}}=1,Y_i^{\mathrm{obs}}=1),\hfill \end{array}$$

where the summations are over i = 1,…,, n. (Note that the double subscripts do not have the same meaning for the n’s as for the ϕ’s and θ’s.) We assume each of the six combinations is observed at least once, that is, n_sy(z) > 0 for (s, y) = (0, *), (1, 0), (1, 1) and z = v, p. Let n(p) = n_0*(p) + n₁₀(p) + n₁₁(p) and n(v) = n_0*(v) + n₁₀(v) + n₁₁(v) denote the number of individuals assigned to placebo and to vaccine. Let n₁.(p) = n₁₀(p) + n₁₁(p) and n₁.(v) = n₁₀(v) + n₁₁(v) denote the number of infected individuals assigned to placebo and vaccine. Let

$${\mathit{AR}}_z=\frac{n_1.\left(z\right)}{n\left(z\right)}\text{for}z=v,p;$$

that is, AR_z is the observed attack rate in the group assigned treatment z. Finally, let

$${\mathit{SAR}}_z=\frac{n_{11}\left(z\right)}{n_1.\left(z\right)}\text{for}z=v,p;$$

that is, SAR_z is the observed secondary attack rate in the group infected given treatment z.

MLEs of the identifiable vaccine efficacy estimands can be found by maximizing the likelihood

$$L(\theta ,\gamma ,\varphi )\propto \prod _{i=1}^n\mathrm{Pr}[Y_i^{\mathrm{obs}}=\mathit{yi},S_i^{\mathrm{obs}}=s_i\mid {\mathrm{Z}}_i=z_i;\theta ,\gamma ,\varphi ],$$

subject to constraints on θ, γ, and ϕ that ensure that (5)–(7) are probability functions. Using the results from the Appendix, it follows that the MLE of VE_S is given by

$${\widehat{\mathrm{VE}}}_S=\{\begin{array}{cc}1-\frac{{\mathit{AR}}_v}{{\mathit{AR}}_p}\hfill & \text{if}{\mathit{AR}}_v\le {\mathit{AR}}_p\hfill \\ 0\hfill & \text{otherwise.}\hfill \end{array}\phantom{\}}$$ (10)

Further, the MLEs of ${\mathrm{VE}}_I^{\mathrm{ITT}}$ and ${\mathrm{VE}}_I^{\mathrm{net}}$ are

$${\widehat{\mathrm{VE}}}_I^{\text{net}}=1-\frac{{\mathit{SAR}}_v}{{\mathit{SAR}}_p}$$ (11)

and

$${\widehat{\mathrm{VE}}}_I^{\mathrm{ITT}}=1-(1-{\widehat{\mathrm{VE}}}_S)\frac{{\mathit{SAR}}_v}{{\mathit{SAR}}_p}$$ (12)

or, equivalently,

$${\widehat{\mathrm{VE}}}_I^{\mathrm{ITT}}=\{\begin{array}{cc}{\widehat{\mathrm{VE}}}_I^{\text{net}}\hfill & \text{if}{\widehat{\mathrm{VE}}}_S=0\hfill \\ 1-\frac{n_{11}\left(v\right)∕n\left(v\right)}{n_{11}\left(p\right)∕n\left(p\right)}\hfill & \text{if}{\widehat{\mathrm{VE}}}_S>0.\hfill \end{array}\phantom{\}}$$ (13)

The causal estimand VE_I is not identifiable because ϕ.1, the denominator of the right side of (8), is not identifiable. But ϕ_1., the numerator of the right side of (8), can be identified by the observable random variables. The corresponding MLE is given by

$${\widehat{\varphi }}_1.={\mathit{SAR}}_v,$$ (14)

that is, the observed secondary attack rate in the vaccine arm. Finally, although ϕ_.1 is not identifiable, we can identify

$$\mathrm{Pr}[Y\left(p\right)=1\mid S\left(p\right)=1;\theta ,\gamma ,\varphi ]={\gamma }_1{\mathrm{VE}}_S+{\varphi }_{.1}(1-{\mathrm{VE}}_S).$$ (15)

The MLE of (15) is SAR_p such that any feasible pair $({\widehat{\gamma }}_1,{\widehat{\varphi }}_{.1})$satisfying

$${\mathit{SAR}}_p={\widehat{\gamma }}_1{\widehat{\mathrm{VE}}}_S+{\widehat{\varphi }}_{.1}(1-{\widehat{\mathrm{VE}}}_S)$$ (16)

is an MLE of (γ₁, ϕ_.1). In the following section we introduce selection models that identify (γ₁, ϕ_.1). These models add an additional constraint to the parameters such that there is only one feasible pair $({\widehat{\gamma }}_1,{\widehat{\varphi }}_{.1})$ that satisfies (16). Because the value of the likelihood remains the same, we have the unique MLE of ϕ_.1 and, therefore, VE_I. Before proceeding, we revisit our examples.

3.4 Applications

3.4.1 Rotavirus Candidate Vaccine

In the rotavirus candidate vaccine study (Vesikari et al. 1990), the observed data were

$$\begin{array}{cc}\hfill n_{0\ast }\left(p\right)=84,\hfill & \hfill n_{0\ast }\left(v\right)=90,\hfill \\ \hfill n_{10}\left(p\right)=3,\hfill & \hfill n_{10}\left(v\right)=5,\hfill \\ \hfill n_{11}\left(p\right)=13,\hfill & \hfill n_{11}\left(v\right)=5.\hfill \end{array}$$

From (10), ${\widehat{\mathrm{VE}}}_S=1$ – (10/100)/(16/100) = .375. It then follows from (13) that ${\widehat{\mathrm{VE}}}_I^{\mathrm{ITT}}=1$ – (5/100)/(13/100) = .62. The secondary attack rates are ${\mathit{SAR}}_v={\widehat{\varphi }}_{1.}=5∕10=.50$ and SAR_p = 13/16 = .81, such that ${\widehat{\mathrm{VE}}}_I^{\mathrm{net}}=1$ – (5/10)/(13/16) = .385.

To consider estimation of _VEI, Table 2 shows the relation of the observed data to the basic principal strata and the strata of joint potential postinfection outcomes within each basic principal stratum. By Assumptions 1–3, we know the following:

• All n₁₀(v) + n₁₁(v) = 10 belong to the doomed stratum S^P0 = (1, 1).

• All n_0*(p) = 84 belong to the immune stratum S^P0 = (0, 0).

• The n_0*(v) = 90 could belong to S^P0 = (0, 0) or S^P0 = (0, 1).

• The n₁₀(p) + n₁₁(p) = 16 could belong to S^P0 = (0, 1) or S^P0 = (1, 1).

Ignoring statistical variability, by Assumption 2 (independence), because there are 10 vaccine recipients in the doomed stratum, there are 10 placebo recipients in the doomed stratum as well. Because there are 84 placebo recipients in the immune stratum, there are 84 vaccine recipients in the immune stratum as well. Thus there must be 6 recipients from each of the vaccinated and unvaccinated groups in the protected stratum. Thus we can estimate the size of the unobserved principal stratum S^P₀ = (0, 1). However, we do not know which 6 of the 16 infected placebo recipients are in the protected stratum S^P₀ = (0, 1) or which 10 of the 16 are in the doomed stratum S^P₀ = (1, 1). This illustrates the need for further assumptions to identify VE_I.

Table 2.

Rotavirus Vaccine Example (Vesikari et al. 1990): Relation of Observed Data to the Basic Principal Strata of the Joint Potential Infection Outcomes and the Strata of Joint Potential Postinfection Outcomes

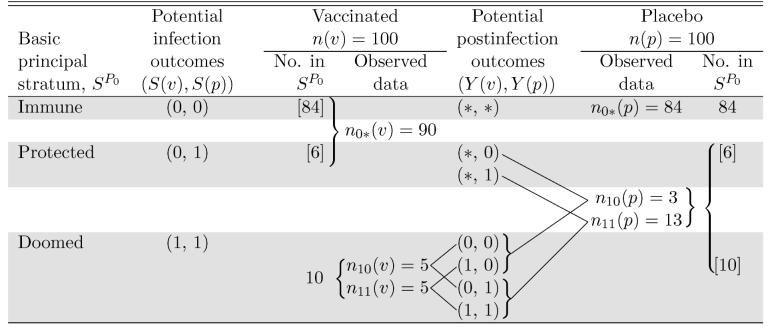NOTE: The shaded regions correspond to membership within the basic principal strata with observations outside the shaded regions having unknown principal stratum. Numbers in [ ] are not observed, but follow from Assumptions 1-3 and the observed data.

3.4.2 Pertussis Vaccine

The pertussis vaccine analysis of Préziosi and Halloran (2003b) included exactly 1 year of follow-up (the calendar year 1993), so that the person-years at risk are a close approximation to the number of persons at risk. Thus we use the person-years at risk for n(v) and n(p). Although vaccine status was not randomized, there was no evidence of systematic differences between the vaccinated and unvaccinated groups, indicating that Assumption 2 (independence) might be reasonable. Active surveillance to find cases makes it unlikely that ascertainment bias plays a role. (See Préziosi and Halloran 2003b for further discussion.) The observed data are

$$\begin{array}{cc}\hfill n_{0\ast }\left(p\right)=814,\hfill & \hfill n_{0\ast }\left(v\right)=3,297,\hfill \\ \hfill n_{10}\left(p\right)=77,\hfill & \hfill n_{10}\left(v\right)=372,\hfill \\ \hfill n_{11}\left(p\right)=129,\hfill & \hfill n_{11}\left(v\right)=176.\hfill \end{array}$$

From (10), ${\widehat{\mathrm{VE}}}_S=1$ – (548/3,845)/(206/1,020) =.29. The secondary attack rates are ${\mathit{SAR}}_v={\widehat{\varphi }}_{1.}=176∕548=.32$ and SAR_p = 129/206 = .63, such that ${\widehat{\mathrm{VE}}}_I^{\mathrm{net}}=1$ – (176/548)/(129/206) = .49, which is the same as ${\widehat{\mathrm{VE}}}_P$ given in (1). Finally ${\widehat{\mathrm{VE}}}_I^{\mathrm{ITT}}=1$ – (176/3,845)/(129/1,020) = .64, which Préziosi and Halloran (2003b) called ${\widehat{\mathrm{VE}}}_S$ for severity.

4. SELECTION BIAS MODELS

In the previous section we showed that VE_I is not identifiable under Assumptions 1–3 (SUTVA, independence, and monotonicity). In particular, the parameterization (5)–(7) defines a family of joint distribution functions of (Z, S(v), S(p), Y(v), Y(p)) for which the resulting conditional distributions of Y(p)|S^P0 = (1, 1) are not identified from the observable random variables (Z, S^obs, Y^obs). In this section we consider different additional assumptions about the selective effect of the vaccine on susceptibility to infection that restrict inference to a subset of this family such that the distribution of Y(p)|S^P0 = (1, 1) and, in turn, VE_I are identifiable. The lack of identifiability of VE_I derives from ϕ_.1 and γ₁ occurring in (9) only through the term

$${\theta }_{01}{\gamma }_1+{\theta }_{11}{\varphi }_{.1}=\mathrm{Pr}[Y^{\mathrm{obs}}=1,S^{\mathrm{obs}}=1\mid Z^{\mathrm{obs}}=p].$$ (17)

Thus for any fixed values of θ₀₁, θ₁₁, and Pr[Y^obs = 1, S^obs = 1| Z^obs = p], all pairs of parameters

$$\{({\gamma }_1,{\varphi }_{.1}):0\le {\gamma }_1\le 1,0\le {\varphi }_{.1}\le 1,\text{and}(17\left)\text{holds}\right\},$$ (18)

will yield the same distribution of (Z, S^obs, Y^obs). The selection models presented in this section place additional constraints on the parameter space such that only one pair of parameters satisfies (18). These selection models are nonparametric in the sense that no additional restrictions are placed on the distribution of (Z, S^obs, Y^obs) (Scharfstein, Rotnitzky, and Robins 1999). Although the observed data do not allow us to distinguish among selection models, through sensitivity analyses we can estimate VE_I under each selection model in a collection of models that represent a range of plausible selective effects of vaccine. Moreover, if we can show that VE_I is significantly greater (less) than 0 over all values of possible selective effects, the observed data provide sufficient evidence to conclude the vaccine has a positive (negative) causal effect on the postinfection endpoint under Assumptions 1–3 only.

We begin in Section 4.1 by assuming there is no selective vaccine effect. In Section 4.2 we present two extreme models that assume maximum possible levels of positive and negative selection bias and, in turn, yield bounds on the MLE of the causal estimand in a fashion similar to the approaches of Manski (1990), Balke and Pearl (1997), and Hudgens et al. (2003). In Section 4.3 we present three approaches to sensitivity analysis that allow a range of selective effects. We discuss making inferences on VE_I accounting for statistical variability in Section 4.4, and then apply the different methods to the two vaccine examples in Section 4.5.

4.1 No Selection Bias

The simplest assumption is that there is no selection; that is, the probability of the postinfection outcome conditional on infection under placebo is independent of infection status under vaccine,

$$\begin{array}{cc}\hfill \mathrm{Pr}\left\{Y\right(p)& =y\mid S^{P_0}=(1,1);\varphi \}\hfill \\ \hfill & =\mathrm{Pr}\left\{Y\right(p)=y\mid S^{P_0}=(0,1);\gamma \}\text{for}y=0,1,\hfill \end{array}$$ (19)

which implies ϕ_.1 = γ₁. It follows immediately that assumption (19) identifies VE_I and, from (16), that the resulting MLE is

$${\widehat{\varphi }}_{.1}={\mathit{SAR}}_p.$$ (20)

From (14), (20), and the definition of VE_I given by (8), it follows that the MLE of VE_I equals ${\widehat{\mathrm{VE}}}_I^{\mathrm{net}}$ as given in (11). In other words, under the additional assumption of no selection bias as specified by (19), the MLE of the causal vaccine effect is the usual secondary attack rate ratio estimator one obtained when conditioning on infection as in (1).

4.2 Upper and Lower Bounds

In this section we present selection models that provide the largest and smallest estimators of VE_I. In particular, the upper bound selection model yields the parameter pair satisfying (18) that has the largest ϕ_.1 (and thus the largest VE_I). Because (18) is simply the intersection of the unit square and a line with negative slope, it follows that the pair with maximal ϕ_.1 must be on the edge of the square, that is, either when

$$\mathrm{Pr}[Y\left(p\right)=1\mid S^{P_0}=(1,1)]={\varphi }_{.1}=1$$ (21)

or

$$\mathrm{Pr}[Y\left(p\right)=1\mid S^{P_0}=(0,1)]={\gamma }_1=0.$$ (22)

In words, the upper bound selection bias model assumes either that (a) all placebo recipients in the doomed principal stratum have the worse postinfection outcome or (b) all placebo recipients in the protected principal stratum have the better postinfection outcome. Under the model assuming either (21) or (22), ϕ_.1 is identifiable; the proof is not shown but is available from the authors. From (16), it follows that the unique MLE of VE_I assuming either (21) or (22) is given by

$${\widehat{\mathrm{VE}}}_I^{\text{upper}}=\{\begin{array}{cc}1-{\mathit{SAR}}_v\hfill & \text{if}{\widehat{\mathrm{VE}}}_S>1-{\mathit{SAR}}_p\hfill \\ {\widehat{\mathrm{VE}}}_I^{\mathrm{ITT}}\hfill & \text{if}0<{\widehat{\mathrm{VE}}}_S\le 1-{\mathit{SAR}}_p\hfill \\ {\widehat{\mathrm{VE}}}_I^{\text{net}}\hfill & \text{if}{\widehat{\mathrm{VE}}}_S=0.\hfill \end{array}\phantom{\}}$$ (23)

All MLEs obtained under Assumptions 1–3 must be less than or equal to ${\widehat{\mathrm{VE}}}_I^{\text{upper}}$.

Similarly, the lower bound selection bias model assumes that under assignment to placebo, the worse postinfection outcome occurs either with probability 0 in the doomed principal stratum,

$$\mathrm{Pr}[Y\left(p\right)=1\mid S^{P_o}=(1,1)]={\varphi }_{.1}=0,$$ (24)

or with probability 1 in the protected principal stratum,

$$\mathrm{Pr}[Y\left(p\right)=1\mid S^{P_0}=(0,1)]={\gamma }_1=1.$$ (25)

This model renders ϕ_.1 identifiable, and from (16) the resulting unique MLE of VE_I is

$${\widehat{\mathrm{VE}}}_I^{\text{lower}}=\{\begin{array}{cc}-\infty \hfill & \text{if}{\widehat{\mathrm{VE}}}_S>{\mathit{SAR}}_p\hfill \\ 1-{\mathit{SAR}}_v∕\left\{\frac{{\mathit{SAR}}_p-{\widehat{\mathrm{VE}}}_S}{1-{\widehat{\mathrm{VE}}}_S}\right\}\hfill & \text{if}0<{\widehat{\mathrm{VE}}}_S\le {\mathit{SAR}}_p\hfill \\ {\widehat{\mathrm{VE}}}_I^{\mathrm{net}}\hfill & \text{if}{\widehat{\mathrm{VE}}}_S=0.\hfill \end{array}\phantom{\}}$$ (26)

In summary, even though VE_I is not identifiable from the data at hand, these extreme selection bias models provide bounds on the MLE. Moreover, we have derived the circumstances when the upper bound will be negative (suggesting harm) and when the lower bound will be positive (suggesting benefit). For example, ${\widehat{\mathrm{VE}}}_I^{\text{upper}}$ will be negative if and only if ${\widehat{\mathrm{VE}}}_S\le 1-{\mathit{SAR}}_p$ and ${\widehat{\mathrm{VE}}}_I^{\mathrm{ITT}}\ll 0$. Similarly, ${\widehat{\mathrm{VE}}}_I^{\text{lower}}$ will be positive if and only if ${\widehat{\mathrm{VE}}}_S\le {\mathit{SAR}}_p$ and ${\mathit{SAR}}_v\ll ({\mathit{SAR}}_p-{\widehat{\mathrm{VE}}}_S)∕(1-{\widehat{\mathrm{VE}}}_S)$. In contrast, for ${\widehat{\mathrm{VE}}}_S\gg \max \{{\mathit{SAR}}_p,1-{\mathit{SAR}}_p\}$, we know that ${\widehat{\mathrm{VE}}}_I^{\text{upper}}$ will be always positive and ${\widehat{\mathrm{VE}}}_I^{\text{lower}}$ will be always negative. In other words, for large enough ${\widehat{\mathrm{VE}}}_S$ we cannot determine the sign of VE_I unless further assumptions are made beyond SUTVA, independence, and monotonicity.

4.3 Sensitivity Analyses

Estimating the causal vaccine effect under an extreme degree of selection bias is useful in bounding the estimate of the postinfection effect above and beyond any possible selective effects. However, the true degree of selection bias is likely less than the foregoing extreme models, such that using ${\widehat{\mathrm{VE}}}_I^{\text{upper}}$ or ${\widehat{\mathrm{VE}}}_I^{\text{lower}}$ may be too conservative. Therefore, we consider classes of selection models that include the foregoing no selection and extreme models. Through sensitivity analysis over a particular class, we can explore the relationship between the assumed degree of selection bias and our inference about VE_I. This approach allows for potentially more realistic models and less conservative inference.

4.3.1 Log Odds Ratio of Infection

Our first approach is similar to that of Scharfstein et al. (1999) and Robins, Rotnitzky, and Scharfstein (2000) and adapted by Gilbert et al. (2003b). We define a sensitivity model in terms of the log odds ratio of having the severe postinfection endpoint under placebo in the doomed versus protected principal strata,

$$\exp \left(\beta \right)=\frac{\mathrm{Pr}[Y\left(p\right)=1\mid S^{P_0}=(1,1)]∕\mathrm{Pr}[Y\left(p\right)=0\mid S^{P_0}=(1,1)]}{\mathrm{Pr}[Y\left(p\right)=1\mid S^{P_0}=(0,1)]∕\mathrm{Pr}[Y\left(p\right)=0\mid S^{P_0}=(0,1)]}.$$ (27)

For example, if exp(β) = 2, then doomed individuals have twice the odds of having the worse postinfection outcome under placebo compared with protected individuals. In terms of our parameterization, this implies that

$${\varphi }_{.1}=\frac{{\gamma }_1\exp \left(\beta \right)}{{\gamma }_0+{\gamma }_1\exp \left(\beta \right)}.$$ (28)

For fixed β, we can solve (16) and (28) for ϕ_.1 and, in turn, VE_I. A sensitivity analysis can then be performed by repeating this process over a range of different β’s.

The selection models given in Sections 4.1 and 4.2 are special cases of the class of logistic selection models given by (27) when β = 0 (no selection), β → ∞ (upper bound), or β → —∞ (lower bound). For example, letting β → ∞

$$\mathrm{Pr}[Y\left(p\right)=1\mid S^{P_0}=(1,1)]\to 1$$ (29)

or

$$\mathrm{Pr}[Y\left(p\right)=1\mid S^{P_0}=(0,1)]\to 0.$$ (30)

Because (29) implies (21) and (30) implies (22), we recover the extreme upper selection bias model. The relation among the log odds ratio, upper bound, and no selection models are depicted graphically in Figure 1.

Figure 1.

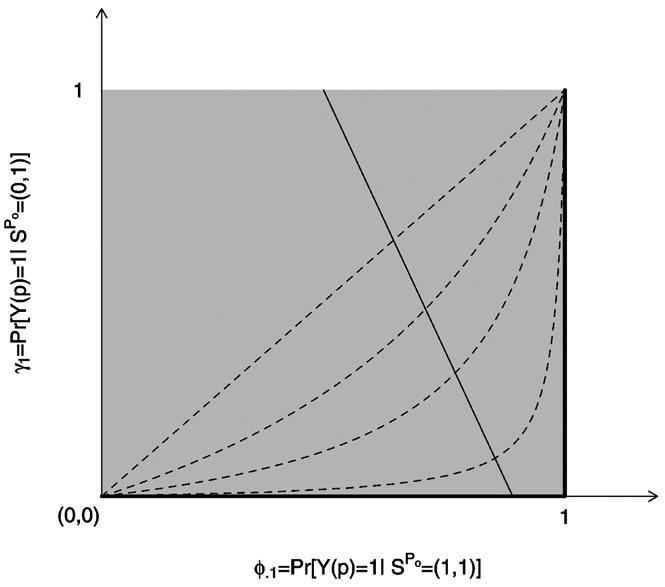
Graphical Depiction of Selection Bias Models Described in Section 4. The four dotted curves depict the log odds ratio selection model for β = 0, 1, 2, 4. The β = 0 model is equivalent to the no selection model. The thick black lines on the edge of the unit square correspond to the upper-bound selection model. The solid thin line with negative slope represents an example of a family of joint distribution functions of (Z, S(v), S(p), Y(v), Y(p)) for which all combinations of parameters (ϕ_.1, γ₁) on this line give rise to the same distribution of the observable random variables (Z, S^obs,Y^obs). Each selection model identifies exactly one pair of parameters (ϕ_.1, γ₁) from this family, rendering VE_I = 1 − ϕ_1./ϕ_.1 identifiable.

4.3.2 Conditioning on γ₁ as the Sensitivity Analysis Parameter

Section 4.3.1 posits a relation between the distributions of the postinfection endpoint under placebo in the doomed and protected strata. Alternatively, we might simply condition on the nuisance parameter γ₁, which governs the postinfection endpoint distribution in the protected stratum. Assuming that γ₁ is known renders ϕ_.1 and, hence, VE_I identifiable. From (16), the resulting MLE of VE_I is

$${\widehat{\mathrm{VE}}}_I=1-{\mathit{SAR}}_v∕\left\{\frac{{\mathit{SAR}}_p-{\gamma }_1{\widehat{\mathrm{VE}}}_S}{1-{\widehat{VE}}_S}\right\},$$ (31)

where γ₁ varies between

$$\max \left\{0,\frac{{\mathit{SAR}}_p-(1-{\widehat{\mathrm{VE}}}_S)}{{\widehat{\mathrm{VE}}}_S}\right\}\le {\gamma }_1\le \min \left\{1,\frac{{\mathit{SAR}}_p}{{\widehat{\mathrm{VE}}}_S}\right\},$$ (32)

with the left side of (32) giving rise to ${\widehat{\mathrm{VE}}}_I^{\text{upper}}$ and the right side of (32) giving rise to ${\widehat{\mathrm{VE}}}_I^{\text{lower}}$.

4.3.3 Complete-Data Model

A third approach to sensitivity analysis regards the unknown basic principal stratum membership of the infected placebo recipients as missing data and formulates the sensitivity analysis in terms of the complete-data likelihood. The observed data are n₁₀(p) and n₁₁(p). If we could know the basic principal stratum membership, then the complete data would be $n_{10}^d\left(p\right)$ and $n_{10}^d\left(p\right)$, the number of infected placebo recipients in the doomed stratum with Y(p) 0 and Y(p) = 1, and $n_{10}^p\left(p\right)$ and $n_{11}^p\left(p\right)$, the corresponding number in the protected stratum. Given the complete data, ϕ_.1 becomes identifiable. The complete-data log-likelihood for (θ, ϕ, γ) is given by

$$\begin{array}{cc}\hfill & n_{0\ast }\left(p\right)\log \left({\theta }_{00}\right)\hfill \\ \hfill & +n_{10}^p\left(p\right)\log \left({\theta }_{01}{\gamma }_0\right)\hfill \\ \hfill & +n_{11}^p\left(p\right)\log \left({\theta }_{01}{\gamma }_1\right)\hfill \\ \hfill & +n_{10}^d\left(p\right)\log {\theta }_{11}(1-\varphi .1))\hfill \\ \hfill & +n_{11}^d\left(p\right)\log \left({\theta }_{11}\varphi .1\right)\hfill \\ \hfill & +n_{0\ast }\left(v\right)\log ({\theta }_{00}+{\theta }_{01})\hfill \\ \hfill & +n_{10}\left(v\right)\log \left({\theta }_{11}(1-{\varphi }_{.1})\right)\hfill \\ \hfill & +n_{11}\left(v\right)\log ({\theta }_{11}{\varphi }_1.),\hfill \end{array}$$ (33)

which factors in terms of θ, ϕ, and γ, say l(θ), l(ϕ), and l(γ). Maximizing l(ϕ) yields the same MLE ${\widehat{\varphi }}_{1\cdot }={\mathit{SAR}}_v$ as before. It also yields the MLE

$$\widehat{\varphi }.1=\frac{n_{11}^d\left(p\right)}{n_{10}^d\left(p\right)+n_{11}^d\left(p\right)},$$ (34)

the secondary attack rate under placebo in the doomed stratum. The sensitivity analysis involves estimating VE_I using (34) for all possible complete-data configurations consistent with the assumptions and the constraints implied by the observed data. Molenberghs, Kenward, and Goetghebeur (2001) called this set of point estimates the region of ignorance, and called the collection of CIs or other measures of precision together with the region of ignorance the region of uncertainty.

4.4 Statistical Variability

Once we assume a particular selection model, we have a finite-dimensional parametric inference problem with a unique MLE. Therefore, conditional on a selection model, we use standard methods to obtain CI estimates for VE_I. For example, CIs can be computed assuming the usual chi-squared limiting distribution of the profile likelihood ratio (Barndorff-Nielsen and Cox 1994). Alternatively, using the observed information and the delta method, Wald-type CIs for VE_I can be determined. The resulting CIs can then be used to determine a region of uncertainty for any of the sensitivity analyses described earlier. A region of uncertainty that excludes 0 will then imply a statistically significant postinfection causal effect of the vaccine.

4.5 Applications, Continued

4.5.1 Rotavirus Candidate Vaccine

For these data, ${\widehat{\mathrm{VE}}}_S\gg 1-{\mathit{SAR}}_p$, so from (23), ${\widehat{\mathrm{VE}}}_I^{\text{upper}}=1-{\mathit{SAR}}_v=.50$. In contrast, $0\ll {\widehat{\mathrm{VE}}}_S\le {\mathit{SAR}}_p$, so, from (26),

$${\widehat{\mathrm{VE}}}_I^{\text{lower}}=1-\frac{5∕10}{\frac{\{13∕16-(1-(10∕100)(16∕100))\}}{(10∕100)∕(16∕100)}}=.29.$$

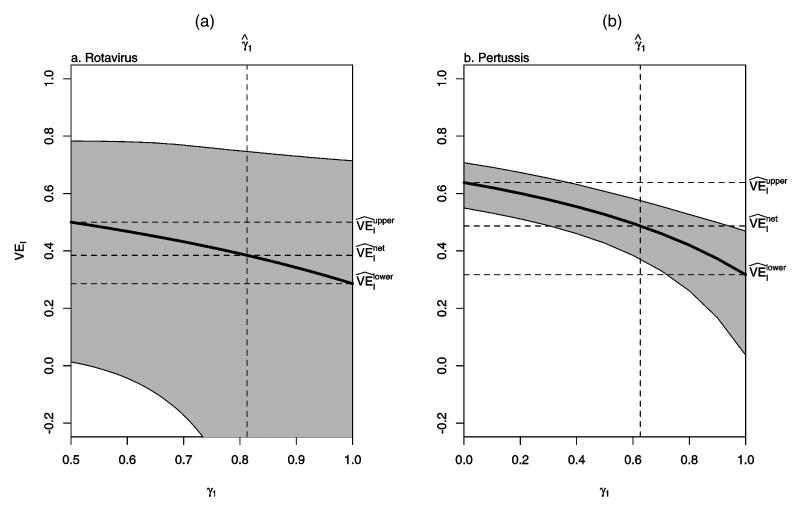
Figure 2(a) shows the sensitivity analysis of ${\widehat{\mathrm{VE}}}_I$ as a function of the odds ratio e^β as described in Section 4.3.1. Figure 3(a) shows the sensitivity analysis of ${\widehat{\mathrm{VE}}}_I$ as a function of γ₁ as described in Section 4.3.2. From (32), the range for γ₁ is [.5, 1.0 in this example. For these figures, profile likelihood–based CIs are presented; Wald-type CIs gave qualitatively similar results. The vertical dotted line in Figures 2 and 3 corresponds to the assumption of no selection bias. In particular, in Figure 3, ${\widehat{\gamma }}_1$ corresponds to the MLE of γ₁ under the assumption of no selection bias.

Figure 2.

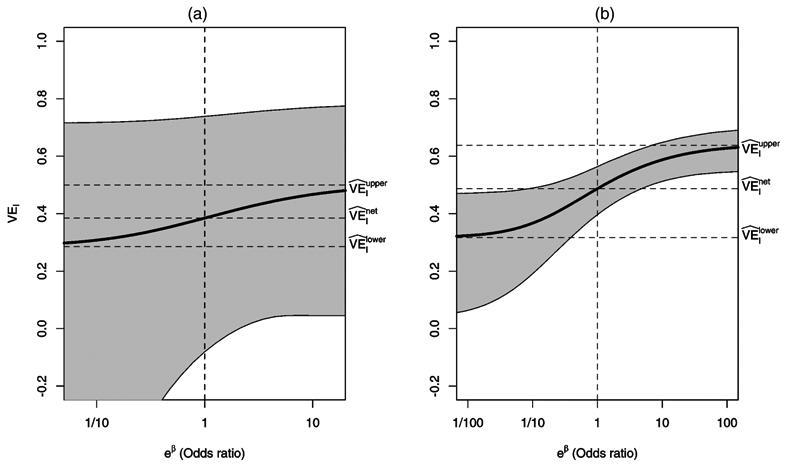
Sensitivity Analysis Using the Odds Ratio of Having the Severe Postinfection Endpoint Under Placebo in the Doomed versus Protected Principal Strata as Described in Section 4.3.1. (a) Rotavirus; (b) pertussis. The vertical dotted line corresponds to the assumption of no selection bias.

Figure 3.

Sensitivity Analysis Assuming γ₁ = Pr{Y(p) = 1|S^P0 = (0, 1); γ} Is Known as Described in Section 4.3.2. (a) Rotavirus; (b) pertussis. The vertical dotted line gives the MLE of γ₁ under the assumption of no selection bias.

Table 3 gives all possible configurations of the complete data for the placebo arm consistent with the observed data and Assumptions 1–3 as described in Section 4.3.3. On the one hand, the complete data are constrained by the observed data to satisfy $n_{11}\left(p\right)=n_{11}^d\left(p\right)+n_{11}^p\left(p\right)=13$ and $n_{10}\left(p\right)=n_{10}^d\left(p\right)+n_{10}^p\left(p\right)=3$. On the other hand, Assumptions 1–3 imply that of the total of 16 infected placebo recipients, 6 must be in the protected stratum and 10 must be in the doomed stratum. There are only four complete-data configurations that satisfy these constraints. These four configurations can be envisaged by assigning the three infected placebo recipients with mild infection to either the doomed stratum or the protected stratum. At one extreme, the three are all in the doomed stratum; at the other extreme, they are all in the protected stratum. The resulting four MLEs of VE_I given in the bottom row of Table 3 compare the region of ignorance. For this dataset, the assumption of no selection bias does not correspond to any possible complete-data configuration. But the extreme lower and upper bound estimates, ${\widehat{\mathrm{VE}}}_I^{\text{lower}}$ and ${\widehat{\mathrm{VE}}}_I^{\text{upper}}$, are included in the region of ignorance.

Table 3.

Rotavirus Vaccine Example (Vesikari et al. 1990): All Possible Configurations of the Underlying Complete Data for the Placebo Arm Consistent With the Observed Data and Assumptions 1–3

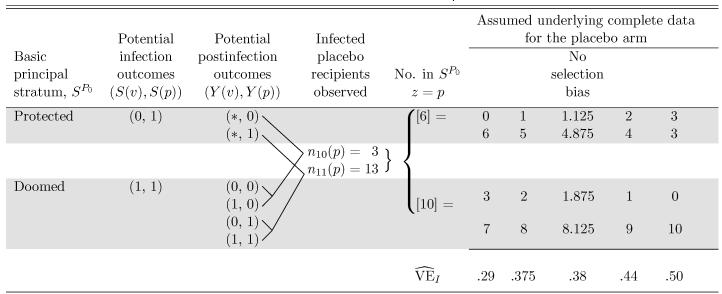NOTE: The shaded regions correspond to membership within the basic principal strata with observations outside the shaded regions having unknown principal stratum. Numbers in [ ] are not observed, but follow from the observed data and Assumptions 1-3. Maximum likelihood estimates of causal VEI are given for each possible complete data configuration. The no selection bias model is also included, although it does not correspond to any of the possible complete data configurations.

This example demonstrates the utility of the sensitivity analyses. For these data, the 95% CI for VE_I covers 0 for the lower bound selection model, indicating that one cannot conclude that the vaccine has a protective causal effect against severe disease at the α = .05 level. In contrast, the upper bound selection model CI excludes 0, indicating a significant protective effect. In this situation, sensitivity analyses can be used to assess at what point significance is attained. For example, Figures 2(a) and 3(a) indicate that even under the assumption of no selection bias, the effect remains nonsignificant.

Finally, the lack of statistical significance in this example may be attributed simply to small sample size. For instance, had the study been such that there were 1,000/arm with the same observed marginal distributions (i.e., 3% mild and 13% severe in the placebo arm, 5% mild and 5% severe in the vaccine arm), then the 95% CI for VE_I under the lower bound model would have been [.09,.46], indicating a significant causal vaccine effect on rotavirus disease severity in individuals who would be infected regardless of vaccination status.

4.5.2 Pertussis Vaccine

For these data, $0\le {\widehat{\mathrm{VE}}}_S\le 1-{\mathit{SAR}}_p$, so from (23), ${\widehat{\mathrm{VE}}}_I^{\text{upper}}={\widehat{\mathrm{VE}}}_I^{\mathit{ITT}}=.64$. In contrast, $0\le {\widehat{\mathrm{VE}}}_S\le {\mathit{SAR}}_p$, so from (26), ${\widehat{\mathrm{VE}}}_I^{\text{lower}}=.32$. Figures 2(b) and 3(b) show the sensitivity analyses of ${\widehat{\mathrm{VE}}}_I$ as described in Sections 4.3.1 and 4.3.2. In both figures, the lower limits of the 95% CIs are well above 0 over the range of both selection models, suggesting that pertussis vaccination causes significant protection against severe disease in children who would develop pertussis regardless of vaccination. The sensitivity analysis using the complete-data likelihood would proceed similarly as for the rotavirus vaccine candidate, with many more possible data configurations and taking the unequal sizes of the vaccinated and unvaccinated arms into account.

5. DISCUSSION

For vaccine studies in which the effect of vaccination on binary postinfection outcomes is of interest, our results will enable researchers to quantify the soundness and limitations of their findings. Combining principal stratification with a maximum likelihood approach, we have developed methods for estimating the causal effect of vaccination on postinfection outcomes in those individuals who would be infected under vaccine and placebo. Closed forms for the MLE of the causal estimand have been derived assuming extreme upper, extreme lower, and no selection bias models. These results indicate specific assumptions under which currently used efficacy estimators have a causal interpretation; for example, the usual net postinfection efficacy estimator is the MLE of our causal estimand under the assumption of no selection bias. In contrast, the usual intent-to-treat estimator provides an upper bound on the postinfection causal vaccine effect when the protective effect of the vaccine against infection is not too large (i.e., ${\widehat{\mathrm{VE}}}_s\le 1-{\mathit{SAR}}_p$). We have also presented three approaches to sensitivity analysis that allow selection models to range from no selection to the extreme maximum possible levels. Coupled with confidence intervals, these sensitivity analyses provide a comprehensive description of the uncertainty regarding VE_I. For example, in the analysis of the pertussis vaccine study, the estimated postinfection vaccine effect was significantly greater than 0 for all selection bias models, including the extreme lower bound model, indicating a significant causal effect in reducing disease severity. In other words, under only the standard assumptions of SUTVA, monotonicity, and independence of treatment assignment, we have shown that there is a definitive causal vaccine effect on severity of pertussis in individuals who would be infected whether vaccinated or not.

Several extensions of this work and avenues for further research merit mention. For instance, further research is needed on the consequences of relaxing several key assumptions. Regarding Assumption 1, SUTVA is clearly violated in many vaccine field studies (Rubin 1990a; Halloran and Struchiner 1995). When SUTVA is violated, an individual can have different potential infection outcomes under the same treatment assignment. Therefore, defining the basic principal stratum for an individual needs to account for the possible treatment assignments of other individuals. Assumption 2 (independence) clearly holds in the rotavirus example because the trial was randomized, and likely also holds in the pertussis field study, as discussed in Section 3.4.2. In general, the effect of nonrandom allocation of the vaccine can be explored through additional sensitivity analyses and other approaches for observational studies (Rosenbaum 1995). In addition, exclusion restrictions not considered here may be necessary if the independence assumption is not made. Assumption 3 (monotonicity) also likely holds for the rotavirus and pertussis examples, because ${\widehat{\mathrm{VE}}}_S\gg 0$ in both studies. Relaxing Assumption 3 to allow for a harmful vaccine effect on infection would make identifiability and estimation of the postinfection causal estimand VE_I more difficult. However, a vaccine that increases susceptibility to infection would be unacceptable from a public health standpoint, so that concerns about postinfection selection bias become less relevant. Finally, we have assumed that assignment to a treatment is equivalent to receipt of that treatment. The increased complexity of defining, identifying, and estimating causal effects in the presence of noncompliance (Angrist et al. 1996) would likely necessitate further exclusion restriction assumptions (e.g., given the actual treatment received, assignment to treatment carries no additional information).

Additional research is also needed to incorporate baseline covariates and allow for missing or mismeasured infection or postinfection outcomes. The operating characteristics of conditional and unconditional (i.e., ITT) tests for binary postinfection vaccine effects remain unknown. Our preliminary comparisons (results not shown) suggest a conditional approach [similar to that of Hudgens et al. (2003)] may be more powerful. These results are consistent with the findings of Mehrotra, Li, and Gilbert (2005). Finally, as pointed out by a reviewer, the multivariate literature on characterizing the set of possible joint distributions given fixed marginal or conditional distributions (see, e.g., Joe 1997) may have direct application in the principal stratification setting.

Correct assessment of vaccine effects on postinfection endpoints has important public health consequences. For example, there is precedent and concern for vaccine-induced immune responses causing disease enhancement (Kliks, Nisalak, Brandt, Wahl, and Burke 1989; Burke 1992; Mascola et al. 1993; Nabel 2001). If the estimated net postinfection vaccine effect suggested a possible harmful effect, then a vaccine could be wrongfully discounted if, in fact, the apparent negative effect were due to selection bias. Our methods could be used to determine whether such an observed effect was consistent with selection bias. In contrast, if the estimated net vaccine effect were positive, then one might be less compelled to distinguish (a) a selective effect of the vaccine on infection from (b) the causal effect of the vaccine in the doomed principal stratum, because either effect is beneficial from a public health perspective. Disentangling (a) from (b) could be quite valuable from a scientific standpoint, however. For example, our analysis of the pertussis vaccine study provides evidence that vaccination has an effect on disease severity above and beyond that attributable to selection bias, suggesting the vaccine produces an immune response that directly hinders severe symptoms, such as paroxysms with whoops. This could suggest directions for further biological research. Another example arises in HIV, where researchers are considering both antibody and T-cell–based vaccines (McMichael, Mwau, and Hanke 2002; Nabel 2001) under the hypothesis that the former will protect from infection and the latter will protect from disease or death. If a combination vaccine proves effective in reducing the risk of morbidity or mortality, then researchers will be interested in understanding the mechanism of protection, that is, to which vaccine component is such an effect attributable. Analysis revealing a signifi-cant post-infection causal vaccine effect in the doomed stratum would provide evidence of T-cell–based protection. Separating (a) and (b) also might be helpful in predicting the success of particular vaccination programs (Hayes, Alexander, Bennett, and Cousens 2000).

Although in this article we have handled the postinfection outcomes of transmission and disease severity or death similarly, there are important differences. In particular, vaccine efficacy for infectiousness (VE_I) involves transmission to another susceptible individual, whereas vaccine efficacy for severity or progression (VE_P) involves only the infected individual. Thus, unlike VE_P, VE_I can depend on the characteristics of the individuals susceptible to secondary infection, as well as on the type of contacts between individuals. Also, an infected individual could expose more than one individual, so that there could be several potential postinfection outcomes, one for each exposed individual; for example, the study be in Préziosi and Halloran (2003a), more than 20 individuals were exposed to one infected individual in some cases. Alternatively, an infected individual may expose no other susceptibles, and then the potential postinfection outcome would be undefined. Our method needs to be extended to such multiple outcomes and possible dependencies.

In most vaccine studies in humans, whether or not an individual becomes infected is not under the control of the investigator. The potential postinfection outcomes for individuals who would not become infected under either vaccine or placebo are undefined, or are a priori counterfactual (Frangakis and Rubin 2002), resulting in our defining the postinfection causal estimand in the doomed stratum only. However, there are a few infectious agents that can be used in infection-challenge studies in either human or animal. For these types of studies, a more appropriate approach might be that of Robins and Greenland (1992, 1994), which assumes that the posttreatment variable is controllable; that is, the investigator can force the individuals to take on any possible value of the posttreatment variable. Comparison of the different approaches merits further research.

APPENDIX: MAXIMUM LIKELIHOOD ESTIMATION

Let ξ = θ₀₁γ₁ + θ₁₁ϕ_.1 and consider maximizing the log-likelihood,

$$\begin{array}{cc}\hfill & n_{o\ast }\left(p\right)\log \left({\theta }_{00}\right)\hfill \\ \hfill & +n_{10}\left(p\right)\log ({\theta }_{01}+{\theta }_{11}-\xi )\hfill \\ \hfill & +n_{11}\left(p\right)\log \left(\xi \right)\hfill \\ \hfill & +n_{0\ast }\left(v\right)\log ({\theta }_{00}+{\theta }_{01})\hfill \\ \hfill & +n_{10}\left(v\right)\log \left({\theta }_{11}(1-\varphi .1)\right)\hfill \\ \hfill & +n_{11}\left(v\right)\log ({\theta }_{11}{\varphi }_1.),\hfill \end{array}$$

subject to the constraints

$${\theta }_{00}+{\theta }_{01}+{\theta }_{11}=1,$$

$$0\le {\theta }_{ij},i,j=0,1;i\le j,$$

$$0\le \xi \le {\theta }_{01}+{\theta }_{11},$$

$$0\le {\varphi }_1.\le 1.$$

The maximum of ϕ_1. is given by ${\widehat{\varphi }}_1.=n_{11}\left(v\right)∕n_1.\left(v\right)$, such that we are left with the simpler problem of maximizing

$$\begin{array}{cc}\hfill & l(\theta ,\xi )=n_{0\ast }\left(p\right)\log \left({\theta }_{00}\right)\hfill \\ \hfill & +n_{10}\left(p\right)\log ({\theta }_{01}+{\theta }_{11}-\xi )\hfill \\ \hfill & +n_{11}\left(p\right)\log \left(\xi \right)\hfill \\ \hfill & +n_{0\ast }\left(v\right)\log ({\theta }_{00}+{\theta }_{01})\hfill \\ \hfill & +n_1.\left(v\right)\log \left({\theta }_{11}\right),\hfill \end{array}$$

subject to (A.1)–(A.3).

The function 1(θ,ξ) is strictly concave over the closed, convex parameter space defined by (A.1)–(A.3) such that a unique MLE exists and the (first-order) Kuhn–Tucker conditions are necessary and sufficient for optimality (Fletcher 1987). In particular, define Lagrange multipliers λ₀,λ₁,…,λ₅ and Lagrangian function

$$\begin{array}{c}L(\theta ,\xi )=l(\theta ,\xi )+{\lambda }_0\left(1-\sum {\theta }_{ij}\right)+{\lambda }_1{\theta }_{00}+{\lambda }_2{\theta }_{01}\hfill \\ \hfill +{\lambda }_3{\theta }_{11}+{\lambda }_4\xi +{\lambda }_5({\theta }_{01}+{\theta }_{11}-\xi ),\end{array}$$

where the summation is over i, j = 0, 1 such that i≤j. Then $(\widehat{\theta },\widehat{\xi })$ is an MLE iff it is a feasible point according to (A.1)–(A.3) and satisfies

$$\frac{\partial L(\theta ,\xi )}{\partial {\theta }_{ij}}=0,i,j=0,1;i\le j,$$

$$\frac{\partial L(\theta ,\xi )}{\partial \xi }=0,$$

$${\lambda }_i\ge 0,i=1,...,5,$$

and

$$\begin{array}{cc}\hfill {\lambda }_0\left(1-\sum {\theta }_{ij}\right)={\lambda }_1{\theta }_{00}& ={\lambda }_2{\theta }_{01}={\lambda }_3{\theta }_{11}={\lambda }_4\xi \hfill \\ \hfill & ={\lambda }_5({\theta }_{01}+{\theta }_{11}-\xi )\hfill \\ \hfill & =0.\hfill \end{array}$$

Under the assumption n_sy(z) > 0 for all possible combinations of s, y, and z, we must have ${\widehat{\theta }}_{00},{\widehat{\theta }}_{11}$, and $\widehat{\xi }$ strictly greater than 0 to maximize l(θ, ξ), such that λ₁ = λ₃ = λ₄ = 0. Similarly, we must also have $\widehat{\xi }\ll {\widehat{\theta }}_{01}+{\widehat{\theta }}_{11}$, such that λ₅ = 0. Multiplying (A.5) and (A.6) by θ_ij and ξ and summing,

$$\sum {\theta }_{ij}\frac{\partial L(\theta ,\xi )}{\partial {\theta }_{ij}}+\xi \frac{\partial L(\theta ,\xi )}{\partial \xi }=0$$

can be shown to yield λ₀ = n. It follows that $(\widehat{\theta },\widehat{\xi })$ is an MLE iff it satisfies (A.1)–(A.3) and

$$\frac{\partial l(\theta ,\xi )}{\partial {\theta }_{00}}=\frac{n_{0\ast }\left(p\right)}{{\theta }_{00}}+\frac{n_{o\ast }\left(v\right)}{{\theta }_{00}+{\theta }_{01}}=n,$$

$$\frac{\partial l(\theta ,\xi )}{\partial {\theta }_{01}}=\frac{n_{10}\left(p\right)}{{\theta }_{01}+{\theta }_{11}-\xi }+\frac{n_{0\ast }\left(v\right)}{{\theta }_{00}+{\theta }_{01}}\le n,$$

$$\frac{\partial l(\theta ,\xi )}{\partial {\theta }_{11}}=\frac{n_{10}\left(p\right)}{{\theta }_{01}+{\theta }_{11}-\xi }+\frac{n_{10}\left(v\right)+n_{11}\left(v\right)}{{\theta }_{11}}=n,$$

and

$$\frac{\partial l(\theta ,\xi )}{\partial \xi }=\frac{n_{11}\left(p\right)}{\xi }-\frac{n_{10}\left(p\right)}{{\theta }_{01}+{\theta }_{11}-\xi }=0.$$

We can show the MLE of θ has the following closed form that depends on the data. In particular, if

$$\frac{n_{0\ast }\left(v\right)}{n\left(v\right)}\ge \frac{n_{0\ast }\left(p\right)}{n\left(p\right)},$$

then the MLEs are given by

$${\widehat{\theta }}_{00}=\frac{n_{0\ast }\left(p\right)}{n\left(p\right)},$$

$${\widehat{\theta }}_{01}=\frac{n_{0\ast }\left(v\right)}{n\left(v\right)}-\frac{n_{0\ast }\left(p\right)}{n\left(p\right)},$$

and

$${\widehat{\theta }}_{11}=1-\frac{n_{0\ast }\left(v\right)}{n\left(v\right)}.$$

Otherwise,

$${\widehat{\theta }}_{00}=\frac{n_{0\ast }\left(p\right)+n_{0\ast }\left(v\right)}{n},$$

$${\widehat{\theta }}_{01}=0,$$

and

$${\widehat{\theta }}_{11}=1-\frac{n_{0\ast }\left(p\right)+n_{0\ast }\left(v\right)}{n}.$$

In either case, the MLE of ξ is given by

$$\widehat{\xi }=\frac{n_{11}\left(p\right)}{n_1.\left(p\right)}({\widehat{\theta }}_{01}+{\widehat{\theta }}_{11}).$$