Local refinement

Abstract

A critical problem in electron tomography is the deformation of the specimen due to radiation, or “shrinkage,” which interferes with image alignment and thereby limits resolution. Here, we describe a general strategy for refining preliminary reconstructions which allows the damage due to the shrinkage of plastic-embedded thin sectioned specimens (50−80 nm) to be corrected. The basic steps of the strategy involve: a) the partition of the preliminary reconstruction into sub-volumes; b) the extraction of corresponding sub-areas for each sub-volume from the micrographs of the tilt series; c) the re-projection of each sub-volume according to the orientation parameters; and d) the refinement of these parameters by correlating each sub-area to the corresponding computed projection.

We tested the strategy by refining chemical synapses reconstructed from series imaged with conical, double and single tilt geometries. The results gathered with local refinement were evaluated by visually inspecting the structure of biological membranes in the maps. In an effort to quantify these improvements, we studied the refined maps using correlation criteria and mapped the corrections applied to the orientation parameters in each sub-volume of the reconstruction. Simulation experiments complemented the data gathered by correlation analysis. Based on these criteria, we concluded that local refinement significantly improves the overall quality of the reconstructions of chemical synapses calculated from series imaged with conical and double tilt geometries.

Introduction

Electron tomography is a general technique for studying the 3D structure of biological macromolecules in their cellular environments. It has been used to reconstruct macromolecular assemblies (e.g. Hart, 1968; Hoppe et al., 1974), sections of plastic embedded tissues (e.g. Mc Ewen et al., 1986; He et al., 2003), frozen hydrated organelles extracted from the cell (Al-Almoudi et al., 2004; Beck et al., 2004) and large macromolecular complexes and viruses in frozen solution (Grünewald et al., 2003). In all cases, the 3D reconstructions are calculated without imposing symmetry or using averaging methods, which can be applied later, if necessary, to improve the signal to noise ratio (Liu et al., 2004; Nicastro et al., 2005; Zhu et al., 2006).

In electron tomography, the specimen is imaged many times along different directions (the “tilt series”) to produce the images used to calculate the 3D maps. Since biological specimens are comprised of elements with low atomic numbers, for many samples inelastic scattering predominates during image formation. Energy is transferred to the specimen and hence makes radiation damage a key limitation when calculating 3D reconstructions.

The deleterious effects of radiation damage on the chemical and structural integrity of specimens include formation of free radicals that rupture bonds, fragmentation of large macromolecules, mass loss and establishment of new cross-links between adjacent molecules in the tissue (for review, see Cosslett, 1978). After radiation damage, the specimen is highly cross-linked and bears little resemblance to the original sample. At room temperatures, these changes occur at very low electron doses (0.5−1 e/A²), which make the study of the detailed structure of these specimens impossible. Since the changes depend on the temperature at which the specimen is imaged (Siegel, 1970; Salih and Cosslett, 1975), stopping mass loss and preserving the order of organic crystals necessitates imaging specimens cooled at liquid helium temperatures (Dubochet and Knapek 1979).

Sections that are stained with heavy metal atoms and imaged at room temperatures can provide information about the boundaries between the stain and the macromolecule (the “envelope”). Since the stain is far more stable than the biological specimen, these envelopes can be obtained at moderate levels of resolution (2−5 nm). Often, however, even 2−5 nm resolutions are difficult to accomplish because shrinkage interferes with the alignment of the tilt series. While procedures introduced to reduce the shrinkage due to radiation during data collection (i.e., pre-irradiation), have been successful, even small changes in position of the fiduciary points used for alignment (i.e., gold particles added to the specimen’ surface) cause inconsistencies that limit resolution.

For these reasons, it is necessary to correct specimen shrinkage with computational strategies (Mastronarde, 1997; Lawrence et al., 2006). In a series collected with single-tilt geometry, correcting for magnification compensates for gross deformations while adjusting the rotation and shift parameters corrects small geometric inaccuracies that occur during image recording. These corrections improve primarily the resolution in the center of the reconstruction volume while leaving a resolution gradient from the center to the periphery. In series collected with double-tilt geometry, the effect of shrinkage becomes apparent when the fiduciary markers of reconstructions calculated from the two independent series do not properly match up. Mastronarde (1997) introduced a strategy based on the 3D layout of these reference points whereby the independent tomograms are brought into a common reference system by finding the transformation that best allows the coordinates of the fiduciary markers to superimpose. If linear transformations fail to superimpose these coordinates, non-linear corrections are used. Since this strategy, highly successful for double-tilt geometry, is deeply embedded in the reconstruction algorithm, its generalization to single and conical tilt geometries is not straightforward.

In this paper, we describe a strategy to cope with specimen shrinkage and distortions in a reconstruction from tilt series recorded with different geometries. Since shrinkage is a local phenomenon, the reconstruction is first subdivided into smaller cubes (64), processed independently and refined by projection matching (Zampighi et al., 2005). Pasting together the refined cubes reconstitutes the entire volume of the region (Lanzavecchia et al. 2005). We followed the refinement process by mapping the corrections applied to the orientation parameters of the projections of each sub-volume of the reconstruction and assessed the improvements in the refined maps using correlation criteria. Simulation experiments complemented the data gathered using correlation analysis. Based on these criteria, we concluded that local refinement significantly improves the overall quality of the reconstructions of chemical synapses calculated from series imaged with conical as well as double axis tilt geometry.

Material and Methods

Preparation of thin sections

The preparation of the specimens has been described in (Zampighi et al., 2005; 2006). In brief, three Sprague-Dawley adult rats 90−120 days of age were sacrificed and fixed by perfusion with about 1 liter of 3% glutaraldehyde, 4% paraformaldehyde in 0.2 M cacodylate buffer pH 7.4. The brains were removed and sliced in a vibrotome in sections 100−150 μm. Tissue from the frontal association and motor neocorticies was dissected from these thick sections and processed for thin sectioning electron microscopy. After OsO₄ post-fixation and block staining, the tissue was embedded in Epon 812. Thin sections of thickness with gray-to-silver interference color (50−80 nm) were cut, collected on 200 mesh grids with carbon substrate and stained with solutions of uranyl and lead citrate. Gold particles, 10 nm in diameter, deposited on the surfaces of the thin sections were used for centering the conical series, estimating the thin section thickness, and calculating preliminary 3D reconstructions.

Electron microscopy

We used the Gatan 650 Single Tilt Rotating Holder in a FEI Tecnai 12 electron microscope operated at 120 KV to collect 22 tomographic tilt series. The holder allowed up to 70° tilts and controlled rotations in the azimuth. The images were collected in a 2k × 2k CCD Gatan camera at 34,230X final magnification (pixel size 0.409 nm). Imaging was carried out using a minimum-dose method: searching was done at 2,700X magnification with minimum illumination and the regions of interest imaged by focusing ∼2 μm away. The total electron dose was ∼800 e/A2, which we previously found to decrease the overall thickness of the thin section by ∼15% (Zampighi et al., 2005).

Data Collection

Tilt series of thin sections were recorded using different geometries as follows:

a) Single axis series: 72 projections were recorded from −60° to +60° in steps of 1.667 degrees. b) Dual axis series: 36 projections were recorded from −60° to +60° in steps of 3.3 degrees. The holder was then rotated by 90° in the XY plane and a second series was recorded in the same way. c) Conical series: many series of 72 projections were collected after tilting the stage by 55° or 60°, while rotating the holder in steps of 5°. Other series were collected at an angular spacing of 3.5 degrees (103 projections). Images were acquired using a CCD camera in a 2048×2048 pixel map, later compressed to 1024×1024 pixels, with one pixel corresponding to 0.818 nm.

Alignment of the series and 3D reconstruction

For the three different tomographic geometries, projections were manually pre-aligned by selecting a specific gold particle and shifting each image such that the particle was in the center of the field. The series were then aligned, with the technique depending on the type of geometry used to record the projections. For single and dual axis series, we performed alignment and preliminary reconstructions using the program Imod (Kremer et al., 1996). After tracing a number of gold particles, we exported the coordinates of the points, and continued the analysis with our library of programs. In this way, we were able to compare the results obtained for each type of geometry. The final 3D reconstructions were computed using the weighted back projection (WBP) for general geometry (Radermacher, 1992).

In single tilt tomography, the alignment parameters were obtained as described by Jing and Sachs (1991), using the coordinates of about 20 points, obtained from Imod. In this procedure we corrected for magnification, as well as for variation in the tilt angle, with a limit to the maximum amount of tilt correction, in case of small tilt angles. Furthermore, we checked to make certain that the computed orientation parameters coincided with those furnished by Imod.

In dual axis tomography, each series was first aligned as described above, yielding the coordinates of the reference points. Then the parameters of all the projections were put into a common reference system, by finding the transformation which optimizes the superposition of the reference points common to both series. In so doing, we introduced an additional scale correction for magnification, which was applied in the projection space, directly to the micrographs, for the purpose of minimizing the residual difference.

3D reconstructions were computed using a program of weighted back projection for arbitrary geometry (Radermacher, 1992). In the computation of the weights we considered an object dimension corresponding to the thickness of the sections divided by the cosine of the maximum tilt angle. The program is fed with orientation parameters comprising Euler angles and shifts, plus the pre-aligned projections, corrected for magnification.

Conical data

The conical series were first aligned using reference points, as described in Lanzavecchia et al., (2005). For each projection, we determined the orientation parameters (α,β,γ, Δx, Δy) using several gold particles and set the tilt angle (β) and lay out of the tilt axis (γ) to the values used during data collection. The azimuth (α) and shifts (Δx, Δy) varied slightly at this step (Lanzavecchia et al., 2005). We then searched for the best match between the original micrographs and the re-projections calculated from the preliminary reconstructions (global refining, Zampighi et al., 2005). Briefly, each Euler angle was refined independently, starting from the azimuth (α). For every projection (i) of the series, a number (n) of re-projections were computed at different azimuth angles (αj = αi ± jδ; j=−n/2 ..0..n/2), after which the projection (i) was compared by cross-correlation with the n re-projections. Typical values were n=7−9 and δ=0.1 − 0.2 degrees. The re-projection with the highest correlation was assumed to represent the best angular value and the parameter αi was replaced with the corresponding αj. The shift parameters were also updated in accordance with the azimuth values in order to maximize correlation. The tilt angle (β) and the tilt axis (γ) were refined in the same way.

Though the analysis of the 3D space of the Euler angles is often explored exhaustively and simultaneously in single particle analysis, this is not the case in tomography for two reasons: First of all, the final angles do not diverge more than ∼0.5 degrees from the preliminary alignment so it is unproductive to explore outside this range. Secondly, the dimensions of the reconstructed volume are too unwieldy to justify the computational time required for a multi-axial exploration of even a small quadrant of Euler space. In this way, we alternated single refinement cycles on each of the angles in the order α, ϑ, φ. A typical refinement process took 10 triple cycles. In a few cases, we also corrected for magnification, either during the initial alignment, or in the subsequent refinement.

Local refinement

This algorithm combines the underlying strategy of projection matching as it applies to tomography (Zampighi et al., 2005) with the ability to compute complete reconstructions by pasting together independently reconstructed sub-volumes (Lanzavecchia et al., 2005). The computation of reconstructions yields a 3D volume and a set of orientation parameters for the N projections: {α_i, β_i, γ_i, Δx_i, Δy_i ; i=0,1, .. N}. The reconstructed “slab” volume (Fig 1A) was then divided into M small cubes, for which one edge of each corresponds to the height of the slab: C_j, j = 0,1, .. M. Each cube (Fig 1B) was then reconstructed from sub-regions of the properly extracted original micrographs (Fig 1C). To extract the corresponding areas (256×256 pixels) from the original micrographs, we projected the center of each cube using the orientation parameters that were determined during the preliminary alignment process. Stacks of these small areas (Fig. 1D) were used to reconstruct the cubes, in conjunction with the Euler angles from the original map, calculated with the global refinement strategy. The shift parameters were set to zero since the projections were already centered. So as to allow for reliable re-projections, the size of this new reconstruction (256×256×128) was made larger than the dimensions of the target cube.

Figure 1.

Local refinement of tomographic maps.

The procedure starts in direct space by subdividing the preliminary reconstruction into 64 cubic volumes (A) each of which is treated independently. This processing is illustrated for the generic cube (B), which is shown isolated in the lower left corner of the figure. Working in the projection space (right side of the figure), we extract from the original micrographs the sub-areas from which the sub-volume (B) can be reconstructed. The stack C represents the original micrographs, though only the first projection is shown in full. The elliptical stair of squares represents the sub-areas of the subsequent micrographs containing the data associated with the projection of the cube (B). The vertical axis (n) indicates the order of the projections in series. The position of the squares is computed considering the projection of the center of the cube (B) in the imaging plane during data collection. In conical geometry the projection of every point describes an ellipsis. The sub-areas of the stairs are then organized in a new stack (D). The cube (B) can be reconstructed from (D) using known orientation parameters, because the lay out of Fourier sections in the reciprocal space (E) is the same as for the cube (B) and for the large reconstruction (A). Using the data of the stack (D), the cube (B) is refined as in a standard process of projection matching. Pasting together the refined cubes reconstruct the final volume.

The orientation parameters of each cube were then refined just as was done for the entire reconstruction. The reconstructions of the individual cubes were projected again, along the directions dictated by the Euler angles. The contribution of the projection corresponding to the chosen viewing direction was subtracted from the volume to avoid bias in the subsequent projection matching. To determine a new shift value, the computed projections were correlated with the experimental projections extracted from the micrograph. The 64 cubes were reconstructed independently a second time. The Euler angles were kept constant while varying the shift parameters. In this way, the new reconstruction used 64 parameter files rather than the single file required in the global refinement strategy. Finally, the Euler angles of each cube were independently refined by computing different projections with similar viewing directions. As for the global refinement, the process refined one Euler angle at time, cycling on the three angles by iterative steps. For each step, a number of re-projections n=7−9 and a spacing δ=0.1−0.2 degrees, were used. The 64 parameter files presented differences with respect to the other orientation parameters. If during refinement one of the Euler angles changed, the shifts were changed accordingly, so as to compensate for movements of the center of the cube in the projection (see appendix).

A simulated tomographic experiment

In order to simulate reconstructions from all three geometries, we created a phantom structure, designed to mimic a specimen consisting of many molecular complexes distributed in the plane and at different heights in the volume. This structure consisted of 256 identical “random knots” (Bellon et al., 1998) randomly oriented and contained within the volume of a slab of 1024×1024×128 voxels, with the exclusion of the eight corners. To simulate imaging of these phantom specimens, 72 projections were computed for each type of geometry, using a maximum tilt of 60°. As the generation of these data sets was purely analytic, no interpolation errors occurred. We used a large volume comprised of many objects to reproduce the sparse sampling of the Fourier space with respect to the size of the specimen and the superposition of the structures in projections. The volume of the phantom specimen was reconstructed from the noise-free projections using the exact values of the projection views. The corners of the slab were left empty to avoid any knot falling out of the projection area, so causing inconsistency in the data set. Though this type of inconsistency if quite frequent in tomography, the study of its effects was beyond the scope of this simulation.

For each reconstruction, we measured the discrepancy (or normalized root mean square deviation: Herman et al., 1973) with respect to the original phantom specimen and the relative variance of the 256 reconstructed knots. To do this, the 256 knots were extracted from the reconstructed specimen, aligned and compared pixel by pixel with respect to their average map and with respect to the original model. Each knot fits in a sphere of radius 25, and for each pixel p_i belonging to the sphere we computed:

$${\stackrel{‒}{p}}_i=\frac{1}{256}\sum _{j=1}^{256}{p}_{ij},{\sigma }_{1i}=\sqrt{\frac{1}{256}\sum _{j=1}^{256}\left(p_{i,j}^2-{\stackrel{‒}{p}}_i^2\right)}\text{and}{\sigma }_{2i}=\sqrt{\frac{1}{256}\sum _{j=1}^{256}\left(p_{i,j}^2-k_i^2\right)}$$

j being an index running on the series of reconstructed and aligned knots and i being an index running on the 65117 pixel of the sphere. The symbol k_i indicates the pixel of the original knot used to generate the phantom. In this way we obtained 65117 values of σ_1i and σ_2i. Within these sets we computed the minimum, maximum and average value of both σ_i for the three geometries considered. In doing this operation, we did not attempt to align the reconstructed knots experimentally. Rather, we used the exact orientation parameters used to construct the original knots.

Results

Analysis of series imaged using conical geometry

a) “Preliminary reconstruction and global refinement”. We began by aligning and refining the maps with the same strategy used in previous studies: marker based alignment (Lanzavecchia et al., 2005) and refinement by projection matching (Zampighi et al., 2005). We found that while this global strategy improved the overall quality of the maps, the resolution at the center was always better than at the periphery. These “globally refined” maps, referred to here as “preliminary” since global refinement is the first step in the refinement process, were then compared with maps refined using the local strategy.

b) “Local refinement”. In this strategy, the preliminary reconstruction (1024×1024×128 voxels) was subdivided into an array of 8x8 cubes (128³ voxels) that were refined independently by projection matching (Fig. 1). The local refinement strategy for plastic sections requires ∼10 cycles (1 for the shifts and 3 for each of the angles). Improvements in the reconstructions were assessed visually by examining single planes of the structure of biological membranes at the periphery of the reconstructed volume (Fig. 2). The membrane and vesicles exhibited trilayer structures comprised of two dense bands flanking a central electron lucent region (the “unit membrane” pattern), indicating a bilayer configuration (for review, see Robertson, 1987). Maps refined using the “local refinement” strategy always exhibited the “unit membrane” pattern in views oriented both parallel and orthogonal to the XY plane, while in those calculated using only information from the position of the gold particles, the unit membrane was not resolved.

Figure 2.

Results of local refinement in conical geometry.

The reconstructed volume was inspected by cutting sections along the X-Y, X-Z and Y-Z planes. Before refinement (A, C, E), the unit membrane pattern in the vesicles and plasma membrane is unevenly resolved since alignment was optimized for the center of the maps. After local refinement (B, D, F), the presence of the unit membrane pattern was independent from the location in the map. The larger arrows point to a group of three vesicles where the improvement is most noticeable. The smaller arrows indicate a vesicle of the same group in the X-Z plane

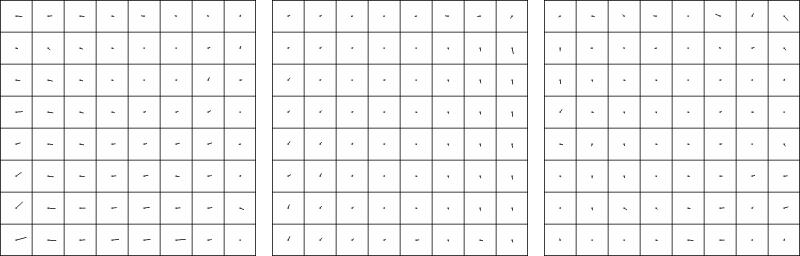
We also followed the results of the refinement process by constructing maps of the shift vectors created by correlating the projections of the cubes with the corresponding regions from the original micrographs. These maps show that local refinement warped differently in different projections, collected at the beginning, middle and at the end of the series (Fig. 3). The direction of the vectors indicate that the squares at the periphery move more than those at the centre of the map. This behaviour indicates that global refining aligns the central region properly (compare, panels A-C in Fig. 3).

Figure 3.

Distortion maps for conical geometry.

The three images refer to the first, the middle and the last projection in conical series. The short lines at the center of each small square represent the 64 shift vectors detected by correlating the projections of the cubes with the corresponding regions extracted from the micrograph. For clarity of presentation, the shift vectors are drawn as segments starting from the centre of a set of squares which reproduce the lay out of the 64 cubes. In scale to the edge of the square, the length of the drawn segment is four times the real value. The vectors denote how the specimen warps during shrinkage. The movements follow a non-linear transformation with respect to both the speed of the changes and the shape of the final volume.

Application of the local refinement to series imaged with single and double tilt geometries

We also refined reconstructions calculated from double-tilt series with the same local refinement strategy as used for conical geometry. There was, however, a small difference with the refinement of the tilt angle β. In single or dual axis geometry, every micrograph M_i possesses two neighbouring items (M_i−1 and M_i+1) at short Δβ distance. During refinement, the 3D volume is projected after subtracting the contribution of M_i, thus reducing the density of the Fourier space sampling. M_i is then correlated with the n re-projections computed at close β angles (β_j= β_i+jδ; j=−n/2 .. n/2). These re-projections appear somehow more defined as β_j approaches β_i+1 or β_i−1, because they approach a region of the Fourier space which is better sampled by the tomographic series. This may affect the cross-correlations in such a way that the tilt parameters β_i tend to near each other, at least at small tilt angles (β<15°), where the consecutive micrographs are often quite similar. This problem, which does not appear in conical geometry because of the different sampling of the Fourier space, is solved by decreasing the value of the correction of β by one half, at small tilt angle. We found that the local refinement strategy, so adapted, improved the quality of the reconstructions, as determined by visual inspection of the reconstructed volumes (Fig. 4). Despite significant improvement in these reconstructions, maps of the shift vectors created by correlating the projections of the cubes with the corresponding regions from the original micrographs, showed that the movements were less pronounced than when refining reconstructions from conical series (Fig. 5). This was probably due to the good performances of the preliminary alignment strategy, which already took into account a magnification correction between the two series (see methods). Accordingly, the number of local refining cycles was reduced to ∼7 cycles (1 for the shifts and 2 for each of the angles).

Figure 4.

Results of local refinement in dual axis geometry.

The reconstructed volume was inspected by cutting sections along the X-Y, X-Z and Y-Z planes. Before refinement (A, C, E), the unit membrane pattern in the vesicles and plasma membrane is unevenly resolved since alignment was optimized for the center of the maps. After local refinement (B, D, F), the presence of the unit membrane pattern was independent from the location in the map.

Figure 5.

Distortion maps for dual axis geometry.

The three images refer to the first, the middle and the last projection of the first the dual axis series. Like in Figure 3, the short lines at the center of each small square represent the 64 shift vectors detected by correlating the projections of the cubes with the corresponding regions extracted from the micrograph. For clarity of presentation, the shift vectors are drawn as segments starting from the centre of a set of squares which reproduce the lay out of the 64 cubes. In scale to the edge of the square, the length of the drawn segment is four times the real value. The vectors denote how the specimen warps during shrinkage. The movements follow a non-linear transformation with respect to both the speed of the changes and the shape of the final volume.

We also applied the local refinement strategy to series imaged using single tilt geometry. The procedure was the same as the one for series collected using double tilt geometry. In the refinement of single tilt series, however, we did not use corrections for the tilt angle. A single cycle was required before terminating the refinement process. The improvements of the map were detected as small variations of statistical indices (see below) but were not evident to visual inspection.

Quantitative measurements

Fourier ring correlation (FRC), among the original micrographs and the projections computed from the 3D maps (noise-compensated leave-one-out, NLOO), as well as Fourier shell correlation (FSC), among independent reconstructions, have both been proposed as a means of measuring the quality of tomograms (Cardone et al., 2005). We planned to use these criteria to compare the quality of our tomograms before and after the application of the local refinement protocol. However, the computation of NLOO after applying the local refinement strategy became too cumbersome since each individual micrograph associates as many orientation parameters as the number of squares (64). For this reason, we estimated the resolution by computing a local 3D FSC.

The reconstructed volumes were partitioned in the 64 cubes previously defined, and each cube was reconstructed two times using either even or odd projections of the original series and then compared with FSC in order to measure local resolution. This calculation produces an undervalued estimate of the resolution, since these reconstructions were calculated from one half the data set. A more realistic estimate was obtained using the equation described by Cardone et al. (2005) which availed the correlation curve defined by the equation: even/odd FSC = 2FSC/(FSC+1). In this case, we estimated the resolution by cutting the curve either at 0.5 or at 0.3.

Table I reports the local resolution from both conical and dual axis geometry data, estimated before and after the local refinement protocol. The values associated to each square indicate that the local refinement strategy was able to improve resolution at the periphery of the volumes, bringing them closer to those estimated for the central area. The improvement was observed for both geometries and is independent of the criteria used to calculate resolution. Therefore, Table 1 represents a numerical description of the visual improvements observed in figure 2 and 4, and coincides as well with figure 3 and 5, which show that the peripheral regions underwent the largest corrections in shift parameters.

Table I.

Assessment of Resolution We estimated resolution before and after the application of local refinement using the even/odd FSC criterion, in maps calculated from conical (a), dual (b) and single (c) axis geometries. In each case we cut the FSC curve using either the 0.3 criterion or 0.5 criterion. For conical and dual axis geometries we report the mean, minimum and maximum value of the 64 cubes as well as the local resolution in the 8×8 cubes of the reconstruction. The locations of the values in the table correspond to the locations of the cubes in the map. Notice the stronger improvement at the periphery of the volume. For single axis series, only the mean, minimum and maximum value of the 64 cubes are included. All values reported are expressed in nm.

(a) Conical geometry.
Global Refinement (0.3 criterion)								Local Refinement (0.3 criterion)
Ave.			min.		Max.			Ave.			min.		Max.
4.7			3.5		8.0			3.6			3.3		5.3
8×8 sub-volumes								8×8 sub-volumes
5,7	5,1	5,2	4,9	4,7	5,2	5,9	6,3	4,0	3,7	3,6	3,6	3,4	3,7	4,1	4,2
5,6	4,9	4,3	4,3	4,5	4,6	4,8	5,4	3,7	3,6	3,6	3,6	3,4	3,5	3,7	4,1
5,1	4,5	3,9	3,8	3,9	3,9	4,2	4,8	3,6	3,6	3,4	3,4	3,4	3,4	3,4	4,0
4,8	3,8	3,6	3,6	3,7	3,6	4,0	4,6	3,5	3,4	3,4	3,4	3,3	3,3	3,3	3,6
4,7	3,9	3,5	3,5	3,6	3,7	3,7	4,3	3,6	3,5	3,4	3,4	3,3	3,3	3,3	3,5
5,2	4,8	4,5	3,7	3,7	3,8	4,4	5,1	3,9	3,7	3,7	3,4	3,4	3,3	3,4	3,7
5,5	5,2	4,9	4,8	4,6	4,6	4,9	5,6	3,7	3,6	3,6	3,7	3,6	3,4	3,3	4,1
5,9	5,1	5,5	5,9	5,6	6,2	6,3	8,0	4,1	3,5	3,6	3,9	3,8	4,1	3,8	5,3
Global Refinement (0.5 criterion)								Local Refinement (0.5 criterion)
Ave.			min.		Max.			Ave.			min.		Max.
6.4			4.6		10.4			5.2			4.2		8.1
8×8 sub-volumes								8×8 sub-volumes
7,4	7,2	6,8	6,8	6,3	7,3	7,9	8,1	5,7	5,2	5,5	5,5	4,7	5,6	6,2	6,2
7,3	6,5	6,2	6,2	5,9	6,2	7,0	7,3	5,5	5,1	4,9	4,9	5,1	5,1	5,5	6,3
6,9	6,1	5,5	5,2	5,2	5,7	5,6	6,8	5,4	4,9	4,6	4,8	4,7	4,6	4,6	5,8
6,9	5,5	4,8	4,9	4,9	5,2	5,5	6,3	4,9	4,6	4,4	4,6	4,4	4,3	4,4	5,1
6,2	5,6	4,9	4,6	4,6	5,2	5,9	6,3	5,0	4,9	4,7	4,6	4,2	4,2	4,6	5,1
6,8	6,2	5,9	5,2	5,2	5,5	6,2	7,3	5,4	5,2	5,2	4,6	4,6	4,6	4,9	5,6
7,3	6,8	6,2	6,3	6,3	6,4	6,9	8,1	5,6	5,2	5,2	5,4	5,1	4,9	4,9	6,0
7,3	6,9	7,3	7,3	7,5	7,4	8,3	10,4	5,9	4,8	5,4	5,9	5,6	6,2	6,4	8,1

(b) Dual axis geometry.
Reference points (0.3 criterion)								Reference points (0.3 criterion)
Ave.			min.		Max.			Ave.			min.		Max.
4.1			3.4		5.1			3.4			3.2		4.2
8×8 sub-volumes								8×8 sub-volumes
5,0	5,0	4,7	3,9	4,7	5,1	4,8	4,0	3,6	4,0	4,2	3,6	4,0	4,1	3,9	3,6
4,6	4,2	3,9	3,4	3,8	4,4	5,0	4,5	3,3	3,3	3,4	3,3	3,6	3,7	3,7	3,5
4,2	4,0	3,6	3,4	3,6	4,0	4,3	4,5	3,3	3,3	3,2	3,3	3,4	3,4	3,3	3,3
4,1	3,8	3,7	3,6	3,6	3,7	4,0	4,0	3,3	3,2	3,3	3,2	3,4	3,4	3,3	3,3
4,5	3,9	3,8	3,8	3,6	3,7	3,7	3,9	3,5	3,2	3,2	3,3	3,3	3,3	3,3	3,3
3,9	3,6	3,8	4,1	3,8	3,9	3,9	3,9	3,5	3,2	3,2	3,2	3,2	3,3	3,3	3,3
3,8	3,6	3,8	3,9	4,0	4,2	4,5	4,2	3,4	3,3	3,3	3,2	3,3	3,3	3,4	3,3
3,9	3,6	3,5	3,7	3,9	4,0	5,0	5,0	3,6	3,3	3,2	3,3	3,3	3,3	3,6	3,7
Reference points (0.5 criterion)								Reference points (0.5 criterion)
Ave.			min.		Max.			Ave.			min.		Max.
5.8			4.5		7.4			4.6			4.0		6.4
8×8 sub-volumes								8×8 sub-volumes
7,1	6,9	6,9	5,1	6,6	6,8	6,9	5,8	5,3	6,4	6,4	5,0	5,9	5,7	5,4	4,6
6,3	5,6	5,3	4,5	5,6	6,0	6,6	6,4	4,4	4,4	4,5	4,3	5,0	5,0	5,3	4,6
5,8	5,4	4,8	4,5	5,2	5,5	5,6	6,0	4,4	4,2	4,2	4,3	4,9	4,8	4,5	4,3
6,0	5,5	5,0	4,6	5,6	5,3	5,3	5,4	4,3	4,2	4,1	4,3	4,9	4,8	4,5	4,2
6,6	5,5	5,2	4,9	4,9	5,0	5,0	5,3	4,9	4,2	4,2	4,3	4,4	4,5	4,3	4,3
6,3	5,6	5,8	5,4	5,2	5,0	5,2	5,6	4,7	4,2	4,1	4,2	4,0	4,1	4,2	4,3
6,4	6,1	6,2	5,7	5,8	6,0	6,1	6,0	4,7	4,2	4,3	4,2	4,2	4,2	4,4	4,4
6,6	5,6	5,8	6,6	6,7	6,2	7,4	6,8	5,0	4,3	4,3	4,3	4,4	4,3	5,4	5,2

(c) Single axis series.
Reference points (0.3 criterion)			Reference points (0.3 criterion)
Ave.	min.	Max.	Ave.	min.	Max.
3.2	3.1	3.6	3.1	3.0	3.4
Reference points (0.5 criterion)			Reference points (0.5 criterion)
Ave.	min.	Max.	Ave.	min.	Max.
3.8	3.6	4.2	3.7	3.5	4.1

Simulation

The performances of the three geometries previously considered were also studied with a simulated tomographic experiment. We constructed a phantom specimen consisting of many identical complexes dispersed in random orientations (Fig. 6) and generated three different sets of projections for the three types of geometries (conical tilt, single and dual axis). The three reconstructions were analyzed to assess the quality of the tomogram with regard to anisotropic deformations of the volume, introduced by the geometry. The 256 complexes in the reconstructed phantom specimen were extracted from the volume, brought to a common orientation and compared pixel by pixel to study the variance of these reconstructions. The results are shown in Table 2 and the maps of variance in Fig. 7. The table shows that for the single axis series there are large differences between the reconstructed knots, as evidenced by the high value of their variance. These differences originate from a strong anisotropy in the reconstruction introduced by the geometry (Penczek et al, 1995), whereby the reconstruction of each knot depends upon its orientation with respect to the tilt axis.

Figure 6.

A phantom structure was reconstructed using single, double and conical tilt geometries to assess the quality of the tomograms with regard to anisotropic deformations of the volume. The phantom was comprised of 256 analytically constructed “knots”, randomly oriented and displaced in the slab. An individual knots is shown at the bottom left corner.

Table II.

Results of the Simulated Tomographic Experiment The phantom specimen comprised of 256 knots in random orientation (Fig. 6) was projected and reconstructed using the geometries in the first column. The value of the discrepancy between the entire reconstructed volume and the original specimen is in column 2. The root mean square deviation (rmsd) values in column 3−4 represent the differences between the knots in the reconstructed volume and their average map (1). The rmsd values in columns 5−6 represent the differences between the knots in the reconstructed volume and the original knot (2). In each case, we computed the average (aver) rmsd of pixels comprising the knots, as well as the maximum value (max) of the set of pixels. All rmsd values are expressed in the original dynamic range of the phantom specimen [0,255].

geometry	discrepancy	aver. rmsd 1	max rmsd 1	aver. rmsd 2	max rmsd 2
Single	0.55	26	64	33	109
Dual	0.42	19	51	24	94
Conical	0.42	17	28	22	91

Figure 7.

Maps of variances obtained from the reconstructed phantom. For each geometry the 256 random knots enclosed within the reconstruction were extracted and aligned with the exact orientation parameters used during the generation of the phantom. The aligned knots were compared pixel by pixel with their average 3D map. The figure presents the variance of the difference maps in common scale: (a) single axis geometry; (b) dual axis; (c) conical geometry. See table 2, columns 3 and 4 (rmsd1).

Anisotropy is reduced for dual axis geometry and, at least in the XY plane, is totally excluded from conical tilt geometry. Looking at figure 7, the difference between conical tilt and dual axis tomography seems glaring. However, the differences in the images are not reflected in table 2, where the average variance between the knots was approximately the same for the two types of tomography. The differences in the images seen in figure 7 B and C most likely reflect the large maximum rmsd value (51). Though this experiment was performed as a simulation, and should be construed as such, it is important to stress that the analysis is quite “real” since the technique of simulation remained constant for each type of tomography. It is equally important to note, that in experiments not performed as simulations, the problem of aligning the complexes creates an additional variable, likely to diminish the accuracy of comparisons among the geometries.

Discussion

The interest in studying specimen deformation arises from the fact that collection of multiple exposures of the same region changes the specimen and interferes with the accurate alignment of the tilt series. Principal strategies introduced to ameliorate this problem involve corrections for magnification based on fiduciary points (Mastronarde, 1997) and the use of a revised back projection algorithm based on non linear transformation (Lawrence et al., 2006).

The first strategy changes the magnification of the projections of the series based on the coordinates of gold particles deposited on the surface of the specimen (Kremer et al., 1996). The principal advantages of this strategy involve the high contrast of the gold particles, which allows their identification along the entire series as well as the computational speed of the calculations. Our results indicate that with this strategy, it is possible to align the series, particularly when the gold particles were evenly spread on the surface of the specimen. Corrections based on this strategy, however, cannot be perfect since shrinkage is a non-linear phenomenon and the average values of the refinement depend principally on how the regions which are closest to the particles changed during imaging. For this reason, the periphery is often poorly aligned with respect to the central region. Moreover, this strategy implemented in Imod is limited to dual axis geometry.

The second strategy takes into account lens aberrations and curvilinear electron paths in addition to specimen deteriorations, all of which contribute to misalignment and poorly reconstructed tomograms (Lawrence et al., 2006). The solution proposed deals with a revised back projection algorithm based on non linear transforms. The algorithm of Lawrence et al. clearly improved the quality of the reconstruction when compared to traditional back projection approaches.

Likewise, our algorithm produces highly improved reconstructions. It remains to be seen which approach will give the best results. It may turn out that the quality of the results achieved with either algorithm will depend on specific specimen features and experimental conditions. This question can be answered when much more experience will have accumulated by the application of both algorithms to a variety of specimens recorded with different imaging conditions and geometries.

To this end, we have introduced a novel strategy to correct for shrinkage that is based on local refinement and projection matching. In this strategy, the coordinates of a few gold particles are still required since optimization of the Euler angles and the shifts are done reliably only when they start from a point close to the final solution. As demonstrated in a previous study (Zampighi et al., 2005), a free search of the orientation parameters, as done in single particle methods (see, e.g., Frank, 1996), is not practical since in electron tomography the Fourier space is sparsely sampled. Key advantages of our strategy are that it can be applied without specific knowledge of the imaging conditions, and that it is driven by the structures under study, rather than exogenous particles with no biological significance.

We used several methods to determine the efficacy of the local refinement strategy based on projection matching. First, we relied on visual inspection of structures contained in the reconstructed volume (Figs. 2, 4). In particular, we focused on the structure of membranes that have phospholipids arranged in a bilayer configuration. In the tomograms, membranes show up as trilayer structures comprised of two electron dense layers flanking an electron lucent central band (the “unit membrane” pattern). As reported in previous studies (Zampighi et al., 2005; 2006), maps refined using the “global” strategy resolved the unit membrane pattern clearly in the central region but not in the periphery of the volume (see also Fig. 2A). In contrast, maps refined using the “local” strategy resolved the pattern equally at the periphery of the reconstructed volume (Fig. 2B). More importantly, the improvement was also evident along the X-Y and X-Z planes (Fig. 2 C-F). Therefore, the local refinement based on projection matching greatly improved the overall resolution of biological membranes, a key cellular structure, throughout the reconstructed volume.

We also followed the refinement process by studying the deformation from the shift vector maps (Fig. 3, 5), which indicated that shrinkage modifies the plastic section non-linearly. In addition, our strategy provided a detailed description of how these distortions affect each projection of the series. After the shifts were used to refine the reconstruction, the overall quality of the tomogram improved. We also used quantitative measurements to monitor the effect of the local refinement strategy. Measurements using FSC methods indicate that the local strategy improves the overall resolution of the tomograms, particularly in the periphery (Table 1). More importantly, this improvement was not dependent on the criteria used to cut the correlation curve (Table 1). Therefore, the quantitative measurements support the results gathered by resolving the unit membrane pattern.

The thickness of the sample, however, must be small enough so that the projection matching is feasible. When the thickness increases, the high tilt projections contain the superposition of an increasing amount of matter, not all of which belongs to the cube under refinement. This extra matter is amenable to noise and impedes the projection matching process since it cannot find any correspondence with the re-projections of the reference. Our specimen had a thickness of about 50−100 nm, which are typical values for plastic sections. In the case of thicker material, serial sectioning and tomography of adjacent slices would be a viable strategy (Soto et al., 1994; see also McEwen and Marko, 2001).

Although every example reported here deals with reconstructions partitioned in 64 cubes, this number is not fixed or mandatory. We were limited by the requirement of using cube edges corresponding to a power of 2, because of our FFT routines. However, in theory, any edge can be used. Furthermore, our choice that the cube edge coincides with the height of the reconstructed slab was largely a result of practical convenience. In a few cases, we tested different sub-volumes, like tetragonal prism sizing 256×256×128 or small cubes with a size of 64³ voxels. In this latter case the subdividing grid acted also in the Z direction, creating 2 layers of 256 cubes each. We found that every sub-volume is feasible, with the quality of the results being determined by the reliability of the projection matching process. A sparse grid assures large areas and good correlations but reduces the ability of detecting very local deformations. A finer grid assures detection of small deformations but increases the risk of using insufficient signal during correlation. The best balance depends on the type of sample and on the signal to noise ratio of the images. In our reconstructions, this balance coincided with the choices reported here while other choices gave worse results.

The local refinement strategy works best with conical series since in this geometry, the Fourier sections share a different line with every other section of the set. In single axis geometry, the refinement that can be attained was limited since all the sections share the same line. This limited refinement results from the fact that the tilt angle beta cannot be refined. If beta is allowed to vary, the Fourier sections are “attracted” by neighbouring sections with which they form pairs. This effect alters the spacing of the Fourier sections, downgrading the quality of the reconstructions. In dual axis geometry this “attraction” of consecutive sections is tempered by combining two independent series. Even so, the beta correction has to be relaxed in order to avoid oscillations (see Results).

The quantitative measurements we reported offer an estimate of the resolution for the tomograms obtained with three different geometries. The data in table 1 show that the measured resolution for conical and dual axis geometries are about the same, i.e. around 3 to 5 nm, depending upon the thresholds selected. Surprisingly, for single axis geometry, resolution seems to be even better (3 − 3.5 nm). Better FSC values, however, do not signify better resolution, but rather a higher level of correlation between the reconstructions coming from the split data. The number of Fourier coefficients recovered from the tomographic experiment in turn depends upon the number of projections and in this study it was the same for all three geometries. In the case of single axis, the missing region is larger than for the other geometries and the coefficients are sampling a smaller space. It must be stressed here that the missing region is excluded from FSC computation, since the two reconstructions, both equaling zero, are perfectly identical in this region. In other words, the smaller the tilt angle and larger the missing region, the better the FSC values.

Many tomographic studies deal with the reconstruction of volumes containing multiple copies of equivalent structures in different orientations. This is true for viruses in frozen solution (Zhu et al. 2006) and also for tissue sections and cells (see, e.g. Baumeister, 2005; Frey et al., 2006). In these studies, copies of the complexes were detected in the tomogram, extracted and aligned with the goal of either attaining the computation of an average model or studying the variability of complexes (Beck et al., 2004). Here, the quality of the tomogram is especially important, with regard to anisotropic deformations of the volume, introduced by the geometry. For alignment and classification purposes, the effect of the missing region in Fourier space must be taken into account as its effect on the complexes is directly dependent on their orientation.

To study the effect of the geometry on the tomogram we used a phantom structure consisting of identical “random knots” (Bellon et al., 1998) randomly oriented and displaced in a slab volume (Fig. 6). The larger the volume, the closer the simulation comes to mimicking an actual tomographic experiment, including the sparse sampling of the Fourier space with respect to the size of the specimen and the superposition of the structures in projections. The simulation using a phantom specimen shows that from a strict geometrical point of view, conical geometry is superior to the other two types considered here. In this experiment we took into account only the layout of the projections, which were free of noise. Due to the nature of the simulation, it was, of course, not possible to take into consideration the imaging problems at the microscope, the alignment strategy, or the recording condition. In conical geometry all micrographs are taken at a high tilt angle, adding further to the complexity to the data recording. With our microscope, operating at an accelerating voltage of 120kV, we realized that conical tomography is successful at 55°, while many problems arise at 60°. Collecting the series tilted at the same angle does simplify the normalization of the data and provide an additional advantage with respect to single or dual axis tomography. Furthermore, conical tomography represents the best way to reduce the missing region in Fourier space. In theory, single axis can be pushed up to 70° or 80°, which could be very difficult for conical geometry. However, it must be remembered that the high tilt cannot solve the problem. For section material, the specimen is not finite, so that, at high tilt, a lot of signal comes from portions of the specimen which cannot fit in the reconstruction. This signal superimpose to the “good” signal and can be considered as noise (Cardone et al., 2005). It is a structured noise, whose effects are difficult to predict.

We have demonstrated the good performances of the local refining strategy on conventional plastic sections analyzed at room temperature, for which shrinkage problems are often significant. The same problems and the same behavior is expected also for plastic samples obtained after freeze substitution, provided that a similar contrast is achieved. In cryo-tomography, the cooling stage reduces the risk of macroscopic shrinkage. However, irradiation causes sublimation of the vitreous ice and movement of the gold particles, so that alignment based on gold particles loses its accuracy (Frey et al. 2006). In this case, the local refining could be a viable strategy to improve the alignment, while global corrections are probably useless. Clearly, the results will depend upon the signal to noise ratio of the images and the feasibility of projection matching.

In conclusion, specimen shrinkage and distortions can be corrected a posteriori with the combination of global and local refinement techniques presented here, resulting in a substantial improvement in the reconstruction. The techniques presented here are general and applicable to images recorded with any of the three major data collection geometries.

Appendix

Shift Composition

Consider a refining cube centred at X,Y,Z (usually Z=0), and a micrograph (M), with orientation parameters (α, β, γ). The position (x,y) of the projection of the center of the cube on M is given by:

$$\begin{array}{cc}\hfill \mathrm{x}& =\mathrm{a}{}^{\ast }\cos (-\gamma )-\mathrm{b}{}^{\ast }\sin (-\gamma )\hfill \\ \hfill \mathrm{y}& =\mathrm{a}{}^{\ast }\sin (-\gamma )+\mathrm{b}{}^{\ast }\cos (-\gamma )\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill \mathrm{a}& =\mathrm{X}{}^{\ast }\cos (-\alpha ){}^{\ast }\cos (-\beta )-\mathrm{Y}{}^{\ast }\sin (-\alpha ){}^{\ast }\cos (-\beta )+\mathrm{Z}{}^{\ast }\sin (-\beta )\hfill \\ \hfill \mathrm{b}& =\mathrm{X}{}^{\ast }\sin (-\alpha )+\mathrm{Y}{}^{\ast }\cos (-\alpha )\hfill \end{array}$$

and the vector (a,b) corresponds to the projection of the vectors pointing to XYZ for the given viewing direction (α, β).

After a refining cycle, a new set of parameters: (α', β', γ') and a possible shift Δ’ dictated by the correlation function are assigned to the projection of the cube. If one of the Euler angle changes, the projection of the center of the cube falls at (x’,y’). If this new position differs from the previous position (x,y), the difference vector (x’- x, y’- y) must be subtracted from the shift Δ’ to avoid misalignment.