Responses of Areas 3b and 1 in Anesthetized Squirrel Monkeys to Single- and Dual-Site Stimulation of the Digits

Abstract

Stimulation of the skin evokes topographically organized activation in somatosensory cortex. This representation is context dependent, however, since a different cortical topography is observed in area 3b when stimulated with complex tactile stimuli that evoke the von Békésy funneling illusion. Here we report on the population responses, as observed with intrinsic optical imaging, of area 1 and area 3b in the anesthetized squirrel monkey to pressure indentation of distal finger pads. Individual finger pad stimulation revealed that area 1 exhibited a smaller magnification factor than 3b, as evidenced by a smaller area of activation elicited by distal finger pad stimulation. Effects of paired finger pad stimulation produced largely similar effects in area 1 and area 3b. Paired finger pad stimulation produced reductions in the area of digit activation in area 1, suggesting the presence of lateral inhibition and funneling of information in area 1. Suppressive effects were stronger for paired stimulations at adjacent than at nonadjacent sites. Single-unit recordings revealed a mixture of either a summation or a suppression of the response to paired finger stimulation, compared with single finger pad stimulation of the primary digit. However, the average population response showed that paired finger pad stimulation resulted in response suppression. Based on this study and previous studies, we suggest the presence of at least three distinct ranges of lateral inhibition in areas 3b and 1.

INTRODUCTION

Pressure stimulation of individual distal finger pads evokes topographically organized activation in area 3b of primary somatosensory cortex (SI) as revealed with intrinsic signal optical imaging (Chen et al. 2001). This well-established systematic body map in area 3b changed when activity was evoked by the von Békésy (1960, 1967) funneling illusion (Chen et al. 2003). In the funneling illusion simultaneous stimulation at multiple sites leads to an illusory percept of stimulation at a single central site rather than separate sensations at each of the individual sites (Chen et al. 2003; Gardner and Spencer 1972a; Gardner and Tast 1981; Hashimoto et al. 1999; Laskin and Spencer 1979a; Sherrick 1964). Psychophysically, subjects report a sensation that a single centered object is stimulating the adjacent pairs of fingers (as if holding a pen across two fingers). We discovered that simultaneous stimulation of adjacent finger pads evoked a centrally merged cortical activation as detected with optical imaging in area 3b (Chen et al. 2003). This finding suggested that area 3b is involved in coding the perceived location of a stimulus and not simply the physical features of stimulation.

In SI, area 3b and area 1 are thought to have a hierarchical relationship, as suggested by anatomical, functional, and ablation studies (Costanzo and Gardner 1980; Garraghty and Sur 1990; Hyvarinen and Poranen 1978; Iwamura et al. 1983; Mountcastle and Powell 1959; Sur et al. 1985). Little is known concerning how areas 3b and 1 work in concert in somesthesis other than the existence of topographically organized feedforward and feedback connections between the two areas (Burton and Fabri 1995; Jones and Powell 1969). One known difference is the lack of slowly adapting responses of area 1 neurons compared with area 3b that has led to the conjecture that neural information in area 3b is recoded in area 1 (Jiang et al. 1997; Luna et al. 2005; Salinas et al. 2000). Comparison of activation patterns between areas 3b and 1 would provide valuable data regarding the nature of this interareal relationship and representation of stimuli in and across cortical areas.

In this study we examined SI cortical responses to two-digit versus one-digit pressure stimuli with intrinsic optical imaging and neurophysiology in the anesthetized squirrel monkey. Specifically, we examined how multiple versus single finger pad pressure stimulation is represented in area 1 and contrasted those findings to observations in area 3b. We discovered that area 1 exhibited a smaller magnification factor (mm of cortex/mm skin) than that of 3b, but otherwise exhibited a similar funneling response to paired finger stimulation. Neural unit recordings were consistent with imaged responses. The combined optical imaging and electrophysiological results suggest that area 1 does not, at least in the context of the funneling paradigm, elaborate further on the multidigit interactions initiated in area 3b.

METHODS

Eight adult squirrel monkeys (Saimiri sciureus) were used for these experiments. Surgical, imaging, and stimulation procedures, detailed previously (Chen et al. 2001, 2003, 2005; Friedman et al. 2004; Ramsden et al. 2001), will be described in the following sections. All procedures were conducted in accordance with National Institutes of Health guidelines and approved by University Animal Care and Use Committees.

Surgical preparation

After a preanesthetic dose of ketamine hydrochloride (10 mg/kg) and atropine sulfate (0.05 mg/kg, administered intramuscularly), anesthesia was maintained throughout the experiment with either isoflurane (0.9 to 1.5%) or pentothal (sodium thiopental, 1–2 mg·kg⁻¹·h⁻¹, administered intravenously [iv]) and a paralytic (vercuronium bromide, 100 μg·kg⁻¹·h⁻¹ iv). Animals were artificially ventilated to maintain an end-tidal CO₂ of 3.5–4%. Rectal temperature was maintained at 37°C. Anesthetic depth was assessed by monitoring heart rate, electroencephalograms (EEGs; via implanted wire electrodes), and by regular testing of the response to toe pinch. The anesthetic state was maintained at neurosurgical anesthesia Level 2 (light to moderate anesthesia) in which the EEG is characterized by large-amplitude (≤150 μV), low-frequency (one every 1–3 s) bursts (Kiersey et al. 1950; Pichlmayr et al. 1984).

With aseptic technique, a circular craniotomy about 1.5 cm in diameter and a durotomy were made over the anterior parietal cortex. The relatively shallow central sulcus was a landmark used to locate the primary somatosensory cortex. An electrophysiological mapping procedure was used to locate the finger pad region of areas 3b and 1 prior to imaging. Area 3b units were discriminated on the basis of small receptive field size (restricted to a single finger pad), brisk responsiveness to light tapping, and a lateral-to-medial topography of digits D1–D5 (Nelson et al. 1980; Pons et al. 1987; Sur et al. 1982). Area 1 units typically have larger receptive fields covering more than one finger (Iwamura et al. 1993; Sur et al. 1982). Cortical representations of the distal finger pads in area 3b and area 1 were segregated by the representations of the middle phalanges and palm (Sur et al. 1982). Following the brief electrophysiological mapping session, 4% agar covered with a coverglass was used to stabilize the cortex.

Mechanical stimulation

Fingers were secured by gluing small pegs to the fingernails and fixing these pegs firmly in plasticine, leaving the glabrous surfaces available for tactile stimulation by a mechanically controlled probe (Chen et al. 2001, 2003; Friedman et al. 2004). The distal finger pad was stimulated with a 3-mm-diameter probe that was attached to a force- and position-feedback–controlled motor (Aurora Scientific, Aurora, Ontario, Canada). With two such motors we were able to stimulate two finger pads in any single block of trials. The standard pressure stimulus was a single trapezoidal indentation with a duration of 4 s [ramp rates: 150 g/s; amplitude: 30 g (30.6 mN, ∼0.79 mm); baseline offset: 2 g (2.04 mN)]. When we investigated the coding of stimulus intensity, three plateau force amplitudes were used: 15, 30, and 60 g. Trapezoidal indentation is known to predominantly stimulate slow-adapting mechanoreceptors (Cohen and Vierck Jr 1993). Between vibrotactile stimulus presentations and during blank conditions, the stimulus probe remained in contact with the skin with a baseline contact force of 2 g (2.04 mN).

Optical imaging and analysis

The optical imaging procedures we used were similar to those used in previous studies (Chen et al. 2001, 2003; Friedman et al. 2004).

IMAGE ACQUISITION.

Images of reflectance change (intrinsic hemodynamic signals) were acquired by a video CCD camera and Imager 2001 and 3001 imaging systems (Optical Imaging, Germantown, NY) with 630-nm wavelength illumination. A blood vessel map, used for landmark purposes, was collected with 570-nm illumination. During image acquisition, stimuli were presented to two different finger pads. Thus each imaging acquisition block contained four stimulus conditions: two single-digit stimulation conditions (e.g., D2 or D4 alone), a paired-digit stimulation (e.g., D2 + D4), and a null stimulus (Blank) condition. To study the effect of different stimulus intensities, a control stimulus of 30 g was presented to one finger whereas one of four stimulus intensities (0, 15, 30, 60 g) was presented to the other finger. Within blocks of trials, stimuli were presented in a randomly interleaved manner with an 8- to 10-s interstimulus interval. In a typical imaging session, in all 40–60 trials were averaged (10 trials per block). Maps were collected at five image frames/s for 3 s starting 200 ms prior to stimulus onset.

IMAGE ANALYSIS.

For each stimulus condition, image frames, collected from 1.8 to 2.8 s after trial onset, were summed to maximize signal-to-noise ratios. Prior to averaging, images were examined to remove blocks that contained high-amplitude noise (usually due to significant blood vessel artifact near the central sulcus). As a further control, we also compared images obtained by summing different blocks of trials. The presence of a sporadic signal would result in different half-trial maps, whereas a consistent, reliable signal would produce similar half-trial maps (cf. Bonhoeffer and Grinvald 1996; Chen et al. 2001). These methods were used to confirm that the imaged signals were consistent and repeatable and were not due to noise signals occurring in one or a few of the trials.

The functional maps presented herein are single-condition maps. Single-condition maps were obtained by the subtraction of the blank condition from the stimulus condition (blank subtracted) or by subtracting the first prestimulus frame from each subsequent frame of the stimulus condition (first frame subtracted). Such subtraction maps not only measure changes from baseline, but also reduce blood vessel artifacts and minimize effects of uneven illumination.

OUTLINING ACTIVATION HOTSPOTS.

Thresholding procedures were used to delineate regions of strongest activation (Chen et al. 2003; Ramsden et al. 2001). Images were low-pass filtered (4-pixel rectangular kernel) and, at times, high-pass filtered (to minimize the effects of uneven illumination). Identical image processing parameters were used for all images acquired within each case. Maps were thresholded at the top 15% of the gray pixel value distribution to outline regions (hotspots) of strongest activation. We have found that with different high- and low-pass thresholding criteria (10 and 25%), activation boundaries shift only slightly (Chen et al. 2003); thus our conclusions were not dependent on a specific threshold criterion. To determine the area of activation, the total pixel number was converted into square millimeters based on image magnification.

MEASURES OF CORTICAL MAGNIFICATION.

The cortical magnification factor for digit stimulation was estimated by dividing the cortical area of activation in areas 3b and 1 by the area of the 3-mm-diameter probe (7.07 mm²). Additionally, we calculated the distance (in mm) between the centers of activation of digit pairs stimulated sequentially and used this as a measure of cortical distance separating digits. After filtering and thresholding, the linear distance between the centers of activation of pairs of digits in areas 3b and 1 was measured and converted to millimeters based on image magnification. Although the distance between the centers of digit activation is not a true measure of cortical magnification (a contiguous patch of skin does not connect the distal finger pads), it does provide a comparable measure that may be independent of the effects of anesthesia on activation area.

TIME-COURSE ANALYSIS.

The time course of the percentage reflectance change, during the period of image acquisition (3,000 ms, 15 frames including the prestimulation frame), was obtained over regions of interest in areas 3b and 1. The sample size within the regions of activity measured about 200 μm. Percentage change from baseline was calculated by either first-frame subtraction, where the first 200-ms frame is subtracted from each of the subsequent 200-ms frames, 100 × {[Rstim(ti) − R(tff)]/R(tff)}, or by blank subtraction, which is the time-matched difference between the stimulated and blank conditions, 100 × {[Rstim(ti) − Rblank(ti)]/Rblank(ti)}. The peak percentage change in reflectance was used as a measure of peak signal amplitude. To further confirm that the reflectance change was indeed related to functional activation, control samples were also obtained from regions distant from the activated region.

Electrophysiological recording

Extracellular recordings of the spike discharge activity of single SI neurons and local neuron populations were obtained subsequent to the optical imaging phase of the experiments. Glass-coated tungsten microelectrodes (Ainsworth, Northampton, UK) were inserted into superficial cortical layers and used to record unit activity. The receptive fields (RFs) of multiple or single units were determined through a series of indentations with a 2-mm-diameter handheld probe. Isolated or multiple units were classified as having response properties similar to either slowly or rapidly adapting type I mechanoreceptors (SA and RA, respectively), based on their sustained or slowly adapting response (SA) or transient or rapidly adapting (RA) response to static indentation (Mountcastle et al. 1969; Talbot et al. 1968). To evaluate whether the unit activity had rapidly adapting type II activity (high vibration-sensitive Pacinian response-like properties), we determined whether the unit had a relatively large RF and responded to indirect distant vibrations (tapping on the table). For a subset of units with RFs near the center of the finger pad, we stimulated with the same stimuli we used for the intrinsic imaging. Conventional techniques were used to amplify, filter, and display unit activity. To collect, store, and analyze records of neuronal spike trains, we used Spike2 hardware and software (Cambridge Electronic Design, Cambridge, UK). We found that cortical units with cutaneous RFs away from the stimulated site (e.g., on the middle or proximal finger pads) did not respond to the probe stimulation on the distal finger pad, confirming that our imaged responses were due specifically to distal finger pad stimulation. Poststimulus time histograms (PSTHs) were generated and used to evaluate the neuronal responses.

Statistical analysis

Statistical analyses were performed on the population of samples. ANOVA procedures, paired or unpaired t-tests, were used to compare the effects of the independent variables (area 3b vs. area 1 or stimulus intensity) on the dependent variables (peak signal amplitude, area of activation, discharge rates). A z-test was used to evaluate the significance of the frequency of responses (neural or optical) that fell in different categories (suppressive, facilitative). The criterion for significance for each statistical test was P < 0.05.

RESULTS

Using optical imaging, we examined topography, funneling, and intensity coding in area 1. Data from area 3b, often collected in the same field of view, are also reported for comparison. Typically, following our imaging sessions, we then collected some single and multiunit data to relate individual neuronal responses with imaged activity observed in the cortical population. Our electrophysiological data are meant to be supportive of the imaging data and to provide single examples of neuronal response.

Optical imaging

TOPOGRAPHIC REPRESENTATION OF THE DISTAL FINGER PADS.

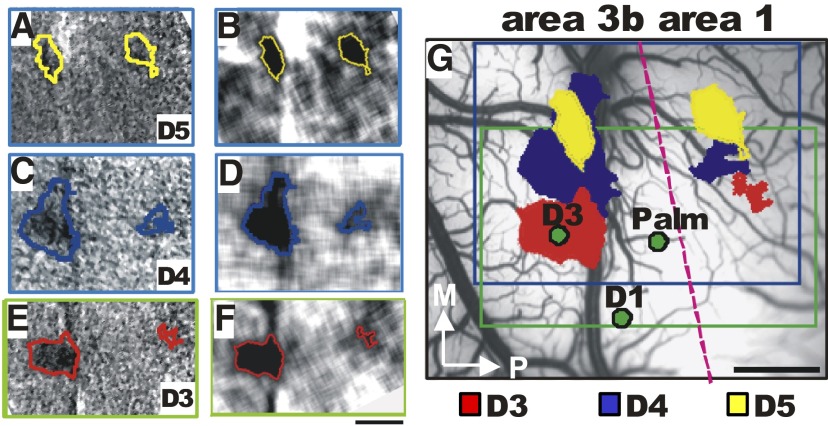
Prior to imaging, we performed a brief electrophysiological mapping procedure to determine the location of a few digit representations in areas 3b and 1. As shown in Fig. 1, stimulation of distal finger pads D5 (Fig. 1, A and B), D4 (Fig. 1, C and D), and D3 (Fig. 1, E and F) elicited focal activations in area 3b (see approximate 3b/1 border indicated by red dashed line in Fig. 1G), consistent with digit topography shown in previous studies (Chen et al. 2001; Sur et al. 1982; Tommerdahl et al. 2002) and with our brief electrophysiological recordings (Fig. 1G, penetrations indicated by green dots). In area 1, a similar topographic map was observed, with focal activations to stimulation of distal finger pads D5 (A and B), D4 (C and D), and D3 (E and F) in area 1. Also consistent with previous reports (Sur et al. 1982), we found the representation of receptive fields on the palm between the representations of the fingers in areas 3b and 1 (Fig. 1G). Topographic organization was always observed in area 3b and in area 1 [activation was present in area 1 in seven of eight cases, D2/D3 (Fig. 3) and D2/D4 (Figs. 3 and 4)]. Thus optical imaging revealed two topographic maps, one in area 3b and another in area 1 located posterior to area 3b.

FIG. 1.

Topography of distal finger pads in areas 3b and 1. A–F: maps of single digit stimulation. Single condition maps (left column) and same maps low-pass filtered (right column). A and B: D5 (yellow outlines). C and D: D4 (blue outlines) and D3 (red outlines). G: regions of activation overlaid on the blood vessel image. Red dashed line indicates the approximate border between areas 3b and 1. The field of view in E and F was shifted relative to A–D. The respective fields of view are indicated by the blue (A–D) and the green (E and F) boxed outlines in G. Green dots indicate electrode penetrations. Scale bar in F applies to A–F and in G applies to G: 1 mm. M, medial; P, posterior.

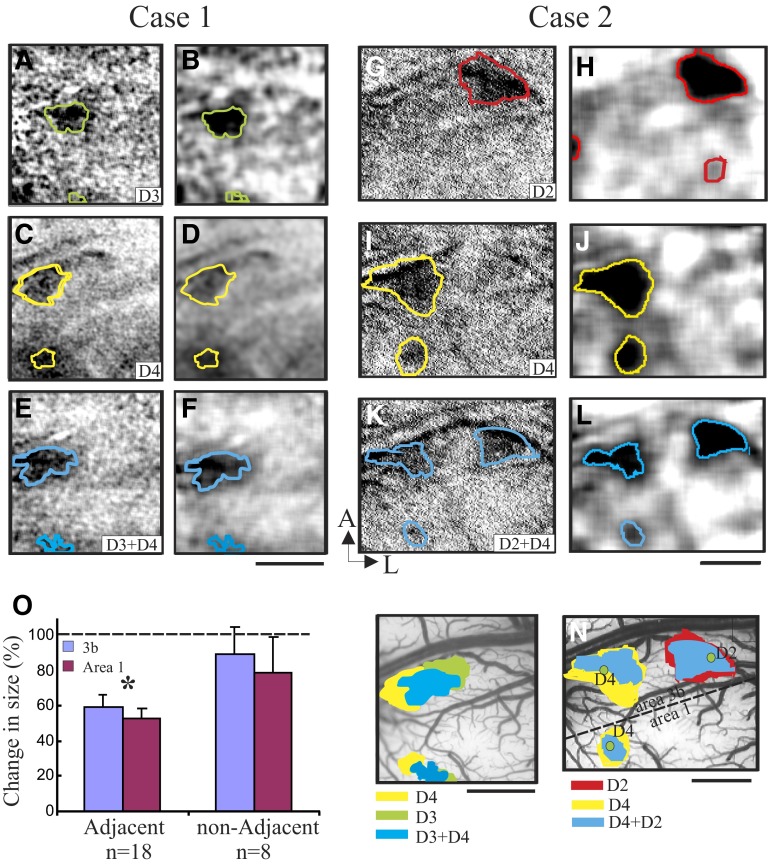
FIG. 3.

Cortical activations to single and paired finger pad stimulation. Case 1 (adjacent digits): images acquired during stimulation of D3 alone (A and B), D2 alone (C and D), and D3 + D4 (E and F). Case 2 (nonadjacent digits): images acquired during stimulation of D4 alone (G and H), D2 alone (I and J), and D2 + D4 (K and L). Thresholded outlines are overlaid on the single-condition map (A, C, E, G, I, K) and on Gaussian-filtered images (B, D, F, H, J, L). Activation sizes are overlaid on blood vessel maps (M, Case 1; N, Case 2). M (Case 1) and N (Case 2): borders between areas 3b and 1 are indicated by dashed lines in the blood vessel images. Green dots: electrophysiological penetrations reveal somatotopy consistent with imaged maps. O: changes of the activation size in areas 3b (blue) and area 1 (red) in response to paired finger pad stimulation (adjacent and nonadjacent) in comparison to single finger pad stimulation (indicated by dashed line as 100%; *P < 0.05). Error bars = SE. Scale bar: 1 mm. A, anterior; L, lateral.

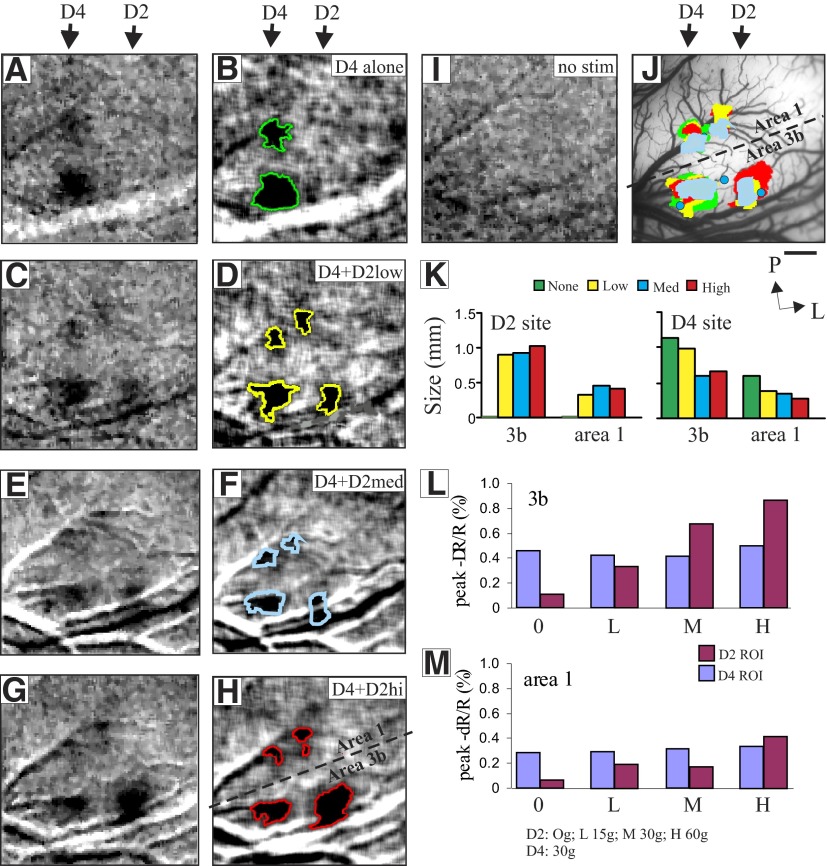
FIG. 4.

Cortical activation size correlates with stimulus intensity. Cortical responses in areas 3b and 1 to medium pressure intensity stimulation of D4 (A–H) and a low (C and D: 15 g), medium (E and F: 30 g), and high (G and H: 60 g) pressure intensity stimulation of D2, and to no stimulus (I: D2 + D4; A and B: D2). Shown are single-condition (A, C, E, G, I) and Gaussian-filtered images (B, D, F, H) with overlaid thresholded outlines. J: activations as indicated by solid color-coded regions to different stimuli in both D2 and D4 locations are overlaid on blood vessel map. K: area of activation vs. pressure intensity for activation regions in areas 3b and 1 for both D2 (left) and D4 (right) locations. Rough border between areas 3b and 1 is shown by dashed back line. Blue dots indicate the location of electrophysiological penetrations. L and M: response amplitude vs. pressure intensity for activation regions in areas 3b and 1. Scale bar: 1 mm. P, posterior; L, lateral.

Cortical magnification factors.

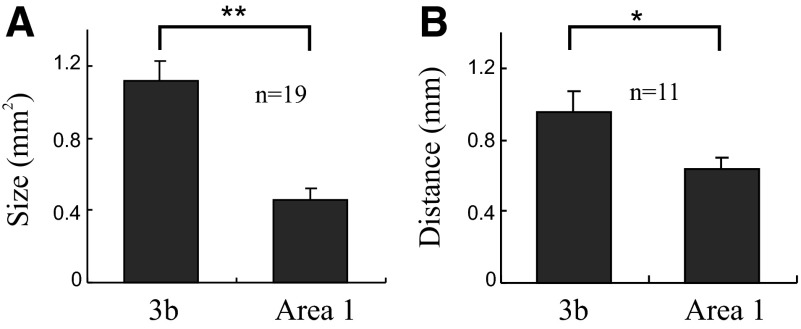
Two differences between area 3b and area 1 in the anesthetized animal are apparent: the separation and activation sizes of active areas are smaller in area 1 than those in area 3b. We quantified the activation areas for a total of 19 digits. The average size of activation in area 3b (1.12 ± 0.10 mm²) was significantly larger than that in area 1 (0.45 ± 0.07 mm², P < 0.001) (Fig. 2A). With a probe diameter of 3 mm, these sizes convert to cortical magnification factors of 0.16 in area 3b and 0.06 in area 1 (area of cortex/area of skin surface). The average ratio of activations in area 3b to area 1 was 2.5.

FIG. 2.

Comparison of area 3b and area 1 activations. A: size of single-digit activations in areas 3b and 1. Mean activation sizes (in mm²) for areas 3b and 1 are significantly different (**P < 0.001, n = 19). B: cortical distance (in mm) between adjacent digit pairs for areas 3b and 1 are significantly different (*P < 0.005, n = 11). Error bars = SE.

As a second measure of cortical magnification we measured, based on the center of activations, the cortical distances separating digits. We used this measure of cortical magnification because in the previous mapping studies, which were conducted under different types of anesthesia, the maps of digit topography with respect to interdigit spacing have remained fairly constant (for a helpful comparison of different studies see Fig. 9 in Pons et al. 1987). The same may not be true for receptive field sizes that are highly influenced by anesthesia and can therefore affect measures of cortical magnification (mm of cortex/mm skin). For a total of 11 adjacent digit pairs, the average cortical separation distance in area 3b was 0.95 ± 0.12 mm and that in area 1 was 0.63 ± 0.07 mm. Thus separation distances in area 3b were larger than those in area 1 (paired t-test, P < 0.005), consistent with the larger cortical magnification factor in area 3b (Fig. 2B).

SPATIAL FUNNELING IN AREA 1.

To examine the response of area 1 to the funneling illusion we used a paired-digit stimulation paradigm, a paradigm that induces a bridged sensation between two stimulated finger pads and a “funneled” activation in area 3b (see supplemental material in Chen et al. 2003). Two examples of cortical responses to simultaneous stimulation of the paired digits are shown in Fig. 3. Case 1 illustrates a funneled response to simultaneous adjacent-finger stimulation. Case 2 illustrates the nonfunneled response to simultaneous nonadjacent-finger stimulation. In Case 1, activations to stimulation of D3 alone and D2 alone are shown in Fig. 3, A and B (red outlines) and Fig. 3, C and D (yellow outlines), respectively. Digit activation revealed a larger focal activation in area 3b and a slightly smaller one in area 1 (see area 3b/1 border in Fig. 3M, dotted line). Paired stimulation of D2 + D3 produced only a single central locus of activation in areas 3b and 1 (Fig. 3, E and F, blue outlines), consistent with the “funneled” response in area 3b (Chen et al. 2003). The location of this funneled response overlaps and lies between the single-digit activation locations (see Fig. 3M for red, yellow, and blue overlays).

In Case 2, activations to stimulation of D4 alone and D2 alone are shown in Fig. 3, G and H (red lines) and Fig. 3, I and J (yellow lines), respectively. Paired stimulation of D2 + D4 (Fig. 3, K and L, blue outlines) did not produce a funneled response, but rather produced two separate activations that overlapped with that of the single-digit activations (see Fig. 3N for red, yellow, and blue overlays). This was observed in area 3b (see area 3b/1 border, in Fig. 3N, dotted line). In area 1, although paired stimulation activation was relatively weak, the activation, when detectable, remained in the same location as the single-digit activation (see overlay in Fig. 3N). In three cases of paired nonadjacent digit stimulation (six locations), no spatial shift in activation was observed in either area 3b or area 1. In contrast, a funneled response was observed in five of five adjacent digit pairings in area 1 and seven of seven pairings in area 3b.

SIZE OF CORTICAL ACTIVATION IS REDUCED IN BOTH AREA 3B AND AREA 1 IN RESPONSE TO PAIRED VERSUS SINGLE FINGER PAD STIMULATION.

We found that simultaneous stimulation of two digits resulted in smaller activation zones relative to single-digit activations. For illustration, in Case 1, stimulation of D3 alone (Fig. 3, A and B, green lines) and D4 alone (Fig. 3, C and D, yellow lines) produced larger responses than paired D3 + D4 stimulation (Fig. 3, E and F, blue line; see Fig. 3M for green, yellow, and blue overlays). Similarly, in Case 2, activations at the D2 (Fig. 3, G and H, red lines) or D4 (Fig. 3, I and J, yellow lines) locations were larger for D4-alone or D2-alone stimulation than for paired D2 + D4 stimulation (Fig. 3, K and L, blue line; see Fig. 3N for red, yellow, and blue overlays). This effect was more pronounced for adjacent than that for nonadjacent digit pairs (Fig. 3O). For a total of 26 digit pairs in areas 3b and 1 there was a significant reduction in the size of cortical activation with paired-digit stimulation relative to single-digit stimulation (Fig. 3O, ANOVA, P < 0.05) that was not observed for nonadjacent-digit pairs. This reduction did not differ between area 3b (59.8 ± 7.8%) and area 1 (53.3 ± 5.3%) (P = 0.16, single-digit activation treated as 100%, as indicated by the dashed line in Fig. 3O). Thus spatially distributed pressure stimulation to finger pad pairs evokes a reduced cortical response in both area 3b and area 1. This effect—which was greater for adjacent than for nonadjacent stimulation—is consistent with our previous observations of a funneling illusion with finger stimulation (Chen et al. 2003) and parallels interpretations for the psychophysical aspects of the funneling illusion (Gardner and Spencer 1972a,b; Gardner and Tast 1981).

INTENSITY OF STIMULATION CORRELATES WITH THE AMPLITUDE OF THE OPTICAL SIGNAL.

Cortical neurons in SI have the capacity to encode the intensity of tactile stimuli (Mountcastle et al. 1969). Previously, we showed that increasing stimulus intensity increased the amplitude of the cortical response in area 3b (Chen et al. 2003). In this study we examined whether areas 3b and 1 similarly code stimulus intensity. As shown in Fig. 4, we presented four different stimulus intensities on D2 while simultaneously presenting a constant 30-g stimulus on D4 as a control. When only D4 was stimulated (Fig. 4, A and B), a single focal activation was obtained in each of areas 3b and 1 (see 3b/1 border in Fig. 4J) at the D4 location (see arrow above Fig. 4, A and B). When D4 stimulation was accompanied by simultaneous low (15 g, Fig. 4, C and D), medium (30 g, Fig. 4, E and F), or high (60 g, Fig. 4, G and H) intensity stimulus on D2, an additional focal activation was obtained at the D2 location in each of areas 3b and 1 (Fig. 4, C–H, D2 location). The activations are shown overlain in Fig. 4J. There were two consequences of adding stimulation at the D2 site.

First, consistent with our previous observations (Chen et al. 2003) and what others have reported (Simons et al. 2005, 2007), as shown in Fig. 4K, in both areas 3b and 1, the size of the D2 activation increased abruptly with a low intensity of stimulation (15 g), but thereafter the area of activation increased only slightly with increases in stimulus intensity (compare 15 g low, to 30 g medium, to 60 g high on digit D2). However, consistent with the finding shown in Fig. 3, paired stimulation reduced the area of activation at the D4 site in both areas 3b and 1 (compare single: green, vs. paired: yellow, blue, and red bars). In this case increasing stimulus intensity reduced the area of activation of the paired site in an intensity-dependent manner. The log relationship between stimulus intensity and the area of activation of a nonadjacent finger was greater for area 3b than that for area 1 (slopes: 3b, −0.08 mm/mN, R² = 0.9; area 1, −0.06 mm/mN, R² = 0.99).

We next evaluated the relationship between stimulus intensity and the amplitude of the cortical response. The amplitude and time course of the optical signal was measured for regions of interest located within the activation areas found in areas 3b and 1. Consistent with the nature of the optical signal, the amplitude of the intrinsic signal was on the order of 0.1–1.0% and increased over a period of 2- to 3-s poststimulus onset (Bonhoeffer and Grinvald 1996; Chen et al. 2001, 2003). For D4 stimulation the response to a medium (30 g) intensity stimulus in 3b and area 1 (Fig. 4, L and M, blue bars) remained constant (since this is a nonadjacent digit) as stimulus intensity varied on D2 (red bars). Reflectance values at D2 with no stimulus (see 0 g in Fig. 4, L and M) were not different from baseline (compare Fig. 4, A and I). As stimulus intensity increased from low (15 g) to medium (30 g) to high (60 g), the percentage changes of peak optical reflectance (amplitude of optical signal) at the D2 location increased gradually from 0.36 to 0.72 to 0.89% in area 3b (Fig. 4L, red bars) and from 0.19 to 0.18 to 0.41% in area 1 (Fig. 4M, red bars). For both areas 3b and 1 the amplitude of the optical signal correlated with the intensity of pressure stimulus. However, area 3b exhibited a stronger relationship [slope = 0.013 (% change/gram force), R² = 0.49] and area 1 exhibited a less linear, weaker relationship (slope = 0.005, R² = 0.28). Whereas signal amplitudes were significantly different for different pressure intensities in area 3b (one-way repeated-measures ANOVA, P < 0.005; Holm–Sidak post hoc; all P values <0.05, except 0 vs. 15 g and 30 vs. 60 g), in area 1, only the higher-pressure intensity stimuli were significantly different from the no-stimulus condition (one-way repeated-measures ANOVA, P < 0.05; Holm–Sidak post hoc; all P values >0.05, except 0 vs. 30 g and 0 vs. 60 g). In summary, both the size and amplitude of cortical activity correlated with the magnitude of the pressure stimulus, but area 3b was better than area 1 at distinguishing stimulus intensity. Note that increasing the stimulus intensity at D2 had little effect on the reflectance signal amplitude at D4 site, but it led to diminishment of the D4 activation area.

Previously for area 3b we reported that paired stimulation of nonadjacent fingers did not significantly alter the amplitude of the cortical response compared with single-finger stimulation (Chen et al. 2003). For area 1 the peak reflectance change (dR/R) for a 30-g pressure stimulus was 0.33 ± 0.15% (n = 5) with single-digit stimulation and 0.26 ± 0.09% for two-digit nonadjacent stimulation. As in area 3b, the reduced response with nonadjacent two-digit stimulation relative to single-digit activation was not significantly different (paired t-test, P > 0.05).

Electrophysiology

RESPONSES OF CORTICAL NEURONS IN SI ARE MODULATED BY PAIRED FINGER PAD STIMULATION.

Figure 5 presents the responses from four neurons from areas 3b and 1 to single- and paired-digit stimulation. Typically, responses were characterized by an initial transient response that was related to the dynamic phase of the pressure stimulus (Cohen and Vierck Jr 1993; Salimi et al. 1999), followed by a short period of inhibition (which for some neurons suppressed firing rates below background levels), followed by a sustained response, related to the plateau phase of the stimulus, lasting for ≤750 ms after stimulus onset. As previously described, we observed RA neurons that exhibited a robust rapidly adapting response and little sustained response and SA neurons that exhibited both transient and sustained response phases.

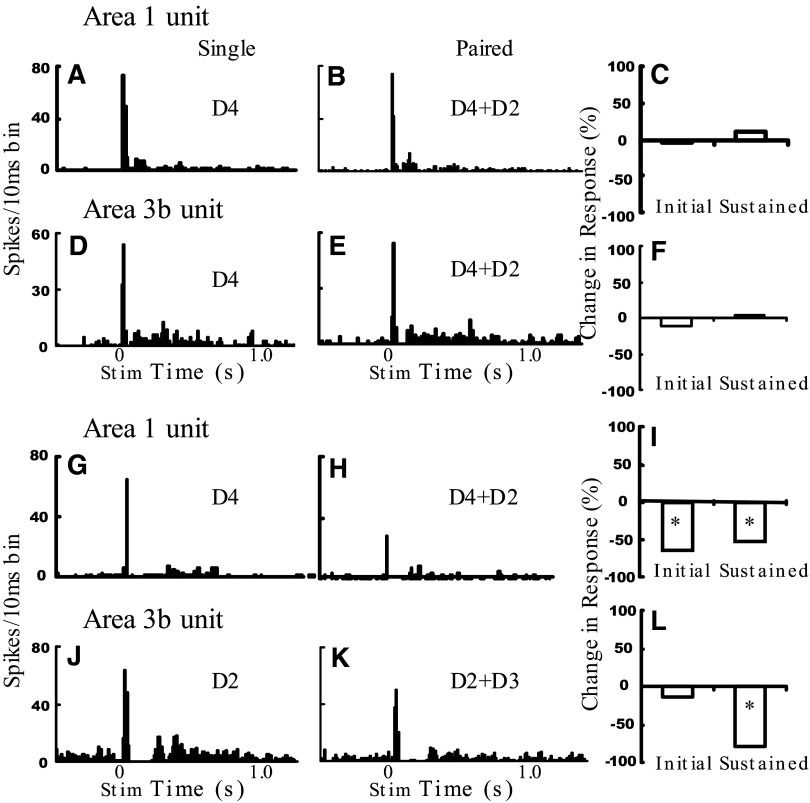
FIG. 5.

Area 1 and area 3b neural responses to digit stimulation. Sample area 1 (A–C, G–I) and area 3b (D–F, J–L) unit responses to single- (D4) and paired-digit stimulation (K: D2 + D4; L: D2 + D3). Left 2 panels: poststimulus time histograms showing the total number of spikes per 10-ms bin summed for 20 trials. Shown are responses to single-digit stimulation in the center of the unit's receptive field (far left) and paired-digit stimulation of 2 distal finger pads (middle). Right: bar graphs show the percentage change in spiking activity with paired stimulation for the initial transient and sustained response periods. *P < 0.05.

To examine the effect of paired-digit stimulation, we isolated units with receptive fields on the distal finger pad and recorded the response to stimulation of the primary digit. We then recorded response to simultaneous stimulation of that digit plus a second digit. The second digit was either adjacent (e.g., D3 + D4) or nonadjacent (e.g., D2 + D4) to the primary digit. We found different effects across our population, ranging from no effect to facilitatory to suppressive. Because we did not find any statistical differences between adjacent and nonadjacent pairs (perhaps due to our limited data set), we report them together.

No effect.

Figure 5, A–C (area 1 unit) and Fig. 5, D–F (area 3b unit) illustrate units with transient and sustained phases that exhibited little effect of paired-digit stimulation compared with single-digit stimulation. These units were recorded at a D4 location, had a relatively restricted receptive field, and exhibited a robust response to D4 stimulation (Fig. 5, A and D). Simultaneous stimulation of D2 had little effect (Fig. 5, B and C); effects for this unit are quantified at the right (Fig. 5, C and F, graphs). Of our population of 43 digit pairs (area 1, n = 16; area 3b, n = 27), there were 12 units (3 in area 1 and 9 in area 3b) that exhibited little to no effect (<25% modulation) of second-digit stimulation on the response of the primary digit.

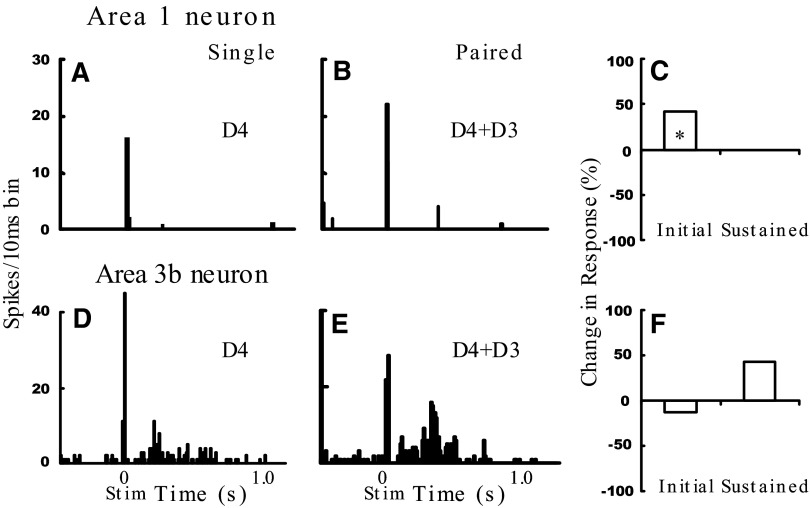
Facilitatory.

One anticipated effect of simultaneous second digit stimulation was an augmentation of unit responses (for examples, see Fig. 7). Of our population of 43 units, paired stimulation led to a significant increase (>25% increase, compared with single-digit stimulation) in 14 units [area 1: 6 of 16 units (37%), area 3b: 8 of 27 units (30%)]. Of these neurons, comparable increases in responses were observed in areas 3b (36.2 ± 4.8%) and 1 (41.7 ± 6%). However, augmentation of the sustained response (53 ± 7%) was significantly larger than that of the transient response (23 ± 3.8%, P < 0.05). Only a trend was observed for adjacent stimulation to have greater effects than nonadjacent pairings (transient response: adjacent 26 ± 5%, nonadjacent 11 ± 11%; sustained response: adjacent 54%, nonadjacent 52%; two-way ANOVA, all P values >0.05). Thus for a subset of units, the transient and sustained responses both showed evidence of augmentation to paired stimulation with the effect being greater for the sustained response.

FIG. 7.

Funneled neural responses to digit stimulation. Sample area 1 (A–C) and area 3b (D–F) unit responses to single- (D4) and paired-digit stimulation (D3 + D4). Unit from D4 penetration shown in Fig. 4J. *P < 0.05. In F, the increase in the sustained response was only a statistical trend (P = 0.12). See Fig. 5 legend for figure format.

Suppressive.

More frequently, a primary effect of simultaneous second-digit stimulation was a suppressive effect on the response. Figure 5, G–I (area 1 unit) and J–L (area 3b unit) illustrate suppressive effects. In Fig. 5G, the area 1 neuron had a receptive field that covered multiple digits but responded best to stimulation on D4. A diminished initial transient and sustained response was observed when D2 stimulation was added (Fig. 5H, quantified in Fig. 5I, >50% reductions). Another example of paired suppression is illustrated in Fig. 5, J–L. This area 3b unit exhibited suppression in the initial transient (14%) and greater suppression in the sustained portion of the response with paired stimulation (Fig. 5K, quantified in Fig. 5L, 79% reduction). Thus the transient and sustained responses both showed evidence of suppression to paired stimulation.

Of our population of 43 units, paired stimulation led to significant reduction (>25% reduction, compared with single digit stimulation) in 19 units [area 1: 9 of 16 units (56%), area 3b: 10 of 27 units (37%)]. For the transient response, a reduction was observed in about 25% of the area 1 units (4 of 16 units) and 15% of area 3b units (4 of 27). In comparison to the transient response, a larger number of units showed a greater reduction in the sustained portion of response (z-test, P < 0.05): 50% of area 1 units (6 of 12) and about 45% of area 3b units (9 of 20).

Averaged across the entire population, a slight reduction was observed in the unit responses to paired stimulation (transient response: 8.5 ± 4.2% SE; sustained response: 24 ± 11.3% SE). For area 1 these respective reductions were 11 ± 7.8% transient and 11 ± 14% sustained (11 ± 7% overall), whereas for area 3b the reductions were 7 ± 4.9% transient and 31 ± 16% sustained (17.5 ± 7.5% overall). Thus these suppressive effects were observed in approximately one third to one half of the units in our sample, consistent with a net overall reduction in the responses to paired stimulation that could lead to the diminished optical response observed in Fig. 4.

PAIRED FINGER PAD STIMULATION.

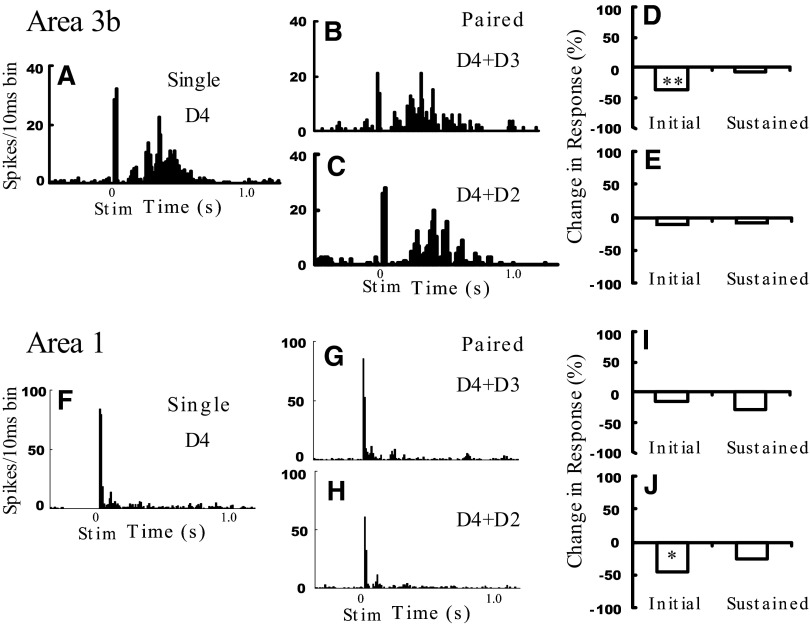
Effect of distance. Because of the difficulties in moving a stimulating motor to a different digit while holding a neuron on-line, we only infrequently attempted to stimulate both adjacent and nonadjacent digits. However, we present here the small body of data that we have accumulated (area 3b, n = 3; area 1, n = 2).

To test whether the suppressive effect of a second digit depended on the distance between the two digits, we compared the effects of paired nonadjacent and paired adjacent digit stimulation. Figure 6 illustrates two examples. The area 3b unit (top unit) illustrated is an SA unit that, in response to D4 stimulation, exhibits both transient and sustained response components (Fig. 6A). The response to paired D4 + D3 stimulation results in reduction of the transient response (Fig. 6B, arrow) without much effect on the sustained phase (quantified in Fig. 6D). This same neuron's response to paired D4 + D2 stimulation (Fig. 6C) shows little impact of paired nonadjacent digit stimulation (quantified in Fig. 6E), suggesting a greater effect of adjacent than nonadjacent digit stimulation. The second unit (bottom) was recorded from area 1. Overall, the response to paired stimulation resulted in reduction in the transient and sustained responses (quantified in Fig. 6, I and J) compared with single-finger stimulation alone (Fig. 6F). However, nonadjacent stimulation produced a larger reduction on the transient response (Fig. 6H) than adjacent-finger stimulation (Fig. 6G). This unit was located at a peripheral location within the activation region of D4 (case not shown), thus providing direct neural support for the effect of lateral interactions from nonadjacent digits in area 1 (cf. Fig. 4K).

FIG. 6.

Effect of digit separation on neural modulation. Sample D4 area 3b unit response to single (A) and paired adjacent (D4 + D3, B and D) or paired nonadjacent (D4 + D2, C and F) stimulation. Unit from D4 penetration shown in Fig. 3N. Sample D4 area 1 unit, same format.**P < 0.001, *P < 0.05. See Fig. 5 legend for figure format.

In our population of units recorded in digit center locations (>10% reduction, adjacent pairs n = 14, nonadjacent pairs n = 9), we observed greater suppression with adjacent (36 ± 6.7%) versus nonadjacent pairs (18.2 ± 4.5%, P < 05, two-way ANOVA: variables, initial vs. sustained response, and adjacent vs. nonadjacent). Although not statistically significant, the sustained response showed a slightly greater reduction (37.9 ± 5.6%) than the transient response (24 ± 5.6%). This is consistent with our optical imaging result (Fig. 3) that adjacent-digit stimulation results in a greater reduction of response than nonadjacent-digit stimulation (cf. Chen et al. 2003).

Funneling.

Electrophysiological examples of sensory funneling are elegantly documented in SI (Gardner and Costanzo 1980). Therefore we did not attempt to duplicate this work. However, to support our finding that in between the single-digit centers we find the funneled response during two-digit activation, in one experiment we did record a few units located in between the representations of adjacent digits. Figure 7 illustrates one example. This unit was recorded in area 1 and exhibited prominent response to D4 stimulation (Fig. 7A) and weak response to D3 stimulation. Consistent with optical imaging results (Chen et al. 2003), paired stimulation of D4 + D3 (Fig. 7B) resulted in an enhanced response (quantified in Fig. 7C). In another example, shown in Fig. 7, D and E, there was little change in the transient response but a significant enhancement of the sustained response (quantified in Fig. 7F).

DISCUSSION

Summary

We have used intrinsic signal imaging methods to study cortical responses to pressure stimulation of the distal finger pad. By simultaneously imaging area 3b and area 1, we were able to directly compare responses of these two closely associated areas in primary somatosensory cortex of the squirrel monkey. We find that activations in area 1 are smaller and spaced more closely together than those in area 3b, consistent with a smaller cortical magnification factor in area 1 reported in previous electrophysiological studies. Stronger tactile stimulation produced greater reflectance changes in both area 3b and area 1, indicating that both areas are sensitive to stimulus intensity. We also observed that areas 3b and 1 exhibited comparable “cortical funneling” response to paired-digit stimulation. Similar to area 3b, area 1 funneling occurred only with paired-adjacent (and not with paired-nonadjacent) digit stimulation.

Electrophysiological recordings supported these findings. Although neuronal responses were mixed, the averaged response in our sample was consistent with the observed imaged response. We found single-unit examples that illustrated 1) paired suppression (compared with single-digit stimulation), 2) greater suppression by adjacent- than nonadjacent-digit stimulation, and 3) funneled (enhanced) response at locations in between paired stimulation sites. With respect to paired finger pad stimulation, we observed a range of single-unit responses, including suppression, summation, or no change in unit response. Over the entire population, we observed a net suppression with paired stimulation, a finding consistent with our imaging results. Also consistent with imaging, the modulations of neural responses were greater for adjacent than for nonadjacent stimulation.

Cortical magnification in area 1 versus area 3b

Our two independent measures of cortical magnification found that the amount of cortex dedicated to the distal finger pads was greater in area 3b than that in area 1. We found that cortical magnification of area 3b was estimated to be 1.5- or 2.5-fold greater than that of area 1. Our values for cortical magnification are larger than those reported by Sur et al. (1982). One reason is that their digit magnification factor includes the entire digit, whereas ours include only the distal finger pad. Our calculation methods are also different from those used by Sur et al. (1982). We used the diameter of the probe and the area of activation to determine the magnification factor. Our calculation was as follows: A probe diameter of 3 mm provides a skin contact area of about 7.1 mm² [∏ r² = 3.14 × (1.5 mm)²]. For imaged activation sizes of 1.12 mm for area 3b and 0.45 mm for area 1, this produces cortical magnifications of 0.16 (=1.12/7.1) for area 3b and 0.06 (=0.45/7.1) for area 1. We also used the cortical distances separating the different digits and the diameter of the distal finger pad and got similar values. If one converts the measure of digit separation into cortical magnification (assuming circumference of the distal finger pad is ∼10 mm for the squirrel monkey), then one obtains comparable magnitude estimates for area 1 (0.063) and for area 3b (0.095). In contrast Sur et al. (1982) used the distances separating electrode penetrations and skin receptive field locations. Although the values and methods are different, the relative differences in cortical magnification values between areas 3b and 1 should be valid. Thus in effect our values are obtained from the digit tips and reflect the highest cortical magnifications on the hand, whereas the values from Sur et al. (1982) are presumably averaged over the entire digit and hand.

Relative roles of area 3b and area 1 in the funneling illusion

There are two psychophysical consequences induced by multipoint stimulation. One is a nonlinear summation of sensation magnitude. Gardner and Tast (1981) used reaction time as a measure of stimulus detectability (d′) and found that sensation magnitude was greater with multipoint stimulation. Magnitude estimation tasks have further characterized the growth of sensation magnitude with multipoint stimuli (Greenspan et al. 1997). Thus a functional significance of spatial funneling could be its ability to amplify weak stimuli. The other is the funneling illusion, where brief tactile stimuli presented simultaneously at multiple points on the skin produce a summed single sensation at a central location, even if the central site is not directly stimulated (Chen et al. 2003; Gardner and Spencer 1972a; Gardner and Tast 1981; Greenspan et al. 1997; Hashimoto et al. 1999; Laskin and Spencer 1979a; Sherrick 1964; von Békésy 1960, 1967). This suggests that multipoint integration is useful not only for detection but also for localization of tactile objects.

Neurophysiological studies also support these suggestions. Laskin and Spencer (1979b) described that the classic center surround inhibitory receptive field was present in single neurons in cat somatosensory cortex. The spatial distribution of inhibitory activity was found to be unimodal, had a peak of inhibition corresponding to the functional center of the excitatory receptive field, and extended beyond the excitatory receptive field, forming an inhibitory surround region. Studies using multipoint stimuli (n > 2) observed additional nonlinear affects. Gardner and Costanzo (1980) studied in primate SI the spatial distribution of unit activity in response to multipoint stimulation of the forearm. In contrast to peripheral mechanoreceptors (Gardner and Spencer 1972a), the cortical units did not resolve three-point stimuli; instead multipoint stimulation evoked activity in a broad population of neurons. Peak responses to three stimuli were no different from peak responses to single stimuli in most (73%) but not all neurons; the other neurons showed summation (23%) and suppression (3%), respectively. This led Gardner and Spencer (1972b) to propose that detection of the peak of the population response correlates with the location of the funneling illusion, whereas stimulus intensity is coded by a broad population integration.

This proposal has been further supported by studies of population response using optical imaging methodology. Consistent with neurophysiology, our previous study of the funneling illusion in area 3b revealed that simultaneous stimulation of two finger pads produced activation central to the sites of single finger pad activation. This suggested that area 3b maps not simply the physical location of stimuli, but rather their perceived location (Chen et al. 2003). Here, we find a parallel phenomenon in area 1: stimulation of adjacent digits evoked a single locus of activation in area 1. Because of the relative similarities in the responses of areas 3b and 1 and the combined optical imaging and electrophysiological results, we suggest that the lateral interactions between digits originate in area 3b and that area 1, at least in the context of the funneling paradigm revealed by optical imaging, does not elaborate further on those multidigit interactions. However, one needs to be cautious regarding such conclusions. For example, the distinctions between orientation-selective response in visual areas V1 and V2 were not apparent until these areas were probed with the appropriate higher-order stimuli that then revealed in V2 invariance across multiple types of luminance, texture, and motion borders (Lu et al. 2007; Ramsden et al. 2001; von der Heydt and Peterhans 1989). Thus it will take the right stimulus probe to elucidate the key transformational role(s) that area 1 performs on its inputs from area 3b.

Spatial inhibition in area 3b and area 1

We find that in both area 1 (this study) and in area 3b (Chen et al. 2003) an effect of paired stimulation is a suppression relative to single-site stimulation. As suggested by the electrophysiological recordings reported here, although there is a mixture of summation and suppression in response to paired stimulation, the majority of neurons exhibit suppressive effects. For example, in raccoon SI, stimulation of an adjacent digit produced predominantly suppression effects on single-unit activity of the target digit (Greek et al. 2003). In their population of neurons, depending on interdigit interstimulus interval, between 54 and 78% of the units showed a >10% reduction in unit activity. Only a small percentage (5–14%) showed a >10% increase in response. In humans, as first demonstrated by Gandevia and associates (1983), simultaneous stimulation of two fingers also produces smaller somatosensory evoked potentials (SEPs) and magnetoencephalographic signals. Subsequent research by Hsieh and associates (1995) with intraoperative SEP recordings observed that, consistent with our imaging results, adjacent- versus nonadjacent-finger stimulation produced greater suppression in human area 3b (N20).

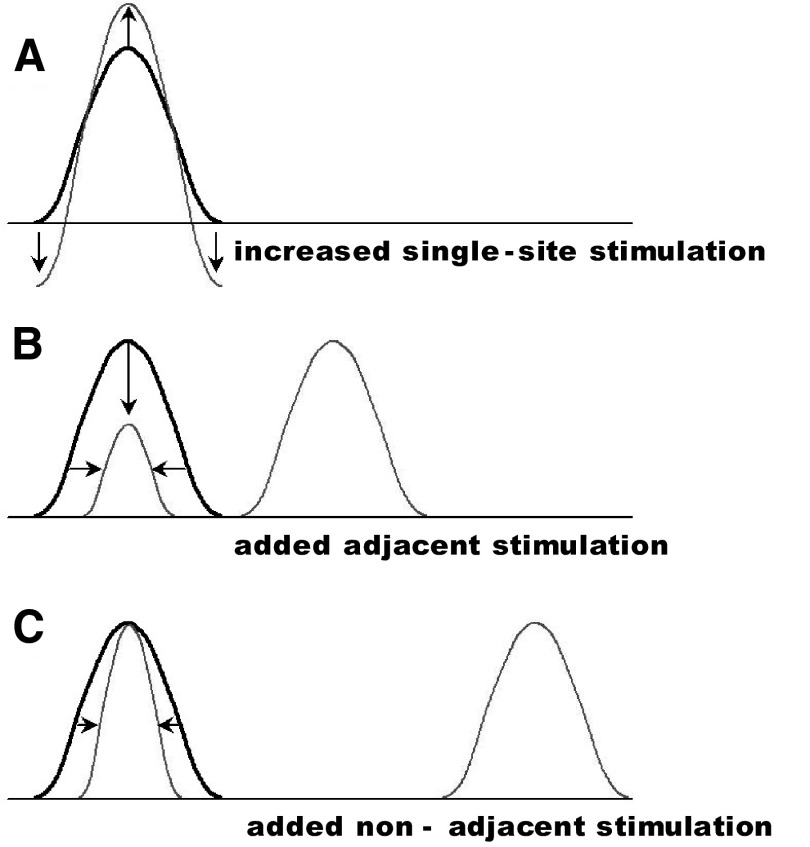
Our studies are largely consistent with and extend studies by Tommerdahl and associates (Simons et al. 2005, 2007). Some differences between these studies may be due to methodological differences: 630-nm light in our study, which focuses on changes in oxygenation of hemoglobin, and 830-nm light in their studies, which has a larger component contributed by light scattering due to tissue swelling. However, both studies find a distinction in effects on response area and amplitude. Simons and associates (2005) reported, with single-site stimulation, that although response amplitude increases with increasing stimulus intensity, the response area does not (Fig. 8A), leading them to hypothesize that increased intensities are accompanied by increased local inhibition. This inhibition is enhanced by prolonged (>1-s) periods of stimulation (Simons et al. 2007). They further report increasing stimulus intensity or duration can result in below-baseline reflectances in the surround (Fig. 8A), something we did not observe perhaps due to the wavelength used in our study. Consistent with Tommerdahl's data, we found an increase in response amplitude with increasing stimulus intensity but relatively little additional increase in area with suprathreshold stimulation (Fig. 4K).

FIG. 8.

Schematic of 3 inhibitory surrounds. A: increased single-site stimulation produces increased amplitude without change in area of activation. In addition, local surround falls below baseline (cf. Simons et al. 2005, 2007). B: addition of a second stimulus at an adjacent digit leads to decreased amplitude (vertical arrow) and area (horizontal arrows) of response. C: addition of a second stimulus at a nonadjacent digit leads to decreased area (horizontal arrows) but little change in response amplitude. Adjacent digit stimulation produces a stronger suppressive effect than nonadjacent digit stimulation (compare horizontal arrows in B and C).

In addition, we found differential effects on amplitude and area by stimulation at different distances, suggestive of additional surround effects. We find that stimulation at an adjacent site suppresses both the area (Fig. 3O) and the amplitude (Fig. 3, B and O; Chen et al. 2003) of activation (Fig. 8B). Increased stimulation at a nonadjacent site led to decreasing area of activation (Fig. 4K, D4 site) without any change in activation amplitude (Figs. 4M and 8C). Our data additionally suggest a decreasing suppressive effect on response amplitude with distance because two-digit stimulation produced greater inhibition at adjacent than nonadjacent sites (Fig. 3O) (compare horizontal arrows in Fig. 8, B and C).

Thus these findings suggest a complex lateral interaction. Single-site stimulation reveals a prominent local suppression surrounding the activation site, which can bring the surround to below-baseline levels (decreased absorbance). Addition of a second stimulus in the surround reveals secondary surround effects. This secondary surround suppresses the response in an activation area–dependent (stronger surround stimulation leads to smaller activation area), distance-dependent (closer stimulation leads to greater suppression), and, at greater distances, amplitude-independent manner (no change in amplitude with increasing stimulation at a second site). These data could suggest the presence of three distinct surrounds. The possibility that these three effects could be achieved by differential integration of a single mechanism implemented at different distances may perhaps be best addressed by modeling studies and by further studies on local intracortical circuitries within area 3b and area 1 (cf. Burton and Fabri 1995; Fang et al. 2002; Lund et al. 1993; Manger et al. 1997). In combination with previous studies (Chen et al. 2003; Lipton et al. 2007; Reed et al. 2007; Simons et al. 2005, 2007), we propose that the tactile landscape sculpts the cortical response profile in a complex, but predictable, manner. Our comparison of area 3b and area 1 responses suggests that the bulk of these surround effects may be established in area 3b and forwarded to area 1. However, further studies are needed to illuminate the additional transformations that area 1 undoubtedly performs on inputs from area 3b.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant NS-044375.