Watching Hydrogen Bonds Break: A Transient Absorption Study of Water

Abstract

Ultrafast infrared transient absorption measurements of the complete hydroxyl OD stretching mode spectrum of HOD in water, from 100 fs to tens of picoseconds, observe hydrogen bond breaking and monitor the equilibration of the hydrogen bond network in water. In addition, the vibrational lifetime, the time constant for hydrogen bond breaking, and the rate of orientational relaxation are determined. The reactant and photoproduct spectra of the hydrogen bond breaking process are identified by decomposing the transient spectra into two components, the initial spectrum associated with vibrational excited states (reactants) and the long-time spectrum associated with broken hydrogen bonds (photoproducts). By properly taking into account the perturbation of the reactant spectrum decay by the growth of the photoproduct spectrum, it is found that the vibrational relaxation (1.45 ps) and orientational relaxation (1.53 ps) are wavelength independent and, therefore, independent of the degree of hydrogen bonding. Energy deposited into water by vibrational relaxation does not immediately break a hydrogen bond by predissociation nor produce a thermally equilibrated hydrogen bond distribution at an elevated temperature. Following deposition of energy by vibrational relaxation, the hydrogen bond breaking time is 800 fs, and there is a transient period of several picoseconds during which the hydrogen bond distribution is not in thermal equilibrium.

I. Introduction

The properties of water are dominated by its ability to form hydrogen bond networks.^1–9 The networks are dynamic, with the strengths and numbers of hydrogen bonds associated with a particular water molecule constantly fluctuating.^10,11 Because the time scale for the evolution of the hydrogen bond networks is extremely fast, the characterization of network dynamics requires ultrafast infrared methods that are sensitive to the time evolution of the number (0–4) and strengths of hydrogen bonds.^10–13 The frequency of the hydroxyl stretching mode is very sensitive to hydrogen bond network properties and, therefore, can be used as a spectroscopic probe of hydrogen bond dynamics in transient nonlinear infrared experiments, particularly pump–probe^5,9,14–17 and vibrational echo experiments. ^18–27 Pump—probe (transient absorption) experiments are particularly useful for the investigation of population dynamics.

A considerable amount of research has been directed toward understanding the nature and origin of the ultrafast dynamics of water as probed by third-order nonlinear spectroscopies.^{5,8,18,23–33} Some of the questions are as follows: (i) What are the time scales and frequency dependence if any of the vibrational lifetime and the orientational anisotropy of the hydroxyl stretch? This is of particular importance because the frequency of the hydroxyl stretch vibration is related to structural parameters and can be used to obtain information on the structural evolution of the hydrogen bond network. The vibrational and orientational relaxation rates are also important parameters for the analysis and simulation of water dynamics. (ii) Since many experiments are performed on the OH stretch of HOD in D₂O, probing heavy water dynamics, an important question is, what are the dynamics in H₂O as opposed to D₂O? (iii) What is the mechanism of hydrogen bond breaking induced by vibrational relaxation? Is it vibrational predissociation where the hydrogen bond mode is excited directly from the hydroxyl stretch and breaks immediately, or does hydrogen bond breaking follow vibrational relaxation into a collection of lower frequency intra- and intermolecular modes that are coupled to the hydrogen bond and subsequently induce hydrogen bond breaking? (iv) Given an energy input, in this case from vibrational relaxation, how long does it take for hydrogen bonds to break, and how fast is hydrogen bond equilibration? That is, how rapidly does the making and breaking of hydrogen bonds bring the hydrogen bond distribution into thermal equilibrium?

To address these questions, we present the first broad-band pump–probe experiments on the OD stretch of HOD in H₂O that covers the entire band including the 0 → 1 and 1 → 2 transitions. Ultrafast (50 fs) pulses, which have sufficient bandwidth to span the entire hydroxyl stretch region, are used to excite and probe the time evolution of the spectrum. Frequency resolution of the dynamics is obtained by frequency resolving the probe pulse after it interrogates the sample. Thus, frequency resolution is obtained without sacrificing time resolution. Initially, a model free decomposition of the time-dependent spectrum is used to identify one decaying spectral component and one growing spectral component, which are the short-time reactant (vibrationally excited) spectrum and the long-time thermally equilibrated photoproduct (modified hydrogen bond) spectrum, respectively. The reactant spectrum and the photo-product spectrum differ significantly. In the low-frequency spectral region, the photoproduct spectrum is positive (long-term bleach), while on the high-frequency side of the spectrum it is negative (increase in absorption). If analysis of the pump–probe signal does not account for both a decay of the excited states and the growth of the photoproducts, the decays will appear to be wavelength dependent. As shown below, analysis of both the reactant decay and the photoproduct growth combined with analysis of the decay of the 1 → 2 transition demonstrates that the vibrational lifetime is wavelength independent and has a value of 1.45 ps. Determination of the orientational dynamics using parallel and magic angle pump–probe experiments requires the same type of considerations of the growth of photoproducts.

Previously, transient absorption experiments on the OH stretch in D₂O have used a two-color approach, where only a part of the hydroxyl stretch band is pumped and only a part of the band is probed.^{14,16,31,33,34} Usually, a model is invoked that comprises wavelength-dependent dynamic parameters such as vibrational relaxation and spectral diffusion to reproduce the data.^14,33,35 The lifetime of the OH vibration in D₂O has been reported to be in the range of 0.7–1.0 ps for HOD,^14,34 while lifetimes of 1.8 ps have been reported for the OD vibration of HOD in H₂O.^33,34 Orientational relaxation has only been examined in HOD in D₂O and reported to be wavelength dependent.^16,36 Bakker et al. found nonexponential anisotropy decay with a mild frequency dependence to occur at ~1 ps,³⁶ while Laubereau and co-workers found longer orientational relaxation times of 3, 8, and 12 ps with pronounced frequency dependence.¹⁶ While a shift of the hydroxyl stretch band is found in all these experiments, the production of photoproducts has not been included in the analysis of these experiments, although it has been considered in an echo peak shift experiment on HOD in D₂O²⁵ and experiments on methanol.¹⁷

Here we report the OD vibrational lifetime (1.45 ps) of HOD in H₂O, the orientational relaxation time (1.5 ps), and the photoproduct spectrum that grows in. Comparisons of the transient photoproduct spectra to linear temperature difference spectra allow us to monitor the relaxation of the nonequilibrium hydrogen bond distribution that exists after vibrational excited-state decay and determine the hydrogen bond equilibration rate. The results show that the distribution of hydrogen bonds is not initially in thermal equilibrium at an elevated temperature. Rather, following the deposition of energy from vibrational relaxation equilibration is not complete until ~5 ps. The time scale for complete hydrogen bond equilibration has been determined by vibrational echo correlation spectroscopy^20,37 and simulations.^8,38 Examination of time-dependent global generation of photoproducts demonstrates that hydrogen bonds are not broken immediately upon vibrational relaxation. Instead, 800 fs is required for hydrogen bonds to break following the vibrational relaxation of the initially excited hydroxyl stretch. This time is slower than the 250 fs observed previously for the hydrogen bonds of methanol–OD oligomers.¹⁷ These findings argue strongly against a vibrational predissociation mechanism but demonstrate a mechanism of hydrogen bond breaking after hydroxyl stretch vibrational relaxation populates a collection of lower frequency intra- and intermolecular modes that are coupled to the hydrogen bond, leading to breaking.

II. Experimental Procedures

The ultrashort IR pulses were generated using a a Ti:sapphire regeneratively amplified laser/OPA system. The output of the OPA is 50 fs transform limited 2 µJ IR pulses centered at 2500 cm⁻¹ at a 1 kHz repetition rate. The ultrashort pulses provide the bandwidth (>400 cm⁻¹) necessary to examine the 0 → 1 and 1 → 2 transitions of the OD stretch band of HOD in water, which are centered at 2510 and 2348 cm⁻¹,³⁷ respectively. Details of the laser setup are presented elsewhere.^19,20

The IR light is split into a pump and probe beam using a 95%–5% beam splitter. The probe beam travels through a polarizer that permits the probe beam to be set with polarization either parallel to the pump beam or at the magic angle polarization. Pump and probe beams are directed into the sample noncollinearly. After the interaction with the sample the probe beam is frequency resolved using a 0.3 m spectrometer. The dispersed light is detected by a MCT array with 32 elements. The spectral resolution is 2 cm⁻¹. The monochromator is stepped so that 64 cm⁻¹ blocks of data are taken at a time. A small fraction of the probe beam is used as a reference beam that is sent to a separate detector to correct for pulse-to-pulse fluctuations of the laser intensity. The pump beam is chopped. A computer reads the array. Subtraction of the pump-off spectrum from the pump-on spectrum yields the difference spectrum. Chirp on the IR pulses is measured by a frequency-resolved transient grating experiment on pure H₂O in an identical sample cell and adjusted to 0 ± 2 fs over the entire spectrum of the laser pulses in the sample. To remove the contribution of weak pump scattered light that is heterodyne amplified by the probe, we fibrillate the probe beam (vary the probe path length randomly by λ/2), which averages the heterodyne cross term to zero.

The samples, either 5% or 10% HOD in H₂O, were held in a sample cell of CaF₂ flats. At these concentrations, vibrational excitation transfer does not contribute to the dynamics. For some of the experiments, particularly those that examine the 1 → 2 transition, the sample path length was 6 µm and the 5% concentration was used to have an overall lower sample absorbance. The short path length eliminated contributions from the H₂O combination band that absorbs lower in energy than the OD 1 → 2 transition, but has a tail that can influence the results in higher absorbance samples. The peak absorbance of the low absorbance sample was 0.2. In some of the experiments that focused on the 0 → 1 transition region and the photo-products, the 12 µm path length/10% OD sample was used to give a better signal for the relatively weak photoproducts. All experiments were carried out at 297 K.

For the spectrally resolved pump–probe experiments, the change in transmission spectrum was collected as a function of the delay between the pump and probe pulses, T_w. To determine the time-dependent orientational anisotropy, the probe polarization was rotated with respect to the pump beam using a polarizer. Data were taken at the magic angle (54.7°) and at parallel polarization. The time-dependent anisotropy of the hydroxyl stretch vibration was calculated according to

$$r(t)=\frac{I_{\parallel }(t)-I_{\text{ma}}(t)}{2I_{\text{ma}}(t)}$$ (1)

where I_∥(t) has the probe olarization parallel to the pump polarization and I_ma(t) has the probe polarization at the magic angle relative to the pump polarization. The population dynamics were obtained from the magic angle data, which eliminates the influence of orientational relaxation.

III. Results and Discussion

A. Vibrational Lifetime

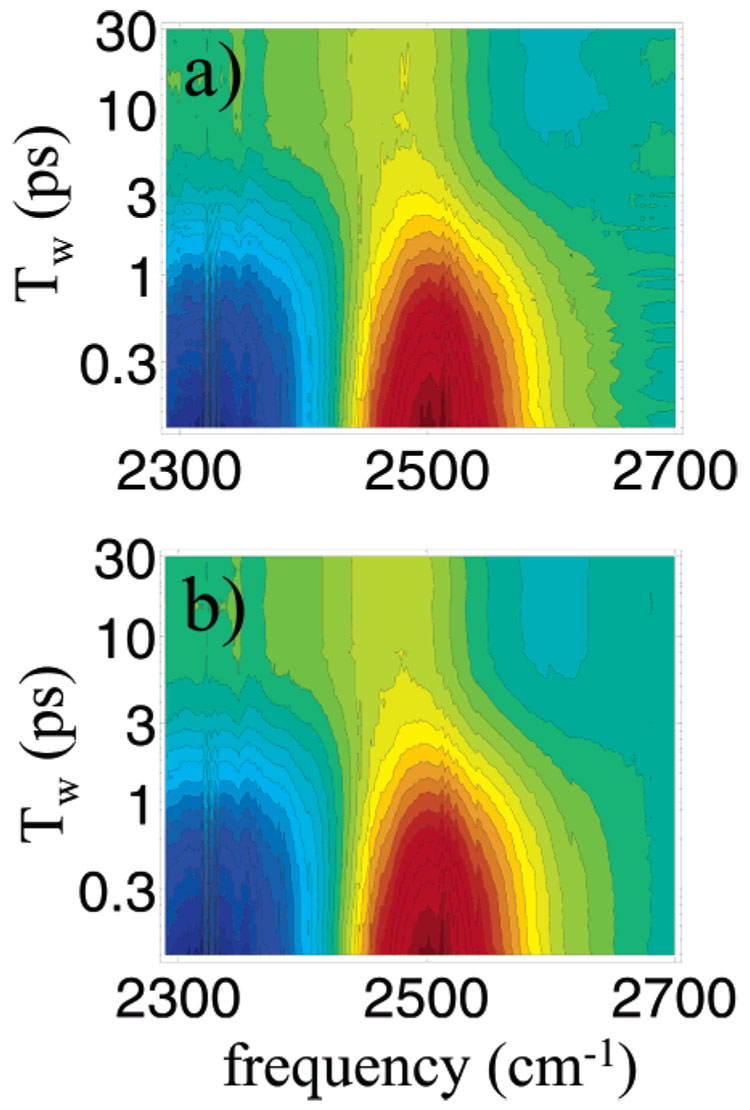
The pump–probe spectra of the OD hydroxyl stretch band of HOD in H₂O including 0 → 1 and 1 → 2 transitions are presented in Figure 1a at time delays T_w from 100 fs to 30 ps. (Note the log time axis.) The figure has 30 contours running from −1 (blue) to +1 (red). The spectra were taken with magic angle probe polarization. Therefore, orientational dynamics do not influence the time dependence. The dominant features of the spectra are the decay of the bleach of the 0 → 1 transition around 2510 cm⁻¹ and the decay of the excited-state absorption 1 → 2 signal around 2350 cm⁻¹. The 1 → 2 signal is negative (blue) because it is an increased absorption that turns on when the pump populates the first vibrationally excited state, 1.

Figure 1.

(a) Experimental transient absorption spectra of the OD stretch of HOD in H₂O as a function of T_w (logarithmic scale). There are 30 equally spaced contours from +1 to −1. The dominant positive (red) decay arises from the bleach of the 0 → 1 transition. The dominant negative (blue) decay arises from the excited-state absorption of the 1 → 2 transition. For long T_w the spectrum does not decay to zero. There is a residual bleach centered at ~2480 cm⁻¹ and a new absorption centered at ~2620 cm⁻¹. (b) Transient absorption spectra reconstructed from the two components found by singular value decomposition.

Only the 1 → 2 region of the spectrum decays to zero for long delay times. By ~6 ps, the 1 → 2 absorption has decayed to 0. The 1 → 2 absorption only exists when there is population in the 1 level. In the 0 → 1 region of the spectrum, the spectral features are not indicative of a simple decay of the excited-state population to the ground state. First, the original bleach centered at 2510 cm⁻¹ does not decay to zero. There is a long-lived component of the bleach centered at ~2480 cm⁻¹ that exists for times much longer than the decay of the 1 → 2 transient absorption. Also, an additional absorption (light blue) develops on the high-frequency side of the band at ~2620 cm⁻¹ that is evident in this contour plot at times greater than ~7 ps. (As discussed below, finer amplitude resolution than afforded by this contour plot shows that the onset of this absorption occurs at earlier times.) These features demonstrate that the system does not relax into the original state on the time scale of our experiment (30 ps).

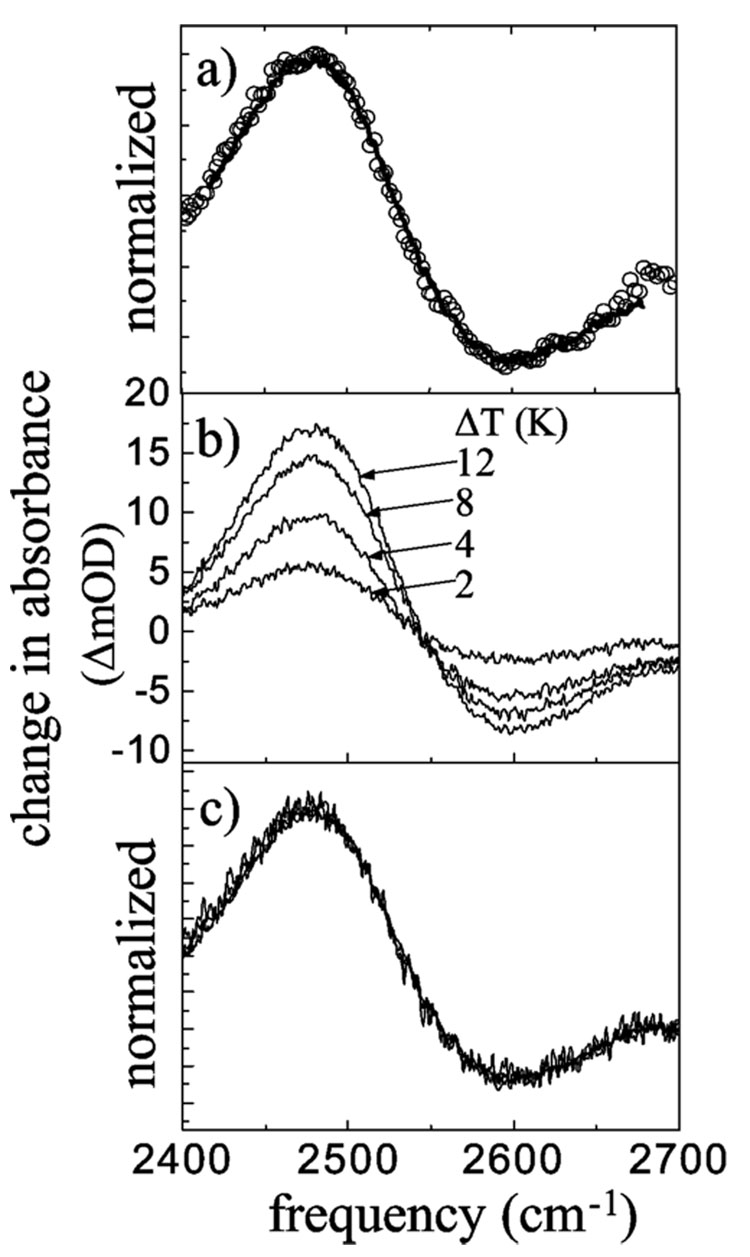
Figure 2a displays a comparison of the pump–probe spectrum (circles) at large T_w (30 ps) to a temperature difference FT-IR spectrum (solid curve). The pump–probe spectrum at 30 ps is a cut across the time-dependent spectrum shown in Figure 1a. The temperature difference spectrum was obtained by subtracting the FT-IR spectrum taken at room temperature from the spectrum taken at higher temperature. The positive portions of the spectra indicate a decreased absorption (a bleach), while the negative portions of the spectra indicate an increase in absorption. The data sets shown in Figure 2a are identical within experimental error. Therefore, at large T_w the system reaches thermal equilibrium at an elevated temperature. Using the laser power, concentration, and sample path length, we estimate that the temperature rises <2 °C. (Calculations based on the thermal diffusion constant of water indicate that the sample has returned to room temperature by the next laser pump pulse.) The temperature difference spectrum shows that a temperature change leads to a spectral change of the hydroxyl stretch band. The change in the spectrum is related to structural changes of the hydrogen bond network toward fewer and weaker hydrogen bonds.¹ More hydrogen bonds to a water molecule shift the hydroxyl stretching frequency to lower frequency.^11–13 The bleach at lower frequency and the increase in absorption at high frequency indicate that the equilibrium number of hydrogen bonds has been shifted to fewer hydrogen bonds.

Figure 2.

(a) Comparison of the transient absorption spectrum of the OD stretch of HOD in H₂O at T_w = 30 ps (circles) to the linear FT-IR temperature difference spectrum for a temperature difference of 2 K (solid curve). The amplitudes of the spectra have been normalized. (b) Temperature difference spectra at 2, 4, 8, and 12 K temperature difference with respect to room temperature. The differences are in units of mOD. (c) The amplitudes of the spectra in (b) are matched. No other changes are made. The spectra for different ΔT values are identical, showing there is only a change in size, not spectral shift or shape. The results are consistent with a hydrogen bond breaking mechanism.

The spectral shift cannot be explained by simply weakening the hydrogen bonds, as can be seen from the temperature difference spectra in Figure 2b,c. Parts b and c of Figure 2 show temperature difference spectra at 2, 4, 8, and 12 K temperature difference with respect to room temperature. Figure 2b displays the absolute change, while the same spectra are normalized in Figure 2c. In Figure 2c, all of the spectra from Figure 2b are superimposed and indistinguishable. It can be seen clearly that the shape of the temperature difference spectrum does not change with increasing temperature difference; only the amplitude increases as the difference is made larger. If an increase in temperature only weakened the hydrogen bonds, a continuous shift of the temperature difference spectrum would be expected with increasing temperature. As the temperature is increased, the bonds would be come weaker and weaker, and the shift would increase. However, only an amplitude change is observed as the temperature is increased. This means by increasing the temperature the amplitude of the unbroken hydrogen bond distribution on the red side of the OD band is decreased while the amplitude of the broken hydrogen bond distribution on the blue side of the OD band is increased. The isosbestic point in the temperature difference spectra (Figure 2b) is indicative of such a behavior. Also, this is in accordance with MD simulations by Skinner et al.,⁸ who found that the dominant change in the hydroxyl stretch frequency comes from changing its hydrogen bond number, especially the hydrogen bond attached directly to the hydroxyl oscillator under investigation. Additionally, a number of MD simulations find that the hydrogen bond length and therefore hydrogen bond strength correlate only weakly with the hydroxyl stretch frequency.^8,27,39 Therefore, we conclude the observed spectral changes in the photoproduct spectrum originate from hydrogen bond breaking.

As will be discussed below, deposition of energy via vibrational relaxation produces spectral changes that are not initially representative of thermal equilibrium. The important point here is that the energy deposition produced by vibrational relaxation following excitation of the hydroxyl stretch produces an apparent frequency dependence of the transient decay rates because of changes in the spectrum. The time-evolving spectrum caused by the growth of the photoproduct spectrum must be taken into account when the decay data are analyzed. The photoproduct signal grows in to ~10–15% of the original signal.

To separate and assign different components contributing to the transient absorption spectrum, we first apply the singular value decomposition (SVD) approach.⁴⁰ SVD is a common technique for analysis of multivariate data. Time and frequency constitute two independent variables in a 2-dimensional matrix. SVD provides the eigenspectra and corresponding eigenkinetics weighted by the so-called singular values. If X is the matrix describing the pump–probe spectrum, then X can be decomposed into X = USV^T so that U contains the eigenspectra, S is the diagonal singular value matrix, and V^T is the transpose of the matrix containing the eigenkinetics. The results give the spectral contributions and their corresponding kinetics and amplitudes (weighting factors). In the analysis as many eigenspectra as there are time points are generated as needed to describe the time-evolving spectrum. Wavelength-dependent lifetimes would result in many eigenspectra with significant amplitude and their associated eigenkinetics describing the decaying component. Wavelength-independent lifetimes would result in only one decaying spectrum with most of the amplitude.

We decomposed the time-dependent spectrum into its major contributions, discarding components that contributed less than 3% to the spectral amplitude. This is an initial procedure that is the first step in the final analysis as discussed below. The time-dependent pump–probe spectrum is found to be composed of two spectra that can be considered as basis functions that are propagated in time by distinct kinetic traces that are described well by exponential functions. The SVD-generated spectrum of water is shown in Figure 1b. The comparison to the pump–probe spectrum (Figure 1a) demonstrates good agreement and provides confidence in the physical significance of the spectra found by SVD. (The long narrow almost rectangular black band at ~2330 cm⁻¹ is caused by CO₂ absorption in the air which was not completely removed by purging the experimental apparatus.) According to SVD, there is one component decaying and one component growing in that combine to make up the time-dependent pump–probe spectrum. Figure 3 presents the spectrum of the decay component that contributes >85% of the overall amplitude of the pump–probe spectrum. The decaying spectrum is dominated by the ground-state bleach (~2510 cm⁻¹) and the excited-state absorption (~2348 cm⁻¹). This component decays with a lifetime of 1.42 ± 0.05 ps and is wavelength independent; that is, the entire spectrum initially generated by the pump pulse decays with a lifetime of 1.4 ps at all wavelengths. The component that grows in is the long-time thermal equilibrium spectrum shown in Figure 2a.

Figure 3.

Spectrum of the decay component that contributes >85% of the amplitude to the pump–probe spectrum. The decaying spectrum is dominated by the ground-state bleach centered at ~2510 cm⁻¹ and the excited-state absorption centered at ~2340 cm⁻¹.

While the calculated time-dependent spectrum shown in Figure 1b is in good agreement with the data, careful comparison shows that it has small but significant deviations on intermediate time scales of 1–5 ps. Physical considerations indicate that energy deposition caused by vibrational relaxation cannot instantly give the thermally equilibrated photoproduct spectrum. Both vibrational echo correlation spectroscopy^20,37 and recent simulations of water using the SPC-FQ water model³⁸ give the hydrogen bond equilibration time as 1.5 ps. This is the time scale on which an initially nonequilibrium distribution of hydrogen bonds will evolve to a new thermal distribution of hydrogen bonds. Therefore, on the 1–5 ps time scale, a nonequilibrium photoproduct spectrum combined with the emerging equilibrium photoproduct spectrum should be observed. We will address the issue of a nonequilibrium photo-product spectrum in section III.B below.

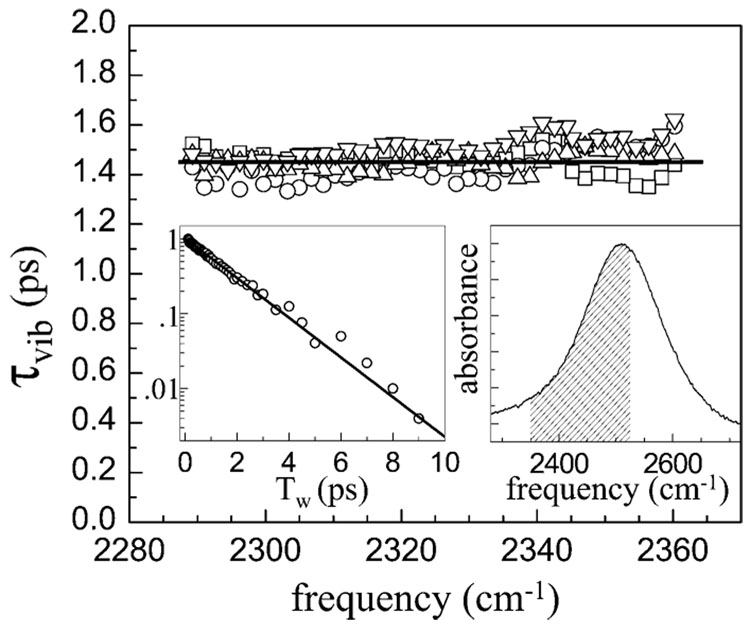
To further analyze the time-dependent spectrum, it is first necessary to confirm that the excited-state decay is in fact wavelength independent as found by the SVD. A number of sets of pump–probe experiments were conducted on the low-absorbance sample to examine the decay kinetics of the 1 → 2 transition. The 1 → 2 transition can be used to determine the vibrational lifetime in the spectral region in which it does not overlap with the 0 →1 transition and the associated creation of photoproducts. The short-path-length low-absorbance sample was used to examine the 1 → 2 transition to prevent the tail of the H₂O combination band, which shifts slightly with a temperature increase, from influencing the measurements. Figure 4 shows the data over the range of the 1 → 2 transition that is not influenced by the 0 → 1 transition. From the four data sets shown, it is clear that the lifetime is wavelength independent within experimental uncertainty. The lifetime is 1.45 ± 0.05 ps, which is virtually identical to the value obtained from the SVD. The inset on the left displays an example at a single wavelength, 2340 cm⁻¹, of a semilogarithmic plot. The line through the data is a fit. The data are clearly exponential over at least 4 factors of e. The fits to all of the wavelengths depicted in the main portion of Figure 4 are also single-exponential decays to four lifetimes within experimental error. The inset on the right side shows the OD absorption spectrum. The shaded area indicates the equivalent range of frequencies for the 0 → 1 transition spanned by the measurements obtained by shifting the 1 → 2 frequencies by the 162 cm⁻¹ OD anharmonicity. ³⁷ The right inset shows that a significant portion of the spectrum has frequency-independent vibrational relaxation lifetime including the peak and most of the low-frequency side of the spectrum. The direct measurements of the lack of frequency dependence of the lifetime confirm the results of the SVD analysis.

Figure 4.

The vibrational lifetime of the OD stretch of HOD in H₂O as a function of frequency was measured on the low-frequency side of the 1 → 2 transition to avoid perturbation by the 0 → 1 transition and its photoproduct spectrum. The vibrational lifetime is frequency independent as found for the full spectrum using singular value decomposition (see Figure 1b). The inset on the left is a semilogarithmic plot of data at 2340 cm⁻¹ and a fit demonstrating that the excited hydroxyl stretch decays exponentially. The inset on the right shows the linear absorption spectrum, and the shaded area shows the range of 0 → 1 transition frequencies spanned by the lifetime measurements of the 1 → 2 transition (see the text).

B. Hydrogen-Bonded Network Equilibration

An important question is, how does the growing in component of the pump–probe spectrum relate to structural changes of the hydrogen bond network? To obtain information on the relationship, we compare the linear temperature difference spectrum to pump–probe spectra at different T_w values. Because energy is deposited into the sample by vibrational relaxation following the IR excitation, the hydrogen bond network has to relax into a new thermal equilibrium. At sufficiently long time, the pump–probe spectrum is identical to the temperature difference spectrum as demonstrated in Figure 2a. The hydrogen bond network, however, is placed in a nonequilibrium state following vibrational relaxation. Therefore, by comparing the temperature difference spectrum to the pump–probe spectrum as a function of T_w, we are able to watch the hydrogen bonds evolve toward their new thermal distribution.

Because the pump–probe spectrum is the sum of the reactant spectrum (excited-state spectrum) and the photoproduct spectrum, it is necessary to subtract the reactant contribution to analyze the photoproduct spectrum. This can be accomplished by subtracting an early time transient spectrum (T_w = 160 fs) from the pump–probe spectrum because at early times very little vibrational relaxation has occurred that would lead to perturbation of the spectrum. At each T_w, the early time spectrum reduced in amplitude by the 1.45 ps exponential decay is subtracted from the total spectrum at that time. The result is the time-evolving photoproduct spectrum. As a consistency check the subtraction was performed using pump–probe spectra at T_w values from 120 to 300 fs. The resulting photoproduct spectra were found to be virtually identical.

Figure 5a shows the comparison of temperature difference spectrum (solid curves; see Figure 2) and photoproduct spectra (circles). Temperature difference spectra were taken for a temperature difference from 1 to 12 °C. Only the amplitude changes with the temperature difference, not the shape. The temperature difference spectrum at ΔT = 2 °C was used for the comparisons. The photoproduct spectra were scaled to match the amplitude of the temperature difference spectrum. Clearly, for T_w smaller than 5 ps, the photoproduct spectra do not match the temperature difference spectrum. For Tw values of 5 ps and greater, the photoproduct spectra and the temperature difference spectra are identical within experimental error. Figure 2 shows the comparison at T_w = 30 ps. At short times, the photoproduct spectra are blue shifted with respect to the temperature difference spectrum, and they shift to the red as time progresses. Therefore, the photoproducts at T_w < 5 ps are not in thermal equilibrium, and hydrogen bond equilibration is not yet complete. From 5 ps on, however, the temperature difference spectrum fits the photoproduct spectrum very well and the long-lived bleach and absorption do not change further.

Figure 5.

(a) Comparison of the transient photoproduct spectrum at T_w values of 1.5, 2.0, 3.0, and 5.0 ps (circles) to the linear temperature difference spectrum (solid curve). The differences for T_w < 5 ps demonstrate that, following vibrational relaxation and subsequent hydrogen bond breaking, the hydrogen bond distribution is initially not thermally equilibrated. (b) Full photoproduct spectral evolution obtained from subtraction of the decaying reactant spectrum. The photoproduct spectrum starts to grow in at ~1 ps after the excitation of the hydroxyl stretch vibration and becomes constant after ~5 ps.

Figure 5b shows the photoproduct spectral evolution that was obtained using the subtraction scheme detailed above. The photoproduct bleach (positive signal) starts to grow in after ~1 ps and shifts from the center of the 0 → 1 transition at 2510 cm⁻¹ to lower frequencies. The somewhat smaller negative photoproduct absorption signal grows in at 2620 cm⁻¹. From ~5 ps on the spectrum does not change significantly as can also be seen in the comparison to the temperature difference spectra in Figure 5a. As mentioned above, the time scale to reach equilibration is consistent with vibrational echo correlation spectroscopy experiments^20,37 and recent molecular dynamics simulations of the vibrational echo experiments using the SPC-FQ water model.³⁸ The molecular dynamics simulations predict a complex time-dependent evolution of the vibrational echo dynamic line width. The slowest component of the calculated time frequency correlation function (TFCF) is 1.5 ps, and it has been identified as associated with hydrogen bond equilibration. The vibrational echo measured dynamic line widths are used to determine experimentally the TFCF, and its slowest component is found to be 1.5 ps,³⁷ although its amplitude is different from that obtained from the simulations. The fact that thermal equilibration is obtained after 5 ps is consistent with 1.5 ps for the inverse of the thermal equilibration time constant.

C. Hydrogen Bond Breaking

Figure 5 shows that the photoproduct spectrum formed when vibrational relaxation leads to hydrogen bond breaking does not initially produce a thermal equilibrium distribution of hydrogen bonds. The differences between the thermally equilibrated spectrum and the short-time photoproduct spectrum are small but observable. To analyze the rate at which hydrogen bonds are broken following vibrational relaxation, we determine the growth of the photo-product spectrum by obtaining its amplitude at each T_w. This is accomplished by fitting it to the thermally equilibrated spectrum at each time. This analysis ignores the small deviations from the thermally equilibrated spectrum at short times, which introduces a negligible error in the amplitude information. Figure 1b shows the results of using the thermally equilibrated spectrum as a model of the photoproduct spectrum. Comparison to the data in Figure 1a shows that the errors introduced are very small.

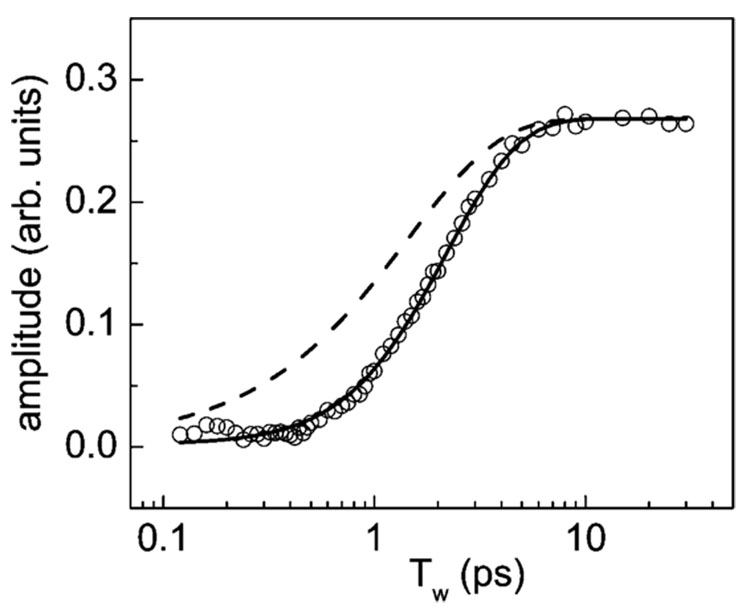
Figure 6 displays the experimentally determined amplitudes of the photoproduct spectrum (circles) as a function of T_w. Note the time axis is logarithmic. At long time, the amplitude levels off because vibrational relaxation and hydrogen bond breaking are complete. At very short time, the signal is essentially zero. The data show the combined time dependence of vibrational relaxation and hydrogen bond breaking. If hydrogen bonds broke immediately upon vibrational relaxation of the excited hydroxyl stretch, the buildup of photoproducts would track the 1.45 ps decay of the vibrational excitations. In detailed studies of vibrational relaxation and hydrogen bond breaking of methanol–OD (MeOD) oligomers in CCl₄, it was found that hydrogen bonds did not break immediately following vibrational relaxation. ¹⁷ In MeOD, the time constant for hydrogen bond breaking was determined to be 250 fs.¹⁷ Therefore, it is necessary to consider the possibility that water hydrogen bonds also require some time following vibrational relaxation to break.

Figure 6.

Experimentally determined amplitudes of the photoproduct spectrum (circles) as a function of T_w. The solid curve through the data is a fit to the data using eq 1. The fit gives the hydrogen bond breaking time following vibrational relaxation as 0.8 ps. The dashed curve would result if the spectral change occurred immediately, which rules out both the direct predissociation mechanism for hydrogen bond breaking and a simple combination band shift caused by excitation of lower frequency modes populated by vibrational relaxation.

Consider a subensemble of HOD molecules with the OD hydroxyl vibrationally excited, e, that will relax with a time constant k_r to an energetic ground state, g. g molecules are the initially excited molecules that are now in the ground state and go on to break hydrogen bonds. g molecules have ~2500 cm⁻¹ of vibrational energy in a combination of intra- and intermolecular degrees of freedom, for example, bending modes and torsional modes. f is the fraction of e molecules that become g molecules, that is go on to break hydrogen bonds and form photoproducts, p, with a time constant k_b. The overall scheme is e → g → p for those initially excited molecules that eventually break hydrogen bonds. The excited molecules that relax and do not break hydrogen bonds will thermalize.

The population dynamics of these processes are governed by the following rate equations, where N_i designates the population in state i:

$$\frac{\text{d}{N}_{\text{e}}(T_{\text{w}})}{\text{d}{T}_{\text{w}}}=-k_{\text{r}}{N}_{\text{e}}(T_{\text{w}})$$ (2)

$$\frac{\text{d}{N}_{\text{g}}(T_{\text{w}})}{\text{d}{T}_{\text{w}}}=k_{\text{r}}f{N}_{\text{e}}(T_{\text{w}})-k_{\text{b}}{N}_{\text{g}}(T_{\text{w}})$$ (3)

$$\frac{\text{d}{N}_{\text{p}}(T_{\text{w}})}{\text{d}{T}_{\text{w}}}=k_{\text{b}}{N}_{\text{g}}(T_{\text{w}})$$ (4)

The solution to the coupled rate equations for the population, N_p, of photoproduct is

$$\begin{array}{c}{N}_{\text{p}}(T_{\text{w}})=\frac{f{N}_{\text{e}}(T_w=0)}{(k_{\text{r}}-k_{\text{b}})}[k_{\text{r}}(1-\text{exp(}-k_{\text{b}}{T}_w))+\hfill \\ \hfill k_{\text{b}}(-1+\text{exp}(-k_{\text{r}}{T}_{\text{w}}))]\end{array}$$ (5)

The long-time solution to eq 5 is Q = fN_e(T_w=0). The T_w = 0 solution is 0. While the absolute magnitude of Q is not known, in the context of the data in Figure 6, it is the value once the data have become flat at long time (>~8 ps). The vibrational relaxation rate is k_r = 1/1.45 ps. Therefore, there is only one adjustable parameter to fit eq 5 to the data in Figure 6, that is, k_b, the hydrogen bond breaking rate constant.

The dashed line in Figure 6 is a result of a calculation using eq 5 and taking k_b = ∞; the hydrogen bonds break immediately upon vibrational relaxation. Clearly, this is not the case. This is a strong argument against a mechanism that assumes a direct excitation of many quanta of the hydrogen bond via relaxation of the hydroxyl stretch mode. In the direct mechanism, the hydrogen bond mode is given sufficient energy through relaxation of the hydroxyl stretch to be above the dissociation threshold. Because the hydrogen bond is above the dissociation threshold, hydrogen bond breaking would require the time for the products to separate, which would be essentially instantaneous compared to the experimental time resolution. Therefore, the photoproduct buildup would follow the dynamics indicated by the dashed line in Figure 6, in clear contradiction to the data. In contrast, the solid line is a fit allowing k_b to vary. The agreement is very good with the resulting value for the inverse of k_b, 1/k_b = 810 fs. A time of 0.8 ps is required for hydrogen bonds to break following the deposition of energy via vibrational relaxation of the hydroxyl stretch. When hydroxyl stretch vibrational relaxation occurs, lower frequency modes are populated. However, population of these modes, which, for example, might be a combination of a bend, torsional modes, and some excitation of the hydrogen bond mode, does not lead to immediate hydrogen bond breaking. Following vibrational relaxation, only a fraction of the vibrational excitations result in hydrogen bond breaking. Only a fraction of the relaxation event may result in the population of the modes that are coupled to the hydrogen bond in the manner required to break it, or further relaxation and dissipation of the energy into the bath may compete with hydrogen bond breaking. In MeOD oligomers, the hydrogen bond breaking time is 250 fs and a much larger fraction of the hydrogen bonds are broken.¹⁷ MeOD makes only two hydrogen bonds.^41,42 It can be a donor and an acceptor. The oligomers are hydrogen bond chains rather than the three-dimensional hydrogen bond networks found in water. The extra restrictions associated with the water networks may be responsible for the longer hydrogen bond breaking time and the small fraction of hydrogen bonds that break measured in water.

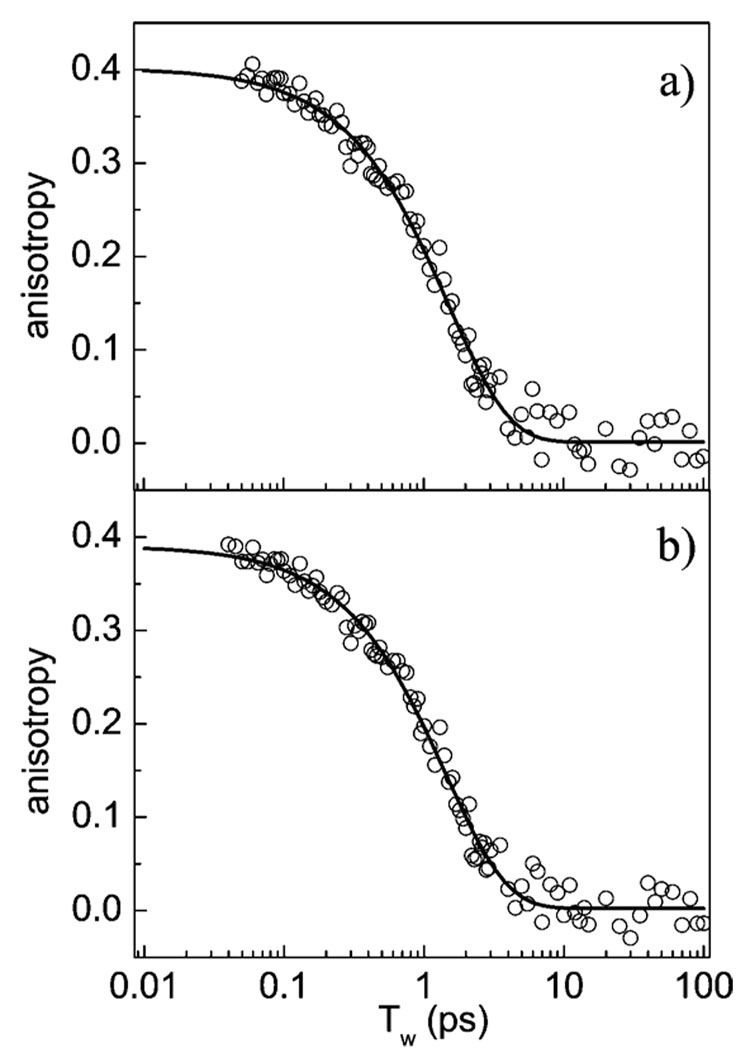
D. Anisotropy

Figure 7a shows the orientational anisotropy of the hydroxyl stretch vibration as a function of T_w (circles), ranging from 50 fs to 100 ps. The data are the results of combining anisotropy data sets for wavelengths over the range 2460–2540 cm⁻¹. The anisotropy, r(t), was determined using eq 1. Anisotropy was calculated from transient spectra taken at magic angle and parallel polarization. The effect of hydrogen bond equilibration on an elevated thermal equilibrium that leads to an apparent frequency-dependent decay of the transient absorption was taken into account by decomposing the parallel and magic angle transients into a decaying and a growing component as discussed above. The anisotropy was calculated from the decaying component, which is not perturbed by the generation of photoproducts.

Figure 7.

(a) Orientational anisotropy decay of the hydroxyl stretch as a function of T_w (circles) for the wavelength range 2460–2540 cm⁻¹. The solid curve is an exponential fit with an anisotropy decay time of 1.53 ps. (b) Orientational anisotropy decay of a single wavelength, 2489 cm⁻¹, and a fit with a 1.5 ps decay time. Orientational relaxation is wavelength independent.

The data were fit to an exponential decay model of r(t) using two adjustable parameters, the decay time and the initial anisotropy, r(t=0). r(t=0) has a theoretical initial value for a dipole transition of 0.40. The solid line through the data is the exponential fit. The fit only included data for times longer than 100 fs because at shorter time some contamination could occur from a nonresonant contribution to the signal. The anisotropy decays exponentially with a time constant of 1.53 ± 0.05 ps. The initial value obtained from the fit is r(t=0) = 0.40 ± 0.05, the maximum possible initial value for a dipole transition. The anisotropy signal decays to 0 at long time. The fact that the data yield r(t=0) =0.40 is important because this value demonstrates that there is no additional ultrafast orientational decay component in the time window when the pump and probe pulses overlap in time (<100 fs) where measurements are not clean because of nonresonant contributions. Figure 7b is an example of a single-wavelength measurement at 2489 cm⁻¹. The exponential fit shown gives the anisotropy decay time as 1.49 ps and r(t=0) = 0.39. The curve in Figure 7a is the average of dozens of curves such as that in Figure 7b over a wide range of wavelengths. There is no systematic wavelength dependence, only small experimental variations in the decay time and the initial value of the anisotropy.

The wavelength-independent anisotropy decay observed here is in contrast to the reports of Laubereau¹⁶ and Bakker,³⁶ who studied the OH stretch of HOD in D₂O. To investigate the possible source of the previously reported wavelength dependence, we analyzed the current data without correction for the generation of photoproducts and foundd a strong frequency dependence of the anisotropy decay ranging from 0.2 to 2.3 ps over a 60 cm⁻¹ frequency range around the center of the hydroxyl band.

As mentioned earlier, it is well documented that the number and strengths of hydrogen bonds influence the frequency of the hydroxyl stretch.^1,10–13 We find that the orientational relaxation is frequency independent. Detailed simulations have shown that the dynamics of HOD in water are the same as the dynamics of water.⁴³ Vibrational echo correlation spectroscopy experiments^20,37 and water simulations³⁸ give the hydrogen bond equilibration time as 1.5 ps. This is also consistent qualitatively with the spectral evolution displayed in Figure 5. Equilibration is a global process that involves more hydrogen bonds than the OD under observation and, therefore, does not depend on the frequency of a given hydroxyl. The frequency independence of orientational relaxation also is consistent with vibrational echo correlation spectroscopy experiments that display a frequency dependence at short times (<400 fs) but not at longer times.²³ The short-time dynamics are correlated with very local hydrogen bond length changes, while the longer time scale dynamics result from equilibration.^20,23 Hydrogen bond breaking and forming processes are likely to be involved with orientational relaxation.

IV. Concluding Remarks

In this paper, we have presented results of ultrafast (50 fs) IR pump–probe spectroscopy of the OD stretch of HOD in H₂O. The experiments and analysis probe hydrogen bond network dynamics in water at room temperature. The broad bandwidths of the ultrashort pulses span the entire hydroxyl stretch spectrum, thereby avoiding the complexity of the time dependence associated with using a narrow bandwidth pump that burns a hole in the spectrum. By frequency resolving the probe after it passes through the sample, we obtain frequency resolution without sacrificing time resolution.

A number of important results emerged from these experiments. (1) The hydroxyl stretch vibrational excited-state decay is wavelength independent and has a decay time of 1.45 ps. (2) Vibrational relaxation generates photoproducts that result from hydrogen bond breaking. The photoproduct spectrum is distinct from the reactant spectrum (excited spectrum). If the rise of the photoproduct spectrum is not separated from the decay of the excited spectrum, the lifetime appears to be wavelength dependent. (3) At long time (>5 ps), the photoproduct spectrum is identical to the linear FT-IR temperature difference spectrum, demonstrating that the system has equilibrated at an elevated temperature. The equilibrated spectrum has increased absorption at high frequency and decreased absorption at low frequency, reflecting a reduction in hydrogen bonding. Temperature difference spectra confirm that the spectral shift is due to hydrogen bond breaking and not weakening of the hydrogen bonds. (4) The photoproducts are not formed in a thermally equilibrated state. At times of <5 ps, the photoproduct spectrum is distinct from the equilibrated spectrum and displays a time-dependent shift as the hydrogen bond network approaches thermal equilibrium. The fact that equilibration is complete in 5 ps is consistent with the 1.5 ps equilibration time obtained from vibrational echo correlation spectroscopy experiments^20,37 and simulations.³⁸ (5) Hydrogen bond breaking does not occur immediately after vibrational relaxation. The time for hydrogen bond breaking following vibrational relaxation is 800 fs. Vibrational relaxation produces an energetic ground state that leads to hydrogen bond breaking. (6) Orientational relaxation is wavelength independent. The orientational anisotropy decay is a single exponential with a decay time of 1.53 ps.

At first glance it may seem surprising that the vibrational lifetime and the orientational relaxation time are frequency independent. The hydroxyl stretch spectrum is very broad. It has a full width at half-maximum of 170 cm⁻¹. Water molecules with the largest number and strongest hydrogen bonds absorb on the low-frequency side of the line. Molecules with the fewest and weakest hydrogen bonds absorb on the high-frequency side of the line. Vibrational relaxation can depend on the frequency because the frequency determines the types of accepting modes and the density of states. Orientational relaxation would seem likely to depend on the number and strength of hydrogen bonds.

The lack of wavelength dependence on the lifetime and the orientational relaxation is caused by the rapid evolution of the frequency in water. Vibrational echo correlation spectroscopy measurements^19,20,23,37 and simulations^38,43 show that spectral diffusion occurs on multiple time scales. A measure of spectral diffusion is the dynamic line width, which can be obtained from the experiments and calculated from simulations. The dynamic line width is a measure of the average range of frequencies sampled by the hydroxyl stretch as a function of time. The ratio of the dynamic line width to the absorption line width at a given T_w is the fraction of the total range of frequencies (total line width) that has been sampled at that time. The experiments show that, at 0.5 ps, 88% of the total line width has been sampled, by 1.0 ps, 95% of the total line width has been sampled, and, by 1.5 ps, 98% of the total line width has been sampled. Therefore, on the time scale of vibrational relaxation and orientational relaxation (1.5 ps), a hydroxyl stretch has moved through virtually all environments. Therefore, the vibrational lifetime and the orientational relaxation time are essentially averages over all environments, eliminating any possible wavelength dependence that would be associated with a particular environment.