Stabilizing effect of knots on proteins

Abstract

Molecular dynamics studies within a coarse-grained, structure-based model were used on two similar proteins belonging to the transcarbamylase family to probe the effects of the knot in the native structure of a protein. The first protein, N-acetylornithine transcarbamylase, contains no knot, whereas human ormithine transcarbamylase contains a trefoil knot located deep within the sequence. In addition, we also analyzed a modified transferase with the knot removed by the appropriate change of a knot-making crossing of the protein chain. The studies of thermally and mechanically induced unfolding processes suggest a larger intrinsic stability of the protein with the knot.

Since the discovery of knotted proteins (1), considerable effort went into to the identification of the types of knots that are present in the protein structure base (2, 3). One interesting subclass identified contains more subtle topological configurations called slipknotted proteins (4). Although structure-based analyses are becoming increasingly available, there are few studies describing the dynamical properties of knotted proteins. Simulations of the folding of the small knotted protein 1j85, combined with experimental results (5, 6), led Wallin et al. (7) to propose that nonnative contact interactions are necessary to fold a protein into a topologically nontrivial conformation. Interestingly, in studies of the tightening of knots under stretching at constant velocity, the knots were found to jump between a set of characteristic sites, typically endowed with a large curvature, before arriving at the final, fully tightened conformation (8). These results are in contrast to the well-studied case of knots in homopolymers that tend to diffuse smoothly along the chain and then eventually slide off (9).

It remains unclear whether knots are responsible for any biological functions or just occur accidentally. One noteworthy suggestion posed is that they provide the additional stability necessary for maintaining the global fold and function under harsh conditions (3). Indeed, RNA methyltransferase derived from thermophilic bacteria appears to require knots for optimal function (10). Consistent with the functional hypothesis, knots are usually found within catalytic domains of enzymes (3). Sometimes they encompass active sites (3) where additional stability or rigidity could enhance catalysis when substrates are bound (2, 3).

Thus, it is important to understand how the presence of a knot may influence the properties and behavior of proteins in solution. In this article, we consider three proteins within the same superfamily that are almost identical and differ by the presence or absence of a topological knot. Two of the proteins are N-acetylornithine transcarbamylase (AOTCase; PDB ID code 1yh1) and ormithine transcarbamylase (OTCase; PDB ID code 1c9y), where the former has a knot (2) and the latter does not contain this topological feature. The third structure is a synthetic construct made from 1yh1 by redirecting the backbone so that the knot is removed. This system will be referred to as 1yh1*. We focus on thermal and mechanical unfolding processes in these systems and compare the properties of these proteins in silico within a structure-based, coarse-grained model as implemented in refs. 11–13. In particular, we consider atomic force microscopy (AFM)-imposed stretching at constant velocity and at constant force and determine the characteristic times for the thermal unfolding and the folding temperature. In all cases, the knotted protein is more stable to unfolding. We compare these results with those observed for the side-chain disulfide-bridged knots.

The Proteins Studied

Proteins 1yh1 (discussed in ref. 14) and 1c9y (discussed in ref. 15) belong to the transcarbamylase superfamily that is essential for arginine biosynthesis (16). The structures are nearly identical, except that 1yh1 contains a knot in its native structure and 1c9y does not (2). The presence or absence of the knot seems to be responsible for the observed differences in enzymatic properties of the two proteins.

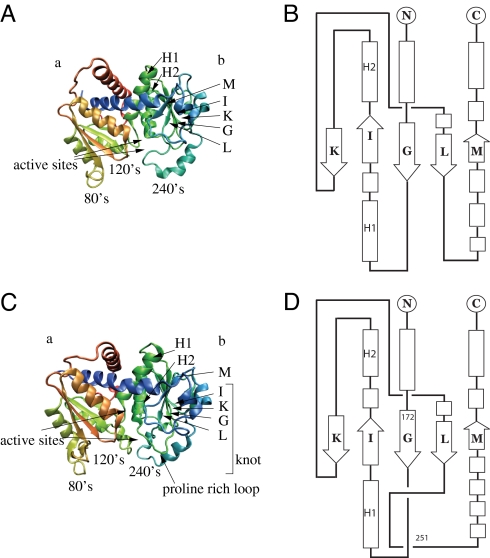
Both proteins 1yh1 and 1c9y comprise two main β-domains denoted as a and b, linked by the two interdomain helices (Fig. 1). The “weaving pattern” in domain b is the structural feature that distinguishes the two proteins topologically. The a domain in 1yh1 incorporates β-strands A(40–45), B(66–70), C(79–80), D(93–94), and E(108–112), whereas the b domain incorporates strands G(172–177), I(202–206), K(232–236), L(248–252), and M(290–292), which create two main β-sheets. Both β-sheets are surrounded by many α-helices. Strands C and D are quite short, but they create an extended loop around site 80, denoted the 80's loop, which is shorter in 1c9y where strands C and D are missing altogether.

Fig. 1.

Native structure of proteins studied in this paper. (Left) The diagrammatic representation of the unknotted 1c9y (Upper) and knotted 1yh1 (Lower) proteins. Both consist of two β-domains, denoted as a and b. (Right) Domain b is topologically trivial in 1c9y (Upper), while knotted in 1yh1 (Lower). The arrows indicating the active sites are arranged in such a way that the upper (lower) arrow corresponds to the first (second) active site. The knot in the native state in 1yh1 extends between amino acids 172 and 251 (whose locations are denoted in a schematic figure on the right).

The sequential positions at which the knot begins and terminates are denoted by n₁ and n₂. These positions are determined by the KMT algorithm (see Materials and Methods). We use this algorithm at every step of our simulations, thereby obtaining the trajectories of knot's ends in the sequential space, such as those shown in Fig. 2Lower. The trefoil knot structure present in 1yh1 extends between amino acids n₁ = 172 and n₂ = 251 making it a relatively rare example of a “deep” knot since it is positioned relatively far from the termini of the protein. The knot encompasses almost the entire domain b, i.e., four β-strands G, K, L, and I, and two nearby α-helices that we denote by H1 and H2 (also present in 1c9y). An important structural difference between 1yh1 and 1c9y is the presence of the proline-rich loop (181–183) in the former, a main building block for the knot-making crossing of the protein chain.

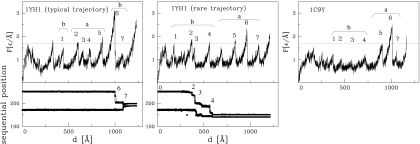
Fig. 2.

Unraveling of the proteins at constant speed of v = 0.005 Åτ. (Upper) Unfolding curves of force versus pulling spring F(d). The horizontal dotted line indicates a reference of F = 1.7 ε/Å corresponding to the height of many of the force peaks. It is drawn to facilitate part-to-part comparisons. The initial force peaks do not relate to the beta sheets in a and b domains. The remaining force peaks are labeled 1 through 7 except that in the Center there is an extra peak between 4 and 5 corresponding to shearing of helices that are coupled to the a domain. In each case, the force peak labeled as 1 arises because of shearing of the L strand against the M strand. Table 1 lists which contacts break (i.e., r_ij > 1.5 σ_ij) at the remaining peaks. (Lower) Sequential movement of knot's ends during the knot-tightening process corresponding to the trajectory shown above.

The two enzymes. OTCase and AOTCase, participate in the arginine biosynthetic pathway, but the presence of the knot in AOTCase makes the corresponding pathway distinct (17). Both proteins contain two active sites—the first binds carbonyl phosphatase (CP), whereas the second site (which is modified by the knot structure) binds either N-acetylornithine or L-ornithine, in the case of 1yh1 and 1c9y, respectively. The second site facilitates the chemical reaction with carbamyl phosphate to form acetylcitrulline or citrulline, correspondingly (14, 15). We use the notation for the active sites introduced in refs. 14 and 18, as shown in Fig. 1. The first active site, located between the two domains, is the same in the two proteins (14). In 1yh1 the second active site is formed by Glu-144 (within the extended 80's loop), Lys-252 (from the 240's loop), and the proline-rich loop (which creates the knot). However, in 1c9y the second active site is localized near the 240's loop (14, 15). Thus, the proline-rich loop in 1yh1 does not allow the formation of contacts between a ligand and the 240's loop (which is possible in 1c9y) and leads to a different functional and topological motif.

The OTCase pathway shows ordered two-substrate binding with large domain movements, whereas in the AOTCase pathway the two substrates are bound independently with small reordering of the 80's loop, small domain closure around the active site, and a small translocation of the 240's loop (17). Thus, it seems that the knot plays two roles here: it changes the environment for the second substrate N-acetylcitrulline binding, and—as shown in this article—makes the structure more stable. As a result, the functional and thermodynamic properties of the fold are affected by the presence of the knot.

Proteins 1yh1 and 1c9y have similar numbers of native contacts [as determined based on the van der Waals radii of heavy atoms (19)], 943 and 919, respectively, so any differences in properties must arise primarily from rearrangements in connectivities in the contact map.

The folding, thermal, and mechanical properties of these two proteins have not been compared up to now, mostly because the structure of AOTCase has not been known until recently and because the presence of the knot makes experimental data harder to interpret. However, some experimental work has been performed on them as detailed in supporting information (SI) Materials.

We have also analyzed a modified 1yh1, in which the knot was removed by reversing the crossing created by the parts of the backbone contained between amino acids 175–185 and 250–260. The cutting and pasting of these two parts of structure was done by using all-atom techniques described in refs. 20 and 21. The resulting structure 1yh1* has the same unknotted topology as 1c9y, but it has 14 fewer contacts than the original 1yh1. This procedure affects the contacts in the vicinity of the original knot-making crossings, but it leaves the global contact map intact. The idea of rebuilding proteins to test their properties is a familiar one—another interesting example of such protein engineering was discussed recently in ref. 22.

Resistance to Mechanical Stretching

One way to probe the stability of a biomolecule is to perform mechanical manipulations on it, such as stretching. The corresponding experimental data on the two proteins are not yet available; thus, we have resorted to computer modeling. We consider the case in which the termini are connected to elastic springs. The N-terminal spring is anchored to a substrate and the C-terminal spring is pulled either at a constant velocity, v_p, or at constant force.

Stretching at Constant Velocity.

In this mode of manipulation, one monitors the force of resistance to pulling, F, as a function of the pulling spring displacement, d. We usually take v_p = 0.005 Å/τ which is ≈100 times faster than typical experimental speeds. Results obtained for v_p = 0.001 Å/τ are found to be similar. In the absence of thermal fluctuations a single unfolding trajectory is followed. At finite temperatures, however, differences between various trajectories arise. Usually, these differences are small. Such is the case for the unknotted 1c9y for which a typical F(d) trajectory is shown in Fig. 2 Right. However, for 1yh1 we identify two distinct pathways. The major pathway is shown in Fig. 2 Center and the alternative pathway in Fig. 2 Left. In fact, that pathway is quite rare: it has been found just once in 50 trajectories. The locations of the knot ends during stretching are displayed in the Fig. 2 Lower Left and Center. The immediate conclusion is that the knotted protein 1yh1 is typically more resistant to stretching than 1c9y because the maximum force peak, F_max, is ≈3.3 compared with 2.6 ε/Å (2.9 and 1.7 ε/Å for v_p = 0.001 Å/τ), with the energy scale ε as defined in Materials and Methods. It is only for the rare trajectory that the values of F_max for the two proteins are nearly the same, but even then the unfolding pathways are distinct as evidenced in Table 1. Based on the data presented in refs. 23 and 24, the unit of force, ε/Å, used here should be on the order of 70 pN. There are uncertainties in this estimate (on the order of 30 pN), but the important observation is that we compare similar proteins with a similar effective value of the ε. Table 1 shows that the unraveling of both proteins proceeds along different pathways. Unfolding of the unknotted 1c9y starts from domain b (which is stabilized by the knot in 1yh1) and once this domain is fully unraveled the unwinding of domain a follows. In the knotted 1yh1 also the domain b begins to unfold first. However, in the typical pathway, its unfolding stops relatively soon, just after strands L and M are pulled apart, because the next step would disarrange the knot. Instead, domain a is unfolded, and only then does the process of knot tightening begins.

Table 1.

The order of the contact breaking for different pathways

Order	Constant velocity						Constant forceF > 1.9ε/Å
	1yh1(typical)	1yh1(rare)	1yh1*(typ.)	1yh1*(rare)	1c9y	1c9y(with SS)	1yh1 & 1c9y
1	L + M (b)	L + M (b)	L + M	L + M	L + M	L + M	L + M
2	A + E (a)	G + L (b)	G + L	A + E	G + L	A + B	G + L,I + K,G + I
3	C + D (a)	G + I, H1,H2 (b)	G + I,H1,H2	C + D	I + K,H1,H2	A + E	A + E, E + F
4	E + F (a)	I + K (b)	I + K	E + F	G + I	E + F	A + B
5	A + B (a)	A + B (a)	A + E,E + F	A + B	E + F	G + L, G + I,H1,H2
6	G + L,I + K,H1,H2(b)	A + E,C + D (a)	A + E,C + D	G + L,I + K,H1,H2	A + E	I + K
7	G + I (b)	E + F (a)	A + B	G + I	A + B

We note that the first broad peak for each trajectory from Fig. 2 corresponds to the shearing motion between two domains, which are connected by two α-helices. It has been established experimentally (17) that the interdomain interactions in 1yh1 are slightly stronger than in 1c9y and are mainly hydrophobic, which is consistent with our observation that the first peak in 1yh1 is higher than in 1c9y. Also. the origin of the main force peak is different in the 2 proteins: in 1yh1 (typical pathway) it coincides with knot tightening within domain b, which is accompanied by shearing of the β-strands G+I, G+L, I+K. In contrast, in 1c9y the main peak is associated with shearing the β-strands A+B, A+E within domain a. However, the rare unfolding pathway of 1yh1 shares many features with that of 1c9y. Nonetheless, because of the presence of the knot, pulling the strands in domain b apart involves a higher force than in 1c9y (where the b-domain-related peaks appear at distances 400–700 Å).

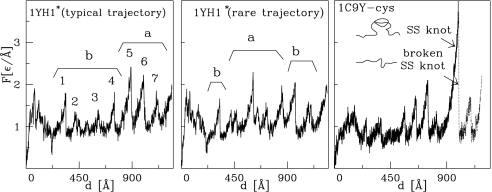
We now consider constant speed stretching of the synthetic protein 1yh1*. Two alternative stretching pathways are also observed in this case, as shown in Fig. 3. The typical pathway (8 of 10 trajectories) yields F_max of just <2.5 ε/Å, which is smaller than F_max for the typical pathway in 1yh1 by ≈0.5 ε/Å. The minor pathway yields F_max which is smaller by ≈0.2 ε/Å than the corresponding value in 1yh1. This lowering in the value of F_max clearly points to the dynamical significance of the knot. In the typical case, the unfolding process is found to proceed in the same way as in the unknotted 1c9y: domain b unfolds first, followed by a. However, in the alternative trajectory, domain b first unfolds partially, then complete unfolding of a follows, and only then is the unraveling of b completed. This pathway is analogous to the typical unfolding of the original knotted 1yh1. However, it is the unfolding of domain a (and not b) that is responsible for the main force peak in 1yh1*. The corresponding value of F_max ≃ 2.4 ε/Å is close to the F_max observed for the unknotted 1c9y (where it also arises from unfolding of domain a). All of these observations indicate that the dynamical differences between 1yh1 and 1c9y can indeed be attributed to the presence or absence of a knot. We now discuss the process of knot tightening and focus on the knotted 1yh1. Similar to what has been found in other proteins with knots (8), the knot ends in 1yh1 make sudden jumps to selected metastable positions. Fig. 2 shows that those jumps are correlated with the force peaks corresponding to unfolding events in domain b. In the typical case (Left), the knot moves to one of the metastable places at ≈1,000 Å (where F becomes F_max), which is followed by tightening of the knot, usually in 2 additional steps. As shown in ref. 8, the set of possible sites at which an end may land corresponds to the sharp turns in the backbone (usually with proline or glycine). In our case, the sites Gly-200, Pro-210, and Gly-230 are found to be the most likely choices. It is interesting to note that for the rare pathway the ends of the knot move even outside the native position (172, 251) to (Val-140, Gln-151). The new knot end positions are close to Pro-139 and Pro-149, which makes this location stable. In proteins comprising <151 aa, F_max tends to arise at the beginning of the stretching process (13). Here, however, the proteins are large and adjust to pulling by first rotating to facilitate unfolding of other parts in their structure, and only then by unraveling the harder knotted part.

Fig. 3.

F(d) curves for the synthetic 1yh1* without the knot (Left and Center) and for the synthetic mutated 1c9y with the disulfide bridge (Right). In the latter, the solid line corresponds to ζ = 20 and the dotted line to ζ = 10.

We also analyzed stretching of tandem linkages of the proteins. Two proteins 1c9y linked together are found to unravel in a serial fashion. This is not the case, however, for two domains of 1yh1. When the unfolding process in one domain reaches the knot region, the other domain starts to unfold. In the final stages, both knots tighten simultaneously.

Comparison Between the Effects of Knots and of Disulfide Bridges.

In the current study we demonstrate that knots provide extra mechanical stability to proteins. Thus, one may think of knots as acting analogously to disulfide bridges between cysteines. Like knots (with the exception of a situation in which pulling unmakes the knot), the disulfide bridges cannot be removed from proteins by stretching. However, unlike knots, they cannot slide along the sequence. Furthermore, the bridges can be weakened through application of the reducing agent DTT as in refs. 25 and 26. As a theoretical analogue of the cysteine knot-containing hormones studied by Vitt et al. (27), we consider a hypothetical mutated version 1c9y in which amino acids at sites 195 and 265 (one could also consider 194 and 262) are replaced by cysteines. The resulting disulfide bridge linking the two sites would close a knot-like loop. The presence of a disulfide bridge can be imitated by strengthening the amplitude of the Lennard–Jones contact potential to ε_ss = ζε. We consider ζ = 20, which makes the bridge essentially indestructible.

Fig. 3 Right shows that the resulting F(d) pattern is quite similar to the typical trajectory for 1yh1 shown in the Fig. 3 Left except for a diverging force peak toward the end of the process. One can endow the disulfide bond with more pliancy by reducing ζ to the value of 10 and thus allowing for the continuation of the stretching process (the dotted line in Fig. 3). The corresponding sequence of the rupture events is different from any of 1yh1 unfolding pathways (Table 1). However, the order of events seems closest to the typical trajectory found for 1yh1: partial unwinding of domain b, followed by unwinding of a, and then returning to unravel b. We conclude that even though the disulfide bridges act dynamically similar to the knots, there are also differences in the details.

Stretching at Constant Force.

The dynamical differences between the knotted and unknotted proteins should also be visible when performing stretching at a constant force, F. In this mode of manipulation, one monitors the end-to-end distance, L, as a function of time as illustrated in Fig. 4 for selected trajectories. In each trajectory, L varies in steps indicating transitions between a set of metastable states that depend on the applied force. For F̃ < 1.7 (where F̃ denotes F in units of ε/Å), domain b in 1c9y gets unraveled first and domain a remains intact. Once the system reaches L, which is just >900 Å, it stays at this extension indefinitely. For larger forces, the b domain also unravels and the ultimate value of L reached is ≈1,200 Å. The pathways observed for the knotted protein 1yh1 are rather different. For F̃ < 1.7, neither domain a nor b unfolds, indicating again the stabilizing role of the knot. It is only the remaining parts of the structure that unravel leading to the largest L of 600 Å. For F̃ between 1.7 and 1.9, two pathways are possible. In the first one, domain a remains nearly intact but domain b gets unfolded, leading to tightening of the knot and to a maximum value of L of 950 Å. This situation is analogous to the one found for 1c9y. In another pathway, the a domain unfolds first, but again full extension of the chain is not achieved. For F̃ > 1.9 the b domain is always the first to unfold. The related movement of knots' ends is shown in Fig. S1. The knot-tightening process looks similar to the one observed in the rare trajectory for the constant velocity stretching (Fig. 2 Center). In this case, domain a eventually unfolds, leading to full extension of the chain. For F̃ > 1.9, the scenarios of unfolding for 1yh1 and 1c9y are almost identical (except for the breakage of C+D bonds, which are absent in 1c9y) and are summarized in Table 1. However, the time intervals between consecutive steps are typically longer for 1yh1, indicating a slower unfolding process. An analysis of the results of stretching with constant velocity led us to expect an interesting behavior for the results for F ≈ F_c = 1.7 ε/Å, because the heights of force peaks (corresponding to domain b) for 1c9y seen in Fig. 2 are much lower than F_c, whereas for 1yh1 some of them are above F_c (both in the typical and rare trajectories). The characteristic value F_c is indicated in Fig. 2 by the horizontal dotted line. Indeed, for stretching with a force ≥F_c, we do not observe any steps in the curves L(t) that are related to peaks 1–4 for 1c9y (Fig. 2 Right). However, we still observe such structures (corresponding to the highest among peaks 1–5 in Fig. 2 Left and Center) during stretching of 1yh1 with F = F_c (and slightly higher). Such a behavior is seen in Fig. 4 for F = 1.9 ε/Å. We also analyzed in detail an example of a constant force pathway for 1yh1 for F > 1.9 ε/Å and average over many trajectories for different forces (see SI Materials).

Fig. 4.

The time dependence of the end-to-end distance when stretching by constant force for the indicated values of the force. Left and Right Center refer to the unknotted protein and the Left Center and Right refer to the knotted one. Schematic pictures of the conformations corresponding to the metastable state are displayed on the right-hand side of each section where the a and b domains are depicted as blobs.

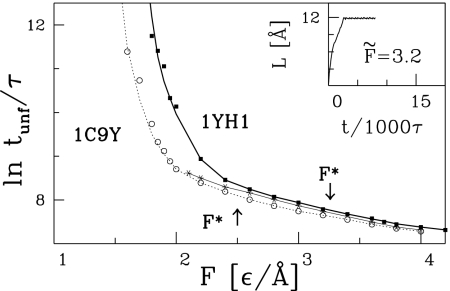
One can quantify the timescales of the force induced unfolding by determining the mean time, t_unf, needed to break all contacts with a sequential distance |j − i| bigger than a threshold value l_c (a somewhat different criterion has been used in ref 28.); see also a related study by Socci et al. (29). The smaller the l_c, the longer the corresponding t_unf In practice, we have found it feasible to take l_c = 8. As shown in Fig. 5 the resulting unfolding times, t_unf(F), are longer for 1yh1 than for 1c9y, which is another manifestation of the higher stability of the knotted protein. The stability of 1yh1 is significantly reduced on replacing 1yh1 by its synthetic variant 1yh1*. Fig. 5 also indicates the values of F*—a force above which the unfolding commences instantaneously. Again, F* for 1yh1 is substantially higher than for 1c9y and 1yh1*.

Fig. 5.

The unfolding times t_unf as a function of the force applied. The solid thick line (with squares) and solid fine line (with asterisks) are for 1yh1 and 1yh1*, respectively; the dotted line (with circles) is for 1c9y. (Inset) For F̃ = 3.2 the protein is stretched instantaneously, without formation of any metastable states, and with small trajectory-to-trajectory variations.

Thermal Stability

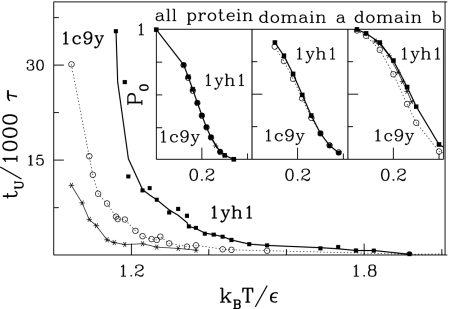
We now consider unfolding via thermal fluctuations following the approach of ref. 30. We define the unfolding time, t_u, as the median duration of a trajectory that starts in the native state and stops when all contacts within |j−i| > l_c get broken. For consistency with the mechanical studies, we choose l_c = 8. The temperature dependence (T) of t_u for both proteins is shown in Fig. 6. Clearly, for any given T, it takes substantially longer to unravel 1yh1 than either 1c9y or 1yh1*. For instance, at k_BT/ε = 1.3 the ratio of t_u between 1yh1 and 1c9y is ≈2.

Fig. 6.

The dependence of the median unfolding time on temperature. The solid thick line (with squares) and solid fine line (with asterisks) are for 1yh1 and 1yh1*, respectively; the dotted line (with circles) is for 1c9y. (Inset) The temperature dependence of the probability of preserving all of the native contacts in 1yh1 and 1c9y.

It should be noted that the mere fact that the contacts with the sequential length larger than l_c are broken does not necessarily mean that the knot itself has loosened and become untied. In fact, according to our studies of thermal unfolding, the knotted proteins unfold in 2 steps: first, the long-ranged contacts break and only then, at much longer timescales, does the knot become undone. Thus, the unfolding follows the N → U K → U path, where N stands for the native state, U K for the unfolded knotted state and U for the totally unfolded, unknotted state. Because of the topological constraints present in the U K state, its entropy is considerably lower than that in U state; thus, the free-energy difference between U K and N is much higher than that between U and N, which leads to the increased stability of the native state. Similar entropy-based strategies for increased stabilization are found in other topologically constrained proteins (31), e.g., in proteins with circular backbones, which has been shown to be highly resistant to enzymatic, thermal, and chemical degradation (32). There is also another, energy-based, reason for the increased stability of 1yh1 and, possibly, of other knotted proteins. Namely, nontrivial topology of a protein may lead to a more energetically favored conformational state. This is the case for the three proteins considered here: the knotted 1yh1 has the lowest native state energy. The native state energy of 1yh1*, the unknotted counterpart of 1yh1, exceeds that of 1yh1 by 14 ε, whereas that of 1c9y is higher than 1yh1 by ≈24 ε. Thus one of the reasons why knots may be preferred in certain proteins is that they lead to deep native state minima.

Apart from the higher stability of 1yh1, its longer unfolding times can also be explained in terms of topological frustration (22, 33). It arises when only a particular order of contact breaking allows the protein to unfold. When this order is incorrect, certain geometrical constraints arise that do not allow for unfolding, and some contacts are forced to form back again. Therefore, a protein unfolds in a series of steps, also called a backtracking, which involve refolding and unfolding. The consequence of this geometric bias is an unusually long unfolding time. There are obvious geometrical constraints present in 1yh1 related to its knotted structure, so it is likely that its unfolding is dominated by topological frustration and takes more time than unfolding of unknotted 1c9y or 1yh1*. A particular example of backtracking, which arises in 1yh1 is presented in detail in SI Materials.

To assess the magnitude of fluctuations around the native state we measured P₀(T) defined as the fraction of time during which all native contacts are established for the trajectory starting in the native conformation. This quantity can be regarded as yet another measure of stability. However, even though P₀ is calculated based on relatively long trajectories of 10⁵ τ, this is still only a small fraction of the expected unfolding time in this range of temperatures. These trajectories are therefore not ergodic and probe vicinity of the native state basin. The results shown in Fig. 6 Inset Left show the data for the entire length of proteins, and Center and Right show the a and b domains, respectively. In Fig. 6 Inset Right for domain b (which contains the knot in 1yh1) the data points corresponding to 1c9y are shifted toward lower temperatures relative to 1yh1. A similar, but smaller shift toward lower temperatures is also observed for the synthetic 1yh1*. However, data points for domain a (Inset Center) and for the whole protein (Inset Left) are similar. Thus, differences in P₀ are confined to domain b and indicate a higher stability of domain b in the knotted protein.

Thermal Untying of a Knot in 1yh1 Protein.

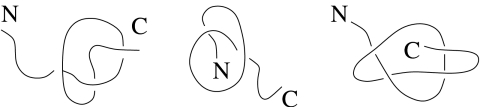
As mentioned above, untying of the knot involves much longer timescales than those of long-range contact breaking. However, the unknotting times decrease with increasing temperature. Meaningful studies could be performed for k_BT/ε = 1.2 (and higher). We have found that the knot opens more readily on the side closer to the C terminus, whereas its N terminus side is more stable. This is in agreement with the results of ref. 34 on the asymmetry of (slip)knots, and the fact that they arise much more often closer to the N terminus. Examples of conformations corresponding to different ways of thermal untying of a knotted loop are shown in Fig. 7 (see also Fig. S2). For each terminus, there are two possibilities: either it is the last site to leave the knot or else it is a leader that pulls the rest of the knotted loop behind it. The latter circumstance is known as a formation of a slipknot (4). It is interesting to note that application of a high temperature has occasionally been found to generate short-lived additional (slip)knots, especially when the native knot has disappeared.

Fig. 7.

Three possible ways of thermal untying of the knot. In the trefoil knot one part of a protein chain is threaded through a loop, which we refer to as the “knotted loop”. Such a knot can be thermally untied in the following ways. From the left to the right: simple from the C terminus, simple from the N terminus, and through formation of a slipknot.

As generally expected and demonstrated in ref. 30 explicitly, the process of thermal unfolding is statistically the reverse to folding. Thus, the phenomena we observe for unfolding should also be observed in folding processes. This also suggests that the presence of the nonnative attractive contacts is not necessary for formation of a knot. Indeed, in a subsequent article we show that proteins of nontrivial topology have the ability to fold to their native states without any nonnative interactions involved. Such nonnative contacts have been vital in folding simulations of Wallin et al. (7). More details and particular examples of thermal untying and backtracking by which it may be accompanied are presented in SI Materials and Fig. S3.

Discussion and Conclusions

We have considered three very similar proteins—one with a knot and two without—and determined their properties by using a coarse-grained, native-geometry-based model. Both mechanically and thermally, the protein with the knot has been found to be more robust and is characterized by longer unfolding times, which we attribute to topological and geometric frustration. The larger robustness of 1yh1 relative to 1c9y relates to the experimental results on OTCase and AOTCase pathways (see Movies S1 and S2). The OTCase pathway shows the two-substrate binding involving large domain movements. In this pathway, the order in which the substrates are bound is well defined. On the other hand in the AOTCase pathway, the 2 substrates are bound independently. This process involves small reordering of the 80's loop, small-domain closure around the active site, and a small translocation of the 240's loop (17).

Other findings can be summarized as follows. The unknotted variant of 1yh1 has been found to behave like the unknotted 1c9y. Therefore, we conclude that this is the nontrivial knot topology that is responsible for the peculiar properties of 1yh1. Disulfide bridges may imitate existence of knots to some degree. The kinetics of the knot untying and thus, by a reversal, the kinetics of formation of the knot may involve generation of other knots and slipknots. According to ref. 14, the presence of the knot motif in AOTCase affects the way the N-acetylcitrulline is bound to the second active site and thus changes the arginine biosynthetic pathway. This observation can provide important information on potential targets for specific inhibition of bacterial pathogens. Such inhibitors would not affect the more common OTCase and thus provide a specific nontoxic method for controlling certain pathogens.

Taken together, these findings show that relatively small structural differences between the proteins which, however, alter the topology of the backbone, result in dramatic changes in their mechanical properties and stability. This research reveals that there is a strong relationship between the topological properties and functional features of biomolecules.

Materials and Methods

Coarse-Grained Model.

The coarse-grained molecular dynamics modeling we use is described in detail in refs. 11–13. In particular, the native contacts between the C^α atoms in amino acids i and j, separated by the distance r_ij, are described by the Lennard–Jones potential V_LJ = 4ε[(σ_ij/r_ij)¹² − (σ_ij/r_ij)⁶]. The length parameter σ_ij is determined pair-by-pair so that the minimum in the potential corresponds to the native distance. The energy parameter ε is taken to be uniform. As discussed in Ref. 23, other choices for the energy scale and the form of the potential are either comparable or worse when tested against experimental data on stretching. Folding is usually optimal at temperature k_BT/ε at ≈0.3 (k_B the Boltzmann constant) which will be assumed to play the role of an approximate room temperature. Implicit solvent features come through the velocity-dependent damping and Langevin thermal fluctuation in the force. We consider the overdamped situation, which makes the characteristic timescale, τ, to be controlled by diffusion and not by ballistic motion, making it on the order of a nanosecond instead of a picosecond. The analysis of the knot-related characteristics is made along the lines described in ref. 8.

KMT Algorithm.

We determine the sequential extension of a knot, i.e., the minimal segment of amino acids that can be identified as a knot, by using the KMT algorithm (35). It involves removing the C^α atoms, one at a time, as long as the backbone does not intersect a triangle set by the atom under consideration and its 2 immediate sequential neighbors. The knots can be identified also by protein knot server (36).