Genetic architecture of complex traits: Large phenotypic effects and pervasive epistasis

Abstract

The genetic architecture of complex traits underlying physiology and disease in most organisms remains elusive. We still know little about the number of genes that underlie these traits, the magnitude of their effects, or the extent to which they interact. Chromosome substitution strains (CSSs) enable statistically powerful studies based on testing engineered inbred strains that have single, unique, and nonoverlapping genetic differences, thereby providing measures of phenotypic effects that are attributable to individual chromosomes. Here, we report a study of phenotypic effects and gene interactions for 90 blood, bone, and metabolic traits in a mouse CSS panel and 54 traits in a rat CSS panel. Two key observations emerge about the genetic architecture of these traits. First, the traits tend to be highly polygenic: across the genome, many individual chromosome substitutions each had significant phenotypic effects and, within each of the chromosomes studied, multiple distinct loci were found. Second, strong epistasis was found among the individual chromosomes. Specifically, individual chromosome substitutions often conferred surprisingly large effects (often a substantial fraction of the entire phenotypic difference between the parental strains), with the result that the sum of these individual effects often dramatically exceeded the difference between the parental strains. We suggest that strong, pervasive epistasis may reflect the presence of several phenotypically-buffered physiological states. These results have implications for identification of complex trait genes, developmental and physiological studies of phenotypic variation, and opportunities to engineer phenotypic outcomes in complex biological systems.

Genetic analysis of complex traits is proceeding at an accelerating pace, with the discovery of susceptibility factors for many traits and diseases in both humans and model organisms (1, 2). Although the individual genes shed important light on the specific molecular functions and pathways controlling phenotypic variation in organismal biology, we remain largely ignorant of the overall genetic architecture of complex traits, including the total number of genes, the typical effect sizes for risk alleles, and the genetic interactions among them. Although readily addressed in organisms such as yeast (3–5), studying these issues with precision is particularly difficult in heterogeneous genetic backgrounds, as in human populations. New genetic resources now enable adequately powered, genome-wide studies of the genetic architecture of quantitative trait loci (QTLs) effects in mammalian model organisms.

Chromosome substitution strains (CSSs) are a novel paradigm for studying complex traits (6). A CSS is created by selecting an inbred strain as the “host” and, with successive backcrossing, by replacing a single chromosome with the corresponding chromosome from a different inbred “donor” strain (6). A CSS panel is a collection of strains, in which each nuclear and mitochondrial chromosome has been independently substituted in its own CSS. Because of the way in which a CSS panel systematically partitions the genome, one can analyze the genetic basis of a trait simply by comparing the trait value in each CSS with the trait value in the host strain (6–10). A significant difference between a CSS and the host strain implies that the corresponding chromosome carries at least 1 QTL. A complete mouse CSS panel and 2 partial rat CSS panels have been constructed (7, 8). With these panels, it has become possible to systematically assess the magnitude of QTL effects associated with each chromosome and to study their genetic interactions.

Several recent CSS studies (7–9, 11, 12) have suggested unexpected results about the genetic architecture of complex traits, by finding that QTL effects associated with individual chromosomes can sometimes be remarkably large and that epistasis may be common. Three traits from a published survey for the mouse C57BL/6J-Chr^A/J/NaJ CSS panel illustrate these points (7). In studies of resistance to diet-induced obesity in males, 16 CSSs were significantly leaner than the host strain. The average reduction in mean body weight per strain was 8.4 g, corresponding to 75% of the 11.1 g difference between the parental strains, and the sum of the phenotypic effects was 928% of the parental difference, suggesting strongly nonadditive effects. Similar results were found for plasma sitosterol levels in males: 12 CSSs differed from the host strain, with the average phenotypic effect being 79% of the difference between the parental strains. Most strikingly, study of cholesterol levels in mice fed a regular chow diet revealed 9 significant CSSs with the average phenotypic effect per strain being nearly 100% of the difference between the parental strains. These results stand in sharp contrast to expectations based on decades of QTL studies of segregating crosses or outbred populations, which typically find that individual QTL tend to have small and additive effects (1, 2, 13–18).

Given these observations, we undertook a systematic analysis of QTL effects in CSSs. In this study, we analyzed data on 90 traits in a mouse CSS panel and 54 traits in a rat CSS panel. We present the analysis of phenotypic effects here and will report the mapping and functional results elsewhere (H.S., L.C.B., D.S.S., A.E.H., E.S.L., and J.H.N., unpublished data).

Results

Traits in Mouse CSS Panel.

We studied 90 blood, bone, and metabolic traits in the mouse C57BL/6J-Chr^A/J/NaJ CSS panel. The study included 42 previously unpublished assays: 22 traits involving bone composition, geometry, and fragility in females and males; 3 traits involving the level of total homocysteine in plasma from females and males; and 17 traits involving diet-induced metabolic syndrome in males [supporting information (SI) Table S1], as well as 48 traits from a published survey of amino acid and sterol levels in plasma samples from females and males (7).

Large Phenotypic Effects.

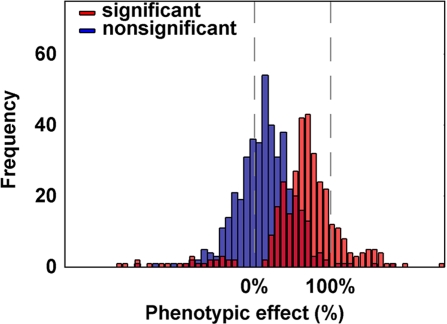
Of the 90 traits studied, 56 were classified as multigenic (based on at least 3 CSSs showing significant differences from the C57BL/6J host strain). We focused on the 41 of these traits that showed significant differences between the 2 parental strains (Table S1). Across these traits, there was an average of 8 significant CSSs per trait (range 3 to 16) and a total of 342 significant CSSs (Table 1). The average phenotypic effect for a CSS was 76% of the total difference between the parental strains. Remarkably, many of the CSSs (18%) showed phenotypic effects that were greater than the difference between the parental strains, with 49% of the traits having at least 1 such CSS, and 2 traits having 7 such CSSs (Fig. 1).

Table 1.

Phenotypic effects for traits in mouse and rat CSSs

Species, trait class	No. of assayed traits	No. of multigenic traits, >2 CSSs (% total)	Mean no. significant CSSs per multigenic trait (min, max)	Mean phenotypic effect per CSS per trait, % (min, max)
Mouse, blood	51	24 (47%)	7 (3, 16)	102 (53, 130)
Mouse, bone	22	17 (77%)	6 (3, 11)	72 (24, 148)
Mouse, metabolism	17	15 (88%)	12 (3, 16)	66 (47, 96)
Mouse, total no.	90	56 (62%)	8 (3, 16)	76 (24, 148)
Rat, total no.	54	31 (57%)	6 (3, 11)	77 (38, 186)

Fig. 1.

Frequency distribution of phenotypic effects in C57BL/6J-Chr^A/J/NaJ CSSs. For the 41 traits that differed significantly between the parental strains, phenotypic effects for CSSs that differed significantly from C57BL/6J are indicated in red, and those that did not differ significantly are indicated in blue. Phenotypes are normalized, so that C57BL/6J = 0% and A/J = 100%.

Chromosome substitution typically results in phenotypic shifts in the direction of the donor strain (92% of cases). The direction tended to be consistent across a trait, with 30 traits showing all significant shifts shifted toward the donor, 4 traits with all significant shifts away from the donor, and only 7 traits with mixed results (Fig. S1). Even among the 435 CSSs whose difference from C57BL/6J was not statistically significant, these shifts showed a significant bias (2:1) toward the donor strain (χ² = 47.0, P < 0.001).

The large phenotypic effects observed with individual CSSs may reflect a single QTL, a few large-effect QTLs, many small-effect QTLs acting in the same direction, or strong gene interactions among the QTLs on the chromosome. We return to this point below.

Substantial Epistatic Interactions.

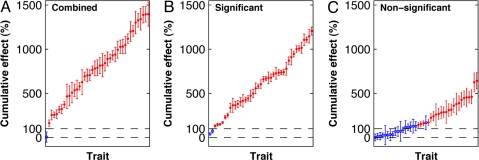
In addition to the large phenotypic effects of individual chromosome substitutions, we also found strong evidence of epistasis among the QTLs across the various chromosomes. For each of 41 traits, we summed the phenotypic effects (that is, the difference from the host strain) for each strain in the CSS panel to obtain a “cumulative phenotypic effect.” If the QTL effects were largely additive, the cumulative phenotypic effect should approximately equal the phenotypic difference between the parental strains; additivity would be true regardless of whether the CSS effects are due to single or multiple QTLs per chromosome. Remarkably, the cumulative phenotypic effect for 40 of the 41 traits was typically much larger than 100% of the parental difference (Fig. 2A). Similar results were obtained regardless of whether we summed only over those CSSs that showed significant differences from the host strain or only over those that did not differ significantly from C57BL/6J (Fig. 2 B and C). In short, significant epistasis was the rule rather than the exception for these quantitative traits.

Fig. 2.

Cumulative combined, significant, and nonsignificant phenotypic effects in the survey of mouse CSSs. For each of the 41 traits that differed significantly between the parental strains, we calculated the cumulative phenotypic effect (sum across the CSSs) and the corresponding SEM. (A) Absolute value of the cumulative phenotypic effect for each trait, given in rank order. For additive interactions, the cumulative phenotypic effect should equal ≈100% (dashed horizontal line). Traits were termed “epistatic” (indicated in red) if the cumulative phenotypic effect exceeded 100% by more than the SEM. Of the 41 traits, 40 were epistatic (median cumulative effect, 803%; range, 164% to 1,397%.). (B and C) The analysis was repeated by using only those CSSs whose phenotypic difference from the host strain that achieved statistical significance (B), or fell short of statistical significance (C).

We formalized this analysis by fitting 2 linear models: (i) an additive model, in which the phenotypic difference between A/J and the host strain is constrained to equal the cumulative phenotypic effect, and (ii) an unconstrained model. We calculated an F-statistic for the fit of the unconstrained model versus the additive model; a P value was calculated as the probability of obtaining an F-statistic as large as or larger than that observed if the additive model were true (Table S2). In cases where the phenotype of a CSS was unavailable, we conservatively assumed that the phenotypic difference for the CSS was zero. We analyzed all 90 traits, including those that did not show significant differences between the strains. Of these, 48% of the traits showed significant deviation from the additive model, demonstrating strong evidence for epistasis.

We emphasize that the observed epistasis was not a subtle deviation from perfect additivity: the deviations were strikingly large. For the 41 traits with significant differences between the parental strains, the cumulative phenotypic effect was at least 200% of the phenotypic difference between the parental strains in 85% of cases and >500% of the phenotypic difference in 56% of cases. In many instances, multiple individual chromosomes each conferred a phenotype that was at least 75% of the phenotypic difference between the parental strains.

Rat CSS Panel.

We similarly studied the genetic architecture of complex traits in a rat CSS panel (8), and found similar results (Table 1; see also Table S1). Among 54 traits studied in the SS-Chr^BN/Mcwi panel, we found that 31 were multigenic and focused on the 11 that also differed significantly between the BN and SS parental strains. These 11 traits involved an average number of 6 significant CSSs per trait (range 3 to 11), for a total of 61 significant CSSs. These CSSs had an average phenotypic effect of 77% of the difference between the parental strains, with 70% in the direction of the donor strain. For 9 of the 11 traits, the cumulative phenotypic effect was >100% of the difference between the parental strains (median 261%, range 169% to 548%). The similar trends in both the mouse and rat CSS panels suggest that the results are not related to the idiosyncrasies of particular traits, strains or species.

Dissecting Genetic Architecture Within Individual CSSs.

As noted above, the large phenotypic effects of chromosome substitution may reflect the cumulative action of multiple QTLs on substituted chromosomes. We explored this question for 2 traits and 2 chromosomes. Specifically, we derived congenic strains containing a nested series of segments from chromosomes 6 and 10 and characterized the strains for diet-induced obesity (CSS-6 and −10) and levels of liver triglyceride (CSS-10) (Fig. 3; Fig. S2). In each case, we detected multiple QTLs within each chromosome, with the number of QTLs ranging from 2 to 4 across the traits and chromosomes.

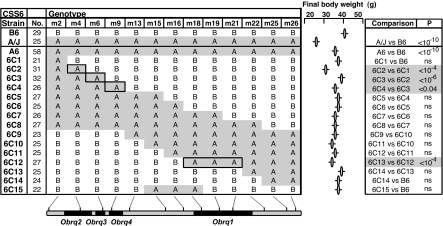
Fig. 3.

QTLs for final body weight in congenic strains derived from CSS-6. Genotypes are shown for various genetic markers (m, defined in SI Materials and Methods), with the genetic map at bottom (centromere at left and telomere at right). Phenotypes are shown by ovals (mean) and whiskers (SEM), with sample size (no.) indicated. Pairwise comparisons between strains are indicated, by using 2-tailed t tests with significance levels (P) corrected for multiple hypothesis testing. The locations of A/J derived segments are indicated in gray, with the breakpoints of the congenic segments arbitrarily placed midway between flanking markers. The locations of QTLs in the key congenic strains (inferred from pairwise comparisons) are indicated in boxes and in black segments on the genetic map, with breakpoints for the most likely location for the QTLs arbitrarily placed midway between flanking markers.

The congenic strains reveal a total of 10 QTLs (Obrq1–4 for obesity in CSS-6; Obrq9–12 for obesity and Ltgq1 and Ltgq2 for liver triglycerides in CSS-10). The average phenotypic effect ranged from 25% (FBW, CSS-6) to 45% (liver triglyceride, CSS-10) of the difference between the A/J and C57BL/6J parental strains, and from 60% (liver triglyceride, CSS-10) to 101% (FBW, CSS-10) of the difference between C57BL/6J and the corresponding CSS. Of the 10 QTLs, the donor allele shifted toward A/J in 7 cases and away from A/J in 3 cases.

The results suggest that the genetic architecture of these 2 traits is similar across chromosomes and within chromosomes, with multiple large effects detectable in both cases. It was not possible to directly study epistasis among the QTLs within a chromosome, because the congenic segments overlapped and thus did not appropriately partition the chromosomes.

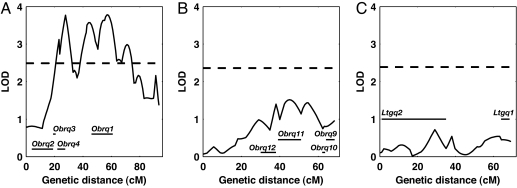
Notably, congenic strains provided considerably greater power to dissect genetic architecture of the traits than intercrosses. We performed intercrosses CSS-6 and separately CSS-10 with C57BL/6J and scored them for final body weight and liver triglyceride levels. Of 10 QTLs detected in the congenic strains, only 3 (Obrq1, 3, and 4) were detected in the intercrosses (Fig. 4).

Fig. 4.

QTL mapping of 2 traits in CSS intercrosses with C57BL/6J. Graphs show logarithm of odds (LOD scores) along chromosomes, with dashed horizontal line denoting threshold for significance (P = 0.05, permutation test). (A) Four QTLs for final body weight (Obrq1–4) in a CSS-6 × C57BL/6J intercross. (B) Four QTLs for final body weight (Obrq9–12) in a CSS-10 × C57BL/6J intercross. (C) Two QTLs (Ltgq1 and Ltgq2) controlling liver triglyceride levels in a CSS-10 × C57BL/6J intercross. Approximate locations of QTLs are derived from surveys of the same traits in 2 panels of congenic strains (Fig. 3 and Fig. S2).

The phenotypic effect of Obrq2 on resistance to diet-induced obesity in the 6C2 congenic strain was particularly striking. Although this strain contains only a small segment of A/J-derived chromosome 6 (≈2% of the donor A/J genome) on the inbred C57BL/6J background, this segment led to dramatically reduced body weight despite presence of both genetic (C57BL/6J host genome) and environmental [high-fat, simple-carbohydrate (HFSC) diet] risk factors (Fig. 3). However, the phenotypic effect of Obrq2 depended heavily on the alleles at neighboring Obrq's in the various congenic strains (Fig. 3), and Obrq2 was not detected in the CSS-6 intercross (Fig. 4A). Therefore, Obrq2 illustrates the large and complex nature of phenotypic effects for QTLs in CSSs and congenic strains derived from them.

Discussion

With the progress in mapping and identifying genetic variants for complex traits in both humans and model organisms (1, 2), it is increasingly important to understand the principles by which polymorphic genetic variants affect development and physiology. CSSs are an important complement to human population studies for studying the genetic architecture of complex traits, because they make it possible to study genetic interactions with greater sensitivity and precision than can be done in natural populations or in crosses.

CSS surveys of multiple traits in both mouse and rat reveal a consistent picture of the genetic architecture of complex traits. First, multiple chromosomes typically conferred a detectable phenotypic shift (average of ≈6–7 per multigenic trait in mouse and rat CSSs). Second, in the 3 cases examined, each chromosome itself harbored multiple distinct QTLs (average of ≈3 loci). These data suggest that the parental strains typically harbor at least 20 distinct QTLs that can be detected experimentally (as well as potentially many more QTLs of smaller effect). These CSS results are compatible with recent studies indicating the presence of dozens of loci affecting such traits as height, type 2 diabetes and inflammatory bowel disease segregating in the human population (1, 20). In fact, the results are particularly striking, because they reveal that a tremendous wealth of genetic and phenotypic variation is readily detected between 2 laboratory strains. Third, the phenotypic effects conferred by individual chromosomes were often unexpectedly large, and usually accounted for a significant fraction of the overall phenotypic difference between the parental strains. Consequently, the overall phenotypic difference between the parental was much less than the sum of the phenotypic differences attributable to individual chromosome substitutions.

Such striking epistasis is rarely detected in humans and model organisms (1, 2, 16–21). One possibility may be that the statistical power to detect pairwise epistasis is typically low both in segregating populations and in crosses with multiple segregating epistatic loci that can obscure pairwise effects (21). Another possibility may be that the genetic architecture varies substantially among traits. In the present study, for example, QTL effects were generally smaller and epistasis weaker for bone traits than for blood and metabolic traits (Table 1). A third possibility is that the study design strongly influences the picture of the genetic architecture obtained. For example, genome-wide association studies of height in the human population, a prototypic quantitative trait (22), revealed many loci with small and additive effects, with little evidence for epistasis (23–25). These human studies necessarily involve large, genetically heterogeneous population samples and are better powered to detect common variants of modest effect than rare variants of larger effects. By contrast, CSS studies measure aggregate effects of whole chromosomes and they involve allelic comparison between 2 defined genetic backgrounds regardless of allele frequencies in the population. Moreover, CSSs enable genome surveys of phenotypic effects in genetically defined individuals, rather than averaging QTL effects across a heterogeneous background.

The presence of strong epistasis may reflect important features of the biological systems that control development and physiology (26–28), but should not affect predictions about the effects of natural or artificial selection (29). We speculate that the underlying systems may have several stable regimes: some genetic perturbations have small phenotypic effects that leave the system in one stable regime, whereas others may propel systems from one region of relative stability to another by crossing critical physiological thresholds. In this way, individual chromosomes could cause significant shifts, but the combination of many such chromosomes might interact in a subadditive manner. It will be interesting to explore the genetic architecture of a wider range of traits, to determine whether the number, magnitude, and interaction of phenotypic effects can be related more precisely to the control networks of the underlying biological systems.

Materials and Methods

All procedures were approved by the Institutional Animal Care and Use Committees.

Phenotypic Effect (ES) Measurement.

We used 2 methods to estimate phenotypic effects in their measured units; these provide a measure of the individual and separately the cumulative phenotypic effect that is attributable to CSSs in a survey of a CSS panel. Detailed information is provided in the SI Materials and Methods and SI Appendix.

Test for Additive Effects.

We assumed that the mean phenotypic value m_i for the ith strain follows (m_i, σ_i²). Taking m₀ to correspond to the average phenotypic value for A/J and m_K+1 to correspond to the average for C57BL/6J, and m_i (i = 1, …, K) to be the average trait value for the ith CSS, the null hypothesis was

SEM for the Cumulative Effect.

The methods for estimating SEM of individual and cumulative effects variable from other variables follow the standard error propagation method. Detailed methods are described in the SI Materials and Methods.

Direction of QTL Action.

To quantify the direction of QTL action, in terms of “moving toward” or “away from” the mean trait value (T) for A/J, we used a variable r, where r = (T_B6–T_CSS)/(T_B6–T_A/J), and where T_B6, T_CSS, and T_A/J were the mean values for the various traits in the corresponding strains. When r > 0, the substituted chromosome shifted the phenotypic trait values toward A/J, whereas when r = 0 or r < 0, the substitutions moved the trait value away from A/J. We focused on traits that differed significantly between C57BL/6J and A/J. For each trait, we sorted the results for the CSS into 2 groups, those whose trait values differed significantly from C57BL/6J, and those that did not. We then estimated the distribution of these 2 groups for these traits and for the combined data.

Clustering of QTL Direction Effects.

K-means was used to cluster the histograms of all 41 traits with CSS entries that differed significantly from C57BL/6J. The maximum cluster number was set to 4, with squared Euclidean distance as the metric and a maximum iteration of 100. Empty clusters were not considered in subsequent analyses.

Metabolic Traits.

Details concerning animal care, serology, dissection, and metabolite and bone assays can be found in the SI Materials and Methods. All phenotyping results were deposited in the Mouse Phenome Database (www.jax.org/phenome).

Physiology Data for Rat CSSs.

Data were downloaded from http://pga.mcw.edu/pga2-bin/strain_profile.cgi (8). We first removed outliers based on 3IQR (InterQuartile Range) criteria and then randomly sampled 45 individual rats from the SS host strain as the reference strain for each CSS comparison (10).

Congenic Strains Derived from C57BL/6J-Chr6^A/J/NaJ and C57BL/6J-Chr10^A/J/NaJ.

Details concerning the construction of the CSS-6 and CSS-10 congenic strains are provided in the SI Materials and Methods.

Genotyping and Statistical Analysis.

DNA and PCR, SSLP, and SNP selection and genotyping are described in the SI Materials and Methods.

Statistical Analysis.

Interval mapping analysis (30) with age as a covariate was performed by using R/QTL (31). To calculate statistical thresholds, 10,000 permutations of the data were used (32). All statistical analyses were performed with the statistical software R (33).

Resistance to Diet-Induced Obesity in C57BL/6J-Chr6^A/J/NaJ Congenic Strains.

At 5 weeks of age, “test” mice were provided the HFSC diet (58 kcal% fat, 26 kcal% carbohydrate, sucrose and maltodextrin, 16 kcal% protein; Research Diets D12331). Mice were weighed every 2 weeks for 100 days. We removed outliers based on 3IQR criteria.