Signaling pathways of PDZ2 domain: A molecular dynamics Interaction Correlation Analysis

Abstract

PDZ domains are found in many signaling proteins. One of their functions is to provide scaffolds for forming membrane-associated protein complexes by binding to the carboxyl termini of its partners. PDZ domains are thought to play a signal transduction role by propagating the information that binding has occurred to remote sites. In the current study, a molecular dynamics simulation based approach, referred to an interaction correlation analysis, is applied to the PDZ2 domain to identity the possible signal transduction pathways. A residue correlation matrix is constructed from the interaction energy correlation between all residue pairs obtained from the molecular dynamics simulations. Two continuous interaction pathways, starting at the ligand binding pocket, are identified by a hierarchical clustering analysis of the residue correlation matrix. One pathway is mainly localized at the N terminal side of helix α1 and the adjacent C terminus of loop β1–β2. The other pathway is perpendicular to the central β sheet toward the side of PDZ2 domain opposite to the ligand binding pocket. The present results extend previous studies based on multiple sequence analysis, NMR and molecular dynamics simulations. Importantly, they reveal the energetic origin of the long-range coupling. The PDZ2 results, as well as the earlier rhodopsin analysis, show that the interaction correlation analysis is a robust approach for determining pathways of intramolecular signal transduction.

Introduction

PDZ domains constitute a class of modules that are important for mediating the interactions between partners along signal transduction pathways ^1–3. They are one of the most abundant interaction domains and have been identified in several hundred of eukaryote proteins ¹. They are often associated with receptors (e.g. NMDA and AMPA/kainite) as well as membrane channels (e.g. Shaker K⁺ and TRP Ca²⁺) and are involved in clustering proteins into functional complexes at the plasma membrane ^1–4. Usually, the PDZ containing protein has several PDZ domains (up to 10 domains ⁵), which can concurrently interact with different protein, and thereby form functional protein complexes. For example, InaD contains five PDZ domains to form homodimer and constitute the formation of the cluster of eight proteins involved in the Drosophila phototransduction cascade ¹, while PSD-95 has three PDZ domains that interact with glutamate receptors at synapses (e.g. in terms of numbering, PDZ3, which has been studied extensively, is the third PDZ domain of PSD-95) ^1,6,7. Moreover, PDZ domain can synergistically binds to inostiol phospholipids with pleckstrin homology domains⁸. Clearly, an understanding of the dynamic properties of PDZ domains and their possible role in allosteric effects is of interest.

Structures of several PDZ domains are available through either X-ray crystallography (PDZ1 ^9,10), NMR studies (PDZ4 ¹¹) or both (PDZ2 ^12–16). PDZ domains adopt an overall globular structure containing two α helices and six β strands (Fig.1a). Most PDZ-mediated interactions occur between the C terminal peptide of the target protein and the binding pocket between the α2 helix and the β2 strand ^1,6. Fig.1b shows an enlarged view of the binding site of the PDZ2 domain with the ligand, which fills a hydrophobic pocket between strand β2 and helix α2 and is capped by the loop β1–β2. The last three residues (P₀, P₋₁ and P₋₂) of the peptide form an antiparallel β-sheet with the β2 strand of PDZ2 (Fig.1b). (P₀ denotes the C terminal residue of the bound peptide and P_−n denotes the nth amino acid up stream from it). In particular, loop β1–β2 contains a conservative glycine-rich motif (Leu18, Gly19 and Ile20), whose mainchain form hydrogen bonds with the carboxylate of the P₀ residue. The sidechains of residue P₀ and P₋₂ are also buried inside the binding groove ¹⁵. Variations in the size and geometry of the hydrophobic binding pockets results in different binding preferences among PDZ domains ¹. However, the hydrophobic recognition is usually not very specific, and helps to explain why some PDZ domains can bind peptides with different sequences¹.

Figure 1.

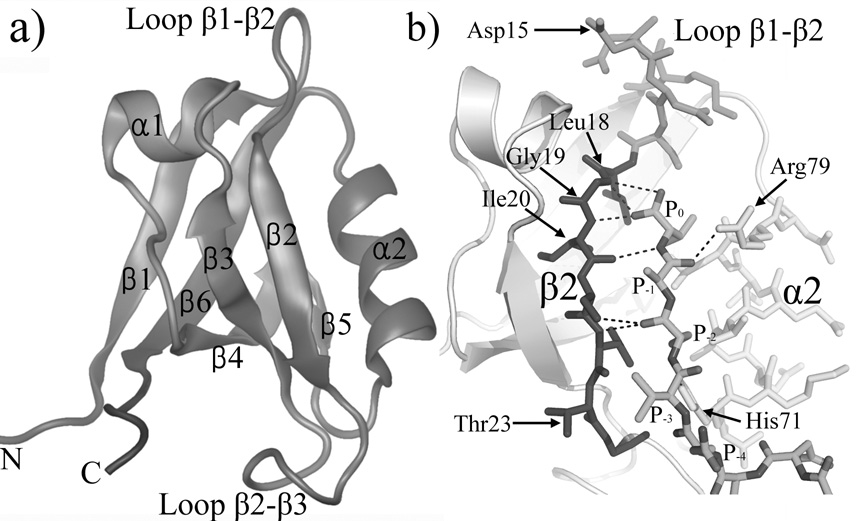
The structure of PDZ2 domain. (a) The overall structure of PDZ2 domain (PDB ID 3PDZ). Image was made with VMD ³⁸. (b) An enlarged view of the ligand peptide and the binding pocket (PDB ID 1D5G). Helix α2, strand β2 and loop β1–β2 are colored yellow, blue and green, respectively. Hydrogen bonds between ligand peptide and PDZ2 domain are shown as dash lines. Images was made by Pymol ³⁹.

The overall structure of the PDZ2 domains studied here does not undergo large changes on binding a peptide ligand; the RMSD between backbone atoms of ligand bound and ligand free structures is about 2.0 Å ^14,15 (The four flexible N and C terminals amino acids are not included in this value). The groove between strand β2 and helix α2 opens slightly to accommodate the binding of the peptide. Specifically, the amplitude of the opening gradually increases away from the P⁰ binding site, e.g. the Cα distances between residue pairs 19/79 and 23/71 increase about 1Å and 4Å, respectively. Also the β1–β2 loop (residue 13–17) moves away from the binding pocket upon peptide binding; e.g. the displacement of residue 15 is about 5Å.

In addition to the fact that PDZ domains recognize and bind the C terminus of target proteins, it has been suggested that they propagate a signal indicatve of binding (i.e. that the target protein is bound) toward other parts of the molecular complex not directly connected to the binding pocket ^17–19. A specific example is that the binding of the guanylate kinase domain with PDZ containing microtubule-associated protein 1A has been shown to be enhanced by a variety of PDZ ligands ²⁰. This type of “allosteric” effect is of intrinsic interest, but it also of more general biological importance. An understanding of the mechanism of intra-molecular signal transduction could be useful for its modification in biologically significant processes. Several analyses concerned with the dynamic response of different PDZ domains have been published; they include the multiple sequence alignment based statistical analysis ¹⁸ which served to stimulated the present study, NMR measurements of the effect of ligands ^12,17,21, a normal mode analysis ²², an anisotropic thermal diffusion calculation at a low temperature ²³ and a pump-probe molecular dynamics study ²⁴. We comment on these alternative approaches in the discussion section.

The objective of the present study is to find communication pathways between the binding region and distant parts of the PDZ molecule that are likely be involved in interaction with the other part of the complex and binding of other partners. Molecular dynamics (MD) simulations of the apo structure PDZ2 domain (96 amino acids) of human phosphatase hPTP1E ¹⁴ and of its ligand bound form (with a 15 amino acid peptide) ¹⁵ were performed with on the available NMR structures. This PDZ2 domain was chosen for study, not only because both the ligand free (PDB ID 3PDZ) ¹⁴ and ligand bound (PDB ID 1D5G) ¹⁵ structures were available when this work was initiated, but also because their existed data for the chemical shift changes upon ligand binding for a close homologue¹². The latter, a mouse PDZ2 domain (PDB ID 1V56) has 95% sequence identity with the human PDZ2 domain that we studied; from the structure, released after much of our work was completed, the RMSD between the two is 2.7Å. The MD simulations were used to calculate the correlations between residue-residue interaction pairs, based on a recently developed method that has been applied to determine the signaling path in rhodopsin ²⁵. This analysis revealed two communication pathways (one novel, the other suggested in ref 17), which originate from the ligand binding pocket and extend to the opposite surface of PDZ2 domain (i.e. the N terminal part of helix α1 and the N terminal of strand β1, see Fig. 1a). Since these pathways are found in the equilibrium simulations of the PDZ2 domain without ligand, the results indicate that pathways are “imprinted” in the structure by evolution. Further, since the coupling is altered by ligand binding, it could serve to signal this fact to other binding partners; i.e., after the ligand binds, the signal could be efficiently propagated toward the target regions through the already existing coupling network.

Results

The interaction correlation method ²⁵ was used to identify the energetically coupled regions and pathways of the PDZ2 domain ^14,15. The method is based on a calculation of the energetic correlations between all interacting residue-residue pairs in an ensemble of protein conformers generated by nanosecond molecular dynamics (MD) simulations. The PDZ2 domain with and without a ligand was studied. A detailed description of the methods used and the MD simulations performed is given in the Methods section.

Dynamically coupled regions identified by interaction correlation

To identify conformational couplings within the PDZ2 domain ^14,15, the equal time correlation, C_i,j|k,l, of the nonbonded interaction energies between all residue pairs were calculated (see Method). To simplify the analysis and remove the thermal noise, two residues are included only if the average interaction energy is larger than 1 kcal/mol in magnitude. Also, neighboring residues in the sequence that are covalently bonded were not included. Based on 10 trajectories with a total simulation length of more than 50ns (see Methods), a 261 × 261 symmetric matrix was generated corresponding to 261 nonredundant residue-residue interactions with absolute values of the interaction energies larger than 1 kcal/mol. Most interaction pairs (there are total of 68260) have no or very weak correlation, as the average correlation value is 0.087 with a standard deviation of 0.084. To avoid the background noise (see Methods), we constructed a condensed version of the interaction correlation matrix with a correlation value cutoff, C_cutoff , in which all correlations less than C_cutoff and larger than − C_cutoff were set to zero, and columns/rows containing all zero elements were not included; In the study of PDZ2 domain, the C_cutoff was set to 0.4 (i.e. only values less that −0.4 and greater than +0.4 were included); the resulting interaction energy correlation matrix dimensions are 136 × 136 (Fig.2a). The index of the residue interaction is shown in Supplemental Table 1. Since each row or column in this matrix corresponds to an individual residue-residue interaction, it is difficult to map the results on the three-dimensional structure and compare them with residue-based experimental data, such as those from mutagenesis and NMR studies. Consequently, the condensed interaction correlation matrix was constructed (see Eq. 4) to obtain the residue correlation matrix (Fig.2b); in this matrix each column and row represents a residue of the protein.

Figure 2.

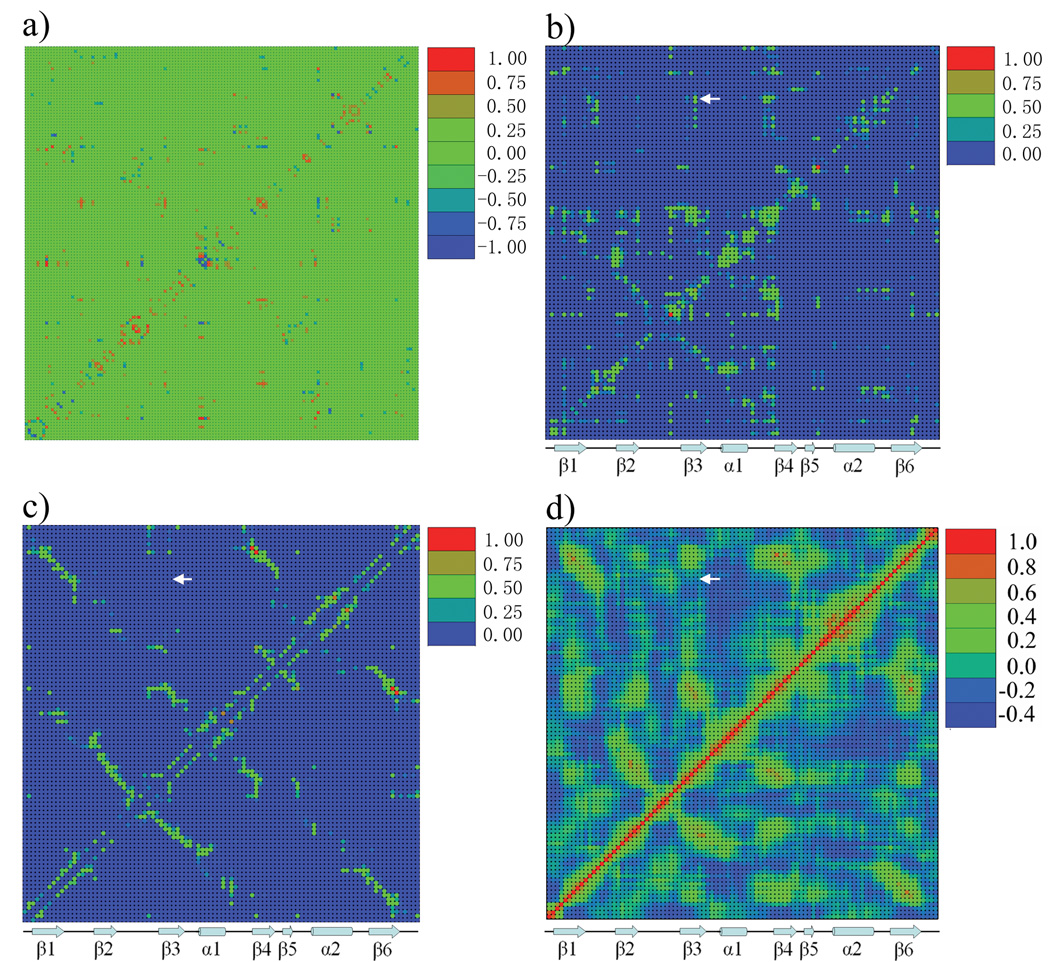
Matrix representation of statistical results for the ligand free PDZ2 domain. a) The interaction correlation matrix. The dimension of this symmetric matrix is 136 × 136, and the range of interaction correlation value is from −0.93 to 0.92. Each column or row represents a specific residue-residue nonbonded interaction. The color scale is from blue (−1) to red (1), and green indicates zero correlation after C_cutoff has been applied (larger than −0.4 and smaller than 0.4). b) The residue correlation matrix. The dimension of this symmetric matrix is 96 × 96, corresponding the number of residues in the protein. Each column or row represents a specific residue of PDZ2 domain. The maximum correlation value was scaled to 1. The color scale is from 0 (blue) to 1 (red). c) The dynamic contact map. This matrix has the same dimension and color scheme as b). Each spot in this matrix indicates the absolute value of average nonbonded interaction energy between two residues, scaled so that the maximum value in this matrix is equal to 1. d) Residue based displacement correlation calculated from quasi-harmonic analysis based on MD trajectories with total length of 50ns (see Text & Methods).

Ligand free state

The residue correlation matrix of the PDZ2 domain in ligand free state shows the magnitude of the average coupling between residue pairs obtained from the MD simulations, which were performed at thermal equilibrium. As shown in the residue-residue absolute interaction energy matrix (Fig.2c) and the displacement correlation matrix (Fig.2d), neighboring residues in the PDZ2 domain secondary structure have strong average interaction energies and their displacement correlations are also relatively high. Overall, residues with strong interactions (Fig.2b) also show strong displacement correlations (Fig.2c,d), because the magnitude of interaction is dependent on the distance. Of primary interest, therefore, are the residue couplings present in the residue correlation matrix (Fig.2b) that are absent in the average interaction energy matrix and in the displacement correlation matrix. For example, residue 37 has strong coupling with residue 82 and 83 in Fig.2b (indicated by white arrow), while there is no corresponding signal in Fig.2c and Fig.2d. These excess correlations correspond to the coupling between different regions within the PDZ2 domain. To relate the results to the possibility of signaling that a ligand is bound, we calculated the cumulative interaction correlation (binding pocket correlation factor, see Methods) of each residue with the ligand binding pocket (residue 16–23 and 70–79), still in the absence of ligand. Based on the geometric distribution of residues with a strong binding pocket correlation factor (Fig.4a), two continuous pathways are identified extending from the binding pocket to the opposite side of the PDZ2 domain. Specifically, pathway I starts at the P₀ binding site on strand β2 and extends along the long axis of helix α1 and pathway II starts at the P₋₂/P₋₃ binding sites on strand β2 and goes perpendicularly across strands β2, β3, β4, β6 and β1. Interestingly, some of residues in pathway I are coupled with residues in pathway II (Fig.2b). To clearly identify the residue subgroups, a clustered correlation matrix (Fig.3a) was generated by a Markov cluster (MCL) algorithm ²⁶ (see Methods) from the residue correlation matrix (Fig.2b). The indexes of rows/columns are rearranged such that residues with more similar coupling patterns have a shorter distance in their indexes. Five major residue clusters with different coupling patterns were identified (Fig.3a). Cluster 1 contains 49 residues and is spread isotropically over the PDZ2 structure (Supplemental Figure 1a). The coupling among these residues is likely to be due to their contacts and the thermal motions of the protein scaffold. Cluster 5 includes 6 residues geometrically clustered on the protein surface opposite to the ligand binding pocket (Supplemental Figure 1b). Cluster 2 (purple, residue 12–16, 68,69,78,81 82 and 89) is mostly localized at the ligand binding pocket, including loop β1–β2 and N and C terminal adjacent loops of helix α2(Fig.3b). Cluster 3 (blue) includes helix α1 (residue 41 and 43–48) and two nearby residues (residue 17 and 18) on loop β1–β2 (Fig 3b). The distribution of cluster 4 shows an approximately linear pattern (it is perpendicular to the central β sheet), which extends from helix α2 (residue 74), through strand β5 (residue 66 and 67), strand β3 (residue 34), strand β4 (residue 58 and 59), strand β6 (residue 90) and N terminal loop (residue 3) to the side of PDZ2 domain opposite to the ligand binding pocket (Fig.3b).

Figure 4.

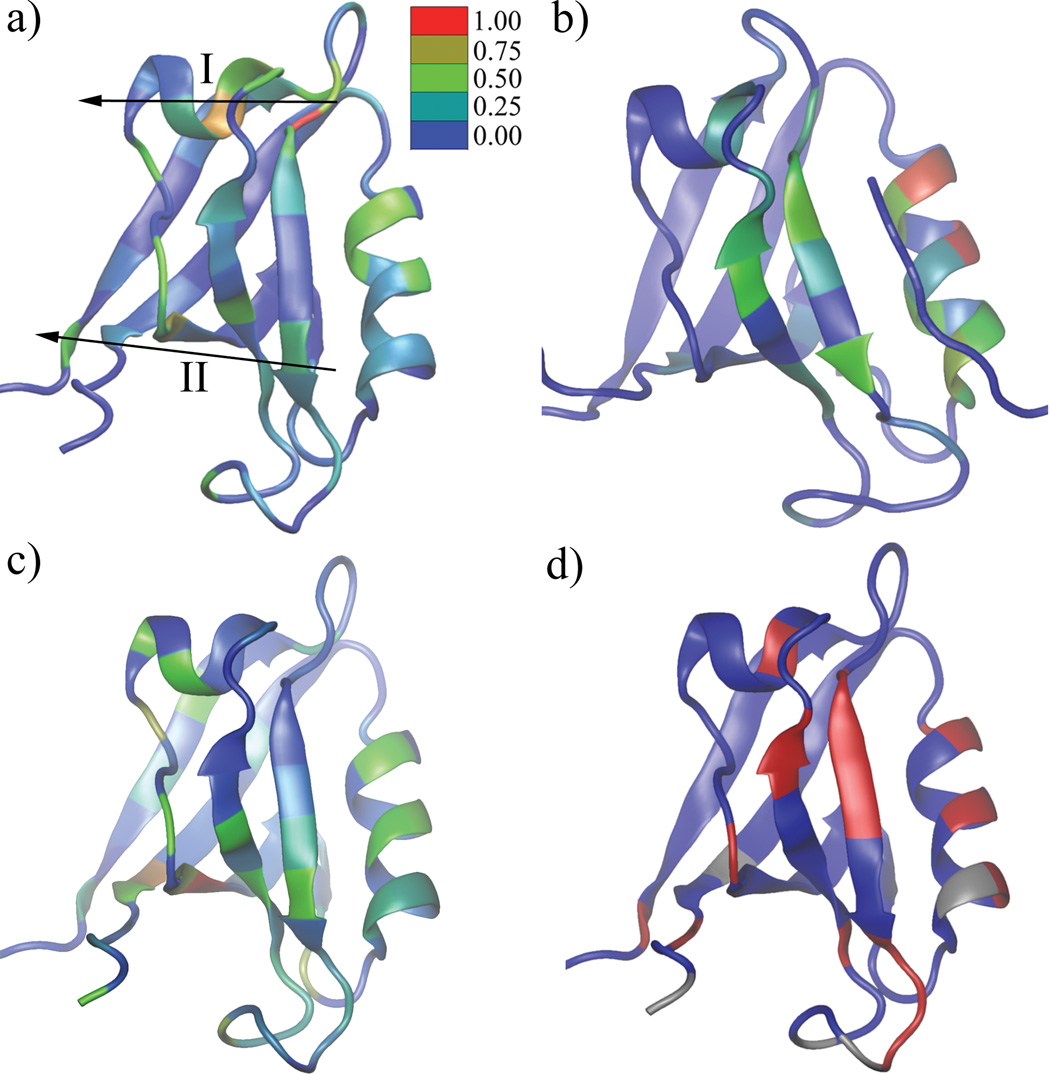
Comparison of interaction correlation results with NMR results and cumulative interaction energy difference on binding. a) The residue correlation factor with the binding pocket (see Methods) calculated from the PDZ2 ligand free dynamics. Two proposed signal transduction pathways (I and II) are labeled. b) The residue correlation factor with the binding pocket calculate from PDZ2 ligand bound dynamics. c) Residues are colored by their cumulative interaction energy difference between the ligand free and ligand bound states (see Methods). d) The backbone hydrogen and nitrogen chemical shift of PDZ2 domain upon titration of human Fas receptor ¹². The blue-to-red gradient represents smaller to larger changes in chemical shift. Grey coloring indicates no data was available. In a), b) and d), the data set was scaled so that the maximum value is equal to 1 and the same color scale is applied. The residue color indicates the coupling strength from blue (none) to red (strongest). All images are made by VMD ³⁸.

Figure 3.

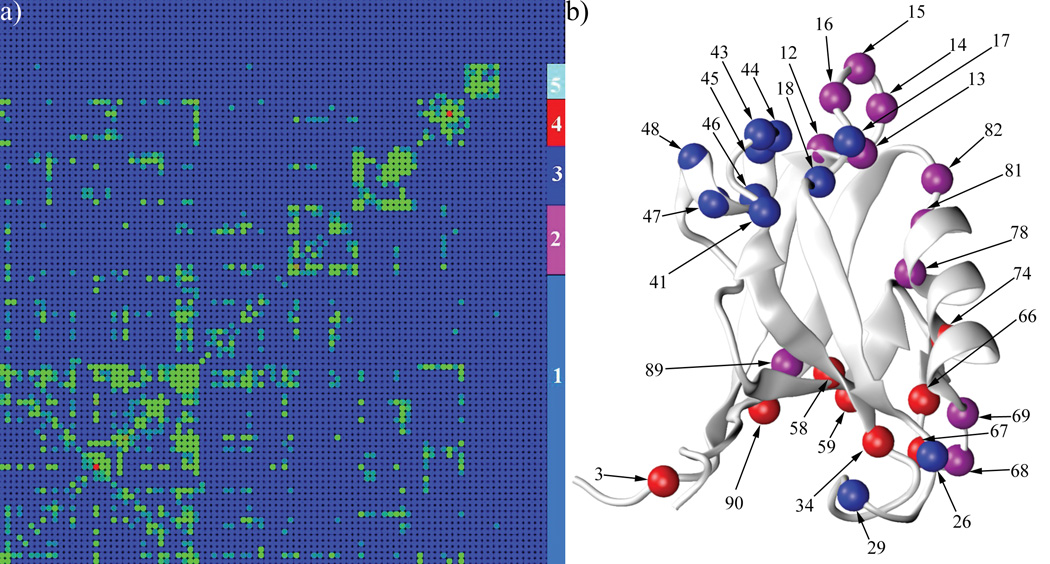
Markov cluster algorithm results. a) The clustered residue correlation matrix (see Methods). This matrix is the same as the one shown in Figure 2b, except the column/row indexes are rearranged according to the clustering results. Five clusters were identified and were colored cyan (1), purple (2), blue (3) red (4) and light blue (5) in the right 4 columns. b) Residues in clusters 2, 3 and 4 are displayed as spheres on the PDZ2 domain structure. The colors of the residues are the same as those in a). Images were made by VMD ³⁸.

The existence of cluster 2 indicates that residues in the binding pocket are in allosterically coupled (i.e. residue 15 and 68) even before the ligand binding, which makes the binding a cooperative process. Residues within cluster 3 and 4 are located in the geometrically identified pathway I and II (Fig.4a), respectively. This analysis indicates that the PDZ2 domain has two internal signal transduction pathways, which not only have physical connections in the protein structure, but also are energetically coupled. In other words, after the ligand binds to the pocket between helix α2 and strand β2, the signal of binding can propagate effectively toward the target regions (i.e. the C terminal part on helix α1 and the N terminal part on strand β1)⁸ because of the preexistence of this long-range coupling.

Ligand bound state

The structure of PDZ2 domain complexed with its ligand is very similar to its ligand-free form (RMSD 1.2Å)¹⁷, so that a direct comparison can be made of the dynamic average interaction results. The ligand-bound state interaction correlation of the PDZ2 domain was characterized by the same procedure as used for the ligand free state; 10 MD trajectories with a total length of 56ns were used (see Methods). There are 124 residue-residue interaction pairs with average interaction energies larger than 1 kcal/mol, and the average correlation for 124 × 124 interaction correlation matrix is 0.084 with a standard deviation of 0.077. The residue correlation matrix is shown in Supplemental Fig.2 and the binding pocket correlation factor is illustrated on Fig.4b. As expected the coupling among residues in the binding pocket becomes stronger (e.g., residues on helix α2) in the presence of ligand. The overall long-distance coupling to the binding pocket, however, becomes weaker than that in the free PDZ2 domain, although residues 40, 44, 45 and 46 on pathway I and residues 35, 36 and 90 on pathway II show similar coupling patterns (Compare Fig.4a and 4b). When the ligand is in the binding pocket between helix α2 and sheet β2, it decreases the flexibility of the system and the signal that a ligand is bound appears as a reduction in the remote coupling.

We used the cumulative interaction energy difference (See Methods) to quantify how each residue is different in it interaction in the ligand-free and ligand-bound states. The results are shown in Fig4c, in which the difference for each residue is mapped to the PDZ2 domain structure. Most residues in the binding pocket are significantly perturbed due the presence of peptide as, expected. Importantly, residues on helix α1 (pathway I) and the continuous residue cluster crossing strands β2, β3, β4, β6 and β1 (pathway II) show different dynamic behavior between two states. The results support the existence of two intra-molecule signal transduction pathways, which were identified without reference to the PDZ2 domain structure or dynamics in the ligand bound form.

Comparison with NMR experiments

A comparison with NMR studies of Walma and colleagues ¹² is of interest. They studied the changes of a mouse PDZ2 domain (95% sequence identity with the human PDZ2 used in the current analysis) backbone hydrogen and nitrogen chemical shifts upon binding of a 12-residue peptide. The sequence of this peptide corresponds to the C terminal end of the human Fas receptor (Fig.4d). The observed changes were interpreted as an alteration of the chemical environment of a given residue, although no quantitative analysis of the origin of the chemical shifts was made. To compare our computational results to the NMR experiments, the binding pocket correlation factor (CF) was used (see Methods, Eq 5). The correlation factor of residue i is defined as the sum of the coupling magnitudes between residue i and all residues in the binding pocket. This parameter provides a measure of the coupling of each residue to the ligand binding site. Thus, the amplitude of the CF_i parameter for a residue is expected to be approximately proportional to the perturbation of a residue in response to ligand binding. Fig.4a shows the values of the CF_i on the PDZ2 structure. Large signals are observed for residues in or near the binding pocket (helix α2 and strand β2) and the correspondence between the NMR shifts (Fig.4d) and the calculated correlation (Fig.4a) is very good. For regions outside the binding pocket, the correlation is also quite good; i.e., relatively strong signals were observed in the N terminal region of helix α1, the N terminal region of strand β1 and the C terminal region of strand β6 in both the NMR and the simulations. However, there are some differences; a correlation was found between the loop region near the C terminus of helix α1 and the binding pocket, but no chemical shift changes were seen. In another study ²¹ of the same PDZ domain, a series of mutations was made within the hydrophobic core to probe their effect on ligand binding. Among them, eleven mutations showed different ligand association rates, dissociation rates or both. The results are consistent with the present study, because seven of the eleven mutated positions are included in or are very close to (within 2 amino acids in sequence) pathway I or II (Fig. 3b and Fig. 4a). This agreement indicates that the interaction correlation analysis provides a more complete description of the allosteric coupling pathways, since it determines the correlation between all possible residue pairs rather than only the selected mutation sites.

It is noteworthy that in both the computational study and the NMR experiment ^12,21, little change was observed on the side of PDZ2 away from the ligand binding pocket (i.e., the middle portions of strand β1, β4 and β6), suggesting that the signal is rather well defined and does not spread isotropically.

Concluding Discussion

A primary function of PDZ domain is to bring together different proteins to form multi-protein complexes, but it has been suggested ²⁰ that they also play a signal transduction (allosteric) role.

The processes of signal transduction often involve significant conformational changes in protein involved. Normal mode analysis ^27,28 and principal component analysis (PCA) ²⁹ are valuable in identifying the functionally related motions by indicating the deformations that require little energy ^30,31, particularly, those involving the relative motion of “rigid” domains with hinges ^30,31. In cases where no significant conformational changes occurs (i.e. activation of G protein coupled receptors and ligand binding to PDZ domains, NMA and PCA are less useful. Although the PDZ2 domain structures in the ligand free and ligand bound state are very similar, a recent study ²² has applied a normal mode analysis to obtain information about the changes in dynamics measured by NMR. In the study, a mode (9^th) obtained from an elastic network model of the PDZ2 domain was selected as being the one with the largest overlap with the (small) conformational change. It was pointed out that the residues with the largest changes in dynamics from NMR are in regions where the fluctuation amplitude was large for that particular mode. This result is interesting but its meaning is not clear since the actual fluctuations predicted by a normal mode model correspond to the sum of the contributions over all the modes, which are effectively the calculated B factors (see their Fig. 7). Also, the identified residues were all in or near the binding pocket.

Two interesting non-equilibrium perturbation MD methods, referred as anisotropic thermal diffusion ²³ and Pump-Probe MD ²⁴ have been used to study the signaling pathway of PDZ domains. In first study, the protein was simulated at a very low temperature (10K) and the signal initiation, ligand binding, was introduced by increasing the kinetic energy of a specific residue in the ligand binding pocket to that corresponding to 300K; the low temperature was used to reduce the realistic thermal noise that would be present if the protein were simulated at 300K so as to make the effect of the perturbation more obvious. In the second study, the protein was simulated at 300K and ligand binding was mimicked by applying strong oscillating forces to selected atoms or residues; the propagation of the perturbation was described in terms of increased RMS fluctuations to other residues. Both studies used the PDZ3 domain and perturbed His76 in the binding pocket, as in the study by Lockless et. al. ¹⁸. They identified a coupling pathway similar to pathway I, but did not find pathway II of our work. We suggest several possible reasons for the difference. First and most likely is that fact that both methods simulated the ligand binding by perturbing a single residue as already mentioned, while the ligand binding process involves all residues of the binding pocket. Second, the perturbations used are much larger than the realistic effect of binding, so that the dynamic response of the protein may not follow the normal pathway. In the present paper, the analysis is based on simulations under thermal equilibrium conditions and the problems cited above did not exist. In addition, we do not exclude the possibility that pathway II is specific to PDZ2 domain, so studies on PDZ3 domain or the PDZ family do not find such a pathway.

The statistical analysis of multiple sequence alignment (MSA) ¹⁸ was used by Lockless et. al. to identify coupling pathways based on residue co-evolution. They identified a signal transduction pathway in their corporative study of all PDZ domains that corresponds to pathway I of present study. Although the statistically analysis has a conceptual similarity to the present approach, the two methods make use of different information sources and so are complementary. The data set for the present method is an ensemble of conformers generated by MD simulations for a single PDZ domain, while that for the MSA method is a series of homologous sequences. The partial agreement of the signal transduction pathways found by the two methods supports the validity of both results. That only pathway I was found, as by the two MD methods mentioned above is due to the fact that His76 alone was used as the perturbation source, rather than the set of binding pocket residues, as in our case. Moreover, application of the two approaches to the same system is important because both methods have limitations. The information extracted from MSA related study represents characteristics of a protein family. Although the sequences are homologous, members of the family have somewhat different structures and probably functions. Consequently, assuming that the statistical results describe the behavior of individual proteins is likely to include significant noise. An important aspect of the interaction energy correlation analysis is that it identifies the energetic source of the coupling but is computationally much more expensive than the MSA method.

We hope that the present analysis and related studies will serve as a stimulus for experimental research to find specific cases where PDZ domains have a signaling function.

Methods

Molecular dynamics simulation

The constant pressure and constant temperature (CPT) molecular dynamics simulation ^32–34 was performed on both the apo and ligand bound PDZ2 domain. The initial coordinates were taken from the Protein Data Bank, PDB ID 3PDZ (ligand free)¹⁴ and 1D5G (ligand bound)¹⁵. Both systems were simulated with periodic boundary in a rectangular water boxes with dimension of 56 × 52 × 44 Å3 for 3PDZ and 64 × 54 × 45 Å3 for 1D5G. In both systems, sodium and chlorine ions were added to the physiological concentration (0.15M). The system of ligand free PDZ2 domain has 13498 atoms including 6 Na⁺, 5Cl⁻ and 4027 water molecules and the system of ligand bound PDZ2 domain contains 16584 atoms with 13 Na⁺, 7Cl⁻ and 4979 water molecules. The CHARMM package ³⁵ was used for the simulations. The all atom potential function Charmm27 ³⁶ was used for both proteins and modified TIP3 water model ³⁷ was used for the water molecules. After 100ps equilibration, 10 independent simulations with were performed on both systems with an integration step size of 2 fs and length of 5ns. The temperature was kept on 298 K and pressure was kept on 1 atmosphere pressure. The coordinates from the molecular dynamics trajectories were save every 0.2 ps.

Calculation of statistical parameters

The analysis of the dynamics trajectories were started by investigating residue-residue interaction energy (only amino acids have been included). For each recorded frame, the nonbonded interaction energy E_i,j between two residues i and j is defined as

$$E_{i,j}=E_{i,j}^{elec}+E_{i,j}^{vdw}\left(\left|i-j\right|>1\right)$$ (1)

,where $E_{i,j}^{elec}$ and $E_{i,j}^{vdw}$ is the electrostatic and van der Waals interaction energy between residue i and j. The interaction energies between any amino acid residue pairs neighboring in sequence were not included, because the nonbond interaction energy between the covalently bonded residue pair is not sensitive to the conformational states of the protein. The average interaction energy between residue i and residue j is defined as:

$${\overline{E}}_{i,j}=\frac{1}{f}{\displaystyle \sum _{t=1}^f{E}_{i,j}^t}\left(\left|i-j\right|>1\right)$$ (2)

, where $E_{i,j}^t$ is the interaction energy between residue i and j in frame t and f is the number or coordinates sets involved in this analysis (Fig.3c). The correlation between two sets of residue-residue interactions i,j and k,l, C_i,j|k,l, is defined as:

$$C_{i,j|k,l}=\frac{{\displaystyle \sum _{t=\mathit{1}}^f(E_{i,j}^t-\overline{E_{i,j}})(E_{k,l}^t-\overline{E_{k,l}})}}{{\displaystyle \sum _{t=\mathit{1}}^f\sqrt{{(E_{i,j}^t-\overline{E_{i,j}})}^2{(E_{k,l}^t-\overline{E_{k,l}})}^2}}}$$ (3)

A particular interaction would be involved in this correlation matrix, only if the absolute value of its average interaction energy is greater than 1 kcal/mol.

Matrix assembly and clustering

From Eq (3), the interaction energy correlation matrix has columns or rows corresponding to all none neighboring residue-residue interactions (Fig.2a). The matrix size is subjected to the correlation cutoff (C_cutoff), although the original distribution is not. In the current study of PDZ2 domain, the C_cutoff was set to 0.4, which generate a 136 × 136 interaction correlation matrix (Fig.2a). The residue correlation matrix is a projection of the interaction energy correlation matrix on the residue space. The correlation between residue I and J, RC_I,J is defined as:

$$\mathit{R}{\mathit{C}}_{i,j}={\displaystyle \mathbf{\sum }_{m=\mathit{1}}^N{\displaystyle \mathbf{\sum }_{n=\mathit{1}}^N\left|{\mathit{C}}_{m|n}\times {\mathit{\delta }}_{m|n}^{i,j}\right|}}$$ (4)

, where the dimension of the interaction correlation matrix is N, ${\mathit{\delta }}_{m|n}^{i,j}$ is equal to 1 only if residue i and j are involved in interaction m and n, or n and m, respectively; otherwise, ${\mathit{\delta }}_{m|n}^{i,j}$is set to zero. For example, if the correlation between interaction pairs 10,25|17,30 is 0.35 and 10,14|17,35 is 0.45, the residue correlation between 10 and 17 would be 0.80 based on these two interaction energy correlations. The dimension of this matrix is equal to number of residues in PDZ2 domain (96).

The residue correlation matrix was clustered by an unsupervised approach, markov cluster algorithm ²⁶. In current implementation, all parameters were used as their default values. The essential idea of this algorithm is to simulate flow within a graph, which can be derived from our residue correlation matrix. By enhancing flow where the current is strong and decreasing flow where the current is weak, the current across borders between different groups will wither away and the clusters in the graph will be revealed.

Calculation of binding pocket correlation factor

Based on the MD simulation of PDZ2 domain bound with the ligand, residues were categorized as in binding pocket if the absolute value of its average interaction energy with the ligand was larger than 1 kcal/mol. The binding pocket related residue correlation matrix was constructed by setting all columns/rows of residue correlation matrix to zero, except for the ones that correspond to residues (residue 16–23 and 70–79) in the binding pocket. The correlation of residue i to the binding pocket is defined as:

$${\mathit{\text{CF}}}_i={\displaystyle \mathbf{\sum }_{j=\mathit{1}}^{NRES}\mathit{R}{\mathit{C}}_{i,j}^{bp}}$$ (5)

where CF_i is the correlation factor of residue i refer to the binding pocket, $R{C}_{i,j}^{bp}$ is the ith row and jth column of the binding pocket related residue correlation matrix and NRES is the number of residue (96) in PDZ2 domain.

Residue deviation between ligand unbound and bound states

The difference between the ligand unbound and bound states is calculated by the cumulative difference in interaction energy of each residue. Based on the average interaction energy matrixes, the interaction energy deviation of residue i, ΔE_i is defined as:

$$\mathrm{\Delta }{\mathit{E}}_i={\displaystyle \mathit{\sum }_{j=\mathbf{1}}^{NRES}\left|\overline{{\mathit{E}}_{i,j}^{apo}}-\overline{{\mathit{E}}_{i,j}^{pept}}\right|}$$ (6)

, where NRES is number of residues (96) in the PDZ2 domain $\overline{E_{i,j}^{apo}}$ and $\overline{E_{i,j}^{pept}}$ are the average interaction energy between residue i and j in the presence and absence of the ligand, respectively.