Minimum mass vascular networks in multifunctional materials

Abstract

A biomimetic analysis is presented in which an expression for the optimum vessel diameter for the design of minimum mass branching or vascular networks in engineering applications is derived. Agreement with constructal theory is shown. A simple design case is illustrated and application to more complex cases with branching networks of several generations discussed. The analysis is also extended into the turbulent flow regime, giving an optimization tool with considerable utility in the design of fluid distribution systems. The distribution of vessel lengths in different generations was also found to be a useful design variable. Integrating a network into a structure is also discussed. Where it is necessary to adopt a non-optimum vessel diameter for structural integration, it has been shown that small deviations from the minimum mass optimum can be tolerated, but large variations could be expected to produce a punitive and rapidly increasing mass penalty.

1. Introduction

Multifunctional engineering materials can be defined as imparting the ability for the material to perform some useful secondary function as well as achieving the primary, usually structural, requirement. Several examples of multifunctional materials have been reported, including self-heating (Chung 2004; Santos et al. 2004), electromagnetic functionality (Nemat-Nasser et al. 2002; Plaisted et al. 2003) and self-healing (e.g. Dry 1996; Bleay et al. 2001; White et al. 2001; Trask & Bond 2006). Both animals and plants use a fluid transport system to perform several roles. Containing a network of vessels within a structural material is a biomimetic way of adding functionality to a material. Such vascular-scale fluid flow has potential applications in multifunctional materials for self-healing, thermal control and adaptive stiffness structures. Examples of these applications are discussed below.

Self-healing has received considerable recent attention in the literature, as a means to mitigate subcritical damage in composite materials, such as fatigue or impact. Liquid-based self-healing approaches involve fluid release from damaged microcapsules (Kessler & White 2001; White et al. 2001; Brown et al. 2002; Kessler et al. 2002, 2003) or hollow glass fibres (Bleay et al. 2001; Pang & Bond 2005; Trask & Bond 2006; Trask et al. 2007b). In liquid-phase self-healing, the storage and delivery of repair agent could disrupt the laminate structure and may incur a mass penalty. Microcapsules and hollow glass fibres couple both delivery and storage functions, an elegantly simple approach but one in which there is a risk that neither is performed optimally. Disruption to the structural role of the material tends to drive the selection of smaller vessels, limiting the available fluid volume. A recent review of biomimetic self-healing (Trask et al. 2007a) has identified that a branched or vascular network approach would allow the contents of a remote reservoir to be delivered into a zone of damage anywhere in a material. Philen et al. (2006) have analysed the concept of an adaptive stiffness structure consisting of flexible matrix composite tubes with different fibre orientations in which the internal pressure can be adjusted via valves to change the overall stiffness by a factor of 3000. In theory, a higher base pressure supplied through a network of channels could expand the available stiffness ratios. There is also interest in microfluidic devices for applications such as enhanced mixing (Therriault et al. 2003, 2005) and ‘lab-on-a-chip’ systems, where fluid handling systems are miniaturized for chemical and biomedical applications (Lim et al. 2003; Emerson et al. 2006). Any high-performance engineering application of a branched network for fluid flow will carry a mass implication, and there is a very real need to optimize any such networks for minimum mass.

The driver for the current work is to optimize the diameter of vessels in an engineering vascular network, especially where the network bifurcates, since it is this feature that allows a large area to be supplied from a single reservoir or pump. A biomimetic approach is adopted whereby the branching of a natural vascular network is investigated to apply a principle from anatomy or biology to the design of vascular networks in high-performance engineering applications. The paper begins with a review of vascular flow in natural and engineering contexts. The literature discussing the applications of Murray's law, a biological optimization principle, to engineering applications is reviewed and found to be limited in scope. The inclusion of a branching network of fluid vessels within a structural material has applications in self-healing, thermal control and adaptive structures but carries an implicit mass penalty. Mass is the prime driver in the structural design of many high-performance engineering systems including multifunctional structures, and using the basic assumptions of Murray's law to develop an engineering method of determining optimum diameters for a minimum mass vasculature has not been considered in the literature. In a structural context, it is also important to consider whether the vascular network could degrade the primary mechanical properties of the material. Finally, a study is undertaken to examine the compromise in structural performance (mass penalty) by varying the structure or vessel diameter from an optimum design. This is linked back to the conclusions of several studies on Murray's law in plants and animals.

2. Review of vascular flow

2.1 Optimum vascular networks in nature

Murray (1926) described a theoretical analysis of the distribution of blood vessel sizes in humans. This work centred on the premise that the human vascular system would have evolved to minimize the power required to maintain and circulate blood. He argued that there were two main components of the power loss: the power required to overcome the friction losses in the vessels and pump the fluid; and the metabolic cost associated with maintaining the blood, a living fluid. The former was modelled using Poiseuille's law, which is stated in appendix A and was reviewed by Sutera & Skalak (1993). The latter, metabolic power, was assumed to be directly proportional to blood volume. Simple calculus was used to demonstrate that a minimum power is required at some given blood vessel size. Qualitatively, smaller blood vessels would require a larger pumping power due to friction losses and larger blood vessels would increase the volume of blood to the point where the metabolic power, required to maintain the blood, competes with the power required for flow. The relationship known as Murray's law followed from this analysis: it was shown that where vessels subdivide, the sum of the cubes of the daughter vessel radii (r_d1 and r_d2) should equal the cube of the parent vessel radius r_p for minimum power

$$r_p^3=r_{d1}^3+r_{d2}^3.$$ (2.1)

Sherman (1981) has reviewed Murray's derivations and physiological studies on various mammals. This work has brought out some subtle points in Murray's work. Murray's law was derived assuming that the maintenance ‘cost’ was a function of the contained volume of the vessel wall, rather than the included volume and the vessel itself. In practice, there will also be a maintenance cost associated with the wall tissue and Sherman showed that Murray's law can also hold for this case if the vessel wall thickness is proportional to internal radius. It was assumed that the vessel wall has the same maintenance cost per unit volume as the included fluid. Physiological studies showed that barring some anomalies (that are explicable in relation to sample preparation or the difference between arterial and venous flow), selected mammalian vascular specimens revealed reasonable agreement with equation (2.1). Later work reported by Sherman & Popel (1989) and originally derived by Milsum & Roberge (1973) showed that the predicted total power demand is relatively insensitive to radius close to the Murray optimum; a 10% change in radius from the optimum was found to increase the power requirement by only 3–5%. Bejan (2000, 2005; Bejan et al. 2000) has used constructal theory—the concept that the survival of a flow network relies on continued evolution to minimize flow resistance—to theoretically investigate fluid flow in networks by minimizing the hydraulic resistance with the network volume constrained. Agreement with Murray's law was shown. This conclusion was independent of network geometry, which verifies the practical utility of Murray's law.

There is a considerable mass of literature comparing Murray's law to physiological studies in animals. Taber and colleagues (Taber et al. 2001) provide a wide selection of references in their paper showing good agreement in the chick embryo. McCulloh has published several papers (McCulloh et al. 2003, 2004; McCulloh & Sperry 2005) discussing the applicability of Murray's law in plants. Broadly, these studies show good agreement except where the vascular conduits provide a direct structural role. In certain cases, the works support Popel & Johnson's (2005) argument that since the penalty of deviating from Murray's law may be small, structural constraints are likely to influence the evolution of these features significantly.

2.2 Vascular networks in engineered structures

Lim et al. (2003) have developed ‘multi-width multi-depth’ miniature fluid channel networks in silicon wafers that effectively follow Murray's law, albeit with a non-circular channel cross-section. Four-generation branching networks were compared by measuring the velocity of fluorescent microbeads suspended in the flowing fluid. One network was multi-width only and does not obey Murray's law, while the other is depth tapered to follow Murray's law. The velocity changes were found to be smaller in the latter network and it is stated that the resistance should be significantly reduced, although measurements are not reported. It is stated that the use of Murray's law to design a vascular network should result in a significantly reduced hydraulic resistance. This is not strictly accurate; Murray's law geometry was derived to obtain minimum system-level power demand and if lowest resistance is required then the largest vessel diameter should be selected at all points.

Emerson et al. (2006) have performed analytical and numerical simulations of microvascular networks, with particular emphasis on the microvascular lab-on-a-chip systems such as those discussed previously (Lim et al. 2003). Analytical expressions for networks of square or trapezoidal cross-section are developed and the total resistance of the flow is considered in an idealized system where the length of each segment scales linearly with the diameter. The use of non-circular cross-sections required a correction based on the equivalent hydraulic diameter. The analysis uses Poiseuille's law (see appendix A) expressed using a resistance analogous to the well-known Ohm's law by assuming that the pressure difference is analogous to a potential difference and the flow rate is equivalent to electrical current. Resistances can then be summed in series and their reciprocals summed in parallel to assemble the total resistance of any network. These expressions were expanded into an elegant method of analytically following the trends and comparing with computational fluid dynamics (CFD) simulations. The latter part of the paper compares the analytical and CFD analysis of flow resistance and shows excellent agreement over a four-generation network, where the junctions obey Murray's law and where the daughter vessels are larger or smaller than the Murray's law optimum. The simple analytical model diverges from the CFD above a flow Reynolds number of approximately 30 due to losses in the 90° bends in the network. The experimental mean flow velocity reported by Lim and colleagues (Lim et al. 2003) was also compared to analytical and numerical simulations using this method. Agreement was reasonable; however, the velocity measurement approach produced a large scatter. This work provides important validation of the engineering application of Murray's and Poiseuille's laws. An assumption made in this analysis is that the length of each section scales with the diameter; this has also been justified in Bejan's studies (Bejan 2000, 2005; Bejan et al. 2000). However, it may be necessary to deviate from this biomimetic principle in practical designs.

The minimization of pumping power for tree networks has been studied by Gosselin & Bejan (2005). This work used the concept of constructal theory to develop a design tool for minimizing the pumping power required to join arbitrary points. This was demonstrated using networks joining 10 points. Constructal theory has also been used in the design of self-healing applications (Bejan et al. 2006; Kim et al. 2006; Wang et al. 2006). In the former two studies, a fully interconnected grid of channels statically pressurized with healing agent was considered, with damage occurring at any point. Fluid from the rest of the grid fills damage when it occurs. The global resistance of flow from the grid into the damage was minimized by numerical methods based on constructal theory, and it was found that the use of two different alternating vessel diameters in the grid approximately halved the global flow resistance into the crack. Optimum ratios of the two vessel sizes were developed, but the absolute value of an optimum size was not considered. More recently (Kim et al. 2006), a tree-shaped configuration has been studied, which is closer to that considered in this paper; it is designed to minimize the resistance of continuous flow through a network with one entry and one exit point. The optimum ratios of diameters in different parts of different-sized and configured networks were studied. The overall choice of configuration was driven by efficient space coverage. The methods all rely on numerical optimization, making them very effective in global system-level optimization, but they do not offer intuitive insight into the basic factors at play, especially in simple systems.

3. Derivation of vessel diameter for minimum system mass

The fundamental premise of the current work is that every individual section of vessel in an engineering vascular system needs to achieve some desired flow rate, using a given fluid and pumping system, in a minimum mass system. To achieve this, there will be some optimum diameter for every section of vessel in the system; the mass of the pump required to circulate the fluid will increase as the resistance rises with falling vessel diameter, but the mass of the tubing and fluid itself will rise as the diameter increases. The derivation of the optimum vessel diameter, $d_i^{*}$, for a single section of vessel is detailed in appendix A, and it yields the following result:

$${{\displaystyle d_i^{*}}}^6=\frac{1024Q^2\mu }{{\pi }^{2}k\left[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}\right]},$$ (3.1)

where Q is the volumetric flow rate; μ is the fluid viscosity; k is the power-to-mass ratio of the pumping system; ρ_tube is the density of the tubing material; c is a constant of proportionality linking vessel wall thickness with internal diameter and effectively incorporating the strength of the tubing material; and ρ_fluid is the density of the circulating fluid. For reasons of completeness, it is convenient to comment further on the derivation of equation (3.1). After initial review, it was brought to the authors' attention that the conflict between system size and overall weight had already been discussed in general terms by Ordonez & Bejan (2003). More specifically, a very similar expression to equation (3.1) has been derived by Bejan & Lorente (2002) and Bejan et al. (2004) using constructal theory. The derivation route was different from that presented in appendix A, assuming that a power penalty was incurred in transporting the additional mass of a flow system in an aircraft rather than a mass penalty in providing an appropriately sized pump. In particular, the former expression required knowledge of the thermodynamic isentropic pump efficiency and the aircraft flight speed. The selection of the cruise speed for an aircraft is an exceptionally complex part of the conventional design process. It is desirable to remove dependence on this variable from the design of subsystems. In practical aircraft or vehicle design, it is common practice to sum the weight of individual components in a ‘mass budget’ rather than considering the individual power penalty of each system. It could be argued that the variables in equation (3.1) are more appropriate for the conventional vehicle design process, since reducing mass is, to a greater or lesser extent, desirable in the design of all vehicles. Fundamentally, agreement has been shown between constructal and biomimetic approaches, in that an adaptation of the method reported by Murray (1926) produces a result of the same form as that obtained through constructal theory.

This expression, therefore, gives an internal diameter for the minimum system mass of a vascular network carrying a volumetric flow rate Q. It is sufficiently general to allow consideration of walled or channelled tubes, with the tube and included fluids being of different densities. Implicitly, it includes an optimization of the tubing wall thickness. It shows agreement with the conventional form of Murray's law, that of cubic scaling at a junction,

$$\begin{array}{c}{{\displaystyle d_i^{*}}}^6\propto Q^2\\ {{\displaystyle d_i^{*}}}^3\propto Q\end{array}.$$ (3.2)

A biomimetic engineering design tool has therefore been developed from the study of a biological principle by re-evaluating in terms of mass, a cost function that is immediately applicable to high-performance engineering systems. A vital distinction between this and the majority of the literature is that with the exception of the original derivation (Murray 1926) and the recent constructal result (Bejan & Lorente 2002; Bejan et al. 2004), focus has been almost exclusively on testing or replicating Murray's cubic scaling law at junctions. In the design of a vascular network for minimum mass, an absolute optimum diameter can now be calculated in terms of accessible quantities. Junctions can then be designed such that the daughter vessels sum to the cube of the parent vessel, since this relationship holds regardless of the absolute size of the vessels. Simply scaling vessels cubically from some arbitrary original diameter will not result in an optimized network. The use of a non-circular channel cross-section based on a hydraulic diameter would produce a different, but analogous, expression to equation (3.1), but the same junction relationship in equation (3.2).

4. Application

4.1 Design of a single section of tube

At the smallest scale, it is desirable to understand the sensitivity of the optimum diameter of a single length of network to certain variables. The key variables that can be expected to influence the design of a section of vascular network—whether for self-healing, thermal control or adaptive structures—are likely to be flow rate, Q, pump mass index, k, and fluid viscosity, μ. A range of practical values corresponding to low Reynolds number flow were selected to establish ranges of typical internal diameters. The variation of other variables, e.g. material densities and tube wall thickness, is likely to be well defined and influenced by wider design factors and is thus fixed here.

The pump mass index, k, is simple to define but difficult to implement owing to the wide range of possible pump designs. Some practical values for mechanical pumps are given in table 1, and they show the large range to be expected. The selection of a specific value will depend on the type of pump chosen and, ultimately, will be at least semi-empirical.

Table 1.

Power–weight ratios for some commercially available pumps of different types.

type	pump index k (W kg−1)	reference(s)
DC peristaltic pump (approx. 7 ml min−1)	0.05	Williamson Pumps Ltd (2004)
VentrAssist artificial heart	10	Ayre et al. (2000), Ventracor Ltd (2002)
fixed displacement hydraulic pump (approx. 6 l min−1)	700	Technova (2006)

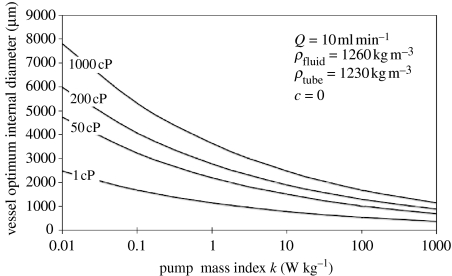
Figure 1 shows that for representative ranges of viscosities and at an appropriate flow rate, the optimum diameter shows only an order of magnitude variation over five orders of magnitude of k. The variation in optimum diameter was similar when the flow rate was varied between 1 and 25 ml min⁻¹. Over the range considered, the effect of viscosity on optimum internal diameter is of similar order of magnitude to the effect of pump index, which is expected from equation (3.1). The values of viscosity selected span the range from water to a typical resin system for self-healing applications. Over the ranges of pump index, k, and viscosity considered, the optimum diameter remains in the millimetre scale for this flow rate.

Figure 1.

Effect of pump mass index on optimum diameter over a range of viscosities.

For design, it will be necessary to obtain reliable values of pump index and viscosity to determine absolute system mass, but these values are tolerant of uncertainties if an optimum internal diameter is required.

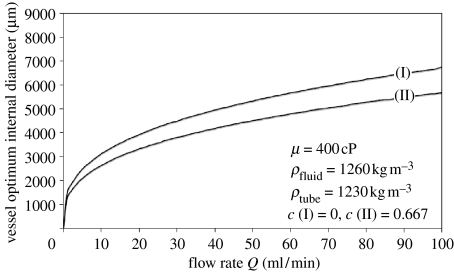
Taking a mid-range viscosity of 400 cP and a pump mass index of unity allows the effect of desired flow rate on vessel internal diameter to be investigated. Figure 2 shows that the optimum diameter is highly sensitive to flow rate at lower rates, but less so at higher rates.

Figure 2.

Influence of desired flow rate on optimum vessel internal diameter for integral vessel, fluid mass only (I) and channel vessel (II).

The effect of the tubing mass is also shown in figure 2. Adding the tube mass term (setting constant c to a non-zero value) is seen to reduce the optimum diameter, as would be expected. Intuitively, this can be seen as accepting an increase in the pump mass to offset some of the mass increase of the network itself. In absolute terms, the effect on diameter is negligible at lower flow rates, which can be seen by inspection of equation (3.1), but at moderate flow rates the difference can exceed a millimetre. In a practical manufacturing environment, tubing is supplied in a range of discrete sizes. This analysis, therefore, has a practical implication since the difference is sufficient to justify the selection of a different tubing diameter.

4.2 Tube length in network design

In principle, networks with multiple branches could be optimized in this analysis. In practical applications, it could be necessary to join tubing of different sizes using joint fittings and this would raise additional optimization questions. At a bifurcation, a joint is a necessary evil, but providing the tube length is much greater than the diameter (l/d_i>30), the influence of the joint on overall network design will be small because losses will be dominated by those in the tube (Wang et al. 2006). It has been shown that a network bifurcating on several levels, forming a dendritic pattern, is the most efficient way to ensure ‘access’ to an area from a point (Bejan 2000). In the work considered here, this takes the form of supplying a fluid flow from a pumping source to channels covering a wide area, and potentially returning the flow to a single channel for return to the pump. A branching system also has the added design freedom of allowing the spacing between channels to be tailored for different regions of a component. The degree of branching will be driven by the component geometry and the desired spacing between channels in each generation. This will be highly application dependent, but in simple cases will reduce to the number of branches, the vessel diameters and the length of each generation. The optimum diameter for each section is independent of vessel length because both the terms in the system mass expression rise linearly with length. In a network with multiple generations, the lengths of each section are, however, also design variables. The total mass m_n per unit length l_n of the nth generation is derived in appendix A, yielding the following result:

$$\frac{m_n}{l_n}=2^{n/3}\left[\frac{128Q_0^2\mu }{\pi d_{i0}^{4}k}+\frac{\pi d_{i0}^2}{4}[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}]\right].$$ (4.1)

The coefficient, 2^(n/3), shows that the total mass per unit length increases through the network generations. For a minimum mass network, the length of vessels in generations with more numerous smaller vessels should always be minimized in favour of longer lengths in generations with fewer larger vessels. It is noteworthy that this conclusion represents a clear driver to keep the degree of branching to the minimum required to achieve the desired network coverage. This is an intuitive but nonetheless important and simply applied design principle. The development in appendix A concludes with an expression for the mass of each generation assuming that the vessel length at each generation is directly proportional to the corresponding diameter. This configuration is often found in natural systems (West 1990) and has formed the basis of other engineering applications of Murray's law (Emerson et al. 2006).

$$m_n=C\left[\frac{128Q_0^2\mu }{\pi d_{i0}^{3}k}+\frac{\pi d_{i0}^3}{4}[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}]\right].$$ (4.2)

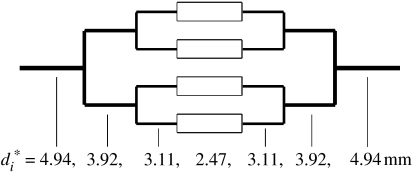
In this special case, the mass of each generation is constant and equal to the mass of the first generation. This is not a minimum mass configuration, but the constant generation mass may make it an elegant solution for use in design. To illustrate the use of equation (3.1) and the understanding of the effect of vessel length, consider a four-level network of channels with variables as given in figure 2, curve (I). If the flow required through each of the smallest tubes is 5 ml min⁻¹, the optimum vessel diameter for this level is 2.47 mm to three significant figures. Figure 3 shows a schematic of the network design with higher levels scaled from this according to the sum of the cubes. Since the volume flow rate sums at a junction (analogous to electrical current), the optimum diameters can also be obtained by reading from figure 2 at 10, 20 and 40 ml min⁻¹. Section lengths have been chosen to be approximately proportional to local diameter.

Figure 3.

A simple vascular network with optimum vessel diameters.

4.3 Advanced network design

The network shown in figure 3 is relatively simple because it is symmetrical and unconstrained by component geometry. Equation (3.1) has utility in describing individual sections of more complex asymmetrical networks such as those that might be required in practical designs. The complication in these cases is that the flow rate at each point cannot be determined by inspection and will be a function of the diameters of different parallel flow paths. An iterative solution will be required in these cases since flow rate and optimum diameter are coupled, with equation (3.1) applied iteratively to each section. It is probable that, in practice, there will be many influences on the vessel length required in each generation. Symmetrical bifurcating branches were assumed in the derivation of equations (4.1) and (4.2). In complex asymmetrical networks, further work would be required to produce a rigorous optimization. However, the general principle that the length of the more numerous smaller vessels should be minimized in favour of fewer larger vessels stands. Clearly, other factors may drive long lengths of numerous small vessels, at which point a trade-off becomes necessary.

5. Turbulent flow

Poiseuille's law is valid only for laminar flow. The applications envisaged in this study all require low flow rates and small diameters and must allow for the use of high viscosity fluids. They are all, therefore, well within the laminar flow regime. However, an optimum diameter could also prove a useful design tool for applications with turbulent flow. Uylings (1977) has extended the derivation of Murray's law to include the power dissipation in turbulent flow. Bejan et al. (2000) has also used the constructal approach to arrive at the same junction relationship as Uylings (1977) for minimum pressure drop within a volume-constrained network, and has suggested that the expression for optimum tube diameter can also be obtained for turbulent flow (Bejan & Lorente 2002; Bejan et al. 2004), although this has not been explicitly derived. A mass-driven analysis that gives absolute values has potential as a useful design tool in this case; hence, the development of an expression for optimum diameter in turbulent flow is detailed in appendix B and yields

$${{\displaystyle d_i^{*}}}^7=\frac{80{\rho }_{\text{fluid}}A}{{\pi }^{3}k({\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}})}{Q}^3,$$ (5.1)

where A is a constant, which is also a function of vessel surface roughness and can be determined by numerical methods or with reference to a Moody chart. An overall trend can be established,

$$\begin{array}{c}{{\displaystyle d_i^{*}}}^7\propto Q^3\\ {{\displaystyle d_i^{*}}}^{2.33}\propto Q\end{array}.$$ (5.2)

As with the analysis for laminar flow, the first point to note is that the scaling or junction relationship agrees with those previously calculated using a different, biologically driven, cost function and using constructal theory. This scaling relationship at a junction is different for turbulent flow when compared with laminar flow. The biomimetic design tool derived in equation (5.1) allows the absolute optimum vessel size to be directly determined in terms of variables accessible to a design engineer. Both terms of the mass expression in equation (B 5) are linear functions of vessel length. For brevity, the expressions will not be developed in full because it can be seen by inspection that the same conclusion regarding the lengths in different generations will apply as in §4.2, namely that a minimum overall mass is achieved with length shifted towards the regions of the network with fewer larger vessels. The design of a minimum mass network with turbulent flow conditions could have many engineering applications incorporating fluid distribution, e.g. hydraulic or pneumatic systems.

6. The cost of deviation from the optimum diameter

In a vascular system consisting of multiple levels, a subtle point concerning the use of the scaling laws in equations (3.2) and (5.2) should be considered. If the optimum tubing diameter at a point is calculated but structural or manufacturing constraints impose an alternative vessel diameter, vessels above or below the design section in the hierarchy must be cubically scaled according to the optimum vessel size. If scaled from the unoptimized size, the original mass penalty would be compounded.

Milsum & Roberge (1973) and Sherman & Popel (1989) have shown that the sensitivity of the total power to variation of diameter from the optimum is relatively small close to the optimum value. Since the constants in the power expression are shown to cancel, it can be seen, almost by inspection, that the mass expression will be directly analogous. The ratio of actual-to-minimum mass can, therefore, be expressed as

$$\frac{m}{m_{\text{min}}}=\frac{{\left(\frac{d_i}{d_i^{*}}\right)}^{-4}+2{\left(\frac{d_i}{d_i^{*}}\right)}^2}{3}=\frac{{\left(\frac{d_{\text{o}}}{d_{\text{o}}^{*}}\right)}^{-4}+2{\left(\frac{d_{\text{o}}}{d_{\text{o}}^{*}}\right)}^2}{3},$$ (6.1)

where $d_i$ and $d_{\text{o}}^{*}$ are the optimum vessel diameters. Close to the optimum diameter, a diameter 10% from optimum will result in only a 3–5% mass penalty; however, this penalty increases rapidly further away from the optimum. Popel & Johnson (2005) state: ‘adherence to Murray's law (or similar minimization principles) could not be expected because moderate deviations from the minimum are not costly and other factors might affect the structure of the network.’ The analysis presented here has incorporated mass, the prime driver in many engineering applications. A 2–3% mass penalty could be significant in high-performance applications and there is a clear need to minimize this mass penalty, especially in load-carrying structures containing a vascular network. Uylings (1977) has also shown that a similar relationship exists for turbulent flow, which is slightly more sensitive but still shows low sensitivity close to the optimum value.

7. Structural factors

The inclusion of a vascular network within a structure could be expected to have an adverse effect on the structural properties since load-bearing material is being replaced. For example, consider a sandwich structure containing a vascular network within its core cross-section. Sandwich structures are extensively used in high-performance engineering applications where structures are subject to bending or compressive loads. They typically consist of thin skins of a high-performance material separated by a lightweight core material, such as a rigid foam (Zenkert 1995). Nature has evolved sandwich structures extensively, most notably bone, effectively a sandwich structure of cortical bone separated by honeycombed cancellous bone (Kalfas 2001). In an engineering structure, the core offers an ideal location for a vascular network, since it can be easily incorporated into a rigid foam. If the network is continuous, the shear connectivity within the core has been compromised, which for shear critical structures may be problematic. Such considerations suggest that a discrete vascular network of spaced vessels is more appropriate because shear connectivity is retained through the core material surrounding the vessels. Then, the key structural properties that are affected are overall flexural stiffness, shear stiffness and effective cross-sectional area of the core. However, such reductions in performance are slight, firstly because flexural stiffness is driven by stiffness of the skins (which are largely unaffected by the presence of a vascular network). Secondly, the reduction in core cross-sectional area will be small if the network density is low and is readily compensated by, for example, slightly increasing the core depth. There remains one further structural consideration that may be of concern, which is fracture mechanics. To illustrate the problem, we consider two hypothetical vascular networks within an axially loaded structure. Contrast a network of cylindrical vessels running parallel with one in which the vessels run transversely to the loading direction. Each may be thought of as introducing stress raisers; in extreme cases, these could be considered cracks. The former case introduces effectively smaller cracks in comparison with the latter and suggests a more favourable approach for design. In a branching vascular network such as that proposed in figure 3, some transverse vessels are unavoidable. These fracture mechanics factors are therefore challenges of detailed design: circular vessels are expected to impart less stress concentration than those with sharper cross-sections; and in a complex practical structure with varying loading, locating the transverse branches in areas of lower stress could alleviate peak stresses.

In summary, the interaction between a vascular network and a structure in multifunctional materials will be highly dependent on the specific configuration and loading state of the structure and the network, with network density being a key factor. To illustrate an example of this interaction, the inclusion of a discrete vascular network of low density (such that the penalty in shear performance is negligible) in the core of a sandwich structure can be considered in more detail. Recent pilot studies of vascular networks in self-healing structures have used this configuration (Trask et al. 2007a).

In engineering design, rules are often used to select the appropriate thicknesses of the skins and core of sandwich structures for given materials and applied loading (Zenkert 1995). The optimum diameter for a vascular network could be selected using equation (3.1). If the optimum vessel outside diameter exceeds the design core thickness of the sandwich structure, then either the core thickness will have to be increased (resulting in a structural mass penalty) or the vascular network diameter must be decreased (resulting in a network mass penalty). A trade-off is therefore required.

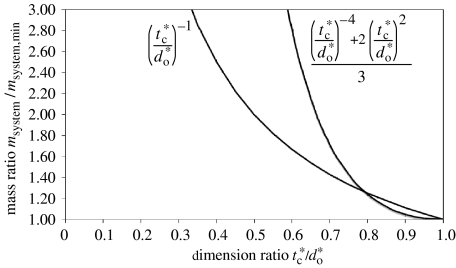
The relative mass penalty of increasing core thickness, t_c, of a constant density core above the design value, $t_{\text{c}}^{*}$, is directly proportional to the ratio of the thicknesses. Equation (6.1) gives the relative mass penalty of reducing the vessel diameter. If the actual diameter in equation (6.1) is set to the design core thickness $t_{\text{c}}^{*}$, then figure 4 can be plotted to show this relationship. The point at which the curves intersect is found by equating the two terms. A numerical solution to three significant figures gives

$$\left(\frac{t_{\text{c}}^{*}}{d_{\text{o}}^{*}}\right)=0.794\text{for}\left(\frac{t_{\text{c}}^{*}}{d_{\text{o}}^{*}}\right)<1.$$ (7.1)

Therefore, this analysis provides useful guidelines:

1. for a dimension ratio (design core thickness to vessel outside diameter) below 0.794, increasing the sandwich thickness incurs less relative mass penalty, and

2. for a dimension ratio between 0.794 and 1, reducing the vessel diameter will incur a lesser relative mass penalty.

Figure 4.

Relative mass penalties for unoptimized tube diameter and sandwich core thickness.

The true optimum could, of course, be a compromise between adjusting both the core thickness and the vessel diameter. In addition, the absolute masses of the baseline systems are an additional factor and should be considered. The model could also be refined to include the influence of core shear properties, but this is beyond the scope of the present work. However, this analysis allows the key drivers to be understood and helps to put the interaction of vascular and structural factors into perspective. If a constraint drives a small deviation in vessel diameter from the optimum (of the order of say 10–15%) or if the mass of the vascular network is much less than that of the overall structure, then changes in diameter offer a lower mass penalty. If the deviation is likely to be larger or if the vascular network forms a significant proportion of the total mass, then the penalty in deviating from the optimum diameter will be more significant. This analysis, therefore, agrees with biological examples of where structural (or other) factors are credited with driving deviation from an optimum vessel diameter (McCulloh et al. 2004; Popel & Johnson 2005).

8. Conclusions

Previous biological, engineering studies and applications of Murray's law have focused on minimizing the power requirement of a vascular system, in most cases only using the junction ‘sum of the cubes’ relationship. In design of high-performance applications such as those for aerospace, minimum mass will be the prime design driver and absolute values are needed for design. In this work, expressions for a minimum mass vascular network have been developed. The cubic relationship between the diameters of parent and daughter vessels originally identified by Murray (1926) is shown to also hold for a minimum mass network. A biomimetic relationship for absolute values of optimum diameter has been derived in terms of useful design variables. This analysis has suggested that flow rate has the most significant effect on the choice of vessel diameter. There is also a significant difference between the optimum diameter of a tubed system and channels within the parent material. In principle, this method could be used in the design of series or parallel vascular networks including any number of branches. A similar relationship has been shown to hold for turbulent flow. Use of this design method to compute the absolute optimum diameter in the turbulent regime requires further analysis but would bring wider application of the method, since it would allow minimum mass design of a wide range of fluid distribution networks. The analysis has been extended to consider the length of each generation of a branching network; the mass per unit length of a network increases with the number of branches, leading to the conclusion that the length of the narrower, more numerous vessels should be minimized.

Qualitatively, the least disruption to the structural performance of a member loaded axially is achieved if the vascular conduits are aligned with the loading direction to avoid stress concentration effects. In a flexural situation, placing a vascular network close to the neutral axis minimizes the influence on structural performance. A case study of a sandwich panel with a vascular network in the core was studied in some detail, in particular to evaluate the mass penalty incurred if the optimum vessel diameter exceeded the thickness of the host sandwich core. It has been shown in this case that small deviations from optimum diameter can be easily justified in terms of mass, whereas large deviations could be expected to produce an increasingly punitive mass penalty. There is a biological precedent for moderate deviation from optimum vasculature for structural reasons, so this final conclusion could itself be considered biomimetic.

Appendix A. Derivation of minimum mass vessel diameter with laminar flow

The relationship between pressure loss and flow rate of a liquid in laminar flow within narrow bore tubes was investigated by Poiseuille in the 1830s and 1840s. A detailed review of the development of Poiseuille's law has been conducted by Sutera & Skalak (1993). This work refers to several of the original French manuscripts. The relationship for the flow of a Newtonian fluid through a circular conduit in laminar flow has come to be used in the form

$$\mathrm{\Delta }p=\frac{128Ql\mu }{\pi d_i^4},$$ (A1)

where Δp is the pressure difference; Q is the volume flow rate; l is the vessel length; μ is the fluid viscosity; and d_i is the vessel internal diameter. The power, P_F, of a flowing fluid is given by

$$P_{\text{F}}=Q\mathrm{\Delta }p,$$ (A2)

where Q is the volumetric flow rate and Δp is the pressure difference. For flow through a narrow bore tube, as described by equation (A 1), it follows that

$$P_{\text{F}}=\frac{128Q^{2}l\mu }{\pi d_i^4}.$$ (A3)

These viscous power losses must be overcome by some form of pump. Assuming that the mass of a pump can be linearly related to its power such that

$$k=\frac{P_{\text{F}}}{m_{\text{pump}}},$$ (A4)

where m_pump is the mass of the pump and k is a constant (intuitively the power-to-mass ratio of the range of pumps on offer), then the mass associated with achieving the desired flow rate can be expressed as

$$m_{\text{pump}}=\frac{128Q^{2}l\mu }{\pi d_i^{4}k}.$$ (A5)

At this point in the derivation, Murray assumed that the power cost function is related only to the blood volume. Sherman (1981) noted that the vessel wall would also require metabolic support. Analogously, it will also inflict a mass penalty. It was assumed that the vessel thickness varied linearly with internal radius. This is a reasonable assumption since this maintains a given wall tension regardless of the radius of the vessel. A structural optimization strategy is therefore tied into the analysis. This gives the vessel wall thickness t_wall as

$$t_{\text{wall}}=c\frac{d_i}{2},$$ (A6)

where c is a constant of proportionality. The selection of c incorporates the strength of the tubing material. This allows the external diameter, d_o, of the tube to be expressed as

$$d_{\text{o}}=d_i+2c\frac{d_i}{2}=d_i(1+c).$$ (A7)

Using equation (A 6), the mass m_tube of the tube can be expressed as

$$m_{\text{tube}}=\frac{{\rho }_{\text{tube}}l\pi }{4}\left[d_i^2(c^2+2c)\right].$$ (A8)

The overall system mass is given by a sum of the pump, tubing and fluid masses. By summing these and collecting terms in d_i², the relationship can be expressed in two terms,

$$m_{\text{system}}=\frac{128Q^{2}l\mu }{\pi d_i^{4}k}+\frac{l\pi d_i^2}{4}\left[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}\right].$$ (A9)

For a minimum mass vascular network with given flow rate, fluid and tube and pump properties, the expression is differentiated with respect to internal diameter and the stationary point found. At this point, the optimum internal diameter can be defined as $d_i^{*}$:

$$\frac{d{m}_{\text{system}}}{d{d}_i}=\frac{-4\times 128Q^{2}l\mu }{\pi {{\displaystyle d_i^{*}}}^{5}k}+\frac{l\pi d_i^{*}}{2}\left[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}\right]=0,$$ (A10)

such that

$${{\displaystyle d_i^{*}}}^6=\frac{1024Q^2\mu }{{\pi }^{2}k\left[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}\right]}.$$ (A11)

This expression is independent of vessel length. It is therefore necessary to suggest how the length of each generation of a network will affect the overall system mass. In the nth generation of a bifurcating network, there will be 2ⁿ vessels. Assuming that the network is symmetrical, the total mass of each generation is therefore given by

$$m_n=2^n\left[\frac{128Q_n^2{l}_n\mu }{\pi d_{in}^{4}k}+\frac{l_n\pi d_{in}^2}{4}[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}]\right].$$ (A12)

The volumetric flow rate through each vessel of the nth generation is given by

$$Q_n=\frac{Q_0}{2^n},$$ (A13)

where Q₀ is the volumetric flow rate in the first generation (n=0). For a network obeying Murray's law, the diameter of the nth generation is given by

$$d_{in}=\frac{d_{i0}}{2^{n/3}},$$ (A14)

where d_i0 is the internal diameter of the first generation. Substituting equations (A 13) and (A 14) into equation (A 12) and simplifying gives

$$\frac{m_n}{l_n}=2^{n/3}\left[\frac{128Q_0^2\mu }{\pi d_{i0}^{4}k}+\frac{\pi d_{i0}^2}{4}[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}]\right].$$ (A15)

This represents the mass per unit length of the nth generation of the network in terms of that of the first generation. In the biomimetic case where the length of each generation is proportional to the vessel diameter,

$$l_n=C{d}_{in}=C\frac{d_{i0}}{2^{n/3}}.$$ (A16)

Substituting equation (A 16) into equation (A 15) gives

$$m_n=C\left[\frac{128Q_0^2\mu }{\pi d_{i0}^{3}k}+\frac{\pi d_{i0}^3}{4}[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}]\right].$$ (A17)

Therefore, for the special case where vessel length is proportional to diameter, the mass of each generation is the same.

Appendix B. Derivation of minimum mass vessel diameter with turbulent flow

The pressure drop of a steady fluid flowing turbulently in a circular pipe is given by the Darcy–Weisbach equation,

$$\mathrm{\Delta }p=\frac{8f{\rho }_{\text{fluid}}{Q}^{2}l}{{\pi }^2{d}_i^5},$$ (B1)

where f is the Darcy or Moody friction factor and is commonly determined from a Moody chart (Moody 1944), as it is a function of the diameter and flow rate. Uylings (1977) defined it as

$$f=\frac{A}{{(R_e)}^B},$$ (B2)

where A and B are constants and R_e is the flow Reynolds number based on internal vessel diameter. The constant B=1 holds for laminar flow, decreasing as the flow transits to fully developed turbulent flow with B=0. The constant A takes the value A=64 for laminar flow, but cannot be so simply defined in transitional or turbulent flow; hence, reference must be made to numerical methods or a Moody chart,

$$R_e=\frac{{\rho }_{\text{fluid}}V{d}_i}{\mu }=\frac{4{\rho }_{\text{fluid}}Q{d}_i}{\mu \pi d_i^2}=\frac{4{\rho }_{\text{fluid}}Q}{\mu \pi d_i}.$$ (B3)

The total mass of the system can be estimated using the pump mass metric k,

$$m_{\text{system}}=\frac{8f{\rho }_{\text{fluid}}{Q}^{3}l}{{\pi }^2{d}_i^{5}k}+\frac{l\pi d_i^2}{4}[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}].$$ (B4)

Substituting equations (B 2) and (B 3) into equation (B 4) and rearranging gives

$$m_{\text{system}}=\frac{8{\rho }_{\text{fluid}}lA}{{\pi }^{2}k}{\left(\frac{\mu \pi }{4{\rho }_{\text{fluid}}}\right)}^B\frac{Q^{3-B}}{d_i^{5-B}}+\frac{l\pi d_i^2}{4}[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}].$$ (B5)

Differentiating (B 5) with respect to internal diameter to find the optimum internal diameter $d_i^{*}$ gives

$$\frac{d{m}_{\text{system}}}{d{d}_i}=-(5-B)\frac{8{\rho }_{\text{fluid}}lA}{{\pi }^{2}k}{\left(\frac{\mu \pi }{4{\rho }_{\text{fluid}}}\right)}^B\frac{Q^{3-B}}{{{\displaystyle d_i^{*}}}^{6-B}}+\frac{l\pi d_i^{*}}{2}[{\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}}]=0.$$ (B6)

Substituting B=1 and A=64 for laminar flow gives equation (3.1). Taking B=0 gives the expression for fully developed turbulent flow,

$${{\displaystyle d_i^{*}}}^7=\frac{80{\rho }_{\text{fluid}}A}{{\pi }^{3}k({\rho }_{\text{tube}}(c^2+2c)+{\rho }_{\text{fluid}})}{Q}^3.$$