INFLUENCE OF BLOOD FLOW AND MILLIMETER WAVE EXPOSURE ON SKIN TEMPERATURE IN DIFFERENT THERMAL MODELS

Abstract

Recently we showed that the Pennes bioheat transfer equation was not adequate to quantify mm wave heating of the skin at high blood flow rates. To do so, it is necessary to incorporate an “effective” thermal conductivity to obtain a hybrid bioheat equation (HBHE). The main aim of this study was to determine the relationship between non-specific tissue blood flow in a homogeneous unilayer model and dermal blood flow in multilayer models providing that the skin surface temperatures before and following mm wave exposure were the same. This knowledge could be used to develop multilayer models based on the fitting parameters obtained with the homogeneous tissue models. We tested four tissue models consisting of 1 to 4 layers and applied the one-dimensional steady-state HBHE. To understand the role of the epidermis in skin models we added to the one- and three-layer models an external thin epidermal layer with no blood flow. Only the combination of models containing the epidermal layer was appropriate for determination of the relationship between non-specific tissue and dermal blood flows giving the same skin surface temperatures. In this case we obtained a linear relationship between non-specific tissue and dermal blood flows. The presence of the fat layer resulted in the appearance of a significant temperature gradient between the dermis and muscle layer which increased with the fat layer thickness.

INTRODUCTION

In our recent paper describing the heating of human skin by mm waves we used a homogeneous skin model [Alekseev et al., 2005]. The Pennes bioheat transfer equation (BHTE) [Pennes, 1948], frequently used in thermal modeling, fitted well to the experimental data obtained in the forearm with low blood flow rates. However, the best fit in a wide range of blood flow was obtained with the hybrid bioheat equation (HBHE), which incorporates into the BHTE a blood flow dependent effective thermal conductivity [Charny et al., 1990; Weinbaum and Jiji, 1989; Wren et al., 2001].

We showed that mm waves in spite of shallow penetration into the skin (0.62 mm at 42 GHz exposure) were able to heat much deeper subcutaneous layers. In the homogeneous model, the skin is considered to be a tissue with uniform physical and thermo-physical properties and with uniform blood flow over the entire tissue volume. In this case, we denoted blood flow as a non-specific tissue blood flow or BF_tissue.Consequently, a non-specific tissue blood flow, a major parameter of the BHTE and HBHE, can not be directly measured or verified. Such a fictional characterization of blood flow complicates the physiological interpretation of the modeling results.

Three-layer models are much closer to the real structure of skin and underlying tissue [Emery and Sekins, 1982; Stolwijk and Hardy, 1977; Xu and Werner, 1997]. They include dermal, fat, and muscle blood flows. As the multilayer models reflect physiological conditions of different tissue layers they are more adequate for describing thermal events in the skin. At the same time they are more complicated. The main question of this study was whether the non-specific blood flow used in the homogeneous uni-layer model could be related to the specific blood flows in multilayer models: the dermal, fat, and muscle blood flows. If so, then the non-specific blood flow in the BHTE and HBHE could be verified by measuring blood flows in cutaneous and subcutaneous layers.

Dermal blood flow varies much more than the other two in responses to environmental temperature and radiant heating [Johnson et al., 1976; Davis et al., 2006]. In this case it is important to know whether the blood flow changes in the dermis alone are enough to produce the same cutaneous cooling effect as the non-specific blood flow changes in the homogeneous tissue. This knowledge could be used to develop a multilayer model based on the fitting parameters obtained with the homogeneous tissue models and dermal blood flow measurements.

The aims of this theoretical study were (a) to develop multilayer models for describing mm wave heating of skin, which utilize the HBHE, (b) to evaluate the adequacy of homogeneous models compared to multilayer models, (c) to determine the relationship between the single-layer non-specific homogeneous blood flow and the corresponding multilayer blood flows that produce the same skin surface temperatures and temperature elevations during mm wave exposures, and (d) to determine the temperature distributions for different amounts of dermal blood flow and different thicknesses of the fat layer.

METHODS

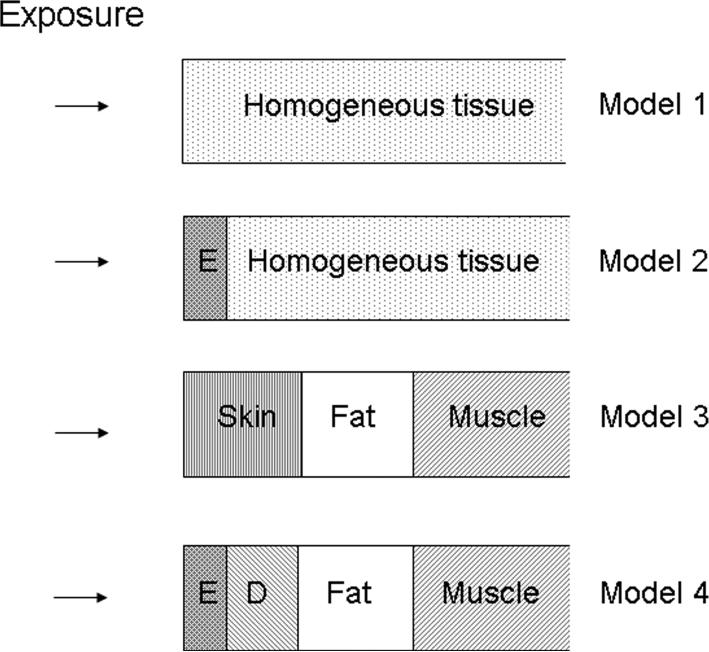
In our calculations we used the four tissue models shown in Fig. 1. Each layer in each of the four models was homogeneous. In the unilayer model, the temperature distributions were calculated for a semi-infinite plane of skin exposed to mm waves with the incident power density (IPD) uniform over the entire exposed area. In this case we used the one-dimensional steady-state heat transfer equation:

$$\frac{{\partial }^{2}T}{\partial z^2}=\lambda \cdot T-\frac{Q\left(z\right)}{k}$$ (1)

where T= T_t —T_b, T_t is the local tissue temperature [°C], T_b is arterial blood temperature [°C], k is the thermal conductivity of tissue [W·m⁻¹·°C⁻¹], λ = BF·ρ_b·C_b/k [m⁻²], where BF is the specific blood flow rate [ml·s⁻¹·ml⁻¹], and ρ[kg·⁻³] and C_b[j·kg⁻¹·°C⁻¹ are the density and specific heat of blood, respectively. Q(z) is the rate of heat deposition per unit volume from mm wave exposure [W·m⁻³], where z is distance into tissue from the skin surface in the direction of the beam axis.

Figure 1.

Tissue models used for modeling mm wave heating. In model 1, the skin and underlying tissues are considered as a homogeneous tissue. In models 2 and 4, E stands for the epidermis. In model 4, D stands for the dermis. The deepest layer in each model has semi-infinite thickness.

Equation (1) is called the steady-state Pennes bioheat transfer equation (BHTE) or the steady-state hybrid bioheat equation (HBHE) depending on what value is represented by k. In the BHTE, k is set equal to k_t, a constant equal to the intrinsic thermal conductivity of a given tissue. In the HBHE, k is set equal to k_eff, the blood flow dependent effective thermal conductivity.

In Eq. (1), a term accounting for metabolic heat production was neglected because its contribution to heat production in resting man is relatively low [Hardy, 1982], and would not change much during mm wave exposure.

Heat deposition for mm wave exposure can be described as follows:

$$Q\left(z\right)=\frac{2\cdot (1-R)}{\delta }\cdot I_o\cdot e^{-\frac{2\cdot z}{\delta }}$$ (2)

where I_o is the IPD, δ is the penetration depth of mm waves into the skin, R is power reflection coefficient. All calculations of mm wave heating were performed for 42 GHz at δ = 0.62 mm and R = 0.43 [Alekseev and Ziskin, 2007].

As shown by Foster et al. [1978], the solution of Eq. (1) is given by:

$$T\left(z\right)=\frac{Q\left(z\right)}{\lambda -\frac{4}{{\delta }^2}}\cdot \left[\exp (-\frac{2z}{\delta })-\frac{\frac{2}{\delta }+\alpha }{\sqrt{\lambda }+\alpha }\cdot \exp (-z\cdot \sqrt{\lambda })\right]+\frac{\alpha \cdot (T_e-T_b)}{\alpha +\sqrt{\lambda }}\cdot \exp (-z\cdot \sqrt{\lambda })$$ (3)

where T_e is the ambient temperature outside the skin, α=h/k, h is the heat transfer coefficient comprising the heat loss from the skin surface due to radiation, convection, and evaporation of water passively diffusing through the skin. To calculate the heat transfer coefficient, we used the same approaches and equations as described in detail by Wissler [1961]. The ambient temperature T_e was set equal to 22°C, T_b = 36.8°C.

In order to better understand the contribution of dermal and deeper blood flow rates, multilayer tissue models were created. For each layer in a multilayer model of tissue, the parameters in Eq. (1) had to be adjusted to account for the differences in IPD and for the presence or absence of blood flow. For example, in 2- and 4-layer models, λ was set equal to 0 (no blood flow) for the epidermis. In 3- and 4-layer models, in which mm wave energy is absorbed entirely within the epidermis and dermis [Alekseev et al., 2008], Q(z) was set equal to 0 in the fat and muscle layers. As the epidermis and dermis had the same permittivities [Alekseev and Ziskin, 2007] we accepted that there were no internal reflections from the boundary between the epidermis and dermis, i.e., Q(z) was continuous function within these layers.

To solve the corresponding equations for multilayer models we applied the following steady-state boundary conditions:

• For the outer surface of the first layer:

  $$\frac{\partial T}{\partial z}\left(0\right)=\alpha \cdot (T+T_b-T_e)$$ (4)
• For the internal boundary surfaces:

  $$T_i\left(Z_i\right)=T_{i+1}\left(0\right)$$

  $$k_i\cdot \frac{\partial T_i\left(Z_i\right)}{\partial z}=k_{i+1}\cdot \frac{\partial T_{i+1}\left(Z_{i+1}\right)}{\partial z}$$ (5)
• For the deepest layer:

  $${\mathrm{T}}_{\text{last}}\left(\infty \right)=0$$ (6)

where Z_i and k_i are the thickness and thermal conductivity of the i^th layer, respectively.

In different tissue models the thermal conductivity of each layer was set either blood flow independent (k=k_t) or blood flow dependent (k=k_eff):

$$\begin{array}{cc}\hfill \text{Model}1({\mathrm{k}}_1={\mathrm{k}}_{1\mathrm{eff}})& \to \mathrm{M}1;\hfill \\ \hfill \text{Model}2({\mathrm{k}}_1={\mathrm{k}}_{1\mathrm{t}};{\mathrm{k}}_2={\mathrm{k}}_{2\mathrm{eff}})& \to \mathrm{M}2;\hfill \\ \hfill \text{Model}3({\mathrm{k}}_1={\mathrm{k}}_{1\mathrm{eff}};{\mathrm{k}}_2={\mathrm{k}}_{2\mathrm{eff}};{\mathrm{k}}_3={\mathrm{k}}_{3\mathrm{eff}})& \to \mathrm{M}3;\hfill \\ \hfill \text{Model}4({\mathrm{k}}_1={\mathrm{k}}_{\mathrm{t}};{\mathrm{k}}_2={\mathrm{k}}_{2\mathrm{eff}};{\mathrm{k}}_3={\mathrm{k}}_{3\mathrm{eff}};{\mathrm{k}}_4={\mathrm{k}}_{4\mathrm{eff}})& \to \mathrm{M}4,\hfill \end{array}$$

where k_i is the thermal conductivity of the corresponding layer i in models 1−4.

The relationship between the non-specific tissue and dermal blood flows resulting in the same baseline skin surface temperature (T_sk) and temperature elevations (ΔT) induced by mm wave heating was determined in the following combinations of models:

$$\begin{array}{cc}\hfill & \mathrm{M}1\iff \mathrm{M}4\left(\mathrm{M}1\text{-}4\right);\hfill \\ \hfill & \mathrm{M}2\iff \mathrm{M}4\left(\mathrm{M}2\text{-}4\right).\hfill \end{array}$$

The coefficient of thermal conductivity depending on blood flow (BF) was found in our previous paper [Alekseev at al., 2005] and expressed as follows:

$$k_{ieff}=k_{it}(1+\beta \cdot B{F}_i)$$ (7)

where i is the tissue layer number, β=975 (ml/s/ml)⁻¹. The typical values of k_it and other parameters necessary for modeling were determined from literature [Gordon et al., 1976; Sekins and Emery, 1982; Duck, 1990]. They are given in Table 1.

Table 1.

Thermophysical parameters of tissues used in models.

Model	Tissue layer	ρ·C [J/m3 °C]	kt [W/m °C]	α [m−1]	BF [ml/s/ml]	Z [mm]
1 and 2	Total Tissue	4.18 · 106	0.32	26.5	variable	∞
3	Skin	3.97 · 106	0.32	26.5	variable	1.5
2, 4	Epidermis	4.18 · 106	0.46	26.5	0	0.01−0.1
4	Dermis	3.97 · 106	0.32	-	variable	1.5
3, 4	Fat	1.88 · 106	0.16	-	0.43·10−5	2
3, 4	Muscle	4.18 · 106	0.32	-	5.33·10−4	∞

List of symbols used in the table is given in the “Methods” section.

RESULTS

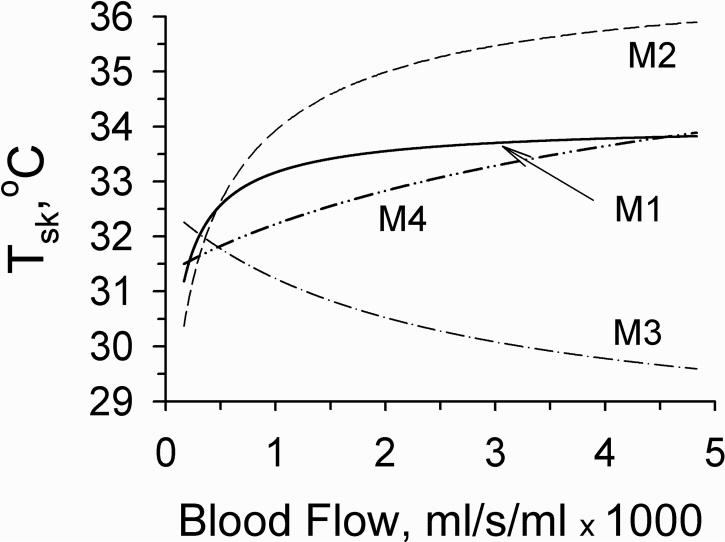
It is well known that the vasodilatation of blood vessels increases the skin surface temperature (T_sk) and vice versa [Rubinstein and Sessler, 1990; Koyama et al., 2000; Walters et al., 2004; Alekseev et al., 2005]. Fig. 2 demonstrates the changes of the skin temperature depending on blood flow in different models in the absence of mm wave heating. All models except model 3 demonstrated skin temperature elevations with increasing blood flow. The opposite effect of blood flow in model 3 could be explained by the greater heat dissipation from skin surface due to the increased k_eff at higher blood flows than due to the radiation, convection and evaporation at constant k_t. The small amount of blood flowing in the thin dermis could not compensate this heat dissipation, while in model 1 the greater amount of total tissue blood flowing at the same velocity was more effective. The results obtained with model 3 conflicted with experimental physiologic data. Therefore, we excluded M3 from further consideration.

Figure 2.

Dependence of skin surface temperature on blood flow in different models in the absence of mm wave exposure. The blood flows graphed in models 3 and 4 were specific for the dermal layer. Blood flows in models 1 and 2 were non-specific and included all blood flow throughout the homogeneous region. Blood flows in fat and muscle layers in multilayer models 3 and 4 were constant, equal to 0.43·10⁻⁵ and 5.33·10⁻⁴ ml/s/ml, respectively.

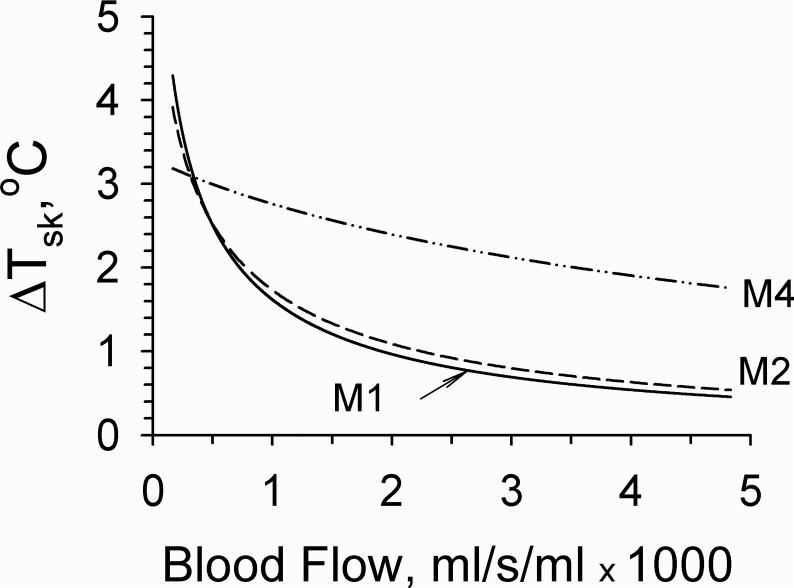
The cooling effect of blood flow on mm wave heating of the skin in different models is shown in Fig. 3. The greatest cooling effect was obtained in model 1. Addition of a thin external layer to this model (M2) produced a small reduction of this effect. In model 4, the elevations of dermal blood flow (BF_sk) producing the same cooling effect were greater than those of non-specific tissue blood flows in models 1 or 2. For example, to reduce ΔT from 3 to 2°C, dermal blood flow had to increase from 0.0005 to 0.0035 ml/s/ml, while non-specific tissue blood flow in Model 1 increased only from 0.0004 to 0.0007 ml/s/ml.

Figure 3.

Skin surface temperature rise following mm wave exposure at 20 mW/cm² versus blood flow in different models. Blood flow in model 4 was dermal. Blood flows in models 1 and 2 were non-specific. The blood flows in fat and muscle in multilayer models were constant, equal to 0.43·10⁻⁵ and 5.33·10⁻⁴ ml/s/ml, respectively.

Next, we searched for the relationship between the dermal and non-specific tissue blood flow giving the same T_sk and temperature elevations, ΔT, produced by mm wave exposure. In order to understand the role of the epidermis layer in skin models we used two combinations of models M1−4 and M2−4. Blood flows in fat and muscle were fixed constant equal to their typical values (Table 1).

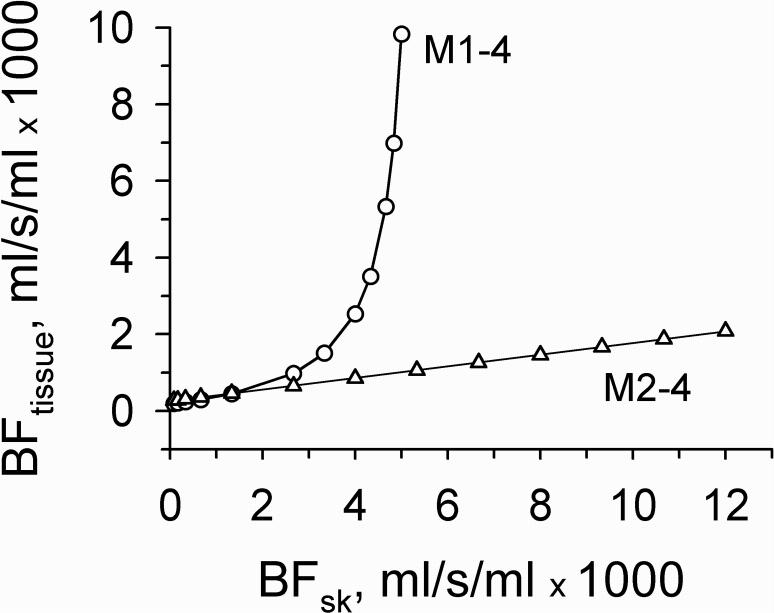
Fig. 4 shows the relationship between dermal and non-specific tissue blood flow giving equal baseline T_sk. In the M1−4, small changes in dermal blood flow above 3.33·10⁻³ ml/s/ml required an exponential increase in non-specific tissue blood flow. This type of relationship is not realistic as the dermal blood flow may reach 0.012 ml/s/ml in the human face [Gordon et al., 1976]. Moreover, only at one value of dermal blood flow were we able to obtain equal ΔT in both models. These results demonstrate that the application of the M1−4 is not appropriate for determination of the relationship between non-specific tissue and dermal blood flows giving the same values of T_sk and ΔT.

Figure 4.

Relationship between the dermal and non-specific tissue blood flows in the combinations of models M1−4 and M2−4 resulting in the same skin surface temperature. In model 4 blood flows in the fat and muscle layers were equal to 0.43·10⁻⁵ and 5.33·10⁻⁴ ml/s/ml, respectively. Solid line through triangles is a fit to Eq. 8.

However, using model 2 in combination with model 4, i.e., M2−4, equal values of T_sk and ΔT were obtainable at any dermal blood flow and exposure intensity. Moreover, the changes of dermal blood flow giving the same T_sk and ΔT were greater than those of non-specific tissue blood flow. Decreasing the thickness of the external layer E from 0.1 to 0.01 mm produced little effect on this relationship. The calculated data obtained at the constant blood flows in fat and muscle equal to 4.33·10⁻⁶ and 5.33·10⁻⁴ ml/s/ml, respectively, were well fitted to the following linear regression equation:

$${\mathrm{BF}}_{\text{tissue}}=0.255\cdot {10}^{\text{-}3}+0.151{\mathrm{BF}}_{\mathrm{sk}}$$ (8)

with the correlation coefficient close to 1. Changes in muscle blood flow up or down did not affect the linearity of the BF_tissue-BF_sk graph but shifted it accordingly up or down with slight change in its slope. Changes in fat blood flow produced little effect on this relationship.

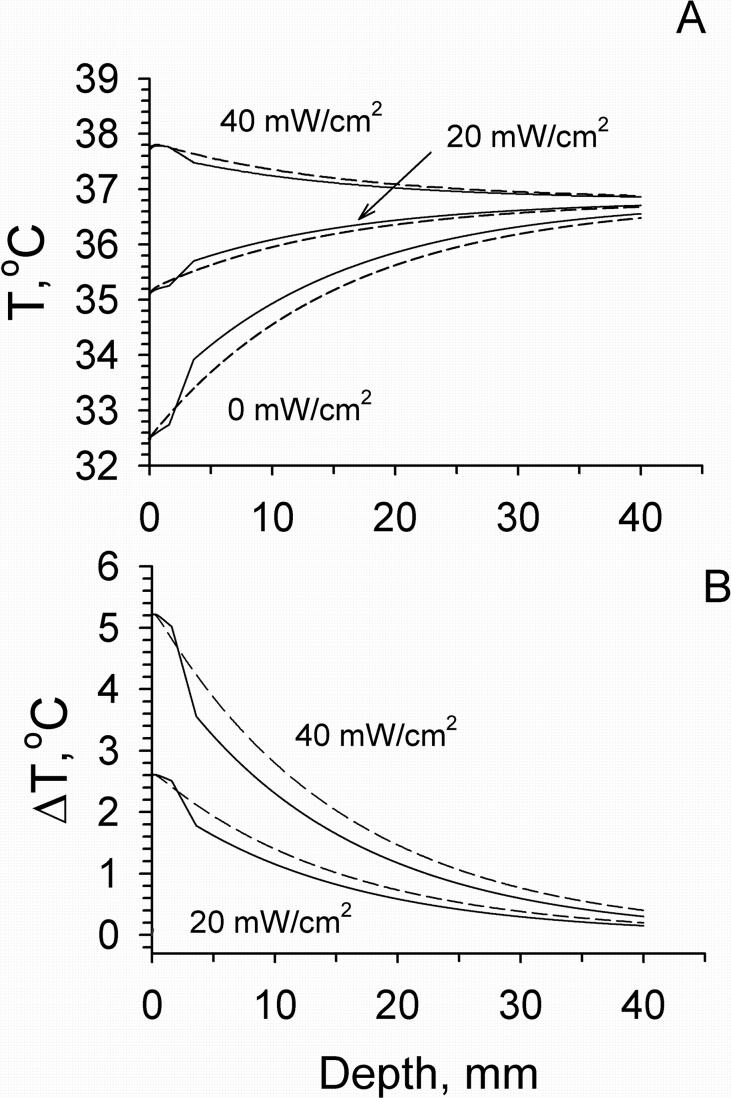
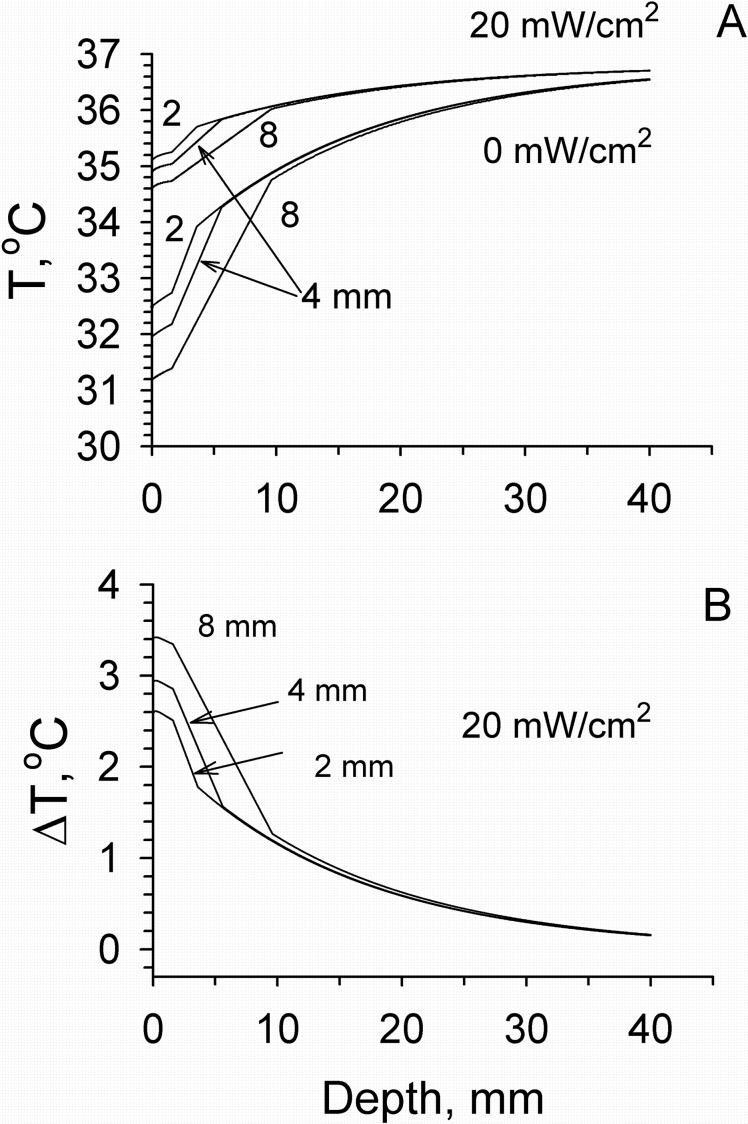
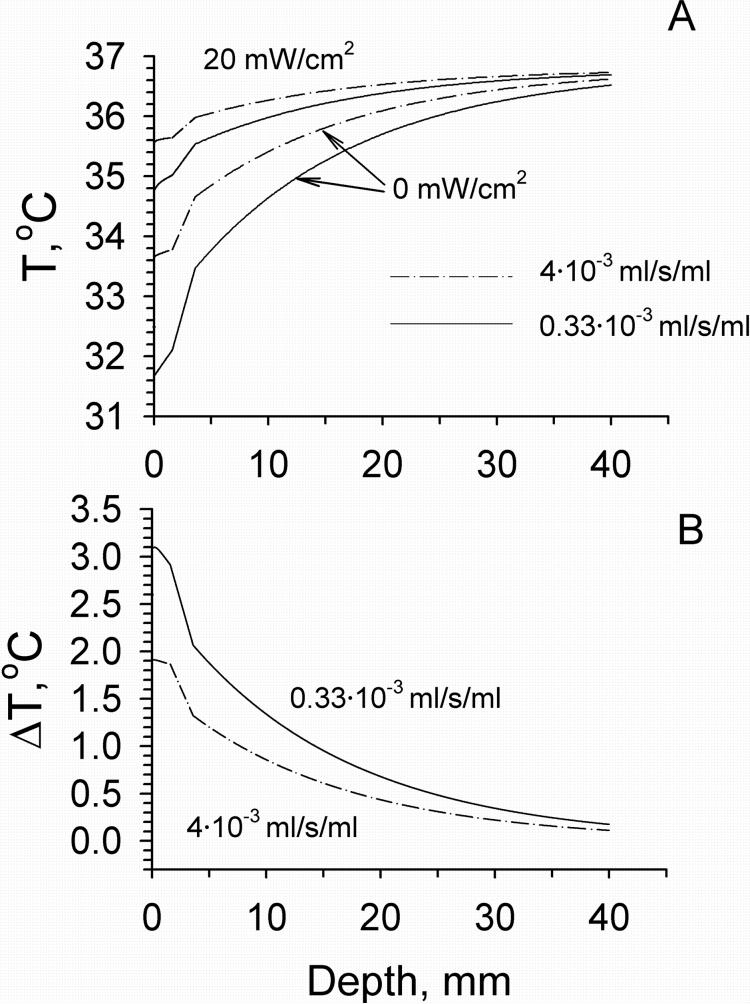
Temperature distributions in tissue calculated using models M2 and M4 before and following mm wave exposure at the IPD of 20 and 40 mW/cm² are shown in Fig. 5. In these calculations we used typical values of blood flow in different layers of the forearm [Gordon et al., 1976; Sekins and Emery, 1982]. The presence of the fat layer resulted in the appearance of a temperature gradient between the skin and muscle layers. The temperature difference between these two layers increased with increasing the thickness of fat layer (Fig. 6). At the same time the temperature distribution within the skin became more uniform in comparison with that obtained from model M2. The greater the thickness of the fat layer, the higher the temperature increment produced by mm wave heating. The effect of the dermal blood flow on the temperature distribution in tissue is shown in Fig. 7. An elevation of blood flow in the dermis could increase T_sk and the temperature of the deeper tissue layers. It also produced a greater cooling effect on mm wave heating on the skin surface and in deeper tissue layers.

Figure 5.

Temperature (A) and temperature increment (B) distributions within tissue calculated for different mm wave exposure intensities using models M2 (dashed lines) and M4 (solid lines). In M2: Tissue blood flow was 4.57·10⁻⁴ ml/s/ml. In M4: Blood flows in the dermis, fat and muscle were constant, equal to their typical values of 1.4·10⁻³, 0.43·10⁻⁵ and 5.33·10⁻⁴ ml/s/ml, respectively. The thickness of the fat layer was 2 mm.

Figure 6.

Temperature (A) and temperature increment (B) distributions within tissue calculated for different thicknesses of the fat layer (2, 4, and 8 mm) in model M4. Blood flows in the dermis, fat and muscle layers were 1.4·10⁻³, 0.43·10⁻⁵ and 5.33·10⁻⁴ ml/s/ml, respectively.

Figure 7.

Effect of dermal blood flow in model M4 on the temperature (A) and temperature increment (B) profiles within tissue before and after exposure with the IPD of 20 mW/cm². The thickness of fat layer was 2 mm.

The sensitivity analysis revealed that some variables of M4 were critical for fitting the model to the experimental data, while others were not (Table 2). The dermal and muscle blood flows were the most influential parameters affecting the skin temperature elevations produced by mm wave exposure. The less influential parameters were blood flow in fat and the thickness of the epidermis layer.

Table 2.

Sensitivity analysis. Effect of a 10% variation in tissue properties on skin surface temperature elevation, ΔT, following mm wave exposure at the incident power density of 20 mW/cm².

Variable	Tissue layer	ΔT, %
Thickness	Epidermis	0.00
	Dermis	1.33
	Fat	1.46
Blood flow	Dermis	2.08
	Fat	0.00
	Muscle	2.69

DISCUSSION

In preliminary calculations we found that the Pennes BHTE could be applied to describe the dependence of T_sk on non-specific tissue blood flows in unilayer homogeneous models. To obtain the relationship between non-specific tissue and dermal blood flows giving the same T_sk and ΔT, it was enough to apply the BHTE to the combination of the one- and three-layer models without the epidermal layer.

In the present study we showed that when applying the HBHE, the homogeneous or any multilayer model should contain the external layer with zero blood flow. The Pennes BHTE and HBHE relate temperature and corresponding blood flows. The blood flow depicted by the BHTE or HBHE in a single- or two-layer model is a fictional characterization of a uniform flow throughout the entire region modeled except the thin epidermis in the two layer model. On the other hand, the blood flows depicted in the multilayer models represent physiological values within the different layers. Our analysis showed that the non-specific tissue blood flow in the HBHE could be expressed via blood flows in the skin, fat and muscle layers in multilayer models and vice versa. In particular, we demonstrated how the non-specific tissue blood flow could be related to the dermal blood flow (Eq. 8). Hence, the blood flow in the HBHE can be experimentally verified at least by measuring blood flow in the skin. The outcome of this type of analysis was not evident a priori. Nevertheless, we were able to find the relationship between the non-specific and dermal blood flows giving the same skin temperatures before and following mm wave exposure in combinations of models M2-M4. In doing so, we were able to confirm that M1 or M2 models using the BHTE or HBHE, respectively, are adequate thermal models providing meaningful physiological values. Thus, the determination of the blood flows in multilayer models to better describe the temperature distribution in different skin layers is possible even when using only the BHTE or HBHE in homogeneous single- or two-layer models. Now, much previously accumulated data using single-layer models and the BHTE or HBHE can be used to better describe temperature distributions and biological responses to mm wave irradiation.

Our calculations showed that the temperature distributions obtained in multilayer models with a thin fat layer were close to those in the homogeneous tissue model. Hence, both types of models may be equally applied to the sites of body with a thin fat layer such as, for example, the forearm. However, in the sites of the body with a thick fat layer the use of multilayer models to describe the temperature distributions during mm wave or other external radiant heating is preferable.

Multilayer models can estimate temperature distributions in different layers of skin, which is difficult to measure experimentally. Furthermore, since different skin structures such as nerve endings, immuno-competent cells, and blood vessels are located in different skin layers, their thermal responses will vary according to local temperature elevations. Thermoreceptors and some nerve endings are very sensitive skin structures responding even to small variations of temperature [Hardy and Oppel, 1937]. Thus, different biological responses will be better explained by consideration of the temperature distributions determined by multilayer models, than would be possible by single-layer homogeneous models.