Pre-power stroke cross bridges contribute to force during stretch of skeletal muscle myofibrils

Abstract

When activated skeletal muscle is stretched, force increases in two phases. This study tested the hypothesis that the increase in stretch force during the first phase is produced by pre-power stroke cross bridges. Myofibrils were activated in sarcomere lengths (SLs) between 2.2 and 2.5 μm, and stretched by approximately 5–15 per cent SL. When stretch was performed at 1 μm s⁻¹ SL⁻¹, the transition between the two phases occurred at a critical stretch (SL_c) of 8.4±0.85 nm half-sarcomere (hs)⁻¹ and the force (critical force; F_c) was 1.62±0.24 times the isometric force (n=23). At stretches performed at a similar velocity (1 μm s⁻¹ SL⁻¹), 2,3-butanedione monoxime (BDM; 1 mM) that biases cross bridges into pre-power stroke states decreased the isometric force to 21.45±9.22 per cent, but increased the relative F_c to 2.35±0.34 times the isometric force and increased the SL_c to 14.6±0.6 nm hs⁻¹ (n=23), suggesting that pre-power stroke cross bridges are largely responsible for stretch forces.

1. Introduction

Activated muscle fibres that are stretched produce a substantial increase in force (Edman et al. 1978, 1981; Flitney & Hirst 1978; Lombardi & Piazzesi 1990; Piazzesi et al. 1992; Stienen et al. 1992; Mansson 1994; Getz et al. 1998; Rassier & Herzog 2004; Bagni et al. 2005). When the stretch is performed at low speeds (less than 2 optimal length (L₀) s⁻¹), the increase in force has two components: (i) a fast phase, in which force increases substantially over a few nanometres per half-sarcomere and (ii) a slow phase, in which force increases a small amount or remains unchanged (Edman et al. 1978, 1981; Flitney & Hirst 1978; Lombardi & Piazzesi 1990; Piazzesi et al. 1992; Stienen et al. 1992; Bagni et al. 2003, 2005; Pinniger et al. 2006; Roots et al. 2007). The transition between these two phases occurs at stretch amplitudes between 7 and 20 nm half-sarcomere (hs)⁻¹. The average critical stretch amplitude (SL_c) is independent of stretch velocity, but the force at the transition phase (critical force; F_c) increases with increasing velocity up to approximately 1 L₀ s⁻¹ (Flitney & Hirst 1978; Lombardi & Piazzesi 1990; Piazzesi et al. 1992; Getz et al. 1998; Pinniger et al. 2006; Roots et al. 2007). The SL_c is commonly associated with a critical strain of attached cross bridges, beyond which they are forcibly detached from actin (Edman et al. 1978, 1981; Flitney & Hirst 1978; Lombardi & Piazzesi 1990; Piazzesi et al. 1992; Getz et al. 1998; Bagni et al. 2003; Bagni et al. 2005; Pinniger et al. 2006; Roots et al. 2007).

The mechanism behind the increase in force during the stretch is still unclear. Several investigators have suggested that stretch forces are a result of an increased cross bridge force or strain during stretch (Getz et al. 1998; Bagni et al. 2005; Colombini et al. 2007). Recently, it has been suggested that an increased force/strain is caused by pre-power stroke cross bridges, in a state that precedes phosphate release, or with the reversal of post-power stroke (Getz et al. 1998; Chinn et al. 2003; Pinniger et al. 2006; Roots et al. 2007). The pre-power stroke cross bridges would not produce substantial isometric force, but large forces when stretched, and could be responsible for low ATP hydrolysis commonly observed in experiments (Abbott et al. 1951; Linari et al. 2003). Studies using permeabilized fibres from mammalian muscles treated with phosphate analogues suggest that this may be the case, as the stretch–isometric force ratio obtained at the transition point increases when cross bridges are biased into pre-power stroke states (Getz et al. 1998; Chinn et al. 2000, 2003). However, in a more recent study, these results were not confirmed by Bagni et al. (2005), who treated intact fibres from frog muscles with the phosphate analogue 2,3-butanedione monoxime (BDM) and observed that the stretch–isometric force ratio was not changed. Even more contradictory results come from investigators who failed to observe a significant increase in cross bridge force or strain, presenting strong evidence that the increase in force during stretch may be caused solely by an increase in the number of cross bridges attached to actin (Linari et al. 2000, 2004).

The force and the critical sarcomere elongation obtained at the transition between the two phases are primary parameters used to investigate cross bridge force and elongation during stretch (e.g. Lombardi & Piazzesi 1990; Getz et al. 1998; Pinniger et al. 2006). These parameters have been investigated previously in studies with isolated muscle fibres or bundles. In these preparations, thousands of sarcomeres arranged in series and in parallel are measured simultaneously, and length measurements are based on average estimates, making conclusions at the molecular (myosin–actin interaction) level limited. To overcome these limitations, the present study evaluated skeletal muscle myofibrils. The small size and short diffusion distance (less than 2 μm) of myofibrils, associated with a fast perfusion switching technique (Stehle et al. 2002; Tesi et al. 2002) allows rapid force development without gradient activation, and an advanced mathematical algorithm (Sokolov et al. 2003) allows the investigation of individual sarcomeres during activation and stretch (Rassier et al. 2003a). The purposes of the current experiments were twofold: (i) to investigate the SL_c and F_c in sarcomeres during stretch and (ii) to test the hypothesis that the force enhancement during stretch is caused largely by pre-power stroke cross bridges, which was done by testing myofibrils before and after BDM administration.

2. Material and methods

(a) Myofibril isolation and solutions

Rabbits were euthanized with barbiturate (pentobarbital) overdose and small strips of the psoas muscles were carefully dissected, tied to wooden sticks and stored in rigor solution (see §2b below) for 12 hours. The muscle strips were transferred to a rigor/glycerol (50 : 50) solution for 12 hours. Both procedures were carried out on ice throughout. The specimen was transferred to a fresh rigor/glycerol (50 : 50) solution and stored in a freezer at −20°C for 7–30 days. All animal procedures were approved by an Animal Ethics Committee from McGill University.

(b) Solutions

The rigor solution (pH 7.4) was composed of (in mM) 50 Tris, 100 NaCl, 2 KCl, 2 MgCl₂ and 10 EGTA. The relaxing solution (pH=7; pCa²⁺=8) was composed of (in mM) 10 MOPS, 64.4 K⁺ propionate, 5.23 Mg²⁺ propionate, 9.45 Na₂SO₄, 10 EGTA, 7 ATP and 10 creatine phosphate. The activating solution (pH=7; pCa²⁺=4.75) was composed of (in mM) 10 MOPS, 45.1 K⁺ propionate, 5.21 Mg²⁺ propionate, 9.27 Na₂SO₄, 10 EGTA, 7.18 ATP and 10 creatine phosphate. Complete protease inhibitor cocktail tablets (Roche Diagnostics) were added to all solutions during muscle storage and experiments.

(c) Force and sarcomere length measurements

Muscle strips were placed in rigor solution for at least 1 hour before experiments. Small pieces of muscle tissue (approx. 2 mm length) were cut using a fine razor blade, and subsequently homogenized in rigor solution according to an established protocol (Rassier et al. 2003a). Myofibrils were transferred into an experimental chamber mounted on a movable stage of an inverted microscope (Nikon T2000U). All experiments were performed with controlled temperature (9–12°C). A myofibril was selected based on its striation appearance, and it was glued (3145 RTV, Dow Corning, Midland, MI) to a rigid glass needle attached to a motor step at one end, and to one of a pair of microfabricated cantilevers used for force measurements at the other end (figure 1). One lever was used as force transducer and the other was used as a static reference to allow differential displacement measurement (Rassier et al. 2003a).

Figure 1.

(a) A myofibril suspended between a glass needle and a pair of microfabricated cantilevers. Note that the sarcomere striation is visible showing the contrast between A- and I-bands. (b) The striation pattern creates a light intensity peak diagram corresponding to the sarcomere bands. Sarcomere length (SL) was measured with an algorithm that calculates the distance between the centroids of the A-bands, representing the SL. In some myofibrils, it was possible to manually track the Z-lines, and the results were used to confirm the SL measurements made with the A-bands. (c) When consecutive peaks (x-axis) are scanned over successive scans (y-axis), a SL–time myogram can be created, during which the behaviour of individual sarcomeres can be tracked during activation, shortening and stretch.

Under low magnification, the attached myofibril was centred in the microscope optical field. Under high magnification provided by an oil immersion phase contrast lens (Nykon plan-fluor, NA 1.30), the image of the myofibril was projected onto a linear photodiode array with 4096 elements (SK4096ZPD, Schafter+Kirchhoff, Germany) connected to the right side port of the microscope. The image of the myofibril was scanned to produce tracings of light intensity versus position along the myofibril. The contrast between the A-bands (dark bands of myosin) and I-bands (light bands of actin) provided a dark–light intensity pattern representing the striation pattern produced by the sarcomeres. Individual sarcomere lengths (SLs) were calculated by a modified minimum average risk algorithm (Sokolov et al. 2003), based on the distance between adjacent A-band centroids (figure 1). In some myofibrils, it was possible to visualize the Z-lines during the experiments, and SL was confirmed based on the distance between adjacent Z-lines. The experiments were also recorded by a 1392×1040 (6.45×6.45 μm pixel pitch) elements CCD camera (CoolSNAP HQ Monochrome, Photometrics-Roper Scientific, Germany), connected to the left side port of the microscope. This camera provided images for confirming the results obtained with the CCD linear photodiode array. Images of the myofibrils were analysed for measurements of diameter and calculation of stress (force/cross-sectional area) produced by the myofibrils.

For the purposes of this study, myofibrils were deemed acceptable when sarcomeres could be clearly visualized and tracked during experiments, except the sarcomeres located at the ends of the myofibrils, close to the attachment of the glass needle and cantilevers.

(d) Experimental protocol

Myofibrils (n=23) were placed in relaxing solution and set at an initial average SL between 2.2 and 2.5 μm, which corresponds to the plateau of the force–length relationship for the rabbit psoas muscle (for the purposes of this paper, L₀=2.3 μm). The relaxing solution was rapidly replaced by activating solution using a computer-controlled perfusion system, whereupon full tension developed. At approximately 1000 ms after the onset of activation, myofibrils were stretched by 5–15 per cent of initial SL, at a nominal velocity of 1 μm s⁻¹ SL⁻¹ (stretch completed in approx. 250–300 ms). Since the velocity was chosen based on the average SL previous to activation and the average SL to be obtained at the end of stretch in a given time, the actual recorded velocity varied slightly as it was dependent on the amount of myofibril shortening during activation. After the end of the stretch, the myofibrils were held isometric for at least 2 s before deactivation. Experiments were followed by the addition of 1 mM of BDM to the activation solution, in order to test whether the increase in force during stretch was associated with cross bridges in the pre-power stroke state. After the contractions with BDM, the solution was exchanged back to control solution to test the reversibility of BDM effects; only when force was reversed to 85 per cent or above of control levels the experiments were deemed as acceptable. Typically, myofibrils were subjected to four activation–stretch cycles before showing significant loss in force production or disarray of sarcomeres. In additional experiments (n=17), myofibrils were stretched at different constant velocities, chosen in a range between 0.25 and 5.5 μm s⁻¹ SL⁻¹ (approx. 0.10–2.4 L₀ s⁻¹).

(e) Data analysis

The transition between the two phases of force increase during stretch was defined by fitting the data with two lines with different slopes (Stienen et al. 1992; Getz et al. 1998; Pinniger et al. 2006; Roots et al. 2007). The point at which the lines intersect was considered the force transition point. Linearity of the data fitting was confirmed by regression analysis, and for the purpose of this study the transition was considered non-existent if the results were not satisfactory (r²<0.98). The F_c was defined as the force obtained at the transition point during the stretch. The SL_c was defined as the stretch amplitude measured from the beginning of stretch to the transition point. In each myofibril, the SL_c was defined for the average SL and for individual sarcomeres. All results are shown as mean±s.e.m.

3. Results

(a) Force during activation and stretch of the myofibrils

When fully activated, force increased rapidly (figure 2). Myofibrils (n=40) produced an average isometric force of 230±20.15 nN, levels comparable to previous studies (Colomo et al. 1997; Rassier et al. 2003b; Telley et al. 2006a,b; Joumaa et al. 2007, 2008a,b). The average stress (force normalized per cross-sectional area) was 96.42±28.11 nN μm⁻², lower than that usually reported in myofibrils; while a difference in temperatures among studies may be responsible for the difference, the cross-sectional area was defined optically, and therefore it may contain small errors. Since this study was concerned mostly with relative force changes during the stretch in a given myofibril, the conclusions should not be affected by this potential limitation. Passive forces were negligible in the SL range investigated.

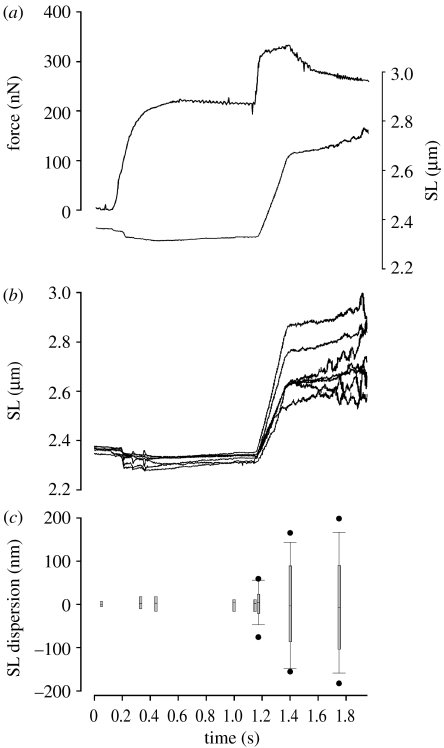
Figure 2.

Experiment performed with a skeletal muscle myofibril. (a) Resting myofibril set at an average SL of 2.36 μm, when maximum sarcomere dispersion was 30 nm. Upon full activation the average SL was shortened by 51.7 nm and maximum sarcomere dispersion was 54.2 nm. Stretch was performed from 2.33 to 2.67 μm (14.4% L₀), at a nominal velocity of 1 μm s⁻¹ SL⁻¹. Force increased during stretch and it was 1.54 times the isometric force at the end of stretch. (b) Individual sarcomere dynamics during activation and stretch. All sarcomeres shortened during activation by different amounts, which increased the sarcomere non-uniformity to reach 38.3 nm just before stretch. During myofibril stretch all sarcomeres stretched, albeit by different amounts. The dispersion of sarcomeres increased significantly during stretch, to reach a maximum of 326.2 nm at the end of stretch. After stretch, the sarcomere dispersion kept increasing to reach a maximum of 355.5 nm. (c) Dispersion of SLs during experiments with control myofibrils. SLs were non-homogeneous at the rest state, and dispersion increased when myofibrils were activated. Stretch increased SL dispersion. Boxplots represent median and 95% confidence intervals, and circles indicate outliers.

(b) Sarcomere dynamics during activation and stretch of the myofibrils

Sarcomeres presented a small non-uniformity at rest (figure 2). In the myofibril shown in figure 2, the maximal SL dispersion at rest was 30 nm, and was not correlated with the sarcomere position in the myofibril. From eight sarcomeres shown in this myofibril, the largest dispersion was observed between the first S1 and the fifth S5 sarcomeres, while the smallest dispersion was observed between the fifth S5 and eighth S8 sarcomeres. This result suggests that the variability in resting SL is randomly distributed, and associated with the properties of passive elements inside the myofibrils, as shown previously (Telley et al. 2006a).

Although sarcomere dynamics were measured continuously, SLs and dispersion was evaluated during chosen fixed times during the experiments for comparisons, as shown in figure 2c. Myofibril shortening increased the dispersion of SLs, but the dispersion did not change significantly while the myofibril was maintained isometric during full activation. During stretch all sarcomeres stretched, albeit by different amounts and at the end of stretch, the maximal sarcomere dispersion was higher than before stretch (figures 2 and 3). Sarcomeres that shortened or stretched more than the average SL were not consistently located in a determined region in the myofibril. However, sarcomeres that were longer before the stretch usually stretched by larger magnitudes than the shorter sarcomeres, especially after the transition in force rise, similar to recent data with permeabilized single fibres (Panchangam et al. in press).

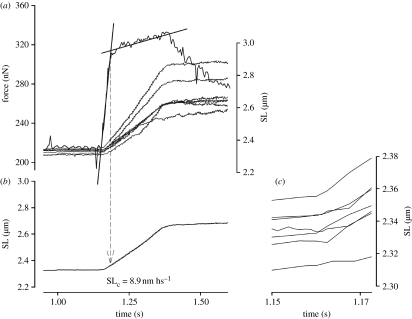
Figure 3.

Close view of the stretch phase in the experiment shown in figure 2. (a) Force trace and superimposed length records for individual sarcomeres. The transition between the fast and the slow phases of force rise was defined by fitting two straight lines. Critical force (F_c), the average critical sarcomere length (SL_c) and critical length for individual sarcomeres were calculated at the transition point between the two force rise phases. In this myofibril, F_c was 1.44 times the isometric force produced before stretch. (b) The SL_c in this myofibril was 8.9 nm hs⁻¹. (c) Superimposed length records for individual sarcomeres. Data were taken from the start of stretch to the point in which SL_c was detected. Note that the maximal dispersion between SLs at the transition phase was 60.9 nm, showing a significant increase from the resting and isometric conditions.

(c) Phase transition on force production and critical sarcomere stretch during stretch

When active myofibrils were stretched, force increased significantly (figures 2 and 3). The increase in force during stretch was divided into two phases, a fast phase and a slow phase (figure 3), as previously observed in experiments with single muscle fibres. The slopes were fitted by two lines and the intersection point was used to define F_c and SL_c.

In the first series of experiments (n=23), the F_c was 1.62±0.24 times the isometric force when the stretch was produced at a nominal velocity of 1 μm s⁻¹ SL⁻¹. The average SL_c was obtained at 8.4±0.85 nm hs⁻¹. Since the sarcomeres stretched by different magnitudes during myofibril stretch, the SL_c in individual sarcomeres were different in a given myofibril (figure 3).

(d) Effects of BDM

Addition of 1 mM BDM to the experimental chamber caused a decrease in isometric force (figure 4) to 21.45±9.22 per cent (n=23) of the isometric force produced during the control situation. This decrease in force was larger than that observed in a previous study with myofibrils, which reported a decrease in force of approximately 30 per cent with the administration of 2 mM of BDM (Tesi et al. 2002). The current experiments were different in that the myofibrils were treated with BDM and then activated, while Tesi et al. (2002) have infused BDM into the experimental chamber during the activation of the myofibrils. While there is no reason to believe that the protocol difference would cause the difference in BDM-induced force inhibition, there is not a clear explanation. Since the variability of BDM-induced force decrease in the myofibrils was small (s.e.m.=9.22%), the results seem to reflect a consistent measurement among all myofibrils in the current experiments.

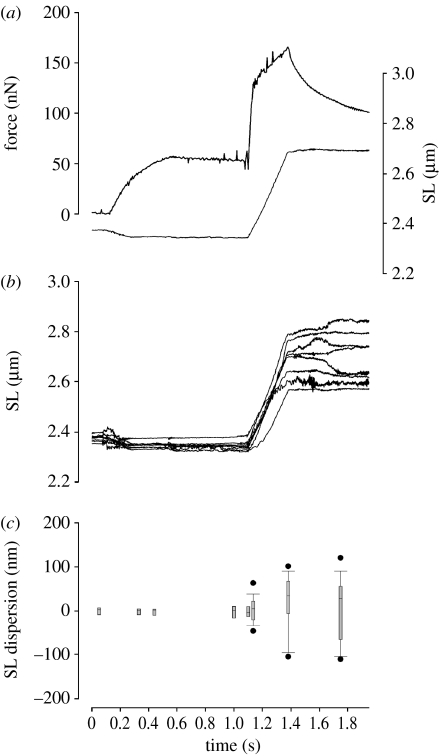
Figure 4.

Typical experiment performed with a skeletal muscle myofibril treated with 1 mM BDM. (a) Resting myofibril was set at an average SL of 2.37 μm, when maximum sarcomere dispersion was 38.7 nm. Upon full activation, the average SL was shortened by 51.7 nm. Stretch was performed from 2.34 to 2.60 μm (11.1% L₀), at a nominal velocity of 1 μm s⁻¹ SL⁻¹. In this example, BDM decreased isometric force to 24.72 per cent P₀. (b) Individual sarcomere dynamics are shown and resemble that observed in control myofibrils. (c) Dispersion of SLs during experiments with BDM-treated myofibrils. The pattern is similar to that observed with control myofibrils—SLs were non-homogeneous at the rest state, and dispersion increased when myofibrils were activated. Boxplots represent median and 95% confidence intervals, and circles indicate outliers.

During this first series of experiments (n=23), the transition point could be identified reliably in most experiments (figure 4), although the increase in force sometimes showed a curvilinear shape. In a few experiments the force dropped more than 85 per cent of the initial value; in these myofibrils the transition force could not be detected. When the stretch was performed at 1 μm s⁻¹ SL⁻¹, the F_c in the BDM-treated myofibrils was 2.35±0.34 times the isometric force. Force at the peak of stretch was 3.01±0.76 times the isometric force.

Sarcomere dispersion was similar to that observed in untreated myofibrils (figure 4). Myofibril shortening increased the dispersion of SLs significantly, but during the isometric period of activation the SL dispersion remained relatively constant. During myofibril stretch, sarcomeres stretched by different amounts, similar to what was observed with control myofibrils (figures 4 and 5). BDM increased the SL_c significantly when compared with the control myofibrils (figures 4 and 5), with an average value of 14.6±0.6 nm hs⁻¹ when stretch was performed at 1 μm s⁻¹ SL⁻¹. The maximal SL dispersion increased during stretch to reach a peak at the end of stretch, as observed in control experiments.

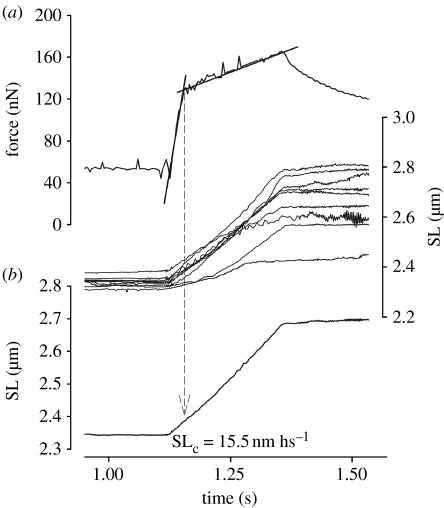
Figure 5.

Close view of the stretch phase in the experiment shown in figure 4. (a) Force trace and superimposed length records for individual sarcomeres. The F_c in this myofibril was 1.92 times the isometric force produced before stretch, and the force at the end of stretch was 3.16 times the isometric force. (b) The average critical SL in this myofibril was 15.5 nm hs⁻¹.

(e) Effects of stretch velocity

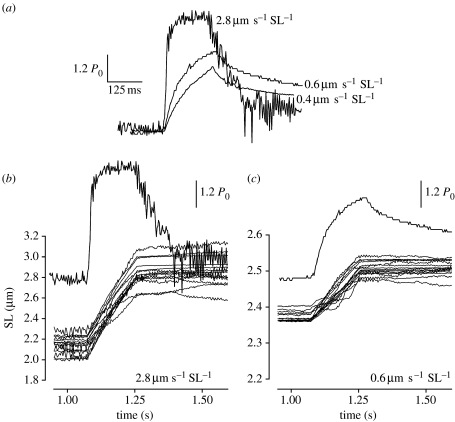
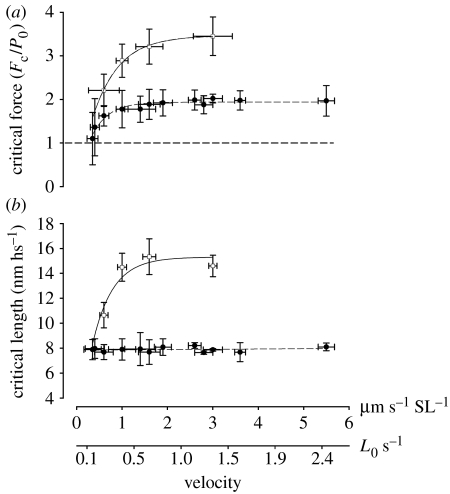
When different velocities were used during the stretch, the pattern of force changed considerably. The transition point was clearly observed in stretches performed at 0.6 μm s⁻¹ SL⁻¹ or higher, and could be visually fitted with two straight lines (figure 6). At velocities of 0.4 and 0.35 μm s⁻¹ SL⁻¹, the transition point was detected only in four myofibrils and at lower velocities it was not detectable. Force at the transition point increased with increasing velocities up to approximately 1.5 μm s⁻¹ SL⁻¹ (figure 7), and then stayed constant. SL_c did not change significantly with different velocities of stretch (figure 7). Furthermore, the SL dispersion at the transition point did not change as a function of velocity.

Figure 6.

The dependence of stretch velocity on the force produced by myofibrils. (a) Activated myofibrils stretched at three constant velocities. The increase in force during stretch is more accentuated at higher velocities. In this example, the transition on force rise could be defined when stretches were performed at 2.8 and 0.6 μm s⁻¹ SL⁻¹, while it was not detectable when stretch was performed at 0.4 μm s⁻¹ SL⁻¹. Peak forces in these examples were 1.84, 1.58 and 1.42 P₀ (from faster to slower stretches), and F_c were 1.80 and 1.40 P₀ (not detected when stretched was performed at 0.4 s⁻¹ SL⁻¹). Bars depict values 20 per cent above isometric forces. (b,c) Force traces and superimposed length records for individual sarcomeres when stretch was performed at 2.8 and 0.6 μm s⁻¹ SL⁻¹, respectively.

Figure 7.

The relationship between critical force (F_c), critical average sarcomere length (SL_c) and velocity of stretch (n=17). Each mean value is a result of four to five experiments. Circles, control myofibrils; squares, BDM-treated myofibrils. (a) In control myofibrils, F_c increased significantly with increasing velocities to reach a plateau at 1.5 μm s⁻¹ SL⁻¹, after which it did not change significantly. BDM-treated myofibrils show a continuous increase in force in long lengths, and a plateau in the F_c-velocity curve was not obtained in the present experiments, although force increase seems to be levelling off at approximately 3.5–3.6 P₀. The horizontal line shows isometric reference force (F_c/P₀=1). Data for BDM and control experiments were fitted by an exponential equation (y=a(1−bx), where a and b are constants). (b) Velocity of stretch did not affect the SL_c, with the exception of BDM-treated myofibrils that showed a sudden increase in SL_c when velocity was changed from 0.6 μm s⁻¹ SL⁻¹ to faster stretches. Data for BDM experiments were fitted by an exponential equation (y=a(1−bx), where a and b are constants) and data for control experiments were fitted by linear regression.

4. Discussion

The first purpose of this study was to investigate the F_c and SL_c at the transition in force increase during myofibril stretch. The experiments showed that force rises to approximately 2 P₀ with increasing velocities of stretch up to 1.5 μm s⁻¹ SL⁻¹, and that the average SL_c was 8.4 nm hs⁻¹. Although these results confirm some of the previous studies with muscle fibres, it is the first time they were observed in isolated myofibrils, preparations in which individual sarcomeres can be evaluated without confounding effects arising from other cellular structures. Numbers taken from the F_c and SL_c are commonly used for cross bridge modelling (e.g. Getz et al. 1998; Roots et al. 2007), and therefore this study contributes effectively to a better understanding of the sarcomeric mechanisms of force produced during stretch. A second purpose of this paper was to test the hypothesis that stretch forces are caused largely by pre-power stroke cross bridges (Getz et al. 1998; Chinn et al. 2003; Pinniger et al. 2006). BDM, which biases cross bridges into the pre-power stroke state (Zhao & Kawai 1994; Regnier et al. 1995), increased F_c and SL_c relative to control (non-treated) contractions, suggesting that pre-power stroke cross bridges are largely responsible for force produced during stretch. These cross bridges acting in lower force states would be able to stretch to longer lengths before reaching a critical strain before detaching from actin. This mechanism would explain the low energy cost for stretch contractions observed in previous experiments (Abbott et al. 1951; Linari et al. 2003).

(a) Comparison with studies using isolated muscle fibres and bundles

The F_c of 1.69±0.24 when stretch was performed at 1 μm s⁻¹ SL⁻¹ (approx. 0.43 L₀ s⁻¹), and forces that increase to approximately 2 P₀ with increasing velocities up to 2.6 μm s⁻¹ SL⁻¹ (approx. 1.13 L₀ s⁻¹) are in the range of most studies performed previously (Colomo et al. 1989a,b; Lombardi & Piazzesi 1990; Stienen et al. 1992; Pinniger et al. 2006; Colombini et al. 2007; Roots et al. 2007), confirming that the myofibrils behave similar to larger scale systems. At velocities higher than 2.6 μm s⁻¹ SL⁻¹ the force did not change significantly, also confirming previous results (Colomo et al. 1989a,b; Lombardi & Piazzesi 1990; Stienen et al. 1992; Pinniger et al. 2006; Colombini et al. 2007; Roots et al. 2007).

Studies with single intact cells from frog and mouse show SL_c between 9 and 13 nm hs⁻¹ when SL is controlled (clamped) during the experiments (Lombardi & Piazzesi 1990; Colombini et al. 2007), and SL_c between 14 and 28 nm hs⁻¹ nm when SL is not controlled (Colomo et al. 1989a,b; Stienen et al. 1992; Pinniger et al. 2006; Roots et al. 2007). In the present experiments the sarcomeres were not controlled at a given length, but the length of all sarcomeres in a myofibril was measured, and therefore the critical stretch for the individual sarcomeres irrespective of non-uniformities that were present during the experiments was evaluated. Although the average SL_c of 8.4 nm hs⁻¹ in the current experiments is lower than that reported in studies in intact fibres, it is consistent with a critical stretch of 8 nm hs⁻¹ in a study performed with permeabilized fibres from the rabbit psoas (similar to the preparation used in this paper) that used SL control (Getz et al. 1998). Therefore, myofibrils follow the same pattern as those observed with single fibres when sarcomeres are controlled.

Significant sarcomere non-uniformity has been observed during muscle contraction and stretch of single muscle fibres and bundles (Julian et al. 1978; Edman & Reggiani 1984; Lombardi & Piazzesi 1990). The dispersion at the end of stretch in the current experiments was larger than previously observed, but most importantly the dispersion at the force transition point, where SL_c was measured, was only approximately 40–100 nm. Such dispersion is probably not responsible for changes in stretch forces when compared with other studies, as sarcomeres are still contracting on the plateau of the force–length relationship, and therefore the forces shared among them are conceptually similar. The reason why the total dispersion of SLs in myofibrils is larger than that observed in muscle fibres is not clear. It may be related to proteins connecting adjacent parallel sarcomeres and myofibrils inside the fibres, which may avoid large sarcomere displacements. More research is needed to understand the causes of such large SL dispersion.

(b) Effects of BDM on force

BDM decreased isometric forces, as shown previously (Fryer et al. 1988; Higuchi & Takemori 1989; Higuchi et al. 1989; Seow et al. 1997; Rassier & Herzog 2004). It is known that BDM decreases stiffness to a lesser extent than isometric forces (Fryer et al. 1988; Higuchi et al. 1989; Higuchi & Takemori 1989; Seow et al. 1997; Rassier & Herzog 2004). Assuming that filament compliance is not significantly affected by BDM, and that stiffness is a good indication of the number of cross bridges attached to actin (Ford et al. 1981), the main effects of BDM cannot be explained uniquely by a decreased proportion of cross bridges; instead, BDM affects the average force per attached cross bridge. Biochemical studies show that BDM binds to the cross bridges and decreases the rate of phosphate release (Higuchi & Takemori 1989; Herrmann et al. 1992; Zhao & Kawai 1994). BDM would therefore stabilize the complex AM-ADP-P_i, which corresponds to the pre-power stroke state. With cross bridges in a pre-power stroke state, and assuming that the stretch forces would be caused mainly by these bridges, an increase in the stretch forces when normalized to the isometric forces, caused mostly by post-power stroke cross bridges, would be expected.

The results of this study agree qualitatively with studies showing that the phosphate analogues vanadate (V_i) and aluminium fluoride (AlF₄), which also bias cross bridges into a pre-power stroke position, reduce isometric force of fibres treated with polyethylene glycol (which promotes myosin–actin interactions), but do not decrease stretch forces by the same magnitude (Getz et al. 1998; Chinn et al. 2000, 2003). Conversely, experiments with muscle fibres tested at increasing temperatures, thought to shift cross bridges towards strongly bound states, show opposite results, i.e. the stretch/isometric force ratios are decreased (Coupland et al. 2001; Wang & Kawai 2001; Piazzesi et al. 2003; Colombini et al. 2008).

Although our results agree with earlier studies using phosphate analogues other than BDM (Getz et al. 1998; Chinn et al. 2000, 2003), they are different from data presented by Bagni et al. (2005). The authors observed that, on using BDM, it reduced isometric and critical forces linearly. While there is not an easy explanation for the discrepant results, they might be explained by different experimental conditions. Bagni et al. (2005) tested fibres isolated from the frog tibialis anterior muscle at approximately 14°C, and used very fast stretches (9.5–33 L₀ s⁻¹), which would avoid cyclic cross bridges contributing to their measurements. Such differences in muscle preparation and specimen, temperature and stretch velocity make comparisons complicated. Especially, the stretch velocity should affect results considerably, as in the current study a small population of cycling cross bridges might have been present during stretch, although it is not clear how that would affect the general pattern of changes observed. While the fast velocities used by Bagni et al. (2005) are highly appropriate to measure cross bridge kinetics, slower stretches as the ones used here and by others (e.g. Edman et al. 1978, 1981; Flitney & Hirst 1978; Lombardi & Piazzesi 1990; Piazzesi et al. 1992; Stienen et al. 1992; Bagni et al. 2003, 2005; Pinniger et al. 2006; Roots et al. 2007) are appropriate to test skeletal muscles in physiological velocity ranges. Future studies using myofibrils should repeat the protocol used by Bagni et al. (2005) to further investigate the reasons for such difference.

(c) Effects of BDM on critical length

Critical length was increased in BDM-treated myofibrils. Although not many studies have consistently measured the effects of phosphate analogues on the critical sarcomere length, Stienen et al. (1992) observed that the critical sarcomere extension increased from approximately 1 to 2 per cent L₀ after addition of 15 mM P_i. These results together with the SL_c changes reported in the present study suggest that the cross bridges populating a pre-power stroke state must be stretched to longer lengths before detaching from actin. If it is assumed that cross bridges detach mechanically at a given strain/force, the results of this study imply that pre-power stroke cross bridges would accommodate greater strains than strongly bound cross bridges before detaching from actin. This argument is online with several kinetic models (e.g. Lombardi & Piazzesi 1990; Getz et al. 1998; Pinniger et al. 2006), suggesting that cross bridges in the AM-ADP-P_i state attach to actin at low strains, and get carried to higher strains during lengthening where they exert increasingly higher forces, and then detach from actin.

Recent experiments performed by Colombini et al. (2007) showed that when single muscle fibres are submitted to fast stretches, the critical length for myosin detachment varies according to the force produced by the cross bridges prior to stretch. When the force is potentiated by a slow stretch (90% force enhancement), the SL_c decreases from 13.04 to 8.19 nm hs⁻¹, indicating that cross bridges are strained 4.85 nm hs⁻¹ more during high forces, and therefore less elongation is needed to detach these bridges. Colombini et al. (2007) suggested that strained cross bridges develop a greater individual force and therefore, compared with isometric conditions, a smaller elongation is needed to raise their force up to the rupture force. Following the same logic, the SL_c should increase progressively with smaller forces and strains in the cross bridges as induced by BDM in the current experiments. With a reduction of approximately 75 per cent of force induced by BDM, the SL_c increased by 6.2 nm hs⁻¹, suggesting that cross bridges are strained by 6.2 nm hs⁻¹ less after BDM treatment, causing the cross bridges to stretch to longer lengths to achieve higher strains before detaching from actin.

(d) Additional mechanisms to explain the differences in F_c and SL_c observed in BDM-treated myofibrils

Potentially, F_c and SL_c values could be affected by (i) SL non-uniformity during stretch (Julian & Morgan 1979; Lombardi & Piazzesi 1990), (ii) the stiffening of passive elements (Bagni et al. 2002, 2004) or (iii) compliance of the myofilaments (Huxley et al. 1994; Wakabayashi et al. 1994). However, it seems unlikely that these mechanisms would alter the interpretation of this study. (i) Sarcomere non-uniformity increased significantly during stretch, but during the transition point where all critical measurements were taken it was still small, as discussed earlier. At the force transition, sarcomeres never shortened during myofibril stretch and never stretched to a non-overlap zone (i.e. they never ‘popped’; Morgan 1994), where passive forces could be significantly high. Previous studies in which slow stretches along the plateau and descending limb of the force–length relationship were applied to myofibrils (Telley et al. 2006b; Joumaa et al. 2008a) also failed to observe ‘popping’ sarcomeres. (ii) It is recognized that passive elements may contribute significantly to force during stretch of activated muscles, independent of cross bridges (Bagni et al. 2002, 2004; Rassier & Herzog 2004; Rassier et al. 2005; Pinniger et al. 2006), most likely through Ca²⁺-induced structural alterations in titin molecules. It is known that titin's persistence length decreases with high Ca²⁺ concentrations, which would increase forces beyond the forces produced during a passive stretch (Labeit et al. 2003). However, the contribution of such passive elements is small during the first phase of force increase during stretch, and would contribute to force significantly only after the break between the two phases (Pinniger et al. 2006). Furthermore, the optimal SL for the force produced by the activity-induced engagement of the passive elements is approximately 2.8 μm (Bagni et al. 2002; Rassier & Herzog 2004), while the current experiments were performed at shorter SLs. (iii) Filaments compliance could affect the force during stretch. The filament compliance accounts for approximately 50 per cent of the sarcomeres compliance (Huxley et al. 1994; Wakabayashi et al. 1994), but their contribution to the total strain–force relationship is unknown, and certainly small. When isolated thick and thin filaments are stretched from zero tension to maximal physiological tensions, strains of 0.3 and 1.5 per cent are observed, respectively (Neumann et al. 1998; Liu & Pollack 2002), a value that is too small to explain the changes observed in this study. Even if one assumes that the compliance would affect the results and explain part of the stretch forces, BDM does not probably affect the compliance of the filaments, and therefore the comparisons made between the two situations are still valid.

5. Summary

The current experiments show that F_c and SL_c increased after myofibrils were treated with BDM, suggesting that most of the increase of tension during stretch is due to cross bridges attached in a pre-power stroke state, which are probably extended into a region of high force by the stretch (Getz et al. 1998; Pinniger et al. 2006; Roots et al. 2007). Such cross bridges would produce small forces during isometric contractions and large forces when stretched.