Stochastic spread of Wolbachia

Abstract

Wolbachia are very common, maternally transmitted endosymbionts of insects. They often spread by a mechanism termed cytoplasmic incompatibility (CI) that involves reduced egg hatch when Wolbachia-free ova are fertilized by sperm from Wolbachia-infected males. Because the progeny of Wolbachia-infected females generally do not suffer CI-induced mortality, infected females are often at a reproductive advantage in polymorphic populations. Deterministic models show that Wolbachia that impose no costs on their hosts and have perfect maternal transmission will spread from arbitrarily low frequencies (though initially very slowly); otherwise, there will be a threshold frequency below which Wolbachia frequencies decline to extinction and above which they increase to fixation or a high stable equilibrium. Stochastic theory was used to calculate the probability of fixation in populations of different size for arbitrary current frequencies of Wolbachia, with special attention paid to the case of spread after the arrival of a single infected female. Exact results are given based on a Moran process that assumes a specific demographic model, and approximate results are obtained using the more general Wright–Fisher theory. A new analytical approximation for the probability of fixation is derived, which performs well for small population sizes. The significance of stochastic effects in the natural spread of Wolbachia and their relevance to the use of Wolbachia as a drive mechanism in vector and pest management are discussed.

1. Introduction

A purely maternally inherited gene, parasite or symbiont will not tend to increase in frequency unless it causes its host to have more female offspring relative to a non-carrier. One way of doing this is to bias the sex ratio towards females, while another way is to be a mutualist and somehow increase host fitness directly. A third approach is to damage the fitness of non-carriers so that the relative fitness of carrier females increases. Wolbachia provide the best-known example of this strategy. These intracellular bacteria (Alpha Proteobacteria) often spread through arthropod host populations by a process called cytoplasmic incompatibility (CI; Hoffmann & Turelli 1997). In a way that it is not yet fully understood at the molecular level, CI-causing Wolbachia modify sperm such that uninfected females that mate with infected males suffer reduced embryo viability and hence lower relative fitness (Werren 1997). Wolbachia infections are found in over 20 per cent of all insects (Werren et al. 1995; Werren & Windsor 2000) and their presence may influence population structure and speciation (Shoemaker et al. 1999; Bordenstein et al. 2001). Wolbachia may also spread in insects through manipulating host reproduction in other ways (Hurst et al. 1999, 2002), and also occur as beneficial symbionts in nematodes (Bandi et al. 1998). Here we concentrate solely on CI-inducing Wolbachia, though our arguments also apply to the unrelated bacterium Cardinium that can also spread by CI (Hunter et al. 2003; Zchori-Fein & Perlman 2004).

The relative fitness of a Wolbachia carrier depends on: (i) any direct fitness costs imposed by the bacteria on the host, (ii) the effective fecundity reduction of uninfected females that mate with a Wolbachia-bearing male, (iii) the probability that Wolbachia is transmitted to offspring, and (iv) the frequency of Wolbachia carriers in the population. Where there are no fitness costs to the carrier but perfect transmission, infected females will always produce more Wolbachia-carrying daughters than uninfected individuals having female offspring and hence the infection will invariably tend to spread, though the rate of increase will be very slow at low frequencies. Assuming random mating (Hoffmann et al. 1990; de Crespigny & Wedell 2007), when Wolbachia reduces host fitness from 1 to 1−s_f<1 and when mating with a Wolbachia-bearing male reduces a non-carrier's fitness from 1 to 1−s_h<1, there is a threshold infection frequency, s_f/s_h, above which Wolbachia is expected to spread to fixation, but below which its frequency is expected to decline to 0 (Caspari & Watson 1959). Mathematically, the threshold and fixation frequencies are, respectively, unstable and stable equilibria. If transmission is not perfect (μ>0) and uninfected ova from infected females are susceptible to CI, then the threshold becomes $\hat{p}$ and instead of becoming fixed the Wolbachia reaches an equilibrium frequency p^*. The values of $\hat{p}$ and p^* are given by (Hoffmann et al. 1990; Turelli & Hoffmann 1991)

$$\begin{array}{c}\hat{p}=\frac{s_{\text{f}}+s_{\text{h}}-\sqrt{{\left(s_{\text{f}}+s_{\text{h}}\right)}^2-4(\mu (1-s_{\text{f}})+s_{\text{f}})(1-\mu (1-s_{\text{f}}))s_{\text{h}}}}{2(1-\mu (1-s_{\text{f}}))s_{\text{h}}}\\ p^{*}=\frac{s_{\text{f}}+s_{\text{h}}+\sqrt{{\left(s_{\text{f}}+s_{\text{h}}\right)}^2-4(\mu (1-s_{\text{f}})+s_{\text{f}})(1-\mu (1-s_{\text{f}}))s_{\text{h}}}}{2(1-\mu (1-s_{\text{f}}))s_{\text{h}}}\end{array}\}.$$ (1.1)

It is thought that Wolbachia infections arise in naive populations through rare interspecific horizontal transfer (Vavre et al. 1999). The initial infection frequency is thus likely to be very low, and this produces a barrier to spread whenever costs are present, as observed in several systems (Hoffmann et al. 1990; Min & Benzer 1997; Poinsot & Mercot 1997; Vavre et al. 1999).

If the initial number of infected hosts is very low, stochastic effects will be important. Even if a Wolbachia with complete CI and perfect transmission (s_h=1, μ=0) has no costs to its hosts (s_f=0) or is beneficial (s_f<0) (Vavre et al. 1999; Dobson et al. 2002; Weeks et al. 2007), the risk of stochastic loss may still be great, especially in large populations where CI will affect the relative fitness of non-carriers only marginally. Conversely, Wolbachia may still establish when its initial frequency is low if stochastic processes carry its frequency above the threshold. Stochastic effects in Wolbachia were first studied by Rigaud & Rousset (1996) who stated that, based on the Wright–Fisher model, the probability of fixation of Wolbachia after the introduction of a single infected individual, u(1/N), was

$$u(1/N)\approx 2\sqrt{\frac{s_{\text{h}}}{\pi N}}\text{exp}\left(\frac{-N{s}_{\text{f}}^2}{s_{\text{h}}}\right),$$ (1.2)

where N is the population size (number of females). (Their expression omits ‘2’, but this is clearly a typographical error.) For cost-free infections (s_f=0), they further write that $u(1/N)=2\sqrt{s_{\text{h}}/\pi N}$. Later, Egas et al. (2002), unaware of this earlier work, simulated the spread of Wolbachia and showed that the probabilities of fixation were low (less than approx. 0.1) for population sizes greater than 100 females, and declined further in the presence of costs to bacterial carriage or imperfect transmission. However, as demonstrated below, equation (1.2) provides a rather poor approximation for the simulation results of Egas et al. (2002) (and our own numerical studies) for the biologically most interesting cases of small N. Here we provide robust new approximations of fixation probabilities applicable to small population sizes, as well as exact results for one particular set of demographic assumptions (which determine the relationship between effective and census population sizes). We also extend the model to include situations when the probability of Wolbachia non-transmission to offspring (μ) is greater than 0.

In addition to their intrinsic interest and importance, Wolbachia are also being widely studied as possible means of driving beneficial genes through populations of pests and disease vectors, or for manipulating host phenotypes in ways advantageous to man (Turelli & Hoffmann 1999; Dobson et al. 2002; Brownstein et al. 2003; Sinkins & Gould 2006). In these situations, Wolbachia-bearing individuals would be mass reared and released at relatively high frequencies, above the threshold at which, as deterministic theory predicts, they should increase in frequency. In designing control strategies involving Wolbachia release, it will be important to understand how stochastic processes affect the probability of bacterial spread or fixation. To address these questions, we determine fixation probabilities (u(p₀)) when an arbitrary fraction of individuals (p₀) carrying Wolbachia are introduced into a population.

2. Model

Our model is a stochastic version of that analysed by Caspari & Watson (1959) and Turelli & Hoffmann (1999). We assume that the population (number of females) is of constant size, N, and that uninfected female fecundity is λ (measured as the number of female offspring with a constant sex ratio of 0.5), with the fecundity of infected females being λ(1−s_f). If there are currently x infected females, they will produce θ_i=xλ(1−s_f)(1−μ) infected offspring, while uninfected female production will be θ_u=((N−x)λ+xλ(1−s_f)μ)[1−s_h(x/N)]. The term in square brackets represents the fitness reduction caused by CI suffered by uninfected eggs fertilized by sperm modified by Wolbachia-carrying males.

We implement this model in two different ways. First, by using the Wright–Fisher method (Crow & Kimura 1970), which assumes that the generations are discrete and that the new generation is a random sample of constant size drawn from the total number of offspring produced by the previous generation. The second implementation is based on the continuous-time Moran process (1958), and assumes overlapping generations (as in the classic birth–death process, Karlin & Taylor 1975, ch. 4). This model assumes that individuals die randomly and sequentially and are replaced by new individuals randomly drawn from the offspring produced by the population. Both approaches thus assume idealized populations, the main biological difference being that the Wright–Fisher model assumes discrete and the Moran model overlapping generations. The Wright–Fisher model has been used extensively in population genetics, facilitating comparisons with previous results. An analysis based on the Wright–Fisher model requires the standard assumptions of a diffusion approximation concerning the strength of selection but allows a flexible connection between census population size (N) and variance effective population size (N_e). The latter is the size of an idealized panmictic population of identical individuals that would experience the same sampling-induced variance of infection frequencies as the actual population under study. The Moran analysis gives exact solutions but assumes a particular demography and hence a specific relationship between census and effective population sizes (Crow & Kimura 1970, ch. 7).

Deterministic models predict that as long as the infection frequency is above the critical threshold, it will become established. By this we mean that it will increase to fixation, p^*=1, or when transmission is incomplete (μ>0) to a stable equilibrium, p^*<1. More formally, if p₀ is the current infection frequency and u(p₀) the probability of establishment, then u(p₀)=0 for $p_0<\hat{p}$ and u(p₀)=1 for $p_0>\hat{p}$, where $\hat{p}$ is given by equation (1.1). In the electronic supplementary material, we describe in detail how expressions for u(p₀) can be calculated for finite populations influenced by stochastic processes using either the Moran or Wright–Fisher approaches. The main mathematical results are given in appendix A.

3. Results

As mentioned in §1, study of the stochastic spread of Wolbachia is relevant to two issues: first, to Wolbachia dynamics in natural populations where transfer between species is rare, most likely involving the infection of very few individuals or even one (i.e. p₀=1/N), and, second, to the applied use of Wolbachia in pest and disease vector management; here the probability of spread with much larger initial numbers of infected individuals (p₀≫1/N) is of interest. We explore each in turn.

(a) Spread of Wolbachia from a very low initial frequency

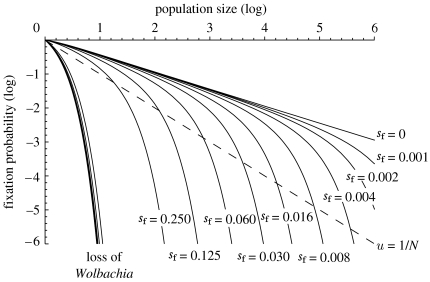
The probability that a neutral or deleterious Wolbachia will spread to fixation in a finite population is shown in figure 1, where it is assumed that CI is complete (s_h=1) and Wolbachia transmission perfect (μ=0). To plot these figures, the exact results from the Moran analysis (equation (A 4) in appendix A) were used. The probability of fixation decreases with population size, as would be expected of a stochastic genetic process. The slope of decline on the double logarithmic plot is −1/2 and hence the fixation probability is proportional to $1/\sqrt{N}$. This is considerably greater than that for a neutral chromosomal gene or maternally inherited element without CI, where the equivalent expression is proportional to the reciprocal of population size (1/N). When the population size is small, the probability of fixation of a weakly deleterious Wolbachia is similar to the neutral value (i.e. s_f=0, s_h>0), but the discrepancy grows rapidly as population size or the magnitude of the deleterious effect increases. We found that decreasing the efficiency of CI (s_h<1) has the same effect as approximately increasing population size by an amount (1/s_h), an observation we confirm analytically below.

Figure 1.

The probability of fixation of Wolbachia following the introduction of a single female into a population of effective population size N. A range of values of costs (s_f≥0) are plotted, and it is assumed that uninfected females are completely incompatible with infected males (s_h=1). For comparison, the probability of fixation of a neutral, maternally inherited element that does not induce CI is also shown (dashed line). The curves marked ‘loss of Wolbachia’ describe the probability that the infection will be lost after the appearance of a single individual without the bacteria (the same values of s_f are plotted, but as all curves are very similar they are not labelled separately).

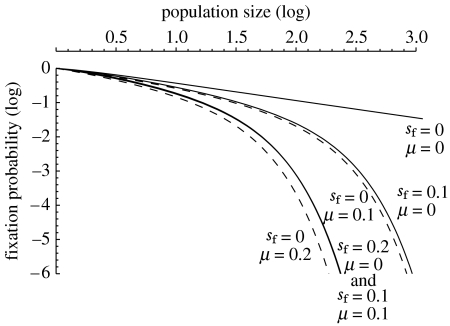
When transmission is imperfect (μ>0), the Wolbachia never reaches a frequency of 1, but we can calculate the probability that it increases in frequency to the stable equilibrium given in equation (1.1) (figure 2). For low values of μ, the reduction in the likelihood of establishment is very similar to the effect of the cost of bacterial carriage (s_f): increasing either by the same amount has similar consequences. The two effects are also roughly additive in the sense that the probability of fixation of a strain with μ=s_f=x is approximately the same as that of a strain with μ=2x and s_f=0 or μ=0 and s_f=2x.

Figure 2.

The probability of fixation of Wolbachia following the introduction of a single female into a population with effective population size N. Probabilities of a neutral Wolbachia and then strains with different combinations of fitness costs (s_f) and probabilities of the non-transmission of the bacterium to offspring (μ) are shown. CI is assumed to be complete (s_h=1).

The equivalent fixation probabilities of a Wolbachia strain that imparts a fitness benefit to its host are shown in figure 3 (which assumes s_h=1 and μ=0). For low population sizes, the probability of fixation is again similar to that of the neutral case; but for stronger benefits and in larger populations, the relative probability of fixation increases. As population size increases, the probability of fixation asymptotes at a figure that is higher for more beneficial bacteria. Note that although the deterministic models always predict beneficial Wolbachia to spread from a single infection, the actual probability, taking into account stochastic effects, is always considerably below 1, whatever the population size is, as is true for beneficial mutations.

Figure 3.

The probability of fixation of Wolbachia following the introduction of a single female into a population of effective population size N. The Wolbachia may now be beneficial (s_f≤0) and a range of different values are plotted.

Further insight into these results can be obtained from approximations of the expressions for the fixation probabilities given in appendix A. First assume perfect transmission (μ=0). In the case of the Wright–Fisher model, the population can be characterized by its variance effective population size, N_e, that allows us to model a variety of demographic assumptions. The price of obtaining exact solutions for the Moran process is the need to make a precise demographic assumption that implies N_e/N=1/2 (Ewens 2004, sec. 3.7). For small s_f and p₀≈1/N, but for arbitrary s_h, both the approaches show that the fixation probability can be approximated by a truncated power law (see the electronic supplementary material)

$$u(p_0)\approx 2p_0\sqrt{\frac{N_{\text{e}}{s}_{\text{h}}}{\pi }}\text{exp}\left(-2s_{\text{f}}\sqrt{\frac{N_{\text{e}}}{s_{\text{h}}\pi }}\right).$$ (3.1)

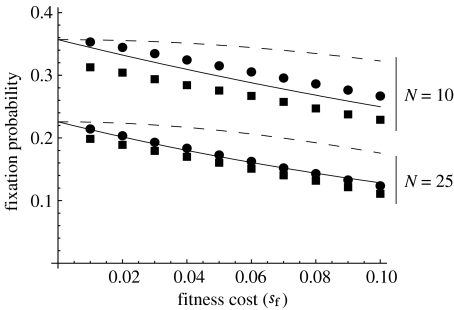
When population size is large, this approximation performs similar to that of Rigaud & Rousset (1996; equation (1.2) above); but when population size is smaller, and fixation probabilities are higher, this result provides a significantly better match to the simulations in Egas et al. (2002) as well as those we have carried out ourselves (figure 4). If the Wolbachia has no effect on host fitness (s_f=0) and N_e/N is constant for populations of different sizes, we obtain

$$u(1/N)\propto \sqrt{s_{\text{h}}/N},$$ (3.2)

which was first derived by Rigaud & Rousset (1996). This matches the patterns in figure 1 and also confirms that the effect of an incomplete CI (s_h<1) is equivalent to inflating population size by a factor 1/s_h.

Figure 4.

Examples of the performance of the diffusion approximations of fixation probability when population size is small (N=10 or 25). The solid lines are the new approximations (equation (3.1)) and the dashed lines the approximations of Rigaud & Rousset (1996, our equation (1.2)). The squares are the results of simulations in Egas et al. (2002) and the circles those from simulations we have carried out. We assumed s_h=1 and μ=0.

Now relax the assumption about perfect transmission. It can be shown (see the electronic supplementary material) that for small s_f and μ, and for p₀≈1/N,

$$u(p_0)\approx 2p_0\sqrt{\frac{N_{\text{e}}{s}_{\text{h}}}{\pi }}\text{exp}\left(-2(s_{\text{f}}+\mu )\sqrt{\frac{N_{\text{e}}}{s_{\text{h}}\pi }}\right).$$ (3.3)

Note that changes in s_f and μ have the same effect on fixation probability, a finding that closely matches the results shown in figure 2.

For the parameter values used in figure 1, the fixation probabilities for deleterious Wolbachia converge to those for the neutral case (i.e. s_f=0, s_h>0) in ‘small’ populations. We can state more generally the conditions under which this is true. As is explained in the electronic supplementary material, the probability of fixation is roughly proportional to $\sqrt{s_{\text{h}}/N}$ for populations smaller than $N_{\text{e}}\approx (\pi /4)s_{\text{h}}{(s_{\text{f}}+\mu )}^{-2}$. Above this threshold, the negative effects of the Wolbachia are much stronger than stochastic drift, and fixation is much less likely.

For Wolbachia with positive effects on host fitness, figure 2 shows that fixation probabilities are again well approximated by the neutral case (i.e. s_f=0, s_h>0, μ=0) for small population sizes and small fitness effects, but asymptote as population size increases. It can be shown that when p₀≈1/N and μ=0, the asymptotic value is 2s_fN_ep₀, which increases with fitness benefit, initial frequency and effective population size. For the particular demography assumed in figure 1 (N_e/N=1/2) and for a single initially infected individual (p₀=1/N), the log probability of fixation is −s_f: the greater the fitness benefit, the higher the probability of fixation. This result is equivalent to Haldane's (1927) classic demonstration that the probability of fixation in the Wright–Fisher model of a single copy to a beneficial allele is approximately 2s in a large population, where s is the (small) selective advantage to heterozygotes.

Once a Wolbachia strain with perfect transmission has become fixed, there is a possibility that it might be lost by chance events, if a single uninfected individual arises. This probability (which can be calculated as 1−u(1−(1/N)) in equation (A 4) in appendix A) is much lower than the equivalent chance that a rare Wolbachia spreads, and it falls exponentially with population size (figure 1). Similar results are found for established strains with imperfect transmission at their equilibrium density. It is thus unlikely that a population will lose an established Wolbachia infection by stochastic processes, although other biological mechanisms might bring this about (Hurst & McVean 1996; Sinkins & Godfray 2004).

(b) The deliberate introduction of Wolbachia

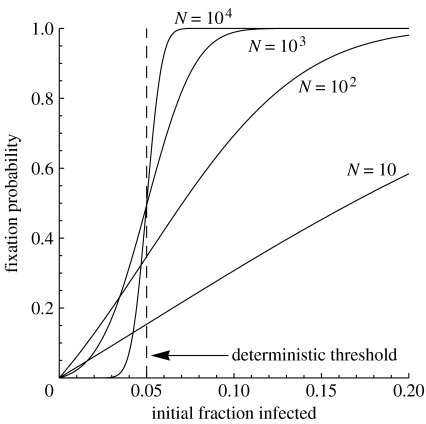
An important question relevant to using Wolbachia to manipulate host populations concerns the number of infected individuals that must be released to ensure establishment with high probability. Deterministic models predict spread and establishment, if the fraction of infected individuals exceeds the threshold given in equation (1.1). The probability of establishment changes from a step to a sigmoid function, when stochastic effects are taken into account (see examples in figure 5). When population sizes are comparatively small, this probability may be substantial at frequencies below the deterministic threshold, while establishment may be far from certain above the threshold. A corollary of this is then that when population size is relatively small, the precise position of the threshold is of less importance and the probability of establishment increases steadily with the number of infected insects released. Note that the probability of fixation or establishment at the deterministic threshold is less than half in finite populations.

Figure 5.

The probability of fixation for different initial frequencies of Wolbachia. We assume s_f=0.05 and s_h=1, so that there is a deterministic threshold infection frequency (dashed line) of 0.05 above which spread occurs. The probability of spread in populations of different size (N) are plotted.

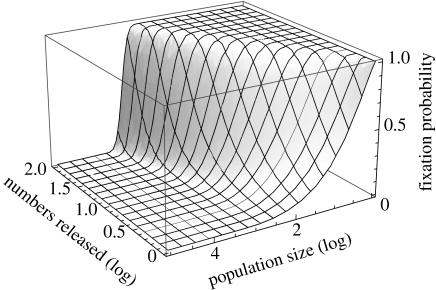
Pest or vector managers involved in practical control programmes will often be faced with decisions about which populations to target with the number of infected insects currently available in the rearing facility, whether to use all the available insects in one population or to split them among several populations; and for host populations that fluctuate in size, whether to release immediately or wait until the wild population is smaller and a higher initial fraction infected can be obtained. The latter is particularly relevant as, almost by definition, pest (and often vector) populations being large and waiting until population bottlenecks occur may be the only feasible way of exceeding the threshold for spread. Even then it is possible that the maximum number of insects available for release is below the threshold, and the pest or vector manager may need to ‘gamble’ on stochastic processes working in his or her favour. Ideally, decisions such as these should be made using a population model tailored to the relevant pest or vector, but where this is unavailable the theory developed here can provide useful guidance. Figure 6 shows the probability of successful establishment when different numbers of Wolbachia-infected insects are released into host populations of different sizes. We have assumed here perfect transmission and complete CI, but both assumptions can be relaxed as appropriate. These probability surfaces, coupled with information about the economics of rearing insects for release and the likely fluctuations in pest or vector population size, can be used to inform of optimum release strategies.

Figure 6.

The probability of fixation as a function of population size and the number of infected individuals released. We assumed s_h=1, s_f=0.05 and μ=0.

4. Discussion

In finite populations, Wolbachia may become established when its initial frequency is below the critical threshold (equation (1.1)), and may be lost when the infection benefits the host or its initial frequency is above the threshold. The presence of CI markedly increases the probability of invasion in the face of stochastic loss compared with equivalent nuclear genes or maternally inherited elements without CI. Our results extend the previous studies of the stochastic dynamics of Wolbachia (Rigaud & Rousset 1996; Egas et al. 2002) and have implications for how Wolbachia spreads and maintains itself in natural populations of insects, as well as how it might be used in pest and disease-vector management.

Information about the fitness effects of Wolbachia on its host is difficult to obtain because costs and benefits may vary depending on the environment as well as factors such as host age and genotype. Examples of costs, benefits and apparent neutrality have been recorded (McGraw et al. 2002; Vala et al. 2003; Duron et al. 2006; Fytrou et al. 2006; Islam & Dobson 2006; Montenegro et al. 2006; de Crespigny & Wedell 2007; Weeks et al. 2007). If transfer between populations does typically occur through rare infections of single or small numbers of individuals, then deterministic models would predict that strains of Wolbachia which impose costs on their hosts would find it very difficult to invade because the threshold for spread would never be exceeded. The stochastic analysis shows that fixation can occur after introduction at a very low frequency, especially in small populations. Egas et al. (2002) concluded after simulating the stochastic spread of Wolbachia that drift was a very unlikely mechanism for the bacterium to establish itself. Although our results closely match and extend theirs, we point out that the fixation probability of neutral or near-neutral Wolbachia markedly exceeds that of an equivalent chromosomal gene. It is widely accepted that drift can lead to the fixation of chromosomal genes and the same processes may be influencing Wolbachia dynamics, though in larger populations.

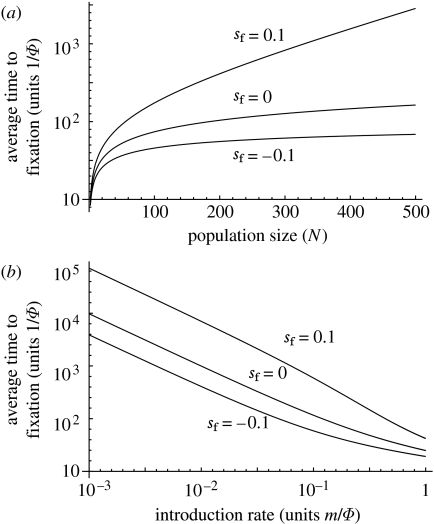
If an uninfected population constantly receives Wolbachia immigrants, the probability that the infection will eventually invade and reach fixation is unity. However, this mathematical truism provides no guarantee that transfer will occur on biologically relevant time scales. In figure 7 we provide examples of average waiting times until fixation as a function of population size, fitness cost and migration rates. They show that populations exposed to a steady influx of Wolbachia-infected individuals, but where frequencies never exceed the critical threshold, can become colonized by the bacterium on medium ecological time scales, especially in small- to intermediate-sized local populations. But without better biological insight into the mechanism and rates of interspecific transfer, it is not possible to make meaningful predictions about likely waiting times.

Figure 7.

The average time until fixation of an uninfected population that receives a constant (small) influx of Wolbachia at rate m. We assume that all individuals die at rate Φ, so that average lifespan is 1/Φ and the number of infected individuals in the naive population at any one time is on average m/Φ. Time is measured in units of average lifetime. (a) Average waiting time as a function of population size for Wolbachia with positive, neutral and negative effects on fitness (s_h=1, m/Φ=0.1) and (b) average waiting times as a function of introduction rates for the same values of Wolbachia fitness effects (s_h=1, N=250). Further details of calculations are given in the electronic supplementary material.

By contrast, the stochastic analysis shows that the spread of a Wolbachia that is beneficial to its host is far from certain after a low-frequency introduction. Just as a beneficial allele, the large majority of beneficial Wolbachia introductions will be lost by chance before they have become abundant enough to ensure fixation.

Exactly how Wolbachia crosses the species boundary is unclear, though such transfers are almost certainly rare events, probably involving only a single or a small number of infections at one time. The overall probability of a successful species jump will be influenced by the number of times a Wolbachia infection occurs in the new species and the probability of an establishment conditional on a new infection. Our and earlier results (Rigaud & Rousset 1996) suggest that the latter depends strongly on population size, the probability being proportional to N^−1/2 for near-neutral bacteria and for low N. But this does not necessarily mean that species jumps are more likely to occur in small populations: this depends on the relationship between population size and the probability of an initial infection occurring. One could envisage situations where transfer dynamics are mass-action and proportional to population size so that the overall dependence on population size scales with N^+1/2. Alternatively, one can imagine processes where the probability of the initial cross-species transfer does not scale with the size of the recipient population, e.g. if transfer occurs during rare interspecific matings. In such cases, the overall dependence on population size might scale somewhere between N^−1/2 and N^+1/2, which includes the case of no influence of population size.

Even when potential host populations are very large, the probability of invasion may still be substantial if the initial establishment of the bacterium occurs in much smaller, partially isolated subpopulations. After this initial establishment, the bacteria can spread through several processes. In a continuous population, the spatial spread of Wolbachia has been modelled by Turelli & Hoffmann (1991) as a ‘Bartonian wave’, mathematically analogous to the spread of an underdominant chromosome (Barton 1979; Schofield 2002). Alternatively, Wolbachia may spread from one partially isolated subpopulation to another as in a stepping stone model, and the theory developed here can be used to calculate the probability of a step occurring in cases when migration is insufficient to increase local frequencies above the threshold. In both the cases, population spread can be arrested at regions of low population density, which cannot produce sufficient migrants to breach the threshold of adjacent high-density populations or regions. A stochastic theory to explore the passage through regions of low density of waves of advance of underdominant chromosomes has been developed (Barton & Rouhani 1991), and this is likely to prove useful in studying Wolbachia spread, both in natural situations and in metapopulations of pests or vectors where managers have to choose populations to be targeted initially.

Pests and important vectors almost by definition have large population sizes and hence applied ecologists employing Wolbachia as a drive element will not normally need to consider stochastic effects. However, it may be possible to temporally reduce densities by insecticide application to a level where relatively small releases cause the threshold for spread to be exceeded. Alternatively, as just discussed, small peripheral populations may be infected, which then act as a bridgehead for further invasion. In these circumstances, the theory developed here may be of use to pest and vector managers.

We chose to analyse stochastic spread using two approaches that have different strengths and in particular differ in how they treat the relationship between the census population size (N) and the variance effective population size (N_e). If the number of offspring per female is Poisson distributed, N_e=N; but if variance is higher than Poisson, N_e<N. The Wright–Fisher approach makes no assumption about N_e/N, while the Moran approach assumes a particular demography with N_e/N=1/2. The consensus from data is that N_e/N<1 (Crow & Kimura 1970), and N_e/N≈0.1 may be common (Frankham 1995). However, if one is willing to accept its underlying demography, then the Moran approach allows exact results. Further, more technical comparisons of the two approaches are given in the electronic supplementary material, though for most biological applications either approach can be used and give similar results.

Deterministically, Wolbachia spreads because it decreases the fitness of individuals that do not carry the bacteria. Several other phenomena have similar properties, specifically providing a frequency-dependent fitness advantage. Medea elements are natural or artificial constructs that in the female heterozygote state place a substance in individual eggs that kills the zygote, unless either the father or mother (or both) bears the medea element (Wade & Beeman 1994; Chen et al. 2007). As in the case of Wolbachia, a medea element codes for a modifier and rescue function, and wild-type homozygotes are disadvantaged relative to other genotypes. More speculatively, evolutionary theorists have explored the dynamics of a dominant gene that it in some way harms individuals that do not carry it. For this to happen, these individuals must be recognizable, and it has become customary to call the identifying trait a ‘green beard’ (Dawkins 1982; Keller & Ross 1998; Axelrod et al. 2004; Summers & Crespi 2005; Jansen & van Baalen 2006). Deterministic theory predicts that both types of gene will spread when initially rare if they have no costs, while if costs are present there will be a threshold frequency above which deterministic spread occurs, analogous to the case of Wolbachia. Although we have not modelled the detailed dynamics, our results suggest that the stochastic spread of neutral medea and green beard genes is similar to that of Wolbachia, with a probability of establishment that scales with $1/\sqrt{N}$.

Appendix A.

As described more fully in the electronic supplementary material, we use the Wright–Fisher and Moran techniques to derive and approximate the probability of Wolbachia establishment. In this appendix, we give the main mathematical results that we use in drawing the figures discussed in the main text.

For the Wright–Fisher analysis, it is necessary to specify values for the mean and variance of the change in frequency per generation, denoted M(p) and V(p), respectively. To understand the initial spread of Wolbachia-like infections, the critical factor is accurately describing the dynamics when the change in frequency is the lowest. Hence for the case of μ=0, we use the approximation

$$\frac{M(p)}{V(p)}\approx N_{\text{e}}(p-\hat{p})\frac{s_{\text{h}}}{1-s_{\text{f}}},$$ (A1)

where $\hat{p}=s_{\text{f}}/s_{\text{h}}$ is the unstable equilibrium infection frequency if s_f>0. Substituting approximation (3.1) into the formula for the probability of fixation (Crow & Kimura 1970, ch. 8), given an initial frequency of p₀, we find

$$u(p_0)=\frac{{\int }_0^{p_0}\text{exp}\left[\frac{M(x)}{V(x)}\right]\text{d}x}{{\int }_0^1\text{exp}\left[\frac{M(x)}{V(x)}\right]\text{d}x}=\frac{\text{erf}\left(\frac{\sqrt{N_{\text{e}}}{s}_{\text{f}}}{\sqrt{s_{\text{h}}(1-s_{\text{f}})}}\right)-\text{erf}\left(\frac{\sqrt{N_{\text{e}}}(s_{\text{f}}-p_0{s}_{\text{h}})}{\sqrt{s_{\text{h}}(1-s_{\text{f}})}}\right)}{\text{erf}\left(\frac{\sqrt{N_{\text{e}}}{s}_{\text{f}}}{\sqrt{s_{\text{h}}(1-s_{\text{f}})}}\right)-\text{erf}\left(\frac{\sqrt{N_{\text{e}}}(s_{\text{f}}-s_{\text{h}})}{\sqrt{s_{\text{h}}(1-s_{\text{f}})}}\right)},$$ (A2)

where erf(.) denotes the error function. Approximation (A 2) is extremely accurate for N_e as small as 20, even with high levels of CI (e.g. s_h=1) and considerable fecundity costs of the infection (e.g. s_f=0.2). Equivalent arguments for the cases of s_f<0 and μ>0 are developed in the electronic supplementary material.

For the Moran model, the probability of fixation can be found in closed form. Starting with a fraction p₀ infected individuals, the probability that Wolbachia becomes fixed is (Goel & Richter-Dyn (1974) and see the electronic supplementary material)

$$u(p_0)=\frac{\sum _{j=0}^{N{p}_0-1}\prod _{i=1}^j\frac{i{\theta }_{\text{u}}}{(N-i){\theta }_{\text{i}}}}{\sum _{j=0}^{N-1}\prod _{i=1}^j\frac{i{\theta }_{\text{u}}}{(N-i){\theta }_{\text{i}}}},$$ (A3)

for μ=0, which simplifies to

$$u(p_0)=\frac{\Gamma \left(n,n(1-s_{\text{f}})\right)-\Gamma \left(n\right)\Gamma \left(n-N{p}_0,n(1-s_{\text{f}})\right)/\Gamma \left(n-N{p}_0\right)}{\Gamma \left(n,n(1-s_{\text{f}})\right)-\Gamma \left(n\right)\Gamma \left(n(1-s_{\text{h}}),n(1-s_{\text{f}})\right)/\Gamma \left(n(1-s_{\text{h}})\right)},$$ (A4)

where n=N/s_h and Γ(x, y) and Γ(x) are gamma functions.

When μ>0, we obtain

$$u(p_0)=\frac{1+\sum _{j=1}^{N{p}_0-1}\prod _{i=1}^j\frac{i(i(1-s_{\text{f}})\mu +(N-i))(N-s_{\text{h}}i)}{(N-i)iN(1-s_{\text{f}})(1-\mu )}}{1+\sum _{j=1}^{N-1}\prod _{i=1}^j\frac{i(i(1-s_{\text{f}})\mu +(N-i))(N-s_{\text{h}}i)}{(N-i)iN(1-s_{\text{f}})(1-\mu )}}.$$ (A5)

Supplementary Material

Stochastic spread of Wolbachia: details of the modelling

Further details of the models described in the main text