Glycolytic Oscillations in Isolated Rabbit Ventricular Myocytes^,

Abstract

Previous studies have shown that glycolysis can oscillate periodically, driven by feedback loops in regulation of key glycolytic enzymes by free ADP and other metabolites. Here we show both theoretically and experimentally in cardiac myocytes that when the capacity of oxidative phosphorylation and the creatine kinase system to buffer the cellular ATP/ADP ratio is suppressed, glycolysis can cause large scale periodic oscillations in cellular ATP levels (0.02–0.067 Hz), monitored from glibenclamide-sensitive changes in action potential duration or intracellular free Mg²⁺. Action potential duration oscillations originate primarily from glycolysis, since they 1) occur in the presence of cyanide or rotenone, 2) are suppressed by iodoacetate, 3) are accompanied by at most very small mitochondrial membrane potential oscillations, and 4) exhibit an anti-phase relationship to NADH fluorescence. By uncoupling energy supply-demand balance, glycolytic oscillations may promote injury and electrophysiological heterogeneity during acute metabolic stresses, such as acute myocardial ischemia in which both oxidative phosphorylation and creatine kinase activity are inhibited.

Previous studies have shown that glycolysis can oscillate periodically, driven by feedback loops in regulation of key glycolytic enzymes, such as phosphofructokinase (PFK),3 by free ADP, ATP, and other metabolites (1, 2). Glycolytic oscillations have been characterized in yeast (1, 3) and pancreatic β-cells (4, 5), but conditions promoting their occurrence in cardiac myocytes are less established. Cardiac myocytes deprived of glucose have been shown to develop oscillations in action potential duration (APD) mediated by activation of ATP-sensitive K (K_ATP) channels, which shorten APD when the free ATP/ADP ratio falls (6). O'Rourke et al. (6) interpreted these as glycolytic oscillations, but their subsequent work (7, 8), as well as that from other groups (9–12), has focused on oscillations arising in the mitochondrial network, in which large scale oscillations in mitochondrial membrane potential (ΔΨ_m) and redox state accompany APD oscillations. Evidence has been presented that such mitochondrial APD oscillations may contribute to arrhythmias during ischemia/reperfusion by creating “metabolic sinks” that promote APD dispersion, conduction block, and reentry (13).

Nevertheless, the potential for primary oscillations driven by glycolysis to complicate energy supply-demand imbalance, as well as electrophysiological heterogeneity, during metabolic stresses remains a real possibility. We hypothesized that glycolytic oscillations would be most likely to occur when the capacity of oxidative phosphorylation and the creatine kinase (CK) system to buffer the cellular free ATP/ADP ratio is limited, conditions that may occur during acute myocardial ischemia (14, 15–17). During acute myocardial ischemia or hypoxia, anaerobic glycolysis becomes the major source of energy production but has a limited capacity to meet the overall energy needs of the beating heart. The onset of irreversible injury after 20–30 min of ischemia coincides with the progressive inhibition of glycolysis due to factors such as lactate accumulation and acidosis (18–22). Efficient coupling of glycolysis to cellular energy needs during this early ischemic window may therefore be critical in deciding cell fate.

To investigate conditions under which metabolic stress might induce glycolytic oscillations, we performed patch clamp studies in isolated rabbit ventricular myocytes subjected to varying degrees and combinations of mitochondrial, glycolytic, and CK inhibition and used modeling to help interpret the findings. In our modeling strategy, we first developed a simplified model, focused on the glycolytic subsystem, with parameters and variables consolidated to the minimum required to analyze the dynamical mechanisms causing oscillations. We then represented the metabolic pathways more realistically in a detailed model, to show that the same dynamical behaviors occur under physiologically plausible conditions, and show good agreement with the experimental observations in isolated myocytes.

EXPERIMENTAL PROCEDURES

Cell Isolation—Ventricular myocytes were enzymatically isolated from the hearts of 2–3-kg rabbits, as described previously (23). Briefly, hearts were removed from rabbits anesthetized with intravenous pentobarbital and perfused retrogradely at 37 °C in Langendorff fashion with nominally Ca²⁺-free Tyrode's buffer containing 1.2 mg/ml collagenase type II (catalog number 4176; Worthington) and 0.12 mg/ml protease type XIV (catalog number P5147; Sigma) for 25–28 min. After washing out the enzyme solution, the hearts were removed from the perfusion apparatus and placed in Petri dishes containing Tyrode's solution. Cells were isolated by gentle mechanical dissociation, stored at room temperature, and used within 6 h. This procedure typically yielded 30–50% of rod-shaped and Ca²⁺-tolerant myocytes.

Patch Clamp Methods—Isolated ventricular myocytes were patch clamped in the whole cell ruptured patch configuration using borosilicate glass pipettes (1–3-megaohm tip resistance). Action potentials were measured under current clamp conditions, using an Axopach 200B amplifier with a Digidata 1440A interface (Axon Instruments, Union City, CA). Data were acquired and analyzed using pClamp software (Axon instruments). Myocytes were superfused at 34–36 °C with Tyrode's solution containing 140 mm NaCl, 5.4 mm KCl, 0.33 mm NaH₂PO₄, 1.0 mm MgCl₂, 1 mm CaCl₂, and 10 mm HEPES (pH 7.4 with NaOH), with or without the following additions: glucose (10 mm), iodoacetate (1 mm), 3-mercaptopropionic acid (0.45 mm), cyanide (5 mm), oligomycin (0.01 mm), FCCP (0.001 mm), rotenone (0.003 mm), dinitrophenol (0.1 mm), DNFB (0.1 mm), cyclosporine A (0.01 mm), and N-acetylcysteine (5 mm), which were added at appropriate dilution from stock solutions in DMSO or distilled water. The pipette solution contained 140 mm KCl, 1 mm MgCl₂, 10 mm 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid, and 10 mm HEPES (pH 7.2 with Tris), to which fluorescent dyes were added as described below. Action potentials were evoked by brief (4-ms) current injections (8 nA) at 1 Hz. All chemicals were obtained from Sigma.

Fluorescence Imaging—To image mitochondrial membrane potential, cells were superfused with Tyrode's solution containing 30 nm tetramethylrhodamine methyl ester (TMRM) for at least 30 min. Myocytes were illuminated with a mercury arc lamp, using a 520/610-nm band pass filter for excitation/emission, respectively. Fluorescence images were recorded at 1 frame/s using an Olympus IX70 inverted microscope (×40, uplanFl, numerical aperture 0.75 dry lens) coupled with a video camera (WAT-120N Pal version; Orangeburg, NY). Images were processed using Imaging Workbench version 5.2 (Indec Biosystems, Santa Clara, CA) software. To image intracellular free Mg²⁺, myocytes were loaded with 100 μm pentapotassium salt of Mg Green through the patch pipette, and imaging was performed using a 480/530-nm band pass filter for excitation/emission, respectively. Although Mg Green is also a low affinity Ca²⁺ indicator (K_d =∼6 μm), under our usual experimental conditions with 10 mm 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid in the patch pipette solution, changes in fluorescence intensity mainly reflected change in free intracellular [Mg²⁺] (24). All dyes were obtained from Molecular Probes.

Mathematical Modeling—Two mathematical models were developed to simulate the metabolic processes in cardiac myocytes: a low dimensional simplified model of glycolysis (based on Refs. 1 and 2) to investigate dynamics and a high dimensional detailed model, including three compartments (cytoplasm, intermembrane space of mitochondria, and mitochondrial matrix) to compare directly with experimental findings. The simplified model focuses on the glycolytic subsystem, incorporating only key steps in the glycolytic pathway regulating the dynamics (see Fig. S1) (i.e. we assumed that glucose 6-phosphate is synthesized from either exogenous glucose or endogenous glycogen at the rate V_S); glucose 6-phosphate is converted to fructose 6-phosphate, and fructose 6-phosphate is converted to fructose 1,6-bisphosphate, accompanied by ATP hydrolysis to ADP; and fructose 1,6-bisphosphate is utilized to generate pyruvate, accompanied by phosphorylation of four ADP to four ATP (reflecting the stoichiometry for glycogenolysis, since exogenous glucose was removed in most experiments). The conversion of fructose 6-phosphate to fructose 1,6-bisphosphate is catalyzed by PFK, which is activated by free ADP, forming the positive feedback loop. The ATP production and consumption by the mitochondria as well as the facilitation of ATP delivery to the mitochondria by the CK system were simply modeled by constants that multiply the ATP consumption rate. In the detailed model (see Fig. S2), we used a more complete model of glycolysis based on Zhou et al. (25) and a mitochondrial metabolism model simplified from Cortassa et al. (26). We also incorporated the CK system, including diffusion of phosphocreatine and creatine between compartments. Action potentials were simulated using an early version of the Luo and Rudy model (27), modified by adding the K_ATP current as formulated by Ferrero et al. (28). The steady state stability of the simplified model was analyzed using Matlab. The differential equations were numerically solved by a fourth order Runge-Kutta method with a time step of 0.0005 s.

RESULTS

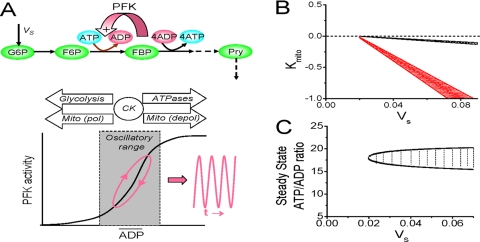
Glycolytic Oscillations; Theoretical Considerations—If glycolytic oscillations are driven by the feedback of free ADP and ATP on PFK (1, 2), then two conditions must be met for glycolysis to oscillate in cardiac myocytes: first, the free ATP/ADP ratio regulating PFK activity must be free to vary (i.e. not clamped by oxidative phosphorylation and the CK system); second, the rates of ATP production and consumption must be balanced in a critical range so that regulatory metabolites, such as free ADP, can engage the steep response region of the PFK activation curve (Fig. 1A). These conditions are not met under normoxic conditions, since well polarized mitochondria actively phosphorylate excess ADP and clamp the free ATP/ADP ratio at a high level, assisted by the CK system; conversely, depolarized mitochondria consume glycolytically generated ATP in an attempt to maintain ΔΨ_m, clamping the free ATP/ADP ratio (with the assistance of the CK system) at too low a level for oscillations. However, if mitochondria are unable to buffer the free ATP/ADP ratio effectively, then glycolysis may be free to oscillate over a critical appropriately balanced range of ATP production and consumption rates.

FIGURE 1.

A, simplified schema of the glycolytic oscillator, based on positive feedback of free ADP on PFK activity. Oscillations (due to a substrate depletion mechanism) develop when the steady-state free ADP level engages the steep portion of the PFK activity curve (lower graph). The arrows indicate how mean ADP levels are regulated by glycolysis, polarized (pol) or depolarized (depol) mitochondria, and cytosolic ATPases, facilitated by CK. V_S, input flux of glycolytic substrate (glucose or glycogen); FBP, fructose-1,6-biphosphate. The dashed arrows represent the molecular steps indicated for clarity of metabolic pathways but not explicitly formulated in the modeling equations. B, phase diagram in V_S - k_Mito parameter space from the simplified model (see supplemental material). Oscillatory regions are indicated with the CK system intact (black lines) or 90% inhibited (red lines). C, phase diagram in steady state free ATP/ADP ratio - V_S parameter space from the simplified model. The oscillatory region is cross-hatched. See “Results” for details.

To test this idea, we designed a simplified model of the glycolytic oscillator, driven by positive feedback of free ADP on PFK (Fig. 1A) to investigate the dynamical mechanisms, as described in detail in the supplemental material. Briefly, in this model, the flux of glycolytic substrate S (either glucose or glycogen) generating ATP is represented by V_S = k_S·[S] (treated as an adjustable parameter instead of a variable, since it changes slowly with respect to the time scale of oscillations). ATP consumption via cytoplasmic ATPases is represented by the flux V_C = k_C·[ATP]. Since glycolytic oscillations occur at low ATP, for simplicity we assume ATP consumption to be proportional to [ATP] (whereas a sigmoid function is used in the detailed model). When mitochondria are polarized, net ATP production is given by the flux V_Mito = k_CKk_Mitoc. Here the CK system, which facilitates the ability of mitochondria to buffer the free ATP/ADP ratio, is phenomenologically represented by the parameter k_CK (with a value of 1 when the CK system is inhibited and 10 when active). When mitochondria are depolarized and consuming ATP, V_Mito = k_CKk_Mito·[ATP], where k_Mito is negative to reflect mitochondrial ATP consumption. This is consistent with the well known reversibility of mitochondrial F₀-F₁-ATPase, which uses the electrochemical proton gradient to synthesize ATP when mitochondria are polarized but consumes ATP to pump protons out of the matrix when mitochondria are depolarized (29). Fig. 1B shows that ATP levels oscillate over a critical narrow range in V_S - k_Mito phase space when k_Mito is negative (i.e. mitochondria are consuming rather than producing ATP). When inhibition of the CK system is simulated by reducing k_CK, the oscillation region in V_S - k_Mito phase space increases considerably (the red region), reflecting the reduced ability of mitochondria to buffer the free ATP/ADP ratio.

Fig. 1C shows the phase space of steady state free ATP/ADP ratio as a function of glycolytic ATP production, with the region of oscillation indicated between the black lines. Note that the steady state free ATP/ADP ratio over which oscillations occur is relatively insensitive to the absolute value of the glycolytic ATP production flux V_s, implying that the relative balance between ATP production and consumption fluxes is the critical factor for oscillations (Fig. 1A).

Induction of Glycolytic Oscillations in Cardiac Myocytes—To test the model's predictions, we exposed isolated patch clamped rabbit ventricular myocytes to a series of interventions in which glycolysis, mitochondrial oxidative phosphorylation, and/or creatine kinase were inhibited to varying degrees (Table 1). We monitored APD to detect ATP oscillations in response to activation/deactivation of ATP-sensitive K (K_ATP) channels, as reported previously (6). Unlike isolated guinea pig ventricular myocytes (6), simple removal of glucose in 36 rabbit ventricular myocytes to reduce glycolytic substrate availability failed to induce APD oscillations, consistent with endogenous substrates (glycogen and fatty acids) allowing oxidative phosphorylation to maintain a high free ATP/ADP ratio (16). If, in addition to glucose removal, the ability of mitochondria to oxidize endogenous fatty acids was inhibited by 3-merc, APD oscillations developed in 5% (3 of 51) of myocytes. The incidence increased to 40% (15 of 38) when cyanide was also added to directly suppress the ability of oxidative phosphorylation to clamp the free ATP/ADP ratio. In contrast, if oxidative phosphorylation was uncoupled with a powerful protophore, such as FCCP or dinitrophenol, APD shortening, once initiated, occurred rapidly without oscillations, even without glucose removal or 3-merc present (data not shown) (30).

TABLE 1.

Incidence of APD oscillations during various types of metabolic inhibition GI, glycolytic inhibition; MI, mitochondrial inhibition; CKI, creatine kinase inhibition; Glu, glucose.

Metabolic inhibition	Experimental conditions	Myocytes displaying APD oscillations
GI	0 mm Glu	0/36 (0%)
MI	Cyanide or FCCP or rotenone or DNP	0/7 (0%)
GI + mild MI	0 mm Glu + 3-merc	3/51 (6%)
GI + moderate MI	0 mm Glu + 3-merc + cyanide	15/38 (39%)
GI + severe MI	0 mm Glu + 3-merc + FCCP	0/6 (0%)
CKI	DNFB	0/6 (0%)
Moderate MI + CKI	Cyanide + DNFB	6/8 (75%)
GI + CKI	0 mm Glu + DNFB	0/7 (0%)
GI + moderate MI + CKI	0 mm Glu + 3-merc + cyanide + DNFB	19/21 (90%)
	0 mm Glu + 3-merc + rotenone + DNFB	5/6 (83%)

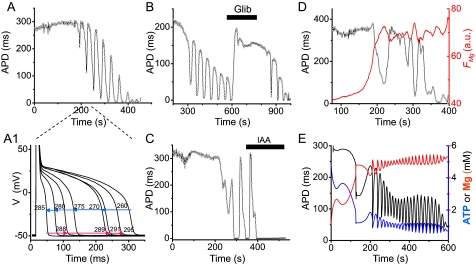
To examine the role of the CK system in facilitating the ability of mitochondria to buffer the free ATP/ADP ratio (31–33), we used the creatine kinase inhibitor DNFB (30, 34). DNFB alone did not induce APD oscillations in six myocytes but, when combined with cyanide, increased the incidence of APD oscillations to 75% (6 of 8), consistent with previous findings in rat myocytes (9). When cyanide and DNFB were further combined with glucose removal and 3-merc, the incidence increased further to 90% (19 of 21). A typical example is shown in Fig. 2A1. APD oscillations (average frequency of 0.045 ± 0.017 Hz, range 0.02–0.067 Hz) were reversibly blocked by the K_ATP channel antagonist glibenclamide (Fig. 2B) and were accompanied by oscillations in intracellular free [Mg²⁺], as expected for an oscillating free ATP/ADP ratio (Fig. 2D). Replacing cyanide with rotenone (3 μm) was similarly effective (5 of 6 cells). In contrast, in the absence of cyanide or rotenone, glucose removal plus DNFB failed to induce APD oscillations in any (0 of 7) myocytes.

FIGURE 2.

APD oscillations during metabolic inhibition. A, APD recorded in the current clamp mode from a whole cell patch clamped myocyte exposed to glucose-free buffer containing 450 μm 3-merc plus 5 mm cyanide and 100 μm DNFB. A1, superimposed action potentials recorded during the oscillation cycle from 260–295 s in A. B and C, inhibition of APD oscillations by the (reversible) ATP-sensitive K channel blocker glibenclamide (10 μm) in B and the (irreversible) glycolytic inhibitor iodoacetate (0.1 mm) in C, under the same conditions as in A. D, Mg Green fluorescence (F_Mg; red line) during APD oscillations (black line) under the same conditions as in A. F_Mg increases, consistent with ATP depletion causing APD shortening via activation of ATP-sensitive K channels, and then oscillates out of phase with APD, as expected if F_Mg is tracking intracellular ATP. E, numerical simulations from the detailed model, showing oscillations in APD, ATP, and free Mg when glucose removal is simulated linearly decreasing in V_S after inhibiting both oxidative phosphorylation and CK to mimic the effects of cyanide and DNFB (see supplemental material). a.u., arbitrary units.

Thus, APD oscillations attributable to oscillations in the free ATP/ADP ratio were most consistently observed when the ability of oxidative phosphorylation, with the assistance of the CK system, to buffer the free ATP/ADP ratio was suppressed, as predicted by the simplified model (Fig. 1). Although useful for analyzing dynamics, the simplified model can only be compared in a limited fashion with experimental data. To provide a more detailed comparison with measurable experimental parameters, such as APD, magnesium, NADH, and ΔΨ_m, we coupled a ventricular action potential model (27, 28) to a detailed three-compartment metabolic model combining glycolysis, oxidative phosphorylation, and the phosphocreatine system (see supplemental material). Fig. 2E shows that when the experimental protocol (glucose removal, 3-merc, cyanide, and DNFB) was simulated in this model, the free ATP/ADP ratio gradually decreased to a critical range inducing APD oscillations. Once in the oscillatory regime, ATP and free [Mg²⁺] oscillated. Thus, physiologically realistic parameter settings in the detailed model replicated the experimental findings.

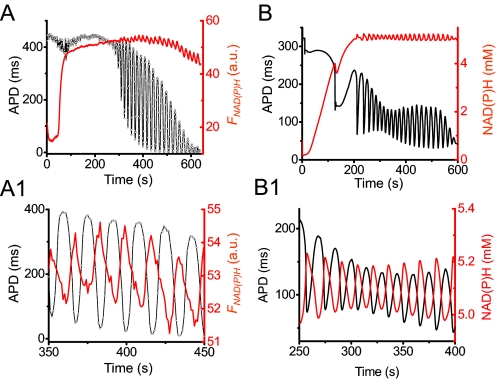
Four key findings established that APD oscillations were driven primarily by glycolysis. First, they occurred in the presence of 5 mm cyanide or 3 μm rotenone, concentrations that should fully suppress mitochondrial ATP generation (35, 36). Second, APD oscillations were inhibited by the glycolytic inhibitor iodoacetate (Fig. 2C). Third, when NAD(P)H fluorescence was simultaneously recorded with APD (Fig. 3A), cyanide caused a large increase in NAD(P)H fluorescence, as expected from reduction of the respiratory chain; during the subsequent APD oscillations, small amplitude NAD(P)H oscillations (averaging 9% of the cyanide-induced increase in seven myocytes) accompanied APD oscillations. The small amplitude is consistent with the cytoplasmic NAD(P)H/NAD(P) pool, which is much smaller than the pool in the mitochondrial matrix (37–39). Moreover, NAD(P)H oscillated out of phase with APD, as predicted for glycolytic oscillations by the detailed model (Fig. 3B and 3B1), since glycolytic flux generating NAD(P)H is highest when the free ATP/ADP ratio is low (i.e. APD is short). In contrast, mitochondrial NAD(P)H oscillated in phase with APD during mitochondrial oscillations (7), since increased ATP synthesis by mitochondria consumes NAD(P)H when the free ATP/ADP ratio is low. Fourth, when ΔΨ_m was simultaneously recorded with APD, ΔΨ_m oscillations were not detected or were very small (Fig. 4, A and B). The detailed model also predicted small ΔΨ_m oscillations, as glycolytically generated ATP was used by depolarized mitochondria to regenerate ΔΨ_m (Fig. 4, A1 and B1). During APD oscillations, ΔΨ_m was only partially dissipated, consistent with mitochondria utilizing glycolytically generated ATP to partially maintain ΔΨ_m. We confirmed that when TMRM-loaded myocytes were illuminated at high light intensity to stimulate ROS-induced APD oscillations, the latter were always accompanied by much larger scale ΔΨ_m oscillations (data not shown), consistent with previous reports (7). In addition, pretreatment of three myocytes with N-acetylcysteine (5 mm), a membrane-permeable antioxidant, did not inhibit APD oscillations induced by glucose removal plus 3-merc, cyanide, and DNFB, unlike ROS-induced APD oscillations driven by the mitochondrial network (7, 8, 10, 40). Cyclosporine A (3 μm) also failed to suppress oscillations in eight myocytes subjected to glucose removal plus 3-merc, cyanide, and DNFB.

FIGURE 3.

NAD(P)H and ΔΨ_m during APD oscillations. A, simultaneous recordings of NAD(P)H autofluorescence (F_NAD(P)H; red) and APD (black) from a myocyte exposed to glucose-free buffer containing 450 μm 3-merc plus 5 mm cyanide. A1, expanded traces between 350–450 s, showing that APD and F_NAD(P)H are oscillating out of phase. B and B1, corresponding simulations from the detailed model (see supplemental material). a.u., arbitrary units.

FIGURE 4.

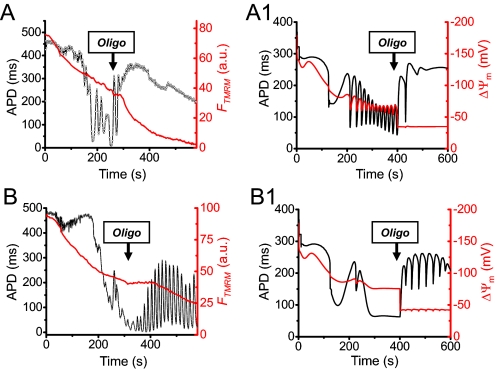
Mitochondrial function and the effects of the F₁-F₀-ATPase inhibitor oligomycin during APD oscillations. A, simultaneous recordings of TMRM fluorescence (F_TMRM; red) and APD (black) in myocytes preloaded with TMRM (30 nm) to measure ΔΨ_m during exposure to glucose-free buffer containing 450 μm 3-merc plus 5 mm cyanide and 100 μm DNFB. Note that ΔΨ_m becomes progressively more depolarized during APD oscillations, with trivial oscillations in F_TMRM. In this myocyte, oligomycin (Oligo) suppressed APD oscillations. Note that after oligomycin, F_TMRM decreased more rapidly, reflecting the loss of the mitochondria's ability to support ΔΨ_m by reverse F₁-F₀-ATPase activity. B, in another myocyte subjected to the same protocol, oligomycin amplified APD oscillations. A1 and B1, corresponding numerical simulations (see supplemental material for details). a.u., arbitrary units.

If the mitochondria's ability to buffer the free ATP/ADP ratio is the key suppressor of glycolytic oscillations, then the F₁-F₀-ATPase inhibitor oligomycin, which blocks the ability of mitochondria to either generate or consume ATP, should have a profound effect. In both model and experiment, oligomycin alone did not induce oscillations (data not shown), presumably because glycolysis was capable of maintaining a high free ATP/ADP ratio under these experimental conditions (high internal calcium buffering, low stimulation rate). When oxidative phosphorylation was inhibited by cyanide, however, oligomycin could either promote or suppress APD oscillations. Fig. 4, A and B, shows two myocytes subjected to glucose removal plus 3-merc, cyanide, and DNFB. In the first myocyte, APD oscillations were suppressed by oligomycin. Note that in the presence of oligomycin, ΔΨ_m declined more rapidly, indicating that the mitochondria were no longer able to use glycolytically generated ATP to support ΔΨ_m. As a result, glycolysis was able to increase the free ATP/ADP ratio (as indicated by the APD lengthening) out of the oscillatory range. This scenario was simulated in Fig. 4A1 using the detailed model. In the second myocyte, APD oscillations were already beginning to dissipate before oligomycin was applied, presumably because partially depolarized mitochondria were avidly consuming glycolytically generated ATP to support ΔΨ_m. This lowered the free ATP/ADP ratio (as indicated by the very short APD) nearly out of the oscillatory range. By reducing ATP consumption by mitochondria, subsequent application of oligomycin allowed glycolysis to increase the free ATP/ADP ratio back into the oscillatory range, reflected by the more rapid decrease in ΔΨ_m and APD lengthening. This scenario was simulated in Fig. 4B1.

DISCUSSION

We have presented theoretical and experimental evidence from patch clamped isolated rabbit ventricular myocytes demonstrating that glycolysis can oscillate when the capacity of oxidative phosphorylation to buffer the cellular free ATP/ADP ratio, assisted by the CK system, becomes compromised. The principle factor regulating the oscillatory dynamics in the simplified model is the free ATP/ADP ratio (Fig. 1C), determined by the balance between ATP production rate and ATP consumption rate. To achieve an ATP/ADP ratio that consistently remained in the critical window long enough to observe glycolytic oscillations experimentally in isolated rabbit myocytes required 1) reducing overall ATP production rate by both inhibiting oxidative phosphorylation (with cyanide or rotenone) and reducing glycolytic substrate availability (glucose removal), 2) concomitantly increasing overall ATP consumption rate beyond the capability of residual glycolysis to support a high ATP/ADP ratio (i.e. using cyanide or rotenone to depolarize mitochondria sufficiently to reverse F₁-F₀-ATPase activity from its ATP-producing mode to its ATP-consuming mode), and 3) inhibiting CK to broaden the window of ATP/ADP ratio inducing oscillations (Fig. 1B). Supporting this proposed dynamic mechanism, the detailed model demonstrated a tight correlation with the experimentally observed effects on APD, ATP, free intracellular Mg²⁺, NADH, and ΔΨ_m during glycolytic oscillations.

Experimental evidence indicates that the observed ATP oscillations, detected as glibenclamide-sensitive APD and/or intracellular free Mg²⁺ oscillations (Fig. 2), were driven primarily by glycolysis, since they 1) occurred in the presence of cyanide or rotenone, 2) were abolished by iodoacetate, 3) oscillated out of phase with NAD(P)H fluorescence, as predicted for oscillations arising from glycolysis but not oxidative phosphorylation, and 4) were accompanied minimal ΔΨ_m oscillations. In addition, the ATP oscillations were not suppressed by antioxidants or cyclosporine, making it unlikely that the ROS-induced mechanism, which can also cause APD oscillations (7, 8, 10), played a significant role.

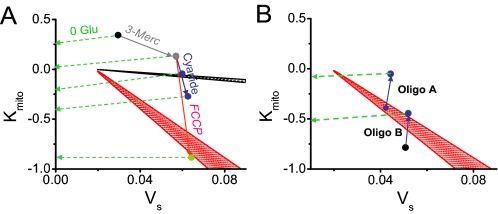
Fig. 5A (based on Fig. 1B) indicates hypothetical trajectories for myocytes subjected to glucose removal in combination with other metabolic interventions. Glucose removal is represented by a gradual slow reduction in V_S horizontally along dashed green arrow(s) as glycogen, now the sole substrate for glycolysis, is progressively depleted. Interventions affecting oxidative phosphorylation along the k_Mito axis, on the other hand, are represented by rapid vertical movement along the solid arrows. With glucose removal alone, k_Mito remains >0, and the myocyte's trajectory (top dashed green arrow) remains above the oscillation region as V_S decreases. If 3-merc is added to inhibit fatty acid oxidation (solid gray arrow), V_S transiently increases due to reflex stimulation of glycolysis, but during glucose removal, the second green arrow still misses the oscillatory region. Adding cyanide rapidly decreases k_Mito (along the solid blue arrow), so that now the trajectory following glucose removal may pass into the black oscillatory region (third dashed green arrow). If cyanide decreases k_Mito too much, however, the trajectory vertically transects the black oscillatory region too rapidly for oscillations to be observed, and no oscillations occur during glucose removal (fourth dashed green arrow). With DNFB, however, either degree of k_Mito reduction causes the trajectory to pass through the red oscillatory region. In contrast, with or without DNFB, FCCP (solid red arrow) decreases k_Mito too drastically and rapidly along the vertical axis for oscillations to be observed (fifth green dashed arrow).

FIGURE 5.

Phase diagrams in V_S - k_Mito parameter space from Fig. 1B. A, dashed green arrows show hypothetical slow trajectories following glucose removal, after various metabolic interventions (as labeled) have rapidly altered K_mito (solid arrows). B, analogous hypothetical trajectories (dashed green arrows) for the suppression (Oligo A) or induction (Oligo B) of glycolyctic oscillations by oligomycin, corresponding to Fig. 4, A and B, respectively. Stippled zones indicate oscillatory regions in the absence (black) and presence (red) of DNFB. See “Discussion” for details.

The ability of oligomycin (which moves k_Mito toward zero) to either suppress or potentiate oscillations can be similarly understood, as shown in Fig. 5B. If, after DNFB and cyanide, glycolysis is already oscillating (Case A from Fig. 4A), the addition of oligomycin makes k_Mito less negative, moving the trajectory vertically out of the oscillatory region (red zone). Conversely, if glycolysis is not oscillating because k_Mito after cyanide is too negative (Case B from Fig. 4B), oligomycin can move the trajectory vertically back into the oscillatory region.

During exposure to the various metabolic interventions listed in Table 1, biological variability among individual myocytes in the levels of glycogen and fatty acid stores, differential efficacy of drugs such as cyanide and DNFB, intrinsic difference in cellular ATPase activity, etc. is likely to determine the fraction of myocytes exhibiting glycolytic oscillations under any given condition.

We characterized glycolytic oscillations under conditions in which intracellular Ca²⁺ cycling was buffered with high 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid or EGTA concentrations in the patch electrode, in order to avoid complicating effects of Ca²⁺ cycling on energy production and consumption. As a major regulator of both energy production and consumption (16), as well as a dynamical subsystem in its own right (41), cardiac Ca²⁺ cycling and its interaction with dynamics of glycolytic oscillations add an additional layer of complexity that will be interesting to explore in future studies.

Conditions producing glycolytic oscillations in isolated myocytes may, in a broad sense, be relevant to acute myocardial ischemia, in which oxidative phosphorylation is inhibited by hypoxia and creatine kinase is inactivated by ROS and other factors (14, 15). Since glycolysis becomes the major source of ATP production under these conditions, glycolytic oscillations may complicate energy supply-demand imbalance during acute ischemia, potentially accelerating the onset of irreversible injury as well as contributing to metabolic sinks that promote ischemic arrhythm (13). Since glycolytic enzymes are also multifunctional signaling proteins, glycolytic oscillations could also be a link to activation of cardioprotective signaling pathways (42). However, further studies will be needed to establish the relevance, if any, to human clinical conditions, such as ischemia/reperfusion injury.