Voltage- and [ATP]-dependent Gating of the P2X₂ ATP Receptor Channel

Abstract

P2X receptors are ligand-gated cation channels activated by extracellular adenosine triphosphate (ATP). Nonetheless, P2X₂ channel currents observed during the steady-state after ATP application are known to exhibit voltage dependence; there is a gradual increase in the inward current upon hyperpolarization. We used a Xenopus oocyte expression system and two-electrode voltage clamp to analyze this “activation” phase quantitatively. We characterized the conductance–voltage relationship in the presence of various [ATP], and observed that it shifted toward more depolarized potentials with increases in [ATP]. By analyzing the rate constants for the channel's transition between a closed and an open state, we showed that the gating of P2X₂ is determined in a complex way that involves both membrane voltage and ATP binding. The activation phase was similarly recorded in HEK293 cells expressing P2X₂ even by inside-out patch clamp after intensive perfusion, excluding a possibility that the gating is due to block/unblock by endogenous blocker(s) of oocytes. We investigated its structural basis by substituting a glycine residue (G344) in the second transmembrane (TM) helix, which may provide a kink that could mediate “gating.” We found that, instead of a gradual increase, the inward current through the G344A mutant increased instantaneously upon hyperpolarization, whereas a G344P mutant retained an activation phase that was slower than the wild type (WT). Using glycine-scanning mutagenesis in the background of G344A, we could recover the activation phase by introducing a glycine residue into the middle of second TM. These results demonstrate that the flexibility of G344 contributes to the voltage-dependent gating. Finally, we assumed a three-state model consisting of a fast ATP-binding step and a following gating step and estimated the rate constants for the latter in P2X₂-WT. We then executed simulation analyses using the calculated rate constants and successfully reproduced the results observed experimentally, voltage-dependent activation that is accelerated by increases in [ATP].

INTRODUCTION

P2X receptors are ligand-gated cation channels activated by extracellular ATP. They are widely distributed in a variety of cell types, including neurons, smooth muscle cells, and blood cells, where they play critical roles in fast synaptic transmission (Edwards et al., 1992; Evans et al., 1992), presynaptic modulation (Gu and MacDermott, 1997; Khakh and Henderson, 1998; Kato and Shigetomi, 2001), regulation of sphincter activity (Cockayne et al., 2000; Yamamoto et al., 2006), and biophylaxis (Ferrari et al., 2006). The primary structure of P2X receptors was determined by isolating its cDNA; so far, seven P2X cDNAs have been identified (Brake et al., 1994; Valera et al., 1994). Although ligand gated, the structural properties of P2X receptor channels are distinct from other ligand-gated channels, such as the Cys loop and glutamate receptors (North, 2002). P2X receptors contain two transmembrane (TM) domains with a large extracellular loop (∼280 amino acid residues), and both the NH₂ and C termini are intracellular (Roberts et al., 2006). Based on the weight of the native protein (Nicke et al., 1998), images obtained with atomic force microscopy (Barrera et al., 2005) and data from a single particle structure analysis (Mio et al., 2005), the functional P2X receptor unit is thought to be composed of three subunits. Moreover, functional heteromultimerization has also been reported (Surprenant et al., 2000; Cockayne et al., 2005; Guo et al., 2007), and the stoichiometry of the P2X₂/P2X₃ heteromultimer was shown to be one P2X₂ and two P2X₃ subunits (Jiang et al., 2003).

Extensive electrophysiological analyses of the P2X receptor channel have also been performed using heterologous expression systems, and several interesting features have been described. For instance, (1) all P2X channels are nonselective cation channels, and some are highly permeable to large cations (Surprenant et al., 1996; Khakh et al., 1999; Virginio et al., 1999); (2) the macroscopic current shows inward rectification, which is also observed in the unitary current (Zhou and Hume, 1998; Fujiwara and Kubo, 2004); (3) upon opening after the application of ATP, some P2X channels show rapid desensitization, as other ligand-gated channels do, but P2X₂, P2X₅, and P2X₆ show very slow desensitization (Ralevic and Burnstock, 1998; Smith et al., 1999; North, 2002; Fujiwara and Kubo, 2006b); and (4) the functional properties of P2X channels are regulated by kinase activities (Boue-Grabot et al., 2000; Hung et al., 2005), membrane lipids (Elliott et al., 2005; Fujiwara and Kubo, 2006b), and their expression density on the membrane (Fujiwara and Kubo, 2004). Because the process of P2X₂ desensitization is slow, and channel activity persists for a considerable period after ATP application, the voltage dependence of the P2X₂ current can be analyzed using voltage step pulses in a manner similar to that used for voltage-gated channels. The inward current through the P2X₂ channel during the semi–steady-state after ATP application is known to gradually increase with hyperpolarization (Nakazawa et al., 1997; Zhou and Hume, 1998; Nakazawa and Ohno, 2005). This interesting phenomenon implies that the ligand-activated P2X₂ channel may behave voltage dependently. Similar observations have also been reported for the nicotinic ACh receptor channel (Charnet et al., 1992; Figl et al., 1996). One of our aims here was to quantitatively analyze the activation of P2X₂ evoked by voltage steps under two-electrode voltage clamp using a Xenopus oocyte expression system. We also quantitatively analyzed the effect of the concentration of the applied ATP ([ATP]) on the voltage-dependent activation. Besides, we performed experiments to exclude a possibility that the apparent voltage-dependent gating is actually due to block/unblock by endogenously contained cytoplasmic blocker(s).

The structural rearrangement of ion channels during activation from a closed to an open state has been extensively studied, and a common model involving a flexible backbone has been proposed. For instance, the TM gate of the nicotinic ACh receptor channel is reportedly opened by taking advantage of the flexibility of a proline pivot situated in the M2-M3 loop (Lester et al., 2004; Lummis et al., 2005). In the case of the voltage-gated potassium (Kv) channel, it is accepted that the activation gate is opened by bending at a flexible glycine hinge in the middle of the S6 region (Jiang et al., 2002a; MacKinnon, 2004; Magidovich and Yifrach, 2004; Ding et al., 2005). Thus, a flexible backbone appears to play a key role in channel gating. With respect to P2X channels, some studies have shown the presence of a TM gate (Rassendren et al., 1997; Egan et al., 1998; Khakh et al., 1999) and have proposed its conformational rearrangement (Khakh and Egan, 2005; Silberberg et al., 2005); however, there are no clear descriptions of the gating dynamics that focus on a flexible backbone. We therefore also aimed to determine the structural basis of the gating of the P2X₂ channel and performed scanning mutagenesis of the second TM helix, focusing on a putative glycine hinge for the gating.

It would also be of interest to obtain additional mechanistic insight into the complex voltage and [ATP] dependence of P2X₂ channel gating. We therefore assumed a standard three-state model consisting of a fast [ATP]-binding step and a following gating step, and estimated the rate constants for the latter in wild-type (WT) channels at various voltages and [ATP] based on the results. We then performed simulation analyses using the estimated voltage-dependent rate constants and the reported voltage-independent binding/unbinding rates to test whether the experimental results could be reproduced.

MATERIALS AND METHODS

In Vitro Mutagenesis and cRNA Synthesis

A BamH1-Not1 fragment of the original rat P2X₂ receptor cDNA (Brake et al., 1994) was subcloned into pBluescript vector. Single- and double-point mutants were made using a QuikChange site-directed mutagenesis kit (Agilent Technologies) and confirmed by DNA sequencing. cRNAs encoding WT and mutant receptors were prepared from the linearized plasmid cDNA using an RNA transcription kit (Agilent Technologies).

Preparation of Xenopus Oocytes

Xenopus oocytes were collected from frogs anaesthetized in water containing 0.15% tricaine; after the final collection, the frogs were killed by decapitation. Isolated oocytes were treated with collagenase (2 mg/ml; type 1; Sigma-Aldrich), after which oocytes of similar size at stage V were injected with ∼50 nl of cRNA solution (Fujiwara and Kubo, 2004). The injected oocytes were incubated for 2–3 d at 17°C in frog Ringer solution. All experiments conformed to the guidelines of the Animal Care Committees of the National Institute for Physiological Sciences (Okazaki, Japan).

Two-Electrode Voltage Clamp Recordings in Xenopus Oocytes

Macroscopic currents were recorded from Xenopus oocytes using the two-electrode voltage clamp technique with a bath clamp amplifier (OC-725C; Warner Co.) (Fujiwara and Kubo, 2002, 2006a). Stimulation, data acquisition, and data analysis were performed on a Pentium-based computer using Digidata 1322A and pCLAMP 8.2 software (MDS Analytical Technologies). All recordings were obtained at room temperature (21–23°C). Intracellular glass microelectrodes were filled with 3 M potassium acetate with 10 mM KCl, pH 7.2. The microelectrode resistances ranged from 0.1 to 0.2 MΩ. Two Ag-AgCl pellets (Warner Co.) were used to pass the bath current and sense the bath voltage. The voltage-sensing electrode was placed near the oocyte (∼1 mm away) on the same side as the voltage-recording microelectrode. The bath current-passing pellet and the current injection microelectrode were placed on the other side. Under these conditions, the series resistance between the oocyte surface and the bath voltage-sensing pellet was ∼200 Ω (Sabirov et al., 1997). As the measured current at the most hyperpolarized potential was 20 μA in the largest case, and was mainly <10 μA, the voltage clamp error due to this series resistance was estimated to be no more than 4 mV and mostly <2 mV. This error, which was not compensated in the experiments, did not change the conclusions drawn from the comparison of WT and mutant channels. Actual clamped membrane potentials were also monitored during the recordings, and data with an error of >2 mV from the command potentials were discarded.

The standard recording bath solution contained 95.6 mM NaCl, 1 mM MgCl₂, 5 mM HEPES, and 2.4 mM NaOH, pH 7.35–7.4. To avoid channel desensitization and a variety of secondary intracellular effects (Ding and Sachs, 2000), Ca²⁺ was not included in the bath solution. When we performed experiments using K⁺-based or gluconate-based external solution, we used KCl or Na gluconate instead of NaCl. For the experiment in which we changed of pH buffer to phosphate, the bath solution (the phosphate buffer solution) contained 88 mM NaCl, 1 mM MgCl₂, 1.5 mM NaH₂PO₄, 3.5 mM Na₂HPO₄, and 1.5 mM NaOH, pH 7.35–7.4. Before recording, the bath was continuously perfused with external solution; however, perfusion of the bath was stopped when recording was begun. ATP disodium salt (Sigma-Aldrich) was dissolved in bath solution just before each experiment, and the pH was adjusted to 7.35 using NaOH to avoid pH-dependent changes in the properties of the P2X channel (Skorinkin et al., 2003). When applied to cells, a one-fifth bath volume of five times–concentrated ATP solution was pipetted into the bath, after which complete exchange of the solution around the oocyte was confirmed to occur within ∼0.5 s (Saitoh et al., 1997). After recordings, the ATP was washed out of the bath by perfusion with external solution without ATP.

All data were recorded by applying a set of step pulses during the steady state (at ∼10 s) after ATP application. All recording pulse protocols are described in Results. Voltage pulses were applied in the range from +60 to −160 mV to avoid activating the oocytes' endogenous channels. We also confirmed using non-cRNA–injected oocytes that the endogenous background current was not evoked by ATP (Fig. S1, which is available at http://www.jgp.org/cgi/content/full/jgp.200810002/DC1). When data were, nevertheless, contaminated by endogenous current, they were discarded. A dataset from an identical oocyte was used for comparison of phenotypes because properties such as the EC₅₀ value for ATP and the I-V relationship differed from cell to cell. Oocytes expressing relatively low levels of P2X₂ (I < 4.0 μA at −60 mV) were used for the recordings to achieve sufficiently correct voltage clamping and to avoid changes of the properties of the channel due to the high expression level (Fujiwara and Kubo, 2004). All recorded currents, except the current traces in Fig. 1 (A and C), were leak subtracted; i.e., the background leak current before ATP application was subtracted to isolate the ATP-evoked current. The leak current was also monitored after the washing out of ATP, and records showing a significant increase in leak current amplitude were discarded.

Figure 1.

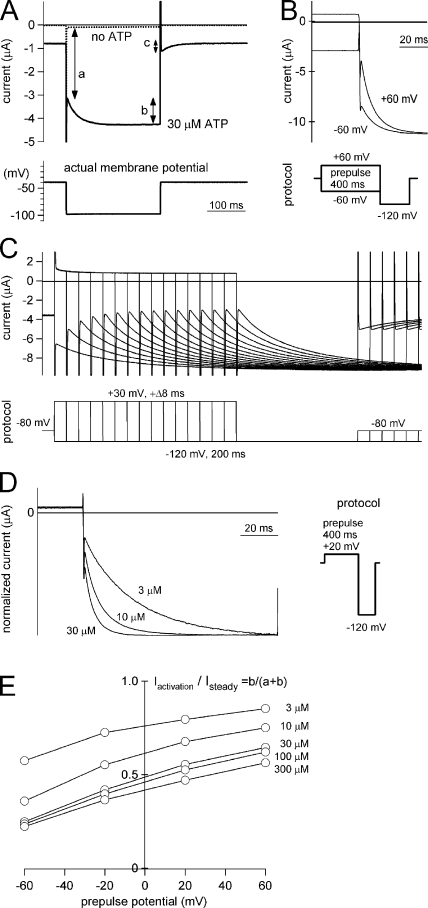
Voltage-dependent activation of P2X₂ during the steady state after application of ATP. Macroscopic currents recorded under two-electrode voltage clamp using Xenopus oocytes in Na-based external solution during the steady state after application of ATP. (A) Current traces from an identical oocyte evoked by a hyperpolarizing step pulse (from −40 to −100 mV) in the absence (dashed line) and presence (solid line) of ATP. The actual membrane potentials recorded are indicated in the bottom panel. The instantaneous component (a), activation component (b), and deactivation component (c) are illustrated. (B) Comparison of macroscopic currents evoked by hyperpolarizing step pulses from two different prepulse potentials, +60 and −60 mV. Pulse protocols are indicated below. These current traces were recorded from an identical oocyte and shown after subtracting data obtained in the absence of ATP. (C) Current traces from an identical oocyte evoked by hyperpolarizing step pulses to −120 from −30-mV prepulses of different durations. The pulse protocols are indicated below. Current traces were overlaid by arranging them relative to the beginning of the prepulse. (D) Comparison of macroscopic currents evoked by hyperpolarizing step pulses during the steady state after the application of various [ATP]. The pulse protocols are indicated on the right. These current traces were recorded from an identical oocyte and shown after subtracting data obtained in the absence of ATP. (E) I_activation/I_steady ratio from an identical oocyte after different prepulse potentials and [ATP]. Data points obtained at the same [ATP] are connected by lines.

Patch Clamp Recordings in HEK293T Cells

The cDNA for WT P2X₂ was subcloned into the pCXN₂ expression vector (Niwa et al., 1991). Then, HEK293T cells (human embryonic kidney cell line) were transfected with the constructed plasmid DNA and a transfection marker, enhanced green fluorescent protein (1/10 the amount of plasmid DNA; Clontech Laboartories, Inc.), using Lipofectamine Plus (Invitrogen), as instructed by the manufacturer. The cells were then cultured for 24 h in Dulbecco's modified Eagle's medium with 10% bovine calf serum. The transfectants were dissociated 12–15 h later by treatment with 0.025% trypsin in Ca²⁺-, Mg²⁺-free PBS and reseeded on coverslips at a relatively low density. Electrophysiological recordings were performed 18–35 h after transfection.

A coverslip with HEK293T cells was placed in a recording chamber containing bath solution (see below) on the stage of an inverted fluorescence microscope (IX70; Olympus), and the transfected cells were identified by the fluorescent signal from the cotransfected green fluorescent protein. Macroscopic currents were then recorded in the whole cell patch and excised inside-out patch configuration using an Axopatch-1D amplifier (Nakajo and Kubo, 2005; Fujiwara and Kubo, 2006a). The resistance of the patch pipettes ranged from 2 to 4 MΩ. 70–80% of the voltage error due to the series resistance was compensated by a circuit in the amplifier. The recorded currents were low-pass filtered at 2 kHz by a circuit built into the amplifier and digitized at 10 kHz. All recordings in this work were performed superfusing the cells with bath solution (0.5 ml/min) at room temperature (23–25°C). In the excised inside-out patch configuration, perfusion pipette was put close to the excised patch membrane (∼500 μm), and the excised membrane was intensively washed by perfusion for 15 min. Under this perfusing system, cytoplasmic organic cations and other ions were removed sufficiently (Fujiwara and Kubo, 2006a).

In the whole cell recordings, the bath (extracellular side) solution contained 150 mM NaCl, 1 mM MgCl₂, 5 mM EGTA, 10 mM HEPES, and various concentrations of Na₂ATP (pH 7.4 adjusted by NaOH). The pipette (intracellular side) solution contained 140 mM KCl, 3 mM MgCl₂, 1 mM CaCl₂, 2 mM EGTA, 2 mM Na₂ATP, and 10 mM HEPES (pH 7.4 with NaOH) (Fig. S2, available at http://www.jgp.org/cgi/content/full/jgp.200810002/DC1). We also used a pipette solution containing 150 mM NaCl, 10 mM EDTA, and 10 mM HEPES (pH 7.2 with NaOH) (Fig. S3).

In the inside-out recordings, the pipette (extracellular side) solution contained 150 mM NaCl, 1mM MgCl₂, 5 mM EGTA, 10 mM HEPES, and various concentrations of Na₂ATP (pH 7.4 with NaOH). The bath (intracellular side) solution contained 150 mM NaCl, 10 mM EDTA, and 10 mM HEPES (pH 7.2 with NaOH) (Fig. 4). Cells with a very high expression level were used for the excised patch experiments to record macroscopic current. The expression level using HEK293 cells and pCXN2 expression can reach up to this level (Fujiwara and Kubo, 2002, 2006a).

Figure 4.

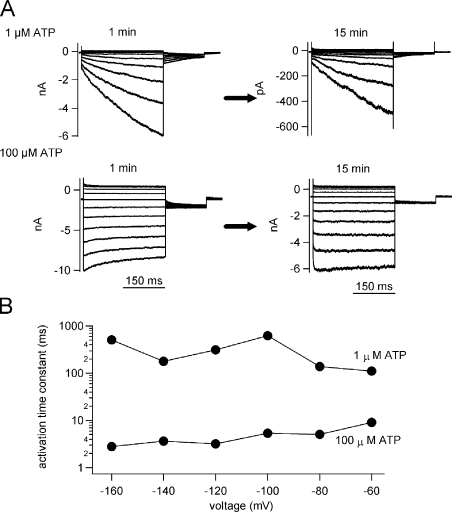
Excised inside-out patch clamp recordings of the macroscopic current through P2X₂ WT expressed in HEK293T cells with intensive perfusion of the bath (intracellular side) solution. (A) Macroscopic currents were recorded by inside-out patch clamp from HEK293T cell using the same voltage step protocols in Fig. 2 in the presence of the indicated [ATP]. Current traces recorded at 1 min (left) after excising the patch membrane and at 15 min (right) after an intensive perfusion by the blocker-free solution described in Materials and methods. (B) Dependence of the activation kinetics on voltage and [ATP].

ATP disodium salt (Sigma-Aldrich) was dissolved in the extracellular solution just before each experiment, and the pH was adjusted to 7.4 using NaOH. The concentration of added ATP is indicated in Fig. 4 and Figs. S2–S3. Leak subtraction was not done for the data from patch clamp recordings.

Data Analysis and Simulation

Data were analyzed using Clampfit (MDS Analytical Technologies), Igor Pro (WaveMetrics, Inc.), and KyPlot (KyensLab, Inc.) software. For the analyses of the G-V relationship in Figs. 3, 7, and 9, inward tail current amplitudes obtained at −60 mV were fitted using pClamp9 software to a two-state Boltzmann equation:

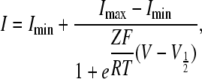where I_min and I_max are the limits of the amplitudes in the fittings, Z is the effective charge, V_1/2 is the half activation voltage, F is Faraday's constant, R is the gas constant, and T is temperature in Kelvin. Here, I_min is the inward current with the largest amplitude. Normalized G-V relationships were plotted using

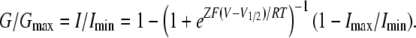Figure 3.

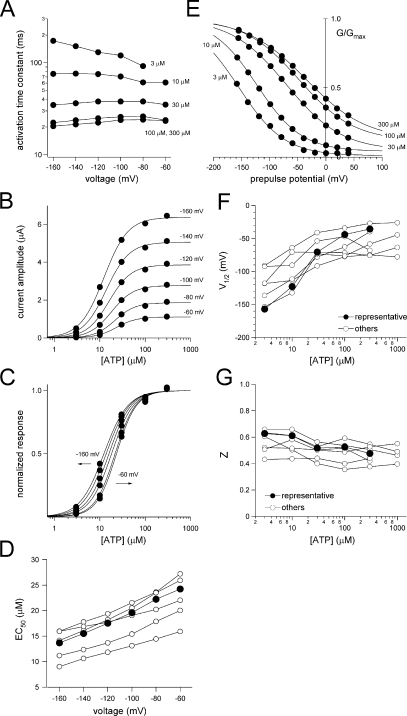
Analyses of the voltage-dependent gating of P2X₂ in the presence of various [ATP]. (A) Dependence of the activation kinetics on voltage and [ATP]. The activation phases of the currents shown in Fig. 2 were fitted with a single exponential function, and the time constants of the fittings at each membrane potential are plotted. (B) [ATP] response relationships are derived from the recordings in Fig. 2. Current amplitudes were measured at the test pulse. Data were fitted with Hill's equation as described in Materials and methods. (C) [ATP] response relationships in B were normalized and replotted. (D) Voltage dependency of EC₅₀ values of the [ATP] response. Representative plots (filled circles) are derived from the data in B and C; the others (open circles) are from other oocytes. (E) Normalized G-V relationships are derived from the recording in Fig. 2. Tail current amplitudes at −60 mV were measured. Data were fitted with the two-state Boltzmann equation as described Materials and methods. (F and G) V_1/2 values (F) and Z values (G) in various [ATP]. Representative plots (filled circles) were derived from the data in E; the others (open circles) are from other oocytes.

Figure 7.

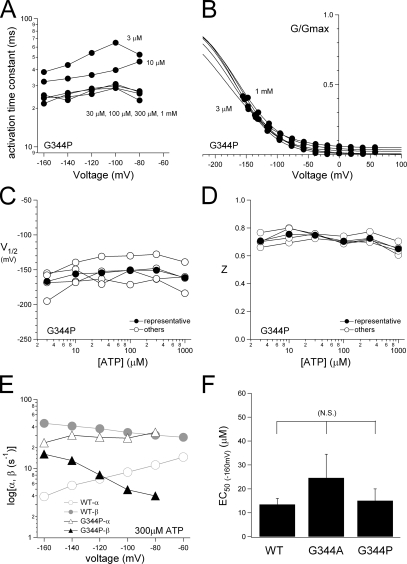
Analyses of the voltage-dependent gating of P2X₂ mutants in the presence of various [ATP]. The data from the mutants were analyzed as in Fig. 2, and representative plots were derived from the data in Fig. 6. (A) Analyses of the activation kinetics of G344P at various [ATP]. (B) Normalized G-V relationships for the macroscopic currents through G344P. (C and D) V_1/2 (C) and Z (D) values for G344P at various [ATP]. (E) Calculated α and β values for G344P in the presence of 300 μM ATP were plotted versus membrane potential. The data from the WT channel in 300 μM ATP were also plotted (gray symbols) for comparison. (F) Comparison of the EC₅₀ values of the [ATP] response relationship for the WT channel and the mutants.

Figure 9.

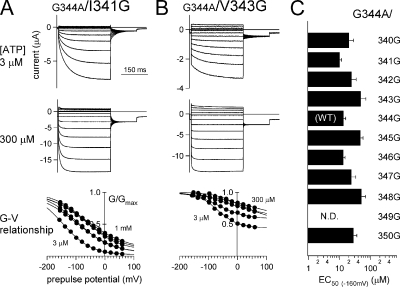
Representative recordings and analyses of two glycine scanning mutants. (A and B) Macroscopic current recordings from G344A/I341G (A) and G344A/V343G (B) in the presence of two different [ATP]. G-V relationships for the two mutants at various [ATP] are shown at the bottom. The recordings and the data analyses were performed as in Fig. 2. (C) EC₅₀ values of the [ATP] response relationship for the mutants. N.D., channels that showed no detectable current.

The activation time constant (τ) shown in Figs. 3, 4, and 7 and Figs. S2–S4 was obtained by fitting the activation phase of the inward currents upon hyperpolarization with a single exponential function. The opening (β) and closing (α) rates shown in Figs. 5 and 7 were calculated using two equations:

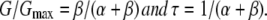(1)

Figure 5.

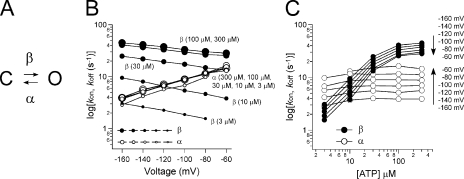
Kinetic analysis with a simple two-state model. (A) Two-state model for P2X channel gating. C represents a closed state, and O represents an open state. α and β represent the transition rates between the closed and open states. (B) Representative α and β at various [ATP] were plotted versus membrane potentials. α and β were calculated from the data in Figs. 2 and 3 using two equations: G/G_max = β/(α + β) and τ = 1/(α + β). (C) α and β in B were replotted versus [ATP].

Current amplitudes evoked by the voltage step with various [ATP] were reproducibly recorded under the present recording condition. Therefore, EC₅₀ values in Fig. 3 (B–D) could be calculated from the data in Fig. 2 by fitting them with the Hill equation, with which the peak current amplitudes at various voltages in the presence of various [ATP] were analyzed. EC₅₀ values in Figs. 7 and 9 were calculated by fitting them with the Hill equation at the peak current amplitudes evoked by applying various [ATP] during the steady state at −160 mV. In Fig. 7, pairs of mean EC₅₀ values were compared among the three groups using Tukey's test.

Figure 2.

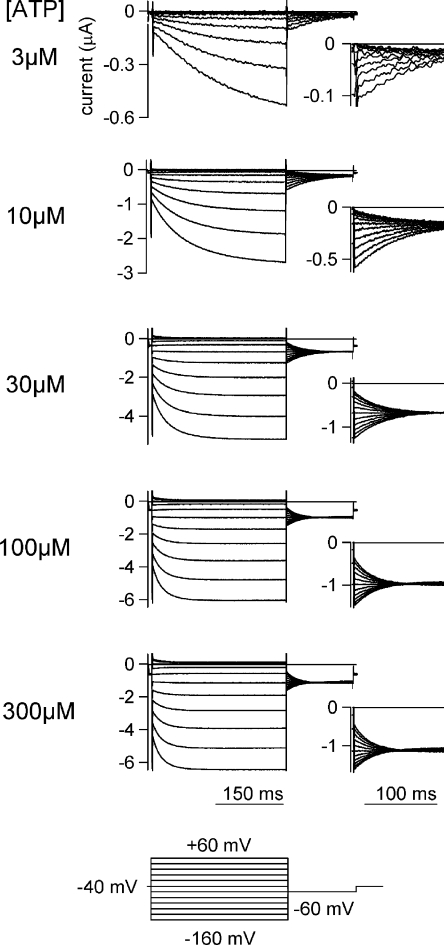
Macroscopic current recordings through P2X₂ evoked by step pulses during the steady state after the application of various [ATP]. Macroscopic currents through WT P2X₂ evoked by step pulses in the presence of various [ATP]. The holding potential was −40 mV. Step pulses from +60 to −160 mV were applied in 20-mV decrements. Tail currents were recorded at −60mV, and their enlarged images are shown in the insets. The pulse protocol is indicated at the bottom. These current traces were recorded from an identical oocyte and shown after subtracting data obtained in the absence of ATP.

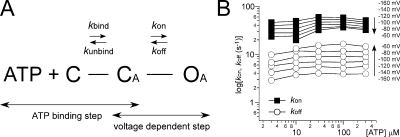
In Fig. 10 A, we propose a standard three-state model consisting of the ATP-binding step and the following gating step. We defined the rate constants for each step: k_bind and k_unbind are for the ATP-binding step, and k_on and k_off are for the gating step. We calculated k_on and k_off from the α and β values obtained in the experiments described above. For the purpose of simplification, we introduced an assumption that the ligand-binding step reaches equilibrium much faster than the gating step. It is generally accepted that the rate constants for ligand binding and unbinding are large; e.g., k_bind = 2.6 × 10⁷ [M⁻¹s⁻¹] and k_unbind = 1.1 × 10³ [s⁻¹] (Ding and Sachs, 1999). We also observed that the activation phase can be fitted with a single exponential function, demonstrating that there is only one rate-limiting step. Both of these findings support the idea that the transition between the C and C_A states reaches equilibrium rapidly, allowing us to define the ratio of C and C_A in practical terms as

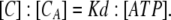Figure 10.

Three-state, two-transition model of voltage- and [ATP]-dependent gating. (A) Simple three-state model consisting of an ATP-binding step and a gating step. C, the closed state with no bound ATP; C_A, the closed state after ATP is bound; O_A, the open state. k_bind and k_unbind represent the binding/unbinding rates for ATP binding to the channel. k_on and k_off represent the rates of the gating step. (B) k_on and k_off were calculated as described in Materials and methods from the data in Fig. 5 (B and C). Membrane potentials are shown in the figure.

The dissociation constant, Kd, is given by:

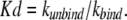The total probability in each step is 1:

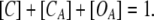Therefore, [C_A] is described as

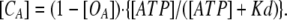(2)

The growing speed of [O_A] is given by

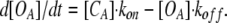By using Eq. 2, d[O_A]/dt can be written as:

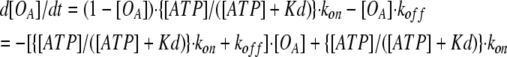(3)

An absolute value of the inverse coefficient of [O_A] in Eq. 3 is the activation time constant (from Eq. 1):

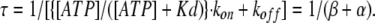Finally, the gating rate constants k_on and k_off are given by the experimentally obtained β and α:

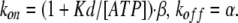Here, we introduce a second assumption that the Kd value is not voltage dependent, and we used a Kd value of 42 μM (Ding and Sachs, 1999) for all voltages and calculated the k_on and k_off values at various voltages and [ATP], as plotted in Fig. 10 B.

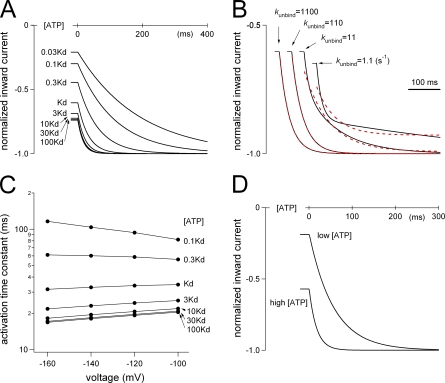
The activation phase evoked by the voltage step was simulated using Igor Pro (WaveMetrics, Inc.) software (Fig. 11). Simulation was performed based on the two-step model in Fig. 10 A. Transitions from each state were represented by differential equations and plotted every 1 ms using numerical integration (Fig. 11). The gating rate constants k_on and k_off were taken from the data in Fig. 10 B, and the rate constants for the ATP-binding step were determined with reference to the single-channel analysis data, k_bind = 2.6 × 10⁷ [M⁻¹s⁻¹] and k_unbind = 1.1 × 10³ [s⁻¹] (Ding and Sachs, 1999). We used a k_unbind value of 1,100, and the value of [ATP] × k_bind was set depending on the [ATP] relative to Kd. The rate constants used for simulation are shown in Table II.

Figure 11.

Simulation analyses of the activation phase evoked by a voltage step in the P2X₂ WT channel. (A) Reproduction of the activation phase by simulation. The activation phases evoked by step pulses from −60 to −160 mV in the presence of various [ATP] were simulated. Rate constants used are shown in Table II (A and B). The applied [ATP] relative to Kd is indicated. (B) Comparison of the simulations of the activation phases using various ATP-binding and unbinding rate constants in the presence of an [ATP] that equals the Kd. The k_unbind values used are shown. Rate constants used are shown in Table II (A and C). Red dashed lines indicate lines fitted by a single exponential function for each current trace. (C) Summary of the simulation of the activation kinetics at various voltages and [ATP]. The activation phases evoked by a voltage step from −60 mV to each voltage were simulated using the rate constants in Table II (A and B). The activation phases of the simulated currents could be fitted satisfactorily with a single exponential function, and the time constants of the fittings at various [ATP] relative to Kd were plotted versus membrane potential. (D) Reproduction of [ATP]-dependent changes in the activation kinetics by a simulation assuming that k_bind is voltage dependent and that k_on and k_off are voltage independent. The activation phases evoked by the step pulse from −60 to −160 mV in the presence of high and low [ATP] were simulated. The rate constants used are shown in Table II D. In the case of low [ATP] here, Kd is equal to 100 × [ATP] at −60 mV and 10 × [ATP] at −160 mV due to the voltage-dependent change of k_bind. In the high [ATP] case, Kd is equal to 10 × [ATP] at −60 mV and 1 × [ATP] at −160 mV.

TABLE II.

Rate Constants Used for the Simulation Study

A	Voltage (mV)	kon (s−1)	koff (s−1)
	−60	33.5	14.8
	−80	36	11.5
	−100	40.5	8.9
	−120	45.7	6.9
	−140	50.7	5.4
	−160	56.3	3.9
B	[ATP] (μM)	[ATP] · kbind (s−1)	kunbind (s−1)
	0.03 Kd	33	1,100
	0.1 Kd	110	1,100
	0.3 Kd	330	1,100
	Kd	1,100	1,100
	3 Kd	3,300	1,100
	10 Kd	11,000	1,100
	30 Kd	33,000	1,100
	100 Kd	110,000	1,100
C	[ATP] (μM)	[ATP] · kbind (s−1)	kunbind (s−1)
	Kd	1,100	1,100
	Kd	110	110
	Kd	11	11
	Kd	1.1	1.1
D	[ATP]	voltage (mV)	[ATP] · kbind (s−1)	kunbind (s−1)	kon (s−1)	koff (s−1)
	Low	−60	10	1,000	100	10
			−160	100	1,000	100	10
	High	−60	100	1,000	100	10
			−160	1,000	1,000	100	10

Rate constants were calculated based on the model in Fig. 10 A. (A) Calculated rate constants for the gating step, K_on and K_off, in Fig. 10 B. These values were used for the simulation study depicted in Fig. 11 (A–C). (B) [ATP] relative to the Kd and rate constants for the ATP-binding step used in Fig. 11 (A and C). (C) [ATP] relative to the Kd and rate constants for the ATP-binding step used in Fig. 11 B. (D) Rate constants used in Fig. 11 D. Here, it was assumed that k_bind increases 10 times with the voltage change from −60 to −160 mV, whereas k_on and k_off are not voltage dependent.

Online Supplemental Material

Negative control recordings were performed with non-cRNA–injected oocytes (Fig. S1). Using the HEK293 cell expression system, the macroscopic currents through the WT P2X₂ were analyzed by whole cell patch clamp recordings with a K⁺-based standard pipette solution (Fig. S2) and with a blocker-free pipette solution (Fig S3). Macroscopic currents through the S378stop mutant expressed in Xenopus oocytes were also analyzed (Fig S4). In these experiments, the activation phases with a highly similar voltage and [ATP] dependence to the WT P2X₂ expressed in Xenopus oocytes were observed (Figs. S2–S4). The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.200810002/DC1.

RESULTS

Voltage- and [ATP]-dependent Activation of P2X₂ Channels

Xenopus oocytes were injected with cRNA encoding rat P2X₂, after which macroscopic currents through the expressed P2X₂ channels were recorded in Na⁺-based standard external solution using two-electrode voltage clamp. To observe the background leak current through the oocyte, we first recorded macroscopic currents in the absence of ATP by applying step pulses. Cells were held at −40 mV, and 250-ms pulses to −100 mV were applied, after which they were stepped back to −40 mV (Fig. 1 A, dashed line). Under these conditions, very small amplitude currents were observed (Fig. 1 A, dashed line). We then used the same step pulse protocol to record macroscopic currents from the same oocyte during the steady state ∼10 s after the application of 30 μM ATP (Fig. 1 A, solid line). The inward current increased instantaneously at the beginning of the step pulses, reflecting the change in the driving force and the inwardly rectifying pore property (I_initial = a), after which there was a gradual increase in the current amplitude (I_activation = b) until a steady state was reached (I_steady = a+b). Then upon depolarization, a gradual decrease in current amplitude was observed (I_deactivation = c). We also recorded the actual membrane potential and confirmed that it promptly followed the applied pulse and was precisely clamped at −100 mV (Fig. 1 A, bottom). This means that the voltage step elicited an activation (the gradual increase in the inward current), even though the ATP-gated P2X₂ channel lacks a voltage sensor domain. We focused on this activation component of P2X₂ in subsequent experiments.

To test whether the observed activation component was dependent on the membrane voltage, we analyzed macroscopic currents in the presence of ATP using various voltage step protocols. In Fig. 1 B, cells were held at −40 mV, and 400-ms prepulses to +60 or −60 mV were applied, after which the membrane voltage was stepped to −120 mV. A set of recordings was obtained from an identical oocyte, and the leak-subtracted data are shown in Fig. 1 B. The current amplitudes at the steady-state levels were the same with both prepulses, but the I_activation/I_steady ratio obtained with a prepulse to +60 mV was larger than that obtained with a prepulse to −60 mV (Fig. 1 B). We also analyzed the activation of P2X₂ by applying prepulses of differing durations. In this analysis, we did not execute the leak subtraction to show the beginning of I_activation clearly. In Fig. 1 C, cells were held at −80 mV, and prepulses to +30 mV were applied, after which the membrane voltage was stepped to −120 mV for 200 ms. In these recordings, the durations of the prepulses increased from 0 to 120 ms in 8-ms increments, and there was a 300-ms interpulse interval. We found that the I_activation/I_steady ratio gradually increased with the increases in prepulse duration.

We also tested whether this activation was dependent on the [ATP]. Cells were held at 0 mV, and 400-ms prepulses to +20 mV were applied, after which the membrane was stepped to −120 mV for 100 ms. Fig. 1 D shows a series of macroscopic currents recorded from an identical oocyte in the presence of three different [ATP]. The current traces were normalized to the peak amplitude at the end of the step pulses, and the leak-subtracted data are shown. The I_activation/I_steady ratio was also clearly dependent on the applied [ATP], and the speed of the activation was accelerated by increases in [ATP]. The I_activation/I_steady ratio was then systematically analyzed in an identical oocyte using various prepulse potentials and [ATP]. When macroscopic currents were recoded using the same pulse protocols as in Fig. 1 D, I_activation/I_steady declined with increases in [ATP] and with hyperpolarization of the prepulse potential (Fig. 1 E); i.e., the ratio was dependent on both voltage and [ATP]. We also confirmed that the voltage- and [ATP]-dependent activation did not depend on the recording solution. No clear differences were observed between experiments performed in K⁺-based, gluconate-based, or phosphate buffer–based external solutions. The outward current at the depolarized potentials was too small in amplitude and was influenced by a leak current. We, therefore, did not analyze it in detail here.

Voltage Step Analyses of the Channel Gating of P2X₂

The macroscopic currents depicted in Fig. 2 were recorded from an identical oocyte in the presence of various [ATP] by applying a set of step pulses during the steady state after ATP application. Cells were held at −40 mV, and 300-ms pulses from +60 to −160 mV were applied in 20-mV decrements, after which the membrane was stepped to −60 mV for 150 ms. Activation of the inward currents in Fig. 2 could be fitted satisfactorily with a single exponential function, and the fitting qualities were not improved by fitting with a double exponential function. The time constants at each potential are plotted in Fig. 3 A. The speed of the activation increased with increases in [ATP] until it saturated at [ATP] > 100 μM (Fig. 3 A). The voltage dependence of the activation kinetics was not very clear, however. The relationship of [ATP] and response current amplitude from Fig. 2 was voltage dependent (Fig. 3, B and C). EC₅₀ values obtained from other oocytes (Fig. 3 D) also showed similar tendencies. Because the single-channel current through the P2X₂ channel shows strong inward rectification (Zhou and Hume, 1998), it is necessary to analyze the G-V relationships of the deactivating tail current to estimate the channel activity (open probability of the channel) at each potential. The G-V relationships were analyzed by measuring the initial amplitudes of the tail currents at −60 mV, and then fitted with a two-state Boltzmann function. Normalized G-V relationships are plotted in Fig. 3 E; also shown are the half-maximal voltages, V_1/2 (Fig. 3 F), and the valence of effective charges, Z (Fig. 3 G). The G-V relationship at each [ATP] showed a clear voltage dependence (Fig. 3 E) and was also dependent on [ATP]; i.e., the curve shifted in a depolarizing direction with increases in [ATP] (Fig. 3 E). Like the activation speed, the shift in the V_1/2 values saturated at [ATP] > 100 μM (Fig. 3 F), whereas the Z values, which reflect the charge movements during channel gating, remained constant (∼0.5) in the presence of the different [ATP]. Data recorded from other oocytes are plotted in Fig. 3 (F and G) and show similar tendencies.

Examination of a Possibility That the Gating Is actually Due to Block/Unblock

The results summarized above show that the activation of P2X₂ channel was voltage dependent as well as dependent on [ATP]. This phenomenon suggests that the P2X₂ channel seemingly has a “gating” depending on the voltage and [ATP], but there is an alternative possibility that the apparent gating we observed might be due to voltage-dependent block/unblock by some positively charged ion(s) or substance(s) contained in the oocytes; i.e., block hypothesis. As it has been reported that the increase in ATP-evoked currents upon hyperpolarization is also observed in PC12 cells by whole cell patch clamp (Nakazawa et al., 1997), and that the main intracellular polyvalent cations Mg²⁺ and polyamines do not block P2X₂ channels (Zhou and Hume, 1998), this possibility is judged to be not likely. To examine the “block hypothesis” by our hands, we analyzed the activation phase under various recording conditions.

We recorded from mammalian HEK293T cells transfected with P2X₂ by whole cell patch clamp configuration and analyzed the activation phase. The activation kinetics and the [ATP] dependency were highly similar to the results from Xenopus oocytes (Fig. S2). Next, we recorded whole cell current through P2X₂ using an intracellular solution that did not include divalent cations or any other blocker candidates. A similar voltage- and [ATP]-dependent activation could still be observed (Fig. S3). Moreover, we analyzed the activation upon hyperpolarization by inside-out patch clamp recording using blocker-free intracellular solution. ATP was added in the pipette solution (extracellular side) to activate P2X₂ channels. Despite a certain degree of desensitization, macroscopic currents could be recorded for a long time. A similar activation phase was still observed even after intensive perfusion for 15 min using the blocker-free bath (intracellular side) solution (Fig. 4). The activation time course was accelerated with the increase in [ATP] (Fig. 4, A and B), and the difference of the tail current shape between low and high [ATP] reflects the G-V shift (Fig. 4 A). These tendencies are similar to those observed in the recordings by the two-electrode voltage clamp (Fig. 2) and by the whole cell patch clamp (Fig. S3).

Like the case of inactivation “ball” of Shaker K⁺ channels, it is postulated in P2X₂ channels that the cytoplasmic construct of P2X₂ itself blocks the channel pore during desensitization (Hoshi et al., 1990; Smith et al., 1999). To examine the possibility that the observed gating might be actually due to block/unblock by the cytoplasmic structure of P2X₂, we made the C terminus deletion mutant, S378stop, and recorded from Xenopus oocytes under two-electrode voltage clamp. The activation phase with a highly similar voltage and [ATP] dependence to WT was still observed in this deletion mutant (Fig. S4).

In sum, these results are clearly against the block hypothesis that the activation evoked by hyperpolarization reflects voltage-dependent relief of channel blockade by unidentified blockers in oocytes or by a part of the channel, and supports that the observed activation upon hyperpolarization reflects gating of the P2X₂ channel depending on voltage and [ATP].

Model Interpretation of the P2X Channel Gating

We next assumed a simple state model in which the activation evoked by a voltage step reflects the channel's transition from a closed to an open state (Fig. 5 A), and calculated the rate constants between the two states using the activation time constants and G/G_max (Fig. 3). We then plotted the rate constants (α and β) calculated for each [ATP] against the membrane potential (Fig. 5 B) and the [ATP] (Fig. 5 C). It can be seen from the plots that the opening (β) and closing (α) rates are reciprocally voltage dependent (Fig. 5 B), and that α remained constant in the presence of various [ATP], whereas β increased with increases in [ATP] (Fig. 5, B and C) until it, too, saturated at [ATP] > 100 μM (Fig. 5 C). This analysis suggests that the closed-to-open transition of P2X₂ is determined in a complex way that reflects both the membrane voltage and the [ATP].

Mutation at Glycine344 in the Second TM Region

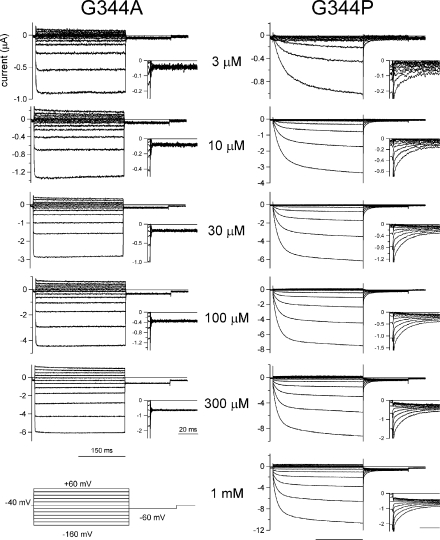
To identify the structural basis of P2X₂ channel gating, we made a set of mutants and analyzed their voltage-dependent gating properties at a steady state after the application of various [ATP]. We observed that the gating kinetics of the channel were clearly altered by mutating the glycine residue (G344) in the second TM helix. Macroscopic currents through the G344A and G344P mutants recorded using the same protocols as in Fig. 2 are shown after leak subtraction in Fig. 6. Enlarged tail currents are also shown in the insets. With the G344A mutant, the activation evoked by a voltage step was instantaneous, even in the presence of a low [ATP] (Fig. 6). The phenotype of the G344V mutant was similar to that of G344A (not depicted). Because the activation and deactivation components of G344A and G344V were instantaneous, they could not be analyzed precisely. In contrast, the activation phase of the G344P mutant (Fig. 6) was similar to, but clearly slower than, that of the WT channel (Fig. 2). And slower changes were also observed in the deactivating tail currents. The activation phase of the inward current through the G344P mutant was fitted with a single exponential function, and the time constants at each potential are shown in Fig. 7 A. The speed of the activation increased with increases in [ATP] until it saturated at ATP > 30 μM (Fig. 7 A). The voltage dependence of the activation kinetics was not very clear in the voltage range studied. The G-V relationships for G344P were analyzed in the same way as in Fig. 3 E and fitted by a two-state Boltzmann function. Normalized G-V relationships are plotted in Fig. 7 B; also shown are V_1/2 (Fig. 7 C) and Z (Fig. 7 D). The G-V relationship for each [ATP] showed similar voltage dependence (Fig. 7 B), and the G-V relationships (Fig. 7 B) and V_1/2 values (Fig. 7 C) were clearly shifted toward hyperpolarized potentials, as compared with those for WT P2X₂ (compare Fig. 3, F and G). Z values remained constant (∼0.7) as [ATP] was varied. Data recorded from other oocytes using the same experimental protocols are plotted as open circles in Fig. 7 (C and D), and the same tendencies can be seen.

Figure 6.

Macroscopic current recordings through the G344A and G344P mutants evoked by step pulses during the steady state after the application of various [ATP]. Macroscopic currents were recorded as in Fig. 2 in the presence of the indicated [ATP]. Tail currents were recorded at −60 mV, and their enlarged images are shown in the insets. All current traces for each mutant were recorded from an identical oocyte and shown after subtracting data obtained in the absence of ATP.

We also calculated the rate constants for the transition between a closed and an open state. The calculated rate constants for the G344P mutant and WT channel in the presence of a saturating [ATP] (300 μM) are plotted versus membrane potential in Fig. 7 E. β for G344P (Fig. 7 E, filled triangles) was smaller than that for WT P2X₂ (filled circles), whereas α for G344P (open triangles) was slightly larger than that for WT (open circles). We also confirmed that the sensitivity of the channel to ATP, which is reflected by the EC₅₀ value, was not significantly affected by the G344P or G344A mutation (Fig. 7 F). G344 mutation–induced changes of the activation kinetics and the EC₅₀ values did not show clear correlation with each other. Furthermore, G344 is clearly distant from the ATP-binding site identified at the extracellular region by systematic mutagenesis study (Ennion et al., 2000; Jiang et al., 2000). Collectively, these data suggest that G344 plays a key role in the channel gating. The activation phase was markedly altered by the G344A mutation, whereas the G344P mutation had a less severe effect. Upon introduction of the G344P mutation, it became harder to induce a transition from a closed to an open state. In contrast, the G344A mutation caused the channel to open easily, as reflected by the instantaneous activation elicited by voltage steps (Fig. 6).

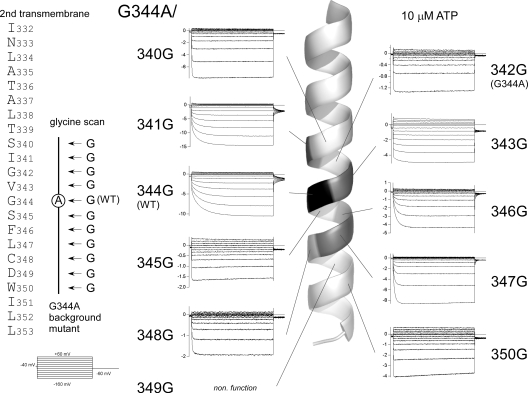
Glycine Rescue Scanning Mutagenesis

We hypothesized that the observed changes in gating kinetics might be caused by changes in the flexibility at the position of G344 (a putative gating hinge) in the middle of the second TM helix. To test that idea, we introduced one glycine residue at a time to the G344A mutant throughout the second TM helix (Fig. 8, left), and then analyzed their gating properties in the presence of various [ATP] with the same protocols used in Fig. 2. Representative current traces recorded in the presence of 10 μM ATP are shown in Fig. 8, and the corresponding locations of the introduced glycine residue are indicated in the helix cartoon. The activation phase was recovered by introducing a glycine residue into the middle of the second TM helix, near the position of 344, but the activation remained instantaneous when a glycine residue was introduced at a position distant from 344. In addition, the G344A/D349G mutant showed no detectable current, and the D349G single-point mutant was also nonfunctional. As the conserved D349 is reported to be critical for the folding and assembly in P2X₅ (Duckwitz et al., 2006), the lack of detectable current here might be due to the disordered channel formation.

Figure 8.

Glycine scanning mutagenesis of the second TM helix of the G344A mutant. Amino acid sequence of the second TM helix of the P2X₂ channel. Macroscopic currents were recorded as in Fig. 2. The pulse protocol used is shown at the bottom left. Current traces recorded in the presence of 10 μM ATP are shown at positions corresponding to the introduced glycine in the TM helix. Current traces are shown after subtracting data obtained in the absence of ATP. In the drawing of the helix, the positions of the amino acid residues that when mutated to glycine rescued the voltage-dependent activation phases are highlighted.

We then analyzed the G-V relationships for the mutants in which the activation phase was recovered, and there were clear deactivating tail currents. All analyzed data are shown in Table I, and representative current traces and G-V relationships for the two mutants are shown in Fig. 9 (A and B). The phenotype of the G344A/I341G mutant resembled that of WT P2X₂. Its G-V curve at a low [ATP] (3 μM) was located at a hyperpolarized position and shifted in the depolarizing direction with increases in [ATP] (Fig. 9 A). The G344A/V343G mutant also showed a depolarizing shift in the G-V relationship with increases in [ATP], but, overall, these curves were located at more depolarized potentials than those obtained with the WT channel. Consequently, the activation included an instantaneous component (low percentage of I_activation/I_steady). V_1/2 values at saturating [ATP] varied in the rescued mutants (Table I), but the depolarizing shift with increases in [ATP] was commonly observed. The [ATP] response of the channel was not significantly altered by introduction of a glycine residue, nor did it clearly correlate with the position of the mutation (Fig. 9 C).

TABLE I.

Analyzed Data of the Glycine Scanning Mutagenesis

Mutants	Activation	V1/2 (mV)	EC50 (μM)
G344A/S340G	(−)		20.3 ± 8.0 (n = 6)
G344A/I341G	(+)	−81.2 ± 7.3 (n = 7)	10.1 ± 1.5 (n = 6)
G344A/G342G (G344A)	(−)		24.6 ± 9.9 (n = 6)
G344A/V343G	(+)	6.4 ± 8.4 (n = 4)	48.4 ± 22.0 (n = 5)
G344A/A344G (WT)	(+)	−54.2 ± 7.5 (n = 7)	13.5 ± 2.5 (n = 6)
G344A/S345G	(−)		47.5 ± 10.0 (n = 5)
G344A/F346G	(+)	−105.6 ± 5.0 (n = 6)	13.3 ± 2.0 (n = 11)
G344A/L347G	(+)	<−200 (n = 8)	24.1 ± 9.3 (n = 6)
G344A/C348G	(−)		51.1 ± 17.8 (n = 5)
G344A/D349G	Nonfunction	Nonfunction	Nonfunctional
G344A/W350G	(−)		28.2 ± 7.8 (n = 5)

Names of the analyzed mutants are shown in the first column. In the second column, (+) indicates recovery of the activation phase; (−) indicates no recovery. For the mutants with recovered activation phase, tail current analyses were performed, and the V_1/2 values in the presence of 300 μM ATP (except 100 μM for G344A/V343G) are shown in the third column. V_1/2 values for the G344A/L347G mutant were too hyperpolarized to analyze precisely. EC₅₀ values for the [ATP] response relationship at −160 mV are indicated in the last column. G344A/D349G showed no detectable current.

In sum, this glycine rescue mutagenesis supports our hypothesis that the activation phase evoked by the step pulse would be mediated by the flexible glycine residue in the middle of the second TM helix.

DISCUSSION

Voltage- and [ATP]-dependent Gating of the P2X₂ Receptor Channel

Here, we analyzed the activation phase of P2X₂ receptor channels evoked by hyperpolarizing voltage steps in the presence of various [ATP] using two-electrode voltage clamp recordings. It was similarly observed in transfected HEK293 cells under the whole cell and the excised inside-out patch condition after intensive bath perfusion (Figs. S2 and S3, and Fig. 4), excluding a possibility that the activation is due to unblock by blocker(s) contained in the oocytes. The activation phase could be fitted satisfactorily with a single exponential function (Fig. 3 A), and the G-V relationships for WT P2X₂ at each [ATP] could be fitted with a single Boltzmann function (Fig. 3 E). On the basis of these observations, we assumed a simple two-state model in which the activation evoked by a voltage step reflects the channel's transition from a closed to an open state (Fig. 5 A) and calculated the rate constants between the two states. We observed that the opening (β) and closing (α) rates were reciprocally voltage dependent (Fig. 5 B), and that β increased with increases in [ATP] until it saturated, whereas α remained constant (Fig. 5 C). In short, our data suggest that the seemingly simple gating of the P2X₂ channel is actually quite complex, and that there is both a voltage-dependent and an [ATP]-dependent step in the gating transition from the closed to the open state.

How then is this complex channel gating explained? For the sake of simplicity, we assumed that P2X₂ channel gating consists of the minimum two steps, although there might be multiple ATP-binding steps before the channel gating. The initial step is the ATP binding, and the second is the gating step (Fig. 10 A). We aimed to express k_on and k_off using α and β obtained experimentally and introduced the assumption that the ligand-binding step reaches equilibrium much faster than the gating step based on the rationale that (1) the rate constants for the ligand binding and unbinding are large—e.g., k_bind = 2.6 × 10⁷ [M⁻¹s⁻¹] and k_unbind = 1.1 × 10³ [s⁻¹] (Ding and Sachs, 1999)—and (2) we could fit the activation phase with a single exponential function, demonstrating that there is only one rate-limiting step.

As described in detail in Materials and methods, k_on and k_off were obtained using the α and β values in Fig. 5 C: k_on = (1+Kd/[ATP]) · β and k_off = α. The Kd values of the ATP-binding step cannot be obtained directly with our electrophysiological data. Therefore, we used a reported Kd value of 42 μM and calculated k_on and k_off values for several [ATP] at various voltages (Fig. 10 B). The transition rates for the gating step were nearly constant at various [ATP] and purely voltage dependent (Fig. 10 B), suggesting that this model can explain the voltage-dependent step. We then simulated the macroscopic current seen during the activation phase evoked by voltage steps at various [ATP] using the calculated rate constants k_on and k_off (Fig. 10 B) and the reported ATP-binding rate constants (Ding and Sachs, 1999). We used 1,100 [s⁻¹] for k_unbind (Fig. 11, A and C), and ([ATP] × k_bind) were set so that these two parameters were equal at the Kd. The rate constants used for this simulation are summarized in Table II.

Normalized activation phases evoked by voltage steps from −60 to −160 mV at various [ATP] are shown in Fig. 11 A. The speed of the activation phase gradually increased with increases in [ATP] until it saturated in the presence of high [ATP]. Relatively fast binding kinetics, as compared with the gating kinetics, enabled us to reproduce the activation steps, which could be fitted with single exponential functions (Fig. 11 A). When relatively small k_bind and k_unbind values (Table II C) were used (Fig. 11 B), the activation phase obviously deviated from the single exponential functions. That the results of this simulation clearly differ from the experimental data is consistent with our assumptions that the binding step is relatively fast and that the gating step is rate limiting (Fig. 11 B). Similar large k_bind and k_unbind values were also reported for the nicotinic ACh receptor channel (k_bind = 1.0 × 10⁸ M⁻¹s⁻¹; k_unbind = 4.0 × 10⁴ s⁻¹) (Sine et al., 1990).

We systematically simulated the activation phase for several [ATP] at various voltages and summarized the activation time constants obtained by fitting with a single exponential function at several voltages. Fig. 11 C shows that using this simulation, we were able to reproduce the situation in which the activation speed was dependent on [ATP], but clearly not on voltage, which is consistent with our experimental data (Fig. 3 A). Thus, our results can be satisfactorily reproduced by a simple three-state model consisting of “a fast and voltage-independent ATP-binding step” and “a rate-limiting and voltage-dependent gating step.”

Unexpected voltage dependence has been reported for G protein–coupled receptors such as the muscarinic ACh receptor (Ben-Chaim et al., 2003, 2006) and the metabotropic glutamate receptor (Ohana et al., 2006). In those cases, the binding affinity of the ligands for their receptors was shown biochemically to change in a voltage-dependent manner (Ben-Chaim et al., 2003; Ohana et al., 2006). By assuming a voltage-dependent k_bind value and voltage-independent values for k_on and k_off, the [ATP]-dependent change in the kinetics of activation elicited by hyperpolarization could be qualitatively reproduced in a simulation using the arbitrary parameters shown in Table II D (Fig. 11 D). Therefore, the possibility that the ATP-binding step is voltage dependent cannot be completely excluded at present. However, the arbitrary parameters here have no experimental basis; therefore, future biochemical analyses of the binding affinity that separate the binding step from the gating step could give informative clues.

Characteristic features of the voltage-dependent activation of the P2X₂ channel are that the valence of the effective charge (Z value) is as low as 0.5–0.7 and that the voltage-dependent activation phase does not show sigmoidicity, which is in clear contrast to the typical voltage-gated channels. These findings, along with the primary structure of the channel, make it very unlikely that gating is mediated by an S4-like voltage sensor. What is the structural basis of the voltage sensing? One possibility is that the weak dipole of the α-helix comprising the TM domain and/or charged amino acid residues (R34 in the first TM and/or D349 in the second TM) are the origin of the voltage sensitivity. A second possibility is that the bound, negatively charged ATP itself or together with the binding site might behave as a voltage-sensing particle. Although the ATP-binding site is schematically drawn to be located at the extracellular loop outside of the electric field (Ennion et al., 2000; Jiang et al., 2000), the structure of the protein has not been solved, so that it remains possible that the bound ATP is located within the extracellular end of the electric field. A third, albeit unlikely, possibility is that a so far unidentified subunit with a voltage sensor domain associates with P2X₂.

The Putative Gating Hinge

In the preceding section, we suggested that a voltage-dependent conformational change after ATP binding is a key to P2X₂ channel opening, and we discussed the structural basis of the voltage sensing. We will next discuss the final step in the opening: the conformational change in the gate. Structural changes in the activation gate of potassium channels have been well studied, and several models have been proposed. In the generally accepted model, the gate opens as a result of kinking at a flexible glycine hinge in the middle of the S6 helix (Doyle et al., 1998; Jiang et al., 2002a,b; Kelly and Gross, 2003; Magidovich and Yifrach, 2004; Zhao et al., 2004; Ding et al., 2005). In the case of the P2X₂ channel, notably, there is also a conserved glycine residue in the middle of the second TM helix. We therefore investigated whether the glycine hinge mechanism is also applicable to P2X₂ channel gating. We found that the slow activation of the WT channel upon hyperpolarization was changed to an instantaneous one in the G344A mutant, whereas slow activation kinetic was conserved in the G344P mutant. In fact, activation of G344P was slower than that of the WT channel because the G-V relationships of G344P were shifted in the hyperpolarizing direction, which would make transition to the open state more difficult. Alanine residues reportedly maximize the stability of helixes (O'Neil and DeGrado, 1990; Chakrabartty et al., 1991), whereas proline, like glycine, residues confer flexibility to them (MacArthur and Thornton, 1991; von Heijne, 1991; Hong et al., 1997). Proline residues also increase torsional flexibility (Tieleman et al., 2001; Cordes et al., 2002; Bright and Sansom, 2003), which facilitates kinking. Thus, the changes in the activation kinetics induced by mutations at G344 appear to reflect alteration of the flexibility of the second TM helix.

With the model depicted in Fig. 10 A, the instantaneous activation of G344A can be explained by an extremely large k_on (also k_on + k_off) value. We would suggest that there is a nominal absence of a closed state after ATP binding (C_A) in the G344A mutant, rather than a fast kinking motion, because alanine is not a flexible residue. It is possible that no kinking motion is needed to induce G344A channel opening after ATP binding. And in the case of G344P mutant, the results could be explained by a decrease in the k_on (also k_on + k_off) value, as seen from the analysis of α and β in Fig. 7 E.

The phenotypes of Kv channels with an alanine, glycine, or proline residue at the hinge position are applicable to our observation. In the Shaker K⁺ channel, G466A mutation at the gating hinge makes the channels nonfunctional, whereas the G466P mutant is functional, with a shift in the G-V curve toward more hyperpolarized voltages (Magidovich and Yifrach, 2004). Although the direction of the effect of alanine mutation on channel opening is opposite in Kv (preference to close state) and P2X₂ (preference to open state) channels, it appears they do have some features in common.

Also supporting our gating hinge hypothesis for the P2X₂ channel are the results of our glycine rescue mutagenesis experiment. In Shaker channel studies, introduction of glycine into the middle of the S6 helix in the nonfunctional G466A mutant rescues channel function, and the phenotypes are similar to those of the WT channel (Magidovich and Yifrach, 2004; Ding et al., 2005), which strongly supports the existence of a glycine gating hinge. We performed glycine rescue scanning mutagenesis in the middle of the second TM helix in the G344A mutant and observed recovery of the activation phase. Some of the rescued channels showed phenotypes similar to those of the WT channel, whereas G344A/V343G was similar to G344A. At any [ATP], the G-V relationships for G344A/V343G were shifted in the depolarizing direction; consequently, most of the activation phase was instantaneous (low percentage of I_activation/I_total) (Fig. 9 B). This phenotype suggests that the G-V relationships for the G344A mutant could be interpreted as being markedly shifted in the depolarizing direction, and an extremely large k_on (also k_on + k_off) value discussed in the previous paragraph would underlie the shift.

In sum, we suggest that Gly344, situated in the middle of the second TM helix, serves as a hinge that mediates channel gating, and that a straight second TM helix is the open conformation, whereas a bent helix is the closed conformation. Consistent with this idea is the earlier finding that the upper part of the second TM in the P2X₂ channel moves so that it approaches the first TM in a state-dependent manner (Jiang et al., 2001). In addition, the interface between the two TM helixes of the P2X₂ channel reportedly changes during channel gating (Khakh and Egan, 2005; Silberberg et al., 2007), and the profile of the energetic contribution in the lower half of the second TM region of the P2X₄ channel reportedly differs from that in the upper half (Silberberg et al., 2005). Our present proposal that there is a bending/kinking motion at a gating hinge (G344) in the P2X₂ channel fits well with these phenomena.