Amphiphilic Blockers Punch through a Mutant CLC-0 Pore

Abstract

Intracellularly applied amphiphilic molecules, such as p-chlorophenoxy acetate (CPA) and octanoate, block various pore-open mutants of CLC-0. The voltage-dependent block of a particular pore-open mutant, E166G, was found to be multiphasic. In symmetrical 140 mM Cl⁻, the apparent affinity of the blocker in this mutant increased with a negative membrane potential but, paradoxically, decreased when the negative membrane potential was greater than −80 mV, a phenomenon similar to the blocker “punch-through” shown in many blocker studies of cation channels. To provide further evidence of the punch-through of CPA and octanoate, we studied the dissociation rate of the blocker from the pore by measuring the time constant of relief from the block under various voltage and ionic conditions. Consistent with the voltage dependence of the effect on the steady-state current, the rate of CPA dissociation from the E166G pore reached a minimum at −80 mV in symmetrical 140 mM Cl⁻, and the direction of current recovery suggested that the bound CPA in the pore can dissociate into both intracellular and extracellular solutions. Moreover, the CPA dissociation depends upon the Cl⁻ reversal potential with a minimal dissociation rate at a voltage 80 mV more negative than the Cl⁻ reversal potential. That the shift of the CPA-dissociation rate follows the Cl⁻ gradient across the membrane argues that these blockers can indeed punch through the channel pore. Furthermore, a minimal CPA-dissociation rate at a voltage 80 mV more negative than the Cl⁻ reversal potential suggests that the outward blocker movement through the CLC-0 pore is more difficult than the inward movement.

INTRODUCTION

Ion channel inhibitors exert their pharmacological effects by reducing the current flow through the channel protein. Inhibitors that work by plugging into the pore of ion channels are commonly referred to as channel blockers. The relief of the block in the channel pore is normally achieved by the return of the blocker to the side of the membrane where the blocker is initially present. In some examples, however, blockers can permeate through channel pores. Divalent cations, for example, can block the voltage-gated Ca²⁺ channel by obstructing the current carried by monovalent cations (Almers et al., 1984; Hess and Tsien, 1984). However, the voltage-gated Ca²⁺ channel allows Ca²⁺ ions to permeate through the pore, and it is the influx Ca²⁺ ions that mediate numerous important physiological functions.

Besides the case of the voltage-gated Ca²⁺ channel mentioned above, previous studies of cation channels have revealed many other examples of permeant blockers. In these studies, the voltage dependence of the blocker affinity is multiphasic, as if the blocker, which carries a charge, first binds to a specific site in the pore, and then traverses the entire pore. These examples include the following: the block of K⁺ channels by methylammonium, Na⁺ and Cs⁺ ions (French and Wells, 1977; Adelman and French, 1978; French and Shoukimas, 1985; Nimigean and Miller, 2002); the acetylcholine block of the ACh receptor channel (Sine and Steinbach, 1984); the block of Na⁺ channels by quaternary ammonium and polyamine molecules (Huang et al., 2000; Huang and Moczydlowski, 2001); and the polyamine block of cyclic nucleotide-gated channels (Guo and Lu, 2000a) and inward-rectifying K⁺ channels (Guo and Lu, 2000b), to name a few. For anion channels, fewer inhibitors are specifically known to be pore blockers. Recently, a group of clofibric acid–derivative compounds, such as p-chlorophenoxy acetate (CPA), was found to inhibit the Torpedo CLC-0 Cl⁻ channel (Pusch et al., 2000, 2001; Accardi and Pusch, 2003). We have recently examined the inhibition of CLC-0 by CPA and several amphiphilic molecules, such as fatty acids or alkyl sulfonate compounds. We found that these molecules, when applied from the intracellular side of the membrane, inhibit pore-open mutants of CLC-0 in a voltage-dependent way: the blocker affinity increases with negative membrane potentials. We suggested that these inhibitors directly plug into the pore, and that the blocking mechanism follows a two-step process: the blocker first docks at a superficial binding site near the intracellular pore entrance, and the hydrophobic part of the blocker then enters the pore to interact with the residue located at position 166 (Zhang et al., 2008). This mechanism is thus similar to the overall scheme of the classical mechanism of the voltage-gated K⁺ channel block by long-chain quaternary ammoniums or by the inactivation ball peptide (Choi et al., 1993; Murrell-Lagnado and Aldrich, 1993a,b; Zhou et al., 2001).

In the process of studying the CPA block of various pore-open mutants of CLC-0, we found that a special mutant, E166G, revealed a paradoxical blocking behavior. The current of the E166G mutant was reduced by CPA or fatty acids, but the voltage dependence of the block appeared to have multiple phases. At the voltage range more positive than −60 to −80 mV, the current decreased with increasing negative potential because of the voltage-dependent block. However, when the membrane potential was further hyperpolarized, more inward current was observed with larger negative voltages. To examine this multiphasic block in the E166G mutant, we studied the dependence of the block on membrane voltages and on the gradient of permeant ions across the membrane. We found that CPA and octanoate, like those permeant blockers described in cation channel studies, may “punch through” the pore of the E166G mutant of CLC-0.

MATERIALS AND METHODS

Mutagenesis and Channel Expression

The construction of the pore-open mutants (E166G and E166A) in pcDNA3 and the channel expression in the human embryonic kidney (HEK) 293 cells are described in more detail in this issue (p. 43) by Zhang et al. (2008). The E166G mutant exhibits a slight inward rectification in the absence of CPA, which can be used to differentiate the E166G current from the leak current. Normally, after 1 d of cDNA transfection, the density of the E166G mutant channels on the surface membrane of HEK 293 cells was large enough for excised patch recordings.

Electrophysiological Recordings

All electrophysiological recordings were made with inside-out patches excised from HEK 293 cells. Except where indicated, the pipette and the bath solutions contained (in mM): 130 NaCl, 5 MgCl₂, 10 HEPES, and 1 EGTA, pH 7.4 (a recording condition with symmetrical 140 mM Cl⁻). For solutions with a lower Cl⁻ concentration, a portion of NaCl was replaced by the same concentration of sodium glutamate. For the 0 Cl⁻ solution, MgCl₂ was also replaced by the same concentration of MgSO₄. The recorded signal was amplified using the Axopatch 200B patch clamp amplifier (MDS Analytical Technologies) and digitized using Digidata 1320 digitizing board and pClamp8 software. For a more detailed description of the electrophysiological recording method, see Zhang et al. (2008).

Blocker Applications

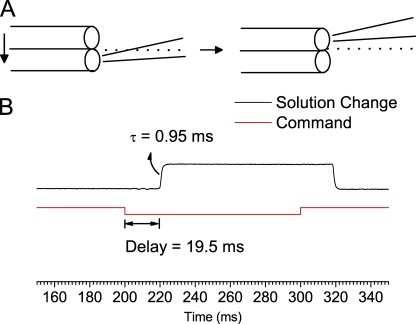
Preparations of the stock and working solutions of CPA and octanoate are described in this issue by Zhang et al. (2008). Solution exchange was achieved using a fast solution exchanger (SF-77; Warner Instruments), which moves the solution-delivering pipe relative to the recording pipette in the orthogonal direction (Fig. 1 A). The time constant of the solution exchange was ∼1 ms based on the single-exponential fit of the change of the junction current generated from the solution change between 100 mM NaCl and KCl solution (Fig. 1 B). This represents the time for the pipette tip to cross the border of two laminar flows from adjacent solution-delivery pipes (dotted lines in Fig. 1 A). However, there was a dead time of ∼20 ms for the SF-77 motor to respond to the digital signal from the Digidata board (Fig. 1 B). Here, we only analyzed the recordings 60 ms after the solution exchange signal—namely, recordings ∼40 ms after the solution was changed.

Figure 1.

Characterization of the solution exchange. The recording pipette contained the normal pipette solution described in Materials and methods. (A) Schematic diagram showing the solution exchange by moving the solution-delivery pipes of the SF-77 rapid solution exchanger. Diameters of the solution-exchange pipe and the electrode tip are not proportionally drawn. Dotted lines indicate the junction plane of laminar flows. (B) Solution exchange characterized by measuring the junction current. The bath solution was changed from 100 mM KCl to 100 mM NaCl. Red line indicates the input of the command voltage signal to the SF-77 controller, and the black curve is the recorded current. The delay from the start of the voltage signal to the start of the current change was 19.5 ± 0.2 ms, and the time constant of the actual solution exchange was 0.95 ± 0.03 ms (n = 4).

Measuring the Dissociation Rate of the Blocker

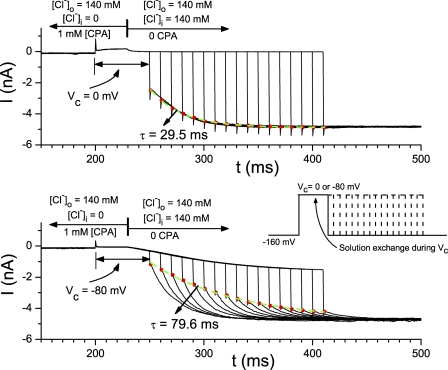
The dissociation rate of the blocker from the binding site in the pore was measured by studying the current recovery process after blocker relief. For the experiments with intracellularly applied blockers, we designed two protocols: a time-based protocol (Fig. 4) and a voltage-based protocol (Fig. 5 A). In both protocols, the blocker (1 mM CPA) was first applied to the intracellular solution, and the membrane voltage was clamped at −160 mV. The membrane potential was then changed to a condition voltage, V_c, where the blocker was removed by a rapid solution exchange. For the time-based protocol (Fig. 4, inset), the duration after removing the blocker was increased at 10-ms steps before the application of a negative voltage at −160 mV to monitor the process of current recovery. For the voltage-based protocol, the duration after the blocker removal was fixed. The membrane potential was stepped from V_c to various voltages 40 ms after the blocker was washed out (see inset in Fig. 5 A). The time course of the current relaxation processes due to the change of solution (Fig. 4) or the change of voltage (Fig. 5 A) was fitted to a single-exponential function. The time constants obtained by these two methods at the same voltage were nearly identical to each other, indicating the validity of the measurement. For the experiment of extracellular block, the blocker was included in the recording pipette. The voltage was first clamped at +80 mV, and was then changed to different stepping voltages from +80 to −160 mV in −20-mV steps. The negative voltage step relieved the block in the pore, and the current increase upon membrane hyperpolarization was fitted to a single-exponential function to obtain the time constant of the process of blocker relief.

Figure 4.

Relief of the CPA block examined by the combination of fast solution exchange and voltage jump. Experiments in both the top and bottom panels were made in excised inside-out patches with 140 mM Cl⁻ in the pipette. The voltage of the patch was first clamped at −160 mV in 0 [Cl⁻]_i and 1 mM CPA. The voltage was then changed to V_c (indicated by the vertical line below the traces), followed by a rapid change of the intracellular solution at the time indicated by the vertical line shown on top. Starting from 40 ms after the fast solution exchange, the membrane voltage was stepped to −160 mV at various time points to monitor the CPA-dissociation process (see inset for the voltage protocol). Red dots are the instantaneous current upon the voltage jump to −160 mV. Green, dashed curves are the single-exponential fit of these red dots with the indicated time constant. Notice that the dissociation of CPA at V_c can also be directly observed from the current relaxation after the solution exchange. This current relaxation is more obvious in the bottom panel because V_c in this experiment (−80 mV) is away from the Cl⁻ reversal potential. The current relaxation course upon stepping the voltage to −160 mV, however, reflects the CPA-dissociation rate at −160 mV.

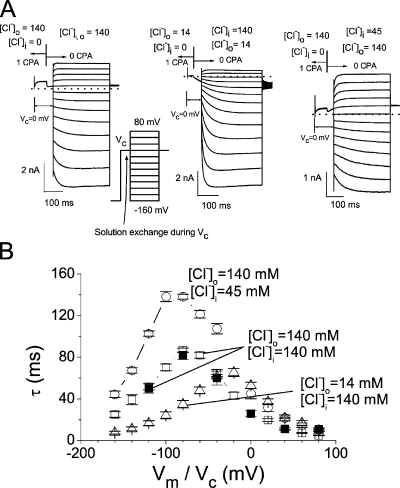
Figure 5.

Voltage-dependent dissociation of CPA from the pore. (A) The experiments were performed in excised inside-out patches similar to those shown in Fig. 4, except that the stepping voltages were applied at a fixed time point (40 ms after the rapid solution exchange) and varied from +80 to −160 mV (in −20-mV steps). See inset for the voltage protocol. The small current spike at the beginning of each recording was due to the switch of the membrane voltage from the initial voltage (−160 mV) to V_c. [Cl⁻]_i and [Cl⁻]_o before (left arrow) and after (right arrow) the rapid solution exchange are as indicated (in mM). (B) Time constants of CPA-dissociation processes obtained from experiments like those shown in A (as a function of the stepping voltage [V_m]; open symbols) and those shown in Fig. 4 (as a function of V_c; filled symbols). The recording conditions were as indicated.

Data Analysis and Modeling

The measurements of the current in the presence and absence of blockers, and the construction of the dose–response curve, are described by Zhang et al. (2008). The fraction of the unblocked current at the steady state was measured by normalizing the current obtained in a particular blocker concentration to the current measured in the absence of the blocker of the same patch. Dose-dependent inhibition curves were thus constructed, and the half-blocking affinity of the blocker was determined from fitting the dose-dependent inhibition curve to a Langmüir function (Eq. 1 in Zhang et al., 2008). All data points in this paper are presented as mean ± SEM averaged from approximately four to six patches.

Modeling the voltage dependence of the CPA and octanoate block followed the models of the voltage-dependent block and punch-through shown by Nimigean and Miller (2002). Thus, the data points in the I-V plot of the E166A mutant were fitted to Eq. 1:

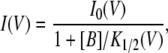(1)

where I₀(V) is the E166A current in the absence of the blocker, and [B] is the concentration of the blocker (CPA or octanoate). The voltage-dependent affinity of the blocker can be described by

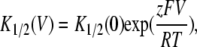where K_1/2(0) is the apparent affinity of the blocker at V = 0 mV. For modeling the voltage-dependent block and punch-through in the E166G mutant, the I-V relationship was fitted to Eq. 2:

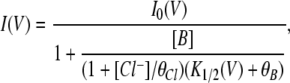(2)

where K_1/2(V) is the same as that shown in Eq. 1, and the two punch-through factors are:

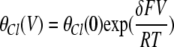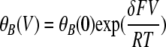RESULTS

Multiphasic Voltage Dependence of the E166G Block by Amphiphilic Blockers

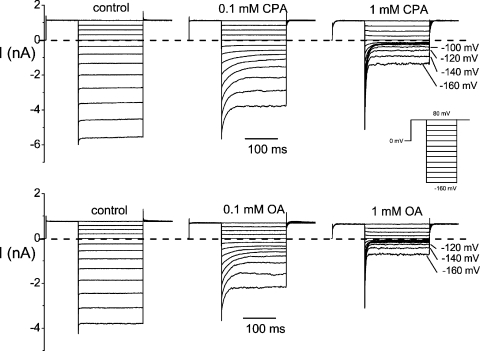
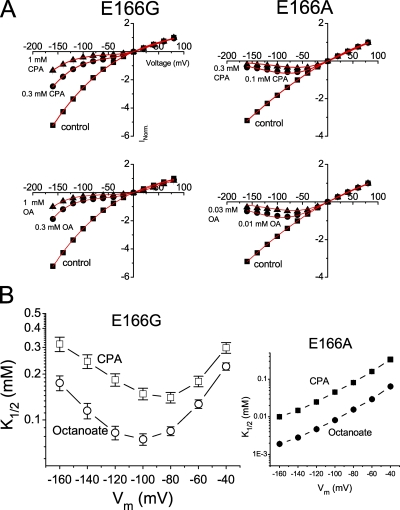
Similar to recordings in many mutants of E166 shown by Zhang et al. (2008), the current deactivation upon membrane hyperpolarization observed in the wild-type CLC-0 is lost in the E166G mutant. Intracellular CPA and other amphiphilic blockers, such as octanoate, can restore this current deactivation at negative voltages, an effect due to the voltage-dependent block. Fig. 2 shows the recording of the E166G mutant in the absence (control) and presence of CPA (Fig. 2, top) and octanoate (Fig. 2, bottom). Compared with the control recording, the steady-state current in the presence of blockers is reduced when membrane potential is hyperpolarized. However, as the voltage is more negative than −80 to −100 mV, the steady-state current is not further reduced by the blocker as would be expected with a simple voltage-dependent blocking mechanism. The blocking effects of CPA and octanoate on the E166G and E166A mutants can be better shown in the I-V plot of the steady-state current (Fig. 3 A). The data points in these I-V plots were well fitted (red curves in Fig. 3 A) to the models of the voltage-dependent block (for E166A) and punch-through (for E166G) proposed by Nimigean and Miller (2002). Compared with the block of the E166A mutant (Fig. 3 A, right, top and bottom), the I-V plot of the E166G mutant shows a paradoxical current increase when the voltage is more negative than −80 or −100 mV.

Figure 2.

Block of E166G by the intracellularly applied CPA (top) and octanoate (OA, bottom). Recordings were taken in symmetrical 140 mM Cl⁻. The top three recordings were obtained from one patch, and the octanoate-blocking experiments in the bottom three panels were from another excised patch. (Inset) Voltage protocol.

Figure 3.

Voltage-dependent block of E166G by CPA and octanoate (OA). (A) Steady-state I-V curves of E166G and E166A in the absence (control) and presence of various concentrations of intracellular CPA (top) and octanoate (bottom). Recordings were made in symmetrical 140 mM Cl⁻, and the current was normalized to that obtained in control at +80 mV. Red curves are the best fit to Eqs. 1 (for E166A) and 2 (for E166G). For the E166A mutant (right), curve fittings gave z = 0.69 ± 0.03 and K_1/2(0) = 0.75 ± 0.08 mM, and the OA block gave z = 0.68 ± 0.03 and K_1/2(0) = 0.12 ± 0.02 mM. For the E166G mutant (left), the parameter θ_Cl(0), which is a Michaelis constant of the Cl⁻ binding to the pore, was set at 60 mM (Chen and Miller, 1996). The fitted parameters were as follows: CPA: z = 0.68 ± 0.08, K_1/2(0) = 0.35 ± 0.04 mM, δ = −0.41 ± 0.03, and θ_CPA(0) = 17.5 ± 2.5 μM; OA: z = 0.35 ± 0.08, K_1/2(0) = 0.16 ± 0.01 mM, δ = −0.61 ± 0.07, and θ_OA(0) = 3.0 ± 1.5 μM. (B) Relationship between the membrane voltage and the blocker affinity. Notice that the highest apparent affinity of the E166G mutant (under the recording condition with symmetrical 140 mM [Cl⁻]) occurs at −80 and −100 mV for CPA and octanoate, respectively.

The apparent blocking affinities of CPA and octanoate in the E166G mutant were estimated by determining the half-blocking concentration (K_1/2) from the dose-dependent inhibition curve. The estimated K_1/2 as a function of the membrane voltage is shown in Fig. 3 B (left). As a comparison, the K_1/2 of E166A is also shown (Fig. 3 B, right). It can be seen that the relation between the K_1/2 and voltage is U-shaped in E166G but not in the E166A mutant. For the CPA block, the smallest K_1/2 occurs at −80 mV, whereas the smallest K_1/2 for the octanoate block occurs at −100 mV. These voltages are the potentials where the paradoxical current increase in the I-V curve starts appearing. The paradoxical increase of the current under larger driving forces, as well as the U-shaped voltage dependence of the K_1/2, mimics the blocker punch-through phenomenon described in previous blocking experiments with many cation channels.

Outward Blocker Punch-through Is Accompanied by a Slow Inward Current-increasing Process

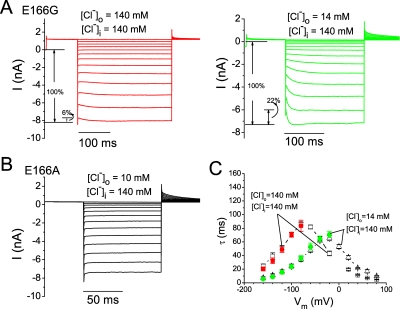
To further explore the above punch-through phenomena, we sought to identify the outward blocker punch-through process, which should be accompanied by a hyperpolarization-induced current increase when the blocker dissociates into the extracellular medium. The current-activation process upon membrane hyperpolarization, however, may be obscured by the simultaneous decrease of the inward current due to a voltage-dependent CPA block from the intracellular side (Fig. 2). To isolate the current-activation process in the intracellular CPA-blocking experiment, we removed the intracellular blocker by a rapid solution exchange before examining blocker dissociation. Two protocols, one varied in time and the other in voltage, were designed for this purpose. Fig. 4 shows experiments using the time-based protocol in which the inside-out membrane patch containing the E166G mutant channel was first exposed to an intracellular solution containing 1 mM CPA and 0 Cl⁻. This allows CPA to enter the pore from the intracellular side. After the recording reached a steady state, the membrane potential was changed to V_c, during which the intracellular solution was switched to one that contains 0 CPA and 140 mM Cl⁻. The change of the recorded current due to the solution exchange should come from two effects: a change in the Cl⁻ reversal potential, a fast process that is completed by the end of the solution exchange (less than 2–3 ms; see Fig. 1); and the dissociation of CPA from the pore, a much slower process. The recorded trace in Fig. 4 shows that the current relaxation lasts for tens of milliseconds, reflecting the CPA-dissociation process at V_c. Thus, the kinetics of the blocker dissociation at V_c can be evaluated either by following the increase of the instantaneous current upon stepping the potential to −160 mV (Fig. 4, red dots and green curves), or by directly following the current recovery at V_c, if V_c was significantly different from the Cl⁻ reversal potential (Fig. 4, bottom).

The experiments in Fig. 4 provide the time constant of the blocker dissociation not only at V_c, but also at the −160-mV stepping voltage. If the relief of CPA block was not complete before the −160-mV voltage step, this negative voltage step would induce a single-exponential increase of the inward current, likely resulting from the outward punch-through of the blocker at this high negative voltage. Performing the same experiments using 1 mM octanoate as the blocker also generated the same phenomenon—namely, the current recovered slowly after the intracellular blocker was washed out, and the negative stepping voltage (−160 mV) induced a slow activation of the inward current (outward Cl⁻ flux).

Voltage Dependence of the CPA Punch-through Rate

The experiments outlined in Fig. 4 reveal that the CPA-dissociation process is voltage dependent. As can be seen by comparing the green dashed curves in the top and bottom panels, in which V_c's are 0 and −80 mV, respectively, the time constants for the CPA-dissociation process in these two experiments are quite different. Besides using variable V_c's in those experiments shown in Fig. 4, we used the voltage-based protocol to examine the voltage dependence of the blocker-dissociation process. In these experiments, the membrane voltage was stepped to various levels (from +80 to −160 mV) at 40 ms after the blocker was removed at V_c (Fig. 5 A). It can be observed from the original recording trace (Fig. 5 A) that the current recovery upon altering the membrane potential happens at all voltages except at the Cl⁻ reversal potential, and the direction of the current recovery can be inward or outward.

From experiments shown in Figs. 4 and 5 A, the time constants of CPA-dissociation processes in various voltage and ionic conditions were measured and plotted as a function of voltage (Fig. 5 B). The time constants from the current-activation process by various stepping voltages (experiments shown in Fig. 5 A), and those from following the process of the current increase upon the washout of CPA at V_c (Fig. 4, red dots), show nearly identical values (compare open and filled squares in Fig. 5 B), indicating that the current activation by voltages shown in Fig. 5 A is indeed due to CPA dissociation but not unrelated voltage-dependent mechanisms. Fig. 5 B also reveals that the peak of the time constant (the smallest CPA-dissociation rate) depends upon the Cl⁻ reversal potential, suggesting that the CPA-dissociation process is affected by both intracellular and extracellular Cl⁻. However, the peak does not occur at the reversal potential; for the symmetrical Cl⁻ condition (Fig. 5 B, open squares), the peak occurs at −80 mV. This is also the voltage where the highest apparent CPA-blocking affinity is observed in the symmetrical 140-mM Cl⁻ condition (Fig. 3 B). For the recording with a 10-fold lower [Cl⁻]_o (Fig. 5 B, open triangles), the peak is at −20 mV. For the recording condition with [Cl⁻]_o = 140 mM and [Cl⁻]_i = 45 mM (Fig. 5 B, open circles), the peak occurs at −100 mV. It appears that the smallest CPA-dissociation rate occurs at a voltage ∼80 mV more negative than the Cl⁻ reversal potential.

Outward Blocker Dissociation Rate of the Extracellular CPA Block

The fact that the CPA dissociation can increase the current in both outward and inward directions strongly suggests that CPA indeed can dissociate to extracellular and intracellular media. If so, we predict that CPA should also block E166G from the extracellular side, and the process of the blocker dissociation back to the extracellular side should be similar to the punch-through process shown above. Thus, we included the blocker in the recording pipette. Fig. 6 A shows examples of the E166G currents under two ionic conditions in the presence of 10 mM CPA on the extracellular side of the membrane. Compared with the recording without CPA (Fig. 2, left panels), both recordings in Fig. 6 A show an increase of the inward current upon stepping the voltage from +80 mV to hyperpolarized voltages. Because Cl⁻ carries a negative charge, the inward current represents an outward Cl⁻ movement through the channel pore. The hyperpolarization-induced increase of the inward current shown in Fig. 6 A likely represents the dissociation of CPA back to the extracellular solution. This hyperpolarization-induced increase of the inward current is not observed in E166A (Fig. 6 B) or in other mutants of E166 with 10 mM CPA in the recording pipette.

Figure 6.

Extracellular CPA effects on the E166G and E166A mutants. (A) Recordings of the E166G mutant in two ionic conditions as indicated, with 10 mM CPA in the pipette. Voltage protocol is the same as that shown in the inset of Fig. 2. The percentage of the hyperpolarization-induced current out of the whole steady-state inward current ranged from 5.1–7.5% in the symmetrical 140-mM Cl⁻ condition and from 20.5–23.2% in the 140-/14-mM Cl⁻ condition. (B) Recordings of E166A with 10 mM CPA in the pipette. No hyperpolarization-activated current is noted at very negative voltages, even in low [Cl⁻]_o (10 mM). (C) Time constants of the current-increasing process shown in A (color symbols) upon stepping the potential from +80 mV to the various test voltages. Only the last several hyperpolarization voltages were able to generate a prominent current activation for a single-exponential fit. For comparison, the time constants presented in Fig. 5 B are reproduced (open symbols).

Fig. 6 also shows that the extracellular CPA block is affected by the extracellular Cl⁻ concentration. Compared with the recording in symmetrical 140 mM Cl⁻ (Fig. 6 A, left), a recording with 14 mM [Cl⁻]_o shows a more prominent extracellular CPA block, as indicated by a larger fraction of the hyperpolarization-induced current (Fig. 6 A, right). At the same time, the kinetics of the hyperpolarization-induced current is also faster with a lower [Cl⁻]_o. Fig. 6 C shows a comparison of the time constant of the current-activation process in the two ionic conditions at those voltage steps where the current activation process is prominent, and the single-exponential curve fitting is possible (color symbols). Reducing [Cl⁻]_o clearly makes the relief of the external CPA block faster at the same voltage (Fig. 6 C). It is possible that the relief of block is facilitated by an outward Cl⁻ movement that knocks off CPA from the pore to the extracellular solution, and the bound CPA may be “locked” in the pore by an extracellular Cl⁻ ion.

To quantitatively examine the CPA-dissociation process, we compared the time constants of the CPA dissociation derived from extracellular CPA-blocking experiments (Fig. 6 A) with those obtained from intracellular CPA-blocking experiments (Fig. 5 A). As shown in Fig. 6 C, the time constants from these two sets of experiments are nearly identical, even though CPA enters the pore from different sides of the membrane. Similar results were obtained when octanoate was used as the blocker.

Longer Fatty Acid Molecules Are Easier to Punch through the E166G Pore

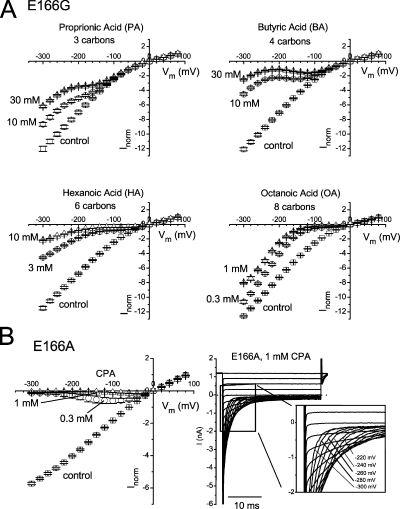
The experiments shown above suggest that amphiphilic pore blockers of CLC-0, such as CPA and octanoate, can punch through the pore of the E166G mutant. Previous studies revealed one peculiar property for the punch-through phenomenon: the larger (and more hydrophobic) the blocker is, the easier for the blocker to punch through the pore (Huang et al., 2000). To test if this behavior also occurs in the anion channel pore, we compared the punch-through of fatty acids with variable lengths of the aliphatic chain. Fig. 7 A shows the steady-state I-V curve of the E166G mutant in the control condition and in the presence of four different fatty acids applied from the intracellular side. The relief of block occurs at different negative voltages for these four molecules. For octanoate, a relatively low concentration of 1 mM already produces a significant block, and the relief of block starts to be prominent at −100 or −120 mV. As the blocker molecule gets shorter, the block requires higher blocker concentrations, and the voltage for the relief of block appears to be shifted toward more hyperpolarized potentials. Thus, the smaller molecule indeed requires a larger driving voltage to punch through the pore.

Figure 7.

Steady-state I-V curves (−300 to +80 mV) of E166G and E166A in symmetrical 140 mM Cl⁻. (A) I-V curve of E166G constructed in the absence (control) and presence of two concentrations of the indicated fatty acids. The measured current was normalized to that obtained in the control condition at +80 mV. Notice that various fatty acids with different molecular lengths all punch through the pore of the E166G mutant. (B) I-V curves of E166A in the absence and presence of CPA. An example of the E166A recording in the presence of 1 mM CPA is shown on the right.

In contrast to the relatively easy punch-through observed in the E166G mutant, E166A does not show a detectable paradoxical current increase in the presence of CPA (Fig. 7 B). The steady-state I-V curve of E166A with octanoate was similar to those shown in Fig. 7 B (not depicted), suggesting that CPA and octanoate do not punch through the pore of E166A down to the voltage of −300 mV.

DISCUSSION

The multiphasic current–voltage relationship of ion channels in the presence of pore blockers and the U-shaped voltage dependence of the blocker affinity have been observed in numerous blocker experiments of cation channels (Bezanilla and Armstrong, 1972; French and Wells, 1977; Sine and Steinbach, 1984; French and Shoukimas, 1985; Guo and Lu, 2000a,b; Huang et al., 2000; Huang and Moczydlowski, 2001; Nimigean and Miller, 2002). It has been generally proposed that the phenomenon results from a blocker punch-through effect—namely, the blocker binds to the pore and can be “pushed” through the pore by a large driving force. However, it was theoretically shown that the multiphasic voltage dependence of the blocker affinity may not necessarily result from the blocker punch-through. If ion channels have multiple open states with different occupancy of ions in the pore, the block can display voltage dependence with a relief of block at high potentials (Heginbotham and Kutluay, 2004).

Like those found in the block of cation channels mentioned above, the steady-state I-V curve of the E166G mutant of CLC-0 in the presence of blockers is multiphasic. The slope of the I-V curve passes a minimum and increases at more negative potentials (Fig. 3 A). We also observed a U-shaped relation between the apparent blocker affinity and the membrane voltage (Fig. 3 B). These phenomena would have been defined as the hallmark of the blocker punch-through effect. However, given the theoretical counterview described above, we look for better evidence to support the idea that these phenomena are indeed due to the punch-through of blockers. We first isolate the current-increasing process accompanied by the relief of blocker using the rapid solution exchange method to remove the intracellularly applied blocker (Figs. 4 and 5). We examined the kinetics of the blocker-dissociation process and found that two phenomena of the blocker dissociation depend upon the Cl⁻ reversal potential.

First, we observed that the direction of current recovery from the block can be either outward or inward (Fig. 5 A). Because the ion-transport pathway of CLC molecules contains very limited space (Dutzler et al., 2002, 2003), it would seem less likely that the current recovery is due to a sideward movement of the blocker to allow permeant ions to pass by the blocker. Therefore, the inward and outward directions of the recovered current (corresponding to the outward and inward Cl⁻ fluxes, respectively) may suggest that the blocker can go either outward or inward, respectively. Furthermore, in the experiment where CPA was applied from the extracellular side, a negative membrane voltage induces an increase of the inward current (Fig. 6). A quantitative comparison shows that the blocker-dissociation rates obtained in the extracellular CPA-blocking experiments are nearly identical with those obtained in the experiments with intracellularly applied CPA (Fig. 6 C). If the hyperpolarization-induced current recovery process in the experiments shown in Fig. 6 A (which are experiments of the extracellular CPA block) represents the CPA dissociation into the extracellular medium, the hyperpolarization-induced increase of the inward current shown in Fig. 5 A (in which CPA was applied from the intracellular side) is also likely to be the same mechanism. Thus, blockers from the extracellular side and from the intracellular side can both bind to the same site in the pore.

The second phenomenon related to the reversal potential is that the maximal time constant of the blocker-dissociation process (or the smallest CPA-dissociation rate) occurs at a voltage 80 mV more negative than the Cl⁻ reversal potential (Fig. 5 B). This observation is consistent with the steady-state affinity measurement in which the CPA affinity in the symmetrical Cl⁻ condition reaches a maximum at −80 mV (Fig. 3 B). It is interesting that the smallest CPA-dissociation rate occurs not at the Cl⁻ reversal potential but at a voltage 80 mV more negative, indicating that the dissociation of CPA into the external medium is probably more difficult than the inward CPA dissociation. It is likely that the narrowest part of the E166G pore is located at a position external to the CPA-binding site. The dissociation of CPA into the external solution thus requires a larger driving force than the CPA dissociation into the intracellular side. This picture is consistent with the observation that only a small percentage of current was blocked by 10 mM of extracellular CPA (Fig. 6 A), likely due to a small association rate for the extracellular CPA to reach the binding site. It seems reasonable to speculate that the narrowest part of the pore is near residue 166 because by adding a methyl group to the side chain of G166 (namely, E166A), the punch-through effect is not observed within the applied voltage range (Fig. 7 B).

All the punch-through phenomena shown by using CPA as the blocker can also be observed when octanoate is used for the experiment. It is quite interesting that large molecules like CPA and octanoate can punch through the pore of CLC-0 because the structure of the bacterial CLC protein does not reveal much empty space in the Cl⁻ transport pathway. Given the precedent in which the bulky tetra-alkyl ammonium molecule can punch through the pore of a mutant voltage-gated Na⁺ channel (Huang et al., 2000), it is perhaps not surprising that more linear molecules like CPA and octanoate can punch through the mutant pore of CLC-0. Similar to the tetra-alkyl ammonium block of the voltage-gated Na⁺ channel, we show here that the longer (and more hydrophobic) the fatty acid molecule is, the less voltage is required for the blocker to punch through the pore. It may seem counterintuitive that the smaller molecule is more difficult to punch through the pore. However, the fatty acid with a shorter aliphatic chain should have a less extensive hydrophobic interaction with pore residues, and thus its dissociation rate back to the intracellular solution is faster than those of the long fatty acid molecules (Zhang et al., 2008). Because the punch-through requires tens of milliseconds (Fig. 5 B), a less hydrophobic molecule is unable to stick to the pore long enough for the punch-through to occur unless the membrane voltage is made negative enough that the inward blocker-dissociation rate is reduced to a comparable level as the outward punch-through rate.

The results shown here argue that CPA and fatty acids enter the deep region of the E166G pore and punch through the pore. Moreover, the hydrophobic region of the blocker is not only important for a stable binding to the pore, but it also helps the blocker to punch through the pore. These results thus reiterate that large amphiphilic molecules, such as CPA and octanoate, can indeed interact with deep pore residues of CLC-0. Although we have shown that the side chain of the residue at position 166 is critical for the hydrophobic interaction with the blocker (Zhang et al., 2008), the pore residues that interact with the blocker should not be limited to only residue 166 because the long blocker appears to have a more extensive interaction with the pore than the short blocker. It would require further mutation work to reveal the extent of interaction between the pore of CLC-0 with these amphiphilic blockers.