Abstract
The distribution of mitochondria is sensitive to physiological stresses and changes in metabolic demands. Consequently, it is important to carefully define the conditions facilitating live imaging of mitochondrial transport in dissected animal preparations. In this study, we examined Schneider’s and the haemolymph-like solutions HL3 and HL6 for their suitability to image mitochondrial transport in motor axons of dissected Drosophila melanogaster larvae. Overall, mitochondrial transport kinetics in larval motor axons appeared similar among all three solutions. Unexpectedly, HL3 solution selectively increased the length of mitochondria in the context of the net-direction of transport. We also found that mitochondrial transport is sensitive to the extracellular Ca2+ but not glutamate concentration. High concentrations of extracellular glutamate affected only the ratio between motile and stationary mitochondria. Our study offers a valuable overview of mitochondrial transport kinetics in larval motor axons of Drosophila under various conditions, guiding future studies genetically dissecting mechanisms of mitochondrial transport.
Keywords: Mitochondria, axonal transport, live imaging, calcium, Drosophila
Introduction
Mitochondria are vital for aerobic respiration, the regulation of Ca2+ homeostasis, apoptosis, aging, and cancer (Wallace 1999; Kuwana et al. 2003; Newmeyer et al. 2003; Rizzuto 2003). The intracellular distribution of mitochondria is not static but adaptable to physiological stresses and changes in metabolic demands (Hollenbeck 1996; Karbowski et al. 2003; Rintoul et al. 2003; Chang et al. 2006c). This plastic control is especially important for neurons, which critically require long-distance transport of mitochondria to satisfy the fluctuating metabolic demands of distantly located synaptic terminals. However, the molecular mechanisms controlling mitochondrial transport remain enigmatic.
Neurons with their long axons and uniform polarity of microtubules (MTs) provide an ideal model system to study mitochondrial transport. Especially, live imaging of fluorescently labeled mitochondria in axons of cultured neurons became instrumental to resolve basic principles of mitochondrial transport (Hollenbeck 1996; Hollenbeck et al. 2005; Chang et al. 2006c). However, it is unlikely that mitochondrial trafficking and distribution in cultured neurons matches that of neurons in their in situ environment since intracellular distributions of mitochondria are sensitive to changes in cellular metabolism, Ca2+ buffering, and the cellular environment (Wong-Riley et al. 1980; Hollenbeck 1996; Karbowski et al. 2003; Rintoul et al. 2003; Li et al. 2004; Yi et al. 2004; Chang et al. 2006c; Chang et al. 2006b; Mironov 2006). In vivo models promise to overcome these limitations and are expected to reduce the potential of experimental artifacts caused by altered cellular bioenergetics.
Recent studies established in vivo models in mice and Drosophila (Pilling et al. 2006; Misgeld et al. 2007a; Misgeld et al. 2007b) that combine the power of genetic manipulations with high-resolution imaging of mitochondrial transport. The Drosophila model takes advantage of the well-established larval neuromuscular preparation (Keshishian et al. 1996; Koh et al. 2000) and facilitates live imaging of mitochondria in motor axons of segmental nerves (Pilling et al. 2006). Although segmental nerves contain glial cells and axons of sensory and motor neurons projecting in opposite directions, only mitochondria in motor neurons are fluorescently labeled due to motor neuron-specific expression of a GFP transgene (mitoGFP) (Pilling et al. 2006). While this in vivo imaging model provides much promise to better understand mechanisms of mitochondrial transport, it remained unclear whether the currently employed Schneider’s solution may compromise the advantages of the preparation since its chemical composition differs from that of larval haemolymph.
Schneider’s solution was originally developed to support the growth of dissected imaginal discs from Drosophila, but was later found to also support the growth of cultured cells derived from Drosophila and other dipterans when supplemented with fetal bovine serum (Schneider et al. 1978; Mitsuhashi 1982; Echalier 1997). Schneider’s solution also supports long-term culturing of dissected Drosophila larvae (Ball et al. 2003), but blocks synaptic transmission at larval neuromuscular junctions (NMJs) and reduces the resting potential of the postsynaptic muscle fiber by at least 50% (Jan et al. 1976; Stewart et al. 1994; Macleod et al. 2002). Notably, the adverse effects of Schneider’s on excitability are often irreversible, indicating that they are unlikely due to just a high glutamate concentration of the solution (Ball et al. 2003). Since changes in neuronal activity can interfere with mitochondrial transport (Yi et al. 2004; Chang et al. 2006b; Mironov 2006), it was important to evaluate alternative solutions that maintain neuronal excitability.
A number of bath solutions have been used to maintain dissected Drosophila larvae for electrophysiological and/or Ca2+ imaging studies, most prominently Jan’s solution (solution A; Jan et al. 1976) and the haemolymph-like solutions HL3 (Stewart et al. 1994) and HL6 (Macleod et al. 2002). While all these solutions initially preserve neuronal excitability and activity, they often fail to maintain the health of the preparation over prolonged periods. In particular, Jan’s solution causes formation of abnormal vacuoles in muscles within minutes of exposure and a progressive loss of the resting membrane potential within 30 minutes (Stewart et al. 1994). HL3 solution greatly attenuates vacuole formation and significantly improves the stability of the larval preparation, but the resting potential still deteriorates after 2 hours (Stewart et al. 1994). The composition of HL6 solution is likely the closest match to larval haemolymph (Macleod et al. 2002). Consistently, HL6 solution eliminates vacuole formation and maintains neuronal excitability and resting potentials over a period of at least 5.5 hours (Macleod et al. 2002). Hence, HL6 solution may be well suited not only for long-term Ca2+ imaging studies but also for imaging mitochondrial transport in larval motor axons.
To define optimal conditions for the imaging of mitochondrial movements in larval motor axons, we surveyed the suitability of Schneider’s, HL3 and HL6 solutions. To facilitate the study, we developed software that automates the analysis of mitochondrial movement tracks. Overall, mitochondrial transport appeared similar among all three solutions, although HL3 increased the length of retrogradely moving mitochondria. We also found that mitochondrial transport in larval motor axons is sensitive to the extracellular Ca2+ concentration. Manipulations of extracellular glutamate affected the ratio between motile and stationary but not mitochondrial transport kinetics.
Materials and Methods
Fly Stocks
Flies (Drosophila melanogaster) were raised on standard medium (http://flystocks.bio.indiana.edu/bloom-food.htm) with dry yeast at 23°–25°C. The strain w1118, P[w+; UAS::mitoGFP] expressing GFP tagged by an N-terminal mitochondrial localization signal derived from human cytochrome c oxidase subunit VIII, was obtained from W. Saxton (Indiana University, Bloomington, IN, USA). To express the mitoGFP transgene in trans, we used the enhancer trap strain w1118; P[w+, OK6::Gal4], which drives expression in all motor neurons, salivary glands, wing discs, and a subset of tracheal branches beginning in the first larval instar persisting until pupation (Aberle et al. 2002). After crossing homozygous w1118; P[w+, OK6::Gal4]; P[w+; UAS::mitoGFP] to w1118 flies, progeny larvae with the genotype w1118; P[w+, OK6::Gal4] / +; P[w+, UAS::mitoGFP] / + were used for analysis.
Imaging solutions
Haemolymph-like HL3 solution supplemented with 4 mM L-glutamate and 1 mM CaCl2, if not otherwise indicated (Stewart et al. 1994): 70 mM NaCl; 5 mM KCl; 20 mM MgCl2; 10 mM NaHCO3; 5 mM trehalose; 5 mM HEPES; 115 mM sucrose, pH 7.3.
Haemolymph-like HL6 solution supplemented with 4 mM L-glutamate and 0.6 mM CaCl2, if not otherwise indicated (Macleod et al. 2002): 23.7 mM NaCl; 24.8 mM KCl; 15 mM MgCl2; 10 mM NaHCO3; 20 mM isothionic acid (Na+); 5 mM BES, 80 mM trehalose; 5.7 mM L-alanine; 2 mM L-arginine • HCl; 14.5 mM glycine; 11 mM L-histidine, 1.7 mM L-methionine; 13 mM L-proline; 2.3 mM L-serine; 2.5 mM L-threonine; 1.4 mM L-tyrosine; 1 mM L-valine; 0.0001 mM TPEN ; 1 mM Trolox; pH 7.2.
Modified Schneider’s medium (according to supplier: Invitrogen, Carlsbad, CA, USA; see also Schneider et al., 1978): 36.2 mM NaCl; 21.3 mM KCl; 3.3 mM KH2PO4; 15.1 mM MgSO4; 5.4 mM CaCl2; 4.8 mM NaHCO3; 4.9 mM NaHPO4; 0.9 mM fumaric Acid; 11.1 mM D-glucose; 1.4 mM α–ketoglutaric Acid; 0.7 mM malic Acid; 0.8 mM succinic Acid; 5.8 mM trehalose; 5.6 mM β-alanine; 2.3 mM L-arginine; 3 mM L-aspartatic Acid; 0.5 mM L-cysteine; 0.4 mM L-cystine, 5.4 mM L-glutamic Acid; 12.3 mM L-glutamine; 3.3 mM glycine; 2.6 mM L-histidine; 1.1 mM L-isoleucine; 1.1 mM L-leucine; 9 mM L-lysine • HCl; 5.4 mM L-methionine; 0.9 mM L-phenylalanine; 14.8 mM L-proline; 2.4 mM L-serine; 2.9 mM L-threonine; 0.5 mM L-tryptophan; 2.8 mM L-tyrosine; 2.6 mM L-valine; 10 mM lactalbumin hydrolysate yeastolate; pH 7.2.
Larval Dissection
Climbing third instar larvae were quickly dissected in the indicated imaging solution, which was pre-cooled to 4°C. Larvae were placed dorsal side up in a 35 × 10 mm Petri dish that was coated with a thin layer of Sylgard resin. Larvae were pinned down at head and tail and cut longitudinally along the dorsal midline. The body wall was filleted and pinned out. Ventral ganglia, segmental nerves and larval body wall muscles were clearly visible after removing viscera. After three rinses, larvae were incubated in the indicated imaging solution at room temperature (20–23°C).
Time Lapse Imaging of Mitochondria
The dissected preparation was viewed at room temperature (20–23°C) with an upright Olympus microscope BX50WI equipped with a confocal laser scanner (FluoView300) and a 60X water immersion objective (LUMPLANFL N.A. 0.9). Larvae were orientated such that the ventral ganglion (VG) appeared on the right of the acquired image and segmental nerves were aligned horizontally across the image. The 488 nm excitation line of the multi-argon laser (Mellet Griot, 150mW) was attenuated to 2–4% of its maximum power, with all other lasers at 0%. Fluorescence emission was monitored through a low-pass optical filter with a cut-off at 510 nM (BA510IF, Olympus). The pinhole was fully opened to allow maximum “focal depth”.
Images of 1024 × 280 pixels (58.868 µm × 16.065 µm) were acquired from individual segmental nerves at about 200 µm from the VG. To allow accurate long-range tracking without obstruction from large stationary mitochondrial clusters, a 872 × 278 pixels (50 µm × 16 µm) region of interest (ROI) was photobleached for 180 seconds with all lasers at full intensity (zoom factor 2X). The position of the ROI was chosen such that the photobleached area was always flanked by large, non-bleached, stationary mitoGFP-positive signals. Immediately after photobleaching, 200 images were acquired at a rate of one frame per 1.006 seconds (zoom factor 2X). The acquired post-bleach images were saved as 8-bit multi-tiff files. Time-lapse images were acquired only from one nerve per animal and within 30 minutes of dissection unless otherwise specified.
Visualization and Analysis of Stationary Mitochondria
Motile and stationary mitochondria in larval motor axons were visualized by merging two differently pseudo-colored images taken at different acquisition time points. Typically, time-lapse images were acquired without photobleaching as described. To visualize motile versus stationary mitochondria, the first image acquired at time 0 was pseudo-colored in green while all subsequent time-lapse images were colored in red. Merging of two images that define a desired time interval (for example: 0–10 s) revealed stationary mitochondria in yellow and motile mitochondria in red or green. Green signals indicated mitochondria that were present at this position at time 0 but moved away during the indicated time interval. Red signals indicated mitochondria that moved into this position during the indicated time interval, which included mitochondria that were present in the imaged area at time 0 as well as mitochondria that moved into the imaged area during the indicated time interval. The percentage of stationary mitochondria from the total mitochondrial population present at time 0 was estimated by calculating the ratio of yellow and green signals in percent. Threshold of movement was a displacement of roughly the size of an individual mitochondrion (2 µm).
Tracking of Mitochondrial Movements
Movements of mitochondria into or through the photobleached ROI were tracked by using NIH ImageJ imaging software (Abramoff et al. 2004) and the plug-in MTrackJ (Meijering, E., Biomedical Imaging Group of Rotterdam, University Medical Center of Rotterdam, Netherlands; http://www.imagescience.org/meijering/software/mtrackj/). Essentially, MTrackJ-mediated tracking marked the position of a given mitochondrion in every consecutive frame via a mouse cursor. We tracked the “anterior” tip of a mitochondrion since the center of highest GFP intensity of an individual mitochondrion was found to be less reliable as it was highly variable from one frame to the next. The displacement of a mitochondrion from one frame to the next was converted from pixels to real distances by calibrating the x-y axes of the analyzed images in MTtrackJ. Up to 12 clearly labeled, motile mitochondria were tracked per animal as long as each remained visible in consecutive frames for no less than 60 frames. In addition, at least one stationary mitochondrial cluster flanking the bleached ROI was tracked for normalization. The stationary nature of such clusters was verified by merging the first image in red (t=0 s) with last image of the time-lapse in green (t=200 s).
Mitochondrial Tracking Analysis
The MTrackJ-derived x-y-t tracking coordinates of mitochondrial movements were exported for automated analysis to Excel-based software that was designed by G.J. Russo and has been made freely available (http://www.neurobio.arizona.edu/faculty/zinsmaier/Software_Site.htm). To reduce the influence of muscle contractions and drift of the segmental nerve, x-y tracking coordinates were normalized to those of a mitochondrial cluster in the non-bleached area that was stationary throughout the entire imaging time (Fig. 2A; 0–200 s image). This normalization step removed a significant number of fast and short-lasting movements that were clearly caused by muscle contractions because they affected many tracked mitochondria of an imaged nerve in a similar manner (not shown).
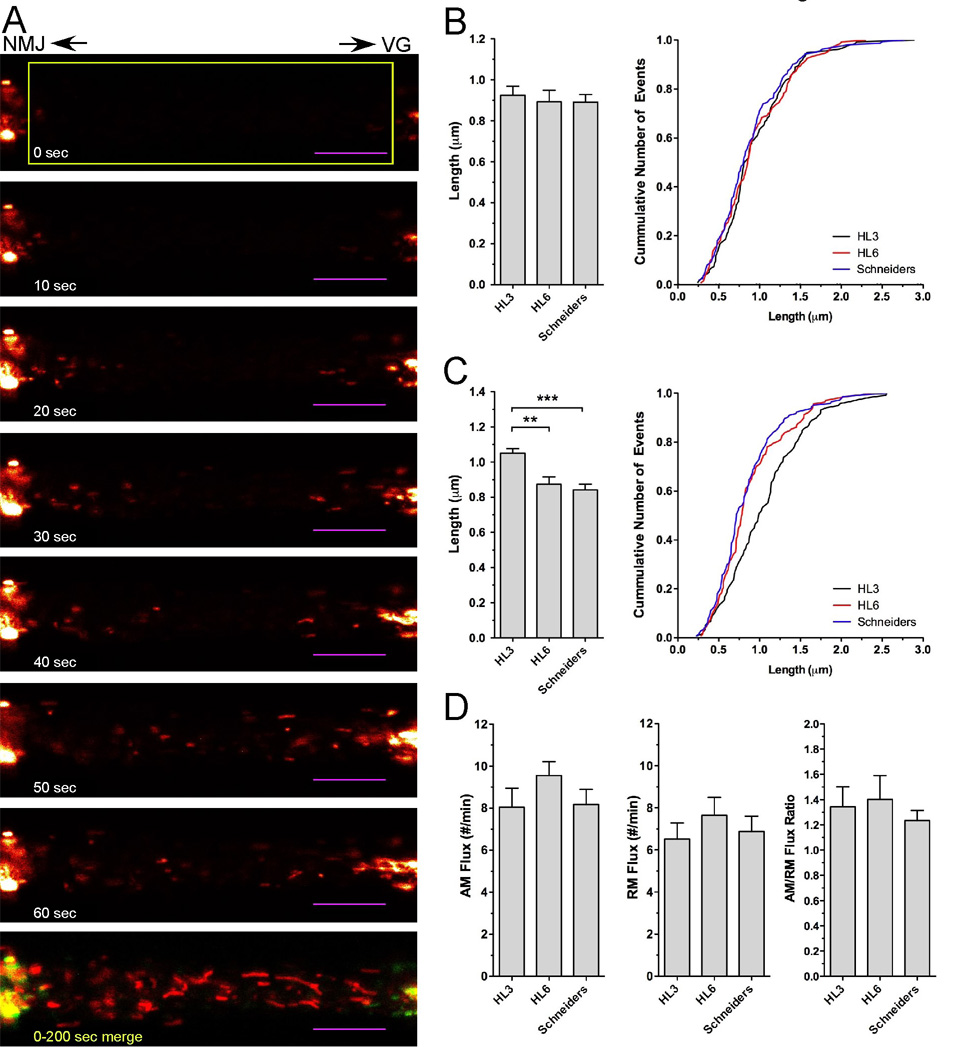
Figure 2. Effects of HL3, HL6 and Schneider’s solution on mitochondrial length and the rate of mitochondrial transport in larval motor axons.
A) Time lapse imaging of mitochondrial transport in larval motor axons after photobleaching. Shown is a selection of confocal time-lapse images (see Suppl. Video 2) that were acquired at the indicated time after photobleaching a region of interest (yellow box) from a segmental larval nerve about 200 µm away from the VG at a rate of 1 Hz. Mitochondria exhibiting net-anterograde (AM) or net-retrogade movements (RM) entered the photobleached area from the left or right boundary, respectively. The last image of the series is a merge of images taken at 0 (green) and 200 seconds (red) to illustrate the long-term stationary (yellow) nature of mitochondrial clusters next to the photobleached area. Scale bar is 10 µm.
B–C) Effects of imaging conditions on the length of mitochondria exhibiting net-anterograde (AM) and net-retrograde movements (RM). The left panels show the average length and right panels show the cumulative frequency distribution of all measurements. No significant differences were observed for AM mitochondria (B) between HL3, HL6 and Schneider’s solution (p>0.05, N=11, n>133, one-way ANOVA). In contrast, the length of RM mitochondria (C) was significantly increased in HL3 solution (p<0.01, N=11, n>118). Significant differences are indicated by asterisks. Error bars represent SEM.
D) Effects of imaging conditions on the flux of AM and RM mitochondria. HL3, HL6 and Schneider’s solution showed no significant effects on the flux of AM mitochondria (left panel), RM mitochondria (middle panel), and the ratio of AM/RM fluxes (p>0.05, N>11, one-way ANOVA). Significant differences are indicated by asterisks. Error bars represent SEM.
To define the motion of a mitochondrion, normalized x-y-t coordinates were modeled as a three state system consisting of anterograde (plus end-directed) runs, retrograde (minus end-directed) runs and stops (stationary phase). A run is defined as a period of uninterrupted movement in one direction. To account for movements in both the x and y coordinate planes, the linear distance between each pair of coordinates was calculated. Antero- or retrograde displacements in the x-coordinate plane were assigned a positive or negative designation, respectively. Movement in the y plane without displacement in the x plane was extremely rare and consequently negligible. Besides fast muscle movements, stage drift of the microscope, and slow drift of the segmental nerve, errors of the manual tracking process were likely to distort the analysis of mitochondrial movements. The effect of these errors was estimated experimentally by analyzing tracks of immobilized, formaldehyde-fixed mitochondria. The mean displacement of such immobilized mitochondria was 26 ± 29 nm (n = 36,501; SEM; Suppl. Fig. 1A). While 75% of such artificial displacements were smaller than 30 nm from frame to frame (1.006 s apart), 2.8% of displacements exceeded 100 nm and consequently contributed to a significant error in the analysis.
To minimize effects of artificial movements without compromising run length and duration unreasonably, we defined runs by two “thresholds of movement”. The first threshold defined the start of a run by requiring a displacement of 0.151 µm from one frame to the next. Applying this threshold to the analysis of immobilized, formaldehyde-fixed mitochondria reduced the tracking error to less than 0.06% (Suppl. Fig. 1B). The second threshold reviewed whether a run truly ended or just slowed down by considering the duration of the stop phase and the direction of the subsequent run: if the displacement from one frame to the next dropped below 0.151 µm for no more than two seconds (up to two frames), and if this slower phase was above the second threshold of 0.12 µm/s, the two runs flanking the slower phase were combined to one extended run, but only if both runs and the slower phase were in the same direction. The second threshold was deemed necessary since manual inspections of individual runs showed that run velocities often slowed down just below the first threshold for less than 2 seconds (data not shown).
After identifying run and stationary phases, mitochondrial tracks were sorted into two classes by their net-direction of movement: mitochondria that either showed net-anterograde movement (AM) or net-retrograde movement (RM). For each class, the following motility parameters were then calculated: duration, distance, and velocities of antero- (plus end-directed) and retrograde (minus end-directed) runs, duration and frequency of stops, frequency of reversals in direction, and frequency of reversals and stops. In addition, we determined the net-velocity (total net-distance during entire tracking time) as well as the “duty cycles” (percentage of time spent in anterograde runs, retrograde runs, and stationary phases).
Statistical Analysis
Track data of individual mitochondria from one segmental nerve were averaged for each animal and then averaged for all animals of the same condition used. The obtained averages were analyzed for statistical significance by ANOVA testing using Prism software Graphpad Software, Inc., 2007. A one-way analysis of variance test was performed for parametric data and a Kruskal-Wallis test for nonparametric data unless otherwise indicated. P values of <0.05, <0.01, and <0.001 were indicated with one, two and three asterisks (*), respectively.
Since most parameters describing mitochondrial transport exhibit a large variance and often do not follow a Gaussian distribution, mean values often represent inadequate descriptions of mitochondrial transport dynamics. Therefore, we also compiled the entire data set for each transport parameter and plotted the relative frequency distribution as well as cumulative frequency distribution of all measurements for more accurate comparisons.
Results
Imaging of mitochondria in axons of larval motor neurons of Drosophila
Larval segmental nerves of Drosophila contain sensory axons, motor axons and glial cells (Hurd et al. 1996). To image mitochondrial transport in relation to the polarity of axonal microtubule, it is consequently critical to selectively visualize mitochondria only in axons of motor neurons or sensory neurons. We used the Gal4/UAS system (Brand et al. 1993) to selectively express a mitochondrial GFP transgene (mitoGFP) in motor neurons with the Gal4-driver Ok6 (Aberle et al. 2002). MitoGFP strongly labels mitochondria in various systems and matches the pattern of MitoTracker staining (Guo et al. 2005; Cox et al. 2006; Glater et al. 2006; Pilling et al. 2006).
In dissected third instar larvae, Ok6-driven mitoGFP fluorescence strongly labeled mitochondria in motor neurons of the larval ventral ganglia and segmental nerves (Fig. 1A). In segmental nerves mitoGFP labeled 3 distinct groups of mitochondria: short ellipsoid or “grape-like” mitochondria; thin elongated or “worm-like” mitochondria; and much larger and relatively round structures that were likely clusters of mitochondria (Fig. 1B).
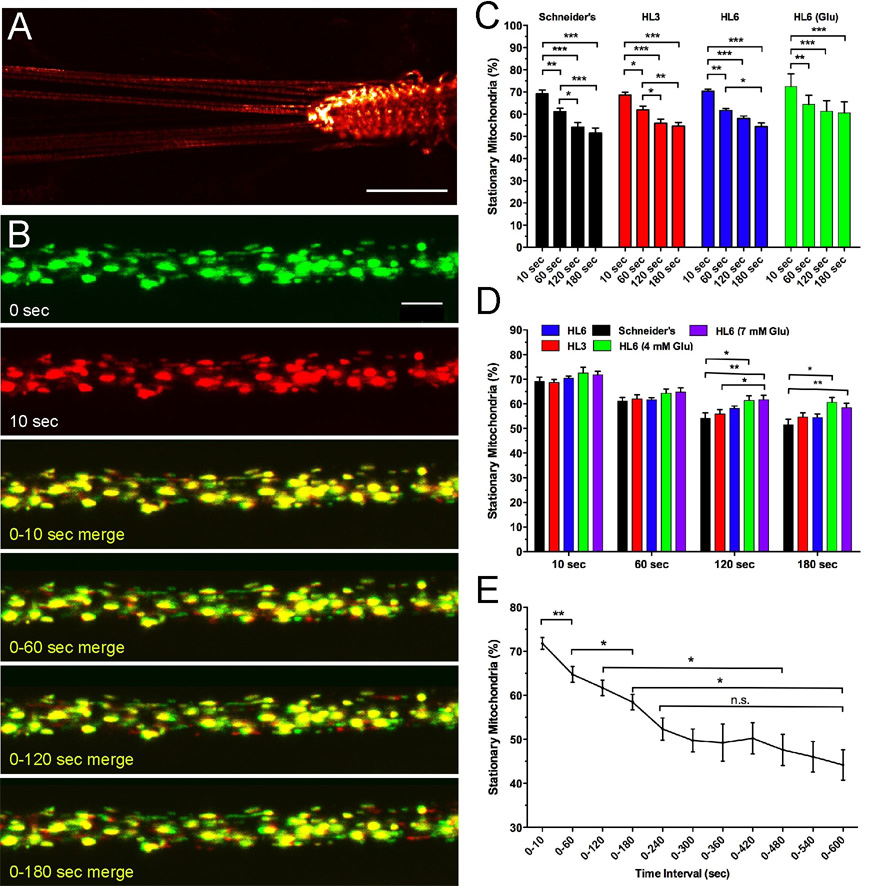
Figure 1. Imaging of Mitochondria in Larval Motor Axons of Drosophila.
A) Ok6-driven mitoGFP expression in motor neurons of 3rd instar larvae. MitoGFP fluorescence strongly labels the ventral ganglia (VG), segmental nerves (SN) and neuromuscular junctions (NMJs). Scale bar is 200 µm.
B) Visualization of motile and stationary mitochondria in larval motor axons. Shown is a selection of confocal time-lapse images that were acquired from a segmental nerve about 200 µm away from the VG at a rate of 1 image per second. To visualize motile versus stationary mitochondria, the first image at time 0 was labeled in green while all subsequent time-lapse images were labeled in red. Merging of two images defining a desired time interval (for example: 0–10 s) reveals stationary mitochondria in yellow and motile mitochondria in red or green. Note the primarily stationary nature of large aggregates of mitoGFP fluorescence. Time intervals are indicated. Scale bar is 5 µm.
C–D) Effects of HL3, HL6 and Schneider’s solution on percentage of stationary mitochondria.
C) The percentage of stationary mitochondria decreases proportionally in HL3, HL6 and Schneider’s solution over 180 seconds (p<0.05, N>8, two-way ANOVA).
D) The number of stationary mitochondria is similar in Schneider’s, HL3, HL6, and HL6 solution supplemented with 4 or 7 mM glutamate (Glu) for time intervals of 10 and 60 seconds. For longer time intervals, the percentage of stationary mitochondria in HL6 solutions with glutamate was significantly higher than that in Schneider’s and/or HL3 solution (p<0.05; N>6; two-way ANOVA). Error bars represent SEM.
E) Percentage of stationary mitochondria for time intervals of 10 seconds to 10 minutes. Note that the number of stationary mitochondria decreases significantly up to 240 seconds. Thereafter, there is no further significant decrease in the percentage of stationary mitochondria. Significant differences are indicated by asterisks (p<0.05, N>6, two-way ANOVA). Error bars represent SEM.
To visualize mitochondrial transport in larval motor axons, we performed time-lapse imaging in a 1024 × 280 pixel large region of a single segmental nerve about 200 µm from the ventral ganglion. Typically, 200 images were acquired at a frequency of 1 frame per 1.006 seconds without deleterious photobleaching of mitoGFP-labeled mitochondria (Suppl. Video 1, Fig. 1B). Since all images were oriented such that motor axon terminals were to the left, mitochondrial movements from the right-to-left were anterograde or plus end-directed microtubule-based movements while left-to-right movements were retrograde and minus end-directed.
A number of mitoGFP-labeled mitochondria displayed quite vigorous movements while others displayed only little or no appreciable movement at all. To differentiate between motile and stationary mitochondria, we displayed the first image of the time-lapse sequence in green (time = 0 s) and all successive images in red. In merged images of time 0 and time X, all mitochondria that were stationary during the respective time interval appeared in yellow, while all mitochondria that exhibited movement appeared in green or red (Fig. 1B).
The large number of stationary mitochondria (~50% in 10 s interval) significantly obscured a precise tracking of motile mitochondria over large distances. To bypass this problem, we photobleached a centrally located 50 × 16 µm wide region, and immediately recorded the movement of GFP-labeled mitochondria into the bleached area from both sides (Fig. 2A; Suppl. Video 2). These motile mitochondria showed saltatory movements consisting of antero- and retrograde runs (uninterrupted movement) that were often separated by brief stops (1–5 s) as is typical of motile mitochondria (Hollenbeck 1996; Hollenbeck et al. 2005). All motile mitochondria showed a strong bias towards one net-direction (Fig. 2A). Consistent with earlier results (Pilling et al. 2006), we never observed a mitochondrion change its net-direction of transport within the limitations of our 50 µm long region of imaging. Accordingly, two major classes of motile mitochondria were distinguished: mitochondria that showed net-anterograde movement (AM) and mitochondria that showed net-retrograde movement (RM). Tracks of mitochondrial movements were automatically analyzed by Excel-based software (designed by G.J.R.) that has been made freely available. The following motility parameters were calculated for AM and RM mitochondria: net-velocity; duration, distance, and velocity of antero- (plus end-directed) and retrograde (minus end-directed) runs (period of uninterrupted motion in one direction); duration and frequency of stops; frequency of reversals in direction; and the percentage of time spent in anterograde runs, retrograde runs, and stationary phases (duty cycle).
Imaging conditions affect the length and the ratio of motile/stationary mitochondria in larval motor axons
Since it is well-known that metabolic conditions can profoundly affect mitochondrial size and transport in cultured cells (Hollenbeck 1996; Karbowski et al. 2003; Rintoul et al. 2003; Chang et al. 2006c), we determined whether the different conditions of Schneider’s, HL3 and HL6 solutions may affect these parameters in larval motor axons. First, we estimated the percentage of stationary mitochondria (see Methods) and found that it was similar within a 10 second time interval among all three solutions, ranging from 67–73% (p>0.05, N>8, two-way ANOVA; Fig. 1C–D). For longer time intervals, the percentage of stationary mitochondria then significantly declined in all examined solutions such that only 54–60% of mitochondria remained stationary over 180 seconds (p<0.05, N>8; Fig. 1C). This decline was roughly proportional in all solutions and started to saturate after 120 seconds (p>0.05, N>8; Fig. 1C).
To examine the percentage of stationary mitochondria over longer time intervals, it was necessary to supplement HL6 with glutamate to suppress spontaneous muscle contractions by attenuating synaptic transmission at larval NMJs. Addition of 4 or 7 mM glutamate to HL6 solution slightly increased the percentage of stationary mitochondria but did not cause a significant difference among HL6 solutions with or without glutamate (Fig. 1D). However, the percentage of stationary mitochondria in HL6 solutions with glutamate was significantly higher than that with Schneider’s and/or HL3 solution for time intervals of 120 and/or 180 seconds (p<0.05 N>6, Fig. 1D). In HL6 solution supplemented with 7 mM glutamate, 72% of mitochondria were stationary within a 10 second interval (Fig. 1E). This percentage then steadily declined to 52% by 240 seconds. After that, there was no further significant decline up to 10 minutes (p>0.05, N>5, Fig. 1E). Many of the long-term stationary mitoGFP-positive signals resembled large aggregates. These structures were likely stationary mitochondrial clusters and were included in the analysis (as one mitochondrion) because we frequently observed motile mitochondria that either originated from or entered a structure for various periods of time. Including these clusters could have limited the interpretability of the data if a given condition would alter mitochondrial clustering without altering the ratio of motile/stationary mitochondria. However, this was not the case since the number and size of the large stationary clusters did not change among the examined solutions (not shown).
Taken together, these data suggest that there may be at least 3 different populations of mitochondria in larval motor axons: a highly motile population of mitochondria that moved at least once within 10 seconds, a moderately stationary population for which movements occurred within 2–3 minutes, and a long-term stationary population of mitochondria that showed no movement within at least 10 minutes and tended to cluster in larger aggregates. A similar pattern has also been observed in cultured cortical neurons where stop durations of <20 seconds, 1.5–2 minutes and >15 minutes defined three populations of mitochondria (Chang et al. 2006a).
To determine potential effects of imaging conditions on mitochondrial size, we analyzed the length of motile mitochondria invading the photobleached area (Fig. 2A). Mitochondrial length varied substantially, ranging typically from 0.24 to 2.9 µm for AM mitochondria and 0.22 to 2.6 µm for RM mitochondria (Fig. 2B–C). Interestingly, the size of AM and RM mitochondria was selectively influenced by imaging conditions. The mean length of AM mitochondria was similar in Schneider’s (0.89 ± 0.03 µm), HL6 (0.93 ± 0.04 µm), and HL3 solution (0.94 ± 0.04 µm; p>0.05, N=11, n<135; Fig. 2B). However, the average length of RM mitochondria was 1.05 ± 0.03 µm in HL3, 0.87 ± 0.04 µm in HL6, and 0.84 ± 0.03 µm in Schneider’s (Fig. 2C). In comparison, RM mitochondrial length in HL3 was increased to at least 121% of that in HL6 and Schneider’s (p<0.01, N=11, n<118). There was no difference between HL6 and Schneider’s solution (p>0.05). The biological significance of the HL3-induced increase in the length of RM mitochondria remained unclear, although it could be a compensatory reaction due to the gravely different metabolic conditions of HL3, which lacks amino acids.
Effects of HL3, HL6 and Schneider’s solution on mitochondrial transport in larval motors axons
Typically, imaging of mitochondria in HL3 and HL6 required addition of 4 mM glutamate to reduce adverse effects of spontaneous muscle contractions by desensitizing glutamate receptors at larval NMJs. Omitting extracellular Ca2+ from the bath solution was not an alternative option as this caused a rapid deterioration of the larval preparation (not shown). Schneider’s solution did not require any supplements because it essentially blocks synaptic transmission at larval NMJs and greatly diminishes neuronal and muscular excitability (Stewart et al. 1994).
To estimate the rate of mitochondrial transport in a net-antero- and net-retrograde direction (AM and RM, respectively), we determined mitochondrial flux by counting mitochondria moving into the bleached area. HL3, HL6 and Schneider’s solutions showed similar mean AM fluxes ranging from 8.1 ± 0.9 min−1 in HL3 to 9.6 ± 0.7 min−1 in HL6 (Fig. 2D, Table 1). Mean RM fluxes ranged from 6.5 ± 0.8 min−1 in HL3 to 7.6 ± 0.9 min−1 in HL6 solution. There was no significant difference in the mean values among the different solutions (p>0.05, N=11). All solutions showed a similar bias towards a higher anterograde flux as indicated by the mean AM/RM flux ratio, which ranged from 1.2 ± 0.2 in Schneider’s to 1.4 ± 0.1 in HL6 solution (Fig. 2D).
Table 1.
Net-Kinetics of mitochondrial transport in larval motor axons.
| Schneider’s 5.4 mM Ca2+5.4 mM Glu | HL3 1 mM Ca2+ 4 mM Glu | HL6 0.6 mM Ca2+ 4 mM Glu | HL6 0.1 mM Ca2+ 4 mM Glu | HL6 1.5 mM Ca2+ 4 mM Glu | HL6 0.6 mM Ca2+ 10 mM Glu | HL6 0.6 mM Ca2+ 4 mM Glu 90 min | |
|---|---|---|---|---|---|---|---|
|
AM Flux (#/min) |
8.18 ± 0.72 (N=11, n=291) |
8.05 ± 0.90 (N=11, n=286) |
9.55 ± 0.65 (N=18, n=563) |
8.35 ± 0.97 (N=5, n=140) |
8.43 ± 0.76 (N=13, n=349) |
9.01 ± 0.95 (N=9, n=272) |
10.92 ± 2.59 (N=8, n=195) |
|
RM Flux (#/min) |
6.89 ± 0.72 (N=11, n=243) |
6.52 ± 0.76 (N=11, n=237) |
7.64 ± 0.86 (N=20, n=506) |
5.49 ± 1.20 (N=5, n=92) |
7.02 ± 0.78 (N=13, n=296) |
74 ± 0.72 (N=9, n=264) |
5.73 ± 1.42 (N=8, n=136) |
|
AM Net-Velocity (µm/min) |
10.53 ± 0.76 (N=9, n=35) |
12.15 ± 0.90 (N=8, n=40) |
12.59 ± 0.49 (N=14, n=71) |
13.94 ± 1.29 (N=5, n=21) |
12.08 ± 0.55 (N=10, n=48) |
12.16 ± 0.88 (N=9, n=47) |
14.91 ± 1.42 (N=5, n=21) |
|
RM Net-Velocity (µm/min) |
16.73 ± 1.42 (N=9, n=30) |
18.08 ± 1.58 (N=8, n=34) |
19.01 ± 1.38 (N=15, n=52) |
21.11 ± 3.91 (N=5, n=16) |
18.15 ± 1.39 (N=10, n=44) |
19.88 ± 0.97 (N=9, n=45) |
23.26 ± 4.27 (N=5, n=12) |
|
AM Time Spent in AR (% time) |
60.17 ± 2.38 (N=9, n=35) |
64.59 ± 2.42 (N=8, n=40) |
65.98 ± 1.91 (N=15, n=71) |
68.89 ± 3.14 (N=5, n=21) |
60.77 ± 1.84 (N=10, n=48) |
64.55 ± 3.00 (N=9, n=47) |
70.95 ± 4.41 (N=5, n=21) |
|
AM Time Spent in RR (% time) |
6.17 ± 0.74 (N=9, n=35) |
7.60 ± 1.14 (N=8, n=40) |
5.96 ± 0.76 (N=15, n=71) |
5.92 ± 1.18 (N=5, n=21) |
3.67 ± 0.96 (N=10, n=48) |
4.32 ± 0.65 (N=9, n=47) |
6.90 ± 0.47 (N=5, n=21) |
|
AM Time Spent ST (% time) |
33.67 ± 2.39 (N=9, n=35) |
27.81 ± 2.28 (N=8, n=40) |
28.06 ± 1.80 (N=15, n=71) |
25.19 ± 3.31 (N=5, n=21) |
35.56 ± 2.30 (N=10, n=48) |
31.13 ± 3.05 (N=9, n=47) |
22.15 ± 4.19 (N=5, n=21) |
|
RM Time Spent in AR (% time) |
9.54 ± 1.05 (N=9, n=30) |
10.89 ± 1.66 (N=8, n=34) |
11.73 ± 1.69 N=16, n=52) |
8.19 ± 2.31 (N=5, n=16) |
8.16 ± 1.26 (N=10, n=44) |
8.46 ± 0.87 (N=9, n=45) |
13.61 ± 2.48 (N=5, n=12) |
|
RM Time Spent in RR (% time) |
60.21 ± 3.29 (N=9, n=30) |
62.64 ± 4.30 (N=8, n=34) |
65.70 ± 2.11 N=16, n=52) |
65.89 ± 2.78 (N=5, n=16) |
59.68 ± 2.54 (N=10, n=44) |
64.23 ± 1.96 (N=9, n=45) |
65.79 ± 3.77 (N=5, n=12) |
|
RM Time Spent ST (% time) |
30.24 ± 3.04 (N=9, n=30) |
26.47 ± 4.53 (N=8, n=34) |
22.57 ± 1.60 N=16, n=52) |
25.92 ± 2.66 (N=5, n=16) |
32.16 ± 2.49 (N=10, n=44) |
27.31 ± 2.26 (N=9, n=45) |
20.61 ± 2.71 (N=5, n=12) |
|
AM Stops (#/min) |
9.77 ± 0.31 (N=9, n=35) |
9.29 ± 0.40 (N=8, n=40) |
8.91 ± 0.31 (N=15, n=71) |
7.90 ± 0.62 (N=5, n=21) |
9.57 ± 0.20 (N=10, n=48) |
8.70 ± 0.28 (N=9, n=47) |
7.07 ± 0.49 (N=5, n=21) |
|
RM Stops (#/min) |
7.80 ± 0.72 (N=9, n=30) |
10.36 ± 3.22 (N=8, n=34) |
7.22 ± 0.38 (N=16, n=52) |
7.22 ± 0.46 (N=5, n=16) |
8.05 ± 0.40 (N=10, n=44) |
7.68 ± 0.35 (N=9, n=45) |
7.41 ± 0.80 (N=5, n=12) |
|
AM Reversals (#/min) |
5.61 ± 0.52 (N=9, n=35) |
6.97 ± 0.84 (N=8, n=40) |
6.46 ± 0.92 (N=15, n=71) |
5.84 ± 0.81 (N=5, n=21) |
3.66 ± 1.01 (N=10, n=48) |
4.33 ± 0.65 (N=9, n=47) |
6.83 ± 0.45 N=5, n=21) |
|
RM Reversals (#/min) |
7.49 ± 0.76 (N=9, n=30) |
6.97 ± 0.84 (N=8, n=34) |
8.75 ± 0.52 (N=16, n=52) |
6.82 ± 1.87 (N=5, n=16) |
6.53 ± 1.31 (N=10, n=44) |
6.67 ± 0.63 (N=9, n=45) |
10.31 ± 1.15 N=5, n=12) |
|
AM Stops & Reversals (#/min) |
15.38 ± 0.66 (N=9, n=35 |
16.23 ± 0.97 (N=8, n=40) |
15.43 ± 1.00 N=15, n=71) |
13.50 ± 0.68 (N=5, n=21) |
13.22 ± 0.93 (N=10, n=48) |
13.03 ± 0.70 (N=9, n=47) |
13.91 ± 0.52 (N=5, n=21) |
|
RM Stops & Reversals (#/min) |
15.25 ± 1.36 (N=9, n=30) |
18.73 ± 2.83 (N=8, n=34) |
15.97 ± 0.58 (N=16, n=52) |
14.04 ± 1.93 (N=5, n=16) |
14.58 ± 1.42 (N=10, n=44) |
14.37 ± 0.62 (N=9, n=45) |
17.73 ± 1.85 (N=5, n=12) |
All values represent means ± SEM that was derived from N animals and n mitochondria. Abbreviations: net-anterograde movement (AM); net-retrograde movement (RM), anterograde run (AR); retrograde run (RR), short stationary phases of motile mitochondria (stops, ST).
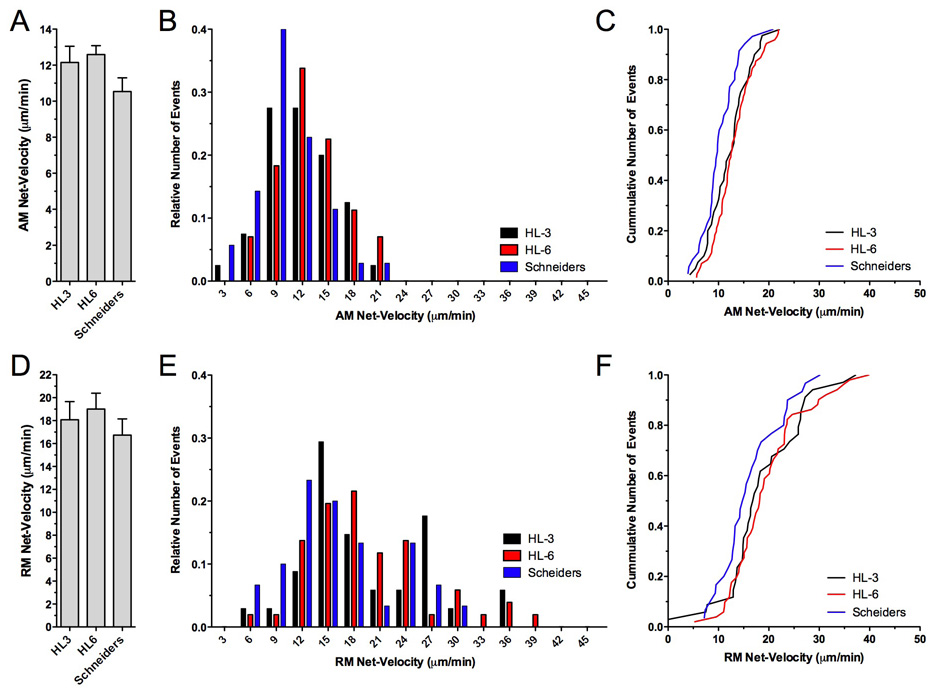
Next, we examined the net-velocity of mitochondria and its underlying key factors including antero- and retrograde run kinetics (distance, duration and velocity), frequency and duration of stops, and the frequency of reversals in direction. Mean net-velocity of AM mitochondria was slightly reduced in Schneider’s solution (10.5 ± 0.8 µm/min) when compared to HL3 (12.2 ± 0.9 µm/min) or HL6 (12.6 ± 0.5 µm/min) solution (Fig. 3A). Although this difference was statistically not significant (p>0.05; N>8), examination of frequency distributions showed that AM mitochondria imaged in Schneider’s solution experienced slower net-velocities more frequently (Fig. 3B–C). In Schneider’s solution, most AM mitochondria (~40%) showed a net-velocity of 9 ± 1 µm/min while most AM mitochondria imaged in HL6 or HL3 solution showed faster net-velocities. This was best illustrated by plotting cumulative distributions, which showed a clear shift of AM net-velocity in Schneider’s solution to the left, suggesting that AM net-velocity was generally slower in Schneider’s solution (Fig. 3C). However, peak AM net-velocities were similar in all three solutions, ranging from 21.0 µm/min to 22.2 µm/min.
Figure 3. Effects of HL3, HL6 and Schneider’s solution on net-velocities of mitochondrial transport.
Shown are the average net velocities for AM (A) and RM mitochondria (D), the middle panels show the relative frequency distribution, and right panels show the cumulative frequency distribution of all measurements.
The average net-velocities of AM (A) and RM mitochondria (D) were similar upon imaging in HL3, HL6 or Schneider’s solution (p>0.05, N>8, n>30, one-way ANOVA) although relative (B, E) and cumulative frequency distributions (C, F) revealed a trend towards slower velocities in Schneider’s solution for both AM (B–C) and RM mitochondria (E–F). Note the much broader range of net-velocities for RM (E) than for AM mitochondria (B).
Mean net-velocity of RM mitochondria was highest in HL6 solution (19.0 ± 1.4 µm/min) although the difference to that in Schneider’s (16.8 ± 1.4 µm/min) and HL3 (18.1 ± 1.6 µm/min) was statistically not significant (p>0.05; N>8, Fig. 3D). Frequency distributions again revealed a trend of RM net-velocities towards slower values in Schneider’s solution (Fig. 3E–F), suggesting that RM, like AM net-velocity, was generally slower in Schneider’s solution. Consistently, peak RM net-velocities were higher in HL6 and HL3 solution where 3% and 6% of RM mitochondria showed a peak net-velocity of up to 45 µm/min and 36 µm/min, respectively. In Schneider’s solution, only 3% reached peak net-velocities of 30 µm/min (Fig. 3E–F). Together these data suggest that HL6 solution facilitates not only fast net-velocities of AM and RM mitochondria but also a balanced flux of antero- and retrograde mitochondria.
In general, the mean net-velocity of RM mitochondria in larval motor axons was much faster than that of AM mitochondria (Fig. 3A, D), consistent with an earlier study (Pilling et al. 2006). AM and RM net-velocity differed by a factor of 1.6 in Schneider’s solution, by 1.5 in HL3, and by 1.7 in HL6. It is also interesting that the range of net-velocities differed between AM and RM mitochondria. Specifically, the overall distribution of AM net-velocities was relatively narrow, spanning from 4 to 22 µm/min. In contrast, the range of RM net-velocities were much broader, ranging from 5 to 46 µm/min (Fig. 3B–C, E–F). The occurrence of two peaks in the RM population was not regarded as significant (Fig. 3E).
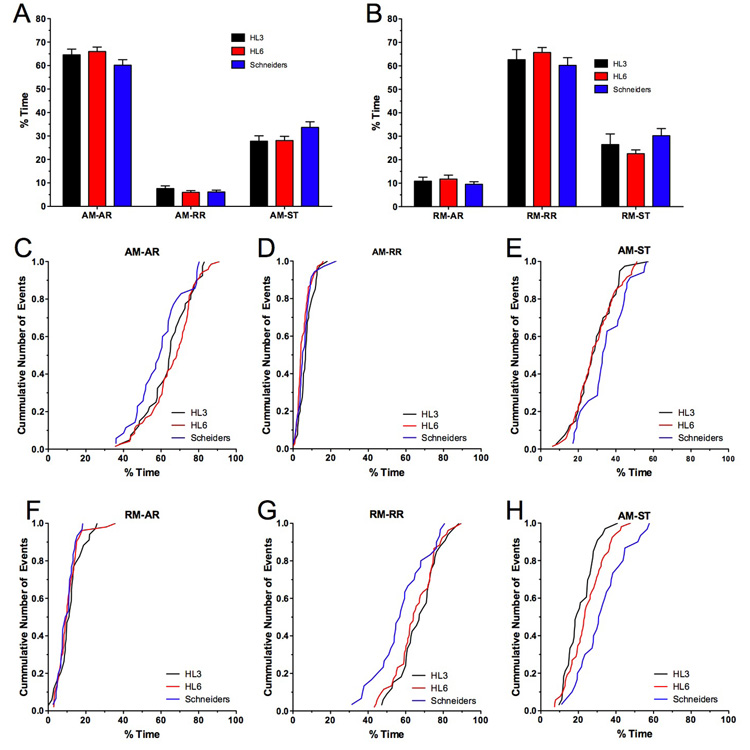
Net-velocity of mitochondrial transport is especially influenced by the difference in the length of antero- (ARs) and retrograde runs (RRs), by the speed of runs, the time between reversals of direction, and the frequency of stationary phases (Welte et al. 1998; Smith et al. 2001; Maly 2002; Welte 2004). One way to estimate the combined effect of these factors is to determine how much time AM and RM mitochondria spend in each phase. In HL6 solution, AM mitochondria spent about 66 ± 2% of their time on ARs, 6 ± 1% on RRs, and 28 ± 2% in short stationary phases (Fig. 4A). For RM mitochondria, the time spent on runs was essentially reversed, while the percentage of time spent stationary remained the same. Specifically, 12 ± 2% of the time was spent on ARs, 66 ± 2% on RRs, and 23 ± 2% in short stationary phases (Fig. 4B). The mean values describing this “duty cycle” of motile mitochondria were similar between all three solutions (p>0.05, N>8, two-way ANOVA, Fig. 4A–B), although AM and RM mitochondria imaged in Schneider’s solutions showed a trend towards spending more time stationary. Specifically, in Schneider’s solution AM mitochondria spent less time on ARs (Fig. 4C) and more time stationary (Fig. 4E) while no differences in the time spent on RRs became apparent (Fig. 4D). In addition, RM mitochondria spent less time on RRs in Schneider’s solution and more time stationary (Fig. 4G–H). Together, these trends in the mitochondrial duty cycle are consistent with a slower net-velocity of AM and RM mitochondria imaged in Schneider’s solution.
Figure 4. Effects of HL3, HL6 and Schneider’s solution on the duty cycle of AM and RM transport.
A–B) The average percentage of time spent in anterograde runs (ARs), retrograde runs (RRs) and short stationary phases (ST) for AM (A) and RM mitochondria (B) are shown. No significant differences were observed between HL3, HL6 and Schneider’s solution (p>0.05, N>8, n>30, two-way ANOVA). Error bars represent SEM.
C–H) Shown are cumulative frequency distributions for the percentage of time spent in anterograde runs (ARs), retrograde runs (RRs) and stationary (STs) of AM (C–E) and RM mitochondria (F–H). Note that AM mitochondria imaged in Schneider’s solution spent less time in ARs (C) and more time stationary (E). A qualitatively similar effect was seen for RM mitochondria, which spent in Schneider’s solution less time in RRs (G) and more time stationary (H).
The mean duration of stops, the frequency of stops, and the frequency of reversals in direction were similar among all examined solutions (Table 1, 2), and could not explain the reduced net-velocity of mitochondria in Schneider’s solution. Retrograde transport showed an insignificant trend towards longer stops for mitochondria imaged in Schneider’s (Table 2) but cumulative histograms showed that the increased mean stop time was mostly due to the occurrence of a small number (0.4%, n=474) of very long-lasting stops up to 31 s (not shown). RM mitochondria imaged in HL3 or HL6 solution never showed stops longer than 15 seconds during the 200 seconds of imaging.
Table 2.
Run kinetics of mitochondrial transport in larval motor axons.
| Schneider’s 5.4 mM Ca2+ 5.4 mM Glu | HL3 1 mM Ca2+ 4 mM Glu | HL6 0.6 mM Ca2+ 4 mM Glu | HL6 0.1 mM Ca2+ 4 mM Glu | HL6 1.5 mM Ca2+ 4 mM Glu | HL6 0.6 mM Ca2+ 10 mM Glu | HL6 0.6 mM Ca2+ 4 mM Glu 90 min | |
|---|---|---|---|---|---|---|---|
|
AM-AR Velocity (µm/s) |
0.31 ± 0.01 (N=9, n=35; e=715) |
0.32 ± 0.01 (N=8, n=40; e=883) |
0.33 ± 0.01 (N=15, n=71; e=1476) |
0.35 ± 0.02 (N=5, n=21; e=424) |
0.31 ± 0.01 (N=10, n=48; e=1062) |
0.31 ± 0.01 (N=9, n=47; e=1047) |
0.37 ± 0.02 (N=5, n=21; e=415) |
|
AM-AR Duration (s) |
3.81 ± 0.30 |
4.22 ± 0.28 |
4.76 ± 0.32 |
4.90 ± 0.30 |
3.91 ± 0.21 |
4.56 ± 0.30 |
5.28 ± 0.48 |
|
AM-AR Distance (µm) |
1.30 ± 0.15 |
1.56 ± 0.13 |
1.82 ± 0.16 |
1.96 ± 0.22 |
1.34 ± 0.09 |
1.62 ± 0.14 |
2.23 ± 0.28 |
|
AM-RR Velocity (µm/s) |
0.26 ± 0.02 (N=9, n=35; e=223) |
0.24 ± 0.01 (N=8, n=40; e=337) |
0.26 ± 0.01 (N=15, n=71; e=461) |
0.25 ± 0.02 (N=5, n=21; e=146) |
0.25 ± 0.01 (N=10, n=48; e=178) |
0.27 ± 0.01 (N=9, n=47; e=284) |
0.28 ± 0.02 (N=5, n=21; e=175) |
|
AM-RR Duration (s) |
1.11 ± 0.04 |
1.15 ± 0.03 |
1.11 ± 0.02 |
1.18 ± 0.06 |
1.09 ± 0.02 |
1.08 ± 0.01 |
1.13 ± 0.02 |
|
AM-RR Distance (µm) |
0.30 ± 0.02 |
0.28 ± 0.02 |
0.29 ± 0.01 |
0.31 ± 0.04 |
0.28 ± 0.02 |
0.29 ± 0.01 |
0.31 ± 0.03 |
|
RM-AR Velocity (µm/s) |
0.27 ± 0.01 (N=9, n=30; e=258) |
0.29 ± 0.02 (N=8, n=34; e=299) |
0.28 ± 0.01 (N=16, n=53 e=430) |
0.26 ± 0.04 (N=5, n=16; e=133) |
0.27 ± 0.02 N=10, n=44; e=298) |
0.28 ± 0.01 (N=9, n=45; e=326) |
0.29 ± 0.03 (N=5, n=12; e=136) |
|
RM-AR Duration (s) |
1.25 ± 0.04 |
1.32 ± 0.06 |
1.31 ± 0.10 |
1.34 ± 0.18 |
1.22 ± 0.03 |
1.26 ± 0.03 |
1.30 ± 0.05 |
|
RM-AR Distance (µm) |
0.34 ± 0.01 |
0.39 ± 0.03 |
0.38 ± 0.05 |
0.37 ± 0.07 |
0.34 ± 0.03 |
0.36 ± 0.02 |
0.40 ± 0.05 |
|
RM-RR Velocity (µm/s) |
0.42 ± 0.01 (N=9, n=30; e=460) |
0.47 ± 0.02 (N=8, n=34; e=480) |
0.45 ± 0.02 (N=16, n=53; e=753) |
0.44 ± 0.04 (N=5, n=16; e=253) |
0.44 ± 0.01 (N=10, n=44; e=576) |
0.47 ± 0.01 (N=9, n=45; e=645) |
0.50 ± 0.07 (N=5, n=12; e=181) |
|
RM-RR Duration (s) |
5.44 ± 0.79 |
5.11 ± 0.43 |
5.93 ± 0.76 |
5.44 ± 0.40 |
5.31 ± 0.38 |
5.62 ± 0.55 |
6.07 ± 1.21 |
|
RM-RR Distance (µm) |
2.93 ± 0.43 |
3.02 ± 0.38 |
3.52 ± 0.56 |
2.92 ± 0.38 |
3.01 ± 0.26 |
3.29 ± 0.35 |
3.95 ± 1.12 |
|
AM Stop Duration (s) |
2.05 ± 0.11 (N=9, n=35; e=689) |
1.82 ± 0.07 (N=8, n=40; e=841) |
1.89 ± 0.11 (N=15 n=71; e=1442) |
1.86 ± 0.13 (N=5, n=21; e=387) |
2.23 ± 0.13 (N=10, n=48; e=1061) |
2.18 ± 0.20 (N=9, n=47; e=1005) |
1.85 ± 0.29 (N=5, n=21; e=335) |
|
RM Stop Duration (s) |
2.55 ± 0.40 (N=9, n=30; e=474) |
1.80 ± 0.17 (N=8, n=34; e=402) |
1.92 ± 0.10 (N=16, n=53; e=697) |
2.16 ± 0.12 (N=5, n=16; e=242) |
2.42 ± 0.21 (N=10, n=44; e=636) |
2.15 ± 0.14 (N=9, n=45; e=628) |
1.65 ± 0.14 (N=5, n=12; e=162) |
All values represent means ± SEM that was derived from N animals, n mitochondria, and an e number of events. Abbreviations: net-anterograde movement (AM); net-retrograde movement (RM), anterograde run (AR); retrograde run (RR), short stationary phases of motile mitochondria (stops, ST).
Kinetics of mitochondrial runs were examined in regard to the net-direction of transport (AM and RM) and the direction of individual runs (AR or RR). The mean duration, distance, and velocity of anterograde and retrograde runs of AM and RM mitochondria showed no statistically significant differences among the examined solutions (Table 2). AM-AR peak run velocities ranged between 0.74 µm/s in HL3 and 1.18 µm/s in HL6, AM-RR peak velocities ranged between 0.88 µm/s in HL6 and 0.97 µm/s in Schneider’s, RM-AR peak velocities ranged between 0.71 µm/s in Schneider’s and 1.01 µm/s in HL6, and RM-RR peak velocities ranged between 0.99 µm/s in Schneider’s and 1.42 µm/s in HL3. Cumulative frequency distributions for all four run types showed no marked differences with two exceptions (Fig. S2). In Schneider’s solution, AM mitochondria showed a trend towards a shorter distance, shorter duration and slower velocity of ARs (Fig. S2A–C). In HL3 solution, RM mitochondria showed an increase in the distance and duration of ARs (Fig. S2G–H), although this increase was proportional and did not produce faster run velocities (Fig. S2I).
In summary, we found no statistically significant differences in the mean values for any of the examined transport parameters between the three imaging solutions. However, cumulative frequency distributions showed a trend towards slower net-velocities of AM and RM mitochondria that were imaged in Schneider’s solution. The trend in lower net-velocities was accompanied by small but consistent changes in the duty cycle of AM and RM mitochondria; AM mitochondria imaged in Schneider’s solution spent typically less time in ARs and more time stationary while RM mitochondria spent less time in RRs and more time stationary.
Effects of extracellular calcium on mitochondrial transport
A number of studies showed that mitochondria respond to Ca2+ signals from external or internal sources (Hollenbeck 1996; Babcock et al. 1998; Rizzuto et al. 2000; Demaurex et al. 2003) and recent reports suggested a direct influence of Ca2+ ions on mitochondrial transport kinetics (Yi et al. 2004; Brough et al. 2005; Beltran-Parrazal et al. 2006; Mironov 2006). Hence, we determined whether extracellular Ca2+ ([Ca2+]e) affects mitochondrial transport in larval motor axons. These experiments were performed in HL6 solution containing either 0.1 mM, 0.6 mM (standard) or 1.5 mM Ca2+, the latter being likely the physiological concentration in larval haemolymph (Stewart et al. 1994).
Antero- and retrograde flux as well as the mean net-velocity of AM and RM mitochondria was statistically not different at all three [Ca2+]es (Fig. 5). At 0.1 mM Ca2+, RM mitochondria showed a slight trend towards faster net-velocities such that ~12% exhibited net-velocities between 36 and 45 µm/min (Fig. 5F). In comparison, only ~3% of RM mitochondria showed similar peak net-velocities at a [Ca2+]e of 1.5 mM.
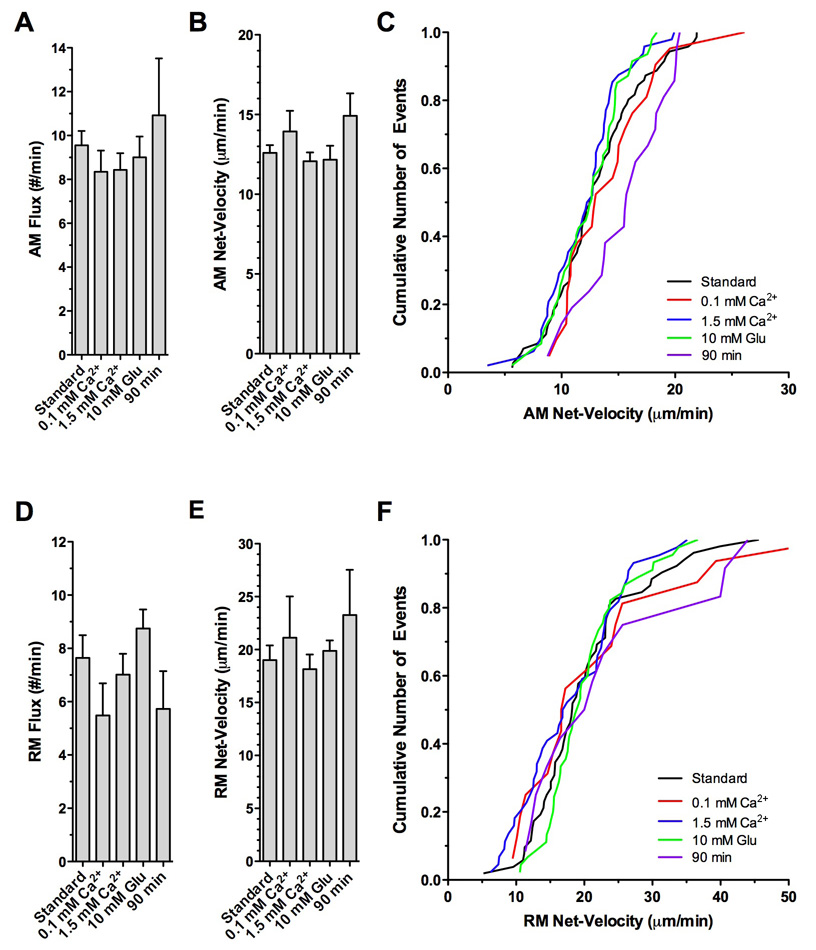
Figure 5. Effects of extracellular calcium, glutamate and time on the rate and net-velocity of mitochondrial transport in larval Drosophila motor axons.
Imaging was initiated within 10 minutes after starting the dissection in HL6 solution supplemented with 4 mM glutamate and 0.6 mM Ca2+ (Standard), HL6 supplemented with 4 mM glutamate and 0.1 mM Ca2+ (0.1 mM Ca2+), HL6 supplemented with 4 mM glutamate and 1.5 mM Ca2+ (1.5 mM Ca2+), HL6 supplemented with 10 mM glutamate and 0.6 mM Ca2+ (10 mM Glu). To examine effects of prolonged exposure to HL6, imaging was initiated 90 minutes after starting the dissection in HL6 supplemented with 4 mM glutamate and 0.6 mM Ca2+ (90 min) without changing the solution (0.7 ml).
A–C) Flux and net-velocity of AM mitochondria. There was no significant difference in the average flux (A) and net-velocity (B) between all examined conditions (p>0.05, N>5, one-way ANOVA). However, note that the cumulative frequency distribution (C) revealed a trend towards AM net-higher velocities after 90 minutes in standard HL6 solution. Error bars represent SEM.
D–F) Flux and net-velocity of RM mitochondria. There was no significant difference in the average flux (D) and net-velocity (E) between all examined conditions (p>0.05, N>5). However, note that the cumulative frequency distribution revealed a trend for a subpopulation of RM mitochondria towards higher velocities after 90 minutes in standard HL6 solution (F).
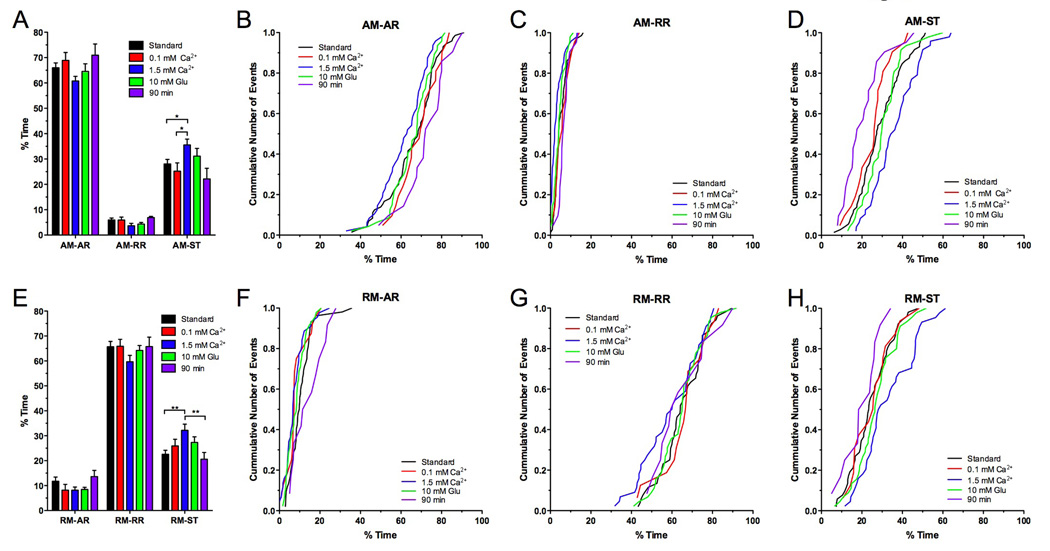
Aspects of the duty cycle of mitochondrial transport were significantly influenced by [Ca2+]e such that AM mitochondria exposed to 1.5 mM Ca2+ spent statistically significantly more time stationary than at lower [Ca2+]es (p<0.05, N>5, two-way ANOVA; Fig. 6A, Table 1). At 0.1 mM Ca2+, AM mitochondria spent 25.2 ± 3.3% of their time stationary while mitochondria at 1.5 mM Ca2+ spent 35.6 ± 2.3% stationary. Consistently, AM mitochondria spent less time on ARs and RRs at a [Ca2+]e of 1.5 mM than at lower [Ca2+]s (Fig. 6A). Although the difference in the respective mean values was not statistically significant (p>0.05), cumulative frequency distributions showed a clear shift towards less time spent on ARs and RRs (Fig. 6B–C) and more time spent stationary (Fig. 6D).
Figure 6. Effects of extracellular calcium, glutamate and time on the duty cycle of mitochondrial transport. Mitochondrial transport was imaged as described in Fig. 5.
A–D) AM mitochondria spent a significantly higher percentage of time stationary (A,D) at a [Ca2+]e of 1.5 mM (p<0.05, N>5, two-way ANOVA) while they spent less time in ARs (A–B) and RRs (A, C). In comparison to standard HL6 solution, addition of 10 mM glutamate (10 mM Glu) or prolonged exposure to HL6 had no significant effects (p>0.05). However, cumulative frequency distributions showed that after 90 minutes in HL6 solution, mitochondria spent more time in ARs (B) and less time stationary (D). Significant differences are indicated by asterisks. Error bars represent SEM.
E–H) RM mitochondria spent a significantly higher percentage of time stationary (E) at a [Ca2+]e of 1.5 mM Ca2+ (p<0.05, N>5, two-way ANOVA). Addition of 10 mM glutamate (Glu) to HL6 or prolonged exposure to HL6 had no significant effect (p>0.05). However, cumulative frequency distributions showed that after 90 minutes in HL6 solution, mitochondria spent less time stationary (H) and more in ARs (F). Significant differences are indicated by asterisks. Error bars represent SEM.
1.5 mM [Ca2+]e also increased the average time RM mitochondria spent stationary, which significantly increased from 22.6 ± 1.6 % at 0.6 mM Ca2+ to 32.2 ± 2.5 % at 1.5 mM Ca2+ (N>10, p<0.01; Fig. 6E, Table 1). While the average time RM mitochondria spent on RRs was similar at [Ca2+]es of 0.1 mM and 0.6 mM, the time was slightly although not significantly reduced at 1.5 mM Ca2+ (p<0.05, Fig. 6E–G).
The mean duration, distance, and velocity of ARs and RRs of AM and RM mitochondria showed no statistically significant differences between the examined [Ca2+]es (Table 2, Suppl Fig. 3). Plots of the cumulative frequency distribution showed also no discernable differences with one notable exception. Upon exposure to 1.5 mM Ca2+, a subpopulation of AM mitochondria showed a trend towards shorter distances and durations of ARs (Suppl. Fig 3A–B) without affecting AR velocities (Suppl. Fig 3C).
In conclusion, high extracellular Ca2+ significantly increased the time AM and RM mitochondria spent stationary while it slightly reduced the time spent in ARs and RRs. The increase in the time spent stationary was accompanied by an, although statistically insignificant, increase in the duration of stop periods and the frequency of stops for AM and RM mitochondria at 1.5 mM Ca2+ (Table 1–2).
Effects of glutamate and preparation time on mitochondrial transport
In contrast to Schneider’s solution, HL3 and HL6 per se do not contain glutamate. Excessive muscle contractions occurred frequently in both solutions, which made reliable imaging of mitochondrial transport cumbersome. Therefore, it was necessary to supplement both HL3 and HL6 with glutamate to essentially block synaptic transmission at larval NMJs by desensitizing glutamate receptors. Previous studies estimated that Drosophila haemolymph contains between 0.8 and 10 mM glutamate (McDonald 1975; Echalier 1997; Pierce et al. 1999; Augustin et al. 2007). Taken together, these studies suggest an average concentration of ~2 mM glutamate in the larval haemolymph, which is consistent with deteriorating effects of lower concentrations of extracellular glutamate on glutamate receptor clustering (Augustin et al. 2007). Accordingly, increasing the glutamate concentration in the imaging solution to 4 mM glutamate appeared reasonable. Since significant effects of glutamate-induced Ca2+ entry on mitochondrial transport and function have been reported in other systems (Nicholls et al. 1998; Atlante et al. 2001; Rintoul et al. 2003; Larsen et al. 2006), we examined whether an even higher concentration of 10 mM glutamate may affect mitochondrial transport in larval motor axons. However, there was no discernable difference between 4 and 10 mM glutamate for all examined parameters, including mitochondrial flux (Fig. 5A,D), net-velocity (Fig. 5B–C,E–F), run kinetics (Suppl. Fig. 3), and duty cycles of AM and RM mitochondria (Fig. 6; Table 1–2).
Finally, we examined the stability of the preparation in HL6 solution over a prolonged time. Specifically, we waited 90 minutes after starting the dissection before we imaged mitochondrial transport. This is in contrast to the 5–10 minutes that are typically required for dissection. Overall, we found no statistical significant differences between 10 and 90 minutes for all examined parameters (Table 1–Table 2). However, plots of the cumulative frequency distribution showed a trend of AM mitochondria towards slower net-velocities (Fig. 5C), while run kinetics of AM and RM mitochondria showed no discernable differences (Suppl. Fig. 3). After 90 minutes, there was also a trend of AM and RM mitochondria to spend less time stationary and more time in runs (Fig. 6B–D, F–H). Nevertheless, the lack of any significant deteriorating effects after a 90-minute exposure suggests that HL6 solution confers a reasonable stability to the larval preparation and mitochondrial transport in larval motor axons.
Discussion
Since it has been developed by Jan and Jan (1976), the larval neuromuscular preparation of Drosophila has been extensively used to genetically dissect numerous molecular mechanisms, including those underlying neuronal function and structure (Keshishian et al. 1996). Recently, the pioneering work by Bill Saxton’s lab added time-lapse imaging studies of mitochondrial transport to its steadily growing repertoire (Pilling et al. 2006). This new in situ model of mitochondrial transport provides much promise to resolve the still enigmatic machinery that controls transport. However, optimal imaging conditions have not been characterized for this new system.
The major goal of this study has been to examine which bath solutions are well suited for the live imaging of mitochondrial transport in larval motor axons. Although a large number of solutions have been developed over the years for the larval preparation (Jan et al. 1976; Schneider et al. 1978; Stewart et al. 1994; Macleod et al. 2002; Ball et al. 2003), we restricted our survey to the most commonly used bath solutions including HL3, HL6 and Schneider’s solution. Overall, our study found surprisingly few differences in mitochondrial transport parameters among the examined solutions, suggesting that all three solutions are in principal suitable to faithfully image mitochondrial transport. However, we also observed a few significant differences and trends that favor HL6 supplemented with glutamate (4–7 mM) and calcium (0.6 mM) over Schneider’s and HL3 solution.
Effects of imaging solutions on length of motile mitochondria
Our study revealed a profound and selective effect of HL3 solution on the length of motile mitochondria. The mean length of RM mitochondria was significantly longer in HL3 solution than in Schneider’s and HL6 solution while the mean length of AM mitochondria was similar among all three solutions. Changes of mitochondrial length have been reported to occur in cultured neurons (reviewed by: (Chang et al. 2006c). For example, mitochondrial length increases in cultured neurons as the development of synaptic connection matures (Popov et al. 2005; Chang et al. 2006b). In addition, mitochondria in axons are usually shorter than in dendrites (Chang et al. 2006a). To our knowledge, the selective effect of HL3 on the length of mitochondria in the context of the net-direction of mitochondrial transport has so far not been reported.
The observed increase in mitochondrial length is likely caused either by fusion or by degradation of small mitochondria in distant regions of the axon. In contrast to an earlier study (Pilling et al. 2006), we observed mitochondrial fusion and fission events often in larval motor axons, even during transport. Degradation of mitochondria in fly motor axons has not been well characterized, but mitochondria together with autophagosomes and lysosomes have been found in large axonal swellings of kinesin and dynein mutants (Gho et al. 1992; Hurd et al. 1996; Martin et al. 1999). The effect of HL3 on mitochondrial length may be due to the gravely different metabolic conditions, as HL6 and Schneider’s solution are rich in amino acids while HL3 lacks amino acids (Schneider et al. 1978; Stewart et al. 1994). Assuming that small mitochondria are more vulnerable than long mitochondria, the effect of HL3 may uncover a homeostatic mechanism that could be triggered by an accelerated decline of mitochondrial function under unfavorable conditions. Since it seems likely that the effect of HL3 solution is triggered by adverse bath conditions, we conclude that HL3 solution may not be ideal for live imaging of mitochondrial transport.
Effects of imaging solutions on mitochondrial transport
Despite the major differences in the ionic and metabolic conditions among the three examined solutions, there were no statistically significant differences in mitochondrial transport among them. AM and RM flux, net-velocity, duty cycle, as well as antero- and retrograde run kinetics were all similar. In addition, there was no significant difference in the percentage of stationary/motile mitochondria among the examined solutions, suggesting that all three solutions are suitable for imaging mitochondrial transport in the larval preparation. However, there are some caveats to consider. HL3 may be less favorable due to its effects on mitochondrial length. Schneider’s solution showed a clear trend towards slower net-velocities, which was likely linked to the trend of spending more time stationary and less time in runs. These trends may be linked to the high Ca2+ concentration of the solution (see below) and/or to the inhibition of neuronal activity that is induced by Schneider’s solution, as it reduces the resting potential by 50% (Stewart et al. 1994).
Since HL6 solution emerged as the most suitable of all examined solutions, we further tested how well HL6 solution can maintain mitochondrial transport over a period of 90 minutes but found no statistically significant differences. However, there was a trend towards faster net-velocities of both AM and RM mitochondria. Consistently, AM (more pronounced) and RM mitochondria spent less time stationary. Both effects were apparently not due to a deterioration of the preparation, which would be expected to decrease mitochondrial motility. The effect may be linked to changes in haemolymph-mediated trophic signaling since, for example, proper circulation of hormones has been abolished in the dissected preparation. In conclusion, the lack of significant effects on mitochondrial transport upon prolonged exposure to HL6 solutions suggests that HL6 solution maintains a reasonable health of the larval preparation. Since HL6 also maintains neuronal excitability, it is a suitable solution for long-term studies of mitochondrial transport.
Effects of extracellular Ca2+ and glutamate on mitochondrial transport
Previous studies reported profound effects of Ca2+ and glutamate-induced Ca2+ entry on mitochondrial function and distributions (Nicholls et al. 1998; Atlante et al. 2001; Rintoul et al. 2003; Yi et al. 2004; Larsen et al. 2006; Mironov 2006). A major effect of raising intracellular Ca2+ is likely an inhibition of mitochondrial transport that may trigger long-term stationary phases (Yi et al. 2004; Brough et al. 2005; Mironov 2006), although this may not be the case in all cells (Beltran-Parrazal et al. 2006). Consequently, it was important to clarify potential effects of Ca2+ and glutamate in the bath solution on mitochondria in larval motor axons.
Our study showed that mitochondrial transport in larval motor axons is indeed sensitive to changes in the [Ca2+]e. While flux and net-velocity of AM and RM mitochondria was similar among [Ca2+]es of 0.1, 0.6 and 1.5 mM Ca2+, a subpopulation of RM mitochondria (12%) showed unusually high peak velocities in 0.1 mM Ca2+ that ranged between 36 and 45 µm/min. In contrast, a high [Ca2+]e decreased the time mitochondria spent in runs and significantly increased the time mitochondria spent stationary. The observed effects of a low and high [Ca2+]e are consistent with observations in cultured mammalian neurons where mitochondrial transport accelerated after inhibition of Ca2+ channels and decelerated after increasing channel activity (Mironov 2006). Our observations are also consistent with studies using cultured myoblasts and HEK-293 cells, suggesting that mitochondrial movements are suppressed after release of Ca2+ from internal stores (Yi et al. 2004; Brough et al. 2005). However, there is an important caveat since we also observed that a complete lack of Ca2+ in the bath solution caused a progressive inhibition of mitochondrial movements (KEZ, pers. communication). A similar effect of Ca2+-free solutions was also observed in cultured neurons, although after membrane depolarization (Brough et al. 2005). It has been speculated that this effect is not directly caused by Ca2+ but by a persistent bursting activity leading to enhanced ATP consumption and possible shortage of ATP (Brough et al. 2005; Mironov 2006). However, this seems an unlikely possibility to explain the effect on transport in larval motor neurons since these were not depolarized.
It is noteworthy that mitochondrial transport parameters in Schneider’s solution did not significantly differ from those obtained in HL6 and HL3 solution (containing 0.6 and 1 mM Ca2+, respectively). This similarity is puzzling since Schneider’s solution contains much more Ca2+ (5.4 mM) than haemolymph (1.5 mM; Stewart et al. 1994). Accordingly, one might have expected slower transport kinetics in Schneider’s solution. While at least cumulative frequency distributions showed trends consistent with effects of a high [Ca2+]e, like slower net velocities and spending more time stationary, these effects were still less pronounced than the effect of 1.5 mM Ca2+ in HL6 on stationary phases. A possible explanation for this discrepancy may be the attenuated excitability of neurons in Schneider’s solution (Stewart et al. 1994) since silencing of neuronal activity by blocking Na+ channels increased mitochondrial transport activity (Chang et al. 2006a; Mironov 2006). Consequently, it is possible that both high Ca2+ and low neuronal activity may cancel out each other’s effects. However, Schneider’s differs in many components from HL6 and contains multi-component ingredients, like yeastolate, that make a careful dissection of the phenomenon difficult. For these reasons, HL6 may be better suited for the analysis of Ca2+- and activity-dependent effects on mitochondrial transport.
Supplementary Material
After dissection in standard HL6 solution, the larval preparation was fixed with 4% formaldeyhde to arrest mitochondrial transport. After washing in HL6, mitoGFP fluorescence from segmental nerves was imaged without photobleaching and tracked through the acquired 200 images. Tracks of fixation-induced stationary mitochondria were analyzed for the presence of any displacement between images.
A) Frequency histogram of 36,501 point-to-point measurements from 180 mitochondria. The point-to-point distance describes the displacement of one mitochondrion from one image to the next. Inset shows a magnification visualizing the relatively rare number of displacement events that were larger than 0.12 µm.
B) Effects of various thresholds on artifactual movements derived from tracking errors and stage drift. Using a threshold (TH) of 0.1 µm, 0.13 µm, or 0.15 µm for movements between successive images limited the tracking error to 2.80%, 1.09%, or 0.06% out of 36,501 measurements, respectively.
Imaging was initiated within 10 minutes after starting the dissection in HL3, HL6 and Schneider’s solution. HL3 and HL6 solution were supplemented with 4 mM glutamate (standard) to reduce spontaneous muscle contractions.
A–C) Kinetics of ARs of AM mitochondria. Note that a subpopulation of mitochondria imaged in Schneider’s solution showed a trend towards a shorter distance (A) and duration of ARs (B), consistent with the trend towards lower AR velocities (C). The cumulative frequency distribution was obtained from >715 events from >35 mitochondria of >8 animals.
D–F) Kinetics of RRs of AM mitochondria. No difference was apparent in the distance (D), duration (E) and velocity (F) of RRs (data from >223 events, >35 mitochondria, >8 animals).
G–I) Kinetics of ARs of RM mitochondria. Note that a subpopulation of RM mitochondria imaged in HL3 solution showed a trend towards a longer distance (G) and duration (H) of ARs without affecting AR velocities (I; data from >258 events, >30 mitochondria, >8 animals).
I–L) Kinetics of RRs of RM mitochondria. No difference was apparent in the distance (J), duration (K) and velocity (L) of RRs (data from >460 events, >30 mitochondria, >8 animals).
Imaging was initiated within 10 minutes after starting the dissection in HL6 solution that was supplemented with 4 mM glutamate (standard) and either 0.1 mM, 0.6 mM (standard), or 1.5 mM Ca2+. In addition, we examined effects of 10 mM glutamate (Glu) in HL6 solution that contained 0.6 mM Ca2+, and effects of a 90-minute exposure to standard HL6.
A–C) Kinetics of ARs of AM mitochondria. Note that a subpopulation of mitochondria exposed to 1.5 mM Ca2+ showed a trend towards a shorter distance (A) and duration (B) of ARs without affecting AR velocities (C). In addition, a prolonged incubation time of more than 90 minutes induced a trend towards higher AR velocities (C). The cumulative frequency distribution was obtained from >415 events from >21 mitochondria of >5 animals.
D–F) Kinetics of RRs of AM mitochondria. No discernable difference was apparent. Data from >146 events from >21 mitochondria of >5 animals.
G–I) Kinetics of ARs of RM mitochondria. No discernable difference was apparent. Data from >133 events from >12 mitochondria of >5 animals.
J–L) Kinetics of RRs of RM mitochondria. No discernable difference was apparent. Data from >253 events from >12 mitochondria of >5 animals.
Acknowledgements
This work was supported by a grant to K.E.Z. from NINDS (R01 NS052664).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aberle H, Haghighi AP, Fetter RD, McCabe BD, Magalhaes TR, Goodman CS. Wishful thinking encodes a BMP type II receptor that regulates synaptic growth in Drosophila. Neuron. 2002;33:545–558. doi: 10.1016/s0896-6273(02)00589-5. [DOI] [PubMed] [Google Scholar]
- Abramoff MD, Magelhaes PJ, Ram SJ. Image Processing with ImageJ. Biophot Int. 2004;11:36–42. [Google Scholar]
- Atlante A, Calissano P, Bobba A, Giannattasio S, Marra E, Passarella S. Glutamate neurotoxicity, oxidative stress and mitochondria. FEBS Lett. 2001;497:1–5. doi: 10.1016/s0014-5793(01)02437-1. [DOI] [PubMed] [Google Scholar]
- Augustin H, Grosjean Y, Chen K, Sheng Q, Featherstone DE. Nonvesicular release of glutamate by glial xCT transporters suppresses glutamate receptor clustering in vivo. J Neurosci. 2007;27:111–123. doi: 10.1523/JNEUROSCI.4770-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babcock DF, Hille B. Mitochondrial oversight of cellular Ca2+ signaling. Curr Op Neurobiol. 1998;8:398–404. doi: 10.1016/s0959-4388(98)80067-6. [DOI] [PubMed] [Google Scholar]
- Ball R, Xing B, Bonner P, Shearer J, Cooper RL. Long-term in vitro maintenance of neuromuscular junction activity of Drosophila larvae. Comp Biochem Physiol A. 2003;134:247–255. doi: 10.1016/s1095-6433(02)00243-x. [DOI] [PubMed] [Google Scholar]
- Beltran-Parrazal L, Lopez-Valdes HE, Brennan KC, Diaz-Munoz M, de Vellis J, Charles AC. Mitochondrial transport in processes of cortical neurons is independent of intracellular calcium. Am J Physiol Cell Physiol. 2006;291:C1193–C1197. doi: 10.1152/ajpcell.00230.2006. [DOI] [PubMed] [Google Scholar]
- Brand AH, Perrimon N. Targeted gene expression as a means of altering cell fates and generating dominant phenotypes. Development. 1993;118:401–415. doi: 10.1242/dev.118.2.401. [DOI] [PubMed] [Google Scholar]
- Brough D, Schell MJ, Irvine RF. Agonist-induced regulation of mitochondrial and endoplasmic reticulum motility. Biochem J. 2005;392:291–297. doi: 10.1042/BJ20050738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang DT, Honick AS, Reynolds IJ. Mitochondrial trafficking to synapses in cultured primary cortical neurons. J Neurosci. 2006a;26:7035–7045. doi: 10.1523/JNEUROSCI.1012-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang DT, Reynolds IJ. Differences in mitochondrial movement and morphology in young and mature primary cortical neurons in culture. Neuroscience. 2006b;141:727–736. doi: 10.1016/j.neuroscience.2006.01.034. [DOI] [PubMed] [Google Scholar]
- Chang DT, Reynolds IJ. Mitochondrial trafficking and morphology in healthy and injured neurons. Prog Neurobiol. 2006c;80:241–268. doi: 10.1016/j.pneurobio.2006.09.003. [DOI] [PubMed] [Google Scholar]
- Cox RT, Spradling AC. Milton controls the early acquisition of mitochondria by Drosophila oocytes. Development. 2006;133:3371–3377. doi: 10.1242/dev.02514. [DOI] [PubMed] [Google Scholar]
- Demaurex N, Distelhorst C. Cell biology. Apoptosis - the calcium connection. Science. 2003;300:65–67. doi: 10.1126/science.1083628. [DOI] [PubMed] [Google Scholar]
- Echalier G. Drosophila: Cells in Culture. Academic Press; 1997. Composition of the body fluid of Drosophila and the design of culture media for Drosophila cells. [Google Scholar]
- Gho M, McDonald K, Ganetzky B, Saxton WM. Effects of kinesin mutations on neuronal functions. Science. 1992;258:313–316. doi: 10.1126/science.1384131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glater EE, Megeath LJ, Stowers RS, Schwarz TL. Axonal transport of mitochondria requires milton to recruit kinesin heavy chain and is light chain independent. J Cell Biol. 2006;173:545–557. doi: 10.1083/jcb.200601067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo X, Macleod GT, Wellington A, Hu F, Panchumarthi S, Schoenfield M, Marin L, Charlton MP, Atwood HL, Zinsmaier KE. The GTPase dMiro is required for axonal transport of mitochondria to Drosophila synapses. Neuron. 2005;47:379–393. doi: 10.1016/j.neuron.2005.06.027. [DOI] [PubMed] [Google Scholar]
- Hollenbeck PJ. The pattern and mechanisms of mitochondrial transport in axons. Front. Biosci. 1996;1:d91–d102. doi: 10.2741/a118. [DOI] [PubMed] [Google Scholar]
- Hollenbeck PJ, Saxton WM. The axonal transport of mitochondria. J Cell Sci. 2005;118:5411–5419. doi: 10.1242/jcs.02745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurd DD, Saxton WM. Kinesin mutations cause motor neuron disease phenotypes by disrupting fast axonal transport in Drosophila. Genetics. 1996;144:1075–1085. doi: 10.1093/genetics/144.3.1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan LY, Jan YN. Properties of the larval neuromuscular junction in Drosophila melanogaster. J Physiol (Lond) 1976;262:189–214. doi: 10.1113/jphysiol.1976.sp011592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karbowski M, Youle RJ. Dynamics of mitochondrial morphology in healthy cells and during apoptosis. Cell Death Differ. 2003;10:870–880. doi: 10.1038/sj.cdd.4401260. [DOI] [PubMed] [Google Scholar]
- Keshishian H, Broadie K, Chiba A, Bate M. The Drosophila neuromuscular junction: a model system for studying synaptic development and function. Annu Rev Neurosci. 1996;19:545–575. doi: 10.1146/annurev.ne.19.030196.002553. [DOI] [PubMed] [Google Scholar]
- Koh YH, Gramates LS, Budnik V. Drosophila larval neuromuscular junction: molecular components and mechanisms underlying synaptic plasticity. Microsc Res Techn. 2000;49:14–25. doi: 10.1002/(SICI)1097-0029(20000401)49:1<14::AID-JEMT3>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- Kuwana T, Newmeyer DD. Bcl-2-family proteins and the role of mitochondria in apoptosis. Curr Op Cell Biol. 2003;15:691–699. doi: 10.1016/j.ceb.2003.10.004. [DOI] [PubMed] [Google Scholar]
- Larsen GA, Skjellegrind HK, Berg-Johnsen J, Moe MC, Vinje ML. Depolarization of mitochondria in isolated CA1 neurons during hypoxia, glucose deprivation and glutamate excitotoxicity. Brain Res. 2006;1077:153–160. doi: 10.1016/j.brainres.2005.10.095. [DOI] [PubMed] [Google Scholar]
- Li Z, Okamoto K, Hayashi Y, Sheng M. The importance of dentritic mitochondria in the morphogenesis and plasticity of spines and synapses. Cell. 2004;119:873–887. doi: 10.1016/j.cell.2004.11.003. [DOI] [PubMed] [Google Scholar]
- Macleod GT, Hegstrom-Wojtowicz M, Charlton MP, Atwood HL. Fast calcium signals in Drosophila motor neuron terminals. J Neurophysiol. 2002;88:2659–2663. doi: 10.1152/jn.00515.2002. [DOI] [PubMed] [Google Scholar]
- Maly IV. A stochastic model for patterning of the cytoplasm by the saltatory movement. J Theor Biol. 2002;216:59–71. doi: 10.1006/jtbi.2002.2531. [DOI] [PubMed] [Google Scholar]
- Martin M, Iyadurai SJ, Gassman A, Gindhart JG, Jr, Hays TS, Saxton WM. Cytoplasmic dynein, the dynactin complex, and kinesin are interdependent and essential for fast axonal transport. Mol Biol Cell. 1999;10:3717–3728. doi: 10.1091/mbc.10.11.3717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald TJ. Neuromuscular pharmacology of insects. Annu Rev Entomol. 1975;20:151–166. doi: 10.1146/annurev.en.20.010175.001055. [DOI] [PubMed] [Google Scholar]
- Mironov SL. Spontaneous and evoked neuronal activities regulate movements of single neuronal mitochondria. Synapse. 2006;59:403–411. doi: 10.1002/syn.20256. [DOI] [PubMed] [Google Scholar]
- Misgeld T, Kerschensteiner M, Bareyre FM, Burgess RW, Lichtman JW. Imaging axonal transport of mitochondria in vivo. Nat Methods. 2007a;4:559–561. doi: 10.1038/nmeth1055. [DOI] [PubMed] [Google Scholar]
- Misgeld T, Nikic I, Kerschensteiner M. In vivo imaging of single axons in the mouse spinal cord. Nat Protoc. 2007b;2:263–268. doi: 10.1038/nprot.2007.24. [DOI] [PubMed] [Google Scholar]
- Mitsuhashi J. Media for insect culture. In: Maramorosch K, editor. Advances in Cell Culture. NY: Academic Press; 1982. pp. 133–196. [Google Scholar]
- Newmeyer DD, Ferguson-Miller S. Mitochondria: releasing power for life and unleashing the machineries of death. Cell. 2003;112:481–490. doi: 10.1016/s0092-8674(03)00116-8. [DOI] [PubMed] [Google Scholar]
- Nicholls DG, Budd SL. Mitochondria and neuronal glutamate excitotoxicity. Biochim Biophys Acta. 1998;1366:97–112. doi: 10.1016/s0005-2728(98)00123-6. [DOI] [PubMed] [Google Scholar]
- Pierce VA, Mueller LD, Gibbs AG. Osmoregulation in Drosophila melanogaster selected for urea tolerance. J Exp Biol. 1999;202:2349–2358. doi: 10.1242/jeb.202.17.2349. [DOI] [PubMed] [Google Scholar]
- Pilling AD, Horiuchi D, Lively CM, Saxton WM. Kinesin-1 and Dynein are the primary motors for fast transport of mitochondria in Drosophila motor axons. Mol Biol Cell. 2006;17:2057–2068. doi: 10.1091/mbc.E05-06-0526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popov V, Medvedev NI, Davies HA, Stewart MG. Mitochondria form a filamentous reticular network in hippocampal dendrites but are present as discrete bodies in axons: a three-dimensional ultrastructural study. J Comp Neurol. 2005;492:50–65. doi: 10.1002/cne.20682. [DOI] [PubMed] [Google Scholar]
- Rintoul GL, Filiano AJ, Brocard JB, Kress GJ, Reynolds IJ. Glutamate decreases mitochondrial size and movement in primary forebrain neurons. J Neurosci. 2003;23:7881–7888. doi: 10.1523/JNEUROSCI.23-21-07881.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzuto R. Calcium mobilization from mitochondria in synaptic transmitter release. J Cell Biol. 2003;163:441–443. doi: 10.1083/jcb.200309111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzuto R, Bernardi P, Pozzan T. Mitochondria as all-round players of the calcium game. J Physiol. 2000;529:37–47. doi: 10.1111/j.1469-7793.2000.00037.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider I, Blumenthal A. Drosophila Cell and Tissue Culture. In: Ashburner M, Wright TRF, editors. Biology and Genetics of Drosophila. vol. 2A. N.Y.: Academic Press; 1978. pp. 266–315. [Google Scholar]
- Smith DA, Simmons RM. Models of motor-assisted transport of intracellular particles. Biophysical Journal. 2001;80:45–68. doi: 10.1016/S0006-3495(01)75994-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart BA, Atwood HL, Renger JJ, Wang J, Wu CF. Improved stability of Drosophila larval neuromuscular preparations in haemolymph-like physiological solutions. J Comp Physiol A. 1994;175:179–191. doi: 10.1007/BF00215114. [DOI] [PubMed] [Google Scholar]
- Wallace DC. Mitochondrial diseases in man and mouse. Science. 1999;283:1482–1488. doi: 10.1126/science.283.5407.1482. [DOI] [PubMed] [Google Scholar]
- Welte MA. Bidirectional transport along microtubules. Curr Biol. 2004;14:13. doi: 10.1016/j.cub.2004.06.045. [DOI] [PubMed] [Google Scholar]
- Welte MA, Gross SP, Postner M, Block SM, Wieschaus EF. Developmental regulation of vesicle transport in Drosophila embryos: forces and kinetics. Cell. 1998;92:547–557. doi: 10.1016/s0092-8674(00)80947-2. [DOI] [PubMed] [Google Scholar]
- Wong-Riley MT, Welt C. Histochemical changes in cytochrome oxidase of cortical barrels after vibrissal removal in neonatal and adult mice. Proc Natl Acad Sci USA. 1980;77:2333–2337. doi: 10.1073/pnas.77.4.2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi M, Weaver D, Hajnoczky G. Control of mitochondrial motility and distribution by the calcium signal: a homeostatic circuit. J Cell Biol. 2004;167:661–672. doi: 10.1083/jcb.200406038. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
After dissection in standard HL6 solution, the larval preparation was fixed with 4% formaldeyhde to arrest mitochondrial transport. After washing in HL6, mitoGFP fluorescence from segmental nerves was imaged without photobleaching and tracked through the acquired 200 images. Tracks of fixation-induced stationary mitochondria were analyzed for the presence of any displacement between images.
A) Frequency histogram of 36,501 point-to-point measurements from 180 mitochondria. The point-to-point distance describes the displacement of one mitochondrion from one image to the next. Inset shows a magnification visualizing the relatively rare number of displacement events that were larger than 0.12 µm.
B) Effects of various thresholds on artifactual movements derived from tracking errors and stage drift. Using a threshold (TH) of 0.1 µm, 0.13 µm, or 0.15 µm for movements between successive images limited the tracking error to 2.80%, 1.09%, or 0.06% out of 36,501 measurements, respectively.
Imaging was initiated within 10 minutes after starting the dissection in HL3, HL6 and Schneider’s solution. HL3 and HL6 solution were supplemented with 4 mM glutamate (standard) to reduce spontaneous muscle contractions.
A–C) Kinetics of ARs of AM mitochondria. Note that a subpopulation of mitochondria imaged in Schneider’s solution showed a trend towards a shorter distance (A) and duration of ARs (B), consistent with the trend towards lower AR velocities (C). The cumulative frequency distribution was obtained from >715 events from >35 mitochondria of >8 animals.
D–F) Kinetics of RRs of AM mitochondria. No difference was apparent in the distance (D), duration (E) and velocity (F) of RRs (data from >223 events, >35 mitochondria, >8 animals).
G–I) Kinetics of ARs of RM mitochondria. Note that a subpopulation of RM mitochondria imaged in HL3 solution showed a trend towards a longer distance (G) and duration (H) of ARs without affecting AR velocities (I; data from >258 events, >30 mitochondria, >8 animals).
I–L) Kinetics of RRs of RM mitochondria. No difference was apparent in the distance (J), duration (K) and velocity (L) of RRs (data from >460 events, >30 mitochondria, >8 animals).
Imaging was initiated within 10 minutes after starting the dissection in HL6 solution that was supplemented with 4 mM glutamate (standard) and either 0.1 mM, 0.6 mM (standard), or 1.5 mM Ca2+. In addition, we examined effects of 10 mM glutamate (Glu) in HL6 solution that contained 0.6 mM Ca2+, and effects of a 90-minute exposure to standard HL6.
A–C) Kinetics of ARs of AM mitochondria. Note that a subpopulation of mitochondria exposed to 1.5 mM Ca2+ showed a trend towards a shorter distance (A) and duration (B) of ARs without affecting AR velocities (C). In addition, a prolonged incubation time of more than 90 minutes induced a trend towards higher AR velocities (C). The cumulative frequency distribution was obtained from >415 events from >21 mitochondria of >5 animals.
D–F) Kinetics of RRs of AM mitochondria. No discernable difference was apparent. Data from >146 events from >21 mitochondria of >5 animals.
G–I) Kinetics of ARs of RM mitochondria. No discernable difference was apparent. Data from >133 events from >12 mitochondria of >5 animals.
J–L) Kinetics of RRs of RM mitochondria. No discernable difference was apparent. Data from >253 events from >12 mitochondria of >5 animals.