Jaw protrusion enhances forces exerted on prey by suction feeding fishes

Abstract

The ability to protrude the jaws during prey capture is a hallmark of teleost fishes, widely recognized as one of the most significant innovations in their diverse and mechanically complex skull. An elaborated jaw protrusion mechanism has independently evolved multiple times in bony fishes, and is a conspicuous feature in several of their most spectacular radiations, ultimately being found in about half of the approximately 30 000 living species. Variation in jaw protrusion distance and speed is thought to have facilitated the remarkable trophic diversity found across fish groups, although the mechanical consequences of jaw protrusion for aquatic feeding performance remain unclear. Using a hydrodynamic approach, we show that rapid protrusion of the jaws towards the prey, coupled with the spatial pattern of the flow in front of the mouth, accelerates the water around the prey. Jaw protrusion provides an independent source of acceleration from that induced by the unsteady flow at the mouth aperture, increasing by up to 35% the total force exerted on attached, escaping and free-floating passive prey. Despite initiating the strike further away, fishes can increase peak force on their prey by protruding their jaws towards it, compared with a ‘non-protruding’ state, where the distance to prey remains constant throughout the strike. The force requirements for capturing aquatic prey might have served as a selective factor for the evolution of jaw protrusion in modern fishes.

1. Introduction

Unlike the fused upper jaws of basal fish lineages and most tetrapods, the upper jaws of many higher teleost species are a flexible, kinetic musculoskeletal system, connected to the braincase by a series of joints that enable their forward protrusion during feeding (Schaeffer & Rosen 1961; Liem 1980; Lauder 1982; Motta 1984; Westneat 2006). Variation in jaw protrusion distance and speed across teleost species is a well-known axis of morphological and ecological diversification (Westneat & Wainwright 1989; Waltzek & Wainwright 2003; Westneat et al. 2005; Westneat 2006). Jaw protrusion is thought to have facilitated the trophic diversity of teleosts (Motta 1984; Albertson et al. 2003, 2005; Stiassny et al. 2004; Westneat et al. 2005) and has been recognized as a major innovation in the evolution of modern fishes (Schaeffer & Rosen 1961; Motta 1984; Westneat 2004). A complex jaw linkage is part of the highly kinetic skull that allows rapid expansion of the buccal cavity during aquatic feeding, which is coupled with the protrusion of the jaws (Lauder 1982; Muller et al. 1982; Motta 1984). The expansion of the buccal cavity is generated by dorsal rotation of the head, lateral expansion of the suspensoria and ventral rotation of the hyoid and lower jaw (Lauder 1982; Motta 1984). Complex jaw protrusion mechanisms have independently evolved multiple times in bony fishes (Motta 1984; Stiassny et al. 2004; Westneat 2004), recruiting different skull elements to push or rotate the premaxilla to its protruded state (Schaeffer & Rosen 1961; Lauder 1982; Motta 1984; Westneat 2004).

The rapid expansion of the oral cavity during suction feeding (often in less than 20 ms) causes water to accelerate into the mouth, and the resulting flow of water external to the fish's head exerts a hydrodynamic force on the prey item, drawing it towards the mouth (Lauder 1980; Liem 1980; Van Leeuwen & Muller 1984; Van Wassenbergh et al. 2006b; Wainwright & Day 2007). Unlike terrestrial predator–prey encounters, where predators have no direct effect on the prey's trajectory during the pursuit (Howland 1974; Weihs & Webb 1984), aquatic suction feeders exert force on an object that is outside their immediate reach by manipulating the water flow around it. Those forces are key to suction feeding success (Van Wassenbergh et al. 2006b; Holzman et al. 2007; Wainwright & Day 2007), countering the force exerted by an escaping or attached prey (Denny et al. 1985; Holzman et al. 2007; Wainwright & Day 2007). Therefore, understanding aquatic predator–prey interactions requires a hydrodynamic perspective.

During suction feeding, acceleration-based forces are major contributors to forces exerted on the prey (Holzman et al. 2007; Wainwright & Day 2007). Acceleration has previously been attributed exclusively to the extreme acceleration of water at the mouth aperture, caused by the rapid expansion of the oral cavity (Holzman et al. 2007; Wainwright & Day 2007), and feeding performance has previously been evaluated by measuring or estimating these accelerations and speeds at the mouth (Van Leeuwen & Muller 1984; Higham et al. 2006; Van Wassenbergh et al. 2006b). However, we suggest that jaw protrusion may increase fluid acceleration around the prey as the mouth moves quickly towards the prey. At that stage, the resultant flow speed around the prey increases more rapidly because the mouth opening, where flow is the strongest, approaches the prey (figure 1; Muller et al. 1982; Day et al. 2005; Higham et al. 2006). The rapid protrusion of the mouth towards the prey occurs in synchrony with the increasing flow at the mouth that is caused by buccal cavity expansion. Our thesis in this paper is that the forward movement of the mouth opening towards the prey (due to jaw protrusion) has the potential to increase the net fluid acceleration around the prey item, thereby increasing acceleration-based forces.

Figure 1.

(a) The effect of spatial displacement of the fish's mouth on acceleration at the prey's location. During suction feeding, fishes protrude their jaws forward, closing the distance to their prey (t₁–t₄). In a simplified case where the prey (cross) does not move and under (unrealistic) conditions of steady flow into the mouth (no acceleration; flow speed indicated by coloured scale), the forward movement of the fast-flow region near the mouth translates into an acceleration of the fluid around the prey. Here, mouth displacement speed determines the magnitude of acceleration in the prey's frame of reference, with a doubling of acceleration in a fast (8 ms) strike compared with a slower one ((b); intervals between consecutive images are 2 and 4 ms in fast and slow strikes, respectively). In a realistic strike, acceleration would also be driven by the increasing flow speed through the gape cycle. Note the rapid nonlinear decay of the flow speed along a transect moving away from the mouth (colour scale bar; Day et al. 2005).

In the context of suction feeding, jaw protrusion can therefore be treated as a mechanism to transform the spatial pattern of the flow in the frame of reference of the mouth (the decay of flow speed away from the mouth; electronic supplementary material, figure S1B) to a temporal pattern of flow in the frame of reference of the prey (the acceleration of the fluid), as the velocity profile moves across the prey (figure 1). It also follows that, all else being equal, faster jaw protrusion will result in higher acceleration in the frame of reference of the prey, because that velocity profile will move faster across the prey (‘fast’ and ‘slow’ strikes in figure 1b). That higher acceleration will increase acceleration-based forces, increasing the ‘suction’ force exerted on the prey. This mechanism of transforming anterior jaw movement to force on the prey may seem somewhat counter-intuitive, as the directions of the movement and the force are opposite. However, that apparent mismatch can be solved if one focuses on the accelerations in the frame of reference of the prey, rather than those in the frame of reference of the mouth.

Our objective in this study was to evaluate the hydrodynamic consequences of jaw protrusion in aquatic suction feeding. We hypothesized that rapid forward protrusion of the oral jaws during suction generation increases the acceleration of the fluid around the prey due to the movement of the velocity profile across the prey (figure 1), caused by the moving mouth. The added acceleration, in turn, increases the hydrodynamic forces exerted on the prey. We used force measurements to find out whether jaw protrusion speed is correlated with the force exerted on the prey, compared the force exerted on the attached prey between simulated scenarios of ‘jaw protrusion’ and ‘fixed distance’ strikes and calculated the fraction of force that can be attributed to the protruding jaws in strikes on evasive prey. We integrated observed strike kinematics of Lepomis macrochirus with results from flow visualization studies to parametrize a model of water flow around the prey (Holzman et al. 2007; Wainwright & Day 2007). Using measured and modelled forces exerted on prey, we showed that jaw protrusion speed has a major effect on suction forces and strike success during aquatic feeding on attached, escaping and free-floating passive prey.

2. Methods

2.1 Force measurements and kinematic analysis

To evaluate whether jaw protrusion speed might affect the forces exerted on the prey, we examined the correlation between feeding kinematics of bluegill, L. macrochirus, to measured forces exerted on their prey. Measurements of the force exerted on attached prey were made for n=60 strikes, using four fish (15 strikes per fish; this is an expansion of the dataset used by Holzman et al. 2007), by letting fish feed on ghost shrimp tethered to a load cell that recorded force, while simultaneously recording strike kinematics with 500 Hz video (Holzman et al. 2007). The prey, 20 mm long live ghost shrimp, were stretched out and their ventral surface was glued with a cyanoacrylate adhesive to a metal wire (0.3 mm in diameter) protruding from a load cell (Futek S-Beam Jr. load cell 1 lb, Irvine, CA, USA). The output of the load cell (voltage) was recorded at 5000 Hz on a PC running a custom LabView script through a DAQpad 6070E data acquisition system (National Instruments, Austin, TX, USA). The camera (NAC Memrecam Ci, Japan) and the load cell were synchronized using an external trigger (Holzman et al. 2007).

The magnitude of the force exerted on the prey is a function of the strike timing, and the acceleration and flow speeds at the mouth (Holzman et al. 2007) besides the hypothesized effect of jaw protrusion. We therefore examined the correlation between the jaw protrusion speed and the force exerted on the prey while controlling for variation in the magnitude of acceleration at the mouth by using a multiple regression. Thus, we separated the effects of the independent factors (effect of acceleration at the mouth and jaw protrusion speed) on the measured force. We predicted that both the speed of jaw protrusion and the magnitude of acceleration at the mouth would be positively correlated with the force exerted on the prey.

A correlation between any two variables (here, the speed of jaw protrusion and the force exerted on the prey) does not demonstrate causality. To understand the mechanical basis of the association between the speed of jaw protrusion and the force exerted on the prey, we integrated observed strike kinematics with results from flow visualization studies to estimate the flow speed and the acceleration at the location of the prey (Day et al. 2005; Holzman et al. 2007; Wainwright & Day 2007) and calculate the forces exerted on the prey (Holzman et al. 2007; Wainwright & Day 2007). This hydrodynamic framework allowed us to find out whether measured forces exerted on prey are consistent with the inferred effects of increased acceleration of water around the prey due to the advancing mouth opening provided by jaw protrusion.

Video sequences taken during prey capture strikes by bluegill, L. macrochirus, were used for kinematic analysis. For each prey capture sequence used in this study, we tracked the position of the upper and lower jaws to calculate gape size throughout the strike. Movement of a landmark on the fish's body (behind the head) was used to calculate body ram, jaw protrusion and mouth displacement speeds (the sum of body ram and jaw protrusion speeds) through the mouth-opening phase of each strike. Speeds were calculated as the maximum slope of the displacement and were only used if based on at least four consecutive measurements of mouth or body position. Only slopes spanning at least two-thirds of the mouth-opening phase and having an R²>0.9 were used (approx. 95% of the analysed strikes). For each strike, we also calculated the time to peak gape (TTPG), defined as the time taken for the fish to open its mouth from 20 to 95% of maximal gape, and evaluated the peak flow speed for the strike based on the tight fit between TTPG and peak flow speed in bluegill (Day et al. 2005). We also measured the length and the maximal height of the prey for each strike. Sequences were digitized using DLTdataviewer2 (http://www.unc.edu/%7ethedrick/software1.html), a free Matlab (MathWorks, Inc., MA, USA) toolbox for automated kinematic analysis.

2.2 Use of strike kinematics to calculate the force exerted on aquatic prey

The framework for deducing the force exerted on the prey from the fish's strike kinematics is described elsewhere (Holzman et al. 2007) and will be discussed here only in brief. First, the temporal pattern of flow at the mouth (u_m(t); table 1) was described as a continuous function using the equation (modified from Muller et al. 1982; see the electronic supplementary material, figure S1A)

$$u_{\text{m}(t)}=u_{\text{max}}{\left[\left(\frac{t-t_{\text{nul}}}{t_{\text{max}}}\right)·\text{exp}\left(\frac{t-t_{\text{nul}}}{t_{\text{max}}}\right)\right]}^{\alpha }.$$ (2.1)

The time of flow initiation (t_nul) and time of peak flow speed (t_max) were set to equal the observed time of 20 and 95% of peak gape (following Day et al. 2005) for each strike. Initial flow speed was 0, and peak flow speed u_max was estimated based on TTPG using the relationships found in Day et al. (2005; see their fig. 9) for similar-sized bluegill. The form coefficient α for the flow speed profile was equated to the observed form coefficient of the gape for each strike. Acceleration at the mouth was calculated as the instantaneous change in flow speed at the mouth (Holzman et al. 2007). Then, flow speed at the location of the prey was estimated at each time step based on the flow speed at the mouth (u_m; equation (2.1)) and the distance from the mouth aperture x′ at time t

$$u_x=f{(u_{\text{m}},x^{\prime })}_{(t)}.$$ (2.2a)

Based on prior studies (Day et al. 2005), that function can be parametrized as

$$u_x=u_{\text{m}}\times [0.348{(x^{\prime })}^4-2.49{(x^{\prime })}^3+6.61{(x^{\prime })}^2-7.78(x^{\prime })+3.56],$$ (2.2b)

where u_x is the flow speed at a distance x′ from the mouth (with distance expressed in units of gape diameters; Day et al. 2005; Holzman et al. 2007; see the electronic supplementary material, figure S1B).

Table 1.

List of symbols.

ρ	density of the medium surrounding the prey
α	form coefficient for flow speed profile
Af	frontal area of an object
Aw	wetted area of an object
Cam	coefficient of the added mass
Cd	drag coefficient
Far	force due to acceleration reaction
Fd	force due to drag
Fpg	force due to pressure gradient of fluid field
Lx	effective length of prey in the x-direction
t	time
tmax	time of peak flow speed
tnul	time of flow initiation at the mouth
u	fluid speed
um	fluid speed at the mouth aperture
umax	peak fluid speed at the mouth aperture
ux	fluid speed at a point x (outside the mouth aperture)
V	volume of the prey
x	absolute position
x′	distance in front of the mouth aperture (relative to the fish)

The speeds and the derived accelerations at the location of the prey were used, in turn, to estimate the forces exerted on the prey. To account for the differences in flow speeds along the long axis of the prey (figure 1), we integrated the forces over a series of 2 mm long bins along that axis (Holzman et al. 2007). This framework, verified by comparing the estimated forces to those measured directly (Holzman et al. 2007), was used here to calculate the total and component forces exerted on the prey (drag, pressure gradient force and acceleration reaction; Batchelor 1967; Wainwright & Day 2007) using observed strike kinematics and measured prey size.

Pressure gradient force (F_pg) was calculated from the temporal and spatial gradients of velocity (local and convective accelerations, respectively; Batchelor 1967) and prey dimensions using the momentum equation (Batchelor 1967; Wainwright & Day 2007), so that

$$F_{\text{pg}}=-\rho ·{\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+u\frac{\mathrm{\partial }u}{\mathrm{\partial }x}\right)}_p·L_x·A_{\text{f}},$$ (2.3)

where ρ is the density of the surrounding medium (kg m⁻³); L_x is the effective dimension of the prey in the x-direction (m); and A_f is the frontal area of the prey (m²).

Local acceleration (∂u/∂t) is defined as the rate of change of flow velocity at a given point in space (the prey, p, in this case) with time t (Batchelor 1967). Local acceleration was calculated at 0.0003 s increments, based on the temporal pattern of flow at the fish's mouth (equation (2.1)), the rate of decreasing flow with distance from the mouth and the distance between the mouth and the location of the prey (equations (2.2a) and (2.2b)), so that

$${\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }t}\right)}_p=\frac{f{(u_{\text{m}},x^{\prime })}_{(t_2)}-f{(u_{\text{m}},x^{\prime })}_{(t_1)}}{t_2-t_1},$$ (2.4)

with equation (2.2b) used to parametrize f(u_m, x′)_(t) (see above).

Convective acceleration u(∂u/∂x) is defined as the rate of spatial change in the flow speed at the prey u along the flow's main axis x (perpendicular to the gape; Batchelor 1967) and was calculated at 0.1 mm increments (Δx), so that

$${\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }x}\right)}_p=\frac{f{(u_{\text{m}},(x^{\prime }-\mathrm{\Delta }x))}_{(t_1)}-f{(u_{\text{m}},(x^{\prime }+\mathrm{\Delta }x))}_{(t_1)}}{2\mathrm{\Delta }x},$$ (2.5)

with equation (2.2b) used to parametrize f(u_m, x′)_(t).

Similarly, acceleration reaction force (F_ar) depends on the sum of local and convective accelerations at the prey, the volume of the prey V (m³), the density of the surrounding water ρ and the coefficient of added mass C_am:

$$F_{\text{ar}}=C_{\text{am}}·V·\rho ·{\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+u\frac{\mathrm{\partial }u}{\mathrm{\partial }x}\right)}_p.$$ (2.6)

Finally, drag was calculated using the prey's drag coefficient (C_d), wetted area (A_w), the density of the surrounding medium and the flow speed (u_x) squared,

$$F_{\text{d}}=0.5·C_{\text{d}}{A}_{\text{w}}\rho {(u_x)}^2.$$ (2.7)

Prey volume, length and diameter were obtained for each sequence from our video records, while drag and added-mass coefficients were measured or estimated for our prey (Holzman et al. 2007).

2.3 Contribution of jaw protrusion to the forces exerted on attached prey

To test the effect of jaw protrusion on forces exerted on attached prey, we calculated the peak force exerted on the prey based on strike kinematics in two simulated scenarios, one where the distance between the mouth and the prey was fixed at a distance of 0.1 mm throughout the strike, and the second where forward displacement of the mouth (i.e. jaw protrusion) took place. The latter jaw protrusion scenario used observed kinematics of a bluegill while the fixed distance scenario simulates a hypothetical fish that cannot protrude its jaws but positions its mouth as close as possible to its prey in order to exert the maximal force on it. In the fixed distance strikes, peak force was calculated using the observed kinematics for gape, but with no mouth displacement throughout the strike, resulting in a fixed prey–mouth distance of 0.1 mm. In jaw protrusion strikes, we used observed gape and mouth displacement kinematics to calculate the force as the mouth was moved towards the prey from afar to a distance of 0.1 mm from the prey (figure 2). The short distance of 0.1 mm was chosen to match the observed patterns in bluegill, where strikes on attached prey end with the prey's head inside the fish's mouth. In these strikes, we varied the timing of jaw protrusion for each strike to find the timing that maximized the force at the distance of 0.1 mm from the mouth. This is because in the fixed distance case peak acceleration of the fluid in the mouth will always occur very close to the prey (at the distance of 0.1 mm), while in the jaw protrusion case it could have occurred when the mouth was further from the prey, thus adding a confounding ‘timing’ effect to the comparison. Therefore, our results report the maximal contribution of jaw protrusion to the force on the prey. This analysis is a pairwise comparison of the force exerted on the prey between two scenarios with identical gape kinematics and flow speeds, both with ‘perfect’ timing of the strike. However, in the fixed distance scenario, the acceleration in the frame of reference of the prey was entirely due to the acceleration of water at the mouth due to buccal cavity expansion (figure 2a,b), whereas in jaw protrusion strikes, acceleration at the prey was due to the acceleration of fluid at the mouth in addition to the movement of the velocity profile across the prey due to the protruding jaws. Calculations of the force exerted on the prey in each scenario were made for n=60 strikes, using the observed kinematics of each strike recorded for four fish (15 strikes per fish).

Figure 2.

Representative time series of the flows, accelerations and the forces experienced by attached prey in two scenarios, ‘fixed distance’ and ‘jaw protrusion’. (a) The flow field in front of the mouth of a suction feeding fish, along with flow speeds experienced by attached prey. Throughout the strike, flow speed at the mouth (distance 0) increases, due to buccal expansion, and then decreases (see also the electronic supplementary material, figure S1A). Elsewhere, flow speeds are a function of flow speed at the mouth and the scaled distance to the mouth (see equations (2.2a) and (2.2b)). If the prey is located at a fixed distance from the mouth (0.1 mm; black line), changes in flow speed in the frame of reference of the prey are solely a function of changes in speed at the mouth aperture (along the ‘time’ axis; red and black lines in (b)). However, if the strike starts from further away and the distance between the prey and the predator is closed rapidly due to jaw protrusion (green line representing mouth trajectory), changes in speed in the frame of reference of the prey are due to the changes in flow speed at the mouth (along the time axis) as well as the change in distance to the mouth (along the ‘distance’ axis). In this case, acceleration in the frame of reference of the prey is faster and more abrupt (green line in (b)). The flow field in front of the mouth is identical for the paired scenarios (as is the acceleration at the mouth; red line in (b)) that differ only in the trajectory of the mouth (green and black lines in (a)). (b) The difference in acceleration in the frame of reference of the prey (green line, ‘jaw protrusion’; black line, ‘fixed distance’; red line, ‘at the mouth’) translates to (c) a higher peak force exerted on the prey. Note the identical acceleration and forces when the jaws have stopped protruding (time above 0.036 in (b,c)).

2.4 Contribution of jaw protrusion to the forces exerted on evasive prey

Fishes often encounter prey that try to escape the approaching predator, rather than cling to their holdfast. In this scenario, direct measurements of the force exerted on the swimming prey are not possible. However, we could still use strike kinematics to estimate the flow speed and the acceleration at the location of the prey (Day et al. 2005; Holzman et al. 2007) and estimate the forces exerted on the prey (Holzman et al. 2007; see below). In the case of evasive prey, the protruding mouth can contribute to strike success by closing the distance between the predator and the prey, in addition to accelerating the water near the prey. Therefore, a comparison with a ‘fixed distance kinematics’ would be confounded for escaping prey. Instead, we quantified the effect of jaw protrusion on the force exerted on escaping prey using only the observed kinematics, where the jaws are protruded to close the distance on the prey, while accounting for the effect of protrusion on the force exerted on the prey. First, we calculated the total force exerted on the prey (‘full kinematic model’). Then, we removed the effect of jaw protrusion by calculating local acceleration as a result of only the acceleration at the mouth such that the distance x′ did not change between t₂ and t₁ (‘partial kinematic model’). This was done by substituting equation (2.4) with the following:

$${\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }t}\right)}_p=\frac{f(u_{\text{m}(t_2)},{x^{\prime }}_{(t_1)})-f{(u_{\text{m}},x^{\prime })}_{(t_1)}}{t_2-t_1}.$$ (2.8)

After calculating local acceleration, the mouth was allowed to advance towards the prey following its observed kinematics (shortening that distance x′ at the next time step) and the calculation was repeated (see the electronic supplementary material, figure S2). For each strike, we recorded the peak force and the outcome of the strike (prey escape/capture). We then compared peak force and accelerations in the partial kinematic model to those obtained from the full kinematic model, where local acceleration was calculated using equation (2.4) (see the electronic supplementary material, figure S2). This way, we compared prey capture with and without the forces that are due to protrusion, with the exact same mouth kinematics. The force exerted on the prey, however, was different and the resulting trajectory of the prey (see below) was therefore different, too.

For these simulations, we used observed strike kinematics of four individual fish striking on live tethered shrimps (n=10 strikes per fish). In this set-up, the shrimps were hanging from a thin metal wire inserted under their carapace (as in Day et al. 2005). The shrimps were relatively mobile, and in many cases escaped the striking fish despite the tether. However, the tether applied a force of unknown magnitude on the prey. Therefore, we used simulated kinematics of escaping prey, which accelerated with a known force away from the fish (perpendicular to the gape). The prey's path was recalculated at each time step (as in Wainwright & Day 2007), by solving the equilibrium of forces on the prey and calculating prey displacement via Newton's second law.

Prey that escape using a flip-tail motion generate a pulse of force, accelerating the prey away from the predator (Nauen & Shadwick 1999, 2001). Owing to the scarcity of data on escape force exerted by the prey organisms encountered by bluegill, we initially simulated the prey in each sequence with an escape force of 2.5×10⁻², expected for our 20 mm shrimp based on the scaling of escape forces in shrimp (Nauen & Shadwick 2001). However, the outcome of these simulations was a 100% escape of the prey. Therefore, we varied the force exerted by the prey from 10⁻³ (resulting in prey capture in less than 5% of the strikes), to 10⁻⁵ N (prey capture in 95% of the strikes). For the purpose of this paper, we used a constant escape force, 2×10⁻⁵ N, simulating a much less efficient prey than our shrimps. That force resulted in a capture rate of approximately 75%, enabling us to investigate the effect of jaw protrusion in successful strikes, but with the prey still exerting force that challenges the fish. Free-floating passive prey were simulated as prey exerting an escape force of 0 N. The temporal profile of the prey's escape force was taken from force measurements for shrimps (R. Holzman 2007, unpublished data; similar to Nauen & Shadwick 2001) and the timing of peak force was equated to that of peak gape. Simulations ended when the prey entered the mouth (prey capture) or when the mouth was closed with the prey outside the mouth (prey escape).

2.5 Statistical analysis

Because fish used in our experiments (two separate groups of four bluegill for attached and evasive prey simulations, respectively) were measured multiple times, the strikes of each fish were not independent. To test the effect of jaw protrusion on the force exerted on attached prey, we used repeated measures ANOVA with scenario as categorical predictor (two levels: fixed distance versus jaw protrusion), strike order as repeated measures factors (15 levels) and the peak calculated force as dependent variable. A similar analysis was conducted to test the effect of jaw protrusion on the force exerted on evasive prey, where repeated measures ANOVA was used with scenario as categorical predictor (two levels: full kinematic model versus partial kinematic model), strike order as repeated measures factors (10 levels) and the peak calculated force as dependent variable. The latter analysis was done only for sequences where partial kinematic model simulations ended with the fish overtaking its prey.

To test the correspondence between jaw protrusion speed and the force exerted on the prey, we used a mixed model approach (following Pinheiro & Bates 2000). In essence, these models enable a regression-like analysis, while accounting for the dependent errors due to repeated measurements on individuals. This framework was used to assess the effect of jaw protrusion speed (independent variable) on the added force or the added local acceleration (dependent variable), defined as the difference in peak force (or local acceleration, respectively) between the jaw protrusion and fixed distance models. A similar analysis was performed to assess the combined effects of acceleration at the mouth and jaw protrusion speed (two independent variables) on the forces exerted on attached prey (dependent variable). In both types of analyses, individual fish were included as random factor.

To ensure that the above statistical models accounted for the correlation structure among the dependent samples, we built for each of the analyses a series of mixed-effects models with increasing complexity and then selected the best model based on AIC score and a likelihood ratio test (Pinheiro & Bates 2000; Johnson & Omland 2004). The basic model included fishes as random factor, while more complex models included a correlation structure in observation order, autocorrelated error and an error correlated with the independent variable. However, in all analyses these models did not provide additional explanatory power, and only results from the basic models are discussed here. In analyses where significant effects were found, we calculated the coefficient of determination R² based on the log-likelihood results of the model using the equation (Magee 1990)

$$R^2=1-\text{exp}\left(-\frac{2}{n}(\text{log}{L}_{\text{m}}-\text{log}{L}_0)\right),$$ (2.9)

where n is the number of observations; log L_m is the log likelihood of the model of interest; and log L₀ is that of an intercept-only model (Magee 1990).

Mixed-effects models were constructed and run using the ‘nlme’ library in the free software R statistics (v. 2.5.0; http://www.r-project.org), after verifying normal distribution of residuals. Repeated measures analysis was done with Statistica (v. 6.0, STATSOFT, Tulsa, OK, USA) after verifying the sphericity assumption. All p-values reported are for two-tailed tests.

3. Results

3.1 Effects of jaw protrusion speed on forces measured on attached prey

To evaluate whether jaw protrusion speed affects the forces exerted on the prey, we examined the correlation between the measured forces exerted on attached prey and the feeding kinematics of bluegill, L. macrochirus (table 2). After controlling for acceleration at the mouth (by using a multiple regression model), the observed speed of jaw protrusion was positively correlated with the peak measured force on the prey (mixed-effects model, whole model R²=0.60; F_1,3=24.7, p=0.003 for jaw protrusion and F_1,3=79.3, p<0.001 for acceleration at the mouth; figure 3a). Similarly, after controlling for the effect of acceleration at the mouth, observed jaw protrusion speed was positively correlated with peak local acceleration (mixed-effects model, whole model R²=0.69; F_1,3=18.6, p<0.01 for jaw protrusion and F_1,3=103.7, p<0.001 for acceleration at the mouth; figure 3b). No such correlation was observed with the magnitude of peak convective acceleration (mixed-effects model, whole model R²=0.41; F_1,3=55.3, p<0.001 for acceleration at the mouth and F_1,3=0.04, p>0.8 for jaw protrusion). These patterns indicate that, independent of acceleration at the mouth, faster jaw protrusion is associated with higher suction forces exerted on the prey, due to increased local accelerations.

Table 2.

Effect of jaw protrusion on forces exerted on attached, evasive and free-floating passive prey.

prey	data	major finding	statistics
attached	measured force	positive correlation between jaw protrusion speed and force	mixed-effects model, R2=0.6, p=0.003	after controlling for acceleration at the mouth
attached	simulation: ‘jaw protrusion’ and ‘fixed distance’ kinematics	force with ‘jaw protrusion’ higher by 32%	repeated measures ANOVA, p<0.002
free-floating	calculation: contribution of protrusion to the force exerted on the prey	force with ‘full kinematic model’ higher by 30%	repeated measures ANOVA, p<0.01	based on observed strike kinematics of bluegill and simulated prey
evasive	calculation: contribution of protrusion to the force exerted on the prey	force with ‘full kinematic model’ higher by 35%	repeated measures ANOVA, p<0.001	based on observed strike kinematics of bluegill and simulated prey
evasive	simulation: contribution of protrusion to strike success	strike success in ‘full kinematic model’ increased by 15%		based on observed strike kinematics of bluegill and simulated prey

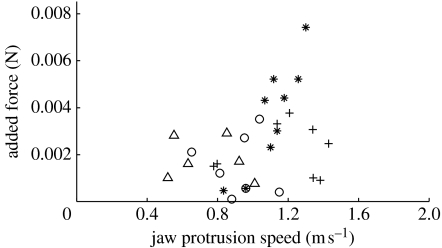
Figure 3.

Effects of jaw protrusion on force and local acceleration for attached prey of L. macrochirus. (a) The contribution of jaw protrusion speed to the observed force on attached prey. Data are residuals of the regression between acceleration at the mouth and observed force, performed to remove the effect of variation in strike effort. The added force was significantly correlated with jaw protrusion speed (mixed-effects model, whole model R²=0.60; F_1,54=24.7, p=0.003 for jaw protrusion and F_1,54=79.3, p<0.001 for acceleration at the mouth). (b) The contribution of jaw protrusion speed to peak local acceleration, calculated based on the observed kinematics. Data are residuals of the regression between acceleration at the mouth and local acceleration (defined as the temporal change of flow at a given point in space; equation (2.4)). The added local acceleration was significantly correlated with jaw protrusion speed (mixed-effects model, whole model R²=0.69; F_1,54=18.6, p<0.01 for jaw protrusion and F_1,54=103.7, p<0.001 for acceleration at the mouth). Local acceleration is a major component of the total acceleration of water around the prey (composed of local and convective acceleration; see text for details) and is positively correlated with the force exerted on the prey. Symbols represent different fish (N=4 fish, 15 strikes each).

3.2 Effects of jaw protrusion speed on forces simulated for attached prey

To quantify the contribution of jaw protrusion speed to the force exerted on attached prey, we used strike kinematics of bluegill feeding on tethered prey and calculated the force exerted during two simulated feeding scenarios (table 2). In the first scenario (fixed distance), we calculated the force when the fish's mouth was held at a constant distance of 0.1 mm from the prey, so that (unlike the observed kinematics) no protrusion occurred, while in the second (jaw protrusion) the jaws were protruded from afar to a distance of 0.1 mm from the prey, with the timing of jaw protrusion (relative to gape) that resulted in maximal contribution to force. The peak force exerted on prey in the jaw protrusion scenario was 32.6% (±s.e.=1.9%) higher than that calculated for the fixed distance strikes (repeated measures ANOVA, F_2,12=12.2, p=0.0013; see figure 2a–c for a representative strike). The magnitude of the added force (defined as peak force exerted in the jaw protrusion scenario minus peak force on the prey in the fixed distance scenario) was positively correlated with jaw protrusion speed (mixed-effects model; R²=0.46, F_1,3=14.1, p<0.005; figure 4a). We attribute the difference in force to the enhancement of peak local acceleration in the jaw protrusion scenario, as indicated by the positive correlation between observed jaw protrusion speed and the absolute change in the magnitude of peak local acceleration (mixed-effects model; R²=0.62, F_1,3=27.8, p<0.001; figure 4b). There was no difference in the magnitude of peak convective acceleration for the two scenarios (average difference±s.e. was 2.4±5.75 ms⁻², corresponding to less than 1% of average local acceleration; median difference=0).

Figure 4.

Effects of jaw protrusion speed on force and local acceleration for simulated attached prey of L. macrochirus. (a) The added force (defined as the difference in peak force exerted on the prey between ‘fixed distance’ and ‘jaw protrusion’ scenarios) was significantly correlated with mouth displacement speed (mixed-effects model; R²=0.46, F_1,55=14.1, p<0.005). That added force is a result of (b) an increased local acceleration, indicated by a significant correlation between the added local acceleration and the mouth displacement speed (mixed-effects model; R²=0.62, F_1,55=27.8, p<0.001). There was no correlation between jaw protrusion speed and convective acceleration (data not shown). Acceleration of the fluid around the prey in the ‘fixed distance’ scenario is due to the acceleration at the mouth, while in the ‘jaw protrusion’ scenario it is due to the acceleration at the mouth augmented by the rapid forward protrusion of the jaws. Symbols represent different fish (N=4 fish, 15 strikes each).

3.3 Effects of jaw protrusion speed on forces exerted on evasive prey

Fishes commonly encounter prey that try to elude the attacking predator, rather than cling to their holdfast. With the prey swimming away from the fish, the forward movement of the mouth is important in closing the distance to the prey, and also in augmenting the force exerted on the prey. We quantified the effect of jaw protrusion on the force exerted on the prey by calculating local acceleration as a result of only the acceleration at the mouth, and found out what is the magnitude of the force compared with that calculated in the full model (electronic supplementary material, figure S2; table 2). In these simulated strikes, parametrized with the observed strike kinematics of bluegill, the contribution of the forward movement of the jaw to the force on the prey was significant (repeated measures ANOVA, F_2,7=22.5, p<0.001; see figure 5a for a representative strike), increasing the force by 35.2% (±s.e.=15.5) compared with the partial kinematic model. That added force, in turn, increased strike success (defined as the number of sequences ending in prey capture) from 30 to 35 (out of 40 strikes) and reduced the time to capture prey by 12% of strike time, on average (±s.e.=2.1; calculated as the difference in time to capture between the two models divided by the TTPG). Similar to the attached prey scenario, there was a positive correlation between the magnitude of the added force and the speed of jaw protrusion (mixed-effects model; R²=0.26, F_1,3=4.7, p<0.05; figure 6) in sequences that ended in prey capture.

Figure 5.

Representative time series of the force exerted on evasive and free-floating passive prey from ‘full kinematic model’ (blue line) and ‘partial kinematic model’ (red line). Here, we compare the gross forces exerted on the prey in sequences with identical jaw kinematics (including protrusion). However, in the ‘partial kinematic model’, the forces that are due to the forward movement of the jaw during the strike are removed. That difference in force affects the trajectory of the prey. Gross force is defined as the sum of the opposing prey's escape force and fish's suction force. (a) Force tracks for escaping prey in the two scenarios. The prey was modelled to escape away from the fish, while exerting a force of 2×10⁻⁵ N. (b) Force tracks for free-floating passive prey for the two scenarios. The prey was modelled to exert 0 N of escape force. Simulations (and force tracks) end when the prey enters the mouth.

Figure 6.

Effects of mouth displacement speed on the force exerted on evasive prey of L. macrochirus. The added force (defined as the difference in peak force exerted on the prey between the ‘full kinematic model’ and ‘partial kinematic model’ scenarios) was significantly correlated with mouth displacement speed (mixed-effects model; R²=0.26, F_1,3=4.7, p<0.05). Symbols represent different fish (N=4 fish, 10 strikes each). Data are only for strikes that ended in prey capture (approx. 75% of strikes).

Similar increase in the force is observed if the prey does not try to evade the fish (escape force is set to 0; increase of 30.3%±s.e.=17.6; repeated measures ANOVA, p<0.01; see figure 5b for a representative strike). Here, however, jaw protrusion reduced the time to capture the prey by only 6% (±s.e.=2.2) of the strike time, and there was no correlation between the magnitude of the added force and the speed of jaw protrusion (mixed-effects model; F_1,3=0.9, p>0.3). This lack of correlation is perhaps due to variations in local accelerations, introduced by the different paths of the prey in the full and partial kinematic models.

4. Discussion

In this paper, we put forward and tested a novel hypothesis for the hydrodynamic effects of jaw protrusion during aquatic suction feeding. Our results indicate that jaw protrusion provides an independent source of acceleration from that induced by the unsteady flow at the mouth aperture, increasing by up to approximately 35% the total force exerted on attached, escaping and free-floating passive prey. The mechanism of augmenting the acceleration of the water around the prey by rapidly moving the source of the flow closer to the prey via jaw protrusion (figures 1 and 2) is a previously unrecognized mechanism for generating and enhancing the forces exerted on the prey in aquatic suction feeding. The force requirements for prey capture were potentially a strong selective factor during the repeated evolution of jaw protrusion in modern fishes, including the evolution of species with extreme jaw protrusion (Westneat & Wainwright 1989; Waltzek & Wainwright 2003; Westneat et al. 2005) or of species that specialize in feeding on evasive prey (Westneat 1995; Higham et al. 2007).

The peak force exerted on attached prey in the jaw protrusion scenario was 32.6% higher than that calculated for fixed distance strikes. The force is augmented due to the increase in local acceleration that is associated with faster jaw protrusion speed (figures 3 and 4), while no difference in the magnitude of convective acceleration was evident. Thus, for the same acceleration at the mouth, the acceleration in the frame of reference of the prey was significantly increased by the rapid anterior jaw movement, resulting in an increased force in an opposite direction. Note that this substantial difference in the force exists despite identical flow speed and accelerations at the mouth, with the only difference being the mouth's trajectory. Thus, jaw protrusion contributes to the success of the strike even for prey that do not attempt to evade the predator, because the enhanced force on the prey increases the probability of detaching it (Denny et al. 1985). In the case of evasive prey, jaw protrusion similarly enhanced the force exerted on the prey (by approx. 35%). The added force, in turn, increased capture success and reduced the time until prey capture. Note again that this substantial difference in force and strike success exists despite identical flow speed and accelerations at the mouth, and the same mouth trajectory.

Strike timing has a critical effect on the force exerted on the prey (Holzman et al. 2007). High flows and accelerations exist only near the mouth (less than 1 mouth diameter away) and persist for a very short time (less than 10 ms; Ferry-Graham et al. 2003; Day et al. 2005; Higham et al. 2006). Therefore, fishes have to accurately coordinate their strike to position the prey near the mouth at the right time (Holzman et al. 2007). Similarly, jaw protrusion has to be coordinated with the temporal pattern of flow in front of the mouth to maximally augment the force exerted on its prey. To illustrate this point, we calculated the force exerted on the prey in a series of strikes with the same gape kinematics, flow speeds and jaw protrusion speeds, but with various timings of peak jaw protrusion relative to peak gape (figure 7). If jaw protrusion occurs before suction begins (so that the jaws are fully protruded when the mouth starts opening), it will contribute very little to the force on the prey, because the velocity profile will not be moved relative to the prey (time −0.013 to 0.003 in figure 7b). Conversely, if jaw protrusion occurs after peak flow speed, then the prey reaches the optimal position near the mouth after peak acceleration has already occurred (time above 0.016 in figure 7b), reducing the peak force. A coordinated strike, however, will increase the peak force on the prey (time 0.006–0.016 in figure 7b). Indeed, the average time of peak jaw protrusion observed for bluegill (relative to peak gape; dashed line in figure 7b) falls within the time frame enabling a contribution of the advancing jaws to the force exerted on the prey. Concomitantly, jaw protrusion increased the force by 17%±2.3 under the observed timing for bluegill, compared with a fixed distance state. An enhancement of the force was observed in 58% of the 60 sequences, with a decrease in force observed only once. This result indicates that bluegill synchronize their strikes to augment the force by jaw protrusion.

Figure 7.

Effect of the relative timing of peak gape and jaw protrusion on the force exerted on attached prey. (a) The force exerted on attached prey in a series of strikes with the same gape kinematics, flow speeds and jaw protrusion speeds, but with various timings of peak jaw protrusion relative to peak gape (time of peak protrusion). (b) Peak force varies due to the relative timing of peak gape and jaw protrusion. If jaw protrusion occurs before suction begins (so that the jaws are fully protruded when the mouth starts opening), jaw protrusion will contribute very little to the force on the prey because the velocity profile will not be moved relative to the prey (peak protrusion at −0.013 to +0.003 s relative to peak gape). Conversely, if jaw protrusion occurs after peak flow speed, then the prey reaches the optimal position near the mouth after peak acceleration has occurred (peak protrusion greater than 0.016 s after peak gape), reducing the effective force on the prey. However, if gape cycle is properly synchronized with protrusion (grey area), the force exerted on the prey is increased. The average time of peak jaw protrusion in bluegill (relative to peak gape; 0.011 s) is indicated as a vertical dashed line in (b). Data in (b) are the relative peak force, compared to ‘fixed distance’ simulation.

Jaw protrusion increases the force exerted on the prey via its effect on acceleration in the frame of reference on the prey, by increasing acceleration-based forces. As the prey size (and Reynolds numbers) decreases, acceleration-based forces become less dominant and drag (which scales with flow speed squared; equation (2.7)) becomes more important (Wainwright & Day 2007). Moreover, acceleration-based forces scale with prey volume, while drag scales with the wetted area of the prey. Hence, jaw protrusion should become less important for small prey, with the relative magnitude of the effect depending on prey characteristics (drag and added-mass coefficient). To test this prediction, we calculated the contribution of jaw protrusion in a representative strike as a function of prey volume (figure 8), with our shrimp scaled isometrically from 0.03 to 250 mm³. The contribution of jaw protrusion to the force was similar (approx. 27%) across most prey sizes under the observed parameters, but dropped sharply at prey size under 2 mm³ (corresponding to less than 4 mm long shrimp-shaped prey; figure 8).

Figure 8.

Effect of prey size on the contribution of jaw protrusion (JP) to the force exerted on attached prey. The contribution of jaw protrusion was defined as the difference between the force exerted on the prey in the ‘jaw protrusion’ case, relative to the force in the ‘fixed distance’ case. The prey was scaled isometrically. The contribution of jaw protrusion to the force was similar (approx. 27%) across most prey sizes under the observed parameters, but dropped sharply at prey size under 2 mm³.

In this paper we assume that the decay of flow speed away from the mouth (equations (2.2a) and (2.2b)) is invariant with jaw protrusion speed. These profiles are based on particle image velocimetry (PIV) work with bluegill that protruded their jaws during the experiments (Day et al. 2005). However, these profiles are in good agreement with those expected based on theory (Muller et al. 1982) calculated for a passive flow into the mouth for a stagnant fish, validating our assumption. However, the magnitude of augmented force due to jaw protrusion may change if evidence is found that the shape of the profiles changes due to protrusion.

Jaw protrusion is not the only mechanism by which forces exerted on the prey can be augmented. In fact, any behaviour that will rapidly shorten the distance between the prey and the predator while suction is being produced might have similar effects on the force exerted on the prey. Such behaviours include forward swimming (ram), fast cranial elevation (Van Wassenbergh et al. 2008) or feeding on prey that is drifting in a current towards the predator, as done by many site-attached coral reef planktivores (Coughlin & Strickler 1990; Westneat 2006). These behaviours are not mutually exclusive to jaw protrusion (at least mechanically) and would have an additive effect on the force and the capture success. This is especially true with the incorporation of body ram, sometimes critical in overtaking evasive prey (Wainwright & Day 2007) as even fishes that are considered ‘ram feeders’ can generate strong suction flows (Higham et al. 2006). However, the evolution of jaw protrusion in acanthomorph fishes was probably under strong selection resulting from the force requirements in catching prey, as jaw protrusion in these fishes is usually mechanically linked to buccal expansion, possibly providing the coordination mechanism needed to augment the force beyond that achieved without protrusion (figure 7b). Moreover, the magnitude of increased force depends also on the speed of jaw protrusion (figures 3 and 4), and jaw protrusion can attain very high speeds (Lauder 1982; Motta 1984; Van Leeuwen & Muller 1984; Osse 1985) that allow significant augmentation of forces on the prey. It is probable that the rapid head rotation during feeding in pipefishes (Van Wassenbergh et al. 2008) also augments the forces these fishes exert on their prey.

Fish species differ in the flow speeds and accelerations they produce at their mouth, and thus differ in the force they exert on their prey. Evolution of suction-related morphology and physiology in centrarchid fishes resulted in significant variation in their ability to produce suction pressure and flows (Carroll et al. 2004; Collar & Wainwright 2006; Higham et al. 2006; Wainwright et al. 2007). It would be interesting to examine the coevolution of the morphological potential for suction production (Carroll et al. 2004; Collar & Wainwright 2006), and the evolution of jaw protrusion speed in this group to learn whether the two evolved as dependent or independent mechanisms of suction enhancement.

In our simulations of the evasive prey, bluegill were unsuccessful in capturing prey that were parametrized with realistic force exerted by a shrimp (Nauen & Shadwick 2001). It might be that a more favourable timing of escape relative to that of the strike (that was fixed at an arbitrary point in our simulations) would have resulted in a higher capture rate, but escape timing could also improve prey escape. However, our simulations reflect the natural state, where shrimp and other highly evasive prey are rare in bluegill's diet (Huish 1957; Flemer & Woolcott 1966; Sadzikowski & Wallace 1976; VanderKooy et al. 2000). With proper parametrization of the fish's and prey's performance, our force model now provides a quantitative tool to study mechanistic aspects of predator–prey interactions such as the force requirements of capturing prey of different escape strategies and sizes and the importance of ram feeding in capturing evasive prey.

Several hypotheses for the selective advantage of jaw protrusion have been previously proposed (Lauder 1982; Motta 1984; Van Leeuwen & Muller 1984; Coughlin & Strickler 1990), related either to the increase in speed of closing on the prey due to protrusion (Lauder 1982; Motta 1984; Van Leeuwen & Muller 1984; Osse 1985) or explained in the context of specific feeding scenarios, such as feeding from a substratum, or in a spatially complex habitat (Lauder 1982; Motta 1984). Here we show a mechanistic ubiquitous function of jaw protrusion that is based on the effect it has on the water flow experienced by prey. The added force exerted on prey items due to protrusion indicates that this innovation has a significant positive effect on fish-feeding performance. The force requirements for capturing aquatic prey are emerging as a rewarding framework for understanding unexpected sources of variation in aquatic feeding performance (Holzman et al. 2007; Wainwright & Day 2007; Wainwright et al. 2007).

Comparative studies of suction performance have focused on strike kinematics (Wainwright et al. 2001; Gibb & Ferry-Graham 2005), the ability to produce low buccal pressure (Carroll et al. 2004; Van Wassenbergh et al. 2006a) and recently the flow of water produced external to the mouth (Higham et al. 2006; Nauwelaerts et al. 2007) as performance metrics. While being informative, these metrics fall short of capturing the predator's ability to perform during aquatic predator–prey interactions. By treating an aquatic predator–prey interaction as a hydrodynamic interaction between fluid and solid in an unsteady flow, we were able to understand the adaptive value of jaw protrusion in the context of aquatic suction feeding. This framework can now be used to more accurately predict suction performance based on kinematic and morphological data, and can be extended to study the coevolution of aquatic predators and prey.

Supplementary Material

Figure S1

Representative time series of the flow at the mouth aperture of a suction feeding fish, and a graphical representation of the decay of flow speed as a function of distance from the mouth

Figure S2

Workflow for escaping prey simulations made with the ‘full kinematic model’ and ‘partial kinematic model’.