The effect of opinion clustering on disease outbreaks

Abstract

Many high-income countries currently experience large outbreaks of vaccine-preventable diseases such as measles despite the availability of highly effective vaccines. This phenomenon lacks an explanation in countries where vaccination rates are rising on an already high level. Here, we build on the growing evidence that belief systems, rather than access to vaccines, are the primary barrier to vaccination in high-income countries, and show how a simple opinion formation process can lead to clusters of unvaccinated individuals, leading to a dramatic increase in disease outbreak probability. In particular, the effect of clustering on outbreak probabilities is strongest when the vaccination coverage is close to the level required to provide herd immunity under the assumption of random mixing. Our results based on computer simulations suggest that the current estimates of vaccination coverage necessary to avoid outbreaks of vaccine-preventable diseases might be too low.

1. Introduction

Infectious diseases such as measles pose a constant threat to the public health worldwide. Measles, a highly contagious disease caused by a virus, is a potentially dangerous infection and a leading cause of vaccine-preventable childhood mortality (Measles. Mortality reduction and regional elimination. WHO, http://www.who.int/vaccines-documents/DocsPDF01/www573.pdf). In many parts of the world, the incidence of measles has declined dramatically since the introduction of vaccination. The wide use of a combined measles, mumps and rubella vaccine since the 1970s has led to high measles vaccination coverage in high-income countries. In the USA, for example, measles was declared eliminated in 2000, an achievement attributed to herd immunity (Anderson & May 1991) resulting from a continued high national vaccination coverage (Anderson & May 1991; Katz & Hinman 2000).

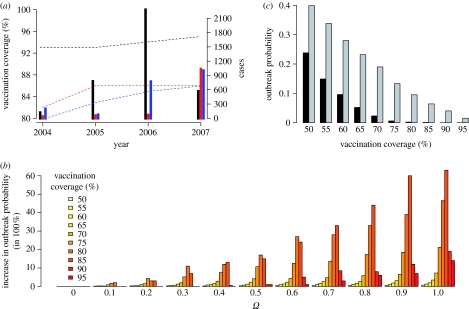
Despite high vaccination coverage, however, many countries continue to experience relatively large measles outbreaks. The general explanation for an increased frequency of such outbreaks in a given time period is that vaccination uptake has declined simultaneously. In England and Wales, for example, the drop in vaccination coverage has coincided with the number of large measles outbreaks a number of years ago (Jansen et al. 2003). However, such an explanation cannot explain the currently observed patterns: Switzerland, for example, where vaccination coverage has steadily increased since 2000, currently experiences the largest measles outbreak since the introduction of mandatory notification for the disease in 1999 (Richard et al. 2008), with more than 2800 reported cases since the beginning of the endemic in late 2006. In 2007, England and Wales reported the highest number of measles cases since surveillance began in 1995 (Heathcock & Watts 2008). Similar patterns are observed in other countries (figure 1a).

Figure 1.

(a) Vaccination coverage and measles prevalence. Data are from Switzerland (red), Germany (black) the UK (blue). The dashed lines show the vaccination coverage and the bars show the number of reported cases in each year. (b) Increase in outbreak probability. Each bar of a given colour (i.e. vaccination coverage) represents the increase in outbreak probability relative to the lowest non-zero outbreak probability at this vaccination coverage. The parameter Ω measures the strength of opinion formation: the probability that an individual swaps opinion is given by the frequency of neighbouring individuals who hold the opposite opinion, weighted by Ω, i.e. Ω=0 indicates that no opinion formation occurs. The data given are based on 220 000 simulations of networks of 2000 nodes, and an outbreak was registered when the initial infection led to at least 10 follow-up infections (for a detailed description of the model see §2.2). For each value of Ω, we tested 11 different levels of vaccination coverage from 0.5 to 0.95. (c) Effect of opinion formation on herd immunity. Outbreak probabilities without opinion formation (black bars, Ω=0) and with opinion formation (grey bars, Ω=1).

An alternative explanation for an increased incidence of outbreaks is that the vaccination coverage, even though it may be rising, is getting more heterogeneous. If an unvaccinated individual is more likely to be in contact with other unvaccinated individuals than would be expected by chance, clusters of susceptible individuals will form and thus constitute a subpopulation in which the disease can spread and cause local outbreaks. Such susceptibility clusters have been observed in the USA (May & Silverman 2003; Parker et al. 2006) and are thought to play a major role in the current outbreaks in Europe (Richard et al. 2008; Schmid et al. 2008).

There is growing evidence that belief systems, rather than access to vaccines, are the primary barrier to vaccination in high-income countries (May & Silverman 2003; Parker et al. 2006; Richard et al. 2008). Vaccination exemption may have many causes such as beliefs about the safety and usefulness of vaccines, religious beliefs, philosophical considerations, etc. However, even though vaccination exemptions are deliberate choices due to a personal opinion about vaccination, susceptibility clustering does not automatically follow. What is necessary for such a susceptibility cluster to form is a process that leads to clustering of individuals who share a negative opinion about vaccination, i.e. individuals with a negative opinion towards vaccination will be more likely to be in contact with other individuals holding the same opinion. Given the evidence of opinion-based access to vaccination, we reasoned that even a simple opinion formation process in a population should affect the probability of disease outbreaks.

2. Material and methods

2.1 Data

The data for vaccination coverage were taken from the WHO website (http://www.who.int/immunization_monitoring/en/globalsummary/time-series/tscoveragemcv.htm) accessed on 23 July 2008. The data for the number of reported measles cases were taken from http://www.euvac.net/ accessed on 23 July 2008.

2.2 Model description

For each simulation, we model the spread of an infection in a contact network where the vertices represent individuals and the edges represent a contact between individuals by which an infection can be transmitted. A generated network remains static during a simulation run.

For each simulation run, the following processes occur sequentially: (i) network generation, (ii) assignment of vaccination opinion, (iii) opinion formation, (iv) vaccination according to opinion, (v) infection of a random susceptible individual, and (vi) spread of infection. We now describe each process in detail.

2.2.1 Network generation

We generate a network with N vertices to represent a population of N individuals (in all simulations, N=2000). The network is generated such that the average degree of a vertex is 10, i.e. each vertex has, on average, 10 connections to other vertices. At any time, each vertex can be in either of the following three states: susceptible; infected; or immune. Initially, the status of each vertex is set to susceptible.

2.2.2 Assignment of vaccination opinion

After the generation of a network, each vertex is assigned either a positive or a negative opinion about vaccination (i.e. an individual decides to be or not to be vaccinated). The probability for each vertex to be assigned a positive opinion is given by the parameter c.

2.2.3 Opinion formation

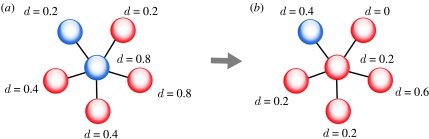
After the assignment of vaccination opinions, an opinion formation occurs as follows. First, for each vertex, we calculate the dissimilarity index d, which is defined as the proportion of neighbouring vertices that have a different (i.e. the opposite) opinion about vaccination from the focal vertex. For example, if the focal vertex has a positive opinion about vaccination, and 4 of its 10 neighbouring vertices have a negative opinion about vaccination, then d=0.4. Thus, d can have any value between 0 and 1.

Then, the following process is repeated N times. We pick a first random vertex from the network and change its opinion with probability d×Ω, where Ω measures the strength of opinion formation. If Ω=0, then no opinion formation process occurs. The maximum value for Ω is 1, i.e. the opinion swapping probability equals d. If the opinion of the first vertex is changed, we recalculate d for this vertex and all its neighbouring vertices (figure 2). In addition, a second random vertex is picked with the constraint that it must have the same opinion about vaccination as the first random vertex after the opinion swap. The second random vertex swaps opinion in the same way, i.e. with probability d×Ω. If no opinion swap occurs in the second vertex, another second vertex is picked in the same manner until an opinion swap occurs. The process of a second opinion swap in the opposite direction of the first opinion swap ensures that the fraction of positive opinions and thus the vaccination coverage remains constant. While this is an artificial assumption, it allows us to compare the effect of different strengths of opinion formation while keeping vaccination coverage constant.

Figure 2.

Visual representation of the opinion formation process. The colours red and blue represent the two possible opinions. After initial assignment of opinions, the dissimilarity index d (i.e. the percentage of neighbouring nodes that are of the opposite opinion) is calculated for each node. An opinion change occurs in the following way. (a) A random node is chosen (in this example, we focus on the central blue node, where d=0.8) and its opinion is changed with probability d×Ω. Note that any non-neighbouring node of the focal node and their edges are omitted for visual clarity. The d values of the neighbouring nodes are chosen randomly as an example and are based on the assumption that every node has five neighbours (in the simulations, the average degree of a node is 10). (b) If an opinion change occurs, the dissimilarity index is recalculated for the focal node and all its neighbouring nodes.

2.2.4 Vaccination according to opinion

After the opinion formation process, each vertex gets vaccinated according to its opinion about vaccination, i.e. vertices with a positive opinion about vaccination will change their status from susceptible to immune. Thus, the above-mentioned probability c also denotes the vaccination coverage or the initial immunization level of the population.

2.2.5 Infection of a random susceptible individual

A random susceptible vertex is picked from the network, and its status is changed from susceptible to infected.

2.2.6 Spread of infection

For 300 time steps, we model the spread of an infection in the following way. At each time step, a susceptible node can become infected with probability 1−exp(−βi), where β is the rate of transmission from an infected to a susceptible vertex and i is the number of neighbouring vertices that are infected (in all simulations, β=0.05). At any time step, an infected node recovers with probability γ=0.1. If recovery occurs, the status of the recovered vertex is set to immune for the rest of the simulation.

Each vertex that becomes infected during these 300 time steps is counted as a follow-up infection. An outbreak is registered if the number of follow-up infections is at least 10.

2.3 Simulations

For each combination of vaccination coverage (ranging from 0.5 to 0.95 in steps of 0.05) and strength of opinion formation (ranging from 0 to 1 in steps of 0.1), we ran 2000 simulations according to the model description above, resulting in 10×11×2000=220 000 simulations.

The data given in figure 1b,c resulted from 220 000 simulations of networks that were generated using an algorithm described by Watts & Strogatz (1998) with a rewiring probability of p=0.02. This algorithm generates so-called ‘small-world’ networks, which are characterized by a high level of vertex clustering and a low average distance between two vertices. We also generated the same dataset using Poisson networks (so-called Erdős & Rényi (1959) networks), where the degree distribution follows a Poisson distribution, and so-called scale-free networks with a highly skewed degree distribution (Barabási & Albert 1999). While different diseases are likely to have different contact patterns, the results obtained do not differ qualitatively.

3. Results

Here, we demonstrate that even a weak opinion formation process will lead to susceptibility clusters and a dramatic increase in disease outbreak probability (figure 1b). For a highly contagious infection such as measles, the vaccination coverage required to eliminate the disease is very high even under the assumption of homogeneous vaccination (more than 90% in the case of measles; Anderson & May 1991). The results presented here suggest that opinion formation impedes the attainment of full herd immunity, as the disease may persist in susceptibility clusters despite high vaccination coverage in the rest of the population.

Furthermore, we find that opinion formation can substantially decrease the herd immunity of a given vaccination coverage. For example, while disease outbreaks at a vaccination coverage of 90 per cent did not occur in the absence of opinion formation, the inclusion of opinion formation led to outbreak frequencies that would be expected in a homogeneously vaccinated population with a vaccination coverage of less than 70 per cent (figure 1c).

4. Discussion

Elimination of dangerous infectious diseases is clearly a top priority for societies worldwide. While health authorities should continue to make sure that vaccines are available for everyone, opinion makers on all levels should also recognize that they can have an enormous impact on the public attitude towards vaccination programmes. The problem of susceptibility clusters is a problem that affects all societies equally, as susceptibility clusters allow an infection to persist for long periods of time during which it can be exported to other susceptibility clusters. The current Swiss outbreak, for example, has already caused secondary infections in various other countries: in Austria, where an outbreak (with more than 200 infected individuals as of April 2008) is currently ongoing, the possible source case is a Swiss student who fell ill in Austria (Schmid et al. 2008). In the USA, exportation of Swiss measles is thought to have led to an outbreak in a community with approximately 10 per cent vaccination exemption due to personal beliefs (Richard et al. 2008). A current outbreak in northern Italy with approximately 1000 cases is thought to be caused by a case imported from the UK (Filia et al. 2008).

Our results show that the effect of opinion formation is strongest when the vaccination coverage is close to or at the level required to provide herd immunity under the assumption of random mixing (homogeneous herd immunity; figure 1c). Given that susceptibility clustering effectively reduces herd immunity, this is not surprising: when vaccination coverage is below homogeneous herd immunity, susceptibility clustering has little effect since an infection can spread relatively easily even in the absence of clustering. Conversely, if vaccination coverage is clearly above homogeneous herd immunity, susceptibility clusters are not only hard to form, but also some of the protection offered by the high vaccination coverage remains. However, if vaccination coverage is approximately at the level of homogeneous herd immunity, susceptibility clustering will have a strong relative effect because it easily breaks the full but fragile protection caused by homogeneous herd immunity. Countries that have over time managed to increase the vaccination coverage to the level where herd immunity would be expected might thus feel the full force of susceptibility clustering. In summary, our results suggest that the current estimates of vaccination coverage necessary to avoid outbreaks of vaccine-preventable diseases are probably too low.