Ontogenetic scaling of foot musculoskeletal anatomy in elephants

Abstract

This study quantifies the shape change in elephant manus and pes anatomy with increasing body mass, using computed tomographic scanning. Most manus and pes bones, and manus tendons, maintain their shape, or become more gracile, through ontogeny. Contrary to this, tendons of the pes become significantly more robust, suggesting functional adaptation to increasingly high loads. Ankle tendon cross-sectional area (CSA) scales the highest in the long digital extensor, proportional to body mass^1.08±0.21, significantly greater than the highest-scaling wrist tendon (extensor carpi ulnaris, body mass^0.69±0.09). These patterns of shape change relate to the marked anatomical differences between the pillar-like manus and tripod-like pes, consistent with differences in fore- and hindlimb locomotor function. The cartilaginous predigits (prepollux and prehallux) of the manus and pes also become relatively more robust through ontogeny, and their pattern of shape change does not resemble that seen in any of the 10 metacarpals and metatarsals. Their CSAs scale above isometry proportional to body mass^0.73±0.09 and body mass^0.82±0.07 respectively. We infer a supportive function for these structures, preventing collapse of the foot pad during locomotion.

1. Introduction

The anatomy of the feet (manus and pes) of Asian (Elephas maximus Linnaeus 1758) and African (Loxodonta africana Blumenbach 1797) elephants is specialized to support the locomotion of the largest living land animals. Elephants, rhinoceroses and hippopotami have large, fatty, fibrous foot pads underlying their manual and pedal digits (Neuville 1935; C. E. Miller & J. R. Hutchinson 2007, personal observation) that are divided into several compartments, supporting the bones of the foot away from direct contact with the substrate (Weissengruber et al. 2006). These pads evolved repeatedly in large tetrapods including dinosaurs (Bonnan 2003, 2005; Moreno et al. 2007), making elephant foot anatomy and function significant to our understanding of large animals, both living and extinct.

An unusual cartilaginous rod is positioned medially within the specialized foot pad of elephants. Although its evolutionary and developmental origins remain uninvestigated, it is described as a sixth digit called the prepollex in the manus and the prehallux in the pes (Ramsay & Henry 2001). These ‘predigits’ articulate proximally with digit I, and articulation surfaces and a joint capsule develop during ontogeny (Hutchinson et al. in press) suggesting significant and regular motion. This is entirely passive—there are no muscle–tendon unit attachment sites. Their function has been postulated as support (Neuville 1935; Ramsay & Henry 2001) as they do not contact the keratinous slipper of the foot (Weissengruber et al. 2006), but this has not been analysed biomechanically.

The mechanics of specialized feet in highly graviportal animals and their apparent correlation with large size remain almost uninvestigated. Here we describe shape change with body mass (scaling) for the predigits of elephants in comparison with other bony, cartilaginous and tendinous features of the feet. Simultaneously, we infer how shape changes may relate to lifetime loading patterns across the whole manus and pes, using scaling to infer relative loading upon structures across an ontogenetic spectrum (using size as a proxy for age, which is reasonably appropriate for the massive size changes and mineralization during elephant growth). Here we use elephants as the exemplar of graviportal quadrupeds, and infer potential lifetime loading regimes for individual elements from their shape changes with increasing body mass. We integrate data for the major support tissues of the wrist and ankle: the tarsal/carpal and metapodial bones and tendons. These are rarely investigated in scaling studies, which mainly concentrate on the proximal long bones and occasionally the metapodials of digit III.

By visualizing and measuring elements in situ using computed tomography (CT) scanning, internal tissues of the feet can be measured in their natural position, as close as possible to the live condition. This also preserves precious cadaveric specimens for further study, and is a method by which future ontogenetic scaling studies could be carried out in live animals using repeated scanning over a lifetime.

Our null hypothesis is that all musculoskeletal structures scale geometrically (without shape change) following Hill (1950), although we predict that, as with other precocial species (and in the proximal long bones of elephants, Christiansen 2007), elephants will show higher relative structural strength in smaller animals (i.e. negative ontogenetic allometry of bone and tendon diameter and area, positive allometry of bone length, Carrier (1983), Carrier & Leon (1990), Heinrich et al. (1999), Main & Biewener (2004) and Main (2007)).

1.1 Scaling

Scaling theory acknowledges that the tissue systems of organisms cannot maintain constant morphology as body mass increases, and that constraints of locomotion and support are different in large and small organisms. Three main scaling models describe various mechanical properties of ideal structures, whose dimensions increase in constant ratio with one another. They assume that all accommodation of increasing size is achieved by maintenance or change in relative shape of supportive tissues. Expected exponents for each of the models (y=ax^b, where b is the scaling exponent and x is body mass; M_b) are given in table 1.

Table 1.

Expected scaling exponents for the three models from the form length, diameter or cross-sectional area (CSA) $\propto M_{\text{b}}^x$, where M_b is body mass and x is the scaling exponent of the best-fit power curve.

	length	diameter	CSA
more gracile than geometric	>0.33	<0.33	<0.67
geometric	0.33	0.33	0.67
elastic	0.25	0.375	0.75
static stress	0.20	0.40	0.80

Geometric similarity (Hill 1950) involves no change in shape with increasing size, isometric scaling. In supportive structures stresses should thus increase as $M_{\text{b}}^{0.33}$.

Elastic similarity (McMahon 1973) describes structures that are similarly threatened by elastic failure under their own weight, based on engineering principles of a beam supported at each end on a base, but able to buckle or bend in the centre. This deformation is maintained at a constant level in elastically similar structures.

Static stress similarity (McMahon 1975) is the maintenance of maximum compressive stress in a cylindrical column during axial compression (standing) with increasing body mass. This also maintains constant skeletal stresses and safety factors (Biewener 1983).

Each of these three models is a point along a continuum of exponent values, which varies from extreme negative allometric to extreme positive allometric via isometric (geometric) scaling.

Changes in bone shape are often explained by Wolff's Law (e.g. Bertram & Swartz 1991; Lieberman et al. 2003), by which bone tissue is redistributed within living animals in response to stress or strain. This creates structures better suited to their functional environment. Tendon CSA is similarly influenced by differential loading, becoming thicker in response to increases in loading regime (e.g. in human long distance runners or in ontogenetic growth/phylogenetic change, Alexander (1981), Ker et al. (1988), Pollock & Shadwick (1994a,b) and Magnusson & Kjaer (2003)). The plasticity of bone and tendon tissues in reaction to differential use, particularly in juvenile animals (Van der Meulen & Carter 1995; Lieberman et al. 2003), allows (with caution, Bertram & Swartz (1991)) the inference of qualitative loading regimes from patterns of intraspecific scaling.

1.2 Elephant foot musculoskeletal anatomy

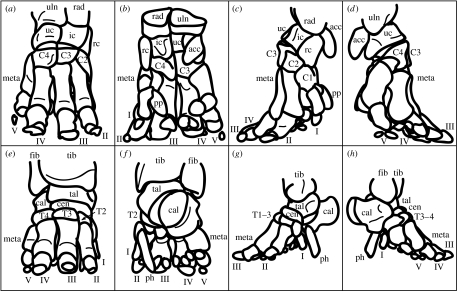
The bony structure of the elephant manus and pes is shown in figure 1. Manual and pedal bones are most robust laterally, digit III is the longest and all toes are tightly bound together in collagenous tissues (Eales 1928; Neuville 1935), except for the cartilaginous predigits that are bound into the foot pad (Weissengruber et al. 2006). The number of toenails can vary between individuals and species. Toenail positions correspond roughly to the locations of underlying digits.

Figure 1.

Bones of the elephant manus and pes (specimens A and B, respectively). Manus (a) cranial, (b) caudal, (c) medial and (d) lateral views. Digits are labelled I–V: acc, accessory carpal; C1–4, carpals I to IV; ic, intermediate carpal; meta, metacarpals; pp, prepollex; rad, radius; rc, radial carpal; uc, ulnar carpal; uln, ulna. Pes (e) cranial, (f) caudal, (g) medial and (h) lateral views. Digits are labelled I–V as for the manus; cal, calcaneus; cen, centrale; fib, fibula; meta, metatarsals; ph, prehallux; tal, talus; T1–4, tarsals I to IV; tib, tibia. Phalanges (1–3, variable between digits) and paired sesamoids are shown but not labelled.

The skeleton of both the manus and pes can be described as digitigrade or subunguligrade, but the manus has the more upright orientation of the two. There is some confusion in the literature about this, as the foot pads which extend from the carpals/tarsals to the ground render elephant feet functionally plantigrade. The manual bones are arranged in a column with the metacarpals positioned almost vertically. The bones of the pes are more horizontal, almost like a human wearing high-heeled shoes, with the calcaneus raised from the floor by the fatty foot pad. Each metatarsal is differently oriented with respect to the vertical: digits I and V are the most vertical and digit III the most horizontal. The functional consequence of the shape of the pes is that digits II, III and IV act like the three supports of a tripod, in contrast to the more unified column of the manus.

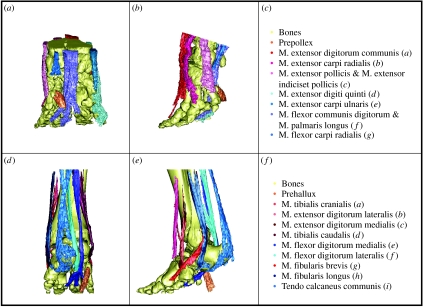
The majority of tendons in elephants act upon more than one skeletal element, partly due to the tightly bound foot bones. This creates a functional hoof-like unit with little scope for movement of individual toes (Eales 1928). Most tendons are relatively robust, the most cranial and caudal of the extensor and flexor tendons having the greatest CSAs (C. E. Miller & J. R. Hutchinson 2007, personal observation). Tendons which might act in pronation or supination are reduced, with lower thicknesses and insertions more consistent with flexor and extensor functions (figure 2). The most noticeable difference between elephants and other animals is the very small size of the tendo calcaneus communis (‘Achilles tendon’) muscles in the shank (Mm. gastrocnemii, M. soleus and M. flexor digitorum superficialis) as a percentage of lower leg musculature (Gambaryan 1974).

Figure 2.

Segmented tendon architecture of the elephant manus and pes (specimens A and B, respectively). Manus (a) caudal and (b) lateral views, (c) tendon colour key. Pes (d) caudal and (e) lateral views, (f) tendon colour key. Bones are displayed in yellow, the predigits in orange and extensor and flexor tendons are coloured red and blue, respectively. Movies of these models rotated in three dimensions are available as electronic supplementary material.

2. Materials and methods

A total of 11 and 12 cadaveric manus and pes specimens were analysed, one of each from African elephants and 10 manus and 11 pedes from Asian elephants (table 2). All specimens were obtained from captive zoo/animal park populations and had died of natural causes or were euthanased for reasons unrelated to this study. Any markedly pathological structures were excluded from our analyses, as were elements that could not be reliably segmented due to fusion. Most carpals were excluded in specimen O because of specimen quality, and in specimen M because the borders of unmineralized structures could not be defined. The same was true for the tarsals of specimens C and Q. Tarsal I of specimen D was excluded due to scan quality in this region. Tendons were excluded where segmentation was impossible due to fusion with, or proximity in grey values to, other tissues. In the manus the flexor carpi radialis tendon was excluded for manus specimens J, K and L, as well as the extensor digitorum communis and extensor carpi radialis tendons for specimen L and the tendo calcaneus communis in specimen N. Tendons were excluded altogether for the manus of specimen M and pes of specimen Q due to scan quality at tendon measurement level.

Table 2.

Specimens used in the analysis. (The one marked with asterisks was of known body mass; all other masses were estimated as described in §2.)

individual	species	gender	element	circumference of foot (m)	mass (kg)	slice thickness (mm)	resolution (pixels mm−1)
A	Asian	female	manus	1.223	3400*	3	1.067
A	Asian	female	pes	1.156	3400*	3	1.067
B	African	female	pes	0.981	1705	5	1.354
C	Asian	female	pes	1.307	4218	1.25	1.024
D	Asian	unknown	pes	0.488	188	1.25	1.430
E	Asian	unknown	pes	1.169	2964	3	1.067
F	Asian	unknown	manus	1.336	4521	3	1.067
F	Asian	unknown	pes	1.219	3384	3	1.067
G	Asian	unknown	pes	1.164	2924	3	1.067
H	Asian	unknown	pes	1.406	5313	3	1.067
I	Asian	unknown	pes	0.726	658	1.5	1.928
J	Asian	unknown	manus	1.251	3673	3	1.067
K	Asian	unknown	manus	1.414	5409	3	1.067
L	Asian	unknown	manus	1.270	3852	3	1.208
M	Asian	unknown	manus	0.438	133	3	1.422
M	Asian	unknown	pes	0.434	133	1.5	2.327
N	Asian	unknown	manus	0.401	101	1.25	1.143
O	African	male	manus	1.656	5872	5	1.024
P	Asian	male	manus	1.254	3438	1.25	1.484
Q	Asian	unknown	manus	0.465	161	1.25	3.066
Q	Asian	unknown	pes	0.476	161	1.25	3.066
R	Asian	unknown	manus	1.211	3311	3	1.067

CT scanning of specimens was carried out at The Royal Veterinary College (Hatfield, UK) and the IZW (Berlin, Germany) using Picker PQ5000 CT scanners (1–5 mm axial slice thicknesses, 120 kV, 200 mA, 512×512 pixels; see table 2 for in-plane resolutions). This provided high-resolution data for bone, cartilage and tendinous structures. The serial X-ray scans were reconstructed three-dimensionally using Mimics v. 9.11 (Materialise, Inc., Leeuwen, Belgium). Thresholds were semi-automatically detected and adjusted as necessary to provide complete cross sections. Previous studies have demonstrated that these methods of measurement are reasonably accurate in calculating true dimensions of musculoskeletal structures from CT scans. Viegas et al. (1993) demonstrated accuracies of 97% for linear dimensions and 94% for volumes, when compared with calliper and water displacement measurements. Our own preliminary work (C. E. Miller, C. Basu & J. R. Hutchinson 2007, unpublished data) and previous work by others suggest that this technique can be applied almost as reliably to magnetic resonance imaging (MRI) scans (99% accuracy for CT length measurements and 97.5% in MRI, compared with lengths from sequential milling; Smith et al. 1989).

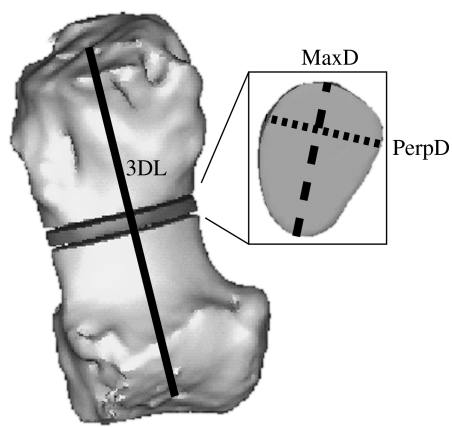
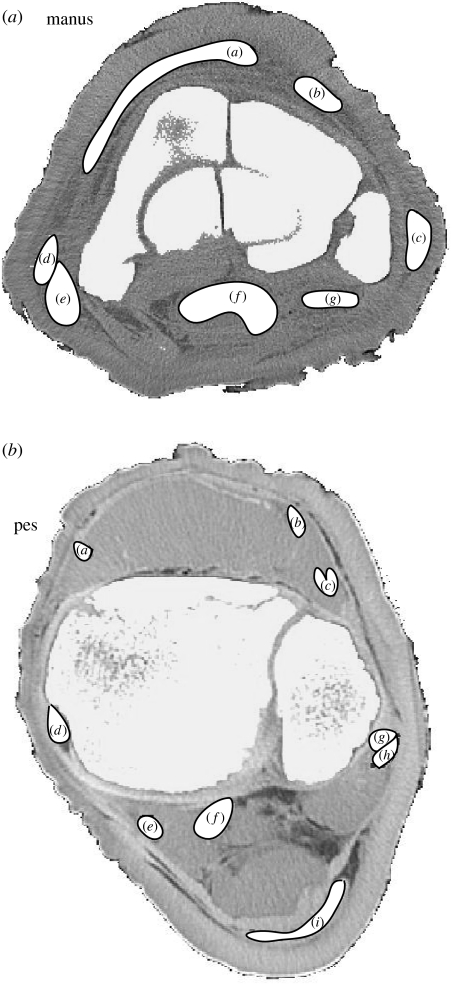
Within Mimics the reconstructions were resliced to isolate and reorient individual musculoskeletal elements for measurement. For bones (plus the prepollex and prehallux) we obtained the three-dimensional bone length, midshaft CSA, maximal diameter (MaxD) and maximal perpendicular diameter (PerpD; figure 3). Three-dimensional length was taken as the distance between articulation centres for each element, except in the accessory carpal and predigits where it was from the centre of the proximal articulation to the tip of the element, and in the calcaneus where it was the maximal craniocaudal length of the calcaneal body and tuber. In juveniles, measurements were taken from cartilaginous structures rather than the ossified mineralization centres to represent the whole skeletal element. Tendon CSAs and diameters were taken from CT scans at 3 cm above the calcaneus in the pes, and at the base of the accessory carpal in the manus. Tendon maps of these locations are shown in figure 4. We chose these positions for their availability in severed cadaveric specimens and for their consistent shapes among specimens; additionally, sensitivity analyses were carried out at 1 cm intervals up to 3 cm proximally and distally to ensure consistency of cross section within this region of tendon.

Figure 3.

Measurements taken. Three-dimensional length (solid line) was measured for each bone, and the mid-point found. This was extracted as a 1 mm thick slice, from which CSA (cut-out segment), MaxD (bold dashed line) and PerpD (perpendicular maximal diameter, dotted line) were calculated. 3DL, three-dimensional length.

Figure 4.

Tendon maps of the manus and pes (specimens A and B, respectively) from cross-sectional CT slices. For tendon labels see figure 2. The cranial aspects are towards the top and the lateral to the right.

Body masses were estimated by comparing with the populations characterized in the literature, except for specimen A which was of known body mass. First, foot circumferences (around the mid-point of the toenail associated with digit III) were measured in Mimics, and then we estimated shoulder height as double the foot circumference, as is generally recognized in the literature (Sukumar et al. 1988; Lee & Moss 1995; C. E. Miller & J. R. Hutchinson 2007, personal observation). Wherever possible this was estimated from the manus. Body mass was approximated from shoulder height using equations for existing Asian (Christiansen 2004) and African (Laws et al. 1975) elephant datasets. A sensitivity analysis of our mass estimates is included in the electronic supplementary material. It is worth noting that we could plot our bone lengths versus diameters as in other studies (e.g. Christiansen 2007) and would obtain identical general conclusions this way, but the approach we take here (plotting against body mass) allows us to tease apart changes of shape and length in elements of elephant feet in a more ontogenetic context.

For one specimen, data were collected twice for each of the bones and tendons to check the repeatability of our measurements. Student's t-tests for bias in bone length, CSA and diameter measurements, as well as tendon diameters, displayed no evidence for bias in repeated measurements, although tendon CSA did show a significant bias (table 3), which itself was fairly small (mean 3.8% error; see electronic supplementary material). British Standards Institution repeatability coefficients (95% of absolute differences being less than the repeatability coefficient) are low enough that they are unlikely to significantly alter our results.

Table 3.

Results of the tests for bias in repeated measures on CT scan reconstructions. (Full test data are available as electronic supplementary material.)

CT repeated measures	t-test for bias (p<0.05)	r	repeatability coefficient
bone
length	none	0.9975	6.6598
CSA	none	0.9997	85.3482
maximum diameter	none	0.9983	4.1688
tendon
CSA	bias present	0.9998	12.8380
maximum diameter	none	0.9930	3.2988

Removal of African elephant samples from datasets (one specimen each for manus and pes) made only very minor differences to individual exponents and had no major qualitative effect on trend data. Prepollex and prehallux exponents decreased slightly more than those in other structures, although we predict that these differences would not be significant with a larger dataset.

Reduced major axis (RMA, model II linear regression) analyses were carried out by plotting each factor with body mass, and obtaining the slope (exponent) of the power curve (on logarithmic axes) in PAST (v. 1.65, Hammer et al. 2001).

3. Results

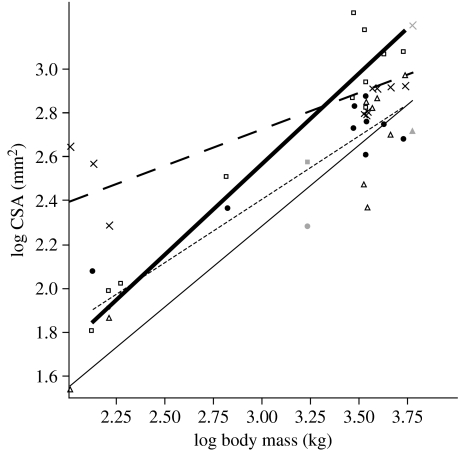
Exponents from all RMA power curve regressions are given in tables 4 (bone) and 5 (tendon). Figure 5 displays four example power curves, describing the relationship between CSA and total body mass for the prepollex, prehallux and their nearest comparable metapodials. The majority of trends are towards increased gracility or maintenance of geometric similarity; only the tendons of the pes become significantly more robust through ontogeny.

Table 4.

Scaling exponents of manus and pes bones±s.e. (Exponents are shaded according to the scaling model to which they most closely approximate (table 1); however, the s.e. overlap more than one scaling model in some cases.)

bone	length	CSA	MaxD	PerpD
manus
carpal I	0.26±0.03	0.48±0.05	0.29±0.03	0.23±0.02
carpal II	0.31±0.03	0.52±0.04	0.30±0.06	0.29±0.05
carpal III	0.30±0.03	0.51±0.02	0.28±0.02	0.24±0.03
carpal IV	0.26±0.04	0.45±0.04	0.24±0.02	0.20±0.02
metacarpal I	0.31±0.02	0.33±0.06	0.18±0.04	0.17±0.03
metacarpal II	0.32±0.02	0.49±0.04	0.24±0.04	0.24±0.02
metacarpal III	0.31±0.02	0.52±0.03	0.27±0.01	0.22±0.02
metacarpal IV	0.33±0.02	0.59±0.04	0.27±0.02	0.26±0.02
metacarpal V	0.39±0.03	0.65±0.05	0.36±0.03	0.30±0.02
accessory carpal	0.36±0.05	0.57±0.04	0.26±0.03	0.31±0.02
ulnar carpal	0.31±0.07	0.49±0.02	0.27±0.02	0.24±0.01
intermediate carpal	0.36±0.07	0.63±0.19	0.27±0.03	0.29±0.03
radial carpal	0.28±0.03	0.57±0.06	0.28±0.03	0.30±0.03
prepollex	0.28±0.01	0.73±0.09	0.34±0.06	0.43±0.04
pes
tarsal I	0.54±0.08	0.79±0.13	0.47±0.08	0.32±0.05
tarsal II	0.40±0.05	0.73±0.08	0.40±0.06	0.41±0.06
tarsal III	0.35±0.03	0.67±0.07	0.41±0.05	0.32±0.05
tarsal IV	0.43±0.05	0.58±0.02	0.28±0.03	0.30±0.02
metatarsal I	0.39±0.03	0.58±0.07	0.35±0.05	0.38±0.07
metatarsal II	0.32±0.02	0.50±0.03	0.28±0.02	0.22±0.01
metatarsal III	0.35±0.05	0.50±0.03	0.28±0.02	0.20±0.02
metatarsal IV	0.34±0.01	0.46±0.03	0.25±0.02	0.21±0.02
metatarsal V	0.32±0.03	0.61±0.05	0.30±0.04	0.32±0.02
calcaneus	0.40±0.02	0.67±0.05	0.36±0.04	0.32±0.03
centrale	0.51±0.06	0.70±0.05	0.35±0.02	0.35±0.04
talus	0.29±0.03	0.62±0.03	0.32±0.02	0.32±0.01
prehallux	0.30±0.03	0.82±0.07	0.42±0.03	0.39±0.04

Table 5.

Scaling exponents for tendons of the wrist and ankle±s.e. (Exponents are shaded according to the scaling model to which they most closely approximate (table 1); however, the s.e. overlap more than one scaling model in some cases.)

tendon	CSA	MaxD	PerpD
manus
M. extensor digitorum communis	0.59±0.07	0.24±0.03	0.31±0.05
M. extensor carpi radialis	0.69±0.09	0.33±0.07	0.32±0.05
M. extensor pollicis and extensor indicis et pollicis	0.51±0.07	0.24±0.04	0.23±0.03
M. extensor digiti quinti	0.61±0.10	0.32±0.07	0.34±0.07
M. extensor carpi ulnaris	0.38±0.11	0.26±0.07	0.25±0.05
Mm. flexor communis digitorum and palmaris longus	0.53±0.08	0.22±0.02	0.33±0.08
M. flexor carpi radialis	0.38±0.06	0.18±0.05	0.19±0.05
pes
M. tibialis cranialis	0.99±0.20	0.44±0.09	0.54±0.11
M. extensor digitorum lateralis	0.85±0.11	0.54±0.11	0.36±0.07
M. extensor digitorum longus	1.08±0.21	0.54±0.10	0.68±0.17
M. tibialis caudalis	0.76±0.10	0.41±0.08	0.33±0.03
M. flexor digitorum medialis	0.92±0.10	0.47±0.05	0.39±0.06
M. flexor digitorum lateralis	1.02±0.09	0.45±0.06	0.53±0.08
Mm. fibularis longus and fibularis brevis	0.78±0.10	0.24±0.05	0.47±0.07
tendo calcaneus communis	0.76±0.08	0.39±0.08	0.30±0.13

Figure 5.

Example power curves: CSA versus body mass for the prepollex, prehallux and metapodials of digit I (manus and pes). Symbols show the individual data points, black symbols are Elephas maximus and grey symbols Loxodonta africana specimens. Thin black line through open triangles, prepollex, y=0.087±0.28x^0.734±0.09, r²=0.93; bold black line through open squares, prehallux, y=0.103±0.22x^0.822±0.07, r²=0.96; bold dashed line through crosses, metacarpal I, y=1.733±0.19x^0.331±0.06, r²=0.82; dashed line through filled circles, metatarsal I, y=0.675±0.20x^0.578±0.07, r²=0.93. Slopes for both of the predigits are significantly higher than those of the metapodials, indicating a greater increase in robusticity of these cartilaginous elements through ontogeny.

3.1 Manus

Manus bone dimension exponents (table 4) display an overall decrease of relative robusticity through ontogeny, but individual diameter exponents tend to be higher in lateral elements, and CSA exponents increase laterally from metacarpals I to V. Metacarpal V showed slight positive allometry of length $(L\propto M_{\text{b}}^{0.39\pm 0.03})$ although its area remained geometrically similar (exponent 0.65±0.05) whereas metacarpal I showed very strong negative allometry of area (exponent 0.33±0.06).

The dimensions of all carpals scale with either geometric similarity or higher length and lower diameter and CSA exponents, suggesting a decrease in overall robusticity. The length exponents of the most medial and lateral of the distal carpals (carpal I and carpal IV) are the exception to this, scaling instead with elastic similarity (exponents 0.26±0.03 and 0.26±0.04, respectively, compared with 0.31±0.03 and 0.30±0.03 for carpals II and III, respectively).

The prepollex has rather different scaling characteristics from the other skeletal elements: prepollex CSA and length scale between elastic and geometric similarities (exponents of 0.73±0.09 and 0.28±0.01, respectively), but the PerpD scales with static stress similarity (exponent 0.43±0.04), greater than the exponent of MaxD (0.34±0.06). This characterizes an increase in cross-sectional circularity through ontogeny, allowing the prepollex to remain more robust than the other mineralized elements of the manus.

Manus tendon cross-sectional properties (CSA and diameters) maintain geometric similarity, or become significantly less thick through ontogeny (table 5). The laterally positioned M. extensor carpi radialis and M. extensor digiti quinti maintain the greatest robusticity with CSA exponents of 0.69±0.09 and 0.61±0.10, respectively, encompassing geometric similarity. This is consistent with the trend of increasing lateral robusticity across the whole manus and stands in sharp contrast to more medial tendons (for example, M. extensor carpi ulnaris exponent of 0.38±0.11, although M. flexor carpi radialis scaling is also weak, with a CSA exponent of 0.38±0.06).

3.2 Pes

In their anatomy the pes bones are similar to those of the manus, being most robust laterally. However, this pattern is not conserved through ontogeny (table 4). CSA exponents increase medially in the tarsals and metatarsals, although most exponents are not significantly different from those predicted by geometric scaling. Tarsals I, II and IV (with III to a lesser extent) have high length and MaxD exponents, remaining relatively longer and wider through ontogeny than the carpals of the manus which are becoming shorter and narrower.

The CSAs of metatarsals I and V scale towards the greatest robusticity with exponents of 0.58±0.07 and 0.61±0.05, respectively (figure 6). Metatarsal I, like metacarpal V, remains longer (in relative terms) than the other metapodials, although both also have relatively high CSA exponents, suggesting that total robusticity is maintained in both structures. Metatarsals II, III and IV all show trends towards decreasing circularity, exponents of MaxDs being smaller than those of the related PerpDs. For example, the MaxD exponent of metatarsal III is 0.28±0.02, greater than its PerpD of 0.20±0.02, so that the cross section changes to become more ovoid.

Figure 6.

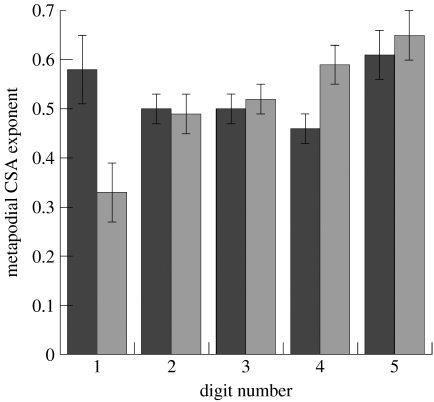
Manual (metacarpal, grey) and pedal (metatarsal, black) metapodial CSA exponents describe differing patterns of change in robusticity mediolaterally, greater robusticity being maintained laterally in the manus and to mediolateral extremes in the pes.

The prehallux is most similar in its scaling trends to the prepollex, with a relatively low length change exponent and high exponents for CSA and diameters. The prehallux becomes more ovoid through ontogeny, making it more similar to the metatarsals than metacarpals. This is the principal difference between it and the prepollex, whose circularity tends to increase.

The pedal tendons of elephants display much greater cross-sectional scaling exponents than any of the musculoskeletal structures in either the manus or pes (table 5). Most flexor and extensor tendon shapes change consistently with static stress similarity or greater, while supinators and pronators have lower exponents more characteristic of elastic or geometric similarity. It is also notable that the superficial flexor tendon, the tendo calcaneus communis, scales rather more weakly than its deeper counterparts.

4. Discussion

The bones of the manus and pes, and tendons of the manus, maintain their shape or become more gracile through ontogeny, scaling with negative allometry. Conversely, the majority of pes tendons have significantly higher scaling exponents than any other manual and pedal elements, displaying strong positive allometry with body mass increase. These differences between fore and hindlimb scaling patterns are intriguing, particularly in the context of different anatomical and locomotor patterns between the two limbs.

The general trend of negative allometry observed in most manual and pedal structures is consistent with observations by Main & Biewener (2004) that some (but not all, e.g. Heinrich et al. 1999) bones of baby animals are ‘overdesigned’ when compared with adults. This is partly related to the differing percentage composition of bone through ontogeny, and the transition from flexible cartilaginous to rigid ossified tissue with increasing elastic modulus (Currey & Butler 1975; Carrier 1983; Carrier & Leon 1990; Main & Biewener 2004). These studies generally concur, however, that in most animals this mineralization cannot fully compensate for negative allometry of bone diameter, area or section modulus. In juvenile elephants, the resulting decrease in total bone strength may be related to their greater athletic ability (larger peak forces with respect to body weight, Hutchinson et al. (2006)), as seen in other animals (Pennycuick 1975; Carrier 1983). The pes maintains greater robusticity than the manus, particularly in the tendons, which become significantly thicker and stronger with body mass increase.

The exceptions to the trend of negative allometry are the tendons of the pes. These become thicker as body mass increases, providing progressively less potential for elastic energy storage (Alexander 1977) but becoming less likely to break under stress during locomotion. The tendons of pedal supinators and pronators scale with elastic similarity, becoming more robust than any of the tendons in the manus, but less so than the majority of pedal extensor and flexor tendons. Pes superficial plantar flexor tendons also scale with elastic or geometric similarity, but these are relatively much smaller than the deep flexors when compared with those of other mammals (Gambaryan 1974). In the elephant pes and ankle it is the deep flexor and extensor tendons that become significantly stronger, scaling with static stress similarity or greater. This is consistent with an increased role of the ankle as a hinge joint, pronation and supination becoming less important features of ankle movement in larger elephants.

The differences in the changes observed between the tendons of the manus and pes may be explained by (or contribute to) the differential use of the fore and hindlimbs during locomotion (Hutchinson et al. 2003, 2006; Ren & Hutchinson 2008). Forelimb mechanics at all speeds are consistent with the inverted pendulum (vaulting mechanics) model of locomotion, by which body mass is vaulted over the limb to conserve energy (Cavagna et al. 1977). Hindlimb mechanics at faster speeds are consistent with the spring–mass model; i.e. a running, bouncing gait (Blickhan 1989). Additionally, the hindlimbs have lower duty factors than the forelimbs, which should bias loading towards slightly higher values in the hindlimb (Hutchinson et al. 2006), although elephants still support approximately 60% of their weight on their forelimbs (Henderson 2006). This fits well with our observations of increased tendon thickness at the ankle through ontogeny, particularly when compared with the decrease in tendon thickness at wrist level. During a bouncing gait greater elastic stretch is required for energy storage, but this must be offset by the resistance of the tissue to damage. In large animals the stresses and strains are likely to be such that greater relative tendon thicknesses would be required through ontogeny to maintain appropriate safety factors.

Differences in manus and pes skeletal anatomy also influence the required ‘antigravity’ support of the wrist and ankle muscles during standing. From simple two-dimensional free body diagram (e.g. Nordin & Frankel 1989) calculations, constructed using known dimensions of a 3400 kg female Asian elephant (individual A, table 2) from our CT data, we have estimated torques (rotational forces) about the wrist and ankle joints at standing. These calculations were made assuming vertical ground reaction forces acting through the centre of the foot sole (C. E. Miller, K. D'Aout & J. R. Hutchinson 2007, unpublished observation; also see Alexander et al. (1979)). At 30% body weight manus load, the torque at the wrist is 295 Nm, compared with the corresponding 20% body weight pes load having a torque of 314 Nm. That torques are slightly (6%) higher in the pes during quiet standing demonstrates the potential contribution of anatomy to differences in stress and strain in the manus and pes, particularly when differences in locomotor style between the fore- and hindlimbs are taken into account. The actual magnitudes of ankle/wrist joint moments, however, are unknown and could be computationally more complex (Gambaryan 1974). Hence more in vitro or in vivo studies of foot pad function are required.

Although the most pronounced differences between the scaling of the elephant manus and pes are seen in the tendons, patterns of bone scaling are by no means identical in the two structures. The bones of the manus and pes are most robust laterally, and exponents for CSAs maintain this lateral robusticity in the manus (figure 6), while the same exponents are the highest towards mediolateral extremes in the pes. This reflects differences in the anatomy and orientation of the bones. Another possible difference in local environment is the location of the overlying proximal limb bones: digit V is placed below the robust ulna in the forelimb and the slender fibula in the hindlimb. If higher loads are transmitted through the ulna (which is probable), then this asymmetry may increase the bias of the manus towards lateral robusticity.

The metatarsals are bound in a tripod-like arrangement, digits I and V angled vertically under compression and metatarsals II, III and IV closer to the horizontal. The orientation of the middle three digits means that they need to be more resistant to bending (and torsion) and require greater cross-sectional robusticity. In contrast the bones of the manus are in a more columnar orientation. All five metacarpals are arranged more vertically and presumably loaded in compression, in line with the presumed direction of force application during stance. Carpal and tarsal bones scale similarly to one another, with carpal and metacarpal bones demonstrating closer scaling similarities than tarsals and metatarsals. This may be similarly related to the different arrangements of metacarpals and metatarsals with respect to the typical direction of force application. These differences in the anatomy of bone orientation between the manus and pes help at least partly to explain the differences between scaling patterns of the bones in the two extremities.

Within the context of these differing functions and anatomies it is also important to look at the changes in the cartilaginous predigits with body mass increase. Both the prepollex and prehallux increase their cross-sectional parameters (CSA, ratio of maximal to perpendicular diameters) through ontogeny. Unit length also remains short, consistent with an increase in robusticity. Scaling exponents suggest that the prepollex and prehallux are more similar to one another in their function and reaction to load than to any of the other bony elements of the manus and pes, and this may be due to their predominantly cartilaginous structure, which becomes progressively more mineralized as elephants age (Hutchinson et al. in press). The scaling exponents for both predigits are most similar to those of tarsal II, one of the blocky, proximal elements, which is presumably loaded in axial compression during stance and locomotion. Also in line with the support hypothesis, length scales most consistently with the carpals of the manus, elements which should be similarly loaded. We have observed greater curvature in the predigits than in other elements, suggesting that they are likely to be loaded in appreciable bending stresses (and perhaps torsion, considering their medial location).

In this context we can infer roles for the predigits in the support and resistance of ground reaction forces vertically through the manus and pes, as well as a possible role in the modulation of foot pad strain. As these flexible cartilage rods are far stiffer than the fatty tissue that surrounds them, these structures may prevent excessive and potentially damaging levels of foot pad compression during loading. The robusticity of the prepollex, in contrast to the more gracile bones of the manus, may be due to its isolated location as a supportive strut within the caudal portion of the foot pad.

The shape changes seen in the tendons of the elephant wrists and ankles contribute further insight into the loading patterns of the manus and pes through ontogeny. The cross-sectional parameters of manus tendons scale consistently with manus bone parameters, the majority of tissues maintaining geometric similarity or becoming significantly more gracile through ontogeny. Scaling exponents tend to be higher laterally in the musculoskeletal structures, suggesting an increase in the levels of load being transmitted through the lateral side of the manus through ontogeny. This hypothesis can easily be tested in future biomechanical studies by studying in vivo forces and foot deformations.

Unusually our study has concentrated on the musculoskeletal structures of the manus and pes alone, making it difficult to compare with many of the other studies published in the literature. Scaling studies tend to focus on more proximal long bones and interspecific datasets. The most well-represented elements of the extremities are the metapodials, with data available for several species and groups of mammal and birds, followed by the calcaneus, and some ankle flexor tendons. We are aware of no other studies examining scaling of all tarsal or carpal bones in animal feet. There are also intraspecific data available for the proximal limb bones of elephantids, which generally scale with negative allometry of length versus circumference (Christiansen 2007), as has been recognized in the manual and pedal elements described here.

The flexor tendons of elephant ankles increase in CSA with a much greater scaling slope than those of birds and kangaroos. In birds (interspecifically) the gastrocnemius and deep digital flexor tendons maintain geometric similarity (Bennett 1996), as do the gastrocnemius and flexor digitorum profundus tendons of kangaroos (again, interspecifically, Bennett & Taylor (1995)). In the same interspecific study, the flexor digitorum superficialis CSA of kangaroos scales similarly to the elephant tendo calcaneus communis tendon (exponents of 0.75 and 0.76, respectively), but values of geometric scaling for other structures lie in stark contrast to the exponents of the elephant medial and lateral digital flexor tendons (0.90 and 1.02). These exponents are far above those predicted by any of the three scaling models outlined above. Carrier (1983) discusses a predicted CSA exponent of 1.0 as a requirement to maintain mechanical advantage in Jack rabbit (Lepus californicus) tendons across ontogeny, and this may be an explanation for the significantly higher CSA exponents in elephant ankles. Tendon anatomy is adjusting to maintain mechanically similar function in an environment of increasingly high forces. This could be further tested by looking for differences in effective mechanical advantage at the wrist and ankle through ontogeny in living elephants.

The changes in elephant metapodial dimensions are similar to those found in the European rabbit (Oryctolagus cuniculus, Lammers & German 2002). This is interesting due to rabbits' locomotor patterns—hind- and forelimbs appear to move in very different ways during locomotion as in elephants (Ren & Hutchinson 2008): the hindlimbs help to vault the body over the forelimbs (e.g. Cavagna et al. 1977). Rabbit and elephant locomotor styles are superficially very different, but stresses and strains upon the metapodial bones through ontogeny appear to have a similar shape change effect in both species.

There are several limitations to our study, the effects of which we have endeavoured to minimize wherever possible. Few of the specimens were taken from animals of known body mass, and therefore some variability in the accuracy of mass estimates is inevitable. Owing to the specimen availability the spread of our data is not ideal—the majority of results fall at the lower and upper limits of body mass range. However, the fit of the power curves to intermediate mass specimens is very good (figure 5), and it is unlikely that this has significantly distorted the trends observed here. All of our specimens were captive animals, and so were presumably less active than wild animals. They may not accurately represent all elephants yet we are confident that at least our general trends, if not their precise quantities, should hold for all elephants. We also assume no change in posture through size increase with ontogeny, and there is evidence to suggest that this is correct (Hutchinson et al. 2006).

The observed decrease in bone robusticity through ontogeny is doubtless influenced by the transition from cartilage to bone, stockier bones compensating for weaker supportive tissue in juveniles (Currey & Butler 1975; Carrier 1983; Keller & Spengler 1989; Carrier & Leon 1990; Main & Biewener 2004, 2007; Main 2007). Therefore, it is important to be cautious when interpreting these data in terms of pure size increase, as they are indicative of ontogenetic shape (but not necessarily strength) transition. As adult morphologies are determined by interactions of mechanical and genetic factors (Bertram & Swartz 1991; Van der Meulen & Carter 1995), future anatomy and ability to withstand typical adult loads are established during ontogeny. Thus our observations are likely to represent the generalized loading patterns of the feet.

5. Conclusions

Here we have completed the most integrative and comprehensive scaling study of foot anatomy in any animal to date. In general, the bones of the elephant manus and pes scale at, or below, geometric similarity. Elements become progressively more gracile, or at the most maintain their shape with increasing size. Contrary to this, the tendons of the pes become significantly stronger through ontogeny, probably in conjunction with differences in manus and pes anatomy and loading during stance and gait.

Both the prepollex and prehallux remain relatively robust in comparison with other mineralized tissues of the feet, strongly supporting the hypothesis that they play a major role in foot support. Although their scaling exponents are most similar to one another, scaling of their cross-sectional parameters is the closest to the tarsals, and length scales closest to the carpals, elements which must be regularly loaded in axial compression.

Further work on the patterns of pressure distribution under the elephant's foot during walking, and patterns of deformation in the internal structures of the foot are needed for comparison with these scaling trends. However, our study demonstrates the value of using intraspecific scaling for generating hypotheses about locomotor loading.

Our results give us an insight into the typical foot loading patterns of large graviportal animals. These same principles can be applied to other animals, and are of particular interest to palaeontologists reconstructing extinct proboscideans, as bony indicators are often all that is available to them. CT scanning is also an important feature of the study as it is non-invasive, allowing living specimens of various animals to be studied through ontogenetic change, and preserves precious cadaveric or fossil specimens for future work.

Supplementary Material

Sensitivity analysis

Sensitivity analysis for body mass estimation using animals of known in vivo mass and dimensions

Repeatability study

Repeatability study for bone and tendon measurements

Video of three-dimensional manus bone and tendon model

Video of three-dimensional manus bone and tendon model. This is the manus model used in construction of figure 2, colours are coded as for this figure

Video of three-dimensional pes bone and tendon model

Video of three-dimensional pes bone and tendon model. This is the pes model used in construction of figure 2, colours are coded as for this figure