Coloration using higher order optical interference in the wing pattern of the Madagascan sunset moth

Abstract

Colour patterns of animals' bodies are usually produced by the spatial distribution of pigments with different colours. However, some animals use the spatial variation of colour-producing microstructures. We have studied one distinctive example of such structurally produced colour patterns, the wing of the Madagascan sunset moth, to clarify the physical rules that underlie the colour variation. It is known that the iridescent wing scale of the sunset moth has the alternate air–cuticle multilayer structure that causes optical interference. The microscopic and optical investigations of various parts of the wing have confirmed that the thickness of the cuticle layers within the scale largely varies to produce the colour pattern. However, it varies in very different ways between the dorsal and ventral sides of the hind wing; the thickness gradually varies on the dorsal side from scale to scale, while the abrupt changes are found on the ventral side to form distinctive borders between differently coloured areas. It is also revealed that an unusual coloration mechanism is involved in the green part of the ventral hind wing: the colour is caused by higher order optical interference of the highly non-ideal multilayer structure. The physical mechanism of the colour pattern formation is briefly discussed with the several mathematical models proposed so far.

1. Introduction

The wing pattern of butterflies and moths is one of the most drastic examples of morphological diversification in the animal world. It is also known that these diverse patterns are essentially produced as a mosaic of differently coloured scales (Nijhout 1991); the scales on the wing contain different pigments, depending on their positions, and the spatial arrangement of the scales forms the pattern as the whole. The physical mechanisms for the position-dependent pigment production have been discussed by using the mathematical models that describe the spatial distribution of the pigmentation-inducing morphogens (Bard & French 1984; Nijhout 1990, 1991; Murray 1993; Sekimura et al. 2000). However, there is a totally different way of coloration, called structural colour, in which the periodic microstructure in submicron size produces brilliant colours through such physical phenomena as optical interference and diffraction (Srinivasarao 1999; Parker 2000; Vukusic & Sambles 2003; Kinoshita & Yoshioka 2005). Since the periodicity of the microstructure mainly determines the wavelength of light that is strongly reflected, the colour pattern can be produced by the spatial variation of the microstructure. The eye pattern of the peacock feather may be the most well-known example of such structurally produced colour patterns (Durrer 1962).

The Madagascan sunset moth, Chrysiridia rhipheus (Lepidoptera: Uraniidae), is another distinctive example that has strong iridescence, as shown in figure 1. The wing pattern of this diurnal moth is quite unusual because various metallic colours are found on the wings and the iridescence exists even on the ventral side of the wings. This is quite in contrast to other structurally coloured butterflies, for example Morpho butterflies, which exhibit the brilliant blue colour only on the dorsal surface, probably for cryptic purposes. The physical origin of the strong iridescence of the sunset moth has been studied for a long time, and it has been revealed that there exists an air–cuticle alternate multilayer structure inside the wing scales causing optical interference (Mason 1927; Lippert & Gentil 1959) accompanied by a special optical effect due to the large-size structural modification (Yoshioka & Kinoshita 2007). Thus, it is naturally expected that the thickness of the cuticle and/or air layers spatially varies to result in the colour variation of the wings. However, careful inspection of the pattern poses a few questions; a small area of the ventral hind wing, shown in figure 1c, contains variously coloured scales: green, blue and purplish red scales. The order of this colour change seems different from that of the wavelength of light. How do the thicknesses of the multilayer structure vary in this region? A similar question can be posed on the whole iridescent part of the wings; what kind of rules exist in the variation? In other words, do the thicknesses change just monotonically or in any other different way? To answer these questions, we have performed microscopic and optical investigations on the various iridescent parts of the wing of the Madagascan sunset moth.

Figure 1.

The wings of the Madagascan sunset moth from (a) dorsal and (b) ventral view. The eight areas with different colours indicated by red arrows are named from C1 to C8. (c) The close-up view of the area between green and purplish red areas that is indicated by the red square in (b). The arrows indicate the position of the scales of which reflectance is shown in figure 6. Scale bar, 2 mm.

2. Materials and methods

The sample of the Madagascan sunset moth, C. rhipheus (also known as Urania ripheus), was purchased from Mushi-sha, Japan. The microstructures inside the wing scales were observed by a transmission electron microscope (TEM; Hitachi H-7650). Ultrathin sections were prepared according to a conventional procedure: the sample was dehydrated by 100% ethanol, embedded in epoxy resin (Quetol-812, Nisshin EM) and finally thin-sectioned by an ultramicrotome (Reichert, UltracutN).

The reflected light spectrum from the single scales was measured using a microspectrophotometer that consisted of a microscope (Olympus BX-50 equipped with a Xe lamp) and a fibre-optic spectrometer (Ocean Optics USB2000 or USB4000). One end of the surface of an optical fibre was placed on the image plane of the microscope, which was slightly above the optical tube of the microscope. Since the fibre had a diameter of 400 μm and an objective lens of magnification 10 was used, the detected light was supposed to come from a circular area with a diameter of 40 μm. This was small enough to examine a part of a single scale, of which typical dimensions are 200 μm in length and 80 μm in width. Reflectance was obtained by dividing the measured spectrum by the reference spectrum of the white standard of a BaSO₄ plate. Because the reflection from the standard plate was too diffuse for all of the reflected light to be collected by the objective lens, this analysis did not give the absolute reflectance but the spectral line shape only. However, the absolute reflectance has already been determined to be several dozen per cent at the maximum by measurements using an optical system, including an integrating sphere (Yoshioka & Kinoshita 2006).

To examine the reflection spectrum in a wider wavelength range from ultraviolet to infrared regions, we employed a UV–Vis–NIR spectrometer (Varian Cary 5G) equipped with a mirror-composed diffuse reflectance accessory (Hogue 1991). The focused spot had an elliptic shape and was approximately 1 and 0.5 mm long in the major and minor axes, respectively. The reflectance spectrum was obtained in the wavelength range between 200 and 2500 nm with KBr powder as the white standard.

To characterize the colour variation, the chromaticity coordinates x and y were calculated by the common formula x=X/(X+Y+Z) and y=Y/(X+Y+Z), where X, Y and Z were obtained by the integration of the product of three wavelength-dependent functions—the standard illuminant D₆₅, the reflectance of the multilayer structure and the colour-matching functions $\overline{x}$, $\overline{y}$ and $\overline{z}$ of a 10° standard observer, respectively—over the wavelength range 380–780 nm (Srinivasarao 1999).

3. Results

3.1 Microscopic observations

The observation of the wings under an optical microscope easily reveals that the regular arrangements of the two kinds of scales form the two layers on the wing; the lower layer consists of flat black scales, called ground scales, while the upper layer of strongly curved scales (cover scales) exists above the layer of ground scales. Since the iridescence comes from the cover scales, the microstructures found in their longitudinal section are shown in figure 2 for eight differently coloured areas of the wings, which are named from C1 to C8 as shown in figure 1. In all the areas examined, the existence of the air–cuticle multilayer structure is clearly confirmed and the layer thickness seems to vary depending on the areas. It has been reported that the number of cuticle layers depends on the position within a single scale; it is less in the proximal part of the scale and most around the tip (Yoshioka & Kinoshita 2007). The TEM images shown in figure 2 correspond to the part where the number of the cuticle layers is maximum. Since the thicknesses of the cuticle and air layers are not perfectly uniform, we have determined the approximate thickness by averaging the thickness of several parts.

Figure 2.

TEM images of the longitudinal cross section of the iridescent cover scales of the eight areas named from C1 to C8 as shown in figure 1. Scale bar, 1 μm.

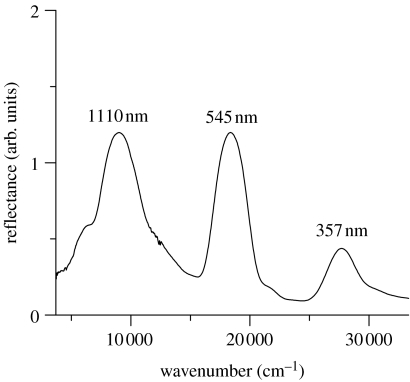
Table 1 summarizes the structural parameters determined from the observed multilayer structures. Although the thickness of both kinds of layer varies, the variation in the cuticle layer is larger than that in the air layer. In particular, the cuticle layer of area C5 is thicker than even double the air layer, and it is the thickest among the eight areas examined. This fact is surprising to us because the colour of this area is green and other areas have orange or red colours, which correspond to light with longer wavelengths. The wavelength λ_p of the reflected light is estimated from the determined structural parameters according to the condition of optical interference under normal incidence, 2(n_cd_c+n_ad_a)=mλ_p, where n_c(n_a) and d_c(d_a) are the refractive index and thickness of the cuticle (air) layer, respectively, and m is an integer called the order of interference in this paper. For the thickest area C5, it is estimated that the first-order interference occurs in the infrared region and the second order occurs at approximately 550 nm, which can cause the green colour.

Table 1.

Structural parameters of the multilayer structure of the eight differently coloured areas named from C1 to C8 as shown in figure 1. (The mean thicknesses of the cuticle and air layers, d_c and d_a, respectively, and the maximum number of the cuticle layer N_max within one scale is determined from observations using a TEM. It is found that in several areas (C1, C2, C7 and C8) the number N_max differs, depending on the scale examined. The wavelengths λ_p are theoretically estimated by the interference condition mλ_p=2(n_cd_c+n_ad_a) for the different order m of the optical interference, where the refractive index of the cuticle layer n_c and air layer n_a are assumed to be 1.55 and 1.0, respectively. The wavelengths λ_p are also determined experimentally from the spectra shown in figure 4 except for area C5, where the spectrum of figure 3 is used for the determination.)

area	colour	Nmax	dc (nm)	da (nm)	λp (nm; estimated)	m	λp (nm; experimental)
C1	pale blue	7–8	100	100	510	1	570
C2	pale green	5–6	110	130	601	1	580
C3	orange	6	140	100	634	1	670
					787	1	800
C4	purplish red	6	170	130	394	2	420
					1097	1	1110
C5	green	4	270	130	549	2	545
					366	3	357
C6	dark red	6	160	150	796	1	750
					398	2	420
C7	orange	5–6	140	130	694	1	600
C8	green	5–6	110	110	561	1	590

To experimentally confirm these estimations, the reflection from area C5 has been examined using a UV–Vis–IR spectrometer in a wide wavelength range. The results, shown in figure 3, clearly confirm an infrared reflection peak at 1110 nm as well as two other peaks at 545 and 357 nm. As it is expected from the general principle of optical interference, the distances between the adjacent peaks are found to be almost the same in wavenumber: they are calculated to be 9340 and 9660 cm⁻¹ between the peaks at 1110 and 545 nm and those at 545 and 357 nm, respectively. These results safely lead us to the conclusion that the reflection of area C5 comes from the optical interference with three different orders and, in particular, the green colour is mainly due to the second order one. Here, we note that the appearance of the higher order peaks is not generally taken for granted in a multilayer system, even when the first-order peak is strongly caused by optical interference. It depends largely on the ratio between the thicknesses of the two kinds of layer, as will be discussed later in detail.

Figure 3.

Reflectance of the green area named C5 in the ventral hind wing. A UV–Vis–IR spectrometer was employed for the measurement in this wide wavelength range.

3.2 Optical characterization of single scales

Next, we have examined the reflection from the single scales of various parts of the wings using the combination of an optical microscope and a fibre-optic spectrometer. It has been reported that the strong curvature of the cover scale causes two paths of reflection that have different reflection spectra from each other; one is the direct reflection from the flat part of the curved scale, and the other is the dual reflection path between the adjacent two scales, which is just like the retroreflection by a right-angle prism (Yoshioka & Kinoshita 2007). Here, we have focused our attention on the direct reflection path, in which the reflection occurs normally to the multilayer system.

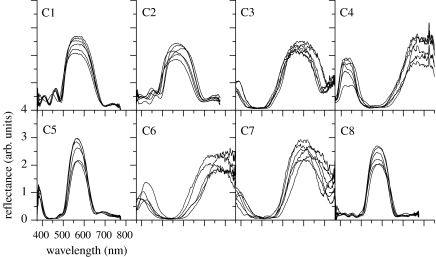
In figure 4 we show the results for the eight areas of the wings, which correspond to those in figure 2. The obtained reflectance spectra have the peaks at totally different wavelengths depending on the areas, and it is found that the wavelengths roughly agree with the estimations from the microscopic observations (table 1). Although the agreement seems not so good in areas C1 and C7, here we will consider that the variation in the wavelength of the reflectance peak corresponds to that in the multilayer structure.

Figure 4.

Reflectance of six different single scales each for the eight areas of the wings shown in figure 1. The spectrum was measured by the combination of an optical microscope and fibre-optic spectrometer. The six scales examined are located next to each other in most cases. Since both the intensity of the light source and the detection efficiency become lower, the spectra look noisy in the longer wavelength range.

Careful inspection of the spectra reveals that the spectral line shapes of different scales in several areas do not perfectly match each other even though the scales are closely located on the wing. In particular, in areas C2, C6 and C7, the wavelength and width of the peaks are largely distributed. On the other hand, in areas C1, C5 and C8, the peak appears at almost the same wavelength, indicating the homogeneous nature of the microstructures among the different scales. Further inspections of the spectral line shape of areas C1 and C2 reveal that there are a few side bands in the shorter wavelength side of the main peak. The appearance of the side bands is commonly known for theoretically calculated spectra of the multilayer system and artificial reflectors actually show this spectral feature. However, it is rarely observed in biological reflectors owing to structurally irregular or non-uniform characteristics. Thus, the observed spectral line shapes contain a lot of structural information on the homogeneous or inhomogeneous characteristics among different scales, and also on regular or irregular characteristics of the multilayer structure inside one scale, which are suggested to be essential in natural structural colours (Kinoshita & Yoshioka 2005). However, detailed analysis of the spectral line shape is too specialized a topic in optics to be described here. In this paper we focus our attention mainly on the wavelengths of the peaks, which directly give us the information on the thickness of the multilayer structure.

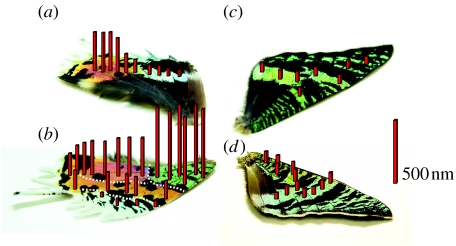
To visualize the spatial variation of the air–cuticle multilayer structure, we draw on the photographs of the wings shown in figure 5; the heights of the red bars shown in this figure are correlated with the wavelength of the first-order reflection peak. As is immediately seen, the highest bars are located in the green area of the ventral hind wing, where the infrared reflection is observed. It seems that the ventral hind wing can be divided into four regions indicated by the broken white lines, as shown in figure 5b. These regions almost correspond to those with four different colours: green, purplish red, orange and pale green regions. In contrast to the ventral side, where sudden changes in the bar height are seen, the dorsal side shows rather smooth variation, as shown in figure 5a, at least with the spatial resolution of the present measurements. As for the front wings, the bar height seems almost constant on the dorsal side (figure 5c), while it is slightly higher in the proximal part on the ventral side (figure 5d).

Figure 5.

Spatial variation of the wavelength λ_p due to the first-order constructive interference depicted as the height of the red bars at various positions of (a) the dorsal hind, (b) the ventral hind, (c) the dorsal front and (d) the ventral front wings. These bars are drawn such that their heights are proportional to (λ_p−500) nm at their positions. The subtraction of 500 nm is simply for the emphasis of the difference. The wavelengths λ_p are determined as the average of the peak position in the reflectance spectra shown in figure 4 and from other spectroscopic measurements at various parts of the wings. When the first-order reflectance peak is out of the range of the fibre-optic spectrometer, it is estimated as double the wavelength of the second-order peak. The red bar on the r.h.s. corresponds to 500 nm.

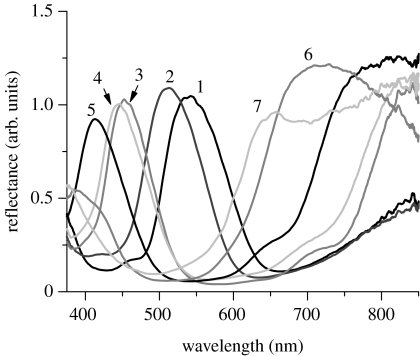
We have a particular interest in the border region between the green and purplish red areas, shown in figure 1c, where variously coloured scales are observed. As shown in figure 6, the spectroscopic measurements of those scales clearly reveal that the reflectance peak gradually shifts with the number that indicates the position of the scale examined: the green scale has a peak at approximately 540 nm, and it shifts to shorter wavelength regions as the colour of the scale changes into blue and violet. In the longer wavelength region, a part of the broad component is noted, and it comes to form a broad peak for the scale of number 6. These spectral features strongly suggest that the layer thicknesses continuously decrease so that the first-order reflection peak, which is in the infrared region for the green scale, comes into the visible range for the purplish red scale.

Figure 6.

Reflectance of seven single scales that are located in the region between the green and purplish red areas of the ventral hind wing. The spectrum was measured by the combination of an optical microscope and fibre-optic spectrometer. The numbers show the positions of the scales examined, as shown in figure 1c.

4. Analysis

4.1 Colour variation between the green and purplish red areas

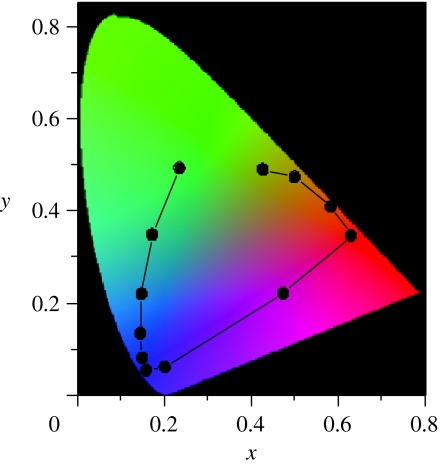
In §1 we posed a question about the structural variation between the green and purplish red areas of the ventral hind wing (figure 1c). The spectroscopic measurements shown in figure 6 strongly indicate that the decrease in the layer thicknesses causes the colour change from green to purplish red. To further confirm this indication, we use the chromatic diagram, since it can clearly show the relation between the shift in the spectral peak and the variation in colour. The chromaticity coordinates, x and y, are calculated for the light reflected from the air–cuticle multilayer structures, of which reflectance is theoretically obtained by the recursive method (Hooper et al. 2006; Noyes et al. 2007). The calculations are performed as a function of the thickness of the cuticle layer, while that of the air layer is kept constant since the thickness is observed to be almost constant at 130 nm in C4 and C5. The results, shown in figure 7, reproduce fairly well the drastic colour change with the locus' movement: when the layer structure is the same as that observed in area C5, the locus is in the green region. As the thickness is decreased, it moves into the regions of blue, violet and purplish red colours and finally reaches the orange region. This movement is almost coincident with the actual colour variation in the region shown in figure 1c. Thus, we can conclude that the thickness of the cuticle layer decreases just monotonically but rather steeply in the border region between green and purplish red areas in the ventral hind wing.

Figure 7.

Chromatic diagram for the reflected light from the multilayer structure as a function of thickness of the cuticle layer. Reflectance is theoretically calculated by the recursive method. The locus at (x, y)=(0.24, 0.50) in the green region is for the multilayer structure observed in the scale in area C5, which consists of four cuticle and three air layers with the thicknesses d_c=270 nm and d_a=130 nm with refractive indexes of 1.55 and 1, respectively. The other loci are calculated for the multilayer structures of which cuticle layer thickness d_c is gradually decreased from 270 to 121.5 nm with intervals of 13.5 nm, keeping other parameters constant.

4.2 ‘Non-ideal’ character of the multilayer structure

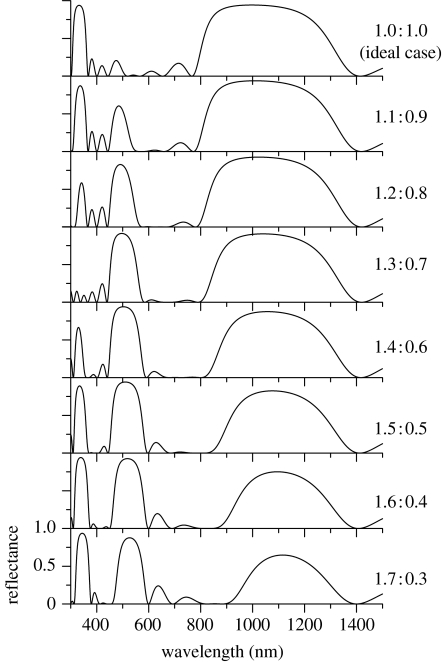
It is known that the second-order interference of the multilayer system does not always cause the reflection peak, even when the first-order one strongly does: when the multilayer structure is said to be ‘ideal’, where the optical thicknesses (the product of the thickness and refractive index) of two kinds of layer are the same as each other, the second (and even)-order peak vanishes, while the first (and odd)-order peak is strongly enhanced by constructive interference (Huxley 1968; Land 1972). On the other hand, when the multilayer is non-ideal, where the optical thicknesses are different, the second-order peak gradually appears as the degree of non-ideal character increases. As expected from this general characteristic of the multilayer system, the air–cuticle multilayer structure found in area C5 is a highly non-ideal one, since the cuticle layer, which has a larger refractive index, is much thicker than the air layer. The ratio of the optical thicknesses of the cuticle and air layer is calculated to be 1.5 : 0.5 (=270×1.5 : 130×1.0). To analyse this high degree of non-ideal character, we have theoretically calculated the reflectance spectrum for ideal and various non-ideal multilayer systems as shown in figure 8, where the sum of the optical thickness is kept constant so that the first-order interference occurs at the same wavelength 1110 nm. It is confirmed that the broadband reflection appears in the infrared region, of which magnitude and width gradually decrease as the non-ideal character increases. On the other hand, the two peaks at 555 and 370 nm, due to the second- and third-order interference, respectively, are found to largely change their magnitude depending on the ratio. In particular, the third-order peak almost vanishes at the ratio 1.3 : 0.7. However, when the ratio becomes 1.5 : 0.5, which is just the case in area C5, both peaks simultaneously appear large. In fact, the two peaks are experimentally observed as shown in figure 3, although their heights differ from each other. This discrepancy is probably due to the thickness variation or other irregular factors of the structure (Yoshioka & Kinoshita 2007), which become more sensitive to reflectance in higher order interference. The tuning of the non-ideal character of the multilayer system to 1.5 : 0.5 may suggest that both the green and ultraviolet reflections are important; they can possibly cause the colour mixing effect in the spectral region for the vision system of the sunset moth.

Figure 8.

Theoretically calculated reflectance of the multilayer structure with the different degrees of ‘non-ideal’ character, keeping the wavelength of the first-order peak constant at 1110 nm. The figures on the r.h.s. indicate the ratio of the optical thicknesses of the cuticle and air layers inside the multilayer structures. The ratio 1.5 : 0.5 is the case in area C5 in the ventral hind wing.

5. Discussion

We have confirmed that the colour pattern of the wing of the sunset moth is produced by the spatial variation in the thickness of the air–cuticle multilayer structure inside the iridescent scales. In general, the structural colour is a more convenient method to produce colour variation than the pigmentary colour, because in the latter case at least several different kinds of pigment molecules with different optical absorption have to be synthesized and properly mixed with each other, if the colourful pattern is to be generated only by means of pigments. On the other hand, the structural colour can be easily modified by tuning the periodicity of the microstructures without changing the overall scheme. Thus, it seems quite natural that the sunset moth uses multilayer optical interference to produce the colourful wing pattern.

However, it is unusual that second-order optical interference causes the green colour, because it can be produced simply by the first-order one as in the dorsal front wing. The thickness control is presumably easier in the lower order interference, because the thickness is less sensitive to the wavelength of reflection. What is the advantage of using the second-order interference in producing the green colour? The infrared reflection is probably not related to that, because it cannot be seen by usual insect or bird vision. One possibility is that the colour mixing effect is intended as mentioned in §4, since it is common that insects detect ultraviolet light. Area C5, which looks green to human vision, may have a completely different colour for the sunset moth, owing to the mixture with ultraviolet light. If the first-order interference causes the green colour, such a colour mixing effect cannot be obtained, because the second-order peak would be located in the wavelength region too short to be detected by usual insect vision.

It has already been reported that the wing of the sunset moth exhibits another colour mixing effect, which is caused by the strong curvature of the scale (Berthier et al. 2006; Yoshioka & Kinoshita 2007): there exist two paths of reflection, direct and dual reflections, and they have different spectra from each other owing to the difference in the incidence angle of light to the multilayer structure. When the direct reflection is assumed to have the reflectance peak at 549 nm, which is estimated by the parameters in table 1 for C5, the dual reflection is expected to cause the peak at 464 nm according to the model proposed previously (Yoshioka & Kinoshita 2007). On the other hand, the third-order interference appears at the much shorter wavelength of 366 nm. Thus, the two mixed colours are much more different in this mixing mechanism, although the polarization effect is not observed. Here we note that a few recent studies suggest that a similar colour mixing mechanism works in the rock dove's vision by comparing the visual sensitivities and the reflectance of the iridescent neck feather (Yin et al. 2006; Yoshioka et al. 2007).

Recently, the mathematical model called the reaction–diffusion system has been successfully applied to the various patterns in animal coats (e.g. Murray 1993; Kondo & Asai 1995; Sekimura et al. 2000; Liaw et al. 2001; Prum & Williamson 2002). The model was originally proposed by Turing (1952), and it relates to the spatial and temporal variations of some chemical materials, called morphogens, which induce pigment production. With regard to the wing patterns of butterflies and moths, the reaction–diffusion system is thought to work, for example, in the first step of the developmental process of the eyespot pattern (Nijhout 1990, 1991). Namely, the centre of the eyespot is determined first by the reaction–diffusion system that assumes the veins as the morphogen source. Second, another morphogen emanates from the centre, and the neighbouring scale-forming cells are induced to produce pigments depending on the local concentration of the morphogen. Even if the simple diffusion phenomenon is considered in the second process, several concentric rings with different colours or other complicated patterns can be generated if the scale-forming cells are capable of having several thresholds of morphogen concentration for the activation of pigment production (Murray 1981; Bard & French 1984; Nijhout 1991).

By inspecting the wing pattern of the sunset moth on the basis of the idea of the morphogen, which is assumed to control the thickness of the cuticle layers, we can note that the structurally produced colour pattern of the dorsal hind wing can be explained similarly to the pigmentary eyespot pattern, because the pattern of the dorsal hind wing seems partially concentric as shown in figure 1a: the dark red part is surrounded by an orange region and by an outer yellow region. Further, the smooth change in the height of the bar in figure 5a may imply that the cuticular thickness is smoothly related to the morphogen concentration, in contrast to the discrete response of the pigment production in the pigmentary eyespot pattern.

However, the simple diffusion model does not seem to explain the pattern formation of the ventral side of the hind wing, because the cuticular thickness rapidly changes in small regions without obvious relation to the venation pattern. This implies abrupt changes in the morphogen concentration, if the smooth response of the cuticular thickness is assumed. A more complicated system such as a reaction–diffusion system, including inhibitors and activators, may work in the patterning process. Theoretical modelling and subsequent predictions for cautery or cutting experiments of the wing will give us a better understanding of the system, as performed for a polymorphic papilio butterfly (Sekimura et al. 2000; Madzvamuse et al. 2002). We have not paid much attention so far to the existence of black patches on the wings. This pattern also implies that another reaction–diffusion system is involved.

The present study reveals that the scale-forming cells of the sunset moth have a surprisingly sophisticated mechanism to develop microstructures, one that uses even higher order optical interference, and also to produce the colour variation by properly controlling the cuticular layer thickness. In addition, the previous study showed that the scale structure is also modified in size much larger than the wavelength of light (Yoshioka & Kinoshita 2007). These sophisticated structural modifications cause the various unusual optical effects, and they look quite interesting, at least from the physical or optical viewpoint. However, their biological significance is still an open question at present. Physiological studies of the vision system and also behavioural studies of the sunset moth are strongly encouraged to clarify whether or not the discovered optical effects actually have adaptive meanings.