The genetic code can cause systematic bias in simple phylogenetic models

Abstract

Phylogenetic analysis depends on inferential methodology estimating accurately the degree of divergence between sequences. Inaccurate estimates can lead to misleading evolutionary inferences, including incorrect tree topology estimates and poor dating of historical species divergence. Protein coding sequences are ubiquitous in phylogenetic inference, but many of the standard methods commonly used to describe their evolution do not explicitly account for the dependencies between sites in a codon induced by the genetic code. This study evaluates the performance of several standard methods on datasets simulated under a simple substitution model, describing codon evolution under a range of different types of selective pressures. This approach also offers insights into the relative performance of different phylogenetic methods when there are dependencies acting between the sites in the data. Methods based on statistical models performed well when there was no or limited purifying selection in the simulated sequences (low degree of dependency between sites in a codon), although more biologically realistic models tended to outperform simpler models. Phylogenetic methods exhibited greater variability in performance for sequences simulated under strong purifying selection (high degree of the dependencies between sites in a codon). Simple models substantially underestimate the degree of divergence between sequences, and underestimation was more pronounced on the internal branches of the tree. This underestimation resulted in some statistical methods performing poorly and exhibiting evidence for systematic bias in tree inference. Amino acid-based and nucleotide models that contained generic descriptions of spatial and temporal heterogeneity, such as mixture and temporal hidden Markov models, coped notably better, producing more accurate estimates of evolutionary divergence and the tree topology.

1. Introduction

Phylogenetic trees and the substitutions between nucleotides that occur on them can tell us about the evolutionary history of sequences and how the biomolecules they encode have adapted to their environment. Inferences about the tree have helped answer the questions ranging from the origins of the metazoa (Baldauf et al. 2000; Rokas et al. 2005) to the detailing transmissions of HIV from chimpanzees to humans (Hahn et al. 2000), whereas inferences about the evolutionary process have helped identify which genes are under adaptive selection in a variety of lineages (Yang et al. 2000; Clark et al. 2003) and can be used to improve the estimates of protein structure (Thorne et al. 1996). The ability to draw reliable inferences about evolution relies on accurately quantifying the number of substitutions that have taken place on different lineages in an evolutionary tree (Yang et al. 1995; Felsenstein 2004).

The conceptually simplest approach for making evolutionary inferences is to use maximum parsimony (MP), which counts the number of changes between sequences (Fitch 1971; Steel & Penny 2000). MP has been shown to have a significant drawback, in that it chronically underestimates the number of changes that have taken place between divergent sequences, because it assumes that for each site in an alignment only a single change may occur on a branch. Felsenstein (1978) showed that this underestimation of changes can lead to systematic errors in the phylogenetic tree estimate, whereby the longer the sequences one uses for tree estimation the more certain one becomes of the wrong answer. This observation of long-branch attraction has acquired the spooky sobriquet of the ‘Felsenstein zone’ and many simulation studies have examined its properties. Early research demonstrated that the Felsenstein zone occurs in real sequence data, where several long branches in a tree appear to incorrectly group together under MP estimates, but the long branches separate when examined using more advanced methodology (Huelsenbeck 1997). Studies on simulated data have shown that statistical methods, such as maximum likelihood or Bayesian inference, can accurately recover trees in the Felsenstein zone (Kuhner & Felsenstein 1994), and research on real sequence data has shown that more realistic models of substitution recover more biologically plausible trees (Baldauf et al. 2000; Delsuc et al. 2005). Furthermore, theoretical work has shown statistical methods are consistent when correct models of substitution are used (Rogers 1997; Allman & Rhodes 2006), in that they become progressively more able to recover a correct estimate of the tree topology as longer sequences are used. The excellent performance of statistical methods and the development of more sophisticated algorithms and user-friendly software (Posada & Crandall 1998; Swofford 1998; Whelan 2007) have led to their widespread use in phylogenetics and growing confidence in the results produced.

What remains open is the question of the conditions under which statistical methods, such as maximum likelihood or Bayesian inference, go awry. Although in many cases statistical methods are reasonably robust, overly simple models have been demonstrated to cause systematic errors (Sullivan & Swofford 1997; Buckley et al. 2001). Several studies have also shown that statistical methods run into difficulties when data come from a single tree, but different sets of branch lengths act on different parts of the sequences. For example, Kolaczkowski & Thornton (2004) used simulations to demonstrate that trees with a mixture of branch lengths can lead to systematic bias in statistical methods, and more theoretical work by Matsen & Steel (2007) showed that such mixtures can also cause non-identifiability of the tree estimate, whereby no amount of data can distinguish between a set of potential tree topologies. Rather than examining mixtures of branch lengths, I investigate how the dependencies between sites in a sequence during evolution affect phylogenetic inference. Such dependencies can take many forms of varying complexity, ranging from simple dependencies between a pair of nucleotides, such as CpG hypermutation, to complex interactions between amino acids in proteins, or nucleotides in RNA, that maintain structure and function.

In this study, I use the dependencies between nucleotides induced by the genetic code as a test system to investigate how the dependencies affect phylogenetic inference. Using the genetic code as the source of dependencies within the data has several benefits: it is well characterized; there are simple models developed to describe it; and it occurs in many of the sequences used for phylogenetic inference. How these dependencies manifest can be demonstrated by considering the pattern of evolution occurring at a nucleotide occupying the third position in a codon. The first two positions in the codon define how this nucleotide evolves: in a fourfold degenerate codon the nucleotide is unconstrained and relatively free to change, in a twofold degenerate codon the nucleotide will tend to accept only transition mutations, whereas in a onefold degenerate codon the nucleotide will be highly constrained because every mutation causes an amino acid change. This dependency between codon positions induces complicated patterns of rate variation across the sequences. Furthermore, a non-synonymous change can alter the degeneracy of the third position, causing its pattern of substitution to differ during time; a phenomenon called temporal heterogeneity (Whelan 2008).

To investigate this effect, I simulate data from a standard codon model under three selective regimes: strong purifying selection; mild purifying selection; and selective neutrality. In addition to describing a range of plausible biological scenarios, these three regimes also serve to provide a measure of the degree of dependencies between the sites in a codon, with the three scenarios representing high, mild and no dependency. I examine how a set of models, describing both nucleotide and amino acid substitutions, that do not explicitly model the dependencies within the data, and have no knowledge of the genetic code, perform when used to estimate the amount of divergence between sequences and when estimating the phylogenetic tree. No single model outperforms all others in all of the simulation conditions examined, although nucleotide models that allow for spatial and temporal heterogeneity in evolution tend to do well. Differences in performance between model types are most evident under the conditions describing strong purifying selection (high dependency between sites), demonstrating that as the dependencies become more prevalent, models become more prone to error. These observations are reflected when examining the performance of different models for performing tree estimation, with models that seriously underestimate evolutionary distance tending to perform badly at tree estimation.

2. Methodology

(a) Simulation

All simulations are performed using the Evolver program from the PAML package (Yang 2007). Simulated sequences are all arbitrarily set to a length of 500 codons (1500 nucleotides), which is intended to represent a reasonably long protein. Varying the length of the sequences has qualitatively little impact on the interpretation of the results, although as one would expect, the variance of parameter estimates is inversely correlated with sequence length (results not shown). Simulations are performed using the M0 codon model (Yang et al. 2000) defined by the following instantaneous rate matrix:

$$Q_{i_1{i}_2{i}_3,j_1{j}_2{j}_3}=\{\begin{array}{cc}{\pi }_{j_1{j}_2{j}_3},& \begin{array}{l}\text{when}{i}_1{i}_2{i}_3\text{and}{j}_1{j}_2{j}_3\\ \text{differ}\text{by}\text{a}\text{single}\\ \text{synonymous}\text{transition},\end{array}\\ \kappa {\pi }_{j_1{j}_2{j}_3},& \begin{array}{l}\text{when}{i}_1{i}_2{i}_3\text{and}{j}_1{j}_2{j}_3\\ \text{differ}\text{by}\text{a}\text{single}\\ \text{synonymous}\text{transversion},\end{array}\\ \omega {\pi }_{j_1{j}_2{j}_3},& \begin{array}{l}\text{when}{i}_1{i}_2{i}_3\text{and}{j}_1{j}_2{j}_3\\ \text{differ}\text{by}\text{a}\text{single}\\ \text{nonsynonymous}\text{transition},\end{array}\\ \omega \kappa {\pi }_{j_1{j}_2{j}_3},& \begin{array}{l}\text{when}{i}_1{i}_2{i}_3\text{and}{j}_1{j}_2{j}_3\\ \text{differ}\text{by}\text{a}\text{single}\\ \text{nonsynonymous transversion},\end{array}\\ 0,& \text{otherwise}.\end{array}$$

The transition-to-transversion rate ratio parameter, κ, was taken to be 2.5 for all simulations. The parameters for the codon frequencies, ${\pi }_{j_1{j}_2{j}_3}$, are defined using the F3X4 model, whereby each codon position has a different nucleotide frequency. I use the frequencies of the β-globin sequences of 17 vertebrates provided in the MCcodon.dat file taken from the PAML, where the frequencies of {A,C,G,T} for the first, second and third codon positions are {0.24,0.23,0.39,0.14}, {0.33, 0.21, 0.15, 0.31} and {0.06, 0.34, 0.33, 0.27}, respectively. These parameters are taken to be the representative of the parameter sets that occur in real sequences and preliminary work indicated that other sets of parameters yielded similar results (not shown).

Three different values of the synonymous-to-non-synonymous rate ratio, ω, are examined in this study. The first, ω=0.05, represents pervasive purifying selection acting in a protein, which is likely to be the case for the majority of coding sequences. A regime of strong purifying selection also represents a high degree of dependence between the three codon positions, introducing the potential of spatial and temporal heterogeneity into the substitution process. Under this regime, there are on average 7.5 synonymous substitutions before a non-synonymous change. The second selective regime, ω=0.5, is representative of moderate purifying selection and represents mild dependencies between the codon positions. There are on average 1.6 synonymous changes per non-synonymous change, which means that little time is spent in, for example, a two- or fourfold degenerate state and the dependencies may not be obvious in the data. The final selective regime, ω=1.0, is the case of a neutrally evolving protein and represents extremely limited dependencies between the codon positions, although the continued lack of stop codons does mean a very small degree of dependency still exists.

(b) Branch length estimates

The effect of the genetic code on branch length estimates is quantified using data simulated under an unrooted six-species tree with leaf labels {s1, …, s6} and equal branch lengths of α: ((s1:α, s2:α):α, (s3:α, s4:α):α, (s5:α, s6:α):α). For this tree, there are six external and three internal branches, which are defined as those leading to a leaf of the tree and those that connect only internal nodes of the tree, respectively. The simulations are used to examine how well models estimate different types of evolutionary distances by varying total simulated tree lengths between 0.1 and 10.0. A total of 50 simulated sets of sequences were produced for each of the tree lengths examined. For each set of sequences, branch lengths are estimated under each of the seven inferential methods described below and three different statistics are computed.

The first statistic, used in figure 1, is the median tree length inferred from the 50 simulated datasets, and reflects how accurate different methods are at inferring the amount of evolution that has occurred on a tree. The second statistic, used in figure 2, reflects the relative amount of evolution that has occurred on internal and external branches in an evolutionary tree. For each of the simulated datasets, I calculate the ratio of the average internal and external branch lengths, and for each set of 50 simulated sequences, I report the median ratio. Note that I chose to present the median for these two sets of statistics because the distribution of inferred tree lengths is non-symmetric and bounded at zero for low values. These conditions can result in high-average inferred tree lengths for divergent sequences and hinder the interpretation of results.

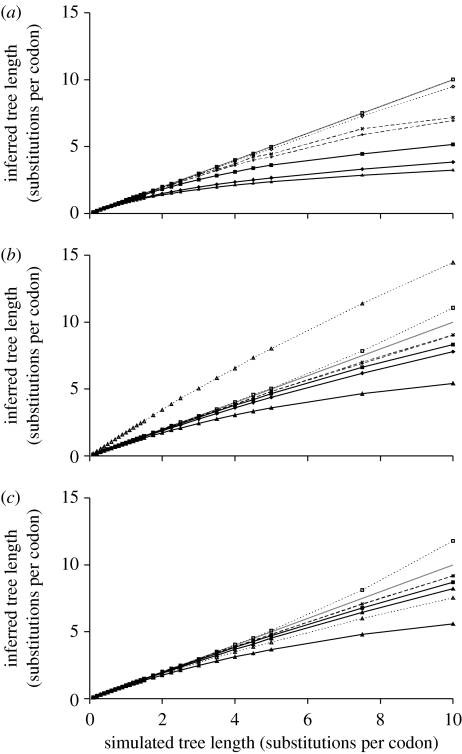
Figure 1.

The degree of evolutionary change inferred by a range of phylogenetic methods compared with the simulated amount of evolutionary change under (a) strong, (b) mild and (c) no purifying selection. Filled triangles, MP; filled diamonds, Jukes Cantor (JC); filled squares, Hasegawa, Kishino Yano (HKY)+Γ; pluses, mixture model (MM); crosses, temporal hidden Markov model (THMM); open diamonds, equiprobable (EQU); open squares, Whelan and Goldman (WAG)+F+Γ; grey solid line, inferred equals simulated.

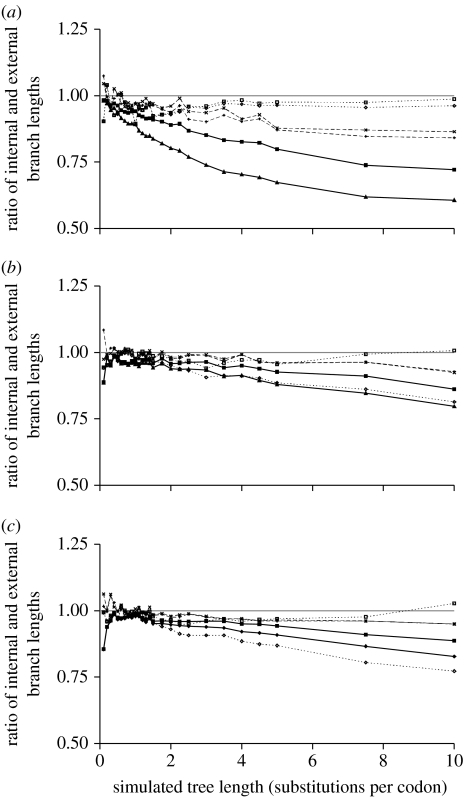
Figure 2.

The ratio of inferred internal branch lengths divided by inferred external branch length under a range of phylogenetic methods under (a) strong, (b) mild and (c) no purifying selection. Filled diamonds, JC; filled squares, HKY+Γ; pluses, MM; crosses, THMM; open diamonds, EQU; open squares, WAG+F+Γ; grey solid line, inferred equals simulated.

The final set of statistics, used in table 1, measures how inferred internal and external branch lengths differ from the simulated values across all simulated tree lengths. For the external and internal branches of each of the six statistical methods, the area between the line describing the simulated branch length and the median inferred branch length is calculated using the standard trapezoid numerical integration. If a method estimates branch lengths accurately, the value of the integral difference will be approximately 0.0, and for the methods that over- and underestimate branch lengths, the integral difference will be greater than and less than 0.0.

Table 1.

Integral difference between the branch length of the tree used to simulate sequences and the average estimated internal and external branch lengths. (Values given are estimates of the area between the simulated and inferred branch lengths. See §2 for details.)

	ω
	0.05		0.5		1.0
	internal	external	internal	external	internal	external
JC	−0.45	−0.35	−0.21	−0.10	−0.21	−0.10
HKY+Γ	−0.37	−0.27	−0.16	−0.08	−0.12	−0.06
MM	−0.23	−0.18	−0.09	−0.05	−0.09	−0.05
THMM	−0.21	−0.16	−0.07	−0.05	−0.07	−0.04
EQU	−0.05	−0.03	−0.19	−0.09	−0.28	−0.20
WAG+F+Γ	−0.01	0	0.07	0.06	−0.12	0.10

(c) Phylogenetic tree estimates

The simulations investigating the performance of phylogenetic tree estimates use an unrooted four-species tree with leaf labels {s1, …, s4} and two sets of branch lengths α and β: ((1:α, 2:β):β, 3:α, 4:β). These simulations follow the experimental design of early studies (e.g. Huelsenbeck & Hillis 1993) for investigating whether the models examined exhibit the evidence of systematic bias in tree estimation: the values of the long branch, α, range between 0.2 and 2.0 in steps of 0.2, whereas the values of the short branch, β, vary from 0.02 to 0.2 in steps of 0.02. For each simulation condition of α and β, a total of 50 sets of sequences are simulated and likelihoods calculated under the three possible unrooted tree topologies linking four sequences (Felsenstein 2004). For each simulation condition, the statistic presented is the overall proportion of times the correct tree is inferred from the 50 sets of sequences. In some sets of sequences, a group of tree topologies may have the same optimal score, defined by having the same MP score or their log likelihood being within 10⁻³ of one another. These sets contribute as one-half or one-third of a correct topology estimate for group sizes of two and three trees, respectively.

(d) Inference

This study examines a range of substitution models to see whether they are capable of recovering accurate estimates of branch lengths and tree topologies from data simulated under a codon model. The models include a range of the most popular choices for phylogenetic inference, and a few more exotic choices that could be expected to perform well under these conditions. The performance of the generative model used for simulation is also briefly discussed in §3. The evolutionary distances (tree lengths) inferred by all models are scaled to the number of substitutions per site per codon, allowing meaningful comparison between models (details not shown). All parameter estimates from the substitution models are obtained using maximum likelihood in the usual manner.

(i) Maximum parsimony

The simplest method for quantifying the amount of substitution occurring on a branch of a tree is MP. This study uses the algorithm described by Fitch (1971) to calculate the minimum number of discrete changes on the tree required to describe the observed sequences. MP has been shown to be inconsistent under many conditions, and I have included it in this study as a benchmark for comparing other methods. Note that MP does not use an explicit statistical model to estimate the number of changes occurring on a tree and is therefore referred to as a method but not a model in the following discussion.

(ii) Nucleotide substitution models (JC/HKY+Γ)

Two simple models of nucleotide substitution are examined. The Jukes Cantor (JC) model provides the simplest description of DNA substitution possible by having all nucleotides replace one another with equal rate, whereas the Hasegawa Kishino Yano (HKY)+Γ model allows for unequal nucleotide composition, transition substitution bias and Γ-distributed rates across the sites (Whelan et al. 2001). For brevity, these two models have been chosen to be the representative of the range of simple models that are frequently used for phylogenetic analysis, with HKY+Γ containing many of the factors used by the generative model. Preliminary studies suggest that the performance of other standard nucleotide models not included in these analyses is fairly predictable, with General Time Reversible (GTR)+Γ performing marginally better than HKY+Γ and other models falling in between the models presented. In common with the amino acid models discussed below, the single most important factor for improving the accuracy of the estimates seems to be the Γ distribution, although the further investigation necessary to confirm this observation is beyond the scope of this study.

(iii) Models of heterogeneous nucleotide substitution (MM/THMM)

The rates at which the nucleotides substitute one another over time are known to be highly variable and this heterogeneity can be broken down into two types. Spatial heterogeneity occurs when individual columns in an alignment evolve differently, such as having different overall rates at different sites, but the evolutionary process at a column remains constant through the evolutionary tree. Temporal heterogeneity occurs when the evolutionary process in a column in a sequence alignment changes through time by varying through the evolutionary tree. Mixture models (MMs) and temporal hidden Markov models (THMMs) provide general methods for describing the spatial and/or temporal heterogeneity in sequence evolution (Whelan 2008). A THMM describes nucleotide substitution using a series of hidden classes, each with a different mode of nucleotide substitution, and all classes switch between one another during evolution. For example, the covarion model (Tuffley & Steel 1998) is a THMM that describes nucleotide evolution using two classes: an ‘on’ class where nucleotide substitution can occur, and an ‘off’ class where the nucleotide cannot change. Over time, an ‘off’ nucleotide will occasionally switch to being an ‘on’ nucleotide, and vice versa. The THMM used in this study is more general and comprises two hidden classes, each described by a separate HKY sub-process. Each observed nucleotide {A, C, G, or T} belongs to one of these two sub-processes, which means that the substitution model needs to describe the rate of change between the labelled nucleotides {A¹, C¹, G¹, T¹, A², C², G², T²}. The THMM can therefore be defined by the following instantaneous rate matrix:

The two light-coloured quadrants describe the two separate HKY substitution sub-processes, with, ${\pi }_{{\text{A}}^k}$, ${\pi }_{{\text{C}}^k}$, ${\pi }_{{\text{G}}^k}$, and ${\pi }_{{\text{T}}^k}$ defining the nucleotide frequencies, κ^k defining the transition-to-transversion rate ratio and μ^k describing the overall substitution rate of the kth process. These two HKY classes are linked by a reversible ‘switching’ process that allows nucleotides to change which hidden class they belong to over time, and are described in the shaded quadrants of Q. The π¹ and π² parameters are the probabilities of the first and second hidden classes, respectively, the ρ parameter controls the overall rate of change between hidden classes and the other parameters are the nucleotide frequencies of the two classes. The stationary distribution of the whole process can be trivially obtained from the ${\pi }_{{\text{X}}^k}$ and π^k parameters.

This THMM is a flexible model that describes both spatial and temporal heterogeneity. At any point in time, each site in a sequence is considered independently and can belong to either of the two classes and has the potential to evolve under very different substitution processes, which allows spatial heterogeneity along the sequence alignment. The switching process enables the sites to change between the two classes during evolutionary time, introducing temporal heterogeneity into the model. The THMM can be reduced to an MM by fixing ρ to 0, which prevents switching between hidden classes (for details, see Whelan 2008). A MM therefore retains its ability to describe spatial heterogeneity in sequence evolution, but cannot describe temporal heterogeneity. Analysis under MMs and THMMs is performed using Leaphy, a program for phylogenetic inference written by the author and available at http://www.bioinf.manchester.ac.uk/leaphy/. Note that numerical parameter estimation for MMs and THMMs can be troublesome, so all analyses using these models take the parameters from the best likelihoods found from three different sets of starting values. This precaution does not guarantee that globally optimal likelihoods are found every time, but preliminary analysis suggests that parameters investigated in this study, and the conclusions drawn, do not appear to be adversely affected by occasional suboptimal parameter sets.

(iv) Amino acid substitution models (EQU/WAG+F+Γ)

Frequently, phylogenetic analysis is performed using amino acid sequences, particularly when looking at deep relationships in the tree. The codon-simulated sequences used in this study can be recoded as amino acid sequences, which will lose some information because it reduces the 64 codons to 20 amino acids. Performing this reduction assumes knowledge of the genetic code, but amino acid models are included in the analysis to investigate whether biological knowledge and recoding can be used to address the problems introduced by the dependencies between sites.

Two standard models of amino acid substitutions are examined in this study, representing a simple and sophisticated description of protein evolution. The first is the simple equiprobable (EQU) model, which is the amino acid equivalent of the nucleotide JC model, and describes all amino acid substitutions as equally likely. The second is the Whelan and Goldman (WAG)+F+Γ model, which allows for different rates of substitution between amino acids, amino acid frequencies of the model to reflect those of the observed data and Γ-distributed spatial heterogeneity in rate.

3. Results

(a) Estimates of evolutionary divergence

Figure 1a–c shows the simulated tree lengths between sequences compared with the median tree length inferred by a range of phylogenetic models under strong, medium and no purifying selection, respectively. The range of tree length in these simulation conditions is quite conservative and covers the kind of data many evolutionary biologists study, with a tree length of 10 representing an average branch length on the tree of 0.37 substitutions per nucleotide site. The number of amino acid substitutions this tree length represents depends on the degree of purifying selection acting: ω=0.05 (high), 0.5 (medium) and 1.0 (none) results in 0.05, 0.22 and 0.28 amino acid substitutions per branch per site, respectively.

All nucleotide-based methods underestimate the tree lengths as the sequences become more divergent, although the range of tree lengths for which they perform well and the degree to which they underestimate the distances varies substantially between the models and the simulation conditions. In general, the degree of underestimation in the tree length correlates with the strength of the purifying selection, with the high purifying selection simulations producing the most extreme underestimates of the tree length. In agreement with many previous studies (e.g. Felsenstein 1978), MP performance is the worst of all of the methods examined and its poor performance was most noticeable for divergent sequences. The second and third worst-performing methods are JC and HKY+Γ, respectively, with the high purifying selection simulations producing the greatest underestimation of the tree length and the greatest difference in their relative performance. The final two nucleotide methods, MM and THMM, all perform very similarly when there is no purifying selection (figure 1c): from a simulated tree length of 10, these methods estimate a median tree length of 9.16 and 9.18, respectively. The different relative performance of these models was only noticeable for the strong purifying selection simulations, where THMM consistently provides better estimates of the tree length than MM. This difference between THMM and MM is approximately the difference between MP and JC, demonstrating that the models that incorporate temporal heterogeneity offer real improvements.

The performance of the amino acid-based methods is highly dependent on the simulation conditions. Under the strong purifying selection conditions, both EQU and WAG+F+Γ provide very good estimates of tree length, with median WAG+F+Γ having near-perfect correlation with simulated tree length. For the medium and no purifying selection regimes, WAG+F+Γ continues to perform very well, with a slight tendency to overestimate the number of amino acid substitutions in more divergent sequences. The estimates provided by EQU, however, were unstable and were the worst of the model-based methods under the other simulation conditions. For example, in the medium purifying selection conditions, it chronically overestimated tree length and performed worse than parsimony for low simulated tree lengths.

(b) Estimates of external and internal branch lengths

The shape of the six-species tree used to simulate data also allows a meaningful comparison between the estimates of external and internal branch lengths because all branches in the tree have the same patterns of connections and the tree has rotational symmetry. Figure 2a–c shows the median ratio of the average internal and external branch lengths estimates (see §2) under strong, medium and no purifying selection, respectively. Under the simulation conditions used, if the inference procedure is unbiased, the average ratio will be 1.0 for both internal and external branches. Figure 2 shows that for many methods internal branch lengths tend to be shorter than the estimates of external branch lengths, particularly for divergent sequences. A different aspect of these results is presented in table 1, which measures the total difference between the branch lengths used to simulate the sequences and the estimated internal and external branch lengths (see §2). The table shows that the majority of methods under all three selective regimes tend to underestimate all branches, and that internal branches are more severely underestimated than external branches.

The relative degree of underestimation in branch lengths is most extreme for the strong purifying selection regime (figure 2a; table 1). For example, under a simulated tree length of 10 with equal branch lengths, HKY+Γ average estimates of internal branches are 0.72 times the length of external branches. The relative performance of different models varies with simulated tree length. For short trees with a tree length of less than 1.0, there is little to choose between the methods, although inference under JC does tend to underestimate internal branches a little more than other methods. Between simulated tree lengths of 1.0 and 5.0, a clearer pattern emerges. All nucleotide-based methods start to significantly underestimate internal branches, with JC, and to a lesser extent HKY+Γ, performing particularly poorly. The other two nucleotide methods all tend to perform reasonably well, although there is a consistent ordering to their performance: THMM tends to outperform MM. For tree lengths of 3.0, for example, the internal-to-external branch length ratio is 0.94 and 0.90 for THMM and MM, respectively. This relative ordering of the nucleotide models is also reflected in the integral differences presented in table 1. From simulated branch lengths of 5.0–10.0, JC and HKY+Γ continue their decline in performance, whereas THMM and MM both tend to perform reasonably. Methods based on amino acid sequences generally performed better than the nucleotide models: EQU and WAG+F+Γ both closely track 1.0 for simulated tree lengths greater than 3.0, with WAG+F+Γ providing marginally better estimates than EQU. Between simulated tree lengths of 0.1 and 3.0, there is little to choose between the better performing nucleotide methods and either of the amino acid methods.

The results for the mild (figure 2b) and no purifying selection (figure 2c) regimes are generally very similar, with the marked exception of EQU, which goes from being the second best-performing model to the worst-performing model. The JC and HKY+Γ models provide the poorest estimates of branch lengths, although are substantially better estimates than under the strong purifying selection regime. The performance of THMM and MM is similar for both regimes, suggesting little benefit of one method over another when there are mild to no dependencies between the codon positions, which is expected because it is these dependencies between the codon positions that introduce temporal heterogeneity. For the amino acid sequences, WAG+F+Γ continues to be the best-performing method, although its supremacy over the nucleotide methods declines.

(c) Phylogenetic tree estimates

Figure 3 shows the overall performance of different methods in estimating phylogenetic trees, and the results reflect many of the observations made about the estimates of evolutionary divergence above. The weakest method for inferring the correct phylogeny is MP, which is expected from previous studies. However, the dependencies between codon sites in the strong purifying selection group exacerbate the systematic bias in MP, further reducing its ability to accurately infer phylogenies. For the mild and no purifying selection regimes, there is an unusual improvement in performance for the method for high values of α and low values of β. This anomaly seems attributable to the unequal base composition between the codon positions (F3X4) in the generative model: when data are simulated with the same base frequencies at each codon (F1X4), the effect disappears (results not shown).

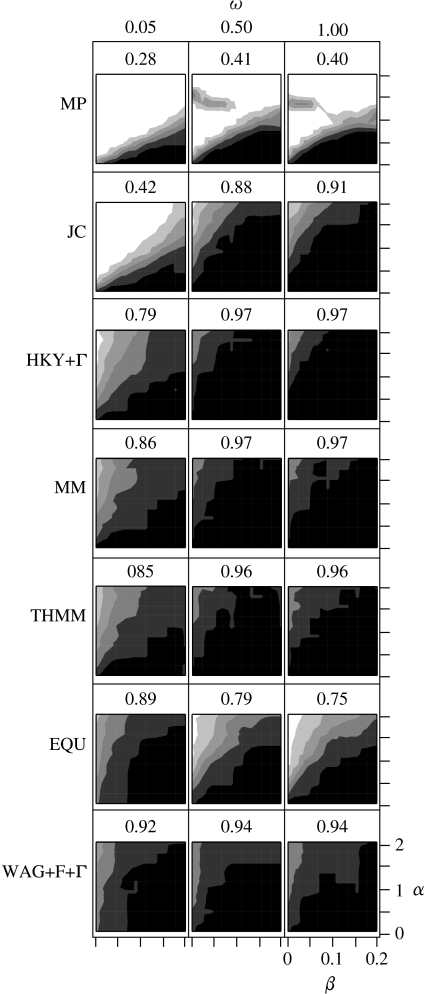
Figure 3.

Performance of phylogenetic tree estimation by a range of methods under different simulation conditions. The numbers above each plot describe the average probability of a method recovering the tree used to simulate the data. The square plots show the distribution of this probability (see text for more details), with probabilities covered by the following ranges: , 1.0; , 0.8–0.99; , 0.6–0.79; , 0.4–0.59; , 0.2–0.39; , 0–0.19.

There is a notable drop in the performance of all the nucleotide-based statistical methods under the strong purifying selection regime relative to the other two regimes, demonstrating that the structure of the genetic code can have a significant effect on tree estimation. The high total accuracy of tree estimates under the mild and no purifying selection also demonstrates the general robustness of statistical methods to model misspecification. The difference in performance between selective regimes is most obvious for JC. The total accuracy of trees estimated by JC under the strong purifying selection regime (0.42) is under half than that observed under the other regimes (0.88, 0.91). This effect is also observable for the other statistical methods, with MM and THMM fairing better than HKY+Γ, particularly in the most difficult cases where α is large and β is very small. Interestingly, the nucleotide-based models marginally outperform the amino acid-based models under the medium and no purifying selection regime.

Tree estimation accuracy under amino acid-based methods also reflects their ability to estimate evolutionary divergence. The WAG+F+Γ model does very well in all conditions, maintaining an overall accuracy of greater than 0.90, and has the highest accuracy of all methods under the strong purifying selection regime. On the other hand, EQU also does well under strong purifying selection, but its performance declines under the other two regimes.

(d) Performance of the generative codon model

The performance of the codon model used to simulate the data is not presented in the results above because, as theory predicts (Rogers 1997; Allman & Rhodes 2006), it successfully estimated the parameters of interest in all cases examined. Estimates of evolutionary distance from the generative model were extremely close to the simulated distances in figure 1 and closely tracked the grey lines. Similarly, the ratio of internal to external branches was accurately estimated under the generative model. For example, for the strong purifying selection (high dependency) simulation of tree length of 7.5, the generative model estimated a median (s.e.) evolutionary distance of 7.6 (0.6), and the median estimated ratio of internal to external branches was 0.98 (0.06). The generative model also performed extremely well at estimating the evolutionary tree (figure 3), recovering the correct tree topology with a probability of 1.00.

4. Discussion

The genetic code introduces complex dependencies between the sites in a coding sequence. Most of the models commonly used for phylogenetic analysis do not incorporate this information and this study demonstrates that these dependencies, and the spatial and temporal heterogeneity they introduce, cause a bias in phylogenetic inference. This study shows that MP performs poorly, both at estimating the number of substitutions on a tree and at inferring tree topologies. For the coding sequences under strong purifying selection (high degree of dependency), this bias most severely affects simple nucleotide models, although none of the generic nucleotide models examined recover accurate estimates in all circumstances. The generic modelling approaches of incorporating rates across sites through a Γ distribution or other forms of heterogeneity with a MM or THMM both perform reasonably well, with the THMM providing notably better estimates of tree length. Models of amino acids, however, perform very well at recovering accurate tree lengths, although the limited number of amino acid substitutions means their performance in tree estimation is similar to that of the best nucleotide models. The strong performance of amino acid models also demonstrates that recoding data to remove or account for some of the stronger dependencies within the data helps phylogenetic inference. Such approaches have been very successful in describing RNA evolution (Schoniger & von Haeseler 1994), although it is unclear how simple recoding could be done for the complicated forms of dependencies resulting from, for example, protein structure.

In the regimes of mild and no purifying selection, which represent mild to no dependencies between the codon sequences, the nucleotide models performed better and this is probably attributable to the reduced dependencies acting within the data. The degree of underestimation in tree length that occurs for these models is likely to be the result of the uneven spread of nucleotide frequencies across the different codon positions. For amino acid sequences, the picture was more complex. The empirically derived WAG+F+Γ model performed reasonably well in all cases examined, but the overly simple EQU model did not. The exact causes of this are unclear, but are likely to be a result of the WAG model being estimated from real sequences, which are, of course, subject to a range of selective pressures and the genetic code.

These results demonstrate that the dependencies induced by the structure of the genetic code can cause problems for phylogenetic inference by nucleotide models. The dependencies that occur in these simulations are, however, only a small fraction, and only one aspect, of those that occur in real data. Protein coding sequences have many layers of selection acting on them beyond the genetic code, including the maintenance of protein structure and function, and interactions with other biomolecules, both at the level of the nucleotide sequence and the protein. These dependencies are unlikely to ‘cancel out’ the biases caused by the genetic code, meaning that the results of this study can be interpreted as a ‘baseline’ of what happens in real sequences. Amino acid models fare much better, but are the product of a priori knowledge of the genetic code, which allows a sequence of nucleotide to be recoded into amino acids. For many of the interactions and dependencies that occur in real data, the recoding into another form of sequence is not currently an option, but when it is, such as in RNA molecules (Schoniger & von Haeseler 1994), it is likely to substantially reduce systematic bias.

The observations in this study therefore led me to three broad conclusions about inferring evolution when there are complex dependencies between the sites in sequence data. First, simple methods erroneously underestimate the amount of evolution that has actually occurred and this underestimation can also lead to systematic error in the phylogenetic tree. Second, branches ‘deep’ within a phylogeny may tend to be underestimated more than ‘shallow’ branches. This result suggests that models that do not adequately describe sequence evolution may tend to infer deep rapid radiations and find it difficult to determine the correct order of branching, which may contribute to the continued difficulty in understanding the origins of some groups of organisms (Rokas et al. 2005; Rokas & Carroll 2006). It may also contribute to explaining node-density artefacts (Fitch & Bruschi 1987) because there is evidence that long branches tend to be underestimated more than short branches in overly simple models. Finally, statistical models describing general patterns of heterogeneity in sequence evolution can perform reasonably well when complex dependencies occur in the data. Of all the types of nucleotide models examined, mixture models and THMMs provide the best estimates of evolutionary distance and tree topology, and it would be interesting to see whether these currently underused models provide more plausible answers to pressing biological questions.