Abstract
Most theoretical models of unsteady aquatic movement in organisms assume that including steady-state drag force and added mass approximates the hydrodynamic force exerted on an organism's body. However, animals often perform explosively quick movements where high accelerations are realized in a few milliseconds and are followed closely by rapid decelerations. For such highly unsteady movements, the accuracy of this modelling approach may be limited. This type of movement can be found during pivot feeding in pipefish that abruptly rotate their head and snout towards prey. We used computational fluid dynamics (CFD) to validate a simple analytical model of cranial rotation in pipefish. CFD simulations also allowed us to assess prey displacement by head rotation. CFD showed that the analytical model accurately calculates the forces exerted on the pipefish. Although the initial phase of acceleration changes the flow patterns during the subsequent deceleration phase, the accuracy of the analytical model was not reduced during this deceleration phase. Our analysis also showed that prey are left approximately stationary despite the quickly approaching pipefish snout. This suggests that pivot-feeding fish need little or no suction to compensate for the effects of the flow induced by cranial rotation.
Keywords: feeding, Syngnathidae, computational fluid dynamics, hydrodynamics, unsteady rotation
1. Introduction
Simple mathematical models are widely applied in biomechanics because they are useful in studies of the relationship between form and function in animals (for a review, see Alexander 2003). Inverse dynamics models, in which motion is prescribed while forces are calculated based on Newton's second law, are probably the most common types of biomechanical models. Examples vary from calculations of the muscular force required to produce tongue projection during prey capture in chameleons (de Groot & van Leeuwen 2004), salamanders (Deban et al. 2007) and toads (Lappin et al. 2006) to studies of aerodynamic forces on flapping wings by modelling them as blade elements (i.e. sectioning the wing along its span into distinct units characterized by a certain width and distance to the axis of rotation; e.g. Osborne 1951; Ellington 1984; Zanker & Götz 1990). However, several studies have shown that the accuracy of simple inverse dynamics models can be limited for structures of complex geometry moving unsteadily through relatively viscous fluids (e.g. Ellington et al. 1996; Liu et al. 1998; Lan & Sun 2001; Nauwelaerts et al. 2005).
One of the most extreme cases of unsteady aquatic movements studied so far in vertebrates is the explosively quick dorsal rotation of the head when fishes of the suborder Syngnathoidei capture prey (Alexander 1970; Muller 1987; Bergert & Wainwright 1997). Since the majority of the species in this group (which includes pipefishes, seahorses and seadragons) have a relatively long snout (Kuiter 2003), the observed cranial rotations of more than 20° in less than 5 ms can rapidly bring the mouth closer to the prey (Bergert & Wainwright 1997; de Lussanet & Muller 2007; Van Wassenbergh et al. 2008). High cranial acceleration (more than 105 rad s−2) followed shortly by deceleration, which is only slightly lower in magnitude, characterizes prey capture in the pipefish Syngnathus leptorhynchus (Van Wassenbergh et al. 2008). After this phase, lateral expansion of the snout causes the prey to be sucked into the mouth (de Lussanet & Muller 2007). This feeding mode, also referred to as pivot feeding (de Lussanet & Muller 2007), differs from what is typically observed in suction-feeding teleost fishes, where the crucial function of cranial dorsal rotation lies in contributing to mouth opening and expansion of the mouth cavity (e.g. Lauder 1985; Carroll et al. 2004; Wainwright et al. 2007) rather than in rapidly decreasing distance to the prey.
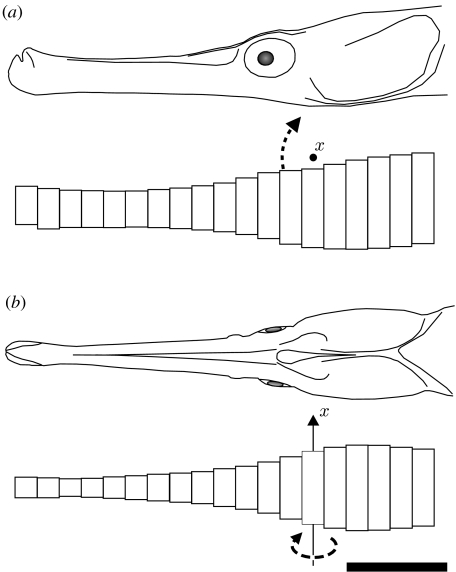
A recent inverse dynamics model indicated that a release of elastic energy from the post-cranial tendons (epaxial and hypaxial tendons) is necessary to explain the observed instantaneous rotational accelerations and velocities of the head of S. leptorhynchus (Van Wassenbergh et al. 2008). In analogy with blade-element models, this model divided the head of the pipefish into a series of elliptical cylinders, each characterized by a specific width, height and distance from a fixed axis of rotation (figure 1; for details, see Van Wassenbergh et al. 2008). For each of these elliptical cylinders, an equation of motion was solved that separated the force exerted by the surrounding water on the pipefish head into two components: steady-state drag force and added mass force.
Figure 1.
Schematic of the elliptical cylinder model of the head of the pipefish S. leptorhynchus (Van Wassenbergh et al. 2008) from a (a) lateral and (b) ventral view. The axis (x) and direction (dashed arrows) of rotation is indicated. Scale bar, 5 mm.
Including these two forces (steady-state drag and added mass) in analytical models of unsteady aquatic movement can be considered as the classical approach (e.g. Lighthill 1975; Daniel 1984; Denny et al. 1985; Gal & Blake 1988; Daniel & Meyhöfer 1989). Several studies on the mechanics of undulatory swimming found reasonably good agreement between the predictions of these mathematical models and in vivo measurements (e.g. Jordan 1992; McHenry et al. 2003). However, the accelerations and decelerations involved during pivot feeding are considerably higher in magnitude than those involved in studies of steadily swimming animals. Since the effect of acceleration magnitude on added mass coefficients is still a subject of discussion, even for flow around simple object such as spheres (Wakaba & Balachandar 2007), the accuracy of the elliptical cylinder model of pipefish pivot feeding (Van Wassenbergh et al. 2008) could be questioned.
In addition to the magnitude of acceleration, the temporal proximity of acceleration and deceleration during pivot feeding may alter the flow conditions during deceleration. This implies that forces associated with the history of the flow, i.e. Boussinesq–Basset history forces (e.g. Thomas 1992; Michaelides 1997; Maxey & Riley 1983; Candelier et al. 2004), may become important. For example, the importance of history forces that are generated by a cylinder encountering its own wake has been shown for impulsive changes in the incident flow around cylinders (Chaplin 1999). Because analytical approximations of Boussinesq–Basset history forces are currently available only for simple bodies such as spheres (Michaelides 1997) or two-dimensional cylinders (Chaplin 1999) at low Reynolds numbers, biological applications of the blade-element approach, such as the pipefish pivot feeding model (Van Wassenbergh et al. 2008), cannot include history forces in their calculations. Since the results of this model (Van Wassenbergh et al. 2008) implied that a novel ballistic mechanism of neurocranial rotation has evolved in fishes, these data have significant implications for the evolution of feeding systems in vertebrates, and since other explosive aquatic movements have been modelled using a similar approach (e.g. Daniel & Meyhöfer 1989), a test of this hydrodynamic theory is appropriate.
In an effort to validate the use of the elliptical cylinder model (Van Wassenbergh et al. 2008) for analysing the dynamics of feeding in syngnathoid fishes, we apply here computational fluid dynamics (CFD). The most general description of the relationship between force and flow in a fluid is given by the Navier–Stokes equations, which are a set of partial differential equations that are based on the conservation of mass and momentum. Finite-volume approaches in CFD solve these equations numerically for a spatial domain discretized into small cells that form a volume mesh. Doing so, we evaluate whether the dynamics of an abruptly accelerating and decelerating aquatic rigid body can still be modelled with simple analytical equations for drag force and added mass (Van Wassenbergh et al. 2008) or whether more realistic, but also more complex and computationally intensive, modelling is necessary for studying the biomechanics of this type of movement.
In addition to characterizing flow around the rotating head and snout, CFD allows characterization of flow in the region where the prey is located. Since dorsal rotation of the snout will probably cause a strong dorsally directed flow, this could result in pushing the prey away from the mouth. To evaluate whether pushing of the prey due to snout rotation is important (and needs to be compensated for by suction), simulations of prey motion due to the flow generated by the rotating snout will be performed.
2. Material and methods
Before outlining the methods used in CFD modelling, a brief description of the elliptical cylinder model will be given. Note, however, that we refer the reader to the original publication (Van Wassenbergh et al. 2008) for a more detailed overview including the mathematical formulation of this model.
2.1 Elliptical cylinder model
The head of the pipefish was divided into a series of 19 elliptical cylinders scaled to match the height and width of the head measured at specific positions on lateral- and ventral-view photographs of a specimen at rest (figure 1). The centre of rotation of the head, as well as kinematic profiles of angular velocity and acceleration, was determined from high-speed videos (2000 Hz) of pipefish capturing mysid shrimp. The moment generated by the post-cranial muscles to rotate the snout dorsally was assumed to balance with the following moments on each of the elliptical cylinders: the moment due to inertia of the head and snout (moment of inertia multiplied by angular acceleration) minus the moment due to drag force and the moment resulting from the effect of added mass (see equation (2.1)).
The drag force on a given elliptical cylinder included in the model was a function of the squared linear velocity of its centre of mass, the external surface area, the angle of attack, the density of seawater (1024.75 kg m−3) and a shape-dependent drag coefficient. Drag coefficients of (infinitely) long elliptical cylinders (Blevins 1984) were included in the model. These coefficients vary as a function of the elliptical cylinder's aspect ratio (width divided by height). It was assumed that the model operates in flow regimes where drag coefficients can roughly be considered independent of the Reynolds number Re (400<Re<2×105).
The force due to the effect of added mass was included as a function of the instantaneous linear acceleration of the centre of mass of the elliptical cylinder, its angle of attack and a shape-dependent added mass coefficient. Added mass coefficients of (infinitely) long elliptical cylinders as a function of aspect ratio, as presented by Daniel (1984), were included in the model (Van Wassenbergh et al. 2008).
2.2 Computational domain and grid
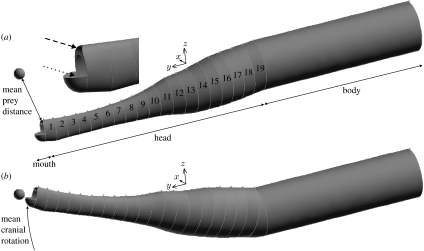
Gambit v. 2.3 (Ansys, Lebanon, USA) was used to create a three-dimensional, unstructured tetrahedral mesh around the pipefish head. The elliptical cross sections of the elliptical cylinder model (figure 1) were also used in generating this volume mesh. In order to allow a realistic three-dimensional flow, three modifications were performed to the CFD model (figure 2) with regard to the elliptical cylinder model (figure 1). Firstly, the dorsoanterior edge of the model was rounded with respect to plane of motion (figure 2). Secondly, a depressed lower jaw was modelled by attaching a hollow quarter spheroid to the ventral side of the anteriormost elliptical cylinder (figure 2). Note that opening of the mouth in pipefish by lower jaw depression occurs gradually during the phase of head rotation. Therefore, it should be kept in mind that our model potentially overestimates the volume of water that is pushed at the level of the mouth by including an opened mouth from the start of the head rotation phase. In order to preserve continuity in the flow domain at the mouth region, an intra-oral zone of water was included as well (figure 3). This intra-oral zone roughly mimics the pipefish's buccal cavity inside the snout. Thirdly, a ‘body’ was attached to the pipefish head to avoid flow around the posteriormost elliptical cylinder (figure 2).
Figure 2.
Outline of the geometry of the CFD model at the (a) start and (b) end of head rotation. The head includes 19 elliptical cylinders with cross sections equal to the model shown in figure 1. The upper jaw edge is rounded (dashed arrow) and the lower jaws are modelled as a hollow quarter spheroid (dotted arrow). The body is modelled as an elliptical cylinder translating ventroanteriorly to follow the rotation of the head.
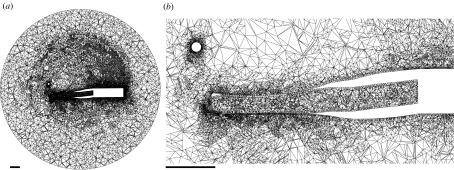
Figure 3.
Three-dimensional, unstructured tetrahedral mesh used for CFD modelling. (a) A midsagittal plane overview of the full domain including the pipefish at rest. In (b) more detailed illustrations of the increased node density around the pipefish head model are shown. Triangle sizes are on average 2 mm at the outer boundary of the domain and less than 0.2 mm at the surface of the pipefish and the prey. Scale bars, 5 mm.
In order to capture the entire flow generated by the pipefish, the flow domain around the 20.8 mm long pipefish head was modelled as a sphere with a diameter of 80 mm. The centre of this sphere corresponded to the point where the axis of rotation intersected the midsagittal plane. The surfaces of the pipefish model were meshed with a uniform triangle size of 0.2 mm (cf. minimal snout width and height are, respectively, 0.9 and 1.82 mm), while a larger spacing between the nodes of the mesh was chosen for the spherical outer boundary surface of the flow domain (triangle size of 2.4 mm).
Next, a solution-adaptive refinement of the mesh was performed in order to add cells where they were needed. To do so, the mesh was imported into the CFD solver Fluent v. 6.3 (Ansys, Lebanon, USA) that solved the Navier–Stokes equations. The model was subjected to a steady rotation of 100 rad s−1 after which additional nodes were added to the mesh at the positions in the grid where a high flow velocity gradient is calculated during this simulation (velocity-gradient hanging node grid adaptation settings: coarsen threshold of 0.3, refine threshold of 0.7, curvature method, scale normalization). This procedure was repeated once (coarsen threshold of 0.5, refine threshold of 1.2). The resulting mesh had a total of 2 606 736 cells with 5 765 011 faces connected by 713 001 nodes (figure 3).
The CFD flow solutions of the pipefish model (figures 2 and 3) rotating steadily at a range of different velocities (10–350 rad s−1; 18 simulations) were used to calculate the drag moment as a function of steady-state angular velocity. This allowed us to use a more accurate estimate of steady-state drag force than in the original model (Van Wassenbergh et al. 2008).
2.3 Moving mesh
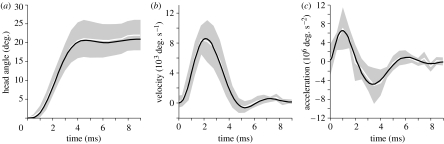
The unsteady rotation of the pipefish head was described using a Fluent user-defined function (UDF). First, a 15th order polynomial fit of the time-averaged angular acceleration profile measured for S. leptorhynchus was calculated using Microsoft Excel equipped with the XLXtrFun add-in functions (Advanced Systems Design and Development, Red Lion, USA; figure 4). After integration, the resulting polynomial function of angular velocity was implemented in a DEFINE-CG-MOTION UDF, and compiled using Microsoft Visual Studio 2005. This motion profile was then assigned to the surfaces of the pipefish head model. Ventroanterior translation of the body was included by a separate UDF that was based on the motion of the posterior margin of the rotating head.
Figure 4.
Kinematic profiles for (a) angle, (b) velocity and (c) acceleration of head rotation in S. leptorhynchus during feeding on mysid shrimps from Van Wassenbergh et al. (2008). White lines represent mean profiles, with grey areas indicating s.d. (N=9). Black lines represent the 15th order polynomial fit of the mean acceleration (c) or the integrals of this function resulting in velocity (b) and angle (a) profiles used in the presented CFD simulations.
Numerical algorithms of Fluent v. 6.3 can automatically update the mesh after each time step relative to the pipefish motion. Here, two methods were combined. Firstly, the spring-based smoothing method was used, in which the edges between nodes are considered as a network of interconnecting springs. To smooth the mesh, a value of 0.5 was used for spring constant factor and 1.0 for boundary-node relaxation factor, while a standard value of 0.001 was used for the convergence tolerance. Secondly, cells that became critically small (less than 0.1 mm), too large (more than 3 mm) or too skewed (more than 0.7) by the movement of the model were automatically remeshed by Fluent.
Grid convergence was confirmed by comparing the force output on the pipefish surfaces with the output from a model in which a boundary-layer refinement was performed after each 0.25 ms (mesh containing more than twice the number of cells). The peak hydrodynamic force on the pipefish model differed only by 2.74% between these two simulations.
2.4 CFD model and boundary conditions
The unsteady flow simulations were also performed using Fluent v. 6.3. The flow was assumed to be laminar because the critical Re for transition to turbulent flow (2×105 for smooth cylinders; Hoerner 1965, Schlichting 1979) is not likely to be reached during head rotation in pipefish. Using a velocity of 3.5 m s−1 (higher than the measured peak velocities of the mouth) and a characteristic length of 20 mm (approximate head length), Re was calculated to be 7×104. Properties of seawater with a salinity of 35 g kg−1 at 20°C were assigned to the fluid: a constant density of 1024.75 kg m−3 and a dynamic viscosity of 1.08 mPa s (Fofonoff 1962).
The no-slip wall condition was enforced at the rotating pipefish head surface, which is the default condition for models of viscous flow in Fluent v. 6.3. The spherical open boundary surface of the flow domain (figure 2a) was modelled as a pressure outlet where a gauge pressure of zero applies (i.e. no changes in pressure due to pipefish rotation is assumed at this boundary) and a backflow normal to the boundary. A steady flow simulation with a considerably larger flow domain around the pipefish showed that this boundary condition was realistic.
The pressure-based solver (chosen to obtain fast-converging solutions) was used with a node-based Green–Gauss gradient treatment. The latter treatment achieves higher accuracy in unstructured tetrahedral grids than the cell-based gradient treatment. The first-order implicit unsteady formulation option was used in the simulation because moving mesh simulations (see above) currently work with only first-order time advancement. The standard pressure discretization scheme was used for the pressure calculation and a second-order upwind scheme was used for the momentum equations. The pressure–velocity coupling was solved using the SIMPLE scheme. The latter is a discretization method that uses a relationship between velocity and pressure corrections to enforce mass conservation and to obtain the pressure field. A fixed time step size of 0.05 ms was used in the calculations. A maximum of 40 iterations per time step was sufficient to reach a converged solution.
The reported moments exerted by the surrounding water on the pipefish head from CFD simulations are always the sum of pressure moments (resulting from pressure forces) and viscous moment (resulting from wall shear forces) on the external surfaces of the pipefish. This means that the forces due to inertia of the intra-oral water (figure 3b) on the internal boundary surfaces of the buccal cavity were not considered. The latter was necessary to allow a comparison with the elliptical cylinder model. The loss or gain of mechanical energy of the rotating pipefish head due to the hydrodynamic forces exerted at its surface was calculated by taking the integral of the moments (viscous moments and pressure moments) multiplied by the instantaneous angular velocity during the acceleration phase and the deceleration phase, and both phases.
2.5 Effects of acceleration and deceleration magnitude
In order to test how the magnitude of acceleration and deceleration affects the accuracy of the elliptical cylinder model (Van Wassenbergh et al. 2008) with respect to the CFD model, two additional simulations were performed: (i) the same rotation (21.15°) is executed in half the time and (ii) the total duration was doubled. The first of these simulations included acceleration and deceleration magnitudes that were quadruple of in vivo observations and peak velocity values that were double. The second simulation implied halved peak velocity and quartered peak acceleration and deceleration magnitudes compared with the original kinematic profile shown in figure 4.
2.6 Prey displacement
A small spherical prey (0.5 mm radius) was included in the CFD model. This sphere was placed at the position where the point on the prey nearest to the mouth aperture was observed in vivo during a previous high-speed video study (Van Wassenbergh et al. 2008; prey position from 10 feeding sequences analysed). Pressure forces and viscous shear forces were obtained from the CFD solver's solution of the previous time step and used to calculate prey acceleration, velocity and displacement in the current time (using a DEFINE-CG-MOTION UDF).
2.7 Forward dynamics simulations
The applicability of the elliptical cylinder model for performing simulations using forward dynamics (i.e. calculating motion from forces) was evaluated. To represent the moment generated by muscle activity and recoil of the post-cranial tendons (initial acceleration) or internal forces such as friction or passive stretching of muscles and tendons (deceleration phase), the same realistic moment (Minput) was used as input into both models. Minput was determined from inverse dynamics using the elliptical cylinder model (Van Wassenbergh et al. 2008).
The following equation of motion was used for the elliptical cylinder model:
| (2.1) |
where α is the angular acceleration; I the moment of inertia; Minput the given input moment; Mdrag the moment due to drag forces; and Madded mass the moment due to the effect of added mass. For the forward dynamic model simulation using CFD, the following equation of motion was incorporated into a DEFINE-CG-MOTION macro in Fluent v. 6.3:
| (2.2) |
where Mpressure and Mviscous are the summations of moments due to, respectively, pressure forces and viscous shear forces on the surface of the pipefish head model. These moments were obtained from the CFD solver's solution of the previous time step. The simulations were run with fixed time steps of 0.025 ms, using the explicit Euler formula to update velocity.
3. Results
3.1 Unsteady flow patterns
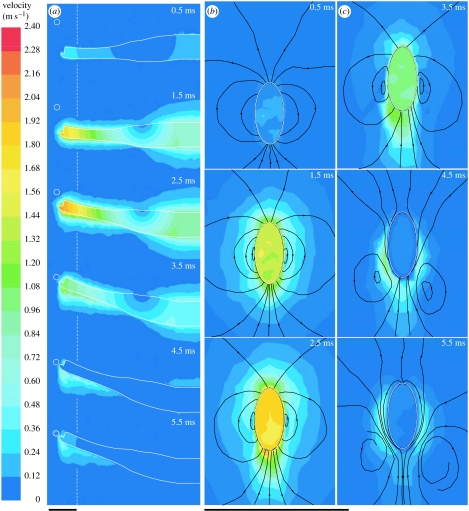
CFD results showed that during the first half of the acceleration of the pipefish head model (approx. 0 ms<t<1 ms), the water surrounding the model formed a boundary layer that is approximately equal in size on the dorsal and ventral sides at a given distance from the axis of rotation (figure 5). During the second half of the acceleration phase (approx. 1 ms<t<2.15 ms), a region of high flow velocities (up to 2.4 m s−1) appeared on the anteroventral side of the head. During the deceleration phase (2.15 ms<t<5.3 ms), this region gradually passed to the lateral sides of the snout (figure 5).
Figure 5.
Time sequence of CFD contour plots of flow velocity along (a) the midsagittal plane and (b,c) within the frontal plane indicated by the white dashed line of the rotating pipefish head. The white circles represent the prey. The initial prey position is indicated on the lower left frame by a dotted white circle. Black lines on the frontal plane plots represent streamlines. The velocity colour scale is indicated on the left. Scale bars, 5 mm.
3.2 Prey displacement
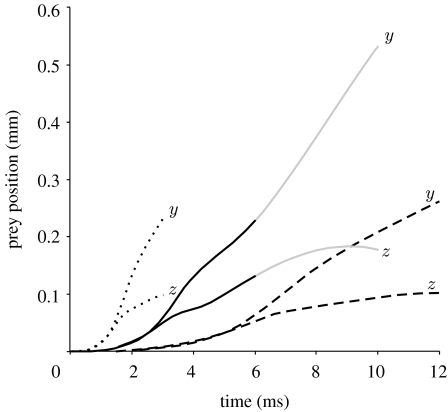
At the instant when prey are typically sucked into the mouth in S. leptorhynchus (approx. 6 ms after the onset of cranial rotation), rotation of the pipefish head model has moved the prey 0.264 mm away from its starting position. Maximal prey velocity was 0.083 m s−1 (reached after 3.3 ms). Prey displacement (figure 6) mainly occurred in the posterior–anterior direction (y-axis figure 2; 0.228 mm) and less in the ventral–dorsal direction (z-axis figure 2; 0.133 mm). At this time the head had ceased rotating and a high velocity (up to 0.75 m s−1) dorsally directed flow was observed passing the lower jaw of the model (figure 7). However, this flow did not impact the prey during the first 6 ms from the time feeding movement started (figures 5 and 7). After 6 ms, the prey was further carried away from the mouth (figure 6) and even reached a second velocity peak near 7.6 ms (0.081 m s−1). Note that the latter situation would occur only if suction did not result in ingestion of the prey.
Figure 6.
Plots of prey displacement along the z-axis (ventral to dorsal) and y-axis (posterior to anterior) due to the pipefish head model (figure 2) rotating at three different speeds (solid black line, cranial rotation S. leptorhynchus; solid grey line, cranial rotation S. leptorhynchus after end of rotation; dotted line, velocity×2, acceleration×4; dashed line, velocity/2, acceleration/4). The ends of the black curves indicate prey position at the time the head has completed the rotation of 21.15°. The grey curve shows prey displacement after the head has stopped rotating (cf. figure 5).
Figure 7.
Velocity vector plot (midsagittal plane) focusing on the mouth near the instant when the prey is sucked through the mouth aperture (5.517 ms after the onset of cranial rotation). Note the upward-directed high-velocity flows just passing the lower jaw region. On the other hand, low flow velocities (less than 0.2 m s−1) characterize the prey's surface region (see also figure 5). The velocity colour scale is indicated on the left. Scale bar, 1 mm.
An increase in the speed of cranial rotation significantly decreased prey displacement (R2=0.99; p=0.038) during the shorter rotation phase. For example, a rotation of 21.15° in 12 ms displaced the prey by 0.282 mm, while performing the same rotation in 3 ms displaced the prey 0.253 mm away from the mouth. On the other hand, prey velocity at the approximate instant when prey capture occurs was roughly proportional to the rotational velocity of the pipefish model: mean angular velocities of the pipefish of 0.03, 0.06 and 0.012 rad s−1 resulted in prey velocities of 28, 69 and 93 mm s−1.
3.3 Elliptical cylinder model versus CFD model
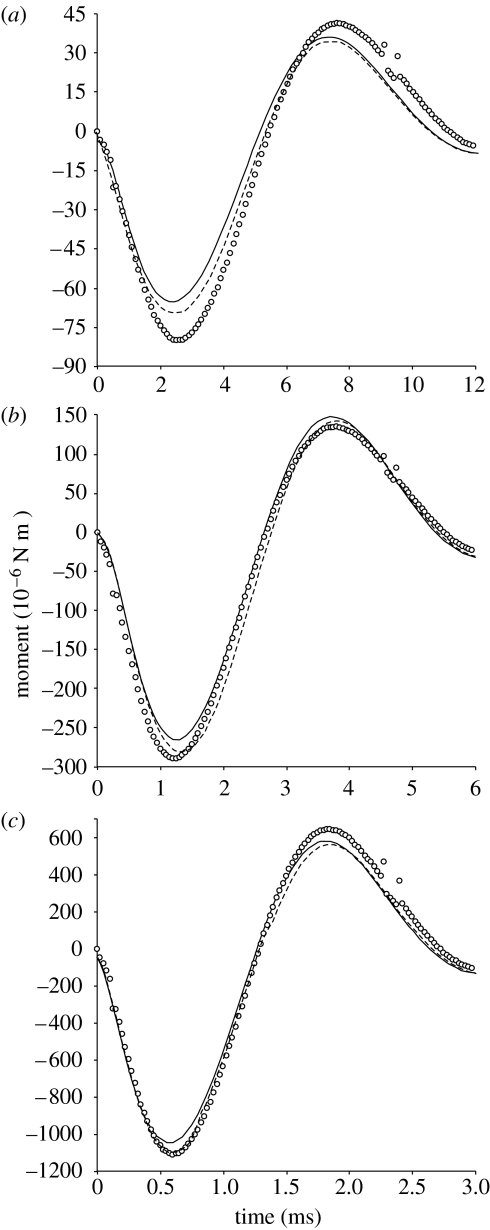
The moments exerted by the water on the rotating pipefish model were compared between the two modelling approaches (figure 8). In general, CFD showed higher magnitudes of hydrodynamic forces than the elliptical cylinder models. In the case of the simulation mimicking in vivo kinematics of S. leptorhynchus (figure 8b), the peak negative moment during the acceleration phase from the elliptical cylinder model was 91.3% of the moment calculated by the CFD simulation. The difference is even lower if a more accurate estimate of steady-state drag (here by using steady-flow CFD solutions) is included: the peak negative moment during the acceleration phase from this improved elliptical cylinder model was 97.4% of the moment calculated by the CFD simulation.
Figure 8.
Comparison of the total moments exerted by the water on the pipefish head as calculated by the original elliptical cylinder model (solid line), the elliptical cylinder model including steady-state drag moment from CFD (dashed line) and the unsteady CFD model (circles) for simulation at three different velocities: (a) using twice the time to perform the rotation observed in vivo (acceleration/4), (b) mimicking the in vivo cranial rotation (figure 4) and (c) the rotation was executed in half the time compared with the in vivo kinematics (acceleration×4). Positive moments contribute to the dorsal rotation of the snout, while negative resist this rotation. Increasing the velocity of the simulation (a<b<c) results in a relatively better fit between the models during the acceleration phase of cranial rotation (water exerting negative moments). Note that the small deviations from synchronicity in the time to peak values depend on which models are compared, with no apparent trend in relation to the magnitude of acceleration.
Increasing the magnitude of acceleration (and deceleration) imposed upon the rotating model decreased the relative difference between the models. The following results illustrate this. Increasing acceleration by a factor of 4 enhanced the fit between the models (figure 8c): the moment calculated by the elliptical cylinder model increased to 94.5% of CFD model output. On the other hand, decreasing the acceleration four times augmented the relative difference between the CFD model and the elliptical cylinder model (peak negative moment 81.6% of CFD; figure 8a). Also for these simulations, the fit between the elliptical cylinder model and the CFD model during the acceleration phase improved by including the more accurate estimate of steady-state drag forces (from steady-flow CFD) than in the original model of Van Wassenbergh et al. (2008).
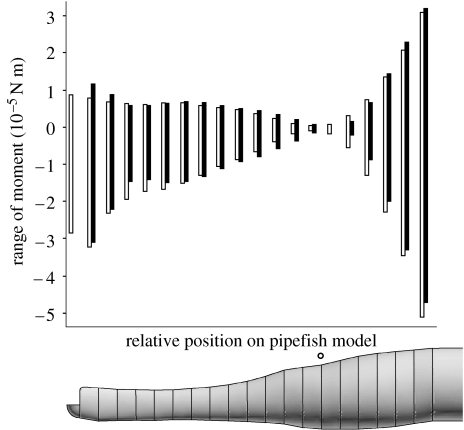
Asymmetries were observed in the agreement between both models in the results from the acceleration phase (negative moments resisting dorsal rotation of the snout) and the deceleration phase (positive moments contributing to snout rotation). However, these asymmetries differed depending on the position on the pipefish model (figure 9). For example, the anteriormost cylinders (numbers 1, 2; see figure 2) and the posteriormost cylinders (numbers 17–19) exhibited an underestimation by the elliptical cylinder model for peak magnitude of negative moment compared with the CFD model, but an overestimation for the peak positive moment. Less temporal asymmetry is observed for the more central cylinders on the pipefish model (figure 9): the elliptical cylinder model either underestimated (cylinders 3–5) or overestimated (cylinders 7–13) the magnitude of both the positive and negative moments compared with the CFD model.
Figure 9.
Comparison of the total moments exerted by the water on the pipefish head as calculated by the elliptical cylinder model (black bars) and the CFD (white bars) in function of the position on the pipefish head model.
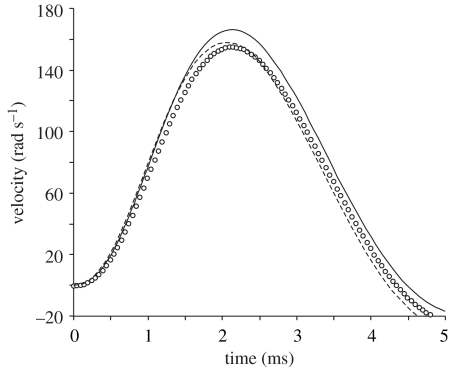
Forward dynamics simulations using the same input moment showed a 7.0% overestimation of maximal velocity by the original elliptical cylinder model compared with the CFD model (figure 10). The elliptical cylinder model that includes steady-state drag based on CFD simulations differed by 1.9% from the unsteady CFD simulation (157.8 versus 154.8 rad s−1).
Figure 10.
Instantaneous velocity output of head rotation from forward dynamics simulations with the original elliptical cylinder model (solid line), the elliptical cylinder model including steady-state drag moment from CFD (dashed line) and the unsteady CFD model (circles). The three models were driven by the same input moment (e.g. from muscle activity). Note that the difference in kinematic output between the elliptical cylinder model and the unsteady CFD model becomes negligible after including the more accurate estimate of steady-state drag force (CFD simulation).
The total loss in kinetic energy of the rotating head due to the surrounding water during the acceleration phase was 12.2% lower in the elliptical cylinder model than calculated by CFD (figure 8b). This difference reduced to 0.1% if the drag force correction was implemented in the model. A similar pattern is observed during the deceleration phase: the total gain in kinetic energy was 19.2% higher in the elliptical cylinder model than calculated by CFD, but was reduced to a 4.4% difference after the drag force correction. Finally, for the entire rotation, we observed an underestimation of the mechanical energy cost of 21.9% for the original elliptical cylinder model with respect to the CFD model that was reduced to only 1.8% after including the CFD-based steady-state drag forces.
4. Discussion
Given the relatively large density and viscosity of water compared with air, it was assumed that suction (by expanding the volume of the oropharyngeal cavity) in aquatic animals that approach their prey quickly is partly used to compensate for the effects of ‘pushing’ the prey by the flow induced by the approaching movement (Muller & Osse 1984; Van Damme & Aerts 1997). However, our results suggested that bringing the mouth close to the prey by cranial rotation in Syngnathidae generated a negligible disturbance of the part of the flow field where prey are typically located (figures 5–7). This was surprising since the mouth is moving at 2.1 m s−1 in the direction of a prey that is only few millimetres away at a certain instant (figure 5).
Relatively high flow velocities at the lower jaw region were too late to reach the vicinity of the prey before prey uptake (figure 7). The total displacement of a small prey induced by cranial rotation was less than 0.3 mm. Given that the prey itself can easily reach 10 mm in length for the size of pipefish modelled (resulting in even less displacement) and that the mouth travels approximately 5 mm, the present results predict that prey pushing by the induced flow will be unimportant in feeding pipefish. Moreover, our model probably even overestimated the flow volume near the mouth by including a lower jaw that was fully depressed from the start of pivot feeding. In turn, this implies that bringing the mouth close to the prey by performing an abrupt rotation of a long and narrow head can be regarded as an efficient strategy to reduce the need for suction to compensate for the flow generated by a sudden approach.
Several other aquatically feeding vertebrates have also evolved feeding strategies involving an oblique strike at the prey. Examples are snakes that sweep their heads laterally when striking at prey (Drummond 1983), and side snapping of long-jawed fishes such as Lepisosteus oculatus (Lauder & Norton 1980). These lateral strikes have also been interpreted as strategies to prevent the prey from being pushed away from the mouth (Young 1991; Hibbits & Fitzgerald 2005). However, the combination of a rotational approach and powerful suction, as observed in pivot-feeding Syngnathoid fish, is probably unique among vertebrates.
The relatively simple elliptical cylinder model for studying the inverse dynamics of the abrupt fast rotation of the head and snout of pipefish during pivot feeding (Van Wassenbergh et al. 2008; figure 1) was reasonably well supported by CFD. Especially during the acceleration phase, the output of both models in terms of moments exerted by the water on the rotating pipefish head differed by less than 9% (figure 8b). Therefore, CFD validated the conclusions of the previous study on the feeding mechanism of pipefish (Van Wassenbergh et al. 2008): a power amplification system is needed to explain the dynamics of head rotation in these fishes. More specifically, the previous study showed that the long epaxial muscle tendons, which insert on the dorsal side of the neurocranium, store energy that is released when the feeding system is suddenly put in motion (Muller 1987; Van Wassenbergh et al. 2008).
Especially for extreme accelerations, the hydrodynamic forces resisting rotation can be modelled fairly accurately by using steady-state drag forces and effects of added mass on a series of elliptical cylinders: an underestimation of less than 6% in the total moment compared with CFD was observed when four times the in vivo acceleration is used in the simulation (figure 8c). When forces on the pipefish become smaller, as illustrated by the simulation where the in vivo acceleration was quartered, the relative accuracy of the elliptical cylinder model decreased (figure 8a). Although the peak forces exerted by the fluid on the pipefish predicted by the elliptical cylinder model still differed by less than 20% from CFD, our analysis indicates that some care is needed when this modelling approach is used for aquatic movements operating at lower Reynolds numbers.
Including a better estimate of steady-state drag force in the simple model will improve the fit with the output from CFD simulations (figures 8 and 10). This can be illustrated by considering the mechanical energy fluctuations of pivot feeding. The original version of the elliptical cylinder model (Van Wassenbergh et al. 2008) and the CFD model estimated the total energy dissipated to the surrounding water for the entire movement (acceleration phase+deceleration phase) to be, respectively, 2.67×10−5 and 3.42×10−5 J. However, if we first used the steady flow CFD solver to calculate drag forces, and then used these values in the elliptical cylinder model, we obtained 3.36×10−5 J (only 2% lower than the value from CFD). Consequently, the accuracy of this type of calculation depends on the quality of the equation for drag force included in the model.
How important are the differences between the two models if we consider the total balance of forces on the pipefish, thus also including the inertia of the pipefish head itself? This total force balance is used when performing forward dynamics simulations. The results of our forward dynamics simulations (figure 10) show that the CFD and elliptical cylinder models are nearly indistinguishable when instantaneous rotation was solved from the balance of forces on the pipefish head. Given the considerable differences in computational time, the simple analytical model (Van Wassenbergh et al. 2008) is an excellent tool for this type of application.
We hypothesized that Boussinesq–Basset history forces (e.g. Loewenberg 1993; Michaelides 1997) may become important during the deceleration phase, since this phase is preceded by acceleration on a very short time scale. Because the history of the flow around the pipefish was not included in the elliptical cylinder model, this may have resulted in a reduced accuracy of this analytical model compared with the computational model during this deceleration phase. Indeed, our results showed that flow patterns during the deceleration phase differed clearly from the acceleration phase: the water that was drawn with the ventral side of the snout passed dorsally along the left and right sides of the snout during cranial deceleration (figure 5). However, the hydrodynamic forces exerted by the water on the pipefish during the deceleration phase are still calculated with similar accuracy relative to the acceleration phase by the elliptical cylinder model compared with the CFD model (figure 8). Our results (figure 9) indicated that strong asymmetries in the fit between the models with regard to the acceleration and deceleration phases occur only near the edges of the model (mouth and pectoral regions), where more complex flow patterns occur (figures 5 and 7). This seems to be supported by our results from a previous version of the present CFD model, which had sharp edges at the mouth and did not include a body. This sharp-edged model resulted in stronger vorticity near the edges and showed a much more pronounced temporal asymmetry in the fit between the models.
In conclusion, our case study of pivot feeding in pipefish showed that a relatively simple analytical model that takes into account drag forces and added mass (Van Wassenbergh et al. 2008) enabled studying inverse dynamics of an explosively fast aquatic movement with, in general, satisfactory accuracy. Despite flow patterns during the phase of deceleration being altered by the preceding initial acceleration, this did not notably reduce the precision of the analytical model. We further observed that, despite the pipefish's snout approaching the prey extremely fast, the prey remains almost stationary. This suggests that subsequent little or no suction needs to compensate for the effects of the flow induced by cranial rotation on the prey in feeding Syngnathidae.
Acknowledgments
S.V.W. is a postdoctoral fellow of the Fund for Scientific Research—Flanders. The University of Antwerp and FWO-Vl (grant no. G 053907 to P.A.) provided financial support. We wish to thank the three reviewers for their valuable suggestions on how to improve this article.
References
- Alexander R.McN. 2nd edn. Hutchinson University Library; London, UK: 1970. Functional design in fishes. [Google Scholar]
- Alexander R.McN. Modelling approaches in biomechanics. Phil. Trans. R. Soc. B. 2003;358:1429–1435. doi: 10.1098/rstb.2003.1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergert B.A, Wainwright P.C. Morphology and kinematics of prey capture in the syngnathid fishes Hippocampus erectus and Syngnathus floridae. Mar. Biol. 1997;127:563–570. doi: 10.1007/s002270050046. [DOI] [Google Scholar]
- Blevins R.D. Van Nostrand Reinhold; New York, NY: 1984. Applied fluid dynamics handbook. [Google Scholar]
- Candelier F, Angilella J.R, Souhar M. On the effect of the Boussinesq–Basset force on the radial migration of a Stokes particle in a vortex. Phys. Fluids. 2004;16:1765–1776. doi: 10.1063/1.1689970. [DOI] [Google Scholar]
- Carroll A.M, Wainwright P.C, Huskey S.H, Collar D.C, Turingan R.G. Morphology predicts suction feeding performance in centrarchid fishes. J. Exp. Biol. 2004;207:3873–3881. doi: 10.1242/jeb.01227. [DOI] [PubMed] [Google Scholar]
- Chaplin J.R. History forces and the unsteady wake of a cylinder. J. Fluid Mech. 1999;393:99–121. doi: 10.1017/S0022112099005480. [DOI] [Google Scholar]
- Daniel T.L. Unsteady aspects of aquatic locomotion. Am. Zool. 1984;24:121–134. doi: 10.1093/icb/24.1.121. [DOI] [Google Scholar]
- Daniel T.L, Meyhöfer E. Size limits escape locomotion of carridean shrimp. J. Exp. Biol. 1989;143:245–265. [Google Scholar]
- Deban S.M, O'Reilly J.C, Dicke U, van Leeuwen J.L. Extremely high-power tongue projection in plethodontid salamanders. J. Exp. Biol. 2007;210:655–667. doi: 10.1242/jeb.02664. [DOI] [PubMed] [Google Scholar]
- de Groot J.H, van Leeuwen J.L. Evidence for an elastic projection mechanism in the chameleon tongue. Proc. R. Soc. B. 2004;271:761–770. doi: 10.1098/rspb.2003.2637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Lussanet M.H.E, Muller M. The smaller your mouth, the longer your snout: predicting the snout length of Syngnathus acus, Centriscus scutatus and other pipette feeders. J. R. Soc. Interface. 2007;4:561–573. doi: 10.1098/rsif.2006.0201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denny M.W, Daniel T.L, Koehl M.A.R. Mechanical limits to size in wave-swept organisms. Ecol. Monogr. 1985;55:69–102. doi: 10.2307/1942526. [DOI] [Google Scholar]
- Drummond H. Aquatic foraging in garter snakes: a comparison of specialists and generalists. Behaviour. 1983;86:1–30. doi: 10.1163/156853983X00543. [DOI] [Google Scholar]
- Ellington C.P. The aerodynamics of hovering insect flight. I. The quasi-steady analysis. Phil. Trans. R. Soc. B. 1984;305:1–15. doi: 10.1098/rstb.1984.0049. [DOI] [Google Scholar]
- Ellington C.P, Van den Berg C, Willmott A.P, Thomas A.L.R. Leading-edge vortices in insect flight. Nature. 1996;384:628–630. doi: 10.1038/384626a0. [DOI] [Google Scholar]
- Fofonoff, N. P. 1962 Physical properties of sea-water. In The sea, vol. 1 (ed. M. N. Hill), pp. 3–33. New York, NY: Interscience Publishers.
- Gal J.M, Blake R.W. Biomechanics of frog swimming. I. Estimation of the propulsive force generated by Hymenochirus boettcheri. J. Exp. Biol. 1988;138:399–411. [Google Scholar]
- Hibbits T.J, Fitzgerald L.A. Morphological and ecological convergence in two natricine snakes. Biol. J. Linn. Soc. 2005;85:363–371. doi: 10.1111/j.1095-8312.2005.00493.x. [DOI] [Google Scholar]
- Hoerner S.F. Hoerner Fluid Dynamics; Bakersfield, CA: 1965. Fluid-dynamic drag. [Google Scholar]
- Jordan C.E. A model of rapid-start swimming at intermediate Reynolds number: undulatory locomotion in the chaetognath Sagitta elegans. J. Exp. Biol. 1992;163:119–137. [Google Scholar]
- Kuiter R.H. TMC Publishing; Chorleywood, UK: 2003. Seahorses, pipefishes and their relatives: a comprehensive guide to Syngnathiformes. [Google Scholar]
- Lan S.L, Sun M. Aerodynamic properties of a wing performing unsteady rotational motions at low Reynolds number. Acta Mech. 2001;149:135–147. doi: 10.1007/BF01261668. [DOI] [Google Scholar]
- Lappin A.K, Monroy J.A, Pilarski J.Q, Zepnewski E.D, Pierotti D.J, Nishikawa K.C. Storage and recovery of elastic potential energy powers ballistic prey capture in toads. J. Exp. Biol. 2006;209:2535–2553. doi: 10.1242/jeb.02276. [DOI] [PubMed] [Google Scholar]
- Lauder G.V. Aquatic feeding in lower vertebrates. In: Hildebrand M, Bramble D.M, Liem K.F, Wake D.B, editors. Functional vertebrate morphology. The Belknap Press (Harvard University Press); Cambridge, MA: 1985. pp. 210–229. [Google Scholar]
- Lauder G.V, Norton S.F. Assymetrical muscle activity during feeding in the Gar, Lepisosteus oculatus. J. Exp. Biol. 1980;84:17–32. [Google Scholar]
- Lighthill J. Regional Conference Series in Applied Mathematics. vol. 17. SIAM; Philadelphia, PA: 1975. Mathematical biofluid dynamics. [Google Scholar]
- Liu H, Ellington C.P, Kawachi K, Van den berg C, Willmott A.P. A computational fluid dynamic study of hawkmoth hovering. J. Exp. Biol. 1998;201:461–477. doi: 10.1242/jeb.201.4.461. [DOI] [PubMed] [Google Scholar]
- Loewenberg M. Sokes resistance, added mass, and Basset force for arbitrarily oriented finite-length cylinders. Phys. Fluids A. 1993;5:765–767. doi: 10.1063/1.858660. [DOI] [Google Scholar]
- Maxey M.R, Riley J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids. 1983;26:883–889. doi: 10.1063/1.864230. [DOI] [Google Scholar]
- McHenry M.J, Azizi E, Strother J.A. The hydrodynamics of locomotion at intermediate Reynolds numbers: undulatory swimming in ascidian larvae (Botrylloides sp.) J. Exp. Biol. 2003;206:327–343. doi: 10.1242/jeb.00069. [DOI] [PubMed] [Google Scholar]
- Michaelides E.E. The transient equation of motion for particles, bubbles, and droplets. J. Fluids Eng. 1997;119:233–247. doi: 10.1115/1.2819127. [DOI] [Google Scholar]
- Muller M. Optimization principles applied to the mechanism of neurocranium levation and mouth bottom depression in bony fishes (Halecostomi) J. Theor. Biol. 1987;126:343–368. doi: 10.1016/0022-5193(82)90287-9. [DOI] [Google Scholar]
- Muller M, Osse J.W.M. Hydrodynamics of suction feeding in fish. Trans. Zool. Soc. Lond. 1984;37:51–135. [Google Scholar]
- Nauwelaerts S, Stamhuis E.J, Aerts P. Propulsive force calculations in swimming frogs I. A momentum–impulse approach. J. Exp. Biol. 2005;208:1435–1443. doi: 10.1242/jeb.01509. [DOI] [PubMed] [Google Scholar]
- Osborne M.F.M. Aerodynamics of flapping fight with application to insects. J. Exp. Biol. 1951;28:221–245. doi: 10.1242/jeb.28.2.221. [DOI] [PubMed] [Google Scholar]
- Schlichting H. 7th edn. McGraw-Hill; New York, NY: 1979. Boundary layer theory. [Google Scholar]
- Thomas P.J. On the influence of the Basset history force on the motion of a particle through a fluid. Phys. Fluids A. 1992;4:2090–2093. doi: 10.1063/1.858379. [DOI] [Google Scholar]
- Van Damme J, Aerts P. Kinematics and functional morphology of aquatic feeding in Australian snake-necked turtles (Pleurodira; Chelodina) J. Morphol. 1997;233:113–125. doi: 10.1002/(SICI)1097-4687(199708)233:2%3C113::AID-JMOR3%3E3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- Van Wassenbergh S, Strother J.A, Flammang B.E, Ferry-Graham L.A, Aerts P. Extremely fast prey capture is powered by elastic recoil. J. R. Soc. Interface. 2008;5:285–296. doi: 10.1098/rsif.2007.1124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wainwright P, Carroll A.M, Collar D.C, Day S.W, Higham T.E, Holzman R.A. Suction feeding mechanics, performance, and diversity in fishes. Integr. Comp. Biol. 2007;47:96–106. doi: 10.1093/icb/icm032. [DOI] [PubMed] [Google Scholar]
- Wakaba L, Balachandar S. On the added mass force at finite Reynolds and acceleration numbers. Theor. Comput. Fluid Dyn. 2007;21:147–153. doi: 10.1007/s00162-007-0042-5. [DOI] [Google Scholar]
- Young B.A. The influences of the aquatic medium on the prey capture system of snakes. J. Nat. Hist. 1991;25:519–531. doi: 10.1080/00222939100770321. [DOI] [Google Scholar]
- Zanker J.M, Götz K.G. The wing beat of Drosophila melanogaster. II. Dynamics. Phil. Trans. R. Soc. B. 1990;327:19–44. doi: 10.1098/rstb.1990.0041. [DOI] [Google Scholar]