Abstract
A two-dimensional multiscale model is introduced for studying formation of a thrombus (clot) in a blood vessel. It involves components for modelling viscous, incompressible blood plasma; non-activated and activated platelets; blood cells; activating chemicals; fibrinogen; and vessel walls and their interactions. The macroscale dynamics of the blood flow is described by the continuum Navier–Stokes equations. The microscale interactions between the activated platelets, the platelets and fibrinogen and the platelets and vessel wall are described through an extended stochastic discrete cellular Potts model. The model is tested for robustness with respect to fluctuations of basic parameters. Simulation results demonstrate the development of an inhomogeneous internal structure of the thrombus, which is confirmed by the preliminary experimental data. We also make predictions about different stages in thrombus development, which can be tested experimentally and suggest specific experiments. Lastly, we demonstrate that the dependence of the thrombus size on the blood flow rate in simulations is close to the one observed experimentally.
Keywords: computational biology, platelet aggregation and coagulation, cellular Potts model, multiscale stochastic systems, blood clot, thrombus development
1. Introduction
The haemostatic system evolves to form a thrombus (clot) at the site of vascular injury to prevent the loss of blood. The response is rapid to limit bleeding and is regulated to prevent excessive clotting that can limit flow. Haemostasis involves complex interactions among multiple molecular and cellular components in the blood and vessel wall, as well as the influence of the flowing blood.
Understanding these processes has significant biomedical values. Improper regulation of thrombus generation can result in haemorrhage following impaired formation of a thrombus on disrupted vessels or thrombosis following inappropriate intravascular coagulation. These processes are involved in stroke (haemorrhagic or thrombotic), thrombotic complications associated with cancer, coronary infarction, and peripheral artery or vein thrombosis. The latter condition results in 250 000 hospitalizations a year in the USA, and the incidence will increase as the population ages. Furthermore, thrombus structure and susceptibility to embolization are important considerations for understanding of pulmonary embolization, an often fatal consequence of deep vein thrombosis (DVT).
While the development of predictive computational models simulating the haemostatic process would be very valuable for basic and applied vascular research, the challenges presented by this complex process are daunting. Such models should take into account both biochemical and mechanical factors which usually occur at different length scales.
Traditionally, almost all attempts to model the coagulation processes computationally and mathematically have focused on continuous models in the form of systems of nonlinear ordinary differential equations (ODEs) or partial differential equations (PDEs), which describe changes in the concentration of activated haemostatic factors and reaction–diffusion systems. Owing to the extremely complicated nature of blood clotting, these attempts usually focused on small subsets of the entire process.
Lobanov & Starozhilova (2005) developed two mathematical models to study the embolus growth in a wall-adjacent flow and the initial stage of the thrombus growing in the haemorrhage into a natural internal space. They showed that the thrombus growth depended on the blood flow and chemical reactions. The extrinsic and intrinsic coagulation pathways have been modelled using feedback loops in Khanin & Semenov (1989), Jesty et al. (1993) and Baldwin & Basmadjian (1994). Multifaceted models have been developed based on a large number of reaction–diffusion equations with parameters related to many aspects of thrombus growth, such as flow rates, membrane binding site density and concentration of calcium (Zarnitsina et al. 1996; Kuharsky & Fogelson 2001; Ovanesov et al. 2002).
Several models concentrated on specific aspects of the coagulation. In Beltrami & Jesty (1995, 2001) it was shown that the activation threshold for an enzyme cascade was affected by the flow rate, the size of the injury and the initial concentrations of active enzymes. The regulation of activation threshold by levels of factors VII and XII and clotting time sensitivity to zymogens concentrations was studied in Zarnitsina et al. (1996a,b) and Barynin et al. (1999) using spatially homogeneous and inhomogeneous systems. Fogelson (1992, 1993) and Sorensen et al. (1999) developed Newtonian fluid models in the form of coupled convection–reaction–diffusion equations without platelet deposits. These models did not include the effect of the growing thrombus on the flow field. In Fogelson & Guy (2004) a PDE model with elastic links was introduced for describing adhesion of platelets to the injured wall and cohesion between activated platelets. A recent viscoelastic liquid thrombus model Anand et al. (2005) incorporates both rheological properties of the thrombus and multiple biochemical reactions. Thrombus formation and dissolution are modelled as the growth/diminishing of a sheer thinning viscoelastic region. Convection–reaction–diffusion equations are used for modelling platelet activation, extrinsic coagulation pathway and fibrinolysis.
In addition, many investigators used experimental approaches or simplified models for studying the blood flow under different physiological conditions leading to haemostasis (see Basmadjian (1990) and David (1997) for a review). For example, Badimon et al. (1986) showed that platelet deposition was strongly influenced by the shear flow rates.
Whereas most models describe continuous dynamics at the macroscale of certain aspects of the platelet aggregation and coagulation process, there is a reason to believe that many aspects of the cascade are better modelled as discrete events at the microscale. First, certain enzymes exhibit threshold effects in activation or inhibition of other proteins. Second, some of the more complex aspects of the coagulation process are poorly understood, and certainly there is no closed-form set of differential equations for the system as a whole. Moreover, more coarse-grained information is available at the microscale, e.g. whether a certain protein factor must be present at some minimal concentration for a reaction to take place, and it can be incorporated into the model in the form of discrete states.
Owing to the multiscale nature of platelet aggregation and coagulation reactions, in order to capture both the discrete events and the continuous mechanics, the thrombus development is best modelled as a hybrid composition of the two. A multiscale approach takes advantage of the simplicity and efficiency of the macroscopic models, as well as the accuracy of the microscopic models and it is particularly helpful for studying the macro–micro relationships of the blood flow and platelet aggregation and coagulation. It allows one to model in detail the formation of the thrombus as well as a boundary layer between the thrombus and the blood flow resulting in the description of different phases in thrombus development and mechanisms determining its shape and internal structure.
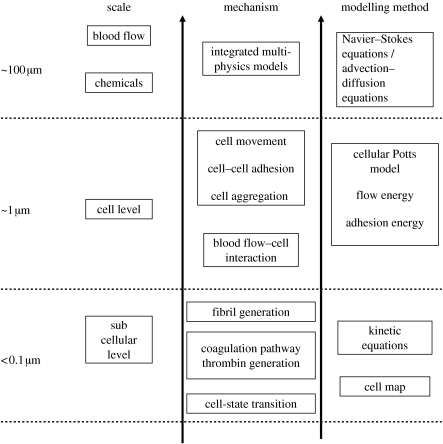
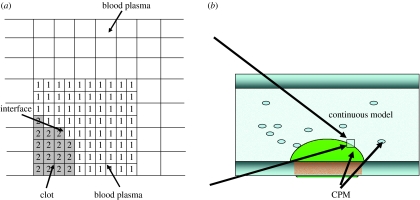
In this paper, we describe a two-dimensional multiscale computational model for thrombus development, which combines the discrete cellular Potts model (CPM) of platelet and blood cell aggregation with the continuous PDEs describing the hydrodynamics of blood flow and the kinetics of coagulation reactions. The model combines all interrelated factors that contribute to the formation of a blood thrombus at three spatial scales demonstrated in figure 1: (i) the vessel wall scale, for which the diameter of the artery is of the order of 100 μm, (ii) the cellular scale, for which the diameter of a platelet is of the order of 1 μm, and (iii) the intercellular scale, on which the fibrin fibril network grows. The hydrodynamics of blood flow and chemical kinetics of coagulation reactions are modelled on the continuous level. Platelet interactions with the vessel wall, leucocytes and other platelets are considered at the cellular level and fibrin generation is modelled at the intercellular level.
Figure 1.
Diagram of the hierarchy of scales from the subcellular level to the blood vessel level together with corresponding mechanisms and modelling approaches.
The CPM approach was initially introduced by Glazier & Graner (1992, 1993) and has become a common technique for biological simulations including embryonic vertebrate limb development (Chaturvedi 2005; Newman et al. 2008), tumour growth (Jiang et al. 2005) and vasculogenesis (Merks et al. 2006). A CPM model consists of a list of biological cells, a list of generalized cells, a set of chemical diffusants and a description of their biological and physical behaviours and interactions embodied in the effective energy, with auxiliary equations to describe absorption and secretion of diffusants and extracellular materials, state changes within the cell, mitosis, cell death and the behaviour of extracellular diffusants. A full model of the thrombus development will require simulation of a large number of cells. Recently, a parallel CPM algorithm capable of modelling 106−108 cells has been developed (Chen et al. 2007).
Owing to the fact that most of the physical features of multiphase hydrodynamic processes can be described using two-dimensional simulations, and that three-dimensional simulations only lead to quantitative characteristics, we replace the cylindrical vessel with a two-dimensional parallel plate chamber in this paper. By doing this, we focus on building a model of moderate computational complexity. Our simulation results also confirm that the two-dimensional model captures significant events of blood clotting, which can be quantitatively compared with the experimental results. In addition, the kinetics constants used in a blood coagulation submodel vary within an order of magnitude in experimental data.
This paper is organized as follows. Section 2 provides biological background and experimental results on thrombus development. Section 3 describes the computational model. Section 4 contains extended discussion of simulation results and proposed experiments for testing model predictions. The paper ends with §5. The numerical algorithms developed to solve the model equations are described in appendix A.
2. Biological and modelling background
2.1 Experimental results
The haemostatic system includes platelets that are fragments of the precursor megakaryocyte found in the bone marrow. In a quiescent state, individual platelets are disc-like structures, approximately 1–5 μm in diameter. They carry receptors on their surface capable of attaching to collagen, a matrix protein in the vessel wall that may be exposed following vessel injury. Other platelet receptors sense components of their chemical environment that are critical for the rapid thrombogenic response to vascular injury. Additionally, prothrombogenic components are stored in granules within the resting platelet; upon activation, these components are released leading to the activation and binding of surrounding platelets into the growing thrombus.
In addition to platelets, blood carries a collection of haemostatic proteins that contribute to the rapid but regulated development and resolution of the thrombus. In a quiescent state, these factors maintain an anticoagulant environment keeping blood in a liquid state capable of flowing through the vasculature. However, upon vascular injury the system is mobilized to form a thrombus at the injury site. These haemostatic factors include coagulation proteases and cofactors which lead to the production of thrombin that converts soluble blood-borne fibrinogen into fibrin fibrils, the primary matrix protein in a thrombus. Thrombin is also a potent activator of platelets. In addition to procoagulant factors, there are anticoagulants that inhibit the coagulant reactions and are essential for the regulation of thrombogenesis. Their importance is demonstrated by the increased risk of thrombosis by the individuals deficient for these anticoagulant proteins. Furthermore, blood contains fibrinolytic proteins that degrade fibrin during the process of thrombus resolution and vessel repair as well as fibrinolytic inhibitors that regulate proteases involved in fibrin degradation. This complex network of reactions is essential for the regulated rapid growth of the thrombus and its resolution following vessel injury. The haemorrhagic or thrombotic complications suffered by the individuals deficient for particular components of this haemostatic system underscore their medical importance.
Haemodynamic processes are also critical to the development of the thrombus. The relationships between the flow field surrounding the thrombus and thrombus development are reciprocal. During the process of blood thrombus development, the geometries of the vessel and growing thrombus change. These shape changes modify the flow field around the thrombus. These include changes in shear and the potential development of turbulence. Thus, the growing thrombus modifies the flow field.
The changes in flow parameters also affect thrombus development and structure. For a thrombus to grow, the adhesive forces among thrombus elements must withstand shear forces exerted by the flowing blood. Thus, changing shear forces affects the incorporation of elements into the growing thrombus. For instance, under high shear, bound von Willebrand factor (vWF) undergoes conformational changes that increase the adhesive forces between platelets and between platelets and the ECM, which are mediated by vWF. Moreover, turbulent flow involves the development of vortices that can entrap blood cells in the growing thrombus (it brings blood cells inside the thrombus and pushes small clusters of platelets towards the centre of the thrombus). Activated platelets can escape from the aggregate. As a result, the structural heterogeneity within the thrombus is influenced by the flow field surrounding the thrombus.
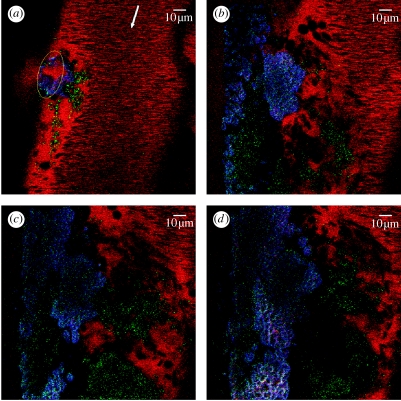
Figure 2 represents results of the experiment which we performed to study internal structure of a developing thrombus. An anaesthetized mouse was injected with three different fluorescent probes in order to visualize platelets, fibrin and plasma: 70 000 dextran labelled with tetramethylrhodamine (750 μg per mouse; Molecular probes) was used to visualize plasma (red channel); rat monoclonal antibody anti-mouse integrin αIIbβ3 (CD41/61) (1 μg g−1 body mass; Emfret Analytics, Germany) mixed with secondary goat anti-rat IgG labelled with Alexa Fluor 488 (0.1 μg g−1 body mass) was used to visualize platelets (green channel); and human fibrinogen (Enzyme Research Laboratories) labelled with Alexa Fluor 350 (350 μg per mouse) was used for fibrin visualization (blue channel). The mesentery vasculature was exposed by an incision in the abdominal area. After positioning the mouse on a microscope stage, a 63×/1.2 W Korr UV–Vis–IR objective was focused on 150 nm vein. A direct titanium–sapphire laser injury was induced with a short (10 s) high-intensity 800 nm laser burst in a small area of the vessel wall. After laser exposure, the progress of thrombus development in the injured vessel was recorded (with approx. 5–7 s delay) by continuous scanning (1 frame s−1) of the entire observation area with a relatively low-intensity 800 nm laser beam for approximately 11 min. Four representative pictures of the thrombus at different times after injury are shown from thrombus formation visualization in figure 2.
Figure 2.
Intravital confocal images of a developing venous thrombus. (a) Initial state of the thrombus immediately after laser-induced injury (time 0 s). (b–d) Status of thrombus at t=296, 480 and 746 s, respectively. During this time, the number of activated platelets incorporated in the thrombus increases, a fibrin network develops on the injured vessel wall covering the observed length (146 μm) and blood cells are incorporated into the growing thrombus. Not evident from the still frames, the growing thrombus induces turbulent flow around the thrombus that affects thrombus development. At the end of the recording period, the thrombus extended 18 μm from the vessel wall (calculated from Z stack; data not included).
2.2 Cell-based models in biology
Stochastic discrete models are used in a variety of problems dealing with biological complexity. One motivation for this approach is the enormous range of length scales of typical biological phenomena. Treating cells as simplified interacting agents, one can simulate the interactions of tens of thousands to millions of cells and still have within reach the smaller-scale structures of tissues and organs that would be ignored in continuum (e.g. PDE) approaches. At the same time, discrete stochastic models can be made sophisticated enough to reproduce almost all commonly observed types of cell behaviour (Alber et al. 2004a–c; Kiskowski et al. 2004; Casal et al. 2005; Chaturvedi 2005; Cickovski et al. 2005; Sozinova et al. 2005, 2006; Knewitz & Mombach 2006; Cickovski 2007).
A recent book by Glazier et al. (2007) reviews many cell-based models. In the centre-based single-cell model developed by Drasdo et al. (1995) and Drasdo & Hoehme (2005), cells are treated in a manner analogous to colloidal particles. The cell–cell interaction force is described using different approaches including the Johnson–Kendall–Roberts model, the Hertz model and the harmonic-like interaction energies with different cell contact geometries. Langevin-type equations describe motion of each cell. In the many-body off-lattice model developed by Newman & Grima (2004), cells are treated as point ‘particles’ and cell–cell interactions are described using short- or long-range intercellular potentials. The model is formulated using Langevin dynamics, which allows for analytic study using methods from statistical and many-body physics. In recent work (Newman 2005), ‘subcellular elements’ are introduced into the model to describe the three-dimensional shape of each cell. In the viscoelastic model developed by Palsson & Othmer (2000), all cells are assumed to be ellipsoids and cell deformations only change the relative lengths of the ellipsoidal semi-axes while cells' volume stays the same. Cells' deformations are determined by active, passive and viscous drag forces.
The shapes of cells and cell–cell adhesion are important in modelling thrombus development. This is why we choose the CPM, a cell-level, energy-minimization lattice model, which uses an effective energy E coupled to external fields, e.g. the local concentrations of diffusing chemicals, to describe the dynamics of the formation of the inhomogeneous internal structure of the thrombus.
We use CPM instead of just a cellular automata (CA) model for several reasons. After the cells aggregate in a clot, they can still move due to the blood flow and motion of other cells adherent to them. It would be rather difficult to describe complex interactions between the cells and the blood flow at an interface with complex geometry using the CA approach. Also, the CA model would involve a large number of specific rules to handle different types of cell movements and interactions, resulting in a very complex and unstable code. In the CPM, the metropolis algorithm automatically leads to the optimal solution through the energy minimization process. Moreover, we have a lot of experience with this model and plan to implement a parallel CPM algorithm capable of modelling 106–108 cells, which we have recently developed Chen et al. (2007), to speed up the simulations.
3. Computational model
3.1 Basic components and processes
Based on the descriptions from §2, we incorporated the following components into our model.
3.1.1 Injury in a vessel wall
We assume that the injury site is smooth and it has higher adhesivity than the vessel wall. Quiescent platelets adhere to it through binding of receptors to molecules that are exposed at the injury site.
3.1.2 Platelets
Platelets can exist in three states: a quiescent (resting) state; an initial activated state; and a final activated state. The concentration of resting platelets is assumed to be constant. The platelets in the two latter states generate molecules to promote coagulation and activation of the neighbouring resting platelets.
3.1.3 Coagulation factors
Coagulation occurs on the surface of individual activated platelets in blood.
3.1.4 Fibrin
Thrombin is considered as the final product of the coagulation system, which converts fibrinogen in the blood into fibrin.
3.1.5 Blood cells
A significant percentage of the volume of blood contains erythrocytes that are responsible for the transport of oxygen throughout the body, and leucocytes that mediate inflammatory responses. While these cells are not traditionally considered in models of thrombus development, experimental images of developing thrombi demonstrate the inclusion of blood cell-rich domains. This is not surprising since leucocyte membranes include ligands for receptors that are present on activated endothelial cells at the site of injury and on activated platelets. In particular, activated endothelial cells and platelets express P-selectin that binds to PSGL-1 exposed on leucocytes. These leucocyte- or erythrocyte-rich domains may affect thrombus stability as differences in elasticity and adhesiveness to surrounding thrombus components could affect structural integrity.
3.1.6 Blood plasma
The blood plasma is treated as an incompressible fluid with constant viscosity.
We identified the following mechanical and biochemical processes that are associated with the elements listed above.
The movement of platelets and blood cells driven by the blood flow.
Platelet–platelet binding and platelet binding to the injury site by means of the platelets binding to molecules exposed on the injury surface. The detailed molecular mechanisms regulating these processes are not considered individually in the model. For instance, while the adhesiveness of platelets is mediated by several receptor–ligand interactions, the adhesive properties in the computational model are considered as a function of the potential energy representing the composite of all these molecular interactions. Individual molecular components may be included in the future if necessary to promote better agreement between the computational model and the experimental data.
Releasing of chemical products by the adherent platelets activates nearby resting platelets and provides anionic lipids on the platelet for surface-dependent coagulation reactions.
Thrombin generation by coagulation reactions subsequently produces fibrin and activates platelets. We implement the tissue factor pathway described in Jones & Mann (1994) for the generation of thrombin involving activation of factors IX, X, V, and VIII, VIIIa–IXa (intrinsic tenase) and factors Va–Xa (prothrombinase).
Fibrin production provides a fibril network adding to the structural integrity of the thrombus. Fibrin conversion is assumed to be proportional to the thrombin concentration. Fibril level is high in the vicinity of platelets in the final activated state. Therefore, the capacity of the platelets to resist external flow force increases when the platelets change from the resting state to the final state.
As described, these processes are interrelated. All these identified biochemical and rheological processes play important roles in the formulation of blood thrombus. The multiscale computational model presented in this paper predicts events at lattice sites by considering multiple parameters that vary in time and space. These include the occupancy of injury and thrombus sites by resting or activated platelets and blood cells; the adhesiveness of flowing platelets to sites within the developing structure; the proximity to thrombogenic surfaces; the concentration of thrombin, which reflects the generation of thrombin by coagulation proteases at the nearby thrombogenic surfaces; the diffusion of thrombin from these surfaces; the effects of blood flow on thrombin distribution; and the haemodynamic forces on elements on the growing thrombus. In addition, the model includes the growth of the fibrin network that stabilizes elements in the grid.
3.2 Submodels
The following are the submodels for the processes involving components described in §3.1.
—Biochemical reaction submodel. The biochemical processes are modelled based on the system of reaction differential equations described in Jones & Mann (1994) with the addition of the fluid transport property. This model describes the role of activation of factors IX, X, V and VIII, in the formation of thrombin, as well as providing rates of coagulation reactions.
—Cell submodel. The discrete stochastic CPM represents different types of cells as well as accounting for platelet–injury adhesion, platelet activation, platelet–platelet binding, cell movements, cell-state changes and platelet aggregation.
—Flow submodel. Incompressible Navier–Stokes equations describe the dynamics of viscous blood plasma.
—Interface submodel. The submodel couples the CPM with the continuous model to describe the thrombus–blood plasma interface. The CPM and the blood flow model are defined on the lattice and the volume filling finite-difference grid, respectively. Two computational grids are spatially superimposed.
In our model, we assume that the thrombus does not change when we are solving for the flow velocity field during one time step. After retrieving thrombus–plasma interface from the CPM grid, the Navier–Stokes equations and reaction–advection–diffusion equations for the flow and chemical distributions are solved. The result in turn is used in the subsequent CPM updates of cell positions, cell shapes and types, and cell production of chemicals. It is also assumed that during the CPM iteration flow conditions (velocity and pressure) remain unchanged. After the CPM step is finished, the latest CPM data (interface geometry and chemical concentrations) provide the updated boundary and initial conditions for the continuous model.
In what follows, we describe in detail each submodel implemented in our multiscale computational environment.
3.2.1 Continuous submodels of the blood flow and biochemical reactions
Blood is a mixture of cellular matter in plasma. The non-Newtonian effect on the blood flow is strong in a capillary, where the size of the blood cells is comparable with the diameter of a blood vessel. A variety of non-Newtonian fluid models have been developed to describe different types of blood behaviour such as shear thinning (Chien et al. 1966) and stress relaxation (Chien et al. 1978).
However, at low shear rates or in relatively large vessels, plasma behaves rheologically as a Newtonian fluid. Therefore, blood plasma is treated in our model as an incompressible fluid with constant viscosity. Namely, we use the following Navier–Stokes equations:
| (3.1) |
| (3.2) |
where u=(u, v) is the flow velocity; ρ is the density of the blood plasma; and p is the pressure. The viscosity μ is assumed to be constant. f is the force density due to cohesion of activated platelets, which generates elastic stresses that influence motion of the blood plasma.
Many of the coagulation reactions occur on the surface of activated platelets (or attached microparticles that are not included in the current model) that expose negatively charged phospholipids. Thus, we do not assume that the thrombin concentration is uniform throughout the environment. If each species present in the environment were to be described using a PDE, it would be too computationally expensive. Therefore, we model coagulation pathway (pathway 1) using Jones & Mann's kinetics model (Jones & Mann 1994) that describes interactions between 18 species such as factors IX, X, V, VIII and IXa and factor Va.Xa. The dynamics of chemical concentration of each species is described by an ODE of the form: , where [Ci] is the concentration of species i and kij, j=1, …, n are the corresponding rate constants.
In each simulation of the thrombus formation, we first calculate the thrombin dynamics using the model of coagulation pathway 1 and store data into a table. Each platelet in the model has a timer associated with it. After the platelet gets activated, the timer is used to determine the rate of thrombin release from the table. The thrombin concentration dynamics is modelled by the following PDE that takes into account the flow effect:
| (3.3) |
where θ is the concentration of the thrombin; N is the number of cells; and Dθ is the diffusion coefficient. Δθi is the thrombin generated by the ith activated platelet. The production of fibrin is modelled by
| (3.4) |
where ψ is the concentration of fibrin and κ is the fibrin production rate set to be 1.0 from Lobanov & Starozhilova (2005). Equation (3.4) does not contain an advection term due to the fact that fibril grows within the platelet aggregates where flow velocity is almost zero.
3.2.2 Discrete cellular Potts model of cellular behaviour
In the CPM, each cell consists of many (lattice sites) pixels. The distribution of multidimensional indices associated with lattice sites determines current system configuration. The effective energy of the system mixes true energies, like cell–cell adhesion, and the terms that mimic energies, e.g. area constraint:
| (3.5) |
We will describe new additional energy terms below.
Given an effective energy, one can calculate the resulting cell motion using the metropolis dynamics algorithm based on the Monte Carlo–Boltzmann acceptance rule (Newman & Barkema 1999). Namely, if a proposed modification of lattice configuration (i.e. a change of the index associated with a pixel) changes the effective energy by ΔE, it is accepted with the probability
| (3.6) |
where T, defined in units of energy, determines effective cell membrane fluctuation amplitude. However, this value cannot be directly measured from the experiments. The value of T is chosen, based on the value of ΔE, in the range of 0.2≤ΔE/T≤2.0 (Glazier et al. 2007). This is done to accept a significant fraction of index copy attempts but not so many that the lattice pattern melts (see Glazier et al. (2007) for details). The pattern of pixels with the same index evolves (and cell moves) to minimize the total effective energy.
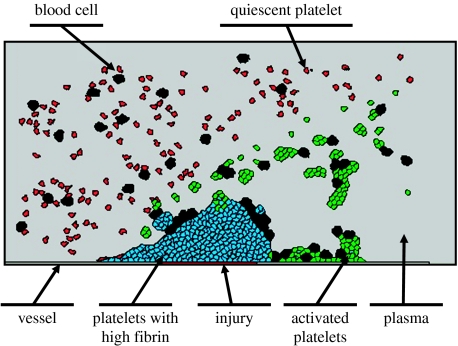
The CPM, developed for the multiscale model of the thrombus formation, contains seven different types of cells as demonstrated in figure 4. Note that cell types ‘injury’ and ‘vessel’ do not represent cells in the CPM and are used only to indicate the boundary of the vessel domain and place of injury. During simulation, their positions and adhesion properties are fixed and platelets can adhere to their surfaces. New platelets (inactivated) and blood cells are introduced from the inlet on the left side at a specified rate and moved to the right. When cells reach the right side of the simulation domain, they are removed from the system. We impose the ‘no-flux’ boundary condition on both upper and lower boundaries so that cells would not move outside of the domain.
Figure 4.
Different types of cells in the model of thrombus development.
On each CPM iteration step, a lattice site (pixel) is randomly chosen and the change of its index (state) is attempted. System energy change is calculated and the probability of its acceptance is determined. A random number generator is used to determine which index to choose. This is followed by adjustment of the lattice site index and update of the corresponding cell properties (cell size, cell boundary position and cell type). For a given CPM lattice of the size (m×n), one Monte Carlo step (MCS) of a simulation consists of (m×n) attempts at index changes of randomly chosen lattice sites.
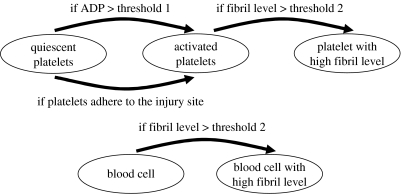
When an inactivated platelet reaches the site of the injury or adenosine diphosphate (ADP) concentration of a platelet becomes higher than the set threshold value, it changes its type to ‘activated’ and starts releasing thrombin that causes fibril generation. The generated fibrils gradually form a fibril network that increases thrombus stiffness and prevents platelets from detaching from the thrombus surface. Fibril level in thrombus and activated platelet cluster increases with the increase in thrombin concentration. Thus, clusters consisting of activated platelets have different fibril levels and stiffness properties at the initial and later stages. We implement in our CPM two different activated platelet states (activated platelet and activated platelet with high fibril level) with different flow responses (see §3.2.3 for more details). If a blood cell is trapped in a platelet cluster with high fibril level, its state changes as well. Figure 5 shows the cell-state transition map.
Figure 5.
Cell-state transition map.
3.2.3 New energy terms for the CPM
Platelet adhesion is mediated by plasma proteins bridging receptors on adjacent platelets (gpIIbIIIa fibrinogen, vitronectin, vWF, gpVI-collagen, etc). However, it is difficult to describe all the details of cell–cell adhesion in the model. In the CPM, the cell–cell adhesion is described as an energy penalty function term: low cell–cell adhesion energy represents strong adhesivity between cells, while high cell–cell adhesion energy represents weak cell–cell adhesivity. Increased complexity will be incorporated as necessary to increase the agreement between simulation and experimental data. In equation (3.5), Eadhesion phenomenologically describes the net adhesion between membranes of different cells
| (3.7) |
where if and if ensure that only the surface sites between different cells contribute to the adhesion energy. Each term under the summation sign is a product of the binding energy per unit length, , and the length of a contact between two neighbouring cells. Adhesive interactions act up to the second nearest neighbours.
A cell of type τ has a prescribed target area atarget(σ, τ), volume elasticity λσ, target membrane length ltarget(σ, τ) and membrane elasticity . Earea imposes an energy penalty for deviations of the actual area from the target area
| (3.8) |
We also introduce two different types of Eflow energy components to describe movements due to flow pressure and flow velocity, as indicated in table 1 for each cell type based on the following considerations. In our simulation, each cell of the Navier–Stokes finite-difference grid corresponds to 25 CPM lattice sites, while each platelet and blood cell area is 30 and 100 sites, respectively. Therefore, a platelet occupies one or two cells of the Navier–Stokes finite-difference grid. Theoretically, the membrane of each cell should be considered as a boundary with specific boundary condition for the Navier–Stokes equation. However, doing this would lead to a significant increase in the computing time. To reduce the computational load, we model only platelets and blood cells with high fibrin levels as obstacles (due to their high stability and flow resistance) and treat membranes of only these cells as boundaries of domains for solving the Navier–Stokes equation. For those cells, flow velocity at the cell–blood interface is assumed to be zero and the flow energy is calculated from the flow pressure. Resting cells and cells in the initial activated state are not treated as obstacles. Therefore, for these cells, the flow velocity at cell–blood interface is non-zero and the flow energy is calculated from the flow velocity. This is justified by the fact that in our model the densities of the cells and blood plasma are set to be equal, and therefore resting and non-activated cells have only weak resistance to the flow.
Table 1.
Flow energy calculation methods for different types of cells.
| cell type | energy calculation |
|---|---|
| quiescent platelet | from flow velocity |
| activated platelet | from flow velocity |
| platelet with high fibrin level | from flow pressure |
| blood cell | from flow velocity |
| blood cell with high fibrin level | from flow pressure |
The flow force applied to a cell i with high level of fibril (platelet or blood cell) is calculated as an integral of blood pressure along a cell membrane
| (3.9) |
where pk is the pressure applied to the blood–cell interface segment k; nk is the inward unit normal of the blood–cell interface segment k; and Sk is the membrane length of the blood–cell interface segment k. For a given state change, the flow energy change for the cell i is
| (3.10) |
where Δdi is the change in the position of the centre of mass of cell i caused by the state change and Ke1 is a flow energy constant. Cells (platelets and blood cells) inside of a cell cluster do not have direct blood contact and flow energy for those cells is zero.
We assume that a cell, which is not considered as an obstacle, has the same velocity value as the blood flow. Thus, the average flow velocity for a cell i is
| (3.11) |
where Vi is the velocity of cell i; vk is the flow velocity at site k; and Voli is the volume of cell i. The flow energy change for cell i caused by state change is equal to
| (3.12) |
where Δdi is the change of the centre of mass of cell i caused by the state change and Ke2 is the flow energy constant.
Improper lattice or neighbour selection in the CPM may cause lattice effects (i.e. lattice pinning). This problem can be resolved either by changing the lattice symmetry configuration (i.e. from square (four nearest neighbours) to hexagonal (six nearest neighbours)) or adding shells of interacting neighbours.
Recently, Dan et al. (2005) developed an advection–diffusion equation solver within the CPM framework. This method handles the advection movement using spin flips in the CPM. However, the CPM is an intrinsically stochastic model, and it is not very fast when modelling the blood flow. Therefore, we implemented a traditional numerical scheme for solving the advection–diffusion equation in our model.
3.2.4 Submodel of thrombus–plasma interface
The typical simulation domain is shown in figure 3b. A section of blood vessel is represented by a rectangle. In our model, the CPM cell lattice (grid) is superimposed on and is aligned with the PDE grid (figure 3b). The PDE grid used in the computational model is a cell-centred grid. The approximate average values of the solution functions are defined at the centres of the cells (see appendix A for the notations of the PDE grid). In the model, a cluster of lattice sites is employed to represent a platelet cell. Owing to the large spatial ratio between the flow scale and the individual platelet diameter, the CPM cell lattice usually is much finer than the PDE grid. We organize them in such a way that the CPM cell lattice is a level of refinement of the PDE grid. The refinement is represented by a factor of 5 in each dimension. Once the sizes of the two grids are specified, the coordination correspondence between the two grids is constructed.
Figure 3.
Diagram of the thrombus–plasma interface. (a) Spatially coupled finite-difference grid and the CPM lattice. (b) The thrombus–plasma interface in the simulation.
To determine the flow velocity field, the flow domain has to be identified. The thrombus is a viscoelastic substance. To simplify calculations, we use a sharp interface model, i.e. we assume that the fluid and thrombus phases are separated by a sharp interface called the thrombus–plasma interface. In this paper, we focus only on the main events in thrombus development and, therefore, neglect diffusion processes of the substances from the thrombus into the blood plasma since they are slow, in comparison with the aggregation and coagulation of the platelets. The evolution of the interface is driven by the platelet aggregation and coagulation and its dynamics is described by the CPM. The thrombus–plasma interface is identified on the CPM lattice as the union of outer boundaries of cells in a surface of a thrombus (figure 3). This interface is projected onto the PDE grid to provide boundary conditions for the PDE solution step. An algorithm similar to the volume-of-fluid method (Noh et al. 1967; Hirt & Nichols 1981; Kothe et al. 1996) is used to construct the thrombus–plasma interface on the PDE grid (numerical algorithms are described in detail in appendix A).
4. Simulation results
A variety of simulations have been performed to calibrate the model for predicting the sequence of events in thrombus formation, as well as the internal structure of the thrombus, which could be verified experimentally.
4.1 Selection of parameter values and sensitivity analysis
We used the simulations parameters listed in table 2. The coagulation reaction rates and initial chemical concentration are from Jones & Mann (1994). The initial concentration of TF.VIIa is 0.5 nm, which is the experimental value corresponding to fast thrombin formation in Jones & Mann (1994). The flow energy parameter is obtained by matching the fluid velocity and the cell response velocity. We gradually change the flow energy parameters until the average velocity of cells in the flow equals the flow velocity. Adhesion energies between different types of cells can be determined from measuring cohesive forces (Benoit et al. 2000). However, systematic experimental values for the cohesive forces of the cells involved in thrombus development are not available at this time. Therefore, we chose adhesion energies based on experimental observations that adhesion between the activated platelets is stronger than that between the quiescent platelets and the activated platelets and between the platelets and the site of injury.
Table 2.
Parameter values used in simulations of the thrombus development. (Note that all energy parameters, including adhesion energy constants, area energy constants, flow energy constants and T, are dimensionless parameters.)
| flow parameters | |
| finite difference grid | 100×50 |
| inlet pressure | 1 bar |
| viscosity | 0.004 |
| inlet velocity u | (200, 0) μm s−1 |
| domain size | 400 μm×200 μm |
| simulation time | 30 s |
| CPM parameters | |
| CPM grid | 500×250 |
| fluctuation temperature, T | 10 |
| adhesion constant, J (equation (3.7)) | a |
| blood platelets | 18.0 |
| quiescent platelet–quiescent platelet | 20.0 |
| activated platelet–activated platelet | 8.0 |
| activated platelet–injury | 2.0 |
| activated platelet–vessel wall | 18.0 |
| target volume atarget platelet (equation (3.8)) | 30 |
| target volume atarget blood cell (equation (3.8)) | 100 |
| volume constant, λ (equation (3.8)) | 2.0b |
| fluid constant, Ke1 (equation (3.10)) | 25.0 |
| fluid constant Ke2 (equation (3.12)) | 0.2 |
| threshold 1 (figure 5) | 0.4c |
| threshold 2 (figure 5) | 1.0c |
| fibrin production rate, K (equation (3.4)) | 1.0 |
| time steps | 20 CPM steps per NS step, 500×250 trials per CPM step |
| coagulation reaction parameters | [TF.VIIa]=5 nm, other parameters are the same as in Jones & Mann (1994) |
Adhesion energy parameters are estimated based on the experimental data. For example, the adhesivity between activated platelets is strong, while it is weak between quiescent platelets.
This value maintains the volume of each cell fluctuating around its target volume value during simulation.
The calculation of the steady state of the coagulation pathway shows that the thrombin concentration generated by activated platelets is in the range from 0 to 1.2 nm. We choose the threshold values based on this range.
The volume constant (λσ in equation (3.8)) represents the cell membrane resistance to cell volume change and it is a function of the Poisson ratio, Young's modulus and the relative adhesive energy constant. However, it is difficult to obtain this value from the known experimental results. The purpose of the area energy term in the CPM is to maintain the volume of each cell fluctuating around its target volume. In this paper, we chose the volume constant to be 2.0 for all cells and the simulation results show that with this value the volume of each cell slightly fluctuates around its target value (30 for platelets and 100 for blood cells).
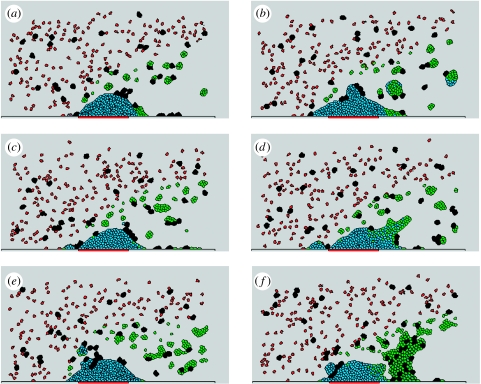
In order to show robustness of the model, we tested its sensitivity with respect to fluctuations of key parameters. In particular, figure 6a–e demonstrates that the model simulations of thrombus growth dynamics are very similar for a range of adhesive energy values. On the other hand, simulation (figure 6f) obtained for a very small activated platelet–activated platelet energy value chosen outside of this range contains a large cluster of activated platelets behind the generated thrombus which was not observed in an experiment.
Figure 6.
Simulation results with different adhesion energy constant values after 24 s. J1 is an adhesion energy constant of activated platelet–activated platelet interaction and J2 is the adhesion energy constant of activated platelet with higher fibrin–activated platelet with high fibrin. (a) J1=J2=4, (b) J1=J2=6, (c) J1=J2=8, (d) J1=12, J2=8, (e) J1=26, J2=4, (f) J1=2, J2=8. Other parameters are listed in table 2.
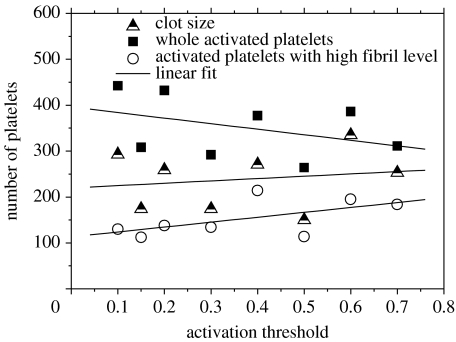
Another important parameter is the platelet activation threshold. The simulation results for different values of this parameter are shown in figure 7. With an increase in the activation threshold, the transition from a quiescent to activated phase becomes more difficult, and the number of activated platelets decreases. However, simulations demonstrate that clot size becomes larger. With low threshold value, a large number of activated platelets aggregate behind the stable part of a thrombus (consisting of platelets with high level of fibril), which prevents the vortical flow from bringing platelets to the back side of the thrombus, leading to a low growth rate.
Figure 7.
The graph represents the number of activated platelets, number of platelets with high fibril level as well as the total number of cells in a clot for simulations with different activation thresholds after 24 s.
4.2 Different stages of thrombus growth
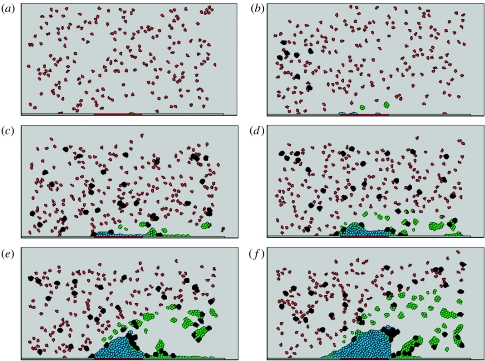
Figure 8 shows different stages of a typical simulation of a thrombus formation. At time 0.72 s, some platelets are activated and some of them are already attached to the injury. At time 4.8 s, injury is fully covered by platelets with high fibril level and some activated platelets with low fibril level accumulate behind the injury in the downstream direction from the thrombus. (An activated platelet at the early stage contains low level of fibril and has relatively high mobility in the blood flow.) At time 12 s, the thrombus is relatively small and it does not affect the flow strongly. At time 18 s, we observe the flow vortices forming behind a large thrombus. At time 24 s, the flow vorticity becomes so strong that the turbulent flow flushes some activated platelet and blood cell clusters back to the downstream side of the thrombus.
Figure 8.
Simulation of different stages of thrombus development: (a) time 0 s, (b) time 0.72 s, (c) time 4.8 s, (d) time 12 s, (e) time 18 s and (f) time 24 s. Parameters used in this simulation are listed in table 2.
The simulations of thrombus development have been compared to images of a growing thrombus collected by intravital microscopy of a laser-induced injury to a vein of the mouse mesentery (figure 2). The mesentery of an anaesthetized mouse was externalized and spread over a support on the stage of a confocal microscope to permit visualization of the blood flow through approximately 150 μm veins. Mice were injected with fluorescent probes to visualize plasma (red), fibrinogen (blue) and activated platelets (green). Figure 2a–d shows captured confocal images at different times following injury induced by high-power laser exposure to the vessel wall. Of particular interest is the development of heterogeneous domains within the thrombus as predicted by the simulations (figure 8). This predicted heterogeneity of thrombus structure contrasts with current models of thrombus development, which incorporate the development of uniform thrombogenic surfaces leading to the development of homogeneous structures. These results suggest that assumptions used in the computational model described in this paper can account for the developing complex structure of the growing thrombus. The incorporation of this structural complexity is likely to have significant biomedical implications as thrombus structural integrity impacts the development of thromboembolic pathology.
4.3 Vortical flow behind the thrombus
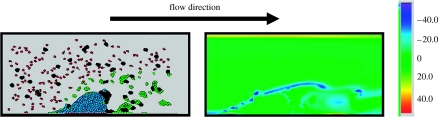
Figure 9 shows flow distribution in the simulation domain after 12 s, which clearly demonstrates strong vortical flow forming behind the thrombus. Figure 10 demonstrates the effect of turbulent flow on cell movements. Namely, some activated platelets and blood cells are flushed back by the rolling of the flow to the backside of the thrombus, which is not observed at the early stage of thrombus formation. The Reynolds number for the flow is of the order of 103. Our simulation results show that the vortical flow effects (or even turbulence), neglected by most of the current models of thrombus development, considerably influence thrombus formation and its structure.
Figure 9.
Vorticity distribution around the thrombus at time 24 s.
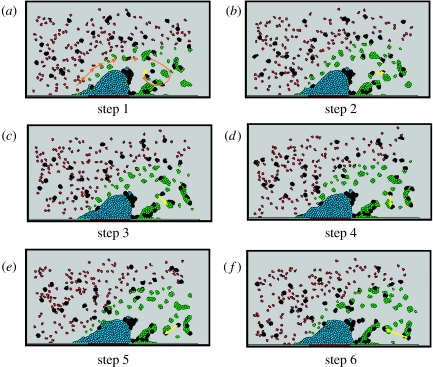
Figure 10.
Vorticity in thrombus formation process. (a–f) Six snapshots from time 23.1 to 24.3 s, with time step 0.24 s. The figure demonstrates the moving direction of platelets and blood cells under vortical flow. Orange arrow, flow direction; yellow arrow, marker for showing two blood cells' moving tracks.
4.4 Thrombus size dependence on blood flow rate
Begent & Born (1970) experimentally studied how the blood flow rate affected the growth rate of a thrombus. They found that the size of the resulting thrombus first increased and then decreased with the increase in the blood flow velocity. To compare with experimental data, we ran simulations with different mean blood flow velocities ranging from 200 to 1200 μm s−1. The size of a simulation domain was chosen to be 250 μm×25 μm and the CPM grid size was 1250×125. We used the following parameter values in the simulations: sinusoidally perturbed inlet flow velocity uin (, ϵ=0.1, ω=2π); inlet pressure=1 bar; quiescent platelet–quiescent platelet adhesion energy=20.0; activated platelet–activated platelet adhesion energy=8.0; activated platelet (high fibre level)–activated platelet (low fibre level) adhesion energy=15; volume energy constant=2.0; and fluid energy constant=Ke1=25.0, Ke2=0.2.
We used a simple coagulation pathway (pathway 2) model in the form of a system of convection–diffusion–reaction equations describing ADP, TxA2, prothrombin, thrombin and ATIII with parameter values and forms of the source terms taken from Sorensen et al. (1999). In the experiment of Begent & Born (1970), factor ADP, which is not included in the pathway 1 submodel, is injected into blood to trigger formation of the thrombus. The reaction rates and initial chemical concentrations were taken from Begent & Born (1970) and Sorensen et al. (1999). We used the Ω (activation function) from Sorensen et al. (1999) to determine the platelet state transition in figure 5 and threshold 1=1.0 and threshold 2=6.0.
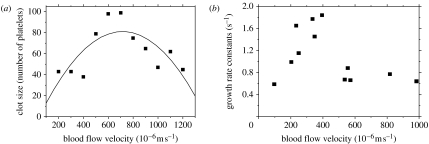
Figure 11a shows the distribution of sizes of simulated clots in a number of coagulated platelets obtained after 20 s for different blood flow velocities. This distribution is very similar to the one observed by Begent & Born (1970; figure 11b). Though our computational model is two dimensional, the simulation results quantitatively agree with the experimental data, meaning that simulation and experimental data are of the same order of magnitude. The simulations also demonstrate that growth of the thrombus is strongly affected by two opposing factors: the rate at which the platelets are supplied by the blood flow to the thrombus and the intensity of shear force that prevents platelets from adhering to the thrombus. When the blood flow rate is low, the platelets supply rate plays the dominant role. When the blood flow rate is high, the shear force increases to such an extent that it prevents platelets from adhering to the thrombus.
Figure 11.
The effect of blood flow rate on clot growth. The clot size refers to the number of platelets the thrombus is composed of at time 20 s. (a) Simulation results and (b) experimental results (reproduced from Begent & Born (1970)). Experimental results show that the clot volume increased exponentially with time and the semi-logarithmic plot of volume against time provided a growth rate constant.
4.5 Experimental verification of model predictions
To summarize, the model predicts that initially due to the small thrombus size, there is no turbulent flow and activated platelets mostly adhere to the front side of the thrombus. The most recently activated platelets end up on the front side of the thrombus. Platelets that were activated first are located in the middle and the back of the thrombus. As the thrombus grows larger, flow around the thrombus becomes turbulent. Unattached, newly activated platelets as well as clusters of blood cells get pushed back to the thrombus, and attach directly to the backside of the thrombus. This results in an inhomogeneous internal thrombus structure which might later contribute to thrombus instability and development of thromboemboli. For instance, deep vein thrombus fragmentation can contribute to emboli being carried by blood flowing from the thrombus in veins of the leg to the vasculature of the lungs. The entrapment of these pulmonary emboli is a significant cause of mortality (10–15%) in individuals suffering from DVT (approx. 250 000 diagnoses per year in the USA).
The structural integrity of a thrombus has important medical consequences, as fragments washed away from an unstable clot in a peripheral vein can embolize to the lungs with sometimes fatal results. The stability of the thrombus is influenced by the structural heterogeneity of the thrombus as the boundaries between discrete domains with different mechanoelastic properties are susceptible to fracture.
A medically relevant test of the computational model would be to determine whether it can predict how haemostatic variables influence thrombus structural heterogeneity. Examination of the experimental video and initial simulations suggests that the growing thrombus induces vortex sheets in the surrounding flow field that contributes to irregular thrombus growth and the entrapment of blood cells.
If the model hypothesis is correct, then manipulating variables affecting flow vortices (or turbulence) such as blood viscosity and flow rate should similarly alter the resulting thrombus structure. The experimental model allows one to modify these variables. Viscosity can be changed by the addition of soluble plasma protein such as albumin which should have no direct effect on thrombus development. Whole blood viscosity can be calculated using the empirical formula (de Simone et al. 2005) as follows:
whole blood viscosity=0.12×(haematocrit)+0.17×plasma protein concentration (g l−1).
Flow velocity can be manipulated by applying slight pressure on a ring placed on the vascular field surrounding the injury site. Using either of these manipulations of parameters, one can monitor thrombus development following laser-induced injury. Collecting stacks of confocal images at different times following injury, one can reconstruct the three-dimensional structure of the developing clot at different time points. Values of flow rate and blood viscosity can similarly be changed in the computational model and the structure of the clot predicted at corresponding time points. Of particular relevance to the hypothesis that vortical flow or turbulence influences thrombus heterogeneity will be the comparison of structural parameters in the resulting experimental and simulation-generated thrombus such as the size, number and distribution of domains containing primarily fibrin, fibrin and platelets, platelets, blood cells or plasma. Similar trends in the structures of the thrombi generated by the computational and experimental models in response to corresponding changes in the input variables will lend strong support to the computational model.
5. Conclusions
In this paper, a multiscale computational model is introduced for simulating different stages of thrombus formation in a blood vessel. The model combines the extended discrete CPM of platelet and blood cell aggregation with the continuous PDEs model describing the hydrodynamics of the blood flow and the kinetics of coagulation reactions. High-resolution numerical schemes have been implemented to solve the Navier–Stokes equations governing blood plasma transport and reaction–diffusion equations governing chemical kinetics. Newly developed computational methods are described for overcoming the difficulties posed by the coupling of events occurring at distinct spatial and temporal scales, by the nonlinearity of the coupled governing equations and by the geometry of the blood vessel.
The model allows one to study the influence of the blood motion on platelet aggregation and coagulation and the feedback of the growth of the growing thrombus on the fluid dynamics of blood. The model also accounts for the vessel and thrombus geometry and provides parameter studies for the effects of changes in geometry on the plasma flow dynamics and coagulation processes.
The model has been shown to be robust with respect to changes in basic parameters such as blood flow rate, adhesion energies and activation threshold. Our simulations confirmed the heterogeneous internal structure of the developing thrombus, suggested by preliminary experimental data, and predicted a particular sequence of events during thrombus development to be tested in the experiment. We also made predictions about different stages in thrombus development, which can be tested experimentally and suggest specific experiments. Lastly, we demonstrated that the dependence of the thrombus growth rate on the blood flow rate in simulations was close to the one observed experimentally.
The simulation results reproduced several specific experimentally observed behaviours of platelets and the blood plasma. For example, on the downstream side, platelets and blood cells behind the thrombus move in the upstream direction towards the thrombus surface. Furthermore, the simulation predicts that blood cells get trapped inside the thrombus during its formation contributing to the heterogeneity of the thrombus structure. Since this heterogeneity probably contributes to thrombus structural instability, understanding parameters involved in these structural considerations has significant biomedical value, given the morbidity associated with thromboembolic disease.
We recently obtained (Alber et al. 2006, 2007a,b) a continuous limit of the CPM for cells in a chemotactic field in the form of a Fokker–Planck equation for the evolution of the cell probability density function. We plan to apply the same methodology to derive continuum limit of the extended CPM described in this paper, and couple it with the Navier–Stokes equations resulting in a coarse-grained model for the thrombus growth.
We are currently working on setting up experiments to test model predictions of the dependence of the specific phases in thrombus development on the blood flow rate. In particular, simulation results suggest that vortices (or potentially turbulence) in the flow fields surrounding the developing thrombus contribute to thrombus structural heterogeneity. By experimentally restricting the blood flow exiting the vascular bed, one can reduce the blood flow through the injured vessels under examination. Additionally, the viscosity of blood can be manipulated experimentally by infusion of albumin, which will not directly affect coagulation parameters. By manipulating haemodynamic properties influencing the flow field, we can test the predictions of the simulation related to the development of thrombus heterogeneity.
Acknowledgments
Adult 6- to 8-week-old C57B1/6 mice were used following NIH guidelines and approval from the Institutional Care and Use Committe of the IU School of Medicine.
This work was partially supported by NIH grant no. 1R0-GM076692-01: Interagency Opportunities in Multiscale Modeling in Biomedical, Biological and Behavioral Systems NSF 04.6071 to M.A. and N.C. and by NIH grant HL073750 to E.D.R.
Appendix A. Computational methods
In this section, we describe numerical methods for solving the PDEs as well as the coupling between the CPM and PDE submodels.
Different scales used in the simulations are as follows. Finite-difference grid used for solving PDEs 100×50 and the CPM lattice grid 500×250 correspond to the physical area 400×200 μm2. The time of a simulation, which is equal to 2500 Navier–Stokes steps and 50 000 Monte Carlo steps, corresponds to 30 s of real physical time. Each Monte Carlo step involves as many as 500×250 state change attempts. Twenty CPM Monte Carlo steps are implemented per each Navier–Stokes step (table 2).
Notations used to describe the computational domain for PDEs and the interface are as follows. The computational domain Ω=[a,b]×[c,d] is decomposed by a rectangular grid with uniform mesh spacing Δx=Δy=h and the boundary of Ω lies on grid lines. The grid lines in each direction are and . The cell centre (xi, yj) of a square cell is and . The indices of cell edges are (i+(1/2), j) and (i, j+(1/2)), respectively. The grid nodes (xi−1/2, yj−1/2) are the cell corners.
The finite volume type discretization is used on this cell-centred Cartesian grid. Corresponding to this grid, variables u, ρ and Ck are given at the cell centres. uij, ρij and Ck,ij are defined to be the cell average values. For example, uij is
| (A1) |
A fractional step approach is employed to update the grid solutions. The sequence of updates for solutions within a time step from time tn to tn+1 is as follows.
Identify the thrombus–plasma interface on the PDE grid. The adhesion and cohesion force densities are calculated from CPM and are added to fn.
The Navier–Stokes equations are solved numerically using a cell-centred projection method to give new velocities un+1 and pressure pn+1/2.
The chemical fields are updated to account for the advection, diffusion and reaction. An operator splitting approach is employed. The updating of the advective transport and the diffusive transport is coupled to the solution of the Navier–Stokes equation step.
The transport of the inactive platelets and platelet aggregation formulation of fibril network are accounted for using CPM.
Steps (i)–(iii) of the sequence belong to the continuous model iteration, while step (iv) belongs to the CPM iteration. The detailed descriptions of each component of the solution updates are presented in the following sections.
A.1 A tracking method for cellular transport
We employ an interface between vessel wall and incompressible viscous flow with no-slip boundary conditions. Therefore, u(x, y) is set to 0 at the wall boundary.
To describe the thrombus–plasma interface on the PDE grid, the ‘stair step’ approach is used as follows.
For every PDE grid cell, find all of the thrombus lattice sites within the PDE cell.
Compute fractional volume of the thrombus within the PDE cell.
If the volume fraction in a PDE cell is less than 0.5, mark this cell as a fluid cell (the cell lies within the fluid), otherwise mark it as a body cell (the cell does not lie within the fluid).
If a fluid cell and a body cell share cell edge, mark this edge as the domain boundary.
We assume that cell motion is negligibly small during one step of the algorithm. Therefore, the thrombus–plasma interface is treated as an internal boundary. The no-slip and no-flux conditions are used on the interface to update the flow state. In principle, the interface should assume the shape adjusted by the flow. However, the reconstructed interface is a ‘stair’ within a finite-difference grid cell. The subcell resolution is omitted by this algorithm, and a displacement error of interface position of order is introduced by this algorithm. As a result, the PDE solution is only first-order accurate near the boundary.
A.2 Forces applied to fluid
We use a method similar to the one used in Pivkin et al. (2006) for describing coupling forces between fluid and cells
| (A2) |
where the coupling force associated with the nth platelet is distributed around its centre of mass yn as
| (A3) |
where α is the platelet radius. The force vector for a platelet n is as follows:
| (A4) |
where vn is the velocity vector of the platelet n and finteraction is an interaction force between platelet n and surrounding platelets.
A.3 Numerical solutions of the PDEs
In the solution domain for the Navier–Stokes equations, the mesh specification introduced at the beginning of §5 applies here. A cell-centred approximate projection method similar to Bell & Colella's approximation projection method (Bell et al. 1991) is used to solve NS equations numerically on the cell-centred Cartesian grid.
The conservative formulation of the momentum equation (3.1)
| (A5) |
where I is the identity matrix and n the outward unit normal on the cell edge is firstly solved for the intermediate velocity u* by the following finite volume approximation equation:
| (A6) |
Here the pressure-incremental formulation is adapted. The projection actually returns an increment to the pressure field.
The chemical reaction equation (3.3) is solved by a Crank–Nicolson time discretization scheme. Standard five-point Laplacian approximation is used to discretize the diffusion term:
| (A7) |
To compute the advective terms and , the fluid velocity on the cell edge is needed. For this reason, equations (A 7) and (A 6) are solved together. These advective terms are computed with the unsplit second-order upwind scheme proposed by Bell et al. (1991). The no-flux boundary condition is used when solving equation (A 7).
The upwind scheme is an explicit scheme, which requires a time-step restriction for stability. The standard CFL condition
| (A8) |
is used to set the time step.
The computed velocity field u* is projected to enforce incompressibility at time tn+1. To decompose the discrete velocity u* into a discretely divergence-free field and a discrete gradient field, equations
| (A9) |
| (A10) |
are solved for the new velocity field un+1 at time tn+1 and ϕ. Here, D and G are discrete divergence and discrete gradient operators, respectively, that act on the cell-centred quantities. To solve for un+1 and ϕ, operator D is applied to both sides of equation (A 9). DG defines a discrete approximation L to the Laplacian
| (A11) |
if Δx=Δy. The stencil for L produces a decoupling of the grid points. This decoupling has been known to cause problems when there are source terms (Lee & Tsuei 1993; Lai 1994). To avoid working with the wide stencil for the discrete Laplacian, the discretely divergence-free constraint on the velocity is relaxed so that the divergence constraint is satisfied approximately. Therefore, L is replaced by the compact, second-order accurate five-point Laplacian operator Lc
| (A12) |
The lagged pressure is updated as follows:
| (A13) |
References
- Alber M, Jiang Y, Kiskowski M. Lattice gas cellular automaton model for rippling and aggregation in myxobacteria. Physica D. 2004a;190:343–358. doi:10.1016/j.physd.2003.11.012 [Google Scholar]
- Alber M, Kiskowski M, Jiang Y. Two-stage aggregate formation via streams in myxobacteria. Phys. Rev. Lett. 2004b;93:068 301. doi: 10.1103/PhysRevLett.93.068102. doi:10.1103/PhysRevLett.93.068102 [DOI] [PubMed] [Google Scholar]
- Alber, M., Kiskowski, M. Jiang, Y. & Newman, S. 2004c Biological lattice gas models. In Dynamics and bifurcation of patterns in dissipative systems, vol. 12 (eds G. Dangelmayr & I. Opera). World Scientific Series on Nonlinear Science, pp. 274–291. Singapore: World Scientific.
- Alber M, Chen N, Glimm T, Lushnikov P.M. Multiscale dynamics of biological cells with chemotactic interactions: from a discrete stochastic model to a continuous description. Phys. Rev. E. 2006;73:051 901. doi: 10.1103/PhysRevE.73.051901. doi:10.1103/PhysRevE.73.051901 [DOI] [PubMed] [Google Scholar]
- Alber M, Chen N, Glimm T, Lushnikov P.M. Two-dimensional multiscale model of cell motion in a chemotactic field. In: Anderson A.R.A, Chaplain M.A.J, Rejniak K.A, editors. Single-cell-based models in biology and medicine. Birkhaauser; Basel, Switzerland: 2007a. pp. 53–72. [Google Scholar]
- Alber M, Chen N, Newman S, Lushnikov P.M. Continuous macroscopic limit of a discrete stochastic model for interaction of living cells. Phys. Rev. Lett. 2007b;99:168 102. doi: 10.1103/PhysRevLett.99.168102. doi:10.1103/PhysRevLett.99.168102 [DOI] [PubMed] [Google Scholar]
- Anand M, Rajagopal K, Rajagopal K.R. A model for the formation and lysis of blood clots. Pathophysiol. Haemost. Thromb. 2005;34:109–120. doi: 10.1159/000089931. doi:10.1159/000089931 [DOI] [PubMed] [Google Scholar]
- Badimon L, Badimon J.J, Galvez A, Chesebro J.H. Influence of arterial damage and wall shear rate on platelet deposition. Ex vivo study in a swine model. Arteriosclerosis. 1986;6:312. doi: 10.1161/01.atv.6.3.312. [DOI] [PubMed] [Google Scholar]
- Baldwin S.A, Basmadjian D. A mathematical model of thrombin production in blood coagulation, part I: the sparsely covered membrane case. Ann. Biomed. Eng. 1994;22:357–370. doi: 10.1007/BF02368242. doi:10.1007/BF02368242 [DOI] [PubMed] [Google Scholar]
- Barynin I.A, Starkov I.A, Khanin M.A. Mathematical models in hemostasis physiology. Izv. Akad. Nauk. Ser. Biol. 1999;1:59–66. [PubMed] [Google Scholar]
- Basmadjian D. The effect of flow and mass transport in thrombogenesis. Ann. Biomed. Eng. 1990;18:685–709. doi: 10.1007/BF02368455. doi:10.1007/BF02368455 [DOI] [PubMed] [Google Scholar]
- Begent N, Born G.V. Growth rate in vivo of platelet thrombi, produced by iontophoresis of ADP, as a function of mean blood flow velocity. Nature. 1970;227:926–930. doi: 10.1038/227926a0. doi:10.1038/227926a0 [DOI] [PubMed] [Google Scholar]
- Bell, J. B., Colella, P. & Howell, H. 1991 An efficient second-order projection method for viscous incompressible flow. In Proc. 10th AIAA Computational Fluid Dynamics Conference, Honolulu, Hawaii, 24–27 June 1991
- Beltrami E, Jesty J. Mathematical analysis of activation thresholds in enzyme-catalyzed positive feedbacks: application to the feedbacks of blood coagulation. Proc. Natl Acad. Sci. USA. 1995;92:8744–8748. doi: 10.1073/pnas.92.19.8744. doi:10.1073/pnas.92.19.8744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beltrami E, Jesty J. The role of membrane patch size and flow in regulating a proteolytic feedback threshold on a membrane: possible application in blood coagulation. Math. Biosci. 2001;172:1–13. doi: 10.1016/s0025-5564(01)00064-5. doi:10.1016/S0025-5564(01)00064-5 [DOI] [PubMed] [Google Scholar]
- Benoit M, Gabriel D, Gerisch G, Gaub H.E. Discrete interactions in cell adhesion measured by single-molecule force spectroscopy. Nat. Cell Biol. 2000;6:313–317. doi: 10.1038/35014000. doi:10.1038/35014000 [DOI] [PubMed] [Google Scholar]
- Casal A, Sumen C, Reddy T.E, Alber M.S, Lee P.P. Agent-based modeling of the context dependency in t cell recognition. J. Theor. Biol. 2005;236:376–391. doi: 10.1016/j.jtbi.2005.03.019. doi:10.1016/j.jtbi.2005.03.019 [DOI] [PubMed] [Google Scholar]
- Chaturvedi R, et al. On multiscale approaches to three-dimensional modelling of morphogenesis. J. R. Soc. Interface. 2005;2:237–253. doi: 10.1098/rsif.2005.0033. doi:10.1098/rsif.2005.0033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen N, Glazier J.A, Izaguirre J, Alber M.S. A parallel implementation of the cellular potts model for simulation of cell-based morphogenesis. Comp. Phys. Commun. 2007;176:670–681. doi: 10.1016/j.cpc.2007.03.007. doi:10.1016/j.cpc.2007.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chien S, Usami S, Taylor H.M, Lundberg J.L, Gregersen M.I. Effect of hematocrit and plasma proteins on human blood rheology at low shear rates. J. Appl. Physiol. 1966;21:81–87. doi: 10.1152/jappl.1966.21.1.81. [DOI] [PubMed] [Google Scholar]
- Chien S, Sung K.L.P, Skalak R, Usami S, Tozeren A.L. Theoretical and experimental studies on viscoelastic properties of erythrocyte membrane. Biophys. J. 1978;24:463–487. doi: 10.1016/S0006-3495(78)85395-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cickovski T.M, Huang C, Chaturvedi R, Glimm T, Hentschel H.G.E, Alber M.S, Glazier J.A, Newman S.A, Izaguirre J.A. A framework for three-dimensional simulation of morphogenesis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2005;2:273–288. doi: 10.1109/TCBB.2005.46. doi:10.1109/TCBB.2005.46 [DOI] [PubMed] [Google Scholar]
- Cickovski T.M, et al. From genes to organisms via the cell: a problem solving environment for multicellular development. Comput. Sci. Eng. 2007;9:50–60. doi: 10.1109/MCSE.2007.74. doi:10.1109/MCSE.2007.74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dan D, Mueller C, Chen K, Glazier J.A. Solving the advection–diffusion equations in biological contexts using the cellular Potts model. Phys. Rev. E. 2005;72:41 909. doi: 10.1103/PhysRevE.72.041909. doi:10.1103/PhysRevE.72.041909 [DOI] [PubMed] [Google Scholar]
- David N.K. Blood flow in arteries. Annu. Rev. Fluid Mech. 1997;29:399–434. doi:10.1146/annurev.fluid.29.1.399 [Google Scholar]
- de Simone G, Devereux R.B, Chinali M, Best L.G, Lee E.T, Welty T.K. Strong heart study. Hypertension. 2005;45:625–630. doi: 10.1161/01.HYP.0000157526.07977.ec. doi:10.1161/01.HYP.0000157526.07977.ec [DOI] [PubMed] [Google Scholar]
- Drasdo D, Hoehme S. A single-cell based model to tumor growth in-vitro: monolayers and spheroids. Phys. Biol. 2005;2:133–147. doi: 10.1088/1478-3975/2/3/001. doi:10.1088/1478-3975/2/3/001 [DOI] [PubMed] [Google Scholar]
- Drasdo D, Kree R, McCaskill J. Monte–Carlo approach to tissue–cell populations. Phys. Rev. E. 1995;52:6635. doi: 10.1103/physreve.52.6635. doi:10.1103/PhysRevE.52.6635 [DOI] [PubMed] [Google Scholar]
- Fogelson A.L. Continuum models of platelet aggregation: formulation and mechanical properties. SIAM J. Appl. Math. 1992;52:1089–1110. doi:10.1137/0152064 [Google Scholar]
- Fogelson A.L. Continuum models of platelet aggregation: mechanical properties chemically-induced phase transitions. Contemp. Math. 1993;141:279–294. [Google Scholar]
- Fogelson A.L, Guy R.D. Platelet–wall interactions in continuum models of platelet thrombosis: formulation and numerical solution. Math. Med. Biol. 2004;21:293–334. doi: 10.1093/imammb21.4.293. doi:10.1093/imammb/21.4.293 [DOI] [PubMed] [Google Scholar]
- Glazier J.A, Graner F.M.C. Simulation of the differential adhesion driven rearrangement of biological cells. Phys. Rev. E. 1993;47:2128–2154. doi: 10.1103/physreve.47.2128. doi:10.1103/PhysRevE.47.2128 [DOI] [PubMed] [Google Scholar]
- Glazier J.A, Balter A, Poplawski J. Magnetization to morphogenesis: a brief history of the Glazier–Graner–Hogeweg model. In: Anderson A.R.A, Chaplain M.A.J, Rejniak K.A, editors. Single-cell-based models in biology and medicine. Birkhaauser; Basel, Switzerland: 2007. pp. 79–108. [Google Scholar]
- Graner F.M.C, Glazier J.A. Simulation of biological cell sorting using a two-dimensional extended potts model. Phys. Rev. Lett. 1992;69:2013–2016. doi: 10.1103/PhysRevLett.69.2013. doi:10.1103/PhysRevLett.69.2013 [DOI] [PubMed] [Google Scholar]
- Hirt C, Nichols B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comp. Phys. 1981;39:201–225. doi:10.1016/0021-9991(81)90145-5 [Google Scholar]
- Jesty J, Beltrami E, Willems G. Mathematical analysis of a proteolytic positive-feedback loop: dependence of lag time and enzyme yields on the initial conditions and kinetic parameters. Biochemistry. 1993;32:6266–6274. doi: 10.1021/bi00075a021. doi:10.1021/bi00075a021 [DOI] [PubMed] [Google Scholar]
- Jiang Y, Pjesivac-Grbovic J, Cantrell C, Freyer J.P. A multiscale model for avascular tumor growth. Biophys. J. 2005;89:3884–3894. doi: 10.1529/biophysj.105.060640. doi:10.1529/biophysj.105.060640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones K.C, Mann K.G. A model for the tissue factor pathway to thrombin. ii. A mathematical simulation. J. Biol. Chem. 1994;269:23 367–23 373. [PubMed] [Google Scholar]
- Khanin M.A, Semenov V.V. A mathematical model of the kinetics of blood coagulation. J. Theor. Biol. 1989;136:127–134. doi: 10.1016/s0022-5193(89)80220-6. doi:10.1016/S0022-5193(89)80220-6 [DOI] [PubMed] [Google Scholar]
- Kiskowski M.A, Jiang Y, Alber M.S. Role of streams in myxobacteria aggregate formation. Phys. Biol. 2004;1:173–183. doi: 10.1088/1478-3967/1/3/005. doi:10.1088/1478-3967/1/3/005 [DOI] [PubMed] [Google Scholar]
- Knewitz M.A, Mombach J.C.M. Computer simulation of the influence of cellular adhesion on the morphology of the interface between tissues of proliferating and quiescent cells. Comput. Biol. Med. 2006;36:59–69. doi: 10.1016/j.compbiomed.2004.08.002. doi:10.1016/j.compbiomed.2004.08.002 [DOI] [PubMed] [Google Scholar]
- Kothe D.B, Rider W.J, Mosso S.J, Brock J.S, Hochstein J.I. Volume tracking of interfaces having surface tension in two and three dimensions. AIAA. 1996:96–0859. [Google Scholar]
- Kuharsky A.L, Fogelson A.L. Surface-mediated control of blood coagulation: the role of binding site densities and platelet deposition. Biophys. J. 2001;80:1050–1074. doi: 10.1016/S0006-3495(01)76085-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai, M. 1994 An approximate projection method for reacting flow in the zero mach number limits. PhD thesis, University of California, Berkeley.
- Lee D, Tsuei Y. A hybrid adaptive gridding procedure for rescirculating fluid flow problems. J. Comput. Phys. 1993;108:122–141. doi:10.1006/jcph.1993.1168 [Google Scholar]
- Lobanov A.I, Starozhilova T.K. The effect of convective flows on blood coagulation processes. Pathophysiol. Haemost. Thromb. 2005;34:121–134. doi: 10.1159/000089932. doi:10.1159/000089932 [DOI] [PubMed] [Google Scholar]
- Merks R.M.H, Brodsky S.V, Goligorksy M.S, Newman S.A, Glazier J.A. Cell elongation is key to in silico replication of in vitro vasculogenesis and subsequent remodeling. Dev. Biol. 2006;289:44–54. doi: 10.1016/j.ydbio.2005.10.003. doi:10.1016/j.ydbio.2005.10.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman T.J. Modeling multi-cellular systems using sub-cellular elements. Math. Biosci. Eng. 2005;2:611–622. doi: 10.3934/mbe.2005.2.613. [DOI] [PubMed] [Google Scholar]
- Newman M, Barkema G. Oxford University Press; Oxford, UK: 1999. Monte Carlo methods in statistical physics. [Google Scholar]
- Newman T.J, Grima R. Many-body theory of chemotactic cell–cell interactions. Phys. Rev. E. 2004;70:051916. doi: 10.1103/PhysRevE.70.051916. doi:10.1103/PhysRevE.70.051916 [DOI] [PubMed] [Google Scholar]
- Newman S, Christley S, Glimm T, Hentschel H, Kazmierczak B, Zhang Y, Zhu J, Alber M. Multiscale models for vertebrate limb development. Curr. Top. Dev. Biol. 2008;81:311–340. doi: 10.1016/S0070-2153(07)81011-8. doi:10.1016/S0070-2153(07)81011-8 [DOI] [PubMed] [Google Scholar]
- Noh, W. & Woodward, P. 1967 SLIC (simple line interface calculation). In Proc. Fifth Int. Conf. on Numerical Methods for Fluid Dynamics (eds A. I. van de Vooren & P. J. Zandbergen). Springer Lecture Notes in Physics, no. 59, pp. 330–340. New York, NY: Springer.
- Ovanesov M.V, Krasotkina J.V, Ul'yanova L.I, Abushinova K.V, Plyushch O.P, Domogatskii S.P, Vorob'ev A.I, Ataullakhanov F.I. Hemophilia a and b are associated with abnormal spatial dynamics of clot growth. Biochim. Biophys. Acta. 2002;1572:45–57. doi: 10.1016/s0304-4165(02)00278-7. [DOI] [PubMed] [Google Scholar]
- Palsson E, Othmer H. A model for individual and collective cell movement in Dictyostelium discoideum. Proc. Natl Acad. Sci. USA. 2000;97:10 448–10 453. doi: 10.1073/pnas.97.19.10448. doi:10.1073/pnas.97.19.10448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pivkin I.V, Richardson P.D, Karniadakis G. Blood flow velocity effects and role of activation delay time on growth and form of platelet thrombi. Proc. Natl Acad. Sci. USA. 2006;103:17 164–17 169. doi: 10.1073/pnas.0608546103. doi:10.1073/pnas.0608546103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorensen E.N, Burgreen G.W, Wagner W.R, Antaki J.F. Computational simulation of platelet deposition and activation: I. Model development and properties. Ann. Biomed. Eng. 1999;27:436–448. doi: 10.1114/1.200. doi:10.1114/1.200 [DOI] [PubMed] [Google Scholar]
- Sozinova O, Jiang Y, Kaiser D, Alber M. A three-dimensional model of myxobacterial aggregation by contact-mediated interactions. Proc. Natl Acad. Sci. USA. 2005;102:11 308–11 312. doi: 10.1073/pnas.0504259102. doi:10.1073/pnas.0504259102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sozinova O, Jiang Y, Kaiser D, Alber M. A three-dimensional model of myxobacterial fruiting-body formation. Proc. Natl Acad. Sci. USA. 2006;103:17 255–17 259. doi: 10.1073/pnas.0605555103. doi:10.1073/pnas.0605555103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarnitsina V.I, Pokhilko A.V, Ataullakhanov F.I. A mathematical model for the spatio-temporal dynamics of intrinsic pathway of blood coagulation. i. The model description. Thromb. Res. 1996a;84:225–236. doi: 10.1016/s0049-3848(96)00182-x. doi:10.1016/S0049-3848(96)00182-X [DOI] [PubMed] [Google Scholar]
- Zarnitsina V.I, Pokhilko A.V, Ataullakhanov F.I. A mathematical model for the spatio-temporal dynamics of intrinsic pathway of blood coagulation. ii. Results. Thromb. Res. 1996b;84:333–344. doi: 10.1016/s0049-3848(96)00197-1. doi:10.1016/S0049-3848(96)00197-1 [DOI] [PubMed] [Google Scholar]