Individual space–time activity-based modelling of infectious disease transmission within a city

Abstract

This paper provides an example of the application of an individual space–time activity-based model (ISTAM) to the simulation of the transmission of infectious disease in Eemnes, a city in The Netherlands. Four questions were addressed: (i) how to build the whole population at the city level, (ii) how to build the structure of the activity bundles for the city, (iii) how to assign daily activity patterns to each individual, and (iv) how to simulate within-AB transmission. The model was calibrated and examples of simulation results such as dynamics of the population during a whole day, infection distribution and network analysis are presented.

1. Introduction

Simulating the processes of infectious disease transmission among the human population, both in time and in space, not only leads to better understanding of transmission mechanisms but also provides practical utility such as the ability to build and test theories, design and analyse epidemiological surveys, forecast trends and test control measures. Faced with diseases such as AIDS, severe acute respiratory syndrome (SARS), foot and mouth disease (FMD) and avian flu, powerful simulation models for infectious disease transmission are becoming increasingly important tools for public health researchers and practitioners.

Cities or urban areas ‘represent large concentrations of diverse peoples living on relatively small parcels of land’ (LaGory 1988). By 2020, 55% of the world's population is projected to live in urban areas (Leautier 2006). Fortunately, the epidemiological environment can be improved by urbanization. For example, urbanization processes can create improved nutrition, housing less vulnerable to vermin and cleaner drinking water (Daily & Ehrlich 1996). However, the large density of population living in urban areas increases the probability of intimate contact between people. Simulating the transmission of infectious disease transmission within urban areas is, thus, of great importance. As reviewed by Daily & Ehrlich (1996), the urban area's ‘amplification’ effect in terms of infectious disease transmission was noted by Decock & Mccormick (1988). The need to investigate the relationship between urbanization patterns, individuals' space–time dynamics and infectious disease transmission has led to an interest in the development of simulation models of both disease transmission and space–time behaviour at the individual level.

1.1 Individual-based models for simulation of infectious disease transmission

Individual-based models (IBMs) for the simulation of infectious disease transmission have been applied frequently. Fox et al. (1971) and Elveback et al. (1976) applied IBMs for immunization studies more than 30 years ago. However, partly due to the lack of both data and advanced computation ability, the potential of IBMs was not recognized widely (Koopman 2002). The twenty-first century has seen a revival of the application of IBMs for the simulation of infectious disease transmission (Eubank 2002; Halloran et al. 2002; Eichner 2003; Ferguson et al. 2003, 2005, 2006; Bian 2004; Carley et al. 2004; Dibble & Feldman 2004; Eubank et al. 2004; Longini et al. 2005). By representing complex social and physical systems through faithful modelling and model space exploration, IBMs can provide insights into different organizational scales that are not possible using other modelling approaches (Prietula et al. 1998).

The most important advantages of IBMs are that they can consider the heterogeneity of both individuals and their environment and incorporate the stochastic nature of infectious disease transmission. However, these advantages also mean that the application of IBMs for modelling the transmission of infectious disease is strongly data dependent, while the required data are not always available. Furthermore, several assumptions have to be made to make the simulation plausible.

1.2 Concept of activity bundle

For the application of IBMs to the simulation of infectious disease transmission, one of the key questions is how to build the transmission network within the population at the individual level. Yang & Atkinson (in press) discussed methods based on spatial adjacency and social relations and proposed an individual space–time activity-based model (ISTAM) as a solution to simulate airborne infectious disease transmission among the human population based on individuals' space–time activities. These activity-based models are rooted in time geography, which provides a framework for describing and defining how individuals perform activities under the constraints of time and space (Hägerstrand 1970). The concept of ‘lifeline’ represents the path taken by an individual in time–space, while ‘bundle’ describes the convergence of human activity in space–time (Hägerstrand 1970). If lifelines of every individual in the population are known, bundles can be identified in which lifelines of multiple individuals interact. Then, it is possible to simulate the transmission of specific infectious diseases on the more detailed level of this bundle (Forer 2002). In this paper, and another paper by Yang & Atkinson (in press), the concept of activity bundle (AB) is borrowed from time geography and defined as a semantic space where contact probability varies as a function of the dynamics of humans inside the bundle.

1.3 Between-AB simulation

Individuals' movements between ABs are determined by both locational supply and individuals' choices. The subset of all locations, which an individual visits as a result of his/her daily activities, is defined as an activity space (Golledge & Stimson 1997). As stated by Golledge & Stimson (1997), the activity space of a typical individual is composed of three parts: (i) movements within and near the home; (ii) movements to and from regular activity locations, such as journeys to work, shop, socialize, and so on; and (iii) movements in and around the locations where these activities occur. Schönfelder & Axhausen (2002, 2003) described and discussed three methods for describing individual activity spaces: (i) confidence ellipses; (ii) kernel densities; and (iii) minimum spanning trees (networks). A similar concept of ‘personal network for usual places’ was presented by Flamm & Kaufmann (2006) to identify a certain number of daily life centres. A large amount of research has been undertaken on individuals' daily activities at the between-AB level, especially in the fields of transportation and urban planning. Both utility maximization (Bowman & Ben-Akiva 2001) and rule-based approaches (Pendyla & Kitamura 1998; Arentze & Timmermans 2007) have been used to describe how households and individuals determine their daily lifeline, including decisions about which activities to undertake, at what locations, at what times, with which persons and how to travel to those locations. These decisions are made subject to spatio-temporal constraints as defined by time geography (Hägerstrand 1970). Activity-based models at this level have been applied widely in transportation (Miller et al. 2004; Batty 2005a,b; Ettema et al. 2006). These models provide a starting point for modelling the presence of individuals in ABs, within which diseases are transmitted.

1.4 Within-AB simulation

At the within-AB level, research on the dynamics of humans inside a small space can be traced to ‘room geography’ (Jackle et al. 1976), which studied how individuals distribute across a specific small area. However, research at fine spatial scales has been slow due to the lack of systematic data and corresponding tools and methods (Batty 2003). Recently, IBMs and object-oriented technology have facilitated further study. One example is the pedestrian model proposed by Batty and colleagues (Batty 2003, 2005a,b; Batty et al. 2003) to study how behaviour emerges from aggregated interactions between fine-scale objects. Applications include pedestrian traffic modelling, disaster evacuation and spreading of infectious diseases.

As reviewed by Ellegård (1999), the importance of the concepts of ‘series’ and ‘group’ was discussed by Jensen & Vestergaard (1979). A number of individuals ‘who occasionally meet at the same place where they intend to do the same thing constitute a series’, while individuals in a group ‘form a social entity which persists over a period of time and in which the individuals share a long-term purpose’. It is believed that role performance and social involvement are influenced by the spatial environment (Baldassare 1978). Baldassare (1978) claimed that ‘individuals must obtain varying degrees of physical separation or closeness to others in order to engage in their activities’. Similarly, Gatrell (1983) claimed that ‘The spacing of individuals depends not only on how the environment has been designed but also on the task or nature of interaction that the individuals must perform’. Furthermore, it is widely accepted that there are social rules about how close humans can approach each other. For example, Hall (1966) identified four distances: intimate; personal; social; and public (table 1).

Table 1.

Distance rules (Hall 1966).

distance type	value (m)	meaning
public	>3	the range of non-involvement
social	3–1.5	the range in which most public interactions are observed. This is a comfortable distance for people who are standing in a group, but maybe not talking directly with one another. People sitting in chairs or gathered in a room will tend to prefer this distance
personal	1.5–0.6	this is a protected area, where strangers would not be welcomed. At its inner limit it holds other people ‘at arm's length’
intimate	<0.6	this range is reserved for lovers, family, small children and very close friends

The contacts between individuals are driven by social purposes or constrained by physical conditions or both, while infection per se is a physical process. Some contacts are indispensable for undertaking some activities. For example, an individual who goes shopping will generally make contact with the salesperson when checking out. Some contacts, although not purposeful, occur owing to the restriction of the environment. For example, in a crowded bus, passengers have to be close to each other when there is no spare space. The first type of contact is voluntary and is determined by the individuals. The second type of contact is involuntary and is not wholly determined by the individuals.

Although the above review is general, it provides a basis for within-AB simulation: focus on the changing distances between individuals and note specifically when the distances are less than the distance required for infection.

1.5 Aim of this research

Previously, an IBM named individual space–time activity-based model (ISTAM) was designed and applied to simulate a hypothetical influenza outbreak among the first-year undergraduate students within the campus of the University of Southampton (Yang & Atkinson in press). The student body provided an example that was relatively simple in terms of daily activity patterns, population structure and AB structure, and this simplicity facilitated modelling. However, a student population is clearly a special case compared with the general human community (e.g. the whole population within a city). To apply the ISTAM at the city level, four additional questions needed to be answered: (i) how to build the whole population in terms of the demographic, social and economic properties; (ii) how to build all ABs within a city in terms of their category, percentage and spatial distribution; (iii) how to assign daily activity patterns to each individual; and (iv) how to simulate individuals' activities at within-AB levels without detailed information about these ABs' physical conditions.

This paper explores the above four questions and attempts to provide answers through the application of the ISTAM to the city of Eemnes in The Netherlands. The aim of the research was to apply the ISTAM at the city level to model a hypothetical influenza epidemic spreading among the population. Section 2 introduces the research methods, specifically the ISTAM and role-based AB simulation. Background and data sources are introduced in §3. Five sub-processes for building the population and city are presented in §4. Section 5 describes the simulation of individuals' movements between ABs and interactions within ABs. Section 6 shows the results of the analysis and simulations, while §§7 and 8 provide a discussion and conclusion, respectively.

2. Individual space–time activity-based model and role-based AB simulation

2.1 ISTAM

Individual space–time activity-based model (ISTAM) is an IBM that integrates the infectious disease evolution process, individual activity patterns and a stochastic infection model (Yang & Atkinson in press). The ISTAM was developed by the integration of Repast (2004, http://repast.sourceforge.net/) and the Java Topology Suite (JTS, 2005, http://www.vividsolutions.com/jts/jtshome.htm). Repast is a toolkit for agent-based modelling and provides the ability to simulate temporal processes and individuals' actions. JTS is a GIS toolkit and provides spatial computation and analysis functionality. Their integration has great potential for simulating the space–time dynamics of individuals.

In the ISTAM, the process of disease transmission is separated into occurrence of contact and infection, the two key factors that need to be captured in a disease transmission model (Zheng et al. 2005). For airborne infectious diseases, it is assumed that transmission probability is inversely related to the distance between the infectious and susceptible individuals (if there are no obstacles between them), and is also directly related to the duration of the contact. A set of time lines are used to describe the evolution of the infection and disease within the host. Generally, time lines include the latent, infectious, incubation and symptomatic periods.

AB is a core concept in the ISTAM. Taking advantage of the concept of an AB, the ISTAM considers the activities of human individuals at two levels: between ABs and within ABs. At the between-AB level, humans' space–time dynamics are modelled as changes in AB per individual during one day within a certain area. At the within-AB level, interest is in capturing each individuals' space–time dynamics at fine space–time scales. Owing to the different degrees of understanding of these two processes and different availabilities of practical data to support modelling, the research approaches at these two levels can be flexible to make the ISTAM suitable for different situations.

If internal physical information about an AB such as its geometry and spatial layout is available, the geographical space inside an AB can be represented using either (i) the raster data model (e.g. a rectangular or hexagonal grid) or (ii) the vector data model (i.e. a continuous space involving the movement of vectors). Furthermore, the raster or vector space can be two- or three-dimensional. Description of these two data models can be found in Yang & Atkinson (2006). By raster or vector space AB simulation, individuals' spatial locations within an AB are modelled explicitly and both the first and second types of contact can be simulated directly and without discrimination. Under most circumstances, internal physical information about an AB is not available. Then, it is assumed that the behaviour of individuals in small areas is among other things determined by the roles that they play in a group, and the individuals' roles within their joint activity are the primary basis for the simulation of the contacts between individuals. Importantly, the spatial pattern of individuals (i.e. relative locations between individuals) is explicit, but individuals' absolute spatial locations are not explicit. These two types of contact need to be simulated separately.

2.2 Role-based AB simulation

The assumption of role-based simulation is that, when people come together for a certain joint activity, their interactions will depend strongly on the different roles that the individuals play. For example, it is obvious that, in a shop, the contacts between salespeople, salespeople and customers, and customers are different not only in frequency but also in intensity. Role-based simulation had been proposed in a previous paper (Yang & Atkinson 2006), but this paper represents the first real implementation of such role-based AB simulation within the ISTAM.

The infection process between two individuals, as discussed before, can be separated into two stages: coming into contact and becoming infected. The probabilities of coming into contact (p_c) and infection during one contact (p_i) were used to express the random properties of these two processes. As discussed before, different distance rules can be applied to determine the distances between individuals who are involved in a variety of activities and play different roles. In the ISTAM, the square of the distance between individuals at a fine spatial scale is assumed to be inversely related to p_i. Also, it is assumed that p_c can be determined by the individuals' roles in their joint activities.

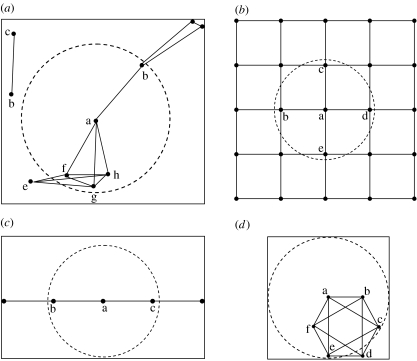
The procedure for simulating interactions within an AB can be summarized as follows. (i) All individuals presented within the same AB are divided into a certain number of groups based on each individuals' role in the joint activity. (ii) A certain spatial pattern (without explicit spatial location at fine spatial scales) is assumed to exist within groups. Interactions between individuals within each group are simulated based on these spatial patterns. Table 2 lists a few general spatial patterns within groups and figure 1 shows four of these spatial patterns. (iii) Interactions between individuals from different groups are simulated based on the activity properties. Table 3 lists a few general interaction types between two individuals belonging to different groups within the same AB.

Table 2.

Spatial patterns within groups.

pattern name	description	value of pi
full	every person is in contact with all other persons	$p_{\text{i}}^2$
loop	static. Fixed before the simulation and does not change. Individuals distribute like a loop, so one person contact with persons first and second above or below with himself/herself in the loop	$p_{\text{i}}^1$ with first above and below and $p_{\text{i}}^2$ with second above and below
queue	static. Fixed linear distribution. One person makes contact with another person just before or after him/her in the queue	$p_{\text{i}}^2$
static random	persons are distributed randomly. Each individual comes into contact with her/his four Von Neumann neighbours. One additional parameter: density	$p_{\text{i}}^2$
static even	persons are distributed evenly in a grid space. Each individual comes into contact with her/his four Von Neumann neighbours	$p_{\text{i}}^1$
dynamic random	every person comes into contact with a number of randomly selected other persons. This process repeats a number of times. Two additional parameters: density and mobility	$p_{\text{i}}^3$

Figure 1.

Spatial patterns of individuals within groups: (a) static random, (b) static even, (c) queue and (d) loop. (The points represent individuals. The solid lines that link between two points represent the possible contacts between these two individuals. Dotted circular line around individual ‘a’ shows all individuals within this area who could come into contact with individual ‘a’.)

Table 3.

Interaction types.

relation type	description or example	default distance	contact distance
cooperation	teamwork or teachers and students, managers and workers	social distance	personal distance
service	service environment. One individual serves another	public distance	personal distance
care	health care facilities. Patients and nurse	social distance, personal distance	intimate distance
random contact	restriction by physical environment	public distance	social distance, personal distance

It is hard to quantify directly the probabilities of coming into contact and becoming infected given contact. Here, both the probabilities of coming into contact and becoming infected given contact are represented at several levels. Five levels of p_c were used to represent different probabilities of coming into contact. The lowest level $p_{\text{c}}^5$ was assumed to take a constant value F, and the ratio between the two adjacent levels was fixed to be 2, i.e. $p_{\text{c}}^1$=2$p_{\text{c}}^2$=4$p_{\text{c}}^3$=8$p_{\text{c}}^4$=16$p_{\text{c}}^5$. The value of F was calibrated after simulation according to related research as discussed in §6. Three levels of p_i were used to represent different probabilities of becoming infected given contact distances of ‘intimate’, ‘personal’ and ‘social distance’. The lowest level was assumed to take a constant value I, and the ratio between the two adjacent levels was fixed to be 2, i.e. $p_{\text{i}}^1$=2$p_{\text{i}}^2$=4$p_{\text{i}}^3$. The value of I was calibrated by simulation according to related research as discussed in §6.

As an example, let us consider the possible contacts within a restaurant. According to their roles, the individuals inside the restaurant can be classified into groups such as the manager, kitchen staff, waiters and customers. The customers can be divided further into several customer groups. Alternatively, to simplify the computation, the individuals could be divided into only two groups (i.e. workers and clients). Different types of contacts could occur between and within different groups. Different values of p_c can be set for different types of contacts. For example, it can be assumed that all the customers belonging to the same customer group prefer to maintain personal distances or intimate distances between each other, while the waiters prefer to maintain a social distance with the customers when they are not providing service and a personal distance when they are providing service. Customers belonging to different customer groups prefer to maintain public distances to retain privacy, but in many circumstances this cannot be satisfied due to the restriction of the physical environment of the restaurant.

3. Background and data sources

The target city was Eemnes in The Netherlands. The municipality of Eemnes is located in the north of the province of Utrecht; it has less than 9000 inhabitants and covers about 3362 ha (from www.eemnes.nl). The Netherlands is one of the most densely populated countries in the world, implying that much interaction takes place between different municipalities in The Netherlands. In order to demonstrate the usefulness of the ISTAM, we selected Eemnes since it is not located in the direct vicinity of larger cities, limiting exchange of individuals with ‘outside’ areas.

The main data sources used in this application are listed in table 4. The activity survey data were assumed to be representative for people residing within Eemnes, although, in fact, it is not surprising that people living in large cities such as Amsterdam or Utrecht have different activity patterns compared with people living in the rural areas. The land use data were PC6 based (in The Netherlands, a complete postcode contains six positions and relates to an average of 17 addresses or delivery points, hence ‘PC6’; The Netherlands has approx. 420 000 postcodes), while synthesized household data were grid based. Preparation was needed to aggregate the household data to the PC6 level.

Table 4.

Data sources for the application of ISTAM to Eemnes.

data source (with short name)	description
activity survey data (ACT)	one activity survey named AMADEUS was taken in 2000 (Ettema 2005). In this data collection, 1997 households (with 3499 people; in the Amsterdam–Utrecht region) filled out a two-day travel/activity diary
synthesized household data (HH)	synthesized household data (at grid space level), above 1 500 000 cases, cover the area of the Amsterdam–Utrecht corridor. Every household within this area is recorded with properties such as number of persons and workers, age of the head household member, household income and car availability (Ettema et al. 2006)
land use data (land)	PC6 based, 433 689 cases, the whole Netherlands. For every PC, the numbers of people engaged with each vocation (such as offices, education, health care, industry and transport) are recorded
PC6 statistical data (PC6)	statistical data about the age and household structure for every PC6 of the whole of The Netherlands

The procedural steps were as follows. (i) Preparation (§4), i.e. build the population and the city of Eemnes. For the population, the key point was to assign properties such as family structure, number of cars and income level to every household, and assign properties such as age and gender and activity patterns to every individual. For the city, the social and spatial structures needed to be built. These simulated data were saved into a database for the next step. (ii) Simulation (§5), i.e. generate individuals' daily activities from their activity patterns and then model individuals' movements between ABs and the interaction of individuals within ABs. During these interactions, infection can occur from contacts between individuals.

In the ISTAM, three parameter groups are defined to describe a specific infectious disease: (i) evolution of the infection and disease within the host (time lines); (ii) disease severity; and (iii) effective contact. Parameters of the time lines including the latent, infectious, incubation and symptomatic periods were used to describe the evolution of the infection and disease within the host. Values of these parameters were taken from the literature as it is believed that time lines for influenza have been relatively invariant over the past half of the century (Longini et al. 2005). In the ISTAM, it is assumed that transmission probability is inversely related to the distance between the infectious and susceptible individuals, if there are no obstacles between them, and is also directly related to the duration of the contact. Thus, if an infectious individual stays within a specific distance of another susceptible individual longer than a specific period (attack duration), the two individuals come into effective contact.

The simulation system was implemented in Java using the Repast library and run on an Intel Pentium (processor 1.5 GHz and 502 MB RAM) laptop. It took approximately 30 min to run a simulation of 100-day duration.

4. Preparation: building the population and city

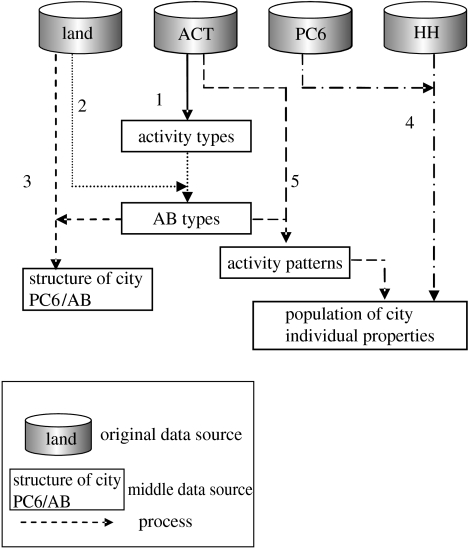
The preparation processes are shown in figure 2. Five sub-processes are represented below.

Figure 2.

Preparation process (see table 6 for data sources).

4.1 Process 1: selecting the activity types

The selection of the activity types to be used in the ISTAM depends strongly on the activity data (i.e. the ACT data source). Some types of activity such as telecommuting were neglected as they were not explicitly related to contact between individuals (and, thus, are not important for infectious disease transmission). Some other activity types needed to be included even if their percentage contribution was small because these activities bring individuals into contact intimately (such as health care). Note that trip activity was neglected in this study to simplify the research and also because of the limited availability of related data sources. All activity types that occur more than 1% in the average time distribution are listed in table 5.

Table 5.

All activity types that take more than 1% in the average time distribution.

activity type	percentage
sleep	32.20
work	14.40
others at home	13.60
trip	7.50
housekeeping	5.40
eating	4.40
waiting	2.90
personal care	2.70
social activity/family, friends	2.20
education (school, study, etc.)	1.80
child care	1.30
telecommunity	1.30
receiving visitors	1.00

4.2 Process 2: selecting the ABs

Specific objects in this application (e.g. different land use units inside one PC6) were classified to reflect the relations between the types of individuals' activities and the types of land use. It was assumed that, within one PC6, no more than one school or industry could exist. Individuals visit certain ABs such as offices, industry and farms for work. However, for certain other ABs such as post offices and banks, some individuals work there while others visit for service. All AB types and corresponding activity types within the ISTAM for this application are listed in table 6.

Table 6.

AB types within ISTAM for application to Eemnes. (The number in brackets is the expected number of staff working in this type of work place while asterisk means one and only one AB of this type within the current PC6.)

AB type	activity type
office (5)	work
industry (*)	work
farm (5)	work
shop (3)	shopping/work
post office/bank (3)	go to post office/go to bank/work
health care place (3)	health care/work
sport place (3)	sport/work
household	sleep/activities within home/visit friend's home
social place (3)	dinner out or other social activities in cafe, bar, club, etc.
relax place	cultural or recreational activities
service place	all other personal service
school (*)	study/work

4.3 Process 3: building the city

Land use data record the numbers of individuals engaged in every vocation. It was assumed that the expected size of a work place (generated from land use data) of a given vocation type was constant across all PC6 zones of Eemnes. Then, from the number of individuals engaged in a given vocation within each PC6, the number of corresponding work places was computed. For example, if the number of individuals engaged in the health care vocation within a given PC6 is 10, and the expected size of a health care work place is set to be five, then it follows that there should be two health care facilities within this PC6.

4.4 Process 4: synthesizing the population

As the synthesized household data were grid based and, therefore, not compatible with PC6 statistical data, all households within all grid cells of Eemnes were pooled together and then each household with its family members were allocated to the PC6 zones of Eemnes as follows.

Firstly, all individuals were classified according to age structure (table 7). Different sub-classifications, and subsequently simulation of activities, were applied to the above four classifications. It is believed that daily activity patterns are related to individuals' socioeconomic characteristics such as household role, lifestyle and life cycle (Vaughn et al. 1997; Kulkarni & McNally 2000). In the study by Janelle et al. (1998), the whole population was divided into 14 role groups based on dimensions of gender, marital status, employment, child care, residential tenure and mobility.

Table 7.

Age structure for the population of Eemnes.

classification	description
children under 5 years	for children under 5 years, it is assumed that they do not have independent activities and always stay inside households
children between 5 and 10 years	since the activity survey data do not cover children in this age range, their activity patterns are assumed to be simple: go to school at school hours and stay inside households at all other times
children between 11 and 18 years	their activity patterns are based on survey data, but delete all work parts. They will be further sub-categorized by four dimensions
adult	same as above, based on survey, but delete all study parts (their studies are taken as work), they will be further sub-categorized by four dimensions

In this research, the following dimensions of information were selected: (i) the average working (or study) hours per week (0, 0 hours; 1, 1–15 hours; 2, 16–30 hours; 3, 31–45 hours; 4, more than 45 hours), role in household (1, no family; 2, single parent with children; 3, child with single parent; 4, parent in couple without children; 5, parent in couple with children; 6, child in couple with children), car availability (1, no car; 2, yes and always; 3, yes and sometimes) and day of the week (Sunday to Saturday). Based on these four dimensions, both children between 11 and 18 years and adults in the population were further sub-classified, and their corresponding activity patterns were generated from the activity survey data. If the survey data could not generate a corresponding activity pattern from a specific value of these four dimensions, a replacement activity pattern was assigned at a more aggregated level, i.e. the number of dimensions was reduced. The sequence of the dimensions to be excluded was car availability index, role in household and working (study) hours. For one individual, her/his daily activity pattern was further classified according to the seven weekdays.

4.5 Process 5: assigning activity patterns to individuals

Within the ISTAM, after the time unit is set (15 and 30 min are in common use), one day is divided into a number of units. Thus, the objective of simulating a person's daily activity is actually to assign these time units with certain activity types.

For each value from the combination of the four dimensions mentioned in the §4.4, aggregated data on the daily distribution of time spent on the main types of activity were computed from the activity survey data (if corresponding data exist). Then, these aggregated data were saved into the database for further use. This activity pattern included not only the average duration for every possible activity but also the probability of the time of commencement for certain activities. Three types of activities were dealt with as exceptions: study time (applicable to children, assuming all children go to school during school hours); working time (applicable to all adult workers, assuming all workers go to work during working hours); and sleeping time. These three types of time were assigned to the individuals as personal properties during the generation of the whole population. For the daily activity of one person of one week day, firstly, these three special types of activities were fixed. Then, from the beginning to the end of the time sequence, the vacant time units were assigned to activity types by the probability weights from the assigned activity pattern in relation to the sociodemographic segment. For spatial location, for every person, her/his household and work place (or school) were fixed from the beginning, and other locations (ABs) were selected randomly (or the spatially closest one was selected). At every time step, individuals can move between different locations.

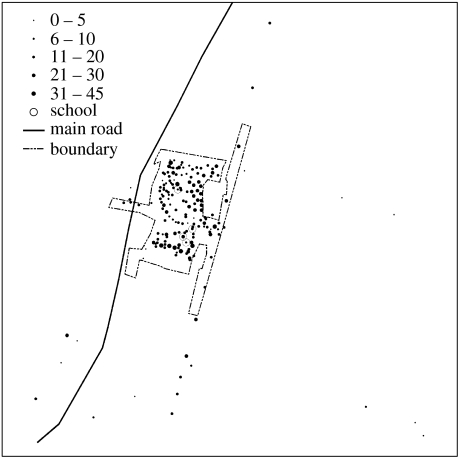
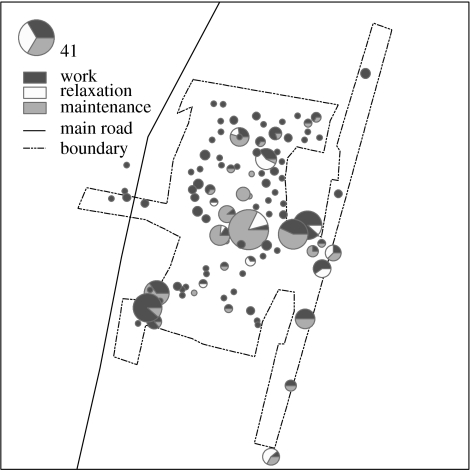
For both children between 11 and 18 years and adults, their activity patterns were assigned according to their properties in the four dimensions. After these processes, the whole population of this city was built and all types of AB were distributed to all PC6 zones. Figure 3 shows the spatial distribution of households and schools at PC6 levels for the whole of Eemnes city. It is clear that most households are within the boundary of the city centre; so in the following sections the spatial display is zoomed within the boundary of the city centre to highlight the area where most contacts between individuals could occur. Figure 4 shows the spatial distribution of the ABs for work (includes office, industry, farm and school), relaxation (includes sports, social and relaxation places) and maintenance (includes shop, post office, bank and health care places) at PC6 levels.

Figure 3.

Spatial distribution of households and schools at PC6 levels. Solid black circles indicate PC6 with a school.

Figure 4.

Spatial distribution of ABs for work, relaxation and maintenance at PC6 levels.

5. Simulation

The most important characteristics of the ISTAM, which distinguish it from other IBMs for simulating the transmission of infectious diseases, are: (i) its two-level simulation structure, between ABs and within ABs and (ii) different options for within-AB simulation depending on the application and data availability.

5.1 Simulation of individuals' movements between ABs

As individuals' movements between ABs are not the focus of this work, a simple method was implemented. For every working individual, the locations (PC6) of her/his household and work place were fixed before the simulation and distributed randomly across the whole city. Owing to the relatively small size of Eemnes, the locations of the only four schools with services for different stages of pupils were fixed before the simulation. Then, for other activities, two methods of selecting ABs were implemented. In the first method, during the simulation, individuals selected an AB randomly from all ABs of specific types from all PC6s (including the current PC6) within a certain distance from the current PC6 if he/she needs to take another activity. In the second method, before the simulation, for every type of activity, every individual was assigned to the fixed AB which has the minimum distance with her/his household. As mentioned before, trip activities were neglected in this research, which means that there are no infections between individuals during travel time.

5.2 Simulation of individuals' interactions within ABs

Eleven types of AB were defined for role-based AB simulation. For each type of AB, its description and the values of its parameters are shown in table 8.

Table 8.

Contacts within AB.

AB type	description	values of parameters (default: pc)
office	loop between all staff	$p_{\text{c}}^2$
industry/farm	the whole staff are divided into a few subgroups (with one as key subgroup, the size of the key subgroup is the same as the total number of other subgroups). Individuals within the same subgroup come into contact with each other as a loop. Each individual from the key subgroup comes into contact with one key number of her/his corresponding subgroup	loop (pc4) between key subgroup and other subgroup ($p_{\text{i}}^2$, $p_{\text{c}}^5$)
shop	loop between workers	loop (pc3)
	dynamic random between all customers	dynamic random (density: 0.5, mobility=1, pc4)
	20% of customers come into contact with one staff member randomly	randomly selected 20% of customers come into contact with one staff (pc3)
post office/bank	loop between workers	loop (pc4)
	queue between clients	queue ($p_{\text{c}}^1$)
health care place	one worker comes into contacts with one client	worker with client ($p_{\text{i}}^1$, $p_{\text{c}}^1$)
	if clients>workers, then Static random between the other clients; if clients<workers, then the other workers stay alone	static random (density=1.0, $p_{\text{c}}^2$)
sport place	loop between workers	loop ($p_{\text{c}}^4$)
	dynamic random between customers	dynamic random (density=0.2, mobility=1.0, $p_{\text{c}}^2$)
household	full between family members	$p_{\text{c}}^2$
social place	loop 1 between workers	loop 1 ($p_{\text{c}}^4$)
	clients are subgrouped, loop 2 contact within each subgroup	loop 2 ($p_{\text{c}}^2$)
	one client randomly selected from each subgroup to come into contact with one worker randomly selected	between clients and workers ($p_{\text{i}}^3$, $p_{\text{c}}^4$)
relaxation place	static random between both workers and clients	static random (density=1.0, $p_{\text{c}}^5$)
service place	every client comes into contact with one worker randomly	clients with workers ($p_{\text{i}}^3$, $p_{\text{c}}^3$)
school	loop between supervisors (all teachers)	loop ($p_{\text{c}}^4$)
	students are subgrouped. Static even within every subgroup	static Even (density=1.0, $p_{\text{c}}^1$)
	one teacher has a fixed subgroup and comes into contact with five students randomly selected from his/her subgroup	teacher with five randomly selected students ($p_{\text{i}}^3$, $p_{\text{c}}^1$)

The simulation results can be recorded into a database during the simulation or after the whole simulation. Currently, simulation results can be recorded as individual based (individuals' disease and activities history), AB based (the changing number of individuals over time), contact based (information related to one contact, such as the time, AB, two individuals and contact result) and PC6 based (the changing of the disease situation over time). Further analysis can then be based on these simulation data.

6. Simulation results and analysis

6.1 Calibration

6.1.1 Calibration of the contact frequency index

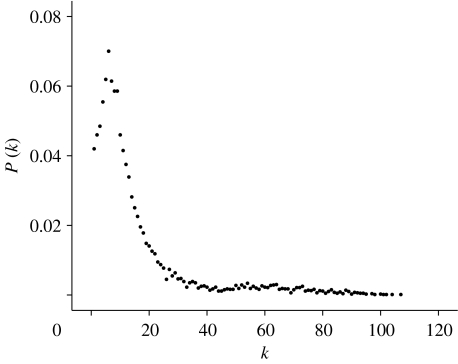
Since all contacts (whether infection is possible or not) can be recorded, the average contact number per person per day can be computed for comparison with related research. An average contact number per day of 16.8 was estimated by Edmunds et al. (1997) from a survey of 92 adults by questionnaire. In the study by Pool & Kochen (1978), the participants had an average of 23 daily contacts (including telephone conversations and letters). In a recent paper by Fu (2005), 14 surveys conducted between 1993 and 2002 in Chinese society were analysed, and it was found that the average number of daily contacts for one person is near the midpoint between two ranges (10–19 and 20–49). According to the above research, F was calibrated to be 0.03, and, at this value, the simulated average contact number for one person per day was 14.7. Figure 5 shows the distribution of the number of contacts of all individuals for one day.

Figure 5.

Distribution of number of contacts for all individuals per day.

6.1.2 Calibration of the contact intimacy index

The basic reproductive number (R₀) is a measure of infectivity. It is defined as ‘the average number of secondary infections produced when one infected individual is introduced into a host population where everyone is susceptible’ (Anderson & May 1992). Different R₀ values exist in different subgroups due to the heterogeneities in the contact rates, transmission probabilities and duration of infectiousness (Halloran 1998). In this study, R₀ was estimated to be less than 2 (Longini et al. 2004).

All contacts during the simulation of the ISTAM can be recorded. This provides the computation of R₀ according to its definition (i.e. trace the number of new infections from the index case). After calibration, I was fixed to be 0.03, and at this value the average R₀ was 1.79.

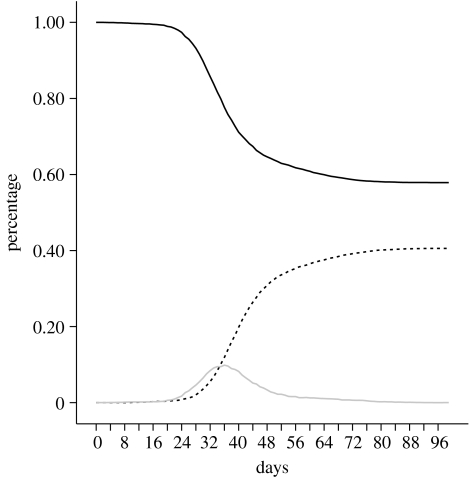
According to Cox & Subbarao (2000), a characteristic pattern for localized epidemics within a community is that the epidemic begins abruptly, peaks within 14–21 days and ends within 35–70 days, and the overall attack rate is estimated to be 10–20%. At I=0.03, the simulated SIR plot is shown in figure 6. The simulated epidemic peaked at approximately 30 days and ended between 70 and 80 days, at which time 40% of the population had been infected. A possible reason for this mismatch is that, in reality, during the epidemic period, humans will change their behaviour according to their own or other people's health states, such as staying at home or going to a health care facility to rest and avoid infecting other people. In the future, the model can be refined (e.g. to include individuals' reactions to the epidemics) to reduce this mismatch.

Figure 6.

SIR plot for one simulation of 100 days (black line, susceptible; dotted line, immune infected).

6.2 Dynamics of the population during a whole day

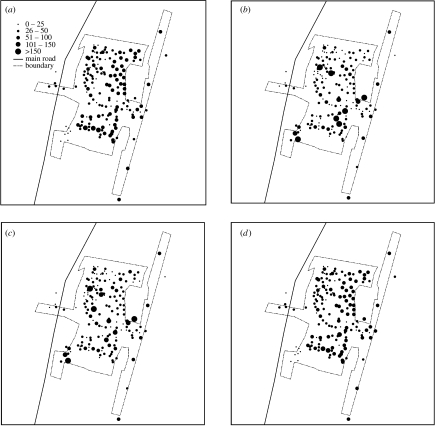
Individuals' daily activities are distributed according to certain patterns both spatially and temporally. Thus, their aggregate patterns (i.e. dynamics of the whole population within the whole city) also exhibit a certain structure during a whole day. This kind of research is especially interesting to the field of transportation, and also has implications for marketing, urban infrastructure and emergency response (Janelle et al. 1998). The word ‘rush hour’ is coined to express the time during this period when the number of individuals present peaks at locations such as transportation networks, shopping centres and other service facilities. The spatial distribution of all individuals at the PC6 level and at a 15 min interval can be generated from the simulation results. Figure 7 shows the spatial distribution of individuals at 04.00, 10.00, 16.00 and 22.00 hours in a given day. It is clear that, at 10.00 and 16.00 h, individuals are more concentrated within a few PC6 zones where a few special ABs such as schools and industrial sites are located.

Figure 7.

Individuals' spatial distribution at (a) 04.00, (b) 10.00, (c) 16.00 and (d) 22.00 hours.

6.3 Infection PC6 distribution

Traditional epidemiological studies take the address of a patient's household or the address of a health care facility where the patient is registered as the spatial location where infection occurred. Also, the ‘lag’ effect, which exists between the times of infection, exhibiting symptoms and visiting health care facilities, is often not represented. Unfortunately, under most circumstances, these data sources are the main resources for research work (sometimes even such data are not guaranteed to be available).

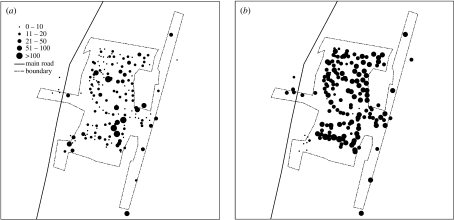
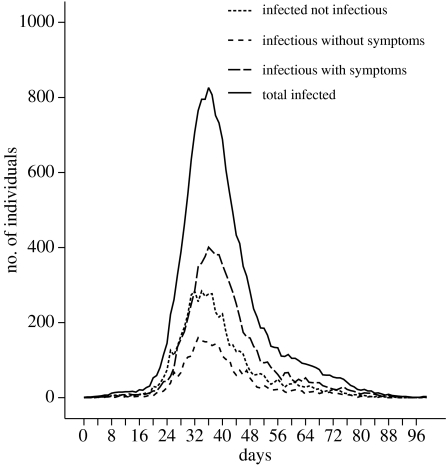
From the simulation results of the ISTAM, for every infection, information such as the attacker, attackee, infection location, infection time and also the change of health state of each patient over time can be accumulated and traced. Figure 8 shows the spatial distributions of infections at PC6 level based on: (i) the ABs where infection really occurred and (ii) the ABs where each patient's household is located. It is clear that infections in figure 8a concentrate within a relatively small number of PC6 zones compared with those in figure 8b, and there were no PC6 zones with more than 100 infections in figure 8b. The reason is that in reality, during the daytime, a large number of individuals stay within a relatively small number of ABs such as schools, industrial sites and farms so that a large number of infections occur there. Figure 9 shows how the number of individuals in the latent stage (i.e. infected but not infectious), the stage of being infectious without symptoms, the stage of infectious with symptoms and the total number of infected individuals change over time.

Figure 8.

Spatial distributions of infections at PC6 level (a) based on the AB where infections occurred and (b) based on the households of infected persons.

Figure 9.

Change over time in the number of individuals infected but not infectious, infectious without symptoms, infectious with symptoms and the total number of infected individuals.

The lag effect in time and the ‘misplace’ effect in space within the empirical epidemic data could be an interesting focus for research. The simulated results from the ISTAM provided the possibility of further analysis, and deeper understanding could be gained in terms of the relations between the empirical data sources and the real situation.

6.4 Infection distribution at different types of AB

In practice, the identification of key ABs for infection is important as this can assist possible infectious disease control measures. If enough information about individuals' activity patterns and ABs' physical condition is available, the percentage of infections at different types of AB for one epidemic outbreak can be generated by AB simulation. One example is given by Longini et al. (2005), as mentioned earlier. They simulated that 28% of infections would occur within the family, 20% at household clusters and 21% at school. Another example is provided by Ferguson et al. (2005), who showed through simulation that infection risk comes from three sources in roughly equal proportions: (i) household; (ii) work place and school; and (iii) random contacts in the community. Table 9 shows the percentage of infections at ABs generated by the ISTAM. Practical statistical data are needed for comparison with the above simulation results for model calibration and validation purposes.

Table 9.

Percentage of infections at different types of AB.

AB type	percentage
household	50.7
school	19.3
industry	9.2
office	8.7
social place	5.1
shop	2.8
cultural place	1.3
sport place	1.0
farm	0.8
post office/bank	0.5
health care place	0.4
other service place	0.1

6.5 Network analysis

The contact network can be obtained from the ISTAM simulation. Taking individuals as nodes and the contacts between them as edges, a contact network can be built from the ISTAM. There can be multiple contacts with different times and contact indices between two individuals. Therefore, the contact network is a dynamic network. Here, the sum of all contacts between two individuals is taken as the value for the edge and the network is simplified to a static network corresponding to one specific period.

The contact network for one day's duration shows that several households exist for which the family numbers did not have contacts with outside persons during a given day. Also from table 9, we know that most infections occurred within households and at school. The arithmetic mean of clustering coefficients of this one-day contact network is 0.52 with a standard deviation of 0.42. This confirms the expected high number of ‘clustered’ contacts between individuals.

7. Discussion

The city has been taken to be a complex system and complexity theory has been applied to study urban dynamics (Batty 2005a,b). Even within a rather small city such as Eemnes, the demographic properties of the population, the physical condition of the landscape and the daily activity patterns of individuals can be very complicated. Inevitably, problems exist with the application of the ISTAM to Eemnes. Data collection was time consuming (e.g. the activity data survey took half a year to complete). Furthermore, because the data (table 4) were not collected for the purpose of this application, much data preparation was needed before the simulation. Owing to the shortage of practical data, certain human activities such as activities related to traffic and outdoor activities were neglected. In reality, human contact within transportation vehicles, especially public transportation, plays an important role in infectious disease transmission among the human population. Some ABs are outdoor, and in such cases weather conditions should not be neglected. To include a climate and weather module is a sensible choice, an example is the model of BioWar (Carley et al. 2004).

Eleven types of AB were simulated within the ISTAM for the above application, but some types of public AB, although very small in number, can play a crucial role. Examples are sports stadia and marketplaces. A large number of individuals aggregate together periodically (e.g. weekends during league match season) or aperiodically (e.g. celebrations during holidays). Within some types of AB such as shopping centres or main traffic stations, individuals are highly mobile and the structures of the AB can be complicated. Thus, a very fine temporal scale is needed to model individuals' complex space–time dynamics.

8. Conclusion

The ISTAM is a novel model for simulating the transmission of infectious disease. The two-level structure (separating the between-AB and within-AB activities) makes the ISTAM flexible such that it can be applied to novel circumstances. The concept of AB plays a key role: both the building of individual activity patterns and simulation within ABs depends on how well the ABs are defined and classified.

One of the merits of the ISTAM is that it is straightforward, conceptually focusing on important factors, neglecting less important factors and including random factors where appropriate in the model. Simulating the interactions between individuals at fine time–space scales imparts particular benefits, including the following:

1. the ability to monitor contacts and transmission through time–space at any level (e.g. in space—individual based, AB based and PC6 based; in time—minutes, hours, days, etc.), including the ability to create a dynamic contact network,

2. providing an experimental environment within which interventions and control strategies can be evaluated,

3. the ability to consider human behaviour, including the roles that people play and individuals' reactions (both active and reactive).

This research provided an example of the simulation of the individual-based transmission of infectious disease at the city level. This involved the building of the population and the spatial and social structure of the city based on data sources of limited quality, and the simulation of contact processes from individuals' movements between ABs and interactions within ABs. Role-based simulation was demonstrated to be an efficient approach for within-AB simulation especially in the present circumstance where detailed spatial structure information for the AB was not available.

As discussed in §1, the ISTAM was applied previously to a university campus. Within this research, through role-based simulation, the model application was extended to a city. This demonstrates the scalability of the ISTAM. By providing the data sources sufficiently, the ISTAM can be extended to larger study areas.

The simulation results can be extracted at any level, thus providing greater opportunities for the calibration and validation of the ISTAM. Research is currently under way to validate the model by comparison of the simulated number of individuals present in different types of AB over time with related research results such as those provided by Eubank et al. (2004).