Abstract
The neuromuscular control of vocalization in birds requires complicated and precisely coordinated motor control of the vocal organ (i.e. the syrinx), the respiratory system and upper vocal tract. The biomechanics of the syrinx is very complex and not well understood. In this paper, we aim to unravel the contribution of different control parameters in the coo of the ring dove (Streptopelia risoria) at the syrinx level. We designed and implemented a quantitative biomechanical syrinx model that is driven by physiological control parameters and includes a muscle model. Our simple nonlinear model reproduces the coo, including the inspiratory note, with remarkable accuracy and suggests that harmonic content of song can be controlled by the geometry and rest position of the syrinx. Furthermore, by systematically switching off the control parameters, we demonstrate how they affect amplitude and frequency modulations and generate new experimentally testable hypotheses. Our model suggests that independent control of amplitude and frequency seems not to be possible with the simple syringeal morphology of the ring dove. We speculate that songbirds evolved a syrinx design that uncouples the control of different sound parameters and allows for independent control. This evolutionary key innovation provides an additional explanation for the rapid diversification and speciation of the songbirds.
Keywords: birdsong, vocal learning, biomechanics, nonlinear dynamics
1. Introduction
The neuromuscular control of vocalization in birds requires complicated and well-orchestrated motor control of the vocal organ (i.e. the syrinx), the respiratory system and upper vocal tract (e.g. Wild 1997). Especially songbirds, which learn their song from a tutor, provide an excellent and widely used model system for sensorimotor learning and human speech acquisition (Doupe & Kuhl 1999). The biomechanics and neuromuscular control of the syrinx, which is a modification of the trachea and/or bronchi located at the bifurcation of the trachea into the bronchi, is very complex and not well understood. An emergent model organism to study the biomechanics of phonation and its control is the ring dove (Streptopelia risoria). The syrinx morphology of this species is relatively simple (figure 1), with only two paired muscles controlling its geometry compared with six to eight pairs in most songbirds (King 1989). Because this non-songbird does not learn the syntax of its species-specific song as songbirds do (Nottebohm 1972), it is of less interest to study vocal learning. However, juveniles of a closely related species still require motor practice to utter the final characteristic coo (Ballintijn & ten Cate 1997), which indicates the individuals must go through numerous iterations to match their vocal output with some sort of neural template.
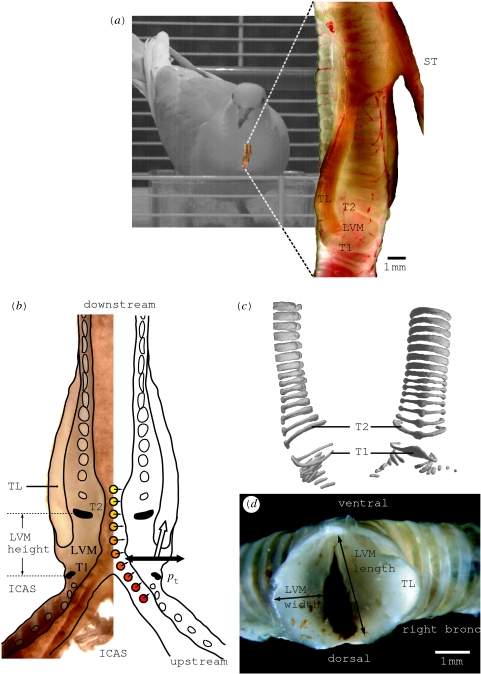
Figure 1.
Syrinx morphology. (a) Toto view of ring dove syrinx. (b) Longitudinal cross section of ring dove syrinx. Several forces acting on the LVMs: a pressure gradient from bronchus to trachea (red to yellow circles), the transmural pressure pt from air sac to syringeal lumen (black arrow) and muscle activity (white arrow). (c) Micro-CT scan of the syrinx. Note that, due to its flattened shape, ring T2 is able to better withstand the torques generated by the m. tracheolateralis (TL). (d) Sagittal cross section through a fresh syrinx slightly below the TL insertion. The right LVM is cut higher, some TL fibres are cut. The arrows indicate LVM width and length as presented in table 1. ICAS, interclavicular air sac; LVM, lateral vibratory mass; pt, transmural pressure; T1–2, tracheal rings; TL, musculus tracheolateralis; ST, musculus sternotrachealis. The syrinx in (a) has been published in a different form as electronic supplementary material accompanying Elemans et al. (2004) and in Elemans et al. (2006). The syrinx cross section in (b) is modified from Zaccarelli et al. (2006).
In pigeons, sound is produced in the syrinx by flow-induced oscillations of membranes (Goller & Larsen 1997; Larsen & Goller 1999). The control of the fundamental frequency of the sound and the gating of sound elements happen at the level of the syrinx (Greenewalt 1968; Goller & Suthers 1996a,b). Despite the seeming simplicity of the dove coo, the syrinx demonstrates surprisingly complex dynamics; sound is produced during expiration and inspiration (Gaunt et al. 1982) and the coo exhibits fast trills (Elemans et al. 2004) and frequency jumps (Beckers et al. 2003a).
Many forces act on the sound-producing lateral tympaniform membranes (LTMs; figure 1b): pressure gradients (Gaunt et al. 1982; Beckers et al. 2003a) and syringeal muscles (Elemans et al. 2004, 2006) affect variations in geometry and tension (Gaunt 1983). These forces affect the tension in the LTM (Gaunt 1983; Fletcher 1992), and most likely also the oscillation amplitude and phonation onsets. This complex interplay of forces is hard to dissect without a quantitative biomechanical approach.
In order to provide a clear overview, it is essential to define some terms on the concepts of modelling. A conceptual biomechanical model is a construct based on physical principles without mathematical analysis (see also Alexander 2003). A mathematical model is a mathematical construct, which describes some mathematical aspects of the system under study. Basic mathematical models are sometimes referred to as ‘toy models’ or ‘normal forms’. A quantitative (or numerical) biomechanical model is the implementation of a mathematical model in a computer program with which simulations can be made for a selected range of values of the input parameters.
Several conceptual models have been proposed to explain the biomechanics of sound production that uses a separation of single physiological correlates with frequency modulation (FM) and amplitude modulation (AM; e.g. songbirds: Goller & Suthers 1996a,b; doves: Beckers et al. 2003a). This separation in functional attributes is most likely a too simple representation. Especially nonlinear oscillators, which are used to mathematically model syringeal vibrations (Fee et al. 1998; Gardner et al. 2001; Laje et al. 2001, 2002; Laje & Mindlin 2002, 2005), can show conversion from AM to FM in certain regions of their parameter space (e.g. the Duffing oscillator in Elemans (2004)).
In this paper, we aim to unravel the contribution of the different control parameters in the coo of the ring dove at the syrinx level. First, we briefly review the literature and aim to integrate older conceptual models and observations into a novel biomechanical framework. Second, we characterize a standardized coo with all physiologically important parameters using earlier studies and additional measurements. Third, we implement a quantitative biomechanical syrinx model that is driven by the derived physiological control parameters. This model provides a consistency check for our formulated biomechanical framework. Furthermore, with our model, we can systematically switch on and off the control parameters to determine how they affect amplitude and frequency modulations. As such, we can also assess if it is reasonable to correlate amplitude and frequency modulations to separate physiological correlates and we can generate new experimentally testable hypotheses.
2. The biomechanics of phonation in ring doves
Over the last decades, the mechanics and physiology of phonation in doves have received some attention, but some data have been interpreted in an older framework that is missing recent insights (e.g. based on the assumption that other structures acted as the principal sound sources). Here, we aim to integrate all observations into a new framework.
Gaunt et al. (1982) show that abdominal muscles generate expiratory pressure pulses passing through the syrinx. However, during the coo, the beak and nares are closed and the air is collected in an inflating oesophageal crop (Riede et al. 2004). Direct observations of the syrinx during induced phonation using brain stimuli in pigeons by Goller & Larsen (1997) show that (i) the LTMs are the sources of the sound and (ii) the syrinx is brought into a ‘phonatory position’ by two paired syringeal muscles, the musculus sternotrachealis (ST) and musculus tracheolateralis (TL) as hypothesized earlier by Gaunt et al. (1982). Whereas the TL directly affects position in the LTM (figure 1a,b), the ST moves the entire syrinx downward (Goller & Larsen 1997). However, the LTMs in ring doves are not thin membranes (see §5), but more resemble labia with larger masses. Therefore, the denomination membrane seems not appropriate and we will argue that lateral vibratory mass (LVM, figure 1) is a more appropriate name than LTM. To avoid confusion, we will consistently use the abbreviation LVM from now on.
Although there are no direct observations in freely singing doves, several indirect measurements support the idea that the syringeal aperture is modulated and controlled by syringeal muscles. First, the duration of TL muscle activity is equal to the duration of sound elements during the trill (Elemans et al. 2004). Second, simultaneous pressure and flow recordings suggest that the syrinx is open during sound production and mostly closed in between sound elements: when sound starts, the bronchial pressure drops and when sound stops flow decreases to almost zero (Gaunt et al. 1982; Beckers et al. 2003a). These observations can be explained by the hypothesis that TL contraction modulates the position of the LVM and as such the syringeal aperture (Elemans et al. 2004, 2006).
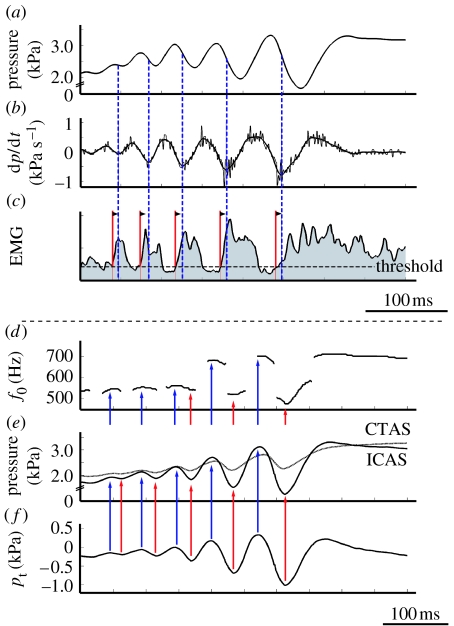
After the initial pressure drop due to opening of the syrinx, the bronchial pressure increases again during every sound element in the trill (figure 2a). Gaunt et al. (1982) suggest that this is due to increased activity of the abdominal muscles synchronized with the TL. Indeed, the pressure slope starts increasing at the inflexion points on the negative slope of the pressure curve (figure 2a–c, local minima of dp/dt in figure 2b), which can be indicative of a start of force generation by the abdominal muscles. We measured the delays between abdominal muscle electromyogram (EMG) activity and pressure by digitizing the data presented in Gaunt et al. (1982). The delay between the onset of abdominal muscle EMG activity and the local minima in dp/dt measures 7.7±2.6 ms for the last five trills (figure 2). The pressure starts increasing 21.0±7.4 ms after the onset of EMG activity. These delays are consistent with a typical delay between electrical activity (EMG) and mechanical muscle action for skeletal muscle (e.g. Norman & Komi 1979; Komi 2000; Carroll & Wainwright 2006) and therefore the claim by Gaunt et al. (1982) is feasible. This again emphasizes that the generation of trills in doves demands a high level of synchronization of syringeal and respiratory muscle activation.
Figure 2.
Function of abdominal muscles and air sac pressure derived from literature. (a–c) Data digitized from Gaunt et al. (1982). Abdominal muscles contract to increase bronchial pressure. (a) Posterior thoracic air sac pressure, (b) time derivative of air sac pressure in (a). (c) EMG activity of abdominal muscles (integrated trace, time constant 1 ms). Onset of muscle activity (red lines) commences 7.7±2.6 ms (mean ±s.d., n=5) before the inflexion points of air sac pressure (blue lines corresponding to local minima in (b)). (d–f) Data digitized from Beckers et al. (2003a). Transmural pressure waveform is in phase with interclavicular air sac (ICAS) pressure waveform. (d) Fundamental frequency (f0) during trill. (e) ICAS (solid line) and cranial thoracic air sac (CTAS) pressure (dotted line) patterns. (f) Calculated transmural pressure (pt) using equation (2.1) and the data in (e). Local maxima (blue arrows) and minima (red arrows) for pt, ICAS and fundamental frequency coincide.
The parameters controlling the fundamental frequency are not well established. The common and most simple assumption is that the fundamental frequency (f0) of LVM oscillation is determined by tension in the LVM (Fletcher 1992). Beckers et al. (2003a) report that the f0 correlates with the pressure in the air sac in which the syrinx is suspended; the interclavicular air sac (ICAS). Birds have a unique and elaborate air sac system for respiratory ventilation (Duncker 1971). Pressure differences between air sacs have been reported during many activities, such as normal respiration (Brackenbury 1972), sound production (Brackenbury 1972) and locomotion (Boggs et al. 1998, 2001). Beckers et al. (2003a) hypothesize that ICAS pressure modulates the tension in the LVM. However, tension in the membrane is the result of the net force that acts on the membrane. When looking at the forces acting on the LVM (figure 1b), it becomes clear that any pressure differences between the air sac surrounding the syrinx (the ICAS) and the syringeal lumen causes a net force to act on the LVM. This so-called transmural pressure pt affects the tension in the membrane (Bertram & Pedley 1982; Bertram 2004). We define the transmural pressure as external pressure minus upstream pressure, where we take ICAS pressure as external pressure and assume that the pressure in the caudal thoracic air sac (CTAS) equals upstream or bronchial pressure (see §3.1)
| (2.1) |
where pICAS and pCTAS are the pressures in the ICAS and CTAS, respectively. When we derive pt from the data presented by Beckers et al. (2003a), we see that the calculated pt is in phase with the pressure in the ICAS (pICAS; figure 2d–f). Therefore, correlation techniques cannot differentiate between pICAS and pt as modulators and as such the function ‘frequency modulator’ cannot be attributed to either one of them using correlation. Considering the mechanics, the LVM tension is affected by both (i) the transmural stress caused by a pressure differential between the bronchus and ICAS and (ii) the stress exerted by muscles.
To summarize, we hypothesize that (i) the tracheolateralis muscle (TL) modulates the position of the LVM and as such the syringeal aperture and (ii) both the transmural pressure and TL stress affect tension in the LVM.
3. Compilation of standardized coo
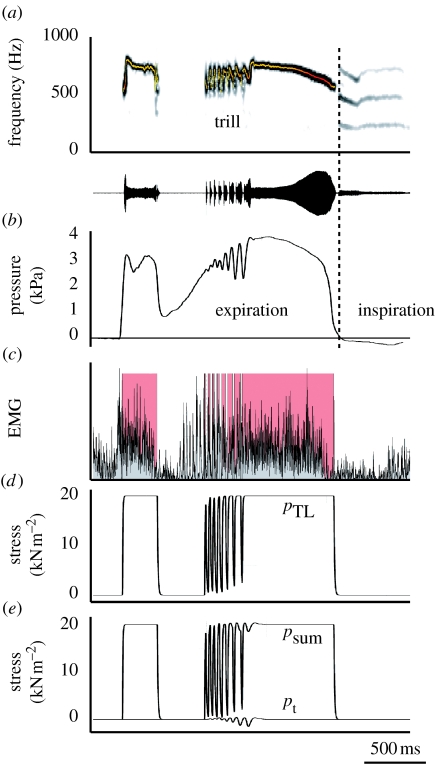
We compiled a quantitative dataset of all the parameters affecting sound production at the syrinx level. Many doves have three different coo types; the nest, bow and perch coo (Goodwin 1983). We did not differentiate between these coos because in ring doves there are no apparent differences in overall acoustic structure (Beckers et al. 2003a). We combined published and additionally collected physiological and morphological data to construct a ‘standard coo’ (figure 3). Our primary focus is the trill where the fastest and most complex interactions occur. If we look at the forces acting on the syrinx membranes (figure 1b), the most important physiological control parameters are (i) the bronchial–tracheal pressure gradient, (ii) the transmural pressure difference and (iii) the stress exerted by syringeal muscles. It should be noted that all these control parameters are the ultimate result of muscle action and therefore all under direct neural control. All pressures mentioned are gauge pressures, i.e. pressure relative to atmospheric pressure. To construct all synchronized time-dependent parameters of the standard coo, we start with simultaneously recorded signals of emitted sound, CTAS pressure and EMGs of the syringeal muscles. These signals were recorded as part of previous studies (Elemans et al. 2004, 2006). These experiments were in accordance with the Institutional Animal Care and Use Committee (IACUC) of the University of Utah, Salt Lake City, USA.
Figure 3.
Standard coo. (a) Spectrogram and oscillogram of dove coo. Superimposed on the spectrograms is a fundamental frequency analysis (colour represents sound amplitude). (b) Bronchial pressure. The vertical dotted line indicates the transition from expiration to inspiration. (c) Rectified EMG of tracheolateralis muscle (TL) and TL activity associated with sound elements (red areas). (d) Stress generated by TL, (e) transmural stress (bottom trace) and sum of transmural and TL stress. pt, transmural pressure; pTL, stress generated by TL; psum, sum of pt and pTL.
3.1 The bronchial–tracheal pressure gradient
To understand the vibrations of the lateral vibratory membrane (LVM), we need to know upstream (i.e. bronchial) and downstream (i.e. tracheal) pressures because the pressure drop along the LVM defines the oscillation regime, analogous to collapsible tube systems (e.g. Bertram 2004; Grotberg & Jensen 2004) and human vocal fold models (Titze 2002).
To estimate upstream pressure, i.e. the bronchial pressure, the common assumption is that pressure in two easily accessible air sacs, either the pressure in the posterior thoracic air sac (PTAS) or CTAS, equals bronchial pressure for most species of birds (e.g. Gaunt et al. 1982; Suthers et al. 1994; Goller & Suthers 1996a; Mindlin et al. 2003; Suthers & Zollinger 2004). To our knowledge, no record of direct bronchial pressure exists of any bird species during song. We studied silicone casts of the air sac system in ring doves and found that the connections or ostia of the lung with CTAS are close to the bronchi (1–3 mm), cf. Duncker (1971). Therefore, also in this case, it is safe to assume that the pressure in the CTAS is a good estimate for bronchial or subsyringeal pressure. Published PTAS and CTAS pressure patterns for ring doves are highly similar (compare PTAS pressure in figs 5–7 in Gaunt et al. (1982) with CTAS pressure in figs 1 and 2 in Beckers et al. (2003a) and CTAS pressure in figure 3b in this paper). A small phase shift between the pressure waveforms of air sacs cannot be ruled out, but from what is known from morphology and airflow pattern models there is no reason to assume large differences in amplitude (Brackenbury 1972). We assume that no phase shift is introduced in the measurements due to the time constant of the technique to measure pressure in air sacs (i.e. an extracorporeal sensor with a short cannula to the air sac).
The maximal pressure in the PTAS and CTAS is 3.5 kPa (equal to 35 cmH2O), with a slight variation introduced by the emotional state of the individual bird (Gaunt et al. 1982). Therefore, it is reasonable to set the maximal pressure for CTAS, PTAS and ICAS in the air sac system to 3.5 kPa. To determine the bronchial–tracheal gradient, we measured CTAS pressure by cannulating CTAS in six male doves (data collected in collaboration with Dr F. Goller as part of previous studies; Elemans et al. 2004). Our results are consistent with earlier measurements; maximal pressure is 3.5 kPa and the temporal pattern is highly similar (figure 3b).
Tracheal pressure gradually increases during the coo, because the air is not exhaled but collected in the oesophagus (Gaunt et al. 1982; Riede et al. 2004). The peak pressure for tracheal pressure rarely exceeds 0.5 kPa (equal to 5 cmH2O) and often only slightly exceeds the respiratory exhalation pressure of 0.1 kPa (equal to 1 cmH2O). Because this pressure is low compared with the bronchial pressure, we will assume that the downstream pressure equals atmospheric pressure (0 kPa). This simplification implies that the CTAS pressure defines the bronchial–tracheal pressure gradient.
3.2 The transmural pressure differential
As discussed above, any pressure difference between the bronchial–tracheal gradient on one hand and the pressure in the ICAS on the other results in a net force on the LVM and therefore in a tension change in the membrane. As can be seen in figure 2e,f, the transmural pressure (pt) oscillates in phase with pICAS and almost in phase with pCTAS. To reconstruct pt from pCTAS, we retained the oscillation in pCTAS, and normalized the magnitude to 1 kPa as measured in figure 2f (bottom trace in figure 3e).
3.3 Syringeal muscles
In ring doves, two syringeal muscles affect LVM position: the paired m. tracheolateralis (TL) and m. sternotrachealis (ST; figure 1). Although the ST seems important for stability of the syrinx (crows: Chamberlain et al. 1968; thrashers: Goller & Suthers 1996a,b; doves: Elemans et al. 2006), they do not act directly on the LVM and we will ignore them here to simplify matters. We use the following algorithm to construct the stress exerted by the TL. First, we define blocks of muscle on/off activity by creating a binary on/off signal from the measured EMG signal (figure 3c). The threshold needed to calculate the binary signal was set to the mean value of the noise level plus three times the standard deviation. Second, we fit exponential rise and fall curves through the tetanic isometric contraction data of Elemans et al. (2004) and calculate their time constants. The maximal stress is set to 20 kN m−2 (equal to maximal isometric stress from Elemans et al. (2004)). Third, we numerically construct the stress signal using the extracted time constants and the on/off EMG signal (figure 3d). We omit the pre-trill pulses of muscle activation (figure 3c) and include only pulses associated with sound elements. The total stress acting on the LVM is psum=pt+pTL (figure 3e).
3.4 Morphology
The thickness of the LVM varies along the syrinx. We assume that action of the TL mostly affects the mass between tracheal rings T1 and T2 (figure 1b), because the tracheal rings T2–T20 form a stiff box and both T1 and T2 are flattened rostrocaudally (figure 1c). Furthermore, endoscopic observations by Goller & Larsen (1997) show that, in the rock pigeon (Columba livia), action of TL and ST especially affects the position and tension of the LVM between T1 and T2. We measured the dimensions and estimated mass of the LVM in four adult male ring doves. LVM height is measured between T1 and T2 (figure 1b), and LVM length and width are measured slightly below the TL insertion between tracheal rings T1 and T2 (figure 1d) using a MicroPhot-FXA microscope (NIKON) and ANALYSISpro software. These experiments were approved by the Committee of Experimental Animal Use of Wageningen University, The Netherlands.
4. Biomechanical model description
We modelled one unilateral LVM with two masses and three massless plates adapted to syrinx geometry (based on Lous et al. (1998), Sciamarella & d'Alessandro (2004) and Zaccarelli et al. (2006)) without tracheal filtering. Because two-mass models have been studied intensively for human and non-human phonations, they provide a well-established starting point. Now we contrast our approach to two previously developed types of mathematical syrinx models (for a review of syrinx models, see Elemans et al. (2003)). The first mathematical model of the syrinx by Fletcher (1988) models the LVM as a thin membrane. However, the LVMs in ring doves are not thin membranes (see §5). Therefore, the denomination membrane seems not appropriate and the structures more closely resemble labia with larger masses (figure 1 and table 1). Furthermore, as also noted by Laje et al. (2002), in order to produce vocalizations with a natural spectral content, the driving pressure in Fletcher's model is composed of a harmonically complex pressure waveform, which does not correspond to the simple pressure traces. Therefore, Fletcher's (1988) model is not a good starting point to model the ring dove syrinx. The second group consists of elegant single-mass models developed by Mindlin, Laje and co-workers. These models are deliberately simplified to the bare minimum to study nonlinear effects caused by control parameters (Gardner et al. 2001; Laje et al. 2001, 2002; Laje & Mindlin 2002, 2005; Mindlin et al. 2003). However, the control parameters cannot be easily translated back to physical properties.
Table 1.
Geometry of the LVM. (For measurements, see figure 1b,d.)
| description | value (mean±s.d.) |
|---|---|
| height T1–T2 (mm) | 2.2±0.4 (n=4) |
| maximal width (=thickness) of LVM between T1 and T2 (mm) | 1.6±0.3 (n=8) |
| length (mm) | 3.2 |
| tracheal diameter (mm) | 3.0 |
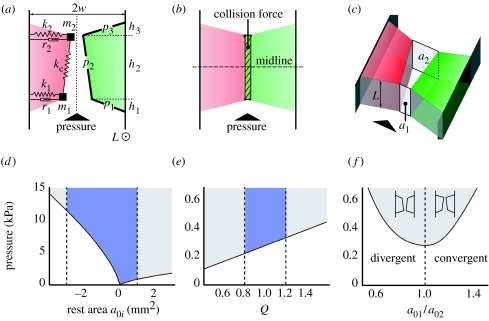
Figure 4 shows cartoons of our biomechanical syrinx model in three different configurations: convergent, rectangular and divergent. The pressure in the syringeal lumen generates a force on the plates (p1,2,3) and pushes the masses (m1, m2) outward, loading the two dampers (r1, r2) and springs (k1, k2). The two masses are interconnected by a single spring with coupling constant kc. Above a threshold value, the subsyringeal pressure induces self-sustained oscillations of the masses. The opening and closing of the syringeal aperture creates pressure waves, i.e. sound.
Figure 4.
Biomechanical syrinx model. The biomechanical syrinx model in (a) convergent, (b) rectangular and (c) divergent configurations. Vertical dotted line in (a) is the symmetry line (x=0) between the two LVMs. Horizontal line in (b) is the midline of the model. Parameters are explained in the text and listed in tables 1 and 2. (d–f) Bifurcation diagrams of oscillation onset pressure versus (d) rest area, (e) tension parameter Q and (f) shape of the rest configuration. The shaded region above the bifurcation line represents self-sustained oscillation. The blue area in between the dotted lines indicates the parameter range used in the simulations.
Following classic two-mass models for human sound production, we obtained the pressures within the syringeal lumen that act directly on the labia using Bernoulli's law and the jet separation assumption. Bernoulli's law states that for a fluid confined in a duct or pipe at any point x along the duct
| (4.1) |
where Ax is the cross-sectional area of the duct at point x; U is the flow; P is the pressure; ρ is the fluid density; and C is a constant. Equation (4.1) is used to derive the mean intraglottal pressure (Pm) acting on the folds in humans, where the airflow passes through the narrower constriction of the glottis. This expression, assuming no vocal fold collision, idealized flow in the glottis and a supraglottal pressure of 0 leads, in the case of a linear shape, to (Titze 2002 and references therein)
| (4.2) |
where Ps is the subglottal pressure and a1, a2 are the areas of the glottis at the position of masses m1 and m2 (figure 4c). From equation (4.2), it follows that Pm is larger for a convergent shape (a1/a2>1, figure 4a) than for a divergent shape (a1/a2<1, figure 4c). Because the lower mass of the fold moves ahead of the upper mass, outward (lateral) movement is associated with a convergent glottis and inward movement with a divergent glottis. Although equation (4.2) assumes no vocal fold collision, this expression shows how the above process leads to an energy transfer from the flow to the tissue and compensates damping.
We assume that the air stream separates from the vocal fold surface at the smallest syringeal opening area to form a jet (Pelorson et al. 1994; Titze 2002). This jet keeps the pressure above the jet separation point close to zero. For the divergent shape, a non-fixed separation point improves the simulated sound (Pelorson et al. 1994) and this method is used in a study of a vocal fold model with applications to prostheses design (Lous et al. 1998). However, because we have no information on the flow field inside the syrinx, we assume a fixed separation point in the divergent case, cf. previous models (Ishizaka & Flanagan 1972; Story & Titze 1995; Steinecke & Herzel 1995). Bernoulli's law and the jet separation assumption imply that the force acting on the labia (i) increases when it is in the direction of the labial movement and (ii) decreases when it is opposite to the direction of the labial movement. This means that the driving pressure and labial velocity are in phase, which is an essential mechanism to explain this self-sustained oscillator.
Our syrinx model deviates from the classical two-mass models in two important points. First, we assume symmetry between the masses (m1=m2, k1=k2 and r1=r2). Second, we introduce a more smooth geometry: on each unilateral side of the LVM the two masses are linked with three massless plates p1,2,3 (figure 4a).
We define a collision force I that pushes the two contralateral LVMs away when they collide. The collision force is a linear function of the area where the two LVMs overlap (figure 4b). To evaluate force on each mass, we assume that all forces below the syrinx midline (horizontal line in figure 4b) act on the lower mass m1, whereas all the forces above act on the upper mass m2. Our model is governed by the following equations of motion:
| (4.3) |
| (4.4) |
| (4.5) |
| (4.6) |
where positions xi are displacements relative to rest position x0i; Fi are the pressure forces derived from the Bernoulli equation and the jet assumption; and Ii represent collision forces. A more detailed description of the equations of motion and pressure evaluation of our model can be found in Zaccarelli et al. (2006). The used tissue properties and geometrical parameters for our default configuration are listed in table 2. The flow derivative is used as an approximation of the suprasyringeal sound (Ishizaka & Flanagan 1972).
Table 2.
Model parameters. (For clarification of geometry parameters, see figure 4.)
| description | symbol | value |
|---|---|---|
| width of syringeal base (mm) | w | 1.5 |
| length of syringeal base (mm) | L | 3.0 |
| height of mass 1 (mm) | h1 | 0.4 |
| height of mass 2 (mm) | h1+h2 | 2.4 |
| LVM height (mm) | h1+h2+h3 | 2.8 |
| massa (g) | m (m1=m2) | 1.7×10−3 |
| stiffnessa (g ms−2) | k1, k2 | 22.0×10−3 |
| damping constant (g ms−1) | r1, r2 | 1.2×10−3 |
| coupling constanta (g ms−2) | kc | 6.0×10−3 |
| rest area of mass 1 (mm2) | a01 | 0.3 |
| rest area of mass 2 (mm2) | a02 | 0.3 |
Parameters are rescaled during coo according to equation (4.9).
4.1 Implementation of time-dependent parameters
In §2, we argue that the syringeal muscles, bronchial pressure and the transmural pressure affect the geometry and tension of the LVM. We hypothesize that (i) activity by the TL muscle modulates syringeal aperture and (ii) the sum of the transmural pressure and muscle stress (psum=pt+pTL) modulates LVM tension. We implemented the above hypotheses in our model. We modulate the syringeal aperture by changing the so-called rest area (a0i) as a function of time. The modulation of rest areas is a linear function of force exerted by the TL (figure 3d). The calculated rest areas a0i are used to determine the rest positions,
| (4.7) |
where L is the length of the syringeal base (figure 4c). Using the position xi (equations (4.3)–(4.6)) and the rest position x0i (equation (4.7)), we can consequently calculate the syringeal aperture (ai) at mass i,
| (4.8) |
We implemented tension modulation of the LVM by means of parameter Q(t), which redefines the masses and the stiffness of the LVM as a function of time: , , where mass m and stiffness k are the default values (table 2). Several implementations of Q have been used in Ishizaka & Flanagan (1972) and Steinecke & Herzel (1995). The definition of Q is motivated by the relation , which defines the natural oscillation frequency (F0) of a single mass–spring system. For a detailed analysis of natural frequencies of oscillations of the classical two-mass model, see Titze (2002). The F0 as a function of time is
| (4.9) |
We systematically explored the bifurcation behaviour of our model using the XPP/XPPAUTO software package (available at www.math.pitt.edu/∼bard/xpp/xpp.html).
4.2 Scaling functions
As discussed above, the measured values of the stress due to TL are in the range [0,20] kN m−2. Simulations of the model indicate that the corresponding range at rest areas a0i is between −3 and 1 mm2. We introduce a scaling factor to transform the range of TL values linearly to the range of rest areas. In a similar way, we rescale the range of psum to Q values between 0.8 and 1.2 to match the frequency range of the coo (figure 4e). We assume that Q(t) varies tissue mass and stiffness around their default values. This requires a slight increase of the default m and k values, closer to the measured values with respect to the set of parameters in Zaccarelli et al. (2006). The damping ratio ()—–a measure for viscous loss of energy in the vocal fold tissue—was kept equal to the values set for human vocal cords (Ishizaka & Flanagan 1972; Steinecke & Herzel 1995). Owing to the increased mass and stiffness values, we slightly increased the damping r accordingly (table 2).
5. Model results
5.1 Model performance
We hypothesized that the TL modulates the syrinx aperture and that the net stress working on the LVMs modulates their tension. Table 1 lists the morphological input parameters. The LVM has a thickness (width) of 1.6±0.3 mm (n=8). Therefore, the term ‘membrane’ in the previously used term ‘lateral tympaniform membrane’ seems not appropriate regarding the connotation in both physics and histology. As introduced before, we will therefore use the abbreviation LVM. We explore the model behaviour during expiration by studying free parameters not provided by measurements. Such parameters allow us to maintain the necessary model assumptions as well as to explore possible different model behaviours. These parameters are rest areas (a0i) and shape of the rest configuration (a01/a02). Bifurcation diagrams of these parameters and tension Q regarding the onset pressure can be seen in figure 4d–f. The shaded area above the bifurcation line represents oscillations of the LVM. These diagrams reveal that: (i) onset of oscillations decreases when the rest area approaches zero (figure 4d). Therefore, oscillation is possible at low pressures when the LVMs are adducted into the lumen. (ii) For rest areas close to zero, a slightly divergent pre-phonatory shape (a01/a02<1, figure 4f) leads to a lower onset of oscillations. Furthermore, a slightly divergent pre-phonatory shape leads to more instabilities, such as period doublings, at low pressure values (data not shown).
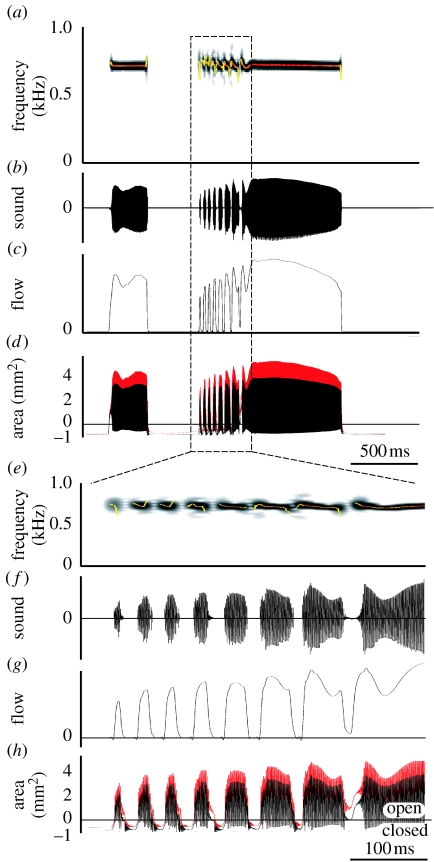
Figure 5 shows the whole coo synthesized with our biomechanical model using the standard coo input signals from figure 3. Both the sound oscillogram and spectrogram closely resemble the sound uttered by the dove (figure 6). When we look closer at the trill, the most dynamic part of the coo, our model reproduces the up and down modulation during on- and offsets during trill elements and the gradual modulation in between very well (figure 5e). Our model also reproduces the sharp onset of trill elements and amplitude modulations in the time domain (figure 5f). Furthermore, flow is zero (figure 5g) and the syringeal aperture areas are negative in between trill elements (figure 5h), implying that the syrinx is closed.
Figure 5.
Simulation of the ring dove coo. (a) Sound spectrogram, (b) sound oscillogram, (c) flow in the trachea, (d) area of syringeal aperture for mass 1 (black trace) and mass 2 (red trace). (e–h) Same signals zoomed in on the trill. Superimposed on the spectrograms is a fundamental frequency analysis (colour represents sound amplitude). Negative areas in (d,h) indicate that the syrinx is closed in between sound elements.
Figure 6.
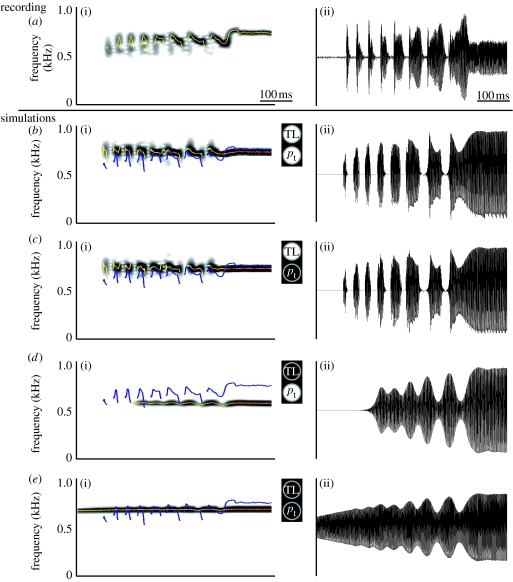
The effect of control parameters on the trill. (a) Recorded sound in vivo. (b–e) Model simulations with (c) no transmural pressure, (d) no TL activity and (e) no transmural pressure and no TL activity. In (c), the rest areas are constant (0.3 mm2). In (d), Q(t)=1 (see equation (4.9)) and rest areas are constant (0.3 mm2). Superimposed on spectrograms are: blue line, f0 analysis of recorded coo in (a); yellow–red line, f0 analysis of current signal. (a(i)–e(i)) sound spectrograms, (a(ii)–e(ii)) sound oscillograms.
5.2 In silico experiments with control parameters
With our model, we can systematically switch on and off the control parameters transmural pressure pt and TL activity to determine how they affect amplitude modulations and frequency modulations. Figure 6 shows what happens when we deactivate the TL muscle, the transmural pressure modulation and both. First, we observe that turning off the transmural pressure has a very small effect on either the onset of sound elements, AM or FM (compare figure 6b,c). Also during the fast trills, both AM and FM closely resemble the original coo recording in figure 6a. However, switching off the TL has profound effects on both gating and FM (figure 6d,e), compared with the original recording. Obviously there is no distinct gating of sound elements anymore. However, the overall amplitude of the sound is still modulated, but now by the bronchial pressure. The remaining small depth of FM is the result of changes in transmural pressure. By turning off both the TL and the transmural pressure as modulators of Q (figure 6e), practically no FM remains and the amplitude is modulated by the bronchial pressure.
5.3 Asymmetry between expiration and inspiration
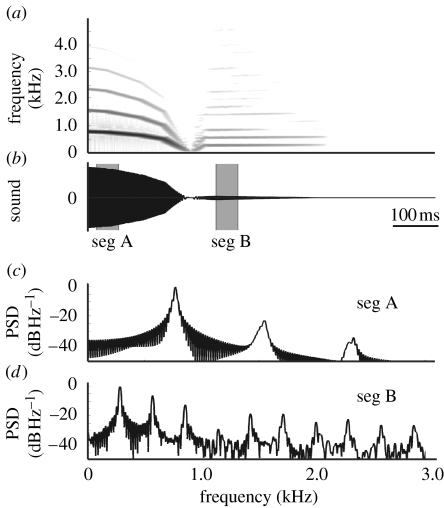
In a typical ring dove coo, nonlinear transitions such as period doublings and chaos are rare during expiration, and the radiated output signal is almost purely tonal. The amplitude of the harmonics 2×f0 and 3×f0 during a steady part of the second syllable for the coo depicted in figure 3a measures −55 and −40 dB, respectively, compared with f0. These values are very similar to published values: both 2×f0 and 3×f0 are 40 dB lower in amplitude, respectively, in Riede et al. (2004) and 40 and 45 dB lower in Beckers et al. (2003b). The inspiratory note following expiration, on the other hand, is characterized by richer harmonic spectra (figure 3a). The amplitude of the harmonics 2×f0 and 3×f0 are 8 and 12 dB higher compared with the fundamental frequency.
Our model also exhibits more rich harmonic spectra during inspiration than during expiration (figure 7). The first and second harmonic measure, respectively, −22 and −34 dB in amplitude compared with the fundamental during expiration, and −6 and −12 dB during inspiration. These results imply that the geometry of the model can influence the harmonic sound spectra, because the shape of the LVM differs between simulated expiration and inspiration.
Figure 7.
Simulation of the asymmetry expiration/inspiration. (a) Spectrogram and (b) oscillogram of expiratory and inspiratory note simulation. (c) Power spectral density (PSD) estimations of segment A (seg A) during expiration and (d) segment B (seg B) during inspiration. Segments are taken from (b) as indicated.
6. Discussion
We establish a novel biomechanical framework for sound production in ring doves (S. risoria). Integrating published experimental data, we hypothesize that (i) the TL modulates the position of the LVM and as such the syringeal aperture and (ii) both TL stress and the transmural pressure affect tension in the LVM. We designed and implemented a quantitative biomechanical model to confirm the validity of these hypotheses. Our simple nonlinear model reproduces the coo with great accuracy and as such provides strong evidence for our biomechanical framework. This is not a trivial result, because nonlinear dynamical systems make the principle of superposition no longer applicable: different excitations may result in different time courses, described by nonlinear dynamics theory (Arrowsmith & Place 1990; Titze et al. 1993; Strogatz 1994). In steady-state simulations with a previous version of our model, we showed that different parameter values can lead to distinct oscillation patterns, and small perturbations induced jumps from one attractor to the other (Zaccarelli et al. 2006). In principle, the interplay of forces that affect rest areas, stiffness and subsyringeal pressure can lead to nonlinear phenomena, such as subharmonics, biphonation or deterministic chaos (Fee et al. 1998; Wilden et al. 1998; Fitch et al. 2002). In a typical ring dove coo, register transitions to aphonia, period doublings or chaos are rare during expiration or inspiration. The simulations with physiological input parameters also (figures 5 and 6) do not exhibit transitions to different dynamical regimes. Ring dove coos can also exhibit punctuated frequency jumps (Beckers et al. 2003a), but these are not reproduced by our model.
We present the first model of bird song that implements a muscle model to calculate force produced by the muscle. The force production by the muscle is based on its actual contractile properties and activation and not simply a function of EMG activity.
Larsen & Goller (1999) observed 0.5–1.0 mm oscillations of the LVM in pigeons. We can derive the maximal oscillation amplitude of one modelled LVM from figure 5d, using equation (4.7). We have to consider mass 2, because Larsen & Goller (1999) had a top view of the syrinx. The maximal oscillation amplitude of our modelled LVM is 0.8 mm (4.8/2×3.0), which corresponds very well with the observed 0.5–1.0 mm. Larsen & Goller (1999) also suggest that a smaller amplitude vibration (0.001–0.1 mm) exists on top of the 0.5–1.0 mm oscillation using a vibration detector that detected light reflectance of the LVM. This signal is hard to interpret in terms of lateral movement of the LVM and could, for example, also represent an oscillation in dorsoventral closure or a tracheal wall vibration. We do not observe this small amplitude oscillation in our simulations.
The thickness (width) of the LVM is 2- to 16-fold higher than reported in other species. In the closely related rock pigeon (C. livia), the LVMs are masses of connective tissue measuring up to 0.1 mm thick (Goller & Larsen 1997). In ducks, reported values range from 360 (Frank et al. 2006) to 750 μm (Warner 1972). The LVMs in ring doves seem to more closely resemble the consistency and geometry of the mammalian vocal folds or songbird's labia. Until direct observations were made in situ of the oscillating LVMs by Goller & Larsen (1997), the medial tympaniform membranes were thought to be the vibrating sound sources. These much thinner membranes (5–20 μm; Casey & Gaunt 1985) inspired the implementation of quantitative models where the sources were modelled as a membrane (Fletcher 1988) or string (Casey & Gaunt 1985). Our model provides a better description of the actual syrinx geometry.
6.1 Harmonics in bird song
The membrane- and string-based mathematical models were initially also implemented because they provided a mechanical basis to explain the almost pure-tone sounds generated by many birds (Casey & Gaunt 1985; Fletcher 1988, 1989). However, sound seems to be predominantly made by colliding syringeal labia (songbirds; Larsen & Goller 2002) or LVMs (Goller & Larsen 1997) just as in humans, other mammals or geckos (Paulsen 1967). As such, the syrinx produces a harmonically rich signal. Recent papers provide an explanation how many birds reduce the higher harmonics and radiate their typical, almost pure-tone sounds. The upper vocal tract acts as a filter in ring doves (Beckers et al. 2003b) and is actively tuned to enhance the fundamental frequency of song during vocalization in some songbirds (Riede et al. 2006) and doves (Riede et al. 2004; Fletcher et al. 2005).
Our model suggests that the geometry and rest position of the syrinx can also influence the harmonic spectra drastically (figure 7). Simulations with constant rest areas demonstrate collision-free oscillations even at high pressures (3.0 kPa=30 cmH2O), mainly because the pressure acts only on the first mass via the lower plate. This leads to an oscillation pattern characterized by weak harmonics compared with standard two-mass models, where avoidance of collisions can be obtained only at pressure values slightly above the onset pressure. During the coo simulation, the syrinx is in a persistent convergent shape (a1/a2>1, figure 4a). As such, the suprasyringeal pressure has little effect on the masses, which might lead to reduced source–tract interaction. This again suggests that filter mechanisms in doves are closer to those in human phonation (Beckers et al. 2003b) in contrast to other possible explanations, such as the soprano model.
6.2 Control of sound production
We can conclude that the complex interplay of bronchial pressure, syringeal muscle force generation and transmural pressure all affect precise amplitude and frequency control. In the case of ring doves, the syringeal muscles have the most profound effect on both AM and FM. Nevertheless, a separated physiological correlate with amplitude or fundamental frequency of the produced sound (Gaunt et al. 1982; Beckers et al. 2003a) seems not to be the case. Even bronchial pressure directly affects the fundamental frequency (figure 6d,e). The implementation of a muscle model to calculate force produced by the muscle, instead of EMG correlates, provides an explanation for the fast frequency rise and fall at the on- and offset of each trill element.
Our model suggests that the control of FM during sound production is relatively independent of a pressure difference between air sacs compared with direct muscular control in ring doves. Brackenbury (1972) shows that a small caudocranial pressure gradient exists in the air sac system. This gradient plays an important role for the gas exchange during ventilation. He provides the only direct measurements of differential pressure between air sacs to our knowledge, and demonstrates that the difference between the ICAS and anterior thoracic air sac is negligible, and that the difference between the ICAS and abdominal air sac is only one-tenth of the parent pressure. During clucking in a chicken the maximal pressure in the ICAS is 1.0 kPa (equal to 10 cmH2O), while the differential with the anterior thoracic air sac maximally measures only 0.03 kPa (Brackenbury 1972). Furthermore, the transmural pressure is very small compared with the pressure that can be exerted on the LVM by the TL muscle (1.0 versus 20 kPa).
Our in silico experiments have their in vivo experimental counterparts and thus lead to testable predictions. Switching off the TL as in figure 6 equals performing a bilateral nerve cut experiment. Switching off the transmural pressure equals an experiment where the ICAS syringeal pressure is levelled, e.g. by making a hole in the bronchus. Therefore, we expect that a coo after a bilateral nerve cut exhibits similarity to figure 6d. Levelling the bronchial and ICAS pressure might be a more difficult experiment, because the structural integrity of the syrinx is easily affected.
The small FM range of 400 Hz in ring doves is limited, but might still play an important role in perception (Beckers et al. 2001). For human listeners, an illustrative example is the two-tone vocalization of the common cuckoo (Cuculus canorus): the two tones are distinct, but their fundamental frequency (650 and 550 Hz, respectively) differs by only 100 Hz. Although many non-oscine's vocalizations may have a limited frequency range, almost every family harbours species capable of considerable FM sweeps or intricate song (Ficken et al. 2000). For example, FM ranges 1–3 kHz in the northern lapwing (Vanellus vanellus, Charadriidae) and the oystercatcher (Haematopus ostralegus), 1–7 kHz in the American woodcock (Scolopax minor), 4–9 kHz in juvenile tawny owls (Strix aluco, Strigidae), 2.5–9 kHz in the woodcock (Scolopax rusticola, Scolopacidae) and even 1.5–9 kHz in the common shelduck (Tadorna tadorna, Anatidae; Bergman & Helb 1982; Kroodsma 2005).
The classification of the songbirds and the mechanisms explaining the radiation of the group into the most diverse and numerically dominant avian order are still under debate (Ericson et al. 2003; Barker et al. 2004). Among other hypotheses, the evolution of a complex syrinx and the ability of vocal learning have been suggested and discussed to contribute to this radiation (e.g. Raikow 1986; Baptista & Trail 1992). The songbird syrinx design is highly conserved in evolution (Ames 1971; King 1989) and has six to eight pairs of muscles (King 1989). However, there seems to be no correlation between syringeal and song complexity (Gaunt 1983; Baptista & Trail 1992). Some syringeal muscles have been correlated with fundamental frequency or amplitude of sound (Goller & Suthers 1996a,b; Suthers et al. 1999), but the biomechanical effects of each individual muscle, let alone potential combinations of differently recruited muscles, e.g. muscle synergies (d'Avella & Bizzi 2005; d'Avella et al. 2003, 2006), are far from understood. Our model suggests that independent control of song characteristics is not possible with the simple syringeal morphology of the ring dove, as suggested before by Gaunt (1983). We speculate that songbirds evolved a syrinx design that allowed for the independent control of sound parameters. Uncoupling the control of different sound parameters as an evolutionary key innovation would lead to a tremendous increase in the possible variation of song, which provides an additional explanation for the rapid diversification and speciation of songbirds.
The authors wish to thank Henk Schipper (Wageningen University, The Netherlands) for the use of microscopes, Sander Kranenbarg (Wageningen University, The Netherlands) for the micro-CT scan of the syrinx, Franz Goller (University of Utah, USA) for the silicone air sac casts and pressure measurements, and four anonymous referees for their critical comments and valuable amendments to the manuscript. This study was supported by the Deutsche Forschungsgemeinschaft.
References
- Alexander R.McN. Modelling approaches in biomechanics. Phil. Trans. R. Soc. B. 2003;358:1429–1435. doi: 10.1098/rstb.2003.1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ames P.L. The morphology of the syrinx in passerine birds. Bull. Peabody. Mus. Nat. Hist. 1971;37:1–194. [Google Scholar]
- Arrowsmith D.K, Place C.M. Cambridge University Press; Cambridge, UK: 1990. An introduction to dynamical systems. [Google Scholar]
- Ballintijn M.R, ten Cate C. Sex differences in the vocalizations and syrinx of the collared-dove (Streptopelia decaocto) Auk. 1997;144:22–39. [Google Scholar]
- Baptista L.F, Trail P.W. The role of song in the evolution of passerine diversity. Syst. Biol. 1992;41:242–247. doi: 10.2307/2992524. [DOI] [Google Scholar]
- Barker F.K, Cibois A, Schikler P, Feinstein J, Cracraft J. Phylogeny and diversitification of the largest avian radiation. Proc. Natl Acad. Sci. USA. 2004;101:11 040–11 045. doi: 10.1073/pnas.0401892101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckers G.J.L, Goossens B.M.A, ten Cate C. Perceptual salience of acoustic differences between conspecific and allospecific vocalisations in African collared-doves. Anim. Behav. 2001;62:511–518. doi: 10.1006/anbe.2001.1768. [DOI] [Google Scholar]
- Beckers G.J.L, Suthers R.A, ten Cate C. Mechanisms of frequency and amplitude modulation in ring dove song. J. Exp. Biol. 2003a;206:1833–1843. doi: 10.1242/jeb.00364. [DOI] [PubMed] [Google Scholar]
- Beckers G.J.L, Suthers R.A, ten Cate C. Pure-tone birdsong by resonance filtering of harmonic overtones. Proc. Natl Acad. Sci. USA. 2003b;100:7372–7376. doi: 10.1073/pnas.1232227100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergman H.-H, Helb H.-W. BLV Verlagsgesellschaft; München, Germany: 1982. Stimmen der Vögel Europas. [Google Scholar]
- Bertram C.D. Flow phenomena in floppy tubes. Contemp. Phys. 2004;45:45–60. [Google Scholar]
- Bertram C.D, Pedley T.J. A mathematical model of unsteady collapsible tube behaviour. J. Biomech. 1982;15:39–50. doi: 10.1016/0021-9290(82)90033-1. [DOI] [PubMed] [Google Scholar]
- Boggs D.F, Butler P.J, Wallace S. Differential air-sac pressures in diving tufted ducks Anthya fuligula. J. Exp. Biol. 1998;201:2665–2668. doi: 10.1242/jeb.201.18.2665. [DOI] [PubMed] [Google Scholar]
- Boggs D.F, Baudinette R.V, Frappell P.B, Butler P.J. The influence of locomotion on air-sac pressure in little penguins. J. Exp. Biol. 2001;204:3581–3586. doi: 10.1242/jeb.204.20.3581. [DOI] [PubMed] [Google Scholar]
- Brackenbury J.H. Lung-air-sac anatomy and respiratory pressures in the bird. J. Exp. Biol. 1972;57:543–550. doi: 10.1242/jeb.57.2.543. [DOI] [PubMed] [Google Scholar]
- Carroll A.M, Wainwright P.C. Muscle function and power during suction feeding in largemouth bass (Micropterus salmoides) Comp. Biochem. Physiol. A. 2006;143:389–399. doi: 10.1016/j.cbpa.2005.12.022. [DOI] [PubMed] [Google Scholar]
- Casey R.M, Gaunt A.S. Theoretical models of the avian syrinx. J. Theor. Biol. 1985;116:45–64. [Google Scholar]
- Chamberlain D.R, Gross W.B, Cornwell G.W, Mosby H.S. Syringeal anatomy in the common crow. Auk. 1968;85:244–252. [Google Scholar]
- d'Avella A.P, Bizzi E. Shared and specific muscle synergies in natural motor behaviours. Proc. Natl Acad. Sci. USA. 2005;102:3076–3081. doi: 10.1073/pnas.0500199102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- d'Avella A.P, Saltiel P, Bizzi E. Combinations of muscle synergies in the construction of a natural behaviour. Nat. Neurosci. 2003;6:300–308. doi: 10.1038/nn1010. [DOI] [PubMed] [Google Scholar]
- d'Avella A.P, Laure F, Lacquaniti F. Control of fast-reaching movements by muscle synergy combinations. J. Neurosci. 2006;26:7791–7810. doi: 10.1523/JNEUROSCI.0830-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doupe A, Kuhl P. Birdsong and human speech: common themes and mechanisms. Annu. Rev. Neurosci. 1999;22:567–631. doi: 10.1146/annurev.neuro.22.1.567. [DOI] [PubMed] [Google Scholar]
- Duncker H.R. The lung air sac system of birds. A contribution to the functional anatomy of the respiratory apparatus. Ergeb. Anat. Entwicklungsgesch. 1971;45:7–171. [PubMed] [Google Scholar]
- Elemans, C. P. H. 2004 How do birds sing? Sound analysis—mechanical modelling—muscular control, PhD thesis, pp. 144. Wageningen University, The Netherlands. ISBN: 90-8504-111-2.
- Elemans C.P.H, Larsen O.N, Hoffmann M.R, van Leeuwen J.L. Quantitative modelling of the biomechanics of the avian syrinx. Anim. Biol. 2003;53:183–193. doi: 10.1163/157075603769700377. [DOI] [Google Scholar]
- Elemans C.P.H, Spierts I.L.Y, Muller U.K, van Leeuwen J.L, Goller F. Superfast muscles control dove's trill. Nature. 2004;431:146. doi: 10.1038/431146a. [DOI] [PubMed] [Google Scholar]
- Elemans C.P.H, Spierts I.L.Y, Hendriks M, Schipper H, Müller U.K, van Leeuwen J.L. Syringeal muscles fit the trill in ring doves (Streptopelia risoria L.) J. Exp. Biol. 2006;209:965–977. doi: 10.1242/jeb.02066. [DOI] [PubMed] [Google Scholar]
- Ericson P.G.P, Irestedt M, Johansson U.S. Evolution, biogeography, and patterns of diversification in passerine birds. J. Avian Biol. 2003;34:3–15. doi: 10.1034/j.1600-048X.2003.03121.x. [DOI] [Google Scholar]
- Fee M.S, Shraiman B, Pesaran B, Mitra P.P. The role of nonlinear dynamics of the syrinx in the vocalisations of a songbird. Nature. 1998;395:67–71. doi: 10.1038/25725. [DOI] [PubMed] [Google Scholar]
- Ficken M.S, Rusch K.M, Taylor S.J, Powers D.R. Blue-throated hummingbird song: a pinnacle of nonoscine vocalization. Auk. 2000;117:120–128. doi: 10.1642/0004-8038(2000)117%5B0120:BTHSAP%5D2.0.CO;2. [DOI] [Google Scholar]
- Fitch W.T, Neubauer J, Herzel H. Calls out of chaos: the adaptive significance of nonlinear phenomena in mammalian vocal production. Anim. Behav. 2002;63:407–418. doi: 10.1006/anbe.2001.1912. [DOI] [Google Scholar]
- Fletcher N.H. Bird song—a quantitative acoustic model. J. Theor. Biol. 1988;135:455–481. doi: 10.1016/S0022-5193(88)80270-4. [DOI] [Google Scholar]
- Fletcher N.H. Acoustics of bird song—some unresolved problems. Commun. Theor. Biol. 1989;1:237–251. [Google Scholar]
- Fletcher N.H. Oxford University Press; Oxford, UK: 1992. Acoustic systems in biology. [Google Scholar]
- Fletcher N.H, Riede T, Beckers G.J.L, Suthers R.A. Vocal tract filtering and the ‘coo’ of doves. J. Acoust. Soc. Am. 2005;116:3750–3756. doi: 10.1121/1.1811491. [DOI] [PubMed] [Google Scholar]
- Frank T, Walter I, Probst A, König H.E. Histological aspects of the syrinx of the male mallard (Anas plathyrhynchos) Anat. Histol. Embryol. 2006;35:396–401. doi: 10.1111/j.1439-0264.2006.00701.x. [DOI] [PubMed] [Google Scholar]
- Gardner T, Cecchi G, Magnasco M, Laje R, Mindlin G.B. Simple motor gestures for birdsongs. Phys. Rev. Lett. 2001;87:208 101–208 105. doi: 10.1103/PhysRevLett.87.208101. [DOI] [PubMed] [Google Scholar]
- Gaunt A.S. An hypothesis concerning the relationship of syringeal structure to vocal abilities. Auk. 1983;100:853–862. [Google Scholar]
- Gaunt A.S, Gaunt S.L.L, Casey R.M. Syringeal mechanisms reassessed: evidence from Streptopelia. Auk. 1982;99:474–494. [Google Scholar]
- Goller F, Larsen O.N. In situ biomechanics of the syrinx and sound generation in pigeons. J. Exp. Biol. 1997;200:2165–2176. doi: 10.1242/jeb.200.16.2165. [DOI] [PubMed] [Google Scholar]
- Goller F, Suthers R.A. Role of syringeal muscles in gating airflow and sound production in singing brown thrashers. J. Neurophysiol. 1996a;75:867–876. doi: 10.1152/jn.1996.75.2.867. [DOI] [PubMed] [Google Scholar]
- Goller F, Suthers R.A. Role of syringeal muscles in controlling the phonology of bird song. J. Neurophysiol. 1996b;76:287–300. doi: 10.1152/jn.1996.76.1.287. [DOI] [PubMed] [Google Scholar]
- Goodwin D. British Museum of Natural History; London, UK: 1983. Pigeons and doves of the world. [Google Scholar]
- Greenewalt C.H. Smithsonian Institution Press; Washington, DC: 1968. Bird song: acoustics and physiology. [Google Scholar]
- Grotberg J.B, Jensen O.E. Biofluid mechanics in flexible tubes. Annu. Rev. Fluid Mech. 2004;36:121–147. doi: 10.1146/annurev.fluid.36.050802.121918. [DOI] [Google Scholar]
- Ishizaka K, Flanagan J.L. Synthesis of voiced sounds from a two-mass model of the vocal cords. Bell. Syst. Tech. J. 1972;51:1233–1268. [Google Scholar]
- King A.S. Functional anatomy of the syrinx. In: King A.S, McLelland J, editors. Form and function in birds. Academic Press; New York, NY: 1989. pp. 105–192. [Google Scholar]
- Komi P.V. Stretch-shortening: a powerfull model to study normal and fatigued muscle. J. Biomech. 2000;33:1197–1206. doi: 10.1016/S0021-9290(00)00064-6. [DOI] [PubMed] [Google Scholar]
- Kroodsma D.E. Houghton Mifflin Company; Boston, MA: 2005. The singing life of birds: the art and science of listening to birdsong. [Google Scholar]
- Laje R, Mindlin G.B. Diversity within a birdsong. Phys. Rev. Lett. E. 2002;89:288 102–288 106. doi: 10.1103/PhysRevLett.89.288102. [DOI] [PubMed] [Google Scholar]
- Laje R, Mindlin G.B. Springer; Berlin, Germany: 2005. The physics of bird song. [Google Scholar]
- Laje R, Gardner T.J, Mindlin G.B. Continuous model for vocal fold oscillations to study the effect of feedback. Phys. Rev. Lett. E. 2001;64:056 201. doi: 10.1103/PhysRevE.64.056201. [DOI] [PubMed] [Google Scholar]
- Laje R, Gardner T.J, Mindlin G.B. Neuromuscular control in vocalizations in birdsong: a model. Phys. Rev. Lett. E. 2002;65:051 921–061 929. doi: 10.1103/PhysRevE.65.051921. [DOI] [PubMed] [Google Scholar]
- Larsen O.N, Goller F. Role of syringeal vibrations in birds vocalizations. Proc. R. Soc. B. 1999;266:1609–1615. doi: 10.1098/rspb.1999.0822. [DOI] [Google Scholar]
- Larsen O.N, Goller F. Direct observation of syringeal muscle function in songbirds and a parrot. J. Exp. Biol. 2002;205:25–35. doi: 10.1242/jeb.205.1.25. [DOI] [PubMed] [Google Scholar]
- Lous N.J.C, Hofmans G.C, Veldhuis R.N.J, Hirschberg A. A symmetrical two-mass vocal-fold model coupled to vocal tract and trachea, with application to prosthesis design. Acta Acust. 1998;84:1135–1150. [Google Scholar]
- Mindlin G.B, Gardner T.J, Goller F, Suthers R.A. Experimental support for a model of birdsong production. Phys. Rev. E. 2003;68:041 909. doi: 10.1103/PhysRevE.68.041908. [DOI] [PubMed] [Google Scholar]
- Norman R.W, Komi P.V. Electromechanical delay in skeletal muscle under normal movement conditions. Acta Physiol. Scand. 1979;106:241–248. doi: 10.1111/j.1748-1716.1979.tb06394.x. [DOI] [PubMed] [Google Scholar]
- Nottebohm F. The origins of vocal learning. Am. Nat. 1972;106:116–140. doi: 10.1086/282756. [DOI] [Google Scholar]
- Paulsen K. Akademische Verlagsgesellschaft; Frankfurt am Main, Germany: 1967. Das Prinzip der Stimmbildung in der Wirbeltierreihe und beim Menschen. [Google Scholar]
- Pelorson X, Hirschberg A, Hassel R.R.V, Wijnands A.P.J, Auregan Y. Theoretical and experimental study of quasisteadyflow separation within the glottis during phonation. Application to a modified two-mass model. J. Acoust. Soc. Am. 1994;96:3416–3431. doi: 10.1121/1.411449. [DOI] [Google Scholar]
- Raikow R.J. Why are there so many kinds of passerine birds? Syst. Zool. 1986;35:255–259. doi: 10.2307/2413436. [DOI] [Google Scholar]
- Riede T, Beckers G.J.L, Blevins W, Suthers R.A. Inflation of the esophagus and vocal tract filtering in ring doves. J. Exp. Biol. 2004;207:4025–4036. doi: 10.1242/jeb.01256. [DOI] [PubMed] [Google Scholar]
- Riede T, Suther R.A, Fletcher N.H, Blevins W.E. Songbirds tune their vocal tract to the fundamental frequency of their song. Proc. Natl Acad. Sci. USA. 2006;103:5543–5548. doi: 10.1073/pnas.0601262103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sciamarella D, d'Alessandro C. On the acoustic sensitivity of a symmetrical two-mass model of the vocal folds to the variation of control parameters. Acta Acust. 2004;90:746–761. [Google Scholar]
- Steinecke H, Herzel H. Bifurcations in an asymmetric vocal-fold model. J. Acoust. Soc. Am. 1995;97:1874–1884. doi: 10.1121/1.412061. [DOI] [PubMed] [Google Scholar]
- Story B.H, Titze I.R. Voice simulation with a body-cover model of the vocal folds. J. Acoust. Soc. Am. 1995;97:1249–1260. doi: 10.1121/1.412234. [DOI] [PubMed] [Google Scholar]
- Strogatz S.H. Perseus Books Publishing; Cambridge, UK: 1994. Nonlinear dynamics and chaos. [Google Scholar]
- Suthers R.A, Zollinger S.A. Producing song: the vocal apparatus. NY Acad. Sci. 2004;1016:109–129. doi: 10.1196/annals.1298.041. [DOI] [PubMed] [Google Scholar]
- Suthers R.A, Goller F, Hartley R.S. Motor dynamics of song production by mimic thrushes. J. Neurobiol. 1994;25:917–936. doi: 10.1002/neu.480250803. [DOI] [PubMed] [Google Scholar]
- Suthers R.A, Goller F, Pytte C. The neuromuscular control of birdsong. Phil. Trans. R. Soc. B. 1999;354:927–939. doi: 10.1098/rstb.1999.0444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titze I.R. Prentice-Hall; Englewood Cliffs, NJ: 2002. Principles of voice production. [Google Scholar]
- Titze I.R, Baken R.J, Herzel H, Titze I.R. Evidence of chaos in vocal fold vibration. In: Titze I.R, editor. Vocal fold physiology. Singular Publishing Group; San Diego, CA: 1993. pp. 143–188. [Google Scholar]
- Warner R.W. The syrinx in the family Columbidae. J. Zool. Lond. 1972;166:285–390. [Google Scholar]
- Wild J.M. Functional anatomy and neural pathways contributing to the control of song production in birds. Eur. J. Morphol. 1997;35:303–325. doi: 10.1076/ejom.35.4.303.13077. [DOI] [PubMed] [Google Scholar]
- Wilden I, Herzel H, Peters G, Tembrock G. Subharmonics, biphonation, and deterministic chaos in mammal vocalisation. Bioacoustics. 1998;9:171–196. [Google Scholar]
- Zaccarelli R, Elemans C.P.H, Fitch W.T, Herzel H. Modelling bird songs: voice onset, overtones and registers. Acta Acust. 2006;92:741–749. [Google Scholar]