Abstract
Nonlinear interactions among coupled cellular oscillators are likely to underlie a variety of complex rhythmic behaviours. Here we consider the case of one such behaviour, a doubling of rhythm frequency caused by the spontaneous splitting of a population of synchronized oscillators into two subgroups each oscillating in anti-phase (phase-splitting). An example of biological phase-splitting is the frequency doubling of the circadian locomotor rhythm in hamsters housed in constant light, in which the pacemaker in the suprachiasmatic nucleus (SCN) is reconfigured with its left and right halves oscillating in anti-phase. We apply the theory of coupled phase oscillators to show that stable phase-splitting requires the presence of negative coupling terms, through delayed and/or inhibitory interactions. We also find that the inclusion of real biological constraints (that the SCN contains a finite number of non-identical noisy oscillators) implies the existence of an underlying non-uniform network architecture, in which the population of oscillators must interact through at least two types of connections. We propose that a key design principle for the frequency doubling of a population of biological oscillators is inhomogeneity of oscillator coupling.
Keywords: oscillator, rhythm, phase-splitting, circadian, suprachiasmatic nucleus
1. Introduction
Rhythmic behaviours of higher organisms can emerge from the temporal coordination of cellular oscillators within tissues. This kind of design may lead to complex states that arise from nonlinear mechanisms (Kuramoto 1984; Strogatz 1994; Winfree 2001), including dysrhythmias (e.g. chaotic activities and abrupt changes of frequency) and anomalous spatial patterns (e.g. turbulence and spiral waves). The control of intercellular synchronization within tissues is likely to underlie a variety of normal functions as well as certain pathologies.
One biologically important behaviour is an abrupt doubling of rhythm frequency; this may be normal, as seen with transitions in locomotor cadence (Grillner et al. 1979), or abnormal, as in cardiac tachyarrhythmias (Ritzenberg et al. 1984). Theoretical analyses of coupled oscillators have suggested a possible mechanism for frequency doubling. A group of synchronized cellular oscillators could double its frequency by spontaneously splitting into two subgroups, each subgroup oscillating with a common frequency but now in anti-phase (Schuster & Wagner 1989; Okuda 1993; Daido 1996). We call this phenomenon phase-splitting, by analogy with terminology used in mathematical physics (Basler et al. 1998; Auffeves et al. 2003). Our aim now is to better understand biological phase-splitting, and here we apply mathematical reasoning to infer the essential design principles, guided by the real constraints of an actual living tissue.
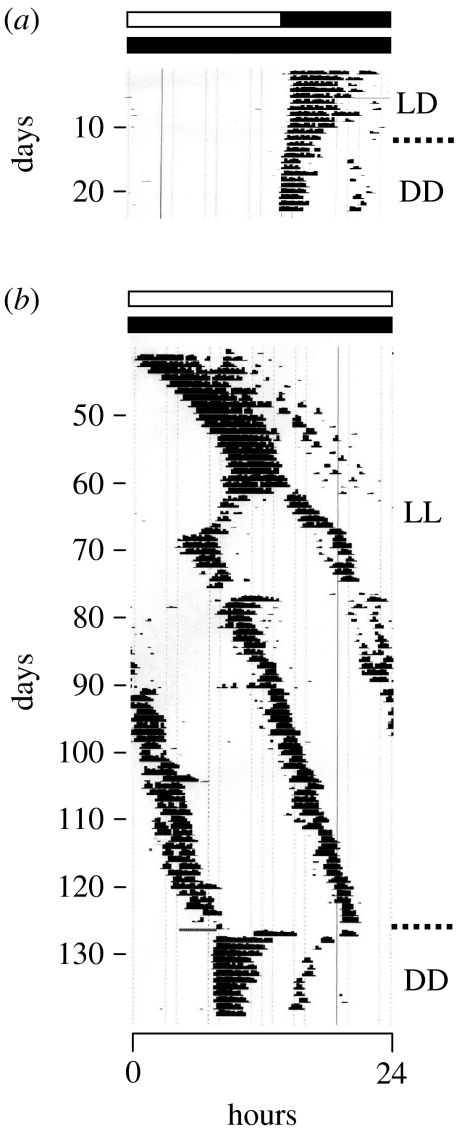
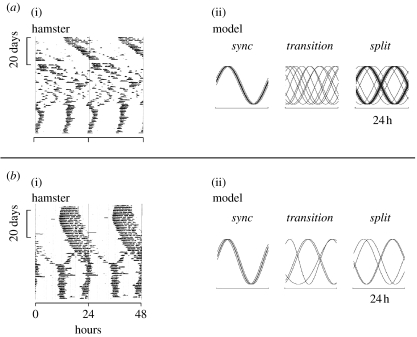
Recently, an example of phase-splitting behaviour in a well-characterized neural tissue has been demonstrated (de la Iglesia et al. 2000). The suprachiasmatic nucleus (SCN), a bilaterally paired cell group in the anterior hypothalamus of the mammalian brain, is the site of an endogenous timekeeping mechanism that regulates 24 hour (circadian) rhythmicity and its entrainment to day and night (Takahashi et al. 2001). It is a tissue clock composed of multiple single-cell circadian oscillators coupled together to generate a circadian output signal. In golden hamsters, as in other rodents, the SCN regulates the night-time expression of locomotor (wheel-running) activity during the light–dark (LD) cycle and its persistent rhythmicity in constant darkness (DD; figure 1a). Hamsters housed in constant light (LL) also show rhythmic locomotion, with a longer period than in DD (figure 1b). After a few months in LL, hamsters can exhibit a phenomenon known as ‘splitting’, in which an animal's single daily bout of locomotor activity dissociates into two components that each free-run with different periods until they become stably coupled approximately 180° (12 hours) apart (figure 1b). DD rapidly restores the split rhythm to its normal unsplit state (figure 1b). Recent data show that the SCN is dramatically reorganized in the split condition; its left and right halves continue to oscillate with a circadian period but now in anti-phase rather than in-phase (de la Iglesia et al. 2000). It has been proposed that this reconfigured phasing of cellular oscillators within the SCN tissue leads to the frequency doubling of the locomotor rhythm.
Figure 1.
Circadian locomotor (wheel-running) rhythms in golden hamsters. The number of wheel revolutions per 15 min interval is plotted for each hamster as an actogram, in which activity over the course of each 24 hour period is plotted horizontally from left to right and succeeding days stacked vertically from top to bottom. (a) Circadian rhythm of a hamster's locomotor activity is shown during LD and during DD. (b) Circadian rhythm in LL shows a longer period than in DD; after approximately two months in LL, the rhythm exhibits ‘splitting’, in which the animal's single daily bout of locomotor activity dissociates into two components that each free-run with different periods until they become stably coupled approximately 180° (12 hours) apart. DD rapidly restores the split rhythm to its normal unsplit state.
2. An idealized model of a population of limit-cycle oscillators
If individual cellular oscillators are governed by limit-cycle processes, and if the attraction to the limit cycle is strong relative to the coupling between oscillators, then the global behaviour of the population can be specified solely by the phases of the oscillators without regard to their amplitude of oscillation. This concept was originally presented as a conjecture by Winfree (1967) and subsequently supported by others using mathematical arguments (Kuramoto 1984; Strogatz 2000). Such a system can be formally described by
| (2.1) |
where θi represents the phase of the ith oscillator; ωi denotes its intrinsic frequency; Kij is the strength of coupling between the ith and the jth oscillator; and f specifies how the coupling varies with phase. Kuramoto (1984) and others (reviewed by Strogatz 2000) described oscillator synchronization in such a system, which also applies to cells that communicate strongly via multiple pulse interactions throughout the limit cycle (Ermentrout & Kopell 1991). If f is an odd periodic function (e.g. a sine function) and the coupling strength is symmetrical (i.e. Kij=Kji), then the overall frequency of the synchronized system (Ω) equals the average of the individual oscillator frequencies (i.e. ). Of note, this averaging principle appears to hold for the SCN (Liu et al. 1997).
We wish to modify equation (2.1) to make explicit the possibility that there exist delays in the coupling terms. For example, intercellular communication within the SCN is not globally instantaneous. In addition, a circadian output signal (e.g. locomotion) feeds back to alter the phase of the SCN itself (Mrosovsky 1996), and the presence of light can modify the strength and timing of this feedback signal (Schaap & Meijer 2001). To incorporate such delays and feedback, we write
| (2.2) |
where represents the internal delay within the population and is the delay in the feedback of the population output upon itself; is the coupling term that specifies the intrinsic interaction between the ith and the jth oscillator; and is the coupling term that specifies feedback effects upon the oscillators.
In the idealized case, we consider N oscillators all uniformly coupled to each other (), uniformly receptive to a feedback signal () and with sine functions governing coupling between oscillators () and feedback upon the oscillators (). In the split condition, we define θm and θn as the phases of the oscillators within the two split subgroups and oscillating with a common frequency Ω but with their phases displaced by an angle α, where 0≤α≤π. We assume that the oscillators are nearly identical such that the deviation of the phases of the individual oscillators from the mean phase during synchronization is negligible, and we define as the difference in the mean frequencies of the two subgroups. Then, and . Substituting in equation (2.2), we obtain
For , α≈π cannot be a solution because α must be in the range of (−π/2, π/2), as defined by inverse sine functions. Hence, for phase-splitting (α≈π), and the solution is
| (2.3) |
The same reasoning and derivation has been presented previously by Schuster & Wagner (1989) for two coupled oscillators without feedback.
Equation (2.3) allows for phase-splitting (α≈π) with the conditions Δω≈0 and . This can be satisfied in a number of ways. For example, if the internal delay is negligible, then the feedback delay must be between T/4 and 3T/4 (where T=2π/Ω) and must be greater than . On the other hand, if both delays are negligible, then must be negative. This analysis shows that the presence of negative coupling terms, through delayed and/or inhibitory interactions, is necessary for phase-splitting in the idealized model.
3. Biological variability precludes phase-splitting in the idealized model
Equation (2.3) is derived for a population of nearly identical, noise-free oscillators, which is biologically implausible. In the SCN, individual cellular oscillators express intrinsic periods over a wide range of 20–28 hours (Welsh et al. 1995; Liu et al. 1997; Herzog et al. 1998; Honma et al. 1998). Each of these cellular oscillators exhibits cycle-to-cycle variability in the period of approximately 2 hours (Herzog et al. 2004). We now show that stable phase-splitting is not possible for the idealized model of equation (2.2) in the face of these known sources of biological variability.
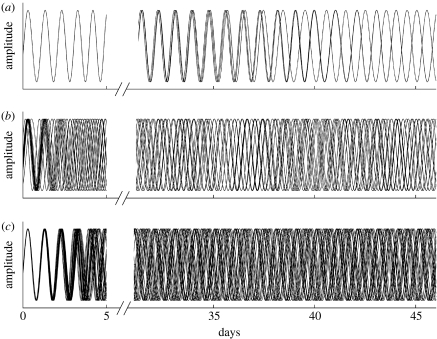
If two subgroups of oscillators are each considered as single oscillator units, the only stable solution would be α→π (Schuster & Wagner 1989), and this would require that . Using the Chebyshev inequality (Papoulis 1984), it can be shown that this is achieved for non-identical oscillators only if the number of oscillators N→∞. In fact, the SCN contains no more than 20 000 oscillators (van den Pol 1980). Furthermore, it can be proved (see appendix A) that noise at any non-zero level will destabilize the split state of the idealized model. Figure 2 illustrates how the idealized phase-splitting (figure 2a) of equation (2.3) becomes destabilized when individual oscillators are non-identical (figure 2b) or when they are subjected to noisy perturbations of phase (figure 2c).
Figure 2.
Phase-splitting in the idealized model is not stable. In (a–c), 20 globally coupled oscillators are simulated with rad s−1 (corresponding to a cycle period of 24.2 hours), , , and hours, and feedback starts on day 0. Numerical integration is by fourth-order Runge–Kutta method with a time step of 0.1 hours. (a) The idealized model exhibits phase-splitting of globally coupled, noiseless, identical oscillators. (b) Phase-splitting is not achieved with variability of the intrinsic oscillator period (the Lorentzian distribution mean period is 24.2±2 hours (s.d.)). (c) Phase-splitting is not achieved with noisy perturbations of phase (the Gaussian variance is 0.005 rad, resulting in s.d. in the period of 0.46 hours).
In actual experiments with hamsters, however, an observer might consider an animal stably split if the two locomotor activity bouts were to persist with a relatively unchanged α≈π for a finite observation period (e.g. 30 days). We ask whether there is any possible solution of the idealized model with a drift sufficiently small such that, for practical purposes, α would appear to be stable. In appendix A, we use stability analysis to estimate the minimum drift of α in the noiseless system and numerical simulations to incorporate noise-induced cycle-to-cycle variability in the period (Herzog et al. 2004). We found that, without noise, the minimum drift of α is 10 hours per week and the addition of noise causes loss of coherence of each split subgroup within 4 hours (see the end of appendix A for simulation parameters and results). Such a change in α over time and loss of coherence in the anti-phase solution would not be misinterpreted as stable splitting in the laboratory.
4. Stable biological phase-splitting requires non-uniform oscillator coupling
We now consider two constraints of the idealized model: the coupling functions ( and ) and the coupling parameters ( and ). Thus far, we have assigned the simplest odd periodic function (a sine function) for the coupling functions in equation (2.2). Hansel et al. (1993) have shown that stable anti-phase solutions can exist for a population of identical phase oscillators if the coupling function includes higher order harmonic terms. For such a solution to be relevant for circadian phase-splitting, the system must evolve from an initially synchronized state to the stable split condition. In appendix B we apply perturbation theory to determine whether such a transition is possible, and we find that the synchronized system of the idealized model (equation (2.2)) cannot evolve to the split state for any continuous or . This analysis does not exclude the possibility that phase-splitting might be achievable with discontinuous coupling functions, or that phase-splitting might be achievable via desynchronization to the incoherent state followed by instantaneous reconstitution of the anti-phase solution (Hansel et al. 1993). We know of no biological observations that would support the existence of such discontinuous behaviours in the SCN.
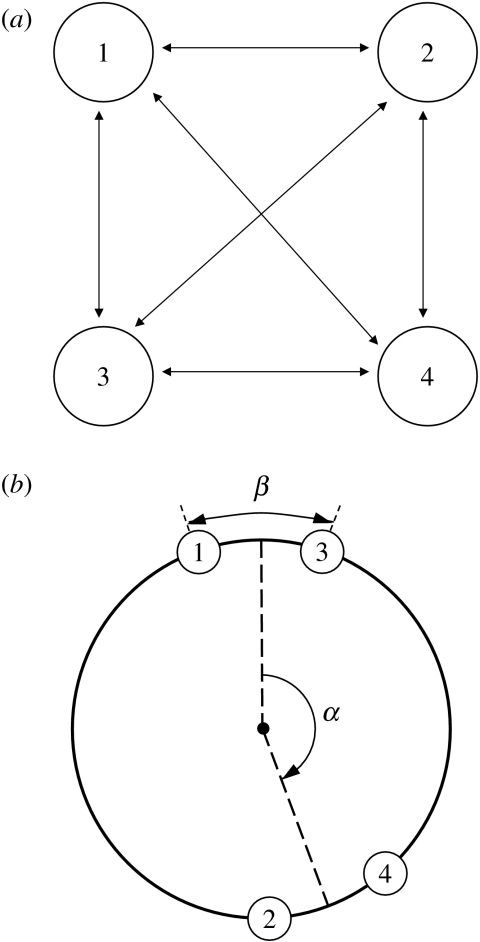
The idealized model also includes the constraint that the oscillator-to-oscillator coupling parameters and are uniform within the population. In fact, the SCN is markedly heterogeneous (Silver & Schwartz 2005), with multiple types of synaptic and non-synaptic connections. To analyse explicitly the impact of non-uniform network connectivity, we consider four coupled non-identical oscillators (figure 3a) whose behaviour is described by , where ψi is the phase displacement of the ith oscillator from the mean phase (Ωt) of the four-oscillator ensemble. The simplest non-uniform configuration of these oscillators is two subgroups defined by two different types of connections. Let and represent the coupling parameters within each subgroup, and and the coupling parameters across the two subgroups. We assign oscillators 1 and 3 to the first subgroup and oscillators 2 and 4 to the second subgroup, and define α as the mean phase difference across subgroups and β as the mean phase difference within each subgroup (figure 3b). If and if , it follows that and . Substituting for each of the four oscillators in equation (2.2), adding the solutions for each subgroup and subtracting between the subgroups, we obtain the following equations in place of equation (2.3):
| (4.1) |
and
| (4.2) |
For α≈π, the numerator of equation (4.1) must be approximately 0 while the denominator must be less than 0 (see §2). This is achieved by
| (4.3) |
and since β must be less than α, we obtain
| (4.4) |
Now consider a population N beyond four oscillators and with noisy perturbations η(t). We write
| (4.5) |
where and represent the mean fields corresponding to oscillators within and across the subgroups, respectively. We previously showed that, for uniform coupling , noise at any non-zero level will destabilize the split state of N identical oscillators. For non-uniform coupling of the simplest type (equation (4.5)) and using , we derive the stability criteria as
| (4.6) |
| (4.7) |
For α=π,
| (4.8) |
Therefore, the system is stably split under the conditions of inequalities (4.3) and (4.4).
Figure 3.
(a) Schematic of four coupled non-identical oscillators. Circles represent each phase oscillator and arrows depict coupling. (b) Definition of phases between oscillators, depicted on the phase circle (full cycle is 2π). Oscillators 1 and 3 are the first subgroup and oscillators 2 and 4 are the second subgroup; α is the mean phase difference across subgroups and β is the mean phase difference within subgroups. In the model, we assume symmetric coupling such that β is identical for both subgroups.
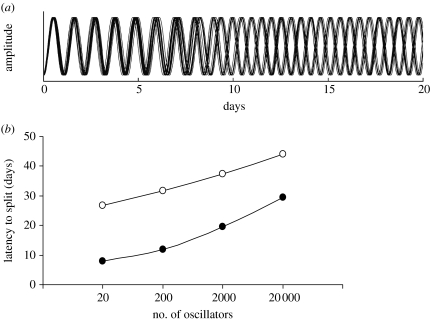
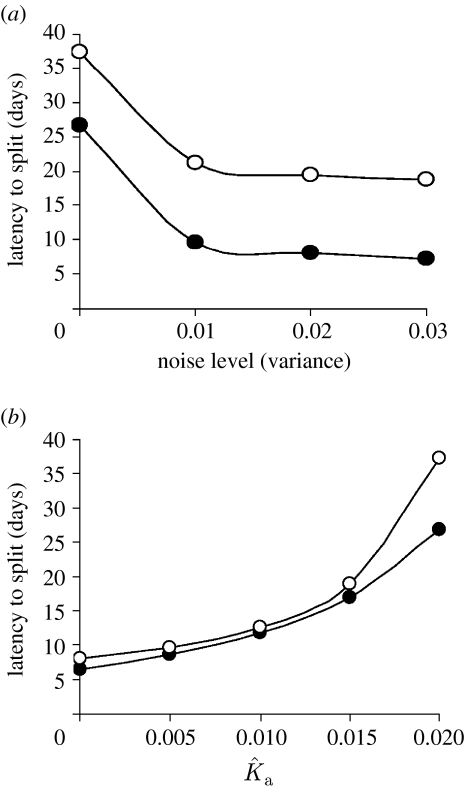
For N non-identical oscillators coupled by sine functions, the stability of phase-splitting of equation (4.5) can be estimated by numerical simulation with various intensities of noise and various coupling strengths and delays (see appendix C). We find that the existence of non-uniform network connectivity enables the system to remain stably split over a wide range of parameters, tested for up to 20 000 oscillators. The latency to onset of stable splitting (figure 4a) is prolonged by increasing the number of oscillators (figure 4b) or reducing the degree of heterogeneity, i.e. increasing towards (appendix C). Notably, over the range of N, the presence of noise reduces the latency to splitting (figure 4b). The angle α will be π if the mean frequency of the two subgroups is identical. A range of stable split angles around π is possible if the mean frequency of the two subgroups is different. For example, in a 20-oscillator network in which the mean frequency of the subgroups differs by 2 hours, , , , and hours, we find that the stable split angle is 167°.
Figure 4.
Stable phase-splitting in populations of oscillators with non-uniform coupling. In all cases, populations are simulated with non-identical oscillators (the Lorentzian distribution mean period is 24.2±2 hours (s.d.)) in the presence of noise (the Gaussian distribution variance is 0.02 rad, resulting in a cycle-to-cycle period with s.d. of 2.1 hours), , , , and hours, and feedback starts on day 0. (a) Twenty oscillators exhibit stable phase-splitting. (b) The latency to split depends on both the number of oscillators and the absence or presence of noise. Open circles, no noise; filled circles, noise with variance equal to 0.02 rad. See appendix C for further details regarding numerical simulation and effects of varying the intensity of noise.
Our numerical simulations show that the transition from synchronized to split states can exhibit different forms. An example similar to the most common transition seen in hamsters from synchronized to the split state (figure 1) is shown in figure 4a, in which there is a progressive separation of the phase difference between the two subgroups. The equation parameters influence the rate at which the two subgroups separate. Other transitions—arrhythmic or tri-branching—exist for certain parameter combinations and such transitions are rarely seen in hamster phase-splitting (see appendix D).
5. Discussion
Here we have sought the essential design principles for a population of synchronized coupled oscillators to spontaneously exhibit stable phase-splitting. We found that the inclusion of biological reality—a finite number of non-identical noisy oscillators—implies the existence of an underlying non-uniform network architecture, in which the population of oscillators must interact through at least two types of connections. This connectivity requirement follows from our assumption of continuous coupling functions. Whether there exist discontinuous coupling functions or instantaneous transitions that would obviate the connectivity requirement for phase-splitting of biological oscillators is a question for further mathematical study. We have also assumed that coupling among SCN cellular oscillators is weak relative to the strength of attraction to each cell's limit-cycle oscillation. This assumption is indirectly supported by the observations of Liu et al. (1997), but further work is needed to test whether SCN cells can act as phase oscillators and to estimate the strength and timing of coupling using quantitative experimental and modelling approaches at the interface between intracellular oscillations of ‘clock’ genes (Forger & Peskin 2003; Leloup & Goldbeter 2003; Becker-Weimann et al. 2004; Ueda et al. 2005) and intercellular coupling of neural activities (Pavlidis 1971; Carpenter & Grossberg 1983; Díez-Noguera 1994; Antle et al. 2003; Kunz & Achermann 2003; Nakao et al. 2004; Gonze et al. 2005; Bush & Siegelmann 2006; Liu et al. 2007; Sim & Forger 2007; To et al. 2007).
Our analyses show how coupling strengths and delays must interrelate in order to functionally partition the population into two split subgroups. The theoretical requirements imposed by inequalities (4.3) and (4.4) could be satisfied by a number of parameter combinations. In the case of hamster phase-splitting, the split subgroups are the left and right halves of the paired SCN, but higher order split clusters may exist (Tavakoli-Nezhad & Schwartz 2005; Yan et al. 2005). We also note that the heterogeneity requirement for stable phase-splitting could be satisfied by feedback coupling acting differentially on the oscillator network, which (in the simplest case of only two types of feedback connections) would yield a canonical phase equation whose form is identical to (4.5).
So how might LL induce phase-splitting of the hamster SCN? One possibility would be that the transition from DD to LL leads to a change in sign of from positive to negative; if all the delays are small relative to the overall circadian period, then conditions for stable phase-splitting are satisfied. Indeed, Oda & Friesen (2002), expanding on earlier models (Daan & Berde 1978; Kawato & Suzuki 1980), have considered this idea and performed numerical simulations using coupled relaxation oscillators. An alternative possibility would be that LL does not alter intrinsic SCN coupling but instead induces phase-splitting by altering feedback coupling . This would require that and are both positive in LL (as they are in DD to achieve synchronization). Since (Liu et al. 1997), all delays in DD must be small relative to the overall circadian period (see appendix A) and must be greater than (inequalities (4.4) and (4.8)). Under these conditions, the feedback delay required for stable phase-splitting can be estimated, given that . If , must be between and ; if , must be between and .
It is important to realize that, although LL is defined as constant light, what the animal actually perceives might be an entirely different matter. Typically measured are rest and activity cycles, but not intermittent sleep bouts, during which time the eyes are closed and the animal assumes a tightly curled, shielded sleeping posture tucked in the bedding. Thus, we predict that the overall photic input to the SCN during the rest phase of an animal in LL must be less than that during the active phase when the animal is awake running in the wheel. Running in the light in LL would therefore generate an oscillating, phase-shifted photic input to the SCN when compared with the usual situation in an LD cycle, in which a nocturnally active animal like the hamster restricts its running bouts to the dark. Our analysis shows that the long latency to splitting onset reflects nonlinearities in the system (equation (4.5)) and does not require any change in parameters during the LL incubation period. However, latency is parameter dependent (figures 4 and 5; appendix C) and there is at least one example in the literature in which latency is dramatically reduced. Administration of a 6 hour dark pulse timed to precede the expected onset of locomotor activity in LL has been reported to induce immediate splitting (Duncan & Deveraux 2000). If reflects the amplitude of a sinusoidal photic input, then an increase in at such a dark-to-light transition could trigger more rapid phase-splitting.
Figure 5.
The latency to split is plotted against (a) noise intensity, with , and (b) , with zero noise. ; ; hours. Filled circles, N=20 oscillators; open circles, N=2000 oscillators.
The central nervous system contains many bilaterally symmetrical neural oscillators in addition to the SCN, including those that underlie respiratory, autonomic and locomotor activities, and frequency and phase control are critical to their function. We suggest that this natural midline symmetry provides an architectural partition that could promote frequency doubling by a phase-splitting mechanism.
Acknowledgments
The hamster wheel running data used in this article are from experiments that were approved by the Institutional Animal Care and Use Committee of the University of Massachusetts Medical School.
We thank Leon Glass for early discussions on circadian splitting and Steven Strogatz, Bard Ermentrout and Daniel Forger for reviewing a previous version of the manuscript. This study was supported in part by the National Institutes of Health R01 grants NS046605 and HL71884. The contents of this article are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.
Appendix A. Stability analysis and estimation of the minimum drift in α of the idealized model of uniformly coupled, noisy oscillators
Consider a population of N oscillators composed of two subgroups θm and θn, each subgroup having N1 and N2 oscillators, respectively, both subgroups oscillating with a common frequency Ω but with their phases displaced by an angle α. Assuming a solution and , we substitute in equation (2.2). Solving for Ω for each subgroup, we obtain
| (A1) |
where m=1, 2, …, N1, and
| (A2) |
where n=1, 2, …, N2.
Consider a perturbation of each oscillator and , where δ represents perturbations due to noise. Using stability analysis of coupled phase oscillators (Strogatz 1994) with time delay (Yeung 1999), we derive
| (A3) |
and
| (A4) |
For stable phase-splitting, the following conditions must be satisfied:
| (A5) |
and
| (A6) |
With sine functions, the stability condition of equations (A 5) and (A 6) becomes
| (A7) |
Inequalities (A 7) will not be satisfied for α=π and therefore the system is not stable.
In actual experiments with hamsters, however, an observer might consider an animal stably split if the two locomotor activity bouts were to persist with a relatively unchanged α=π for a finite observation period (e.g. 30 days). We ask whether there is any possible solution of the idealized model with a drift sufficiently small such that, for practical purposes, α would appear to be stable. To estimate the minimum drift in α, we assume (N1/N)≈(N2/N) and define the growth in α as , where
| (A8) |
and δ0 is the initial perturbation from α=π.
The synchronized frequency of each subgroup during the split state is
| (A9) |
Substituting equation (A 8) into equation (2.3), we obtain
| (A10) |
Similarly, the synchronized frequency during DD (α=0) is
| (A11) |
and the synchronized frequency during LL prior to splitting is
| (A12) |
Biological observations provide some constraints on the minimum drift in α. Experimental studies (Welsh et al. 1995; Liu et al. 1997; Herzog et al. 1998; Honma et al. 1998) suggest that the circadian period of the SCN in DD is approximately the average of the distributed periods of individual oscillator cells, i.e.
| (A13) |
In LL, the circadian period is lengthened (figure 1), which results in
| (A14) |
We further consider the biologically plausible assumptions that the internal delay in intercellular communication is small with respect to the period of the pacemaker, whereas the delay in the external feedback arises from slower mechanisms and is therefore large compared with . This leads to the condition that and during DD. During LL, as before, whereas to satisfy equation (A 14). Since the oscillators are synchronized, and (from equation (2.3)). This results in and .
Substituting equation (A 11) into equation (A 9), we can estimate and if we estimate the difference between ΩDD and Ω in the stable split state. From our experimental records of hamster phase-splitting, we measured ΩDD and estimated Ω as twice the frequency of the split rhythm. Calculating for each hamster, we found for a group of 30 hamsters (mean±s.d.) rad h−1. We assume that the number of oscillators in each subgroup is 10 000; we chose the maximum number of oscillators since fewer leads to a greater drift in α (figure 4). From the Chebyshev inequality (Papoulis 1984) for a probability of 95%, we estimate . We determined the minimum λ using a nonlinear optimization procedure (Press et al. 1992), which enables us to estimate , and from equations (A 10)–(A 14). The estimated parameters are , and . Using these estimates and the measured , the estimate for the minimum λ is 0.988×10−2.
The minimum growth in α is calculated as , where δ0 is the difference between the anti-phase solution (α=π) and the estimated initial split angle (α≈4π/5). Over an observation period of one week, the minimum drift in α is 10.1 hours. This estimate does not account for the destabilizing effects of noise. Using the same estimated parameters and with noise variance equal to 0.02 rad resulting in a cycle-to-cycle period of s.d. of 2.1 hours (Herzog et al. 2004), we find using numerical simulation of 20 000 oscillators that the two split subgroups become incoherent in 4 hours.
Appendix B. Evolution of subgroups from the synchronized to the split states
Based on stability analysis (appendix A), the conditions for stable phase-splitting of N identical oscillators (each subgroup having N1 and N2 oscillators) are
| (B1) |
| (B2) |
Inequalities (B 1) and (B 2) can be satisfied by proper selection of and . For example, if and , the above inequalities can be satisfied (Hansel et al. 1993). We now ask whether the two subgroups will be robust to perturbations as the system evolves from the synchronized state to the split state as the split angle α increases from zero to approximately π. To study the stability of the system during such a transition, we assume (N1/N)≈(N2/N) and consider a small split angle Δα as the perturbation parameter (Yeung 1999).
The synchronized frequency during constant darkness can be expressed as
| (B3) |
Consider a perturbation of the synchronized frequency and a perturbation of the feedback strength at the onset of LL in terms of Δα
| (B4) |
and
| (B5) |
Substituting equations (B 4) and (B 5) into equation (B 3) and comparing the coefficients on both sides of the resulting equation, we obtain
| (B6) |
and
| (B7) |
Now consider a perturbation of the synchronized frequency at the onset of splitting in LL
| (B8) |
Subtracting equation (A 2) from equation (A 1) (appendix A), we obtain
| (B9) |
Substituting equations (B 6)–(B 8) into equation (B 9) and expanding in terms of Δα
| (B10) |
The above condition will be satisfied only if
| (B11) |
and substituting equation (B 11) into equation (B 8), we obtain .
The stability conditions from equations (B 1) and (B 2) become
| (B12) |
For any Δα>0, both the above conditions will not be satisfied and hence the system will become unstable during the transition. Our analysis suggests that, although the anti-phase solution may be stable for certain coupling functions (Hansel et al. 1993), it is impossible for the system to evolve from the synchronized condition to the anti-phase solution in the presence of noise. This analysis does not exclude the possibility that phase-splitting might be achievable via desynchronization to the incoherent state followed by instantaneous reconstitution of the anti-phase solution (Golomb et al. 1992; Hansel et al. 1995).
Appendix C. Latency to splitting is influenced by the strength of coupling between two subgroups of oscillators and by noise impinging upon the individual oscillators
We numerically integrated equation (4.5), using a fourth-order Runge–Kutta method with a fixed time step of 0.8 hours, to simulate the behaviour of a population of N oscillators containing two identical subgroups with N/2 non-identical oscillators, with a Lorentzian distribution of periods having a mean of 24.2 hours and s.d. of 2 hours. The phase of each oscillator was subjected to noisy shifts of phase; the distribution of such stochastic perturbations was Gaussian and had a mean of zero and specified variance that defined the noise intensity.
We assumed that the internal delays were negligible relative to the mean period of the oscillation, and in the simulations we set these delays to zero. The initial phases were randomized across the cycle and we computed the subsequent time evolution of the system. We simulated DD by setting the feedback delay to zero; synchronization of the population corresponds to the normal circadian rhythm of the coupled oscillators. To simulate the effect of LL, we introduced a large feedback delay when the system was in the synchronized condition and observed its subsequent evolution for approximately 90 simulated days. The results of these simulations, shown in figure 5, reveal that the latency to splitting depends on , noise intensity and the number of oscillators.
Appendix D. Arrhythmic and tri-branching transitions from synchronized to split states
Hamsters can exhibit two unusual transitions from unsplit to split rhythms, shown in figure 6. Locomotor activity is plotted for individual animals in double actogram format, with activity over day n followed by day n+1 horizontally, succeeded by day n+1 and n+2 on the next line, and so on. In figure 6a(i),b(i), an arrhythmic locomotor transition to splitting and a tri-branching transition are shown, respectively. These two patterns can be simulated using equation (4.5) with appropriate parameter adjustments. Initially, all delays were set to zero and the initial phases randomized; we computed the subsequent time evolution of the system. When the system synchronized, a large delay in the feedback hours was introduced to simulate the effect of LL, and the system's behaviour was followed for 90 simulated days.
Figure 6.
(a) Arrhythmic and (b) tri-branching transitions in (i) hamster locomotor activity and (ii) phase model. See text for parameter values.
In figure 6a(ii), a transition with dispersion of phases of 20 oscillators is shown, simulating the arrhythmic transition of hamster splitting (figure 6a(i)). The parameters were , , and hours. In figure 6b(ii), a tri-branching transition has been simulated, which is achieved if the s.d. of periods in one subgroup is larger than the s.d. of periods in the other subgroup. In figure 6, we used two oscillators in each subgroup for clarity. In one subgroup, the frequencies were 0.23 and 0.29 whereas in the other subgroup they were 0.255 and 0.265. The parameters were , , and hours.
References
- Antle M.C, Foley D.K, Foley N.C, Silver R. Gates and oscillators: a network model of the brain clock. J. Biol. Rhythms. 2003;18:339–350. doi: 10.1177/0748730403253840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auffeves A, Maioli P, Meunier T, Gleyzes S, Nogues G, Brune M, Raimond J.M, Haroche S. Entanglement of a mesoscopic field with an atom induced by photon graininess in a cavity. Phys. Rev. Lett. 2003;91:230 405. doi: 10.1103/PhysRevLett.91.230405. [DOI] [PubMed] [Google Scholar]
- Basler M, Krech W, Platov K.Y. Rigorous analytical results on phase locking in Josephson junction ladder arrays. Phys. Rev. B. 1998;58:3409–3416. doi: 10.1103/PhysRevB.58.3409. [DOI] [Google Scholar]
- Becker-Weimann S, Wolf J, Herzel H, Kramer A. Modeling feedback loops of the mammalian circadian oscillator. Biophys. J. 2004;87:3023–3034. doi: 10.1529/biophysj.104.040824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush W.S, Siegelmann H.T. Circadian synchrony in networks of protein rhythm driven neurons. Complexity. 2006;12:67–72. doi: 10.1002/cplx.20145. [DOI] [Google Scholar]
- Carpenter G.A, Grossberg S. A neural theory of circadian rhythms: the gated pacemaker. Biol. Cybern. 1983;48:35–59. doi: 10.1007/BF00336883. [DOI] [Google Scholar]
- Daan S, Berde C. Two coupled oscillators: simulations of the circadian pacemaker in mammalian activity rhythms. J. Theor. Biol. 1978;70:297–313. doi: 10.1016/0022-5193(78)90378-8. [DOI] [PubMed] [Google Scholar]
- Daido H. Multibranch entrainment and scaling in large populations of coupled oscillators. Phys. Rev. Lett. 1996;77:1406–1409. doi: 10.1103/PhysRevLett.77.1406. [DOI] [PubMed] [Google Scholar]
- de la Iglesia H.O, Meyer J, Carpino A, Jr, Schwartz W.J. Antiphase oscillation of the left and right suprachiasmatic nuclei. Science. 2000;290:799–801. doi: 10.1126/science.290.5492.799. [DOI] [PubMed] [Google Scholar]
- Díez-Noguera A. A functional model of the circadian system based on the degree of intercommunication in a complex system. Am. J. Physiol. 1994;267:R1118–R1135. doi: 10.1152/ajpregu.1994.267.4.R1118. [DOI] [PubMed] [Google Scholar]
- Duncan M.J, Deveraux A.W. Age-related changes in circadian responses to dark pulses. Am. J. Physiol. 2000;279:R586–R590. doi: 10.1152/ajpregu.2000.279.2.R586. [DOI] [PubMed] [Google Scholar]
- Ermentrout G.B, Kopell N. Multiple pulse interactions and averaging in systems of coupled neural oscillators. J. Math. Biol. 1991;29:195–217. doi: 10.1007/BF00160535. [DOI] [Google Scholar]
- Forger D.B, Peskin C.S. A detailed predictive model of the mammalian circadian clock. Proc. Natl Acad. Sci. USA. 2003;100:14 806–14 811. doi: 10.1073/pnas.2036281100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golomb D, Hansel D, Shraiman B, Sompolinsky H. Clustering in globally coupled phase oscillators. Phys. Rev. E. 1992;45:3516–3530. doi: 10.1103/PhysRevA.45.3516. [DOI] [PubMed] [Google Scholar]
- Gonze D, Bernard S, Waltermann C, Kramer A, Herzel H. Spontaneous synchronization of coupled circadian oscillators. Biophys. J. 2005;89:120–129. doi: 10.1529/biophysj.104.058388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grillner S, Halbertsma J, Nilsson J, Thorstensson A. The adaptation to speed in human locomotion. Brain Res. 1979;165:177–182. doi: 10.1016/0006-8993(79)90059-3. [DOI] [PubMed] [Google Scholar]
- Hansel D, Mato G, Meunier C. Clustering and slow switching in globally coupled phase oscillators. Phys. Rev. E. 1993;48:3470–3477. doi: 10.1103/PhysRevE.48.3470. [DOI] [PubMed] [Google Scholar]
- Hansel D, Mato G, Meunier C. Synchrony in excitatory neural networks. Neural Comput. 1995;7:307–337. doi: 10.1162/neco.1995.7.2.307. [DOI] [PubMed] [Google Scholar]
- Herzog E.D, Takahashi J.S, Block G.D. Clock controls circadian period in isolated suprachiasmatic nucleus neurons. Nat. Neurosci. 1998;1:708–713. doi: 10.1038/3708. [DOI] [PubMed] [Google Scholar]
- Herzog E.D, Aton S.J, Numano R, Sakaki Y, Tei H. Temporal precision in the mammalian circadian system: a reliable clock from less reliable neurons. J. Biol. Rhythms. 2004;19:35–46. doi: 10.1177/0748730403260776. [DOI] [PubMed] [Google Scholar]
- Honma S, Shirakawa T, Katsuna Y, Namihira M, Honma K. Circadian periods of single suprachiasmatic neurons in rats. Neurosci. Lett. 1998;250:157–160. doi: 10.1016/S0304-3940(98)00464-9. [DOI] [PubMed] [Google Scholar]
- Kawato M, Suzuki R. Two coupled neural oscillators as a model of the circadian pacemaker. J. Theor. Biol. 1980;86:547–575. doi: 10.1016/0022-5193(80)90352-5. [DOI] [PubMed] [Google Scholar]
- Kunz H, Achermann P. Simulation of circadian rhythm generation in the suprachiasmatic nucleus with locally coupled self-sustained oscillators. J. Theor. Biol. 2003;224:63–78. doi: 10.1016/S0022-5193(03)00141-3. [DOI] [PubMed] [Google Scholar]
- Kuramoto Y. Springer; Berlin, Germany: 1984. Chemical oscillations, waves, and turbulence. pp. 22–34. [Google Scholar]
- Leloup J.-C, Goldbeter A. Toward a detailed computational model for the mammalian circadian clock. Proc. Natl Acad. Sci. USA. 2003;100:7051–7056. doi: 10.1073/pnas.1132112100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Weaver D.R, Strogatz S.H, Reppert S.M. Cellular construction of a circadian clock: period determination in the suprachiasmatic nuclei. Cell. 1997;91:855–860. doi: 10.1016/S0092-8674(00)80473-0. [DOI] [PubMed] [Google Scholar]
- Liu A.C, et al. Intercellular coupling confers robustness against mutations in the SCN circadian clock network. Cell. 2007;129:605–616. doi: 10.1016/j.cell.2007.02.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mrosovsky N. Locomotor activity and non-photic influences on circadian clocks. Biol. Rev. Camb. Philos. Soc. 1996;71:343–372. doi: 10.1111/j.1469-185x.1996.tb01278.x. [DOI] [PubMed] [Google Scholar]
- Nakao, N., Nishimura, Y., Aoki, K., Katayama, N. 2004 Modeling of the suprachiasmatic nucleus based on reduced molecular clock mechanisms. In: Eng. Med. Biol. Soc., 26th Ann. Int. Conf. IEEE, vol. 2, pp. 2897–2900. IEEE. ( 10.1109/IEMBS.2004.1403824) [DOI] [PubMed]
- Oda G.A, Friesen W.O. A model for “splitting” of running-wheel activity in hamsters. J. Biol. Rhythms. 2002;17:76–88. doi: 10.1177/074873002129002357. [DOI] [PubMed] [Google Scholar]
- Okuda K. Variety and generality of clustering in globally coupled oscillators. Physica D. 1993;63:424–436. doi: 10.1016/0167-2789(93)90121-G. [DOI] [Google Scholar]
- Papoulis, A. 1984 Probability, random variables, and stochastic processes, pp. 149–151, 2nd edn. New York, NY: McGraw-Hill.
- Pavlidis T. Populations of biochemical oscillators as circadian clocks. J. Theor. Biol. 1971;33:319–338. doi: 10.1016/0022-5193(71)90070-1. [DOI] [PubMed] [Google Scholar]
- Press W.H, Teukolsky S.A, Vetterling W.T, Flannery B.P. 2nd edn. Cambridge University Press; Cambridge, UK: 1992. Numerical recipes in C: the art of scientific computing. pp. 420–430. [Google Scholar]
- Ritzenberg A.L, Adam D.R, Cohen R.J. Period multiplying-evidence for nonlinear behaviour of the canine heart. Nature. 1984;307:159–161. doi: 10.1038/307159a0. [DOI] [PubMed] [Google Scholar]
- Schaap J, Meijer J.H. Opposing effects of behavioural activity and light on neurons of the suprachiasmatic nucleus. Eur. J. Neurosci. 2001;13:1955–1962. doi: 10.1046/j.0953-816x.2001.01561.x. [DOI] [PubMed] [Google Scholar]
- Schuster H.G, Wagner P. Mutual entrainment of 2 limit-cycle oscillators with time delayed coupling. Prog. Theor. Phys. 1989;81:939–945. doi: 10.1143/PTP.81.939. [DOI] [Google Scholar]
- Silver R, Schwartz W.J. The suprachiasmatic nucleus is a functionally heterogeneous timekeeping organ. Methods Enzymol. 2005;393:451–465. doi: 10.1016/S0076-6879(05)93022-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sim C.K, Forger D.B. Modeling the electrophysiology of suprachiasmatic nucleus neurons. J. Biol. Rhythms. 2007;22:445–453. doi: 10.1177/0748730407306041. [DOI] [PubMed] [Google Scholar]
- Strogatz S.H. Addison-Wesley; Reading, MA: 1994. Nonlinear dynamics and chaos. [Google Scholar]
- Strogatz S.H. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Physica D. 2000;143:1–20. doi: 10.1016/S0167-2789(00)00094-4. [DOI] [Google Scholar]
- Takahashi, J. S., Turek, F. W. & Moore, R. Y. (eds) 2001 Handbook of behavioral neurobiology Vol. 12. Circadian clocks. New York, NY: Kluwer Academic/Plenum.
- Tavakoli-Nezhad M, Schwartz W.J. c-Fos expression in the brains of behaviorally “split” hamsters in constant light: calling attention to a dorsolateral region of the suprachiasmatic nucleus and the medial division of the lateral habenula. J. Biol. Rhythms. 2005;20:419–429. doi: 10.1177/0748730405278443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- To T.L, Henson M.A, Herzog E.D, Doyle F.J., III A molecular model for intercellular synchronization in the mammalian circadian clock. Biophys. J. 2007;92:3792–3803. doi: 10.1529/biophysj.106.094086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ueda H.R, Hayashi S, Chen W, Sano M, Machida M, Shigeyoshi Y, Iino M, Hashimoto S. System-level identification of transcriptional circuits underlying mammalian circadian clocks. Nat. Genet. 2005;37:187–192. doi: 10.1038/ng1504. [DOI] [PubMed] [Google Scholar]
- van den Pol A.N. The hypothalamic suprachiasmatic nucleus of rat: intrinsic anatomy. J. Comp. Neurol. 1980;191:661–702. doi: 10.1002/cne.901910410. [DOI] [PubMed] [Google Scholar]
- Welsh D.K, Logothesis D.E, Meister M, Reppert S.M. Individual neurons dissociated from rat suprachiasmatic nucleus express independently phased circadian firing rhythms. Neuron. 1995;14:697–706. doi: 10.1016/0896-6273(95)90214-7. [DOI] [PubMed] [Google Scholar]
- Winfree A.T. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 1967;16:15–42. doi: 10.1016/0022-5193(67)90051-3. [DOI] [PubMed] [Google Scholar]
- Winfree A.T. 2nd edn. Springer; New York, NY: 2001. The geometry of biological time. [Google Scholar]
- Yan L, Foley N.C, Bobula J.M, Kriegsfeld L.J, Silver R. Two antiphase oscillations occur in each suprachiasmatic nucleus of behaviorally split hamsters. J. Neurosci. 2005;25:9017–9026. doi: 10.1523/JNEUROSCI.2538-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeung, M. K. S. 1999 Time delay in the Kuramoto model of coupled phase oscillators, pp. 107–116. PhD dissertation, Cornell University.