Scaling of xylem vessels and veins within the leaves of oak species

Abstract

General models of plant vascular architecture, based on scaling of pipe diameters to remove the length dependence of hydraulic resistance within the xylem, have attracted strong interest. However, these models have neglected to consider the leaf, an important hydraulic component; they assume all leaves to have similar hydraulic properties, including similar pipe diameters in the petiole. We examine the scaling of the leaf xylem in 10 temperate oak species, an important hydraulic component. The mean hydraulic diameter of petiole xylem vessels varied by 30% among the 10 oak species. Conduit diameters narrowed from the petiole to the midrib to the secondary veins, consistent with resistance minimization, but the power function scaling exponent differed from that predicted for stems. Leaf size was an organizing trait within and across species. These findings indicate that leaf vasculature needs to be included in whole-plant scaling models, for these to accurately reflect and predict whole-plant transport and its implications for performance and ecology.

1. Introduction

Plants need to deliver copious water to the leaf cells and airspaces via narrow conduits. If the entire vascular system comprised narrow conduits, its hydraulic resistance would be very high because conduit lumen resistance scales inversely with diameter raised to the fourth power (the Hagen–Poiseuille law; Tyree & Zimmermann 2002). Such a high hydraulic resistance would limit the degree to which stomata could remain open for photosynthesis at a given leaf water potential (Meinzer 2002). Trees have overcome this problem by developing vascular systems that have wider vessels in the trunk and branches than in the peripheral stems and leaves, and modelling optimal tapering has attracted substantial recent interest (West et al. 1999; McCulloh & Sperry 2005a,b; Coomes et al. 2006; Weitz et al. 2006). For convenience, these models have considered petioles as the end of the transport system (West et al. 1999). However, the leaf accounts for at least 30% of the plant resistance, and leaf venation architecture contributes to the determination of photosynthetic and transpiration rates (Sack et al. 2003; Brodribb et al. 2005, 2007; Sack & Holbrook 2006). Thus, a closer examination of scaling within leaves is important for predictions at the plant level.

Despite the importance of the leaf xylem, it might be legitimate to omit leaves from hydraulic scaling models if the xylem diameters of petioles (and veins) are invariant (e.g. West et al. 1999, box 1). Alternatively, the leaf xylem might simply follow the same scaling ‘rules’ as the stem. No study so far has tested whether the leaf xylem follows the trends proposed for the stem xylem scaling, i.e. that hydraulically weighted conduit lumen diameter (d_h) tapers with branch diameter (D) as d_h∝D^α (where optimal α=1/6; Anfodillo et al. 2006; Coomes et al. 2006). In fact, the leaf xylem may follow different rules given its different structure and function, e.g. its reticulation and leakiness to the mesophyll surrounding the veins (McCulloh & Sperry 2005a,b).

We examined scaling relationships within the leaf vasculature of 10 temperate oak species (Quercus, Fagaceae). For a given species, and across species, we hypothesized that there would be tapering of d_h in petiole, midrib and secondary veins, and of vascular bundles within veins. Further, we hypothesized that the d_h would increase with leaf size within and across species. Additionally, we tested whether the leaf xylem vessel properties correlate across species with key functional traits, stomatal density (SD) and leaf mass per unit area (LMA).

2. Material and methods

Leaves from 10 oak species were sampled from the University Botanic Garden, Cambridge, UK and the Sir Harold Hillier Gardens, Hampshire, UK. Most of these trees were planted within the last 30 years and their diameters at breast height ranged from 1.2 to 141 cm (mean 40 cm). We sampled disease-free leaves from a sun-exposed, south-facing branch for five trees per species. Lamina areas were determined from digital images using ImageJ (http://rsb.info.nih.gov/ij/). We determined the SD using nail varnish imprints of the abaxial leaf surfaces; we counted stomata within three areas of the peel under an optical microscope (×100; L3000B-HTG, GX Optical, China). LMA was determined by dividing leaf area by mass after drying the leaves for 72 hours at 70°C.

We estimated the diameters of the vascular bundles and vessels from cross-sections at (i) the midpoint of the petiole, (ii) one-third of the way along the midrib, and (iii) one-third of the way along the secondary vein branching closest to the point at which the midrib was cut. We stained the sections with Safranin O (0.01%), for imaging and measurement of diameters of vessel lumens and vascular bundles (including fibres) using a confocal microscope with an Argon laser and analysis software (TCSSP2 model, Leica Microsystems, Germany). The hydraulic conductance of a pipe scales as the fourth power of lumen diameter (d), so we calculated a hydraulically weighted mean diameter, $d_{\text{h}}=\sum d^5/\sum d^4$ (Mencuccini et al. 1997; Anfodillo et al. 2006), using all vessels with a diameter greater than half that of the largest vessel in each sample to eliminate vessels that appear to be narrow because the tapering ends have been sampled (James et al. 2003), and the number of such vessels within a bundle was counted (N).

We determined the scaling of d_h and the vascular bundle diameter D by fitting straight lines to log–log transformed data (i.e. allometric relationships) by using the standard major axis regression (SMA; using the Smatr package in the R statistics software); this also allowed a comparison of whether slopes (α values) and intercepts differed among species. The SMA regression was also used to fit lines to non-transformed data (i.e. isometric relationships).

3. Results

We found a substantial variation across the 10 oak species in petiole xylem characters: d_h varied from 21 to 34 μm; vascular bundle diameter varied from 670 to 1505 μm; and the vessel number per area of vascular bundle varied from 19 to 52 mm⁻² (table 1). Species also varied strongly in these properties for the midrib and secondary veins (figures 1 and 2 and figure A1 in the electronic supplementary material).

Table 1.

Petiole xylem characteristics of the 10 temperate oak species, including hydraulically weighted mean vessel diameter (d_h), vascular bundle diameter (D) and number of vessels (N), as well as the mean individual leaf area (area), LMA and SD. (The final column contains the scaling exponent of the power functions shown in figure 1. All of these properties varied significantly among species (ANOVA, p<0.05). n.d., not determined because leaves were hirsute.)

code	species	dh (μm)	N (no. mm−2)	D (μm)	area (cm2)	LMA (g m−2)	SD (no. mm−2)	α values
1	Q. castaneifolia	27.4	25.6	968	56	105	332	0.55
2	Q. cerris	25.5	51.8	711	26	87	515	0.59
3	Q. georgiana	22.4	51.5	670	22	74	752	0.58
4	Q. ilex	21.2	21.2	705	22	104	n.d.	0.73
5	Q. nigra	26.1	19.2	886	30	74	525	0.48
6	Q. petraea	28.2	27.4	1217	85	49	228	0.42
7	Q. rhysophylla	26.8	31.2	1505	74	110	761	0.47
8	Q. robur	25.5	30.0	1222	61	54	275	0.48
9	Q. rubra	34.0	30.4	1132	128	81	493	0.51
10	Q. serrata	30.6	36.6	847	59	74	653	0.60

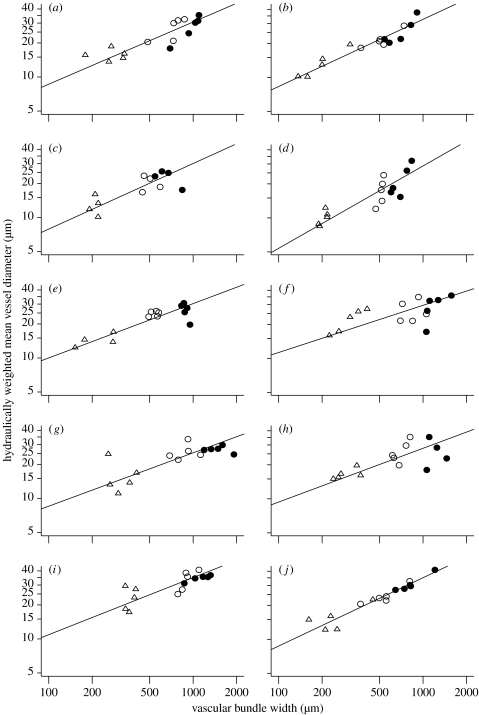
Figure 1.

Scaling of hydraulically weighted vessel diameter (d_h) with vascular bundle diameter (D) within 10 species of oak; standard major axes were fitted to the data. Vessels were sampled from the following: open circles, primary vein; triangles, secondary vein; and filled circles, petiole. (a) Quercus castaneifolia: d_h=0.67D^0.55 and r=0.87, p<0.001; (b) Q. cerris: d_h=0.52D^0.59 and r=0.93, p<0.001; (c) Q. georgiana: d_h=0.53D^0.58 and r=0.68, p<0.001; (d) Q. ilex: d_h=0.18D^0.72 and r=0.85, p<0.001; (e) Q. nigra: d_h=1.07D^0.48 and r=0.78, p<0.001; (f) Q. petraea: d_h=1.61D^0.42 and r=0.61, p<0.001; (g) Q. rhysophylla: d_h=0.95D^0.47 and r=0.67, p<0.001; (h) Q. robur: d_h=1.02D^0.47 and r=0.58, p=0.001; (i) Q. rubra: d_h=1.05D^0.51 and r=0.81, p<0.001; and (j) Q. serrata: d_h=0.52D^0.60 and r=0.98, p<0.001.

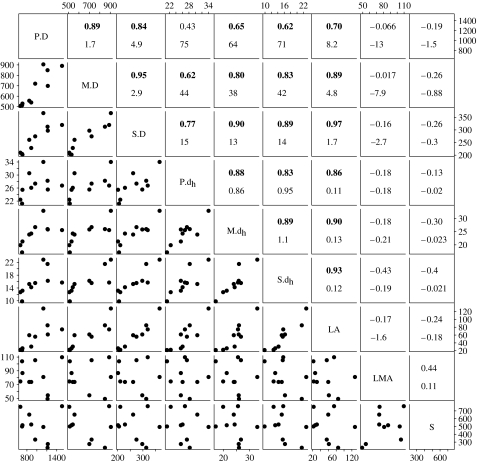
Figure 2.

Correlations among foliar traits measured for 10 species of oak. The upper right panels contain Pearson correlation coefficients (upper number, all values in bold are greater than 0.60 and significant at p<0.05) and SMA slopes (lower number); none of the variables were transformed. The lower left panels show the data points. The traits are abbreviated along the diagonal as follows: P.D, petiole vein diameter; M.D, midrib vein diameter; S.D, secondary vein diameter; P.d_h, petiole vessel mean hydraulically weighted diameter; M.d_h, midrib vessel mean hydraulically weighted diameter; S.d_h, secondary mean hydraulically weighted vessel diameter; LA, leaf area; LMA, leaf mass per unit area; S, stomatal density.

Within and across the 10 species, there were strong scaling relationships between d_h and D (figures 1 and 2). Within and across species, d_h correlated with D for petioles, midribs and secondary veins (figure A1 in the electronic supplementary material, figure 1a–c); additionally, the D of petioles, midribs and secondary veins were intercorrelated (figure 1d–f), as were the d_h in petioles, midribs and secondary veins (figure 1g–i). Across vein orders, for all the 10 species, d_h scaled with D, with α values of 0.42–0.73, substantially greater than the 1/6 predicted by scaling models for stems (figure 1; table 1).

Across species, d_h and D of petioles, midribs and secondary veins scaled tightly with mean leaf area (figure 2). The species' α values correlated negatively with the leaf area, indicating a steeper conduit tapering in smaller leaves (table 1; Spearman's rank test, p=0.032). The leaf xylem properties were not correlated with LMA, SD or the average size of the adult tree (figure 2).

4. Discussion

It is now widely acknowledged that the narrowing of conduit diameters towards the periphery of bulk transport systems reduces the dependency of hydraulic resistance on path length (Becker et al. 2000), but controversy remains over which processes need to be included in models in order to accurately predict the scaling of d_h and D. The pioneering model of West et al. (1999) predicts that the length dependence of hydraulic resistance is practically removed from branching stem systems when d_h∝D^1/6, assuming that the system comprises continuous non-leaky pipes running from trunk to the petioles and that branching systems are fractal-like and volume filling (West et al. 1999; Becker et al. 2000; Anfodillo et al. 2006). We have shown strong relationships between d_h and D for the leaf vasculature of the 10 oak species with scaling exponents consistently greater than 1/6. Several factors will need to be considered in the derivation of a theoretical model of vascular architecture for leaves as distinct from that of stems. Leaf venation is approximately plane filling and typically reticulate (Pelletier & Turcotte 2000). Also, leaf venation is laterally ‘leaky’ to the surroundings (McCulloh & Sperry 2005a,b; Zwieniecki et al. 2006); the tapering of vascular bundles within pine needles is optimized to enable even delivery of water along their length (Zwieniecki et al. 2006). In addition, the cost of constructing the vascular system needs to be considered to determine the theoretically optimal scaling of d_h with D (McCulloh & Sperry 2005a,b). Further investigation is needed of the developmental, hydraulic and economic factors that would determine the optimal tapering of leaf xylem conduits.

Our observations of general scaling between leaf size and vascular properties are consistent with early demonstrations that the leaf area correlates with the petiole vessel diameter for a given species (Salisbury 1913). This scaling supports the classical principle that larger leaves would require a larger ‘pipe’ system to supply a greater transpiration surface (cf. Shinozaki et al. 1964). We also found that the scaling of d_h with D itself scaled with the leaf size across species. More work is needed to determine how far phylogenetically diverse species depart from the scaling trends found for the 10 oak species. The lack of coordination between d_h and D and SD or LMA needs to be confirmed across diverse species sets.

The d_h values given here are within the range reported previously for other tree species (Cochard et al. 2004; Nardini et al. 2005; Sack & Frole 2006), for which the leaf hydraulic conductance was low, 2–20 mmol m⁻² s⁻¹ MPa⁻¹, thus accounting for a major portion of whole-plant resistance. Because the leaf xylem scales differently from tree stem xylem, and species differ in the leaf xylem properties sufficiently to influence their whole-plant hydraulic resistance, realistic models of whole-plant vasculature should explicitly include the scaling of leaf venation architecture.

Supplementary Material

Supplementary figure

Intra-specific relationships between vascular-bundle diameter and vessel diameters