Spatial analysis improves species distribution modelling during range expansion

Abstract

Species distribution models (SDMs) assume equilibrium between species' distribution and the environment. However, this assumption can be violated under restricted dispersal and spatially autocorrelated environmental conditions. Here we used a model to simulate species' ranges expansion under two non-equilibrium scenarios, evaluating the performance of SDM coupled with spatial eigenvector mapping. The highest fit is for the models that include space, although the relative importance of spatial variables during the range expansion differs in the two scenarios. Incorporating space to the models was important only under colonization-lag non-equilibrium, under the expected scenario. Thus, mechanisms that generate range cohesion and determine species' distribution under climate changes can be captured by spatial modelling, with advantages compared with other techniques and in line with recent claims that SDMs have to account for more complex dynamic scenarios.

1. Introduction

Species distribution models (SDMs) for geographical range prediction (Segurado & Araújo 2004; Guisan & Thuiller 2005; Elith et al. 2006) assume that species' occurrence is determined by an immediate response of individuals to environmental variation (equilibrium of species' distribution in relation to climate, sensu Araújo & Pearson 2005). This is expected only under unlimited dispersal (or if dispersal is at least as fast as the changes in environmental conditions) and very high extinction rates outside the limits of species' environmental ‘envelope’.

However, non-equilibrium will arise under different ecological and evolutionary scenarios, so that SDMs may produce biased estimates. First, it could appear by failures in colonization of suitable areas due to recent environmental changes (e.g. habitat destruction, abrupt climatic shifts or physical barriers) or will appear in the initial stages of species' invasion (‘colonization-lag’ non-equilibrium, or CNE, hereafter). In this case, although distribution is actually determined by the environment, generating strong range cohesion (sensu Rahbek et al. 2007), a mismatch between the actual and potential distributions is expected due to historical time lag. Second, complex colonization–extinction dynamics within the species' environmental envelopes, generated by local processes as, for instance, biotic interactions or metapopulation dynamics, will appear as random noise in geographical space. We call this a demographic non-equilibrium (DNE) scenario, which is expected to disrupt range cohesion.

Some recent studies showed that incorporating spatial predictors into SDMs improves model fit (Segurado et al. 2006; Bahn & McGill 2007; Dormann 2007). However, as the two scenarios of non-equilibrium described above will generate different spatial structures (highly structured in CNE and not structured in DNE), it is still necessary to test the performance of autocorrelation models under these scenarios and find how they can be conceptually linked to non-equilibrium dynamics (Araújo & Guisan 2006; Heikkinen et al. 2006). Here we used simulation models, based on cellular automata, to evaluate how a spatially explicit SDM performs under these non-equilibrium scenarios.

2. Material and methods

The use of simulated data is an interesting approach to evaluate SDMs because some important species-range properties affecting modelling efficiency can be controlled for (Hirzel et al. 2001; Austin et al. 2006; Meynard & Quinn 2007). This is usually done by creating a hypothetical species whose occurrences are found within a pre-determined ‘bioclimatic envelope’, and sampled occurrences are then used to evaluate SDM performance by comparison with a known range. As we were interested in dynamic scenarios, we generated non-equilibrium ranges by a spatially explicit simulation of colonization–extinction mechanisms using cellular automata models.

All simulations were based on the premise that species distribution is affected by a simple ‘suitability’ measure, established by the combination of unimodal responses to environmental variables (Meynard & Quinn 2007). This suitability measure was defined for each of the 2545 cells (0.24 decimal degrees cell size) covering the geographical area of the cerrado biome (figure 1), based on four climatic variables (mean annual temperature and its seasonality and mean annual precipitation and its seasonality, from the WORLDCLIM database; available at http://www.worldclim.org) and two topographic variables (altitude and slope, from the Hydro-1K global digital elevation model). The cerrado realm was used here as a computational facility only.

Figure 1.

Simulated range distribution under two scenarios of non-equilibrium (CNE and DNE) at two selected time steps and their predicted distribution obtained by modelling environment alone (ENV) or environment coupled with spatial eigenvectors (ENV+SEVM).

Range expansion processes were simulated based on local colonization and extinction constrained by local suitability (see electronic supplementary material for details). Under the CNE scenario, the range expansion was based on two simple rules: (i) a species automatically colonizes a cell ‘i’ if there is any neighbouring cell ‘j’ successfully colonized at time t−1 and (ii) extinction probability is linearly and negatively related to the suitability. A DNE scenario was simulated by adding stochastic colonization–extinction dynamics to the range expansion model. Thus, we allowed for a suitability-independent persistence probability that increased linearly with the proportion of neighbouring cells successfully colonized at time t−1.

We modelled species' distribution at 15 time steps (cycles), before all possible suitable areas were occupied by the population in both simulation models, using the maximum entropy principle implemented in the program Maxent v. 3.4 (Phillips et al. 2006). At each step, 100 occurrence points were randomly sampled and modelled in Maxent based on the six environmental variables previously described. Model evaluation was done using Cohen's kappa (κ; Allouche et al. 2006) obtained after converting probabilities of occurrence to presence–absence data. Cut-off thresholds were established using receiving operator characteristic curves (Liu et al. 2005). We then added the first five eigenvectors extracted from a truncated double-centred geographical distance matrix as additional predictors, coupling then Maxent with spatial eigenvector mapping (see Diniz-Filho & Bini (2005), Griffith & Peres-Neto (2006) and Dormann et al. (2007), for reviews). These eigenvectors are orthogonal spatial predictors that capture, at different scales, the geometry of the studied area and were obtained in spatial analysis in macroecology software (Rangel et al. 2006).

Spatial autocorrelation in model residuals (i.e. observed occurrence–probability of occurrence given by Maxent at each cell) was investigated using Moran's I coefficients (Dormann et al. 2007). We used an analysis of covariance (ANCOVA) to verify whether the gain in κ values (Δκ) after adding spatial predictors was influenced by the type of scenario simulated (CNE versus DNE). A decrease in κ values is expected with the increase of range size due to the loss of statistical power and reduction in prevalence (Allouche et al. 2006; Jiménez-Valverde & Lobo 2007), since sample size for Maxent analysis was held constant. Thus, to account for this relationship and make Δκ comparable, geographical range size was allowed as a covariate in the ANCOVA.

3. Results and discussion

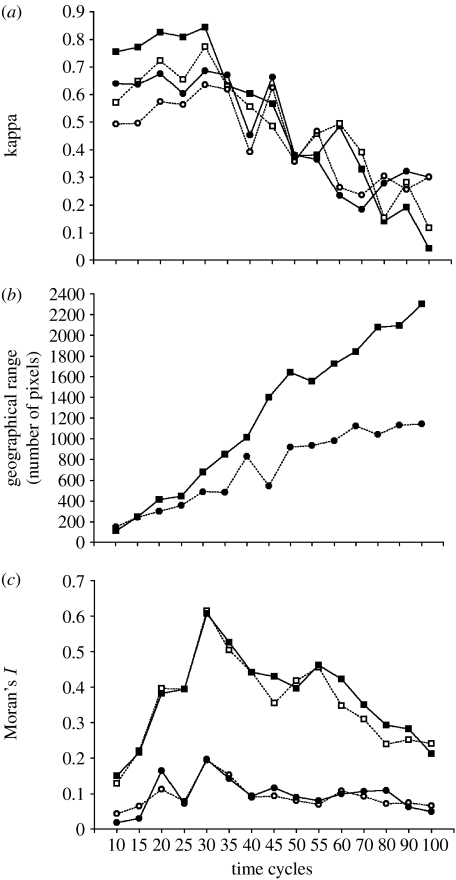
The analyses revealed that, in the initial phases of range expansion, adding spatial variables always provided better fit than using environmental data alone in Maxent (figure 1; figure S1, see also animations in the electronic supplementary material). Under the DNE scenario, models have lower κ values than in their corresponding simulations for the CNE scenario (figure 2a) up to 30 time steps. However, ranges expanded continuously in the second scenario, whereas in the first there was a tendency to stabilization below the maximum expected by suitability (figure 2b). The relationship between gain in κ values after adding spatial predictors (Δκ values) and range size was independent of the scenario, as the interaction between this factor and range size was not significant (F_1,26=1.05; p=0.3144). After accounting for the effect of range size (F_1,27=58.5; p<0.001), a significant effect of scenario was detected (F_1,27=9.14; p<0.01) and the adjusted mean value of Δκ was actually 10 times higher in the CNE (0.06) than in DNE (0.005; see figure S2 in the electronic supplementary material).

Figure 2.

(a) Kappa statistics (open squares, CNE-ENV; filled squares, CNE-ENV-SEVM; open circles, DNE-ENV; filled circles, DNE-ENV-SEVM), (b) range size (squares, CNE; circles, DNE) and (c) residual autocorrelation (Moran's I) in the first distance class for Maxent based on environment and spatial eigenvectors models under CNE and DNE simulations across time cycles (open squares, CNE-ENV; filled squares, CNE-ENV-SEVM; open circles, DNE-ENV; filled circles, DNE-ENV-SEVM).

Under CNE, using environmental variables alone overestimates the range in the initial phases of the range expansion (figure 1). This occurs because in these initial phases the occurrences are sampled within a restricted part of the range, so there is a systematic bias in sampling environmental suitability values. By including spatial predictors, a better fit was obtained because these additional predictors forced range cohesion independently of the spatial distribution of the environmental suitability. Under the CNE scenario, spatial autocorrelation in the residuals was higher than in the DNE scenario, due to the higher levels of range cohesion within a more concentrated part of the potential range defined by suitability (figure 2c). On the other hand, the low levels of spatial autocorrelation in residuals under DNE shows that suitability is enough to ensure accurate predictions and, consequently, this explains why spatial models tend to be ineffective to improve fit in this case (figure 2a).

It is well known that biotic interactions and stochastic colonization processes also determine species' range (Heikkinen et al. 2006; Araújo & Luoto 2007; Soberon 2007). Spatial eigenvector mapping and other spatial autocorrelation techniques can account for these processes only if they are spatially structured. Our analyses reveal that adding spatial components can be a promising approach to modelling CNE processes, such as, for instance, those occurring under fast climate change allowing species' range expansion towards new suitable areas. However, they are ineffective under DNE, in which departures from bioclimatic envelopes are caused by local processes related to biotic interactions or metapopulation structure within species' ranges. This is coherent with theoretical expectations based on the origins of autocorrelation in biogeographical data (Diniz-Filho et al. 2003). So, despite the uncertainty associated with particular SDM techniques (Thuiller 2003, 2004; Araújo & New 2007) and recent criticisms of the limited transferability of Maxent (Peterson et al. 2007; but see Phillips 2008), our main conclusions must hold in general.

Although further studies are necessary to show how these spatial predictors can be coupled with projected environmental changes, spatial eigenvector mapping is particularly suitable for this task as it allows representing spatial relationships at different spatial scales. Also, they can be easily introduced as new predictors in any SDM, with the advantage of not being intrinsically related to observed species' distribution, as it occurs with autologistic terms (Dormann 2007). This is in line with recent suggestions that it is necessary to expand SDMs to incorporate other more complex dynamic scenarios in a spatially explicit context.

Supplementary Material

Detailed methods

Creating simulated species distribution data; modelling method; model evaluation

Additional film

CNE simulation

Additional film

DNE simulation