Calibration of RF Transmitter Voltages for Hyperpolarized Gas MRI

Abstract

MRI with hyperpolarized gases, ³He, ¹²⁹Xe, ¹³C and others, has the potential to become an important diagnostic technique for clinical imaging. Due to the non-reversible loss of magnetization in hyperpolarized gas imaging, the choice of the flip angle is a major factor that influences the signal intensity and hence the signal to noise ratio. Conventional automated RF calibration procedures for ¹H imaging are not suitable for hyperpolarized gas imaging. Herein, we have demonstrated a simple procedure for RF calibration for MRI with hyperpolarized gases that is easily adaptable to clinical settings. We have demonstrated that there exists a linear relationship between the RF transmitter voltages required to obtain the same nutation angle for protons (V^1H) and hyperpolarized gas nuclei (V^3He). For our ¹H and ³He coils we found that V^3He = 1.937·V^1H with correlation coefficient r² = 0.97. This calibration can be done as a one-time procedure during the routine quality assurance (QA) protocol. The proposed procedure was found to be extremely robust in routine scanning and provided an efficient method to achieve a desired flip angle, thus allowing optimum image quality.

Introduction

Hyperpolarized ³He and ¹²⁹Xe gas MR imaging of lung airspaces has developed rapidly during the past decade (see for example recent reviews (1–11)), showing its potential to become an important diagnostic technique for clinical evaluation of lung diseases. The first application of this technology was to produce ventilation images (12,13) which display the distribution of a single bolus of inhaled ³He at breath hold. Subsequently, dynamic ³He MRI was used to show the time evolution of gas distribution, with sub-second time resolution (14,15). A quantitative method for measuring local fractional ventilation (the fraction of gas replaced with each breath) has also appeared (16). The local oxygen concentration and its decrease during breath hold have been determined (17,18) from the ³He T₁. The microstructure of the lung (the acinar airways and alveolar walls) restricts the diffusion of ³He atoms. Measurements of the helium apparent diffusion coefficient (ADC) have detected these microstructural changes in subjects with emphysema (19,20). This effect has also been used to develop the in vivo lung morphometry technique that relates changes in the diffusion rate and anisotropy to alterations in the lung microstructure at the alveolar level (21–23).

In hyperpolarized gas MRI, the gas is prepolarized by optical pumping and its polarization can exceed thermal equilibrium polarization by several orders of magnitude (24). However, since the gas is not in an equilibrium state, it cannot recover its polarization after RF pulses by relaxation as in conventional MRI. However, this allows for fast data acquisition strategies such as high speed gradient echo techniques, as one does not have to wait for relaxation to occur. Since there is a fixed amount of gas polarization available for each MR scan, the use of small flip angle excitation pulses is employed following administration of a bolus of hyperpolarized gas. The choice of flip angle is a major factor influencing the SNR and therefore the achievable resolution in hyperpolarized gas imaging. Several methods have been proposed to optimize the choice of flip angles for improved image quality (25–28). However accurate flip angle quantification is important for any of these proposed optimal imaging protocols.

Differences in subject size and weight can alter RF dissipation and matching and hence vary the RF field strength, B₁. Therefore a predetermined choice of transmitter voltage is not suitable for all imaging subjects. Conventional RF calibration methods used in proton (¹H) imaging, requiring numerous RF pulses, are also not suitable for hyperpolarized imaging due to the non-reversible loss of hyperpolarized gas magnetization. Several RF calibration procedures have been proposed for use with hyperpolarized nuclei. These methods either require the inhalation of an extra portion of hyperpolarized ³He gas, or use a separate bag of gas only for flip angle calibration on each subject (29,30). Mugler et al. have proposed a phase-based method for calibrating transmitter voltage that can be integrated into a breath-hold image acquisition (31). However, this approach requires additional time during the breath-hold scan, potentially reducing the achievable image resolution or slice coverage, and might not be feasible for clinical settings. In addition, the calibration procedure also consumes part of the polarization, resulting in less magnetization available for actual imaging. Hence, none of the existing approaches is ideally suited for clinical studies.

Here we describe a simple procedure for MRI flip angle calibration with hyperpolarized gas that does not consume any hyperpolarization during subject scanning or the presence of an additional phantom in the scanner. It also has advantages for clinical scanning as it requires practically no additional time for calibration and requires only a one-time procedure that can be done during a routine QA protocol. We test this approach using a rigid ³He transmit coil. In case of flexible transmit coil additional testing of our approach is needed.

Methods

Our approach is based on the hypothesis that changes in loading of the transmitter coils (¹H body coil and custom ³He coil) by the subject are proportional for the two coils. Thus, the transmitter reference voltages required to achieve the same nutation of ¹H and ³He spins are also proportional,

$$V^{\mathit{3}He}=\lambda ·V^{\mathit{1}H},$$ [1]

where λ is a proportionality constant. This equation states that a “lossier subject” will require greater transmitter voltage for the same nutation angle, for the same shape and duration of RF pulse, with both nuclei. Once λ is known, the correct setting for ³He RF voltage (V^3He) for a given subject can be determined from Eq. [1] simply by measurement of ¹H RF voltage (V^1H) during flip angle calibration for hydrogen nuclei using the standard automated scanner software program, as part of the routine hydrogen scout scans on the subject. Thus no additional ³He gas or time is needed to find V^3He.

Here we will demonstrate that a linear relation (Eq. [1]) exists between the transmitter voltages of ¹H body coil and ³He coil for a broad range of physiologically relevant loads and present a method to determine the proportionality constant λ.

All experiments were done on a 1.5 T Magnetom Sonata system (Siemens Medical Systems, Erlangen, Germany) with a custom-built ³He coil (32). The helium coil consists of a rigid (does not adapt to differently sized subjects) 48 cm diameter and 58 cm long volume transmitter and a flexible 8-channel receive array.

In order to calibrate the coils over a physiological range, we used 8 subjects ranging in weight from 125 lbs to 226 lbs (8 male and 1 female). The subjects were placed supine inside the ³He coil and positioned in the magnet center. For each subject, we measured $V_{180}^{\mathit{1}H}$, the RF voltage at the ¹H frequency required to nutate ¹H spins by 180° during a 1 ms rectangular RF pulse using the scanner’s automated calibration procedure using the ¹H Body coil. The 180° flip angle was used for convenience as most scanners calibrate RF voltage to this particular flip angle. The RF voltage at the ³He frequency, required to nutate ³He spins by 180° during a 1 ms rectangular RF pulse, $V_{180}^{\mathit{3}He}$, was measured with the aid of a small un-tuned RF pick-up coil (one-turn 2-cm diameter loop) connected to an oscilloscope (50 Ohm input) through 50 ohm coaxial cable. The pick-up coil was mounted as shown in Fig. 1, inside the field of the ³He transmitter coil and above the chest of the subject. We used 100 V (arbitrarily selected value) at the transmitter and recorded the pickup voltage (U₁₀₀) at the oscilloscope. No helium was inhaled by the subjects for this experiment. At our relatively low frequency of 48.5MHz (³He at 1.5 Tesla) changes in RF loading by different subjects are expected to produce uniform fractional changes in the B₁ field without disturbing the spatial pattern of B₁. That is, the frequency is low enough that there are no dielectric resonances and the RF “skin depth” is larger than the subject. Two similar sized subjects with different body composition (high vs. low body fat) will affect the loading of the coils (which our technique accounts for) but will have negligible effect on the spatial pattern of B₁ field. Thus, the RF B₁ field at the position of the pick-up coil is proportional to the RF B₁ field inside a subject or a phantom.

Figure 1.

Picture showing the ³He coil, the pickup loop coil (2 cm diameter) and the green cylindrical phantom used for calibration. The pickup coil was fixed to the transmitter coil with a holder to be in the same position for all subjects, approximately 7.5 cm below the top of the transmitter coil. The pickup loop coil was perpendicular to the vertical RF field generated by the transmitter.

For each subject, we recorded U₁₀₀. Since for each load (subject) the pick-up coil voltage is directly proportional to the transmitter voltage, we can write the following proportionality relationship:

$$V_{180}^{\mathit{3}He}=U_{180}^{\mathit{3}He}·\frac{100V}{U_{100}}$$ [2]

where $U_{180}^{\mathit{3}He}$ is the RF voltage at the pick-up coil required to nutate ³He spins by 180° during 1 ms rectangular RF pulse. Using a ³He phantom we experimentally determined the $U_{180}^{\mathit{3}He}$ voltage in Eq [2]. This was done with a cylindrical Boltzmann-polarized phantom with ³He and O₂ added to give a T₁ of 1 second. The FID signal versus transmitter voltage was measured and a standard sinusoidal fit was used to determine the flip angle and $V_{180}^{\mathit{3}He}$ for the phantom. U₁₀₀ was also measured on the phantom and $U_{180}^{\mathit{3}He}$ was then found from Eq. [2]. Other measurement parameters were: TR/TE = 8000/3.2 ms, averages = 8, vector size = 1024 and spectral width = 2000Hz.

Once $U_{180}^{\mathit{3}He}$ is determined on the phantom, its value is taken as a constant applying to all subjects, as the B₁ spatial dependence (from pick-up coil to subject) is nearly independent of coil loading by the subject, as discussed above. Then, Eq [2] was used to calculate $V_{180}^{\mathit{3}He}$ for the subjects from the measured U₁₀₀. Equation [1] was then used to calculate the proportionality constant λ.

In vivo validation was done on subjects with inhalation of 400 ml of hyperpolarized 3He gas diluted with 600 ml of nitrogen. One coronal slice was acquired with the spin tagging technique (33) using the following imaging parameters: FOV = 448 mm × 336 mm, matrix = 128 × 48 giving a resolution of 3.5 mm × 7.0 mm, slice thickness = 30 mm, TR/TE = 7.5/4 ms, Bandwidth = 390 Hz/pixel, and 21 mm tagging wavelength. A 45° flip angle for tagging pulses and 2.7° flip angle for imaging pulses were used with voltages determined from Eq [1].

Results

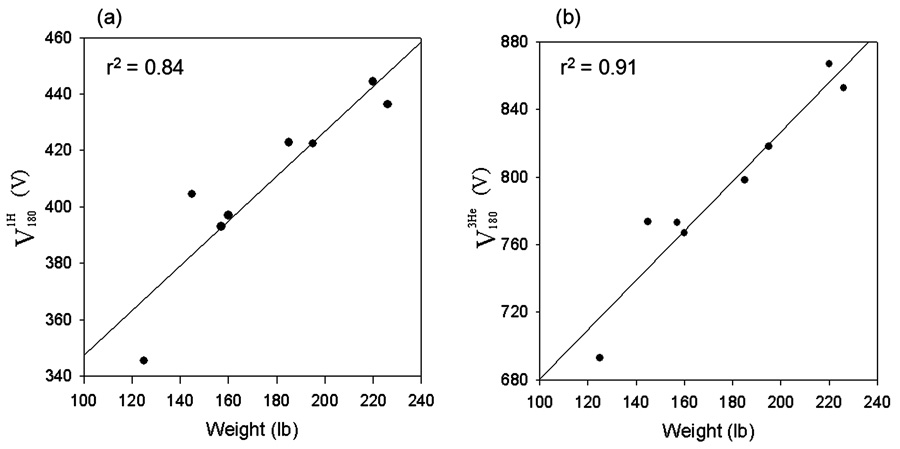
Figure 1 shows a picture of the ³He coil with pickup loop coil attached. The other end of the loop coil is connected to an oscilloscope to record the pickup voltage. The green cylindrical phantom used for calibration is also visible. The voltage, $V_{180}^{\mathit{3}He}$, for the phantom was found to be 320 V. The voltages U₁₀₀ for the phantom and all the subjects are shown in Table 1. The voltages $V_{180}^{\mathit{1}H}$ and $V_{180}^{\mathit{3}He}$ are each plotted as functions of subject weight in Fig. 2. As expected, a larger subjects result in additional RF losses, so $V_{180}^{\mathit{1}H}$ and $V_{180}^{\mathit{3}He}$ both increase with the subject’s weight.

Table 1.

The voltages measured by the pick-up coil corresponding to RF transmitter voltage of 100 V at the ³He frequency.

Subject	Weight (lb)	U100 (V)
1	160	0.685
2	226	0.616
3	195	0.642
4	145	0.679
5	157	0.677
6	220	0.606
7	125	0.758
8	185	0.658
Phantom	N/A	0.845

Figure 2.

¹H reference voltage determined by scanner software (a), and ³He reference voltage determined by pick-up coil measurement and Eq [2] plotted against subjects’ weight.

The voltages $V_{180}^{\mathit{1}H}$ and $V_{180}^{\mathit{3}He}$ are plotted against each other for the eight subjects and phantom, in Fig. 3. The excellent fit to $V_{180}^{\mathit{3}He}=\lambda ·V_{180}^{\mathit{1}H}$ with λ = 1.937 is evident, confirming our hypothesis of a linear relationship between the proton and helium voltages. We note the correlation in Fig. 3 is superior (r² = 0.97) to that in Fig. 2, indicating that weight is not the only variable determining the RF losses of the patient’s chest region. Thus, our procedure is indeed superior to simply determining ³He transmitter voltage based on the subject’s weight.

Figure 3.

Linear relationship $V_{180}^{\mathit{3}He}=1.937·V_{180}^{\mathit{1}H}$ between $V_{180}^{\mathit{1}H}$ (RF transmitter voltage required to nutate ¹H spins by 180° during 1 ms rectangular RF pulse) and $V_{180}^{\mathit{3}He}$ (RF transmitter voltage required to nutate ³He spins by 180° during 1 ms rectangular RF pulse at the ³He frequency). The former was measured using the scanner’s automated calibration procedure. The latter was calculated from Eq. [2] using U₁₀₀ measured by the pick-up coil (see Table 1). Filled circles -data from human subjects; open circle -data from the phantom; solid line -linear fitting curve.

Figure 4 shows a representative image from the in vivo magnetization tagging experiment and plot of the tagged signal profile through the lung. One can see that the signal is nearly zero between the spin tags, confirming the correct setting of the 45° RF pulses.

Figure 4.

(a) Example of a spin tagging image of lung. (b) Signal intensity profile through the lung. In this method (33) two 45° RF pulses separated by a gradient pulse are applied to create sinusoidal modulation of magnetization. The signal intensity is near the noise level in between the stripes confirming the correct setting of the tagging 45° RF pulses.

Conclusions

For hyperpolarized gas lung imaging to be clinically useful, it is important that parameters affecting image quality can be rapidly determined with minimum user interaction. Here we have demonstrated a simple method to calibrate RF pulse voltage – one of the most important parameters for hyperpolarized gas imaging. Our method is based on a proposed linear relationship between the RF transmitter voltages required to obtain a 180° nutation angle for protons $\left(V_{180}^{\mathit{1}H}\right)$ and hyperpolarized gas nuclei $\left(V_{180}^{\mathit{3}He}\right)$.The proportionality constant will be different for different coil setups but linear relationship should hold given that the ¹H coil (usually the scanner body coil) and the ³He transmit coil are rigid volume coils. To determine a coefficient in this relationship we have developed a one-time procedure using a pick-up coil and a ³He phantom. Such a relationship allows determination of $V_{180}^{\mathit{3}He}$ for new subjects based on automated measurement of $V_{180}^{\mathit{1}H}$ during routine hydrogen scout.