Abstract
Large migrating insects, such as noctuid moths and acridoid grasshoppers, flying within the stable nocturnal boundary layer commonly become concentrated into horizontal layers. These layers frequently occur near the top of the surface temperature inversion where warm fast-moving airflows provide good conditions for downwind migration. On some occasions, a layer may coincide with a higher altitude temperature maximum such as a subsidence inversion, while on others, it may seem unrelated to any obvious feature in the vertical profile of meteorological variables. Insects within the layers are frequently orientated, either downwind or at an angle to the wind, but the mechanisms involved in both layer formation and common orientation have remained elusive. Here, we show through the results of numerical simulations that if insects are treated as neutrally buoyant particles, they tend to be advected by vertical gusts (through the ‘turbophoretic’ mechanism) into layers in the atmosphere where the turbulent kinetic energy has local minima. These locations typically coincide with local maxima in the wind speed and/or air temperature, and they may also provide cues for orientation. However, the degree of layering predicted by this model is very much weaker than that observed in the field. We have therefore hypothesized that insects behave in a way that amplifies the turbophoretic effect by initiating climbs or descents in response to vertical gusts. New simulations incorporating this behaviour demonstrated the formation of layers that closely mimic field observations, both in the degree of concentration in layers and the rate at which they form.
Keywords: insect layers, migration, nocturnal boundary layer, temperature inversions, turbulence, turbophoretic model
1. Introduction
1.1 The formation of layers by windborne insect migrants
Because insects are characteristically rather small animals (average body length approx. 7 mm; Dudley 2001), long-distance migration (when it occurs) is most efficiently achieved by flight. A few species, e.g. some butterflies, appear to migrate close to the ground, but the vast majority of taxa ascend high into the air and use the wind as a transporting vehicle. Insect flight at altitudes of several hundred metres is inherently difficult to study, but individuals of the larger sized migrant species (and ‘multi-target echo’ from small species) are amenable to observation by radar techniques. Studies made with both entomological and meteorological radars over the last 40 years (see The Radar Entomology Website http://www.pems.adfa.edu.au/∼s9104004/trews/) have revealed many fascinating phenomena, but among the most frequently reported are the occurrence of layer concentrations (Drake & Farrow 1988; Gatehouse 1997), and the fact that the insects forming these layers often show a degree of common orientation (Riley & Reynolds 1986; Riley 1989; Gatehouse 1997).
Insect layers can occur at various times of the day, e.g. soon after dawn (see references in Reynolds et al. 2008) or later in the daytime (Richter et al. 1973; Campistron 1975; Chapman et al. 2002), but they are most characteristic of night-time migration in fine weather (see references in Vaughn 1985; Drake & Farrow 1988; Drake & Rochester 1994; Burt & Pedgley 1997; Gatehouse 1997; Reynolds et al. 2005). The stratification in insect aerial density is paralleled (and very probably influenced) by the often stratified nature of the nocturnal atmospheric boundary layer (NBL; Drake & Farrow 1988), although the mechanisms leading to the formation of insect layers are often far from clear. In this paper, we briefly outline the state of our knowledge on insect layering, and then use a simple stochastic model to provide some novel perspectives on layer formation and, in particular, to support the proposition that insects preferentially concentrate at heights with local minima in turbulence.
1.2 The phenomenology of layering
Large nocturnal migrants (e.g. noctuid moths and acridoid grasshoppers) take off around dusk, and there follows a period of sustained ascent (at approx. 0.4–0.5 m s−1) to altitudes of several hundred metres above ground. Around the peak of this ascent phase, aerial densities typically show a monotonic (often approx. semi-logarithmic) decrease with height (Drake 1984; Wood et al. 2006). Then, after about an hour or so, the vertical profiles of insect density frequently start to show signs of stratification, and sometimes well-defined layer concentrations form. Drake & Rochester (1994) found that in a sample of 44 nights, the probability of a layer being present rose from 0 to 50% within an hour of dusk. These layers are relatively restricted (approx. 50–150 m) in depth, but of broad horizontal extent (Drake 1984; Drake & Farrow 1988; Drake & Rochester 1994). Layers are most likely to be centred in the height interval of 200–600 m above ground, and the frequency then decreases with height (Drake & Rochester 1994). Sometimes several layers are present simultaneously (Schaefer 1976; Reynolds & Riley 1997)—up to five have been recorded, although this is rare (Schaefer 1976; Vaughn 1985). We are concerned here with insect layers that persist for periods of 1 hour or more at approximately the same altitude (or have shown gradual changes in altitude) under conditions of a stably stratified atmospheric boundary layer; we do not consider layers that may follow the passage of mesoscale disturbances such as density currents (e.g. storm outflows and sea-breeze fronts), bores, hydraulic jumps and solitary waves (Schaefer 1976; Drake 1985a; Drake & Farrow 1988; Reynolds & Riley 1988).
1.3 Layering and the vertical profile of meteorological variables
Insect layers frequently occur near the top of the surface temperature inversion where warm fast-moving airflows provide good conditions for downwind migration (Drake 1984; Drake & Farrow 1988; Reynolds et al. 2005). On some occasions, the layer coincides with a higher-altitude temperature maximum such as a subsidence inversion (Reynolds et al. 2005). It is often assumed that the insect response to temperature is the causal factor in layer formation, and this is very probably the case in regions where night-time temperatures are often suboptimal for extended nocturnal migrations (e.g. in cool temperate places such as New Brunswick, Canada (Greenbank et al. 1980) or Britain (Reynolds et al. 2005)). Even in much warmer climes, certain taxa (e.g. migratory grasshoppers and locusts) may need to migrate at the height of the warmest air because they require relatively high temperatures (more than 20–25°C) to both initiate and maintain flight (Riley & Reynolds 1979; Farrow 1990; Reynolds & Riley 1997).
Layers sometimes occur at high altitude but are unrelated to any distinctive feature in the vertical profiles of wind velocity, air temperature or humidity. Of these layers, some have an abrupt upper boundary at the height at which air temperature becomes too low for flight for a particular species (‘ceiling layers’). For example, the brown planthopper, Nilaparvata lugens, migrating in eastern China showed a density increase up to a well-defined ceiling that corresponded to an air temperature of approximately 16°C, which is known to be close to the minimum required for sustained flight by this planthopper (Riley et al. 1991). The limitation of flight altitude by air temperature is also indicated where the ceilings for particular species are observed to be distinctly higher during seasons, or at locations, with generally warmer air temperatures (Schaefer 1976; Riley & Reynolds 1979).
Temperature is a dominant aspect of the physical environment for insects, and the above discussion shows that there is a good prima facie case for air temperature being a major influence on the cruising altitudes chosen by migrants. However, several caveats must be entered here. Firstly, it is sometimes difficult to know whether the insects in a layer are responding primarily to temperature or to wind-related features because both occur at the same altitude (Drake 1985b). Secondly, there are examples where insect layers (usually composed of noctuid or pyralid moths, e.g. Helicoverpa zea, Helicoverpa armigera or Loxostege sticticalis) clearly do not correspond to temperature maxima, but instead seem to coincide with features of the wind field (Wolf et al. 1986; Westbrook et al. 1987; Beerwinkle et al. 1994; Riley et al. 1995; Feng et al. 2004, 2005). For example, Wolf et al. (1986) found that the migrants were flying preferentially in stable air (lower wind shear and higher thermal stability) near the centreline of a jet, rather than being associated with variables such as temperature, relative humidity and wind direction. In this case, the layer seemed to be located near the base of an (elevated) inversion, rather than in the warmest air. Occasionally, there have been reports that peaks in insect density occurred at the height of maximum wind shear, rather than the height of fastest wind speed (Schaefer 1976; Hobbs & Wolf 1989; Feng et al. 2005).
Another line of evidence that insects may be reacting to intrinsic features of the wind field comes from the ‘common orientation’ phenomenon, in which large, nocturnal, high-altitude migrants adopt a non-random heading distribution, centred about some clearly defined mean. Sometimes the mean appears to be related to wind direction, and in these cases it often tends to be downwind, or at some acute angle to the downwind direction (Drake 1983; Riley & Reynolds 1986; Riley 1989). The mechanisms involved are not clear, but there are indications that orientations are not maintained exclusively by the most obvious mechanism, i.e. visual assessment of the apparent movement of ground features. This has led to suggestions that the insects may be able to use non-visual cues to detect wind direction, such as anisotropic turbulence generated by zones of strong wind shear (Riley & Reynolds 1986; Riley 1989). Layers have, in fact, occasionally been detected in the presence of Kelvin–Helmholtz (K–H) waves (Schaefer 1976; Gossard & Chadwick 1979). K–H waves are formed by, and therefore indicative of, shear. In Schaefer's example, the insect layer formed just below the shear interface, at more or less the same altitude as the apparent K–H waves that had a wavelength of approximately 200 m. The grasshoppers and crickets forming the layer showed very uniform, downwind orientation. Although examples of this sort appear to be uncommon, they suggest that turbulence arising from much smaller K–H instabilities (which are common, but would not be detectable by radar) may provide cues that facilitate both orientation and height selection by insect migrants. The purpose of this paper is to investigate the possible relationship between the height of flight and wind shear-induced turbulence, under fair weather conditions at night.
2. Stochastic modelling of insect flight movements
2.1 The basis of the model
Our model of insect layering assumes that the insects (say, migrant noctuid moths) take off and climb to a height z0 before adopting horizontal cruising flight. It then simulates stochastically the insects' attitudinal motion caused by random vertical air movements induced by turbulence within the stable NBL, and it monitors their resulting drift down gradients in the intensity of turbulence towards layers of low turbulent kinetic energy. The concentration of buoyant inert particles by this ‘turbophoresis’ effect is a well-documented phenomenon that results in a preferential concentration of inertial particles where turbulent kinetic energy is low (Reeks 1983). A second stage of our simulation assumes that flying insects do not simply behave as neutrally buoyant passive particles, but instead respond to vertical buffeting by flying so as to maintain a zero vertical airspeed in gusts above a certain threshold. Finally, we examine the effect of vigorous flight that opposes or, alternatively, amplifies the effect of the vertical gusts. In the ‘amplifying’ case, for example, the migrants climb during upwards gusts and descend in downwards ones.
2.2 Description of the vertical components of turbulent flow
Attention is focused on the stable NBL. The stable stratification of the atmospheric boundary layer develops shortly before sunset, when the radiative cooling of the surface layers results in the development of a thermally stable layer (the stable boundary layer) close to the Earth's surface (Salmond & McKendry 2005). The structure of the NBL is determined by complex interactions between the static stability of the atmosphere and those processes (such as wind shear from the geostrophic, synoptic or terrain-induced flows, or from low-level jets) that govern the mechanical generation of turbulence. These processes can operate at a variety of different heights and scales within the boundary layer, and their dominance may vary in time and space. As a result, equilibrium conditions are rare, and at any given time and location, conditions may vary considerably with altitude. Thus, the NBL may range from fully turbulent to intermittently turbulent or even quiescent at a variety of heights, temporal scales and spatial locations (Salmond & McKendry 2005 and references therein).
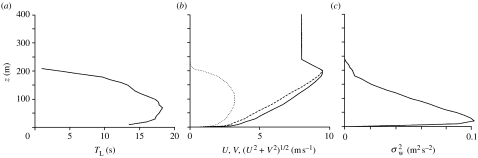
The Eulerian velocity statistics required for the numerical simulations are drawn from the results of a typical large-eddy simulation of a stable NBL (Weil et al. 2006; figure 1). This simulation represents only continuous (non-intermittent) turbulence, and pertains to a geostrophic wind speed of 8 m s−1, a surface cooling rate of 0.25 K h−1 and a surface friction velocity of approximately 0.28 m s−1. The stability index is zi/L=1.6, where zi=200 m is the stable boundary-layer height and L is the Monin–Obukhov length. The potential temperature gradient in the bulk of the layer is ∂Θ/∂z≈0.006 K m−1, but it is greater near the surface and near the top of the stable boundary layer, thus producing a triple-layer structure of the mean potential temperature Θ, which is a characteristic feature of stable boundary layers. The simulations reproduce several characteristic features of a stable NBL including a low-level jet and realistic turbulence profiles. The predicted mean wind profiles are similar to those produced in other large-eddy simulations of stable boundary layers (Brown et al. 1994; Kosovic & Curry 2000). The predicted mean variance profiles are consistent with the measurements of Nieuwstadt (1984) and with the results of other large-eddy simulations (Basu & Porté-Agel 2006). The Lagrangian decorrelation time scale TL for the vertical component of the turbulent air velocity pertaining to the motion of air parcels is here used as a surrogate for the decorrelation time scale T, pertaining to air parcels encountered by an insect along its flight path. This is strictly valid only when the insect is moving with the air but it is approximately correct when the insect is ‘crossing’ through the air parcel trajectories. This is because although the so-called ‘crossing trajectory effect’ (Csanady 1963) will cause the velocities of successive air parcels encountered by the insect to correlate faster than otherwise would be the case, we find that our model predictions are not sensitively dependent upon T.
Figure 1.
(a) The Lagrangian decorrelation time scale TL, for the vertical component of the turbulent air velocity. (b) The east–west U (dashed line) and north–south V (dotted line) components of the mean resolved velocity profile and the overall wind speed (U2+V2)1/2 (solid line) in the simulated stable boundary layer. The variation of U and V with height z leads to an Ekman spiral. (c) The resolved variance in vertical wind speeds.
2.3 The case of passive response to gusts
We assume here that the insects behave as neutrally buoyant, but forward-moving particles that are deflected upwards or downwards by vertical gusts, where the amplitude of deflection is determined by the strength and duration of the gusts, by the ventral/dorsal-aspect aerodynamic drag of the insects and by their mass. The effects of drag and mass may be accommodated in a single term τ, the aerodynamic response time that determines how quickly the insects will respond to changes in the vertical component of the airspeed. That is, after the initial climbing phase to an altitude z0, the vertical position z0+zi and vertical velocity wi of an insect evolve according to
| (2.1) |
where zi is the altitudinal perturbation of the insects' flight trajectory caused by vertical gusts in wind speed and w is the velocity of these vertical gusts. Vertical gusts along the trajectory of the insect are modelled stochastically by
| (2.2) |
where is the variance of the vertical wind speeds, and the quantity dξ are increments of a Wiener (white noise) process and have mean zero and variance equal to the time increment dt. The stochastic model (2.2) was constructed by invoking the well-mixed condition (Thomson 1989), which guarantees that simulated wind velocities along the insect trajectories are exactly consistent with fixed point (Eulerian Gaussian) wind velocity statistics that are used here as model inputs. Thomson's well-mixed condition is equivalent to, or more stringent than, all other criteria that have been established for distinguishing between well and poorly formulated models of particle dispersion (Thomson 1989).
Insects that passively respond to gusts will accumulate in layers where the turbulence is low simply as a result of the classical turbophoretic effect. The accumulation is maximal when the aerodynamic response time is comparable with the Lagrangian decorrelation time scale TL, i.e. when τ∼15 s (Maxey 1990; Reynolds 2004). This value is adopted here because it is sufficient to determine whether classical turbophoresis can account for the degree of layering observed in the field. The aerodynamic response per se is approximately 70 s under the assumption that the insects are spherical with diameter 0.01 m and mass 200 mg.
Predictions for the aerial densities of insects are calculated from the simulated trajectories of 5000 insects obtained by numerically integrating the models (2.1) and (2.2). Numerical integration will be accurate when incremental changes in T and σw occurring in any time step dt are small compared with the parameter values themselves. This was ensured by taking
| (2.3) |
2.4 The case of active responses to gusts
In this case, insects respond to any substantial turbulent gusts (with vertical speeds exceeding some threshold wc) by actively ascending in upwards gusts or descending in downwards ones, with vertical airspeed wf=0.3 m s−1, until the gust speed w falls back below the threshold wc, whereupon horizontal flight is resumed. In other words, the insects actively regulate their lift to maintain horizontal flight in the weaker gusts (w<wc) but, by contrast, actively contribute to the vertical displacement produced by the stronger gusts. Underlying this proposed response is the notion that the insects detect these speed excursions by sensing the vertical accelerations that produce them, perhaps indirectly via changes in wing loading, or by some organ intrinsically sensitive to acceleration (see Sane et al. 2007). With this type of response, after the initial climbing phase to altitude z0, the vertical position and vertical velocity of an insect evolve according to
| (2.4) |
Following Thomson (1989), vertical gusts along the trajectory of the insect are modelled stochastically by
| (2.5) |
where
| (2.6) |
Predictions for the resulting aerial densities of insects are calculated from the simulated trajectories of 5000 insects obtained by numerically integrating the models (2.4)–(2.6) using the time step (2.3).
3. Results from modelling
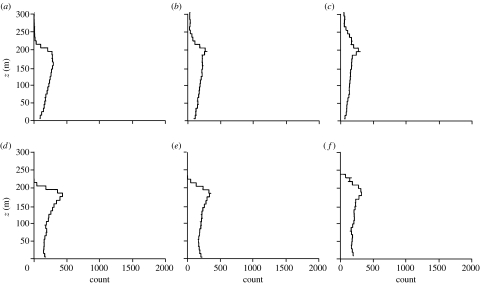
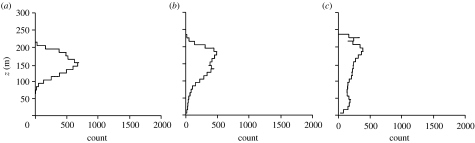
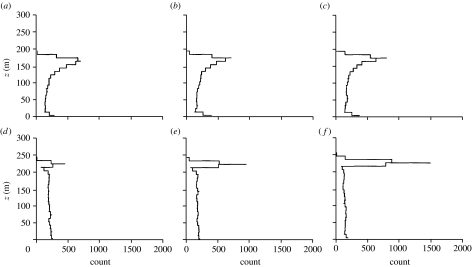
The cases studied are summarized in table 1. The passive response models (2.1) and (2.2) predict that insects tend to accumulate just below the top of the inversion where the air has low turbulence, a result that follows directly from the classical turbophoretic effect (figure 2a–c). However, the degree of layering predicted by this model is far weaker than that observed in the field. The same is true when it is assumed that insects respond to any substantial gusts (with vertical speeds exceeding wc) by regulating their aerodynamic lift to maintain zero vertical airspeed so that they are ‘passively’ advected either upwards or downwards by the gust until the gust speed w falls back below the threshold wc (figure 2d–f). Similarly, insects that attempt to compensate for vertical gust-induced movements by actively flying against the gusts rather than with them are not predicted to form tight layers (figure 3). For these last two cases, a degree of concentration centred approximately at z0 is observed after 2 hours but thereafter this gradually dissipates. Much tighter layering is predicted by the active amplifying response models (2.4)–(2.6). Insects with a turbophoretic response (wc=0.3 m s−1) are predicted to accumulate just below the top of the inversion (figure 4a–c). More responsive insects (wc=0.1 m s−1) will accumulate in a tight layer at the top of the inversion layer close to where turbulence is a minimum and close to where the horizontal wind speed is the fastest (figures 4d–f and 5). In accordance with some radar observations (Drake 1984; Riley et al. 1995), the model predicts that as time progresses, layering becomes progressively tighter and eventually a ‘discontinuity’ arises at the lower edge of the layer where insect counts increase by a factor of approximately 10 over 100 m (figure 4d–f). We found that the predicted density of layers may depend on the airspeed wf at which insects are assumed in our model to ascend in upwards gusts and to descend in downwards gusts. For insects with a low response threshold (wc=0.1 m s−1), layer density does, for instance, increase/decrease by approximately 50% when wf is increased or decreased from 0.3 m s−1 to 0.5 m s−1 or 0.1 ms−1. However, when the threshold is wc=0.3 m s−1, layer density is largely insensitive to such variations in vertical airspeed.
Table 1.
Summary of the cases studied (see text). (Gusts encountered by the insects remain significantly correlated for a time TL. Insects respond to gusts with vertical wind speed exceeding wc by flying with a vertical airspeed wf.)
Figure 2.
(a–c) Predicted profiles of insect numbers within 10 m height intervals in a stably stratified nocturnal boundary layer, (a) 2 hours, (b) 4 hours and (c) 8 hours after climbing to z0=150 m, and thereafter behaving as neutrally buoyant massive particles with response time τ=15 s. (d–f) The results of a simulation where the insects are assumed to actively respond to any substantial gusts (with vertical speeds exceeding wc=0.1 m s−1) by regulating their aerodynamic lift to maintain zero vertical airspeed so that they are ‘passively’ advected either upwards or downwards by the gust until the gust speed w falls back below the threshold wc: (d) 2 hours, (e) 4 hours and (f) 8 hours.
Figure 3.
Predicted profiles of insect numbers within 10 m height intervals in a stably stratified nocturnal boundary layer, (a) 2 hours, (b) 4 hours and (c) 8 hours after climbing to 150 m and thereafter responding to gusts in vertical wind speed by climbing or descending in a direction opposite to the gust with a vertical airspeed of wf=0.3 m s−1 when the vertical wind speed exceeds wc=0.1 m s−1. The stable boundary layer has height z=200 m.
Figure 4.
Predicted profiles of insect numbers within 10 m height intervals in a stably stratified nocturnal boundary layer, (a,d) 2 hours, (b,e) 4 hours and (c,f) 8 hours after climbing to 150 m and thereafter responding to gusts in vertical wind speed by climbing or descending in the direction of the gust with a vertical airspeed of wf=0.3 m s−1. In (d–f) this response arises when the vertical wind speed exceeds wc=0.1 m s−1, while in (a–c) the response threshold is wc=0.3 m s−1. Insects are predicted to preferentially concentrate at the top of the inversion layer where the air is fastest. The stable boundary layer has height z=200 m.
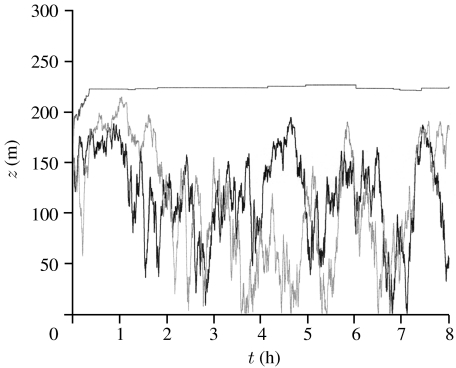
Figure 5.
Three examples of simulated insect altitudinal flight trajectories that, after an initial ascent to 150 m, thereafter responded to gusts in vertical wind speed by climbing or descending in the direction of the gust with a vertical airspeed of wf=0.3 m s−1 when the vertical wind speed exceeds wc=0.1 m s−1. It is evident that insects arriving at the top of the inversion layer can remain there for several hours. The stable boundary layer has height z=200 m.
In our simulations there is an absence of insects at higher altitudes, but radar observations show (e.g. Drake 1984) that some insects, which are adapted to cooler temperatures, will ascend to these altitudes. This is not an intrinsic shortcoming of the model and can be overcome by seeding the model with a few insects at altitudes higher than z0. Once insects have been carried into this quiescent flow, they will accumulate there (because there are few gusts to initiate turbophoretic responses) until the onset of the descent phase of their migratory flight.
4. Discussion
We have shown that an active ‘turbophoretic response’ to vertical gusts in the wind could cause insects flying within the stable NBL to concentrate into a layer near the top of the inversion level, a phenomenon that has often been observed in the field (see references in §1). The response required of the insects in our model is that they should actively climb/descend with a vertical airspeed of approximately 0.3 m s−1 in the direction of the vertical wind gusts they encounter until the gust speed falls back below some threshold, whereupon horizontal flight is resumed. Although only a single layer is predicted by our model, a ubiquitous feature of strongly stratified flows observed in both laboratory-scale experiments and numerical simulations is that the flows are predominately horizontal but develop strong vertical variability and on cooling reorganize themselves into decoupled layers of homogeneous turbulence (often called ‘pancake’ turbulence but also ‘blini’ and even ‘lasagne’ turbulence). These patches of turbulence are commonly observed in the stratosphere (Alisse & Sidi 2000) and given their ubiquity, can be expected to be present in the planetary boundary layer. Our proposed turbophoretic response, taken together with the presence of pancake turbulence could therefore account for the occurrence of multiple insect layers, sometimes separated by only 50–100 m, that have been observed in several radar studies (Schaefer 1976; Reynolds & Riley 1997; Feng et al. 2004, 2005). The dissipation of insect layers observed in airborne radar studies when the observation aircraft encountered mild (intermittent) turbulence (Wolf et al. 1990) would also be predicted by our model. The layers produced by our suggested active turbophoretic response occur at altitudes where the mean horizontal wind speed and/or mean temperature have their maxima (e.g. at the centre of the faster airstreams rather than at their edges); precisely the conditions that would optimize rapid long-distance migration. Cruising at these heights would also minimize flight perturbation by turbulent gusts and thereby presumably reduce the energetic costs of flight control. Given these advantages, it would not be surprising if natural selection had favoured the adoption by migrant insects of an active turbophoretic response that is at least similar to the one we propose here.
In addition to the clear benefits discussed above, it is conceivable that flying at heights where the mean wind speed and/or temperature are locally maximal may also enable insects to use directional cues provided by gravity waves in the atmosphere (Nappo 2002) in order to select and maintain their orientation (see §1.1). There is, in fact, some evidence that the presence of insect layering is associated with higher degrees of common orientation (Hobbs & Wolf 1989; Drake & Rochester 1994; A. S. Edwards 2006, unpublished report). An optomotor response to the relative movement of the ground favours the detection of the absolute flow direction but cannot account for the frequent offsetting of the orientation direction with respect to the mean wind direction (Riley & Reynolds 1986; Riley 1989). These and other candidate orientation mechanisms including, for example, the possibility that some high-flying insects have an adaptive ‘preferred inherited compass direction’ (Chapman et al. 2008) warrant further investigation.
Acknowledgments
We thank David Thomson for fruitful communications regarding the structure of stable NBL and for the suggestion that breaking gravity waves will produce turbulence that cascades to small scales and so be detectable by insects. We thank Alistair Drake for constructive comments pertaining to the temporal development of insect layers and for his careful reading of an earlier version of the manuscript. Rothamsted Research receives grant aided support from the Biotechnology and Biological Sciences Research Council.
References
- Alisse J.-R, Sidi C. Experimental probability density functions of small-scale fluctuations in the stably stratified atmosphere. J. Fluid Mech. 2000;402:137–162. doi: 10.1017/S0022112099006813. [DOI] [Google Scholar]
- Basu S, Porté-Agel F. Large-eddy simulation of stably stratified atmospheric boundary layer turbulence: a scale-dependent dynamic modeling approach. J. Atmos. Sci. 2006;63:2074–2091. doi: 10.1175/JAS3734.1. [DOI] [Google Scholar]
- Beerwinkle K.R, Lopez J.D, Witz J.A, Schleider P.G, Eyster R.S, Lingren P.D. Seasonal radar and meteorological observations associated with nocturnal insect flight at altitudes to 900 metres. Environ. Entomol. 1994;23:676–683. [Google Scholar]
- Brown A.R, Derbyshire S.H, Mason P.J. Large-eddy simulation of stable atmospheric boundary layers with a revised stochastic subgrid model. Q. J. R. Meteorol. Soc. 1994;120:1485–1512. doi: 10.1002/qj.49712052004. [DOI] [Google Scholar]
- Burt P.J.A, Pedgley D.E. Nocturnal insect migration: effects of local winds. Adv. Ecol. Res. 1997;27:61–92. [Google Scholar]
- Campistron B. Characteristic distributions of angel echoes in the lower atmosphere and their meteorological implications. Bound.-Layer Meteorol. 1975;9:411–426. doi: 10.1007/BF00223391. [DOI] [Google Scholar]
- Chapman J.W, Smith A.D, Woiwod I.P, Reynolds D.R, Riley J.R. Development of vertical-looking radar technology for monitoring insect migration. Comput. Electron. Agric. 2002;35:95–110. doi: 10.1016/S0168-1699(02)00013-3. [DOI] [Google Scholar]
- Chapman J.W, Reynolds D.R, Mouritsen H, Hill J.K, Riley J.R, Sivell D, Smith A.D, Woiwod I.P. Wind selection and drift compensation optimise migratory pathways in a high-flying moth. Curr. Biol. 2008;18:514–518. doi: 10.1016/j.cub.2008.02.080. [DOI] [PubMed] [Google Scholar]
- Csanady G.T. Turbulent diffusion of heavy particles in the atmosphere. J. Atmos. Sci. 1963;20:201–208. doi: 10.1175/1520-0469(1963)020%3C0201:TDOHPI%3E2.0.CO;2. [DOI] [Google Scholar]
- Drake V.A. Collective orientation by nocturnally migrating Australian plague locusts, Chortoicetes terminifera (Walker) (Orthoptera Acrididae): a radar study. Bull. Entomol. Res. 1983;73:679–692. [Google Scholar]
- Drake V.A. The vertical distribution of macro-insects migrating in the nocturnal boundary layer: a radar study. Bound.-Layer Meteorol. 1984;28:353–374. doi: 10.1007/BF00121314. [DOI] [Google Scholar]
- Drake V.A. Solitary wave disturbances of the nocturnal boundary layer revealed by radar observations of migrating insects. Bound.-Layer Meteorol. 1985a;31:269–286. doi: 10.1007/BF00120896. [DOI] [Google Scholar]
- Drake V.A. Radar observations of moths migrating in a nocturnal low-level jet. Ecol. Entomol. 1985b;10:259–265. doi: 10.1111/j.1365-2311.1985.tb00722.x. [DOI] [Google Scholar]
- Drake V.A, Farrow R.A. The influence of atmospheric structure and motions on insect migration. Annu. Rev. Entomol. 1988;33:183–210. doi: 10.1146/annurev.en.33.010188.001151. [DOI] [Google Scholar]
- Drake, V. A. & Rochester, W. A. 1994 The formation of layer concentrations by migrating insects. In Proc. 21st Conference on Agricultural and Forest Meteorology–11th Conference on Biometeorology, San Diego, California, 7–11 March 1994, pp. 411–414. Boston, MA: American Meteorological Society.
- Dudley R. The biomechanics and functional diversity of flight. In: Woiwod I.P, Reynolds D.R, Thomas C.D, editors. Insect movement: mechanisms and consequences. CAB International; Wallingford, UK: 2001. pp. 1–18. [Google Scholar]
- Farrow R.A. Flight and migration in acridoids. In: Chapman R.F, Joern A, editors. Biology of grasshoppers. Wiley; New York, NY: 1990. pp. 227–314. [Google Scholar]
- Feng H.-Q, Wu K.-M, Cheng D.-F, Guo Y.-Y. Spring migration and summer dispersal of Loxostege sticticalis (Lepidoptera: Pyralidae) and other insects observed with radar in northern China. Environ. Entomol. 2004;33:1253–1265. [Google Scholar]
- Feng H.-Q, Wu K.-M, Ni Y.-X, Cheng D.-F, Guo Y.-Y. High-altitude windborne transport of Helicoverpa armigera (Lepidoptera: Noctuidae) in mid-summer in northern China. J. Insect Behav. 2005;18:335–349. doi: 10.1007/s10905-005-3694-2. [DOI] [Google Scholar]
- Gatehouse A.G. Behavior and ecological genetics of wind-borne migration by insects. Ann. Rev. Entomol. 1997;42:475–502. doi: 10.1146/annurev.ento.42.1.475. [DOI] [PubMed] [Google Scholar]
- Gossard, E. E. & Chadwick, R. B. 1979 Studies of insects by high resolution radar. In Proc. 14th Conference on Agriculture and Forest Meteorology and 4th Conference on Biometeorology, Minneapolis, Minnesota, 2–6 April 1979, pp. 268–271. Boston, MA: American Meteorological Society.
- Greenbank D.O, Schaefer G.W, Rainey R.C. Spruce budworm (Lepidoptera: Tortricidae) moth flight and dispersal: new understanding from canopy observations, radar, and aircraft. Mem. Entomol. Soc. Can. 1980;110:1–49. [Google Scholar]
- Hobbs S.E, Wolf W.W. An airborne radar technique for studying insect migration. Bull. Entomol. Res. 1989;79:693–704. [Google Scholar]
- Kosovic B, Curry J.A. A large eddy simulation of quasi-steady, stably stratified atmospheric boundary layer. J. Atmos. Sci. 2000;57:1297–1304. [Google Scholar]
- Maxey M.R. On the advection of spherical and non-spherical particles in a non-uniform flow. Phil. Trans. R. Soc. A. 1990;333:289–307. doi: 10.1098/rsta.1990.0162. [DOI] [Google Scholar]
- Nappo C.J. Elsevier; Amsterdam, The Netherlands: 2002. An introduction to atmospheric gravity waves. [Google Scholar]
- Nieuwstadt F.T.M. The turbulent structure of the stable, boundary layer. J. Atmos. Sci. 1984;41:2202–2216. doi: 10.1175/1520-0469(1984)041%3C2202:TTSOTS%3E2.0.CO;2. [DOI] [Google Scholar]
- Reeks M.W. The transport of discrete particles in inhomogeneous turbulence. J. Aerosol. Sci. 1983;14:729–739. doi: 10.1016/0021-8502(83)90055-1. [DOI] [Google Scholar]
- Reynolds A.M. Stokes number effects in Lagrangian stochastic models of dispersed two-phase flows. J. Colloid Interface Sci. 2004;275:328–335. doi: 10.1016/j.jcis.2004.02.039. [DOI] [PubMed] [Google Scholar]
- Reynolds D.R, Riley J.R. A migration of grasshoppers, particularly Diabolocatantops axillaris (Thunberg) (Orthoptera: Acrididae), in the West African Sahel. Bull. Entomol. Res. 1988;78:251–271. [Google Scholar]
- Reynolds, D. R. & Riley, J. R. 1997 The flight behaviour and migration of insect pests: radar studies in developing countries, NRI Bulletin no. 71. Chatham, UK: Natural Resources Institute.
- Reynolds D.R, Chapman J.W, Edwards A.S, Smith A.D, Wood C.R, Barlow J.F, Woiwod I.P. Radar studies of the vertical distribution of insects migrating over southern Britain: the influence of temperature inversions on nocturnal layer concentrations. Bull. Entomol. Res. 2005;95:259–274. doi: 10.1079/BER2004358. [DOI] [PubMed] [Google Scholar]
- Reynolds D.R, Smith A.D, Chapman J.W. A radar study of emigratory flight and layer formation by insects at dawn over southern Britain. Bull. Entomol. Res. 2008;98:35–52. doi: 10.1017/S0007485307005470. [DOI] [PubMed] [Google Scholar]
- Richter J.H, Jensen D.R, Noonkester V.R, Kreasky J.B, Stimmann M.W, Wolf W.W. Remote radar sensing: atmospheric structure and insects. Science. 1973;180:1176–1178. doi: 10.1126/science.180.4091.1176. [DOI] [PubMed] [Google Scholar]
- Riley, J. R. 1989 Orientation by high-flying insects at night: observations and theories. In Orientation and navigation—birds, humans and other animals. Papers presented at the Conference of the Royal Institute of Navigation, Cardiff, 6–8 April 1989. London, UK: The Royal Institute of Navigation.
- Riley J.R, Reynolds D.R. Radar-based studies of the migratory flight of grasshoppers in the middle Niger area of Mali. Proc. R. Soc. B. 1979;204:67–82. doi: 10.1098/rspb.1979.0013. [DOI] [PubMed] [Google Scholar]
- Riley J.R, Reynolds D.R. Orientation at night by high-flying insects. In: Danthanarayana W, editor. Insect flight: dispersal and migration. Springer; Berlin, Germany: 1986. pp. 71–87. [Google Scholar]
- Riley J.R, Cheng X.N, Zhang X.X, Reynolds D.R, Xu G.M, Smith A.D, Cheng J.Y, Bao A.D, Zhai B.P. The long distance migration of Nilaparvata lugens (Stål) (Delphacidae) in China: radar observations of mass return flight in the autumn. Ecol. Entomol. 1991;16:471–489. doi: 10.1111/j.1365-2311.1991.tb00240.x. [DOI] [Google Scholar]
- Riley J.R, Reynolds D.R, Smith A.D, Edwards A.S, Zhang X.-X, Cheng X.-N, Wang H.-K, Cheng J.-Y, Zhai B.-P. Observations of the autumn migration of the rice leaf roller Cnaphalocrocis medinalis (Lepidoptera: Pyralidae) and other moths in eastern China. Bull. Entomol. Res. 1995;85:397–414. [Google Scholar]
- Salmond J.A, McKendry I.G. A review of turbulence in the very stable nocturnal boundary layer and its implications for air quality. Prog. Phys. Geogr. 2005;29:171–188. doi: 10.1191/0309133305pp442ra. [DOI] [Google Scholar]
- Sane S.P, Dieudonne A, Willis M.A, Daniel T.L. Antennal mechanosensors mediate flight control in moths. Science. 2007;315:863–866. doi: 10.1126/science.1133598. [DOI] [PubMed] [Google Scholar]
- Schaefer G.W. Radar observations of insect flight. In: Rainey R.C, editor. Insect flight. Blackwell; Oxford, UK: 1976. pp. 157–197. [Google Scholar]
- Thomson D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1989;180:529–556. doi: 10.1017/S0022112087001940. [DOI] [Google Scholar]
- Vaughn C.R. Birds and insects as radar targets: a review. Proc. Inst. Electr. Electron. Eng. 1985;73:205–227. [Google Scholar]
- Weil, J. C., Patton, E. G. & Sullivan, P. P. 2006 Lagrangian modeling of dispersion in the stable boundary layer. In Proc. 17th Symposium on Boundary Layers and Turbulence, San Diego, 21–25 May 2006 (paper J3.4). Boston, MA: American Meteorological Society.
- Westbrook, J. K., Wolf, W. W., Pair, S. D., Sparks, A. N. & Raulston, J. R. 1987 Empirical moth flight behavior in the nocturnal planetary boundary layer. In Proc. 18th Conference on Agricultural and Forest Meteorology–8th Conference on Biometeorology and Aerobiology, W. Layfayette, Indiana, 15–18 September 1987, pp. 263–264. Boston, MA: American Meteorological Society.
- Wolf W.W, Westbrook J.K, Sparks A.N. Relationships between radar entomological measurements and atmospheric structure in south Texas during March and April 1982. In: Sparks A.N, editor. Long-range migration of moths of agronomic importance to the United States and Canada: specific examples of the occurrence and synoptic weather patterns conducive to migration. US Department of Agriculture, Agricultural Research Service ARS-43; Washington, DC: 1986. pp. 84–97. [Google Scholar]
- Wolf W.W, Westbrook J.K, Raulston J, Pair S.D, Hobbs S.E. Recent airborne radar observations of migrant pests in the United States. Phil. Trans. R. Soc. B. 1990;328:619–630. doi: 10.1098/rstb.1990.0132. [DOI] [Google Scholar]
- Wood C.R, Chapman J.W, Reynolds D.R, Barlow J.F, Smith A.D, Woiwod I.P. The influence of the atmospheric boundary layer on nocturnal layers of moths migrating over southern Britain. Int. J. Biometeorol. 2006;50:193–204. doi: 10.1007/s00484-005-0014-7. [DOI] [PubMed] [Google Scholar]