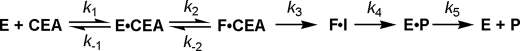Dissection of the Stepwise Mechanism to β-Lactam Formation and Elucidation of a Rate-determining Conformational Change in β-Lactam Synthetase^,

Abstract

Clavulanic acid is a widely used β-lactamase inhibitor whose key β-lactam core is formed by β-lactam synthetase. β-Lactam synthetase exhibits a Bi-Ter mechanism consisting of two chemical steps, acyl-adenylation followed by β-lactam formation. ³²PP_i-ATP exchange assays showed the first irreversible step of catalysis is acyl-adenylation. From a small, normal solvent isotope effect (1.38 ± 0.04), it was concluded that β-lactam synthesis contributes at least partially to k_cat. Site-specific mutation of Lys-443 identified this residue as the ionizable group at pK_a ∼ 8.1 apparent in the pH-k_cat profile that stabilizes the β-lactam-forming step. Viscosity studies demonstrated that a protein conformational change was also partially rate-limiting on k_cat attenuating the observed solvent isotope effect on β-lactam formation. Adherence to Kramers' theory gave a slope of 1.66 ± 0.08 from a plot of log(^ok_cat/k_cat) versus log(η/η^o) consistent with opening of a structured loop visible in x-ray data preceding product release. Internal “friction” within the enzyme contributes to a slope of >1 in this analysis. Correspondingly, earlier in the catalytic cycle ordering of a mobile active site loop upon substrate binding was manifested by an inverse solvent isotope effect (0.67 ± 0.15) on k_cat/K_m. The increased second-order rate constant in heavy water was expected from ordering of this loop over the active site imposing torsional strain. Finally, an Eyring plot displayed a large enthalpic change accompanying loop movement (ΔH^‡ ∼ 20 kcal/mol) comparable to the chemical barrier of β-lactam formation.

Resistance to antibiotics is a consequence of their wide-spread use in the treatment of disease and can arise with dispiriting rapidity after the introduction of a new drug. β-Lactam antibiotics constitute 55% of all antibiotics sold despite their prominent use for more than 50 years (1). Their longevity is because of semi-synthetic structural modifications, the discovery of new members of the family from natural sources, and the growing importance of inhibitors of the principal means of resistance, the β-lactamases (2). Clavulanic acid is a potent serine β-lactamase inhibitor isolated from Streptomyces clavuligerus (3) whose combination with broad spectrum β-lactam antibiotics has proven to be highly effective against resistant infections in humans (4, 5). Inhibitor-resistant β-lactamases are emerging (1), however, and the need for new entities clinically useful against them is growing.

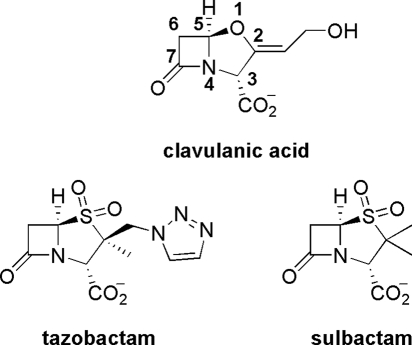
Clavulanic acid is one of only three β-lactamase inhibitors in clinical use (Scheme 1) (6). Although other clavams produced in nature may possess antibacterial and antifungal properties, clavulanic acid is the only known clavam with potent β-lactamase inhibitory activity owing in part to its 3R,5R stereochemistry (7). It is therefore important to understand the steps involved in this pathway to enable the production of derivatives. Substitution at C-6 of clavulanic acid derivatives, for example, led to broader spectrum inhibition toward β-lactamases (8) and encourages efforts at engineering clavulanic acid biosynthesis.

SCHEME 1.

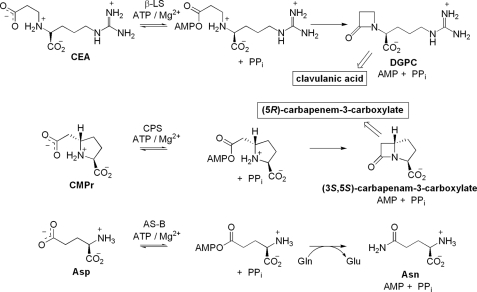
The β-lactam core of clavulanic acid is formed by β-lactam synthetase (β-LS)2 in an early step in clavulanic acid biosynthesis. β-LS converts N²-(2-carboxyethyl)-l-arginine (CEA) to deoxy-guanidinoproclavaminic acid (DGPC) through acyl-adenylate activation followed by intramolecular β-lactam ring closure (9). Formation of the four-membered ring in clavulanic acid is distinct from its well characterized formation in penicillin and cephalosporin. In this respect the biosynthesis of clavulanic acid more closely resembles that of carbapenem biosynthesis (7). This important mechanistic commonality revealed that a second major bacterial pathway to β-lactam-containing compounds existed, separate from the oxidative path to penicillin and cephalosporin derivatives (10).

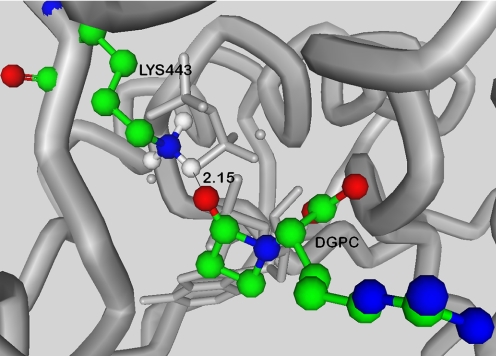
β-LS possesses sequence homology to Escherichia coli asparagine synthetase, class B (AS-B; 33% identity, 49% similarity), and to the large, highly conserved family of other AS-B enzymes. It also has more modest sequence similarity to the β-lactam-forming enzyme carbapenam synthetase (CPS; 26% identity, 46% similarity) in carbapenem biosynthesis (9, 11). β-LS, and its homologs AS-B, and CPS catalyze the production of three chemically distinct compounds, DGPC, asparagine, and (3S,5S)-carbapenam-3-carboxylic acid, respectively, in an ATP/Mg²⁺-dependent fashion (Scheme 2) (12–14). Steady-state kinetic analyses have shown that both β-lactam-forming enzymes, β-LS and CPS, proceed by an ordered Bi-Ter mechanism with ATP the first substrate to bind and PP_i the last product to dissociate (13, 14). X-ray structural studies of β-LS highlighted the importance of enzyme and substrate pre-organization, in particular a conserved mobile loop that is present in the active sites of both β-LS and CPS (15). These pictures of β-LS also revealed a lysine residue, Lys-443, in close proximity to the β-lactam carbonyl of DGPC, which suggested its possible role in chemistry (Fig. 1). This residue is also conserved in CPS, and its mutation to alanine or methionine in this homolog resulted in complete loss of activity (16).

SCHEME 2.

FIGURE 1.

From the crystal structure of β-LS (Protein Data Bank code 1JGT), the position of Lys-443 relative to DGPC can be seen. With hydrogen atoms included, a distance between this residue and the β-lactam carbonyl oxygen of DGPC of 2.15 Å is estimated. Elements are colored as follows: green = carbon, blue = nitrogen, red = oxygen, and white = hydrogen.

In this study, wild-type β-LS was subjected to pH, pD, temperature, and viscosity variation along with radiochemical experiments to probe the kinetics and thermodynamics of substrate capture through the catalytic cycle to product release. Moreover, the first mutagenesis of β-LS is presented, and the kinetic effects of this active site change are reported. Building on the order of substrate binding established previously (13), the experiments presented here elucidate the rate-determining steps on β-LS catalysis, identify a crucial active-site residue in β-lactam formation, and uncover important conformational changes that critically influence the kinetics of β-LS catalysis.

EXPERIMENTAL PROCEDURES

Materials—All buffers, coupled enzymes, and most assay components were purchased from Sigma. NADH, NADP⁺, and UDP-glucose were obtained from Roche Applied Sciences. Nickel-nitrilotriacetic acid-agarose resin was obtained from Qiagen, Inc. (Valencia, CA). D₂O (99.9%) was purchased from Cambridge Isotope Laboratories (Andover, MA). E. coli Rosetta2(DE3) cells were purchased from EMD Biosciences, Inc. (Madison, WI). Na ³²₄P₂O₇ was purchased from PerkinElmer Life Sciences. DGPC was synthesized as described previously (17).

N²-(2-Carboxyethyl)-arginine—To a solution of K₂CO₃ (10.5 g, 0.076 mol) and l-arginine-HCl (16.01 g, 0.076 mol) in distilled H₂O (250 ml), tert-butyl acrylate (9.74 g, 11 ml, 0.076 mol) was added, and the solution was stirred at room temperature for 5 days. The solution was lyophilized to dryness. To crude (S)-2-(3-tert-butoxy-3-oxopropylamino)-5-guanidinopentanoate potassium salt (2.16 g, 6.33 mol), trifluoroacetic acid (20 ml) was added, and the solution was stirred for 90 min under argon (g). The solution was evaporated under reduced pressure at 35 °C to give an oil. The crude CEA was purified as described previously (13).

Construction and Overproduction of cHis₆ β-LS and K443R—The overlap extension method was used to introduce the desired β-LS mutation (18) using codon-optimized pET29b/bls as the template DNA in PCR amplifications with PCR primers incorporating the appropriate mutation. Optimization of the first 21 codons of the gene was achieved using an ApaI cut site within the β-LS sequence. Two primers that were codon-optimized for use in E. coli containing two DNA sequences were annealed to form a DNA linker with NdeI and ApaI overhangs. Ligation of the linker with the appropriately cut pET29b/bls construct created the optimized sequence. The desired gene was cloned into pET29b and transformed into E. coli Rosetta2(DE3) cells for subsequent overproduction and purification. Sequence verification of the entire gene was performed by the DNA Sequencing Facility, Johns Hopkins University, Baltimore. The codon optimization primers are as follows: forward, 5′-TATGGGTGCTCCGGTTCTGCCGGCTGCTTTCGGTTTCCTGGCTTCTGCTCGTACGTGGTGGCCGGGCC-3′, and reverse, 5′-CGGCCACCACCGGTACGAGCAGAAGCCAGGAAACCGAAAGCAGCCGGCAGACCGGAGCACCCA-3′.

β-LS Preparation—E. coli electrocompetent Rosetta2(DE3) cells were transformed with pET29b/bls. Cells were grown at 37 °C in 2× YT medium to an A₆₀₀ of 0.7–0.8, cooled to ambient temperature, and induced with 1 mm isopropyl β-d-thiogalactopyranoside for 18–20 h at 18 °C. Cells were harvested by centrifugation, and the pellet was flash-frozen with liquid nitrogen. All purification steps were carried out at 0–4 °C. 20–30 g of cells was collected in one 3-liter growth for wild-type β-LS. Cells were resuspended in 4 ml of lysis buffer/g of cells (50 mm NaH₂PO₄, 300 mm NaCl, 10 mm imidazole, pH 8), and then 1 mg/ml lysozyme was added, and the cell solution was incubated for 30 min with gentle mixing. The cells were disrupted by sonication, followed by centrifugation (28,000 × g). The supernatant was equilibrated with nickel-nitrilotriacetic acid resin for 1 h with gentle mixing, and the whole solution was loaded onto a column, washed with 20 and 40 mm imidazole wash buffers (50 mm NaH₂PO₄, 300 mm NaCl, pH 8), and finally eluted with 250 mm imidazole buffer. The 250 mm imidazole fractions were dialyzed 2.5 h against 3 liters of dialysis buffer (50 mm Tris-HCl, 1 mm DTT, 50 mm NaCl, pH 8) and loaded onto a pre-equilibrated Q-Sepharose FF column (4.9 cm² × 15 cm). The column was then washed with an equal volume of buffer (50 mm Tris-HCl, 1 mm DTT, 50 mm NaCl, pH 8) and eluted with a 500-ml linear gradient of 50–650 mm NaCl. β-LS eluted at ∼200 mm NaCl. Fractions containing β-LS were pooled and concentrated by ultrafiltration under 30–40 p.s.i. N₂ (g) using an Amicon cell (model 8050) over a YM10 membrane. The concentrated solution was dialyzed against storage buffer (100 mm HEPES, pH 8, 100 mm KCl, 12 mm MgCl₂, 1 mm DTT, or 50 mm Tris-HCl, pH 8, 5% glycerol) overnight with two buffer changes. The volume of the solution was further reduced, and its concentration was determined spectroscopically using the calculated ε₂₈₀ = 48.2 mm^–1 cm^–1 for wild-type β-LS and 41.0 mm^–1 cm^–1 for K443R (19). The concentrated enzyme was flash-frozen dropwise in liquid nitrogen and stored at –80 °C. β-LS and K443R relative purity determined by 12% SDS-PAGE analysis was >95%.

³²PP_i-ATP Exchange Assay—Reaction mixtures of 100 μlat the desired pH contained 12 mm MgCl₂, 1 mm DTT, 4 mm ATP, 1 mm CEA, and 0.10 mm pyrophosphate with 0.5 μCi of ³²PP_i and were initiated with β-LS (0.18 μm) or K443R (0.8 μm). Control assays were run in parallel and contained all components listed above except CEA. These controls were used to calculate the background for each assay. All solutions were incubated for ∼2 h at room temperature and quenched by the addition of 3% (w/v) perchloric acid followed by 100 mm pyrophosphate and 1% (w/v) activated charcoal. The mixture was vortexed and centrifuged for 5 min (28,000 × g). The supernatant was discarded while the pellet was resuspended in 500 μl of 3.5% (w/v) perchloric acid in 100 mm pyrophosphate and centrifuged for 5 min (28,000 × g). This process was repeated twice more with the final remaining pellet resuspended in 500 μl of double distilled H₂O to which 5 ml of scintillation fluid (OptiFluor) was added. The counts per min of ³²P incorporated into ATP were determined with a Beckman LS-5801 scintillation counter. Each reaction was performed in duplicate.

HPLC Product Analysis—DGPC formation from K443R was confirmed using an established HPLC protocol (13). K443R was incubated at room temperature overnight with 1 mm ATP, 1 mm DTT, 12.5 mm MgCl₂ at pH 8.8 (μ = 0.1) in a total reaction volume of 300 μl. Control assays were run in parallel, one containing a reaction mixture without enzyme and another with wild-type β-LS to serve as a positive control. Reactions were quenched by centrifugation (28,000 × g) for 10 min, and the supernatants were subsequently filtered through 0.22-μm membranes. A Luna (5 μm) ODS column was employed at a flow rate of 1 ml/min and a mobile phase of 50 mm sodium phosphate, pH 6.6, to elute DGPC at ∼16 min. This product peak was then verified by co-injection of authentic DGPC standard.

β-LS Assays—ATP hydrolysis products were quantified using AMP and PP_i detection in coupled enzyme assays (see below). Both coupled assays gave identical kinetic parameters to each other for β-LS and K443R and circular dichroism ensured no significant changes to the structural integrity of the mutant relative to wild type (data not shown). The temperature was held constant at 25.0 ± 0.1 °C, unless otherwise indicated, using a water-circulating system. Reactions (500 μl) were initiated by addition of enzyme with ATP held constant at saturating levels (2 mm) with varied concentrations of the second substrate, CEA. The reactions were performed in a 3-buffer system (40 mm MES, 40 mm HEPES, and 20 mm TAPS) or 100 mm 2-amino-2-methyl-1-propanol hydrochloride buffer (AMP-HCl) for high pH values unless otherwise noted, with ionic strength held constant at 0.1 with KCl addition (20). K443R utilized a similar buffer system to that of the 3-buffer system described for wild-type to reach higher pH values (35 mm HEPES, 35 mm TAPS, 35 mm AMP-HCl, μ = 0.1). Overlapping points of the two buffers with K443R ensured appropriateness of the buffer system.

The initial velocity of AMP production was measured as described previously for β-LS (13). PP_i production was monitored using a modified coupled enzyme assay originally determined by Townsend and co-workers (14) and Van Pelt and Northrop (21). The enzyme reaction was followed at 340 nm (ε = 6.22 mm^–1 cm^–1) by the rate of NADPH production. The concentrations of coupled enzymes used were 4–8 units/ml glucose-6-phosphate dehydrogenase, 5–10 units/ml phosphoglucomutase, and 4 units/ml UDP-glucose pyrophosphorylase. Assay mixtures contained 200 μm UDP-glucose, 200 μm NADP⁺, 0.4 μm glucose 1,6-diphosphate, 1 mm DTT, 12.5 mm MgCl₂, and 2 mm ATP. Initial velocity patterns were fitted to Equation 1.

pH Dependence—Initial velocities were measured using the PP_i assay. The 3-buffer system was used for pH 6.8–9.3, and 100 mm AMP buffer was used from pH 9.3 to 10.0. The pH dependence was measured by varying CEA from 5 μm to 1.2 mm. All assays were conducted in duplicate or triplicate at all pH values (6.8, 7.3, 7.8, 8.3, 8.8, 9.0, 9.3, 9.5, 9.8, and 10.0). Based on R² values, the k_cat and k_cat/K_m parameters were best fit to Equations 2 and 3, respectively, and the pK_a values were determined. Profiles were plotted as the log k_cat or log (k_cat/K_m) as a weighted function of pH. The error bars shown were propagated from the uncertainty on each rate to a natural logarithmic function (22).

Solvent Isotope Effects—Initial velocities were measured using the PP_i assay with CEA varied from 4 to 800 μm. Assay components were exchanged in D₂O and evaporated to dryness two times, and then redissolved in the appropriate amount of D₂O and stored under N₂ in an airtight flask. Although controls showed that the 3-buffer system did not require prior exchange in D₂O, the AMP buffer underwent two D₂O exchanges prior to adjusting to each pD. The substrates were dissolved in D₂O prior to the assay and stored under N₂. Buffers were dissolved in D₂O and adjusted to the appropriate pD (pD = pH + 0.4) by the addition of NaOD or DCl and stored under N₂ (23). The 3-buffer system was used at pD 7.3–9.3 and AMP buffer from pD 9.8 to 10.4. Assays were performed in duplicate or triplicate. All assays were performed in either 100% H₂O or >95% D₂O to determine ^D2Ok_cat and ^D2O(k_cat/K_m) using Equations 2 and 4, respectively, after plotting the log of the kinetic parameters as a weighted function of pD. The SIE on k_cat was determined from the alkaline plateau regions, and the k_cat/K_m value was calculated using the x_max values from the fitted data in both solvents. The error on the SIE values was calculated as described previously (24).

Temperature Dependence—Initial velocities were measured using either the PP_i assay or AMP assay from 10.0 to 34.0 °C. Temperature control was achieved by use of water-jacketed cuvettes connected to a water-circulating system with temperature control of ± 0.1 °C. β-LS was tested at pH 8.8 and 9.3 using 100 mm TAPS and AMP, respectively, with the ionic strength held constant at 0.1. Correction for the ΔpK/°C was made for each buffer at the desired pH and temperature (20). CEA was varied from 10 to 800 μm. Reaction mixtures, including all components except β-LS, were incubated for at least 5 min at the desired temperature and were initiated by the addition of β-LS in a volume that was never greater than 3% of the final assay volume. Analyses were performed at two pH values in the optimal activity region of β-LS, pH 8.8 and 9.3. Time-dependent incubation assays of β-LS at temperatures equal to, and greater than, the temperatures used in the assays ensured that β-LS and the assay components were stable throughout the temperature range used. The temperature dependence is shown in Eyring plots. The errors on the Eyring plots were propagated from the uncertainty on each rate to a natural logarithmic function (22).

Viscosity Studies—Viscosity dependence of β-LS of was analyzed at pH 9.0 with CEA varied from 2 to 600 μm using the AMP assay described above. Assays were performed with the microviscogens ethylene glycol (0–35% (w/v)) and glycerol (0–35% (w/v)). The viscosities of the solutions were determined using a Brookfield viscometer at 25 °C and were performed in triplicate. PEG 8000 (6% (w/v)) was the control macroviscogen with η_rel = 3.0. The values of η_rel determined for ethylene glycol were 1.6, 2.1, and 2.4 for 20, 30, and 35% (w/v), respectively. The η_rel values of 10, 20, 30, and 35% (w/v) glycerol buffers were 1.3, 1.7, 2.3, and 2.9, respectively, and agree well with values reported previously (25, 26). Assays were performed in duplicate. The dependence of K443R catalysis on glycerol (0–30% (w/v)) and PEG 8000 (6% (w/v)) was determined at pH 9.3 with saturating concentrations of CEA (4 mm) and were repeated in quadruplicate. The viscosities of the solutions used for K443R were determined as described above. The errors shown in the plots were propagated in quadrature from the fractional uncertainties of the respective rates (22).

Steady-state Kinetic Analysis—All kinetic data were fit using Kaleidograph 4.0. Initial velocity patterns were fit to Equation 1, and x represents the upper or lower limits of the fits in Equations 2, 3, 4.

(Eq. 1)

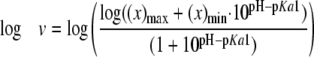(Eq. 2)

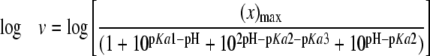(Eq. 3)

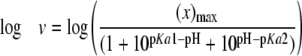(Eq. 4)

RESULTS

Purification of β-LS—The overall yield of codon-optimized His-tagged β-LS was greatly enhanced compared with the native purifications reported previously (27). β-LScHis₆ had essentially the same kinetic behavior as native protein (pH 7.8, β-LS native: k_cat = 0.29 ± 0.01 s^–1, K_{m, CEA} = 0.071 ± 0.008 mm; pH 7.8, β-LScHis₆: k_cat 0.43 ± 0.01 s^–1, K_{m, CEA} = 0.057 ± 0.007 mm).

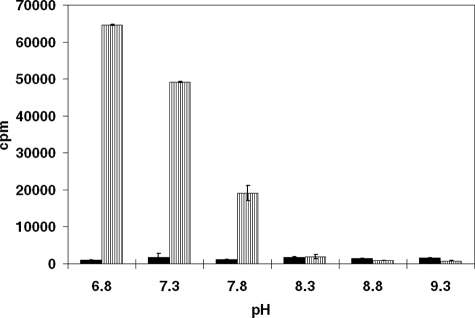
³²PP_i-ATP Exchange Assay—³²PP_i-ATP exchange assays are typically used to test for acyl-adenylate formation by measuring the amount of ³²PP_i incorporated into ATP (28). This experiment operates on the assumption that acyl-adenylations are reversible, as is typically observed. Although an acyl-adenylate intermediate was captured in an x-ray crystal structure of the lower homolog of CEA, N²-(2-carboxymethyl)-l-arginine (CMA), in the enzyme (β-LS/CMA-AMP/PP_i) (15), no ³²PP_i exchange was detected previously with β-LS. In this study, this step was further evaluated over a wider pH range using a procedure modified from that described before (13) to enhance reproducibility and lower the background radioactivity. This method was employed to analyze the acyl-adenylation step at pH 6.8–9.3. In the pH range of 8.3–9.3, no exchange was seen in wild-type β-LS as reported earlier. Increasing concentrations of β-LS (0.18–2.7 μm) and varying CEA (20 μm to 1 mm) still revealed no radioactivity incorporated into ATP. As the pH was lowered, however, appreciable exchange was measured in assays of wild type (pH 6.8–7.8). In contrast, the mutant, K443R, demonstrated significant exchange at pH 8.3 and 9.3 with values 4-fold greater than background.

HPLC Product Analysis—Coupled enzyme assays detected the by-products PP_i and AMP in accord with formation of DGPC in the β-LS reaction. Verification that this β-lactam product was formed in the K443R mutant was achieved through an established HPLC method (13).

β-LS Assays—Because β-LS possesses an ordered binding mechanism, the concentration of the second substrate, CEA, was varied in all the assays with ATP held constant at 2 mm. It was previously established that the products DGPC, AMP, and PP_i are formed in equal ratios (13). Control assays containing all components except the substrate CEA indicated no detectable background ATP hydrolysis by β-LS occurred under the conditions for all experiments. pH Studies—pH profiles of β-LS were performed to identify ionizable groups involved in binding and catalysis (29) and to reveal the optimal pH for β-LS catalysis. The previously published pH profiles of β-LS did not hold ionic strength constant, and points were not overlapped with each new buffer used (13). Although CHES was previously used for β-LS to show pH dependence at high pH, CHES and its analog CAPS were found to be inhibitors of β-LS from buffer crossover experiments and were not used in the present experiments. Moreover, the pH profiles presented here were constructed at a constant ionic strength (μ = 0.1). Crossover experiments with buffers used in the assays along with other commonly used buffers ensured the assay components did not inhibit the β-LS reaction and demonstrated that the buffers used were appropriate in all respects. β-LS and K443R were stable in the entire pH range reported as evidenced by measuring their activity after incubation at the proper pH for at least the duration of the assays.

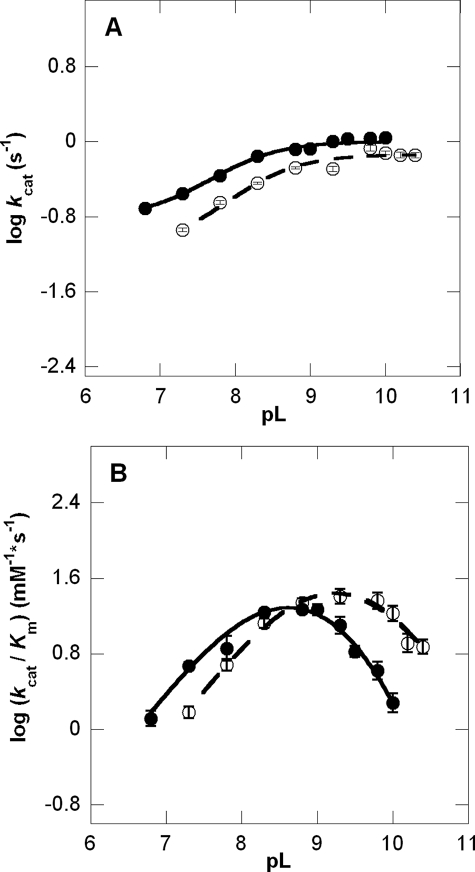
Log k_cat profiles show pK_a values of groups that must be correctly protonated for catalysis, whereas log(k_cat/K_m) profiles reflect ionizable groups that are important from binding of the varied substrate, CEA, to the first irreversible step (29). Although the pH-k_cat profile for β-LS does not change greatly over the entire pH range used, a pK_a of 8.07 ± 0.05 was calculated with activity plateauing at around pH 8.8 (Fig. 2A). The pH-(k_cat/K_m) profile is an asymmetric bell-shaped curve with a steep decline in activity above pH 9.3. Optimal activity at pH 8.8 is 1.86 × 10⁴ ± 7 × 10² m^–1 s^–1 (Fig. 2B). The best fit equation determined three pK_a values. The acidic limb is because of an ionizable group with a pK_a1 of 8.1 ± 0.1, whereas the basic limb can be accounted for by residues having pK_a2 9.2 ± 0.2 and pK_a3 9.9 ± 0.4. The pK_a3, however, is near or at the highest pH attainable with β-LS without loss of activity and may not be a reliable value. A comparison of the kinetic parameters of β-LS and K443R at the β-LS optimal pH values of 8.8 and 9.3 is shown in Table 1.

FIGURE 2.

pL versus log rate profiles at 25 °C of k_cat (A) and k_cat/K_m (B) in 100% H₂O (•) and >95% D₂O (○). The pH-rate profiles gave R² values of 0.99 and 0.99 for k_cat and k_cat/K_m, respectively, and the fit to the pD-rate profiles had R² values of 0.98 and 0.99 for k_cat and k_cat/K_m, respectively. Error bars are shown for all data points and do not exceed the size of the data points when not visible.

TABLE 1.

Comparison of β-LS and mutant K443R kinetic parameters at 25 °C

Standard error is shown in parentheses. Fold changes are shown as Δ; –Δ indicates a fold decrease with the mutant and +Δ represents an increase in the kinetic parameter. WT = wild-type β-LS.

	kcat	Km	kcat/Km	-Δkcat	+ΔKm	-Δ(kcat/Km)
	s-1	m	m-1 s-1
pH 8.8
WT	0.82 (0.009)	4.4 × 10-5 (2 × 10-6)	1.86 × 104 (7 × 102)
K443R	0.0016 (0.0001)	1.9 × 10-4 (2 × 10-5)	8.4 (1.1)	510	4	2040
pH 9.3
WT	1.01 (0.03)	8.2 × 10-5 (7 × 10-6)	1.26 × 104 (1.2 × 103)
K443R	0.0036 (0.0001)	2.4 × 10-4 (2 × 10-5)	15 (1)	280	3	840

Solvent Isotope Effects—The effects of deuterium on the β-LS reaction were analyzed to understand the roles of proton transfer and hydrogen bonding in the steps leading up to the first irreversible step, ^D2O(k_cat/K_m), and isotopically sensitive step(s) contributing to k_cat, ^D2Ok_cat. Although the rate of acyl-adenylation is not expected to be limited by protons in-flight, DGPC formation is proposed to involve proton transfers between heteroatoms, and a significant SIE on k_cat would be consistent with this step being at least partially rate-determining. Solvent isotope effects for ^D2Ok_cat and ^D2O(k_cat/K_m) were determined at equivalent pL values from complete pH and pD profiles to ensure accurate measurement of the effects of heavy water on the correct protomeric form of β-LS (30) (Fig. 2). A small but normal solvent kinetic isotope effect of 1.38 ± 0.04 was determined for k_cat with a pK_a in D₂O of 8.39 ± 0.04. On the other hand, an inverse isotope effect on ^D2O(k_cat/K_m) of 0.67 ± 0.15 was observed. As shown in Table 2, the calculated pK_a values in D₂O were pK_a1 8.7 ± 0.1 and pK_a2 9.7 ± 0.1 from fitting to Equation 4. This resulted in a better fit than to the three pK_a curves fitted to the pH-(k_cat/K_m) profile, presumably because the third pK_a shifted to a greater value than the highest pD obtainable without loss in activity.

TABLE 2.

β-LS kinetic parameters

	kcat	kcat/Km
HpKa	8.07 ± 0.05	8.1 ± 0.1	9.2 ± 0.2
DpK	8.39 ± 0.04	8.7 ± 0.1	9.7 ± 0.1
SIE	1.38 ± 0.04	0.67 ± 0.15
kη	2.5 ± 0.2	-0.32 ± 0.09

^aThe third pK_a calculated from the wild-type pH-k_cat/K_m profile was not included due to its value being at or near the highest pH attainable for wild-type β-LS. ^HpK = pK_a calculated in H₂O. ^DpK = pK_a calculated in >95% D₂O. k^η = slope on the observed rate constant from reciprocal rate versus relative viscosity plots.

Temperature Variation—Eyring plots were constructed from temperature variation of the β-LS reaction to determine the thermodynamic parameters involved in substrate capture by β-LS and the generation of productive forms for catalysis, k_cat/K_m, and to quantify the energetics underlying the rate-determining step k_cat (31). The Eyring plots were derived from transition state theory as shown in Equation 5 to give the Eyring Equation 6,

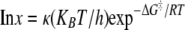(Eq. 5)

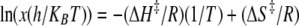(Eq. 6)

where the transmission coefficient κ is equal to 1; x is the observed rate; R is the gas constant; k_B represents the Boltzmann constant; h is Planck's constant, and T represents the absolute temperature.

From the slope of the Eyring plot, the enthalpy of activation was further derived. The Gibbs free energy, ΔG^‡, was calculated from Equation 5, and TΔS^‡ was then determined using the Gibbs-Helmholtz equation. All thermodynamic parameters were evaluated using an absolute temperature of 298 K.

Both Eyring plots of k_cat at pH 8.8 and 9.3 revealed a linear dependence on temperature (supplemental material). The transition state activation parameters at 9.3 are ΔH^‡ = 19.1 ± 1.1, ΔG^‡ = 17.4 ± 0.1, and TΔS^‡ = 1.7 ± 1.1 kcal/mol. These values were very similar to those at pH 8.8. The k_cat/K_m and K_m Eyring plots were nonlinear for both pH values tested (supplemental material). Both k_cat/K_m Eyring plots were concave down where the higher temperature region is temperature-independent, whereas the lower temperature region is largely temperature-dependent.

Viscosity Studies—Viscosity studies were employed to determine whether a diffusion-controlled event influenced the kinetic parameters. Although the rate of the β-LS reaction is not near the diffusion limit, conformational fluctuations that influence reaction rates can be influenced by solvent viscosity.

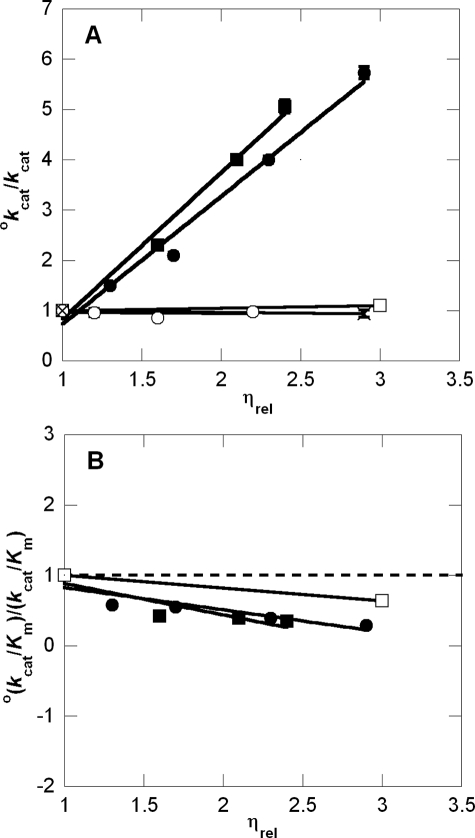
The viscosity dependence of wild-type β-LS was analyzed at pH 9.0 (Table 3). Viscosity dependence was probed using glycerol as the microviscogen and ethylene glycol to serve as a control for nonspecific effects of glycerol. Dependence of k_cat and k_cat/K_m on these viscogens was plotted as reciprocal relative rate versus relative viscosity (Fig. 3). The microviscogens glycerol and ethylene glycol showed similar effects on k_cat and k_cat/K_m, whereas the macroviscogen control, PEG 8000, showed comparatively little effect on k_cat (0.07). The PEG 8000 control, however, did increase k_cat/K_m (slope =–0.18). This slight enhancement could indicate that in addition to viscosity nonspecific effects of glycerol, such as a decreased dielectric, also influence the second-order rate constant. The slopes of the plotted reciprocal rate versus relative viscosity, k_cat^η, are 2.5 ± 0.2 and 2.9 ± 0.2 for glycerol and ethylene glycol, respectively. The k_cat/K_m values increased with increased concentration of microviscogen with slopes of –0.32 and –0.45 for glycerol and ethylene glycol, respectively. Preincubation experiments of β-LS with the microviscogens indicated they did not irreversibly inactivate β-LS. A poor or sluggish mutant was also subjected to viscosity analysis to test if the observed glycerol dependence of β-LS was from nonspecific effects (32). In this case, K443R was examined and displayed no significant viscosity effects giving slopes (k_cat^η) of –0.02 and –0.03 for glycerol and PEG 8000, respectively.

TABLE 3.

Glycerol effects on wild-type β-LS at 25 °C

Standard error on the respective rates is shown in parentheses.

%	η/η°	kcat	kcat/Km	° kcat/kcat	°(kcat/Km)(kcat/Km)
		s-1	m-1 s-1
0	1.0	0.86 (0.02)	2.2 × 104 (1 × 103)	1.0	1.0
10	1.3	0.574 (0.006)	3.8 × 104 (2 × 103)	1.5	0.58
20	1.7	0.414 (0.009)	4.1 × 104 (4 × 103)	2.1	0.54
30	2.3	0.218 (0.003)	5.6 × 104 (3 × 103)	4.0	0.39
35	2.9	0.150 (0.002)	7.5 × 104 (6 × 103)	5.7	0.29

FIGURE 3.

Reciprocal relative rate versus relative viscosity plots of wild-type β-LS and K443R at 25 °C. The viscosity dependence on k_cat and k_cat/K_m is shown in A and B, respectively. The dashed line in B corresponds to a slope of 0. Microviscogens glycerol (0–35% (w/v)) and ethylene glycol (0–35% (w/v)) are shown as • and ▪ for wild-type β-LS, respectively. The control macroviscogen, PEG 8000 (0–6% (w/v)), is denoted as □ and × for wild-type β-LS and K443R, respectively. ○ represents the dependence of K443R on glycerol (0–30% (w/v)). Error bars are shown for all data points and do not exceed the size of the data points when not visible.

DISCUSSION

β-LS Reaction Mechanism—To elucidate the rate-determining steps of this pivotal enzyme in clavulanic acid biosynthesis, the β-LS reaction was analyzed using pL-rate profiles, solvent isotope effects, Erying plots, viscosity variation, site-directed mutagenesis, and radio-pyrophosphate exchange assays. The kinetic assays indicated that the effects on the wild-type k_cat were distinct from those on k_cat/K_m, from which it may be concluded that an irreversible step preceded the rate-determining step or other steps that dominate k_cat (29). The chemical reaction catalyzed by β-LS can be divided into two parts, acyl-adenylation and β-lactam formation. For comparison, the β-LS homologs CPS and AS-B also undergo acyl-adenylation followed by nucleophilic attack to form a β-lactam or the terminal amide bond of asparagine, respectively (12, 14). β-LS, CPS, and AS-B have been previously subjected to ³²PP_i-ATP exchange assays to test for the reversibility of acyl-adenylate formation, and no exchange was detected (12–14). An acyl-adenylate, however, was captured in a crystal structure of β-LS (15). Given that acyl-adenylation reactions are generally considered reversible (28), the lack of exchange in β-LS was attributed to a large forward commitment to β-lactam formation rendering its adenylation event effectively irreversible (13). Because the conserved active site Lys-443 was predicted to play a role in β-lactam formation based on β-LS crystallographic images, the K443R mutant was examined by ³²PP_i-ATP exchange to test for reversibility. This mutant did indeed show exchange at both pH 8.3 and 9.3, values at which wild-type showed no detectable exchange. These positive results supported the proposal that the rate of DGPC formation is decreased in the K443R mutant, lowering the forward commitment to catalysis, thereby allowing reversible acyl-adenylate formation to be detected.

With wild-type β-LS, lowering the pH below optimal values for catalysis gave progressively larger amounts of radiolabeled ATP in the ³²PP_i-ATP exchange assays. This suggested that β-lactam formation, the step following acyl-adenylation, was less favorable as pH was decreased. In fact, a clear trend was observed with an increased amount of ³²P incorporation detected as pH was lowered below the pK_a value of the acidic limb observed in the pH-k_cat profile (Fig. 4).

FIGURE 4.

³²PP_i-ATP exchange assays with wild-type β-LS in a counts/min of ³²P-labeled ATP versus pH plot. At each pH the background is given (all components except CEA) on the left side in black, whereas the results from reactions containing all components are represented on the right with striped bars. The standard deviations are shown as error bars for each set of data.

pL-Rate Profiles—The lack of pyrophosphate exchange at the optimal pH of 8.8 suggested that acyl-adenylation is the first irreversible step. This implied that the groups titrated in the pL-(k_cat/K_m) profiles are those important from substrate binding to acyl-adenylation of CEA. At least two ionizable groups were revealed from the pL-(k_cat/K_m) profiles (Table 2). The observed values in the pD-(k_cat/K_m) profile exhibited a normal pK_a shift (ΔpK_a = 0.4–0.6) from a solvent equilibrium isotope effect consistent with carboxylic acid or nitrogen containing titratable group being responsible for the corresponding pK_a values in this profile (33). Because the pK_a values are only ∼1 pK_a unit apart, however, it may suggest that a reverse protonation mechanism is utilized in β-LS binding (34).

In the pH-k_cat profile a catalytic residue can been seen at pK_a ∼ 8.1 important for both substrate binding and catalysis (Table 2). As noted above, mutation of Lys-443 in CPS to alanine or methionine led to complete loss in activity (16). Mutation to arginine in β-LS, however, gave active protein that showed a large decrease in k_cat, but only a small change to the K_{m, CEA} at the wild-type pH optima of 8.8 and 9.3, which suggests the protonated form of Lys-443 is more favorable for CEA binding (Table 1). A pH-k_cat profile of this mutant was shifted two pK_a units higher (10.1) in accord with replacement of Lys-443 with arginine. Extensive calculations suggest that proton donation from Lys-443 to the acyl-adenylate carbonyl in β-LS plays an important role in stabilizing the tetrahedral transition state of β-lactam synthesis.3 Although this role appears contrary to the pH-k_cat rate profile, it is believed that the reprotonation of Lys-443 after formation of this intermediate is the kinetically significant event seen in this plot. This sort of active site “recharging” is precedented in kinetic studies of aspartyl proteases (35–37) and triose-phosphate isomerase (38, 39). These kinetic and computational studies provide important experimental support of hypotheses based on crystallographic images of the β-LS active site where the Lys-443 primary amine is 3.5 Å away from the activated carbonyl oxygen of the acyl-adenylate (15). In x-ray snapshots of the β-LS·DGPC·AMP·PP_i complex, this nitrogen moves even closer to the β-lactam oxygen (Fig. 1) (15).

SIE—The pD-k_cat profiles revealed a small but significant isotope effect of 1.38 ± 0.04 on k_cat. Although general acid and general base catalysis have typical SIE values of 2–3, solvation catalytic bridges can give rise to values in the range of 1.5–4 (30, 33). Observed values below 1.5 are normally attributed to proton transfer coupled to heavy atom motion in the transition state (40) or to increased viscosity of D₂O relative to H₂O (η_rel = 1.24, see below).

Other nucleophilic acyl substitutions, such as the case of serine proteases, have yielded calculated SIE values as low as 1.5, which can occur where proton transfer is rate-determining (41). Stabilization of tetrahedral intermediates through a proton bridge has also shown SIEs in the range 1.5–2.2 (42). In the case of β-LS, the small SIE of ∼1.4 on DGPC formation supports partially rate-determining proton transfer(s) in the transition state and opens the possibility that a nonchemical step is comparably rate-determining in β-LS catalysis.

An inverse isotope effect of 0.67 on k_cat/K_m in D₂O revealed that reaction in heavy water is faster than that in H₂O. Inverse SIEs in enzyme-catalyzed reactions are frequently attributed to an acid dissociation constant of a thiol group, dissociation of a metal-chelated water molecule, or torsional restrictions (43, 44). These possibilities were further analyzed, and the last was found likely for this system because there are no active site cysteines, and the interactions of Mg²⁺ with solvent are not sufficiently strong to affect fractionation factors of solvating waters (33). An important contribution to the inverse isotope effect observed on substrate capture is proposed to be from restrictions on torsional motions of exchangeable protons. This occurs as enzymes squeeze down on substrate(s) during a conformational change (43, 45), as has been proposed for several aspartyl proteases (46). In fact, this tightening in the transition state could also give rise to a low barrier hydrogen bond(s), which has characteristic low fractionation factors (45–47). Whereas acyl-adenylation is not predicted to involve rate-limiting proton transfer events, and therefore not contribute to the observed SIE, the explanation above would suggest that conversion from an open to a closed form of β-LS is the isotopically sensitive step causing an inverse ^D2O(k_cat/K_m).

From analysis of a series of x-ray snapshots of β-LS, it can be seen that after both ATP and CEA are bound, a heretofore disordered loop comprising residues 444–453 becomes resolved and tightly encloses the acyl-adenylate intermediate. ATP reacted with the CEA analog, CMA, in the crystal to give an accurate model of the adenylated intermediate, which was unable to further cyclize to the α-lactam, thus freezing the otherwise labile acyl-adenylate at excellent resolution.

Germane to the present discussion, movement of reactants and active site residues is evident during product formation despite the fact that the ordered loop remains intact in the structure of β-LS with all three products bound. Not only must relaxation of this structured loop occur prior to product release, but also a corresponding conformational ordering from the open state of β-LS must occur earlier in the reaction coordinate as substrate adenylation is approached. This event is in keeping with the inverse SIE discussed above. The kinetic significance of enzyme conformers after substrate binding is further supported from nonlinear Erying plots (supplemental material). Similar to β-LS, nonlinear temperature dependence was observed on the Michaelis constant and k_cat/K_m of fumarase (48) and was later explained by kinetically significant conformational changes in an iso-mechanism (49).

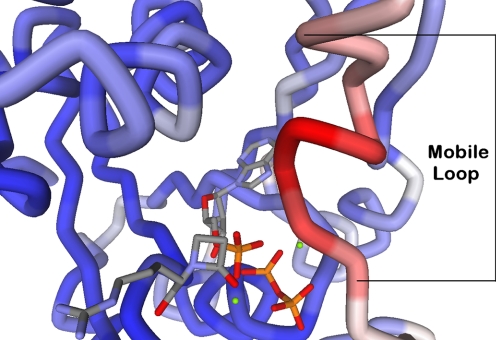
Conformational Change and Viscosity Variation—A direct measure of the importance of conformational change(s) in the dynamics of an enzyme reaction was gained from viscosity studies. The movement of the conserved loop in β-LS is implied in the experiments discussed thus far, and the analogous movement of residues 442–450 (50) is believed to contribute to the overall rate of CPS (16) (Fig. 5). This proposed motion in β-LS was clearly supported by measurements on k_cat using the microviscogens glycerol and ethylene glycol compared with a macroviscogen control in PEG 8000, and a kinetically poor mutant (Fig. 3A).

FIGURE 5.

Crystal structure of β-LS (Protein Data Bank code 1JGT) with a structured catalytic loop. The protein depicted is the β-LS·DGPC·AMP·PP_i complex, and it is colored in blue, white, and red by B-factor using Accelrys Discovery Studio (Accelrys Software Inc., San Diego). Blue represents the most rigid portions of the protein; white is moderate mobility, and red corresponds to the most dynamic portions of the protein. The mobile catalytic loop (residues 444–453) is labeled at the first and last amino acid.

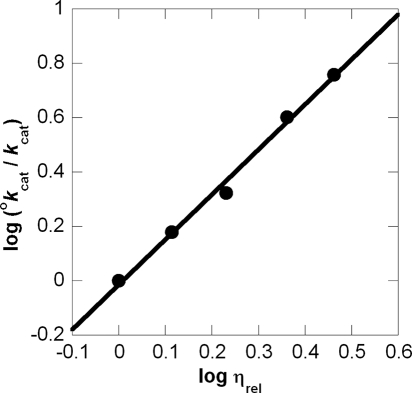
Kramers' theory explains the unimolecular rate dependence on solvent viscosity and demonstrated that for diffusive barrier crossings, rates are inversely proportional to friction (51). The application of Kramers' model to dynamic states of proteins has been successful with solvent viscosity increasing the solvent friction leading to a decreased rate of structural fluctuations (52). Adherence to Kramers' theory predicts a linear relationship between the log of the reciprocal relative k_cat versus log η_rel with an expected slope of 0 < δ < 1 (Equation 7) (53).

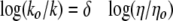(Eq. 7)

A value of 1 shows a tight coupling of the active site to solvent, whereas a value near 0 predicts an enzyme active site largely uncoupled to solvent. Slopes larger than unity obtained from viscosity variation, however, have been observed (54–58).

This study determined a δ value of 1.66 ± 0.08 (R² = 0.993) (Fig. 6). In some cases, deviations from unity can be attributed to factors other than solvent viscosity such as change in dielectric environment or changes in water activity from the co-solvent (59). Although the dielectric constants of ethylene glycol and glycerol are similar, a 6% (w/v) PEG 8000 solution creates a lower dielectric environment than that of even a 50% glycerol/water environment (60). Because virtually no change in k_cat occurred with this macroviscogen, a slope of greater than 1 cannot be explained by change in the dielectric. Next, from lack of dependence on PEG 8000, it is also unlikely that the attenuation in k_cat is from a change in water activity (61). In addition, a 30% (w/v) glycerol pH-k_cat profile ensured pH 9.0 was still in the pH optimum (data not shown). Besides using another microviscogen and a macroviscogen control, a kinetically poor mutant, K443R, was also tested to probe for nonspecific effects of glycerol (32). If chemistry is completely rate-determining in an enzymatic reaction, its rate should not be affected by changes in viscosity (26). Because K443R showed no viscosity dependence, it can be inferred that chemistry is now fully rate-determining in this mutant. From these results it could also be deduced that the large viscosity dependence of wild-type k_cat is indeed from a partially rate-determining conformational change, which is proposed to arise from the active site loop movement that allows products to dissociate.

FIGURE 6.

β-LS viscosity studies applied to Kramers' theory. The log relative reciprocal k_cat versus log relative viscosity plot (0–35% (w/v) glycerol) is given with a linear fit (R² = 0.993).

The δ value greater than unity in β-LS could be explained by the sum of the internal protein friction and the solvent friction. Protein friction can occur when variations on solvent viscosity are partially transferred to the active site, changing the local viscosity of the protein (62). This internal protein viscosity slows the motion of protein atoms relative to each other. For kinetically significant protein conformational changes, these two sources of friction need to be considered (63). These components are additive in the context of Kramers' theory, where σ is the internal protein viscosity; C is an adjustable independent parameter; R is the gas constant; T is the absolute temperature; k is the observed unimolecular rate, and E_o represents the height of the diffusion-controlled energy barrier (Equation 8).

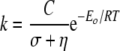(Eq. 8)

Although the η term dominates, the σ component will also attenuate the observed rate in the range of viscosity values used here (63). From these considerations, combined internal and external friction effects could result in the δ > 1 observed in β-LS. A similar explanation has been previously made to account for a higher than predicted δ value in ubiquitin C-terminal hydrolase L3 (55).

Eyring plots of k_cat were linear and gave thermodynamic parameters that indicated β-LS catalysis is under enthalpic control at its optimal pH values. In cases where product dissociation is rate-limiting, ΔH^‡ ≈ 4 kcal/mol is anticipated (64). In the case of β-LS, the k_cat represents the activation barrier from enzyme-adenylate complex to product formation, including a conformational change. Offsetting factors such as changes in translational and rotational degrees of freedom (65) and the reorganization of H₂O (66) leading up to the conformational change all contribute to the small but favorable TΔS^‡, and the enthalpy term manifests the energetics behind bond breaking and formation, with a large positive enthalpy (∼20 kcal/mol) fully in keeping with a conformational change (67).

Conclusion—The proposed β-LS kinetic scheme is shown in Scheme 3. The association and dissociation rate constants are represented by k₁ and k_–1, respectively, for the E·ATP and E·ATP·CEA complex. E and F represent the different conformers of β-LS where E is the open form, and F is the closed form. The second substrate to bind, CEA, is shown, with P representing the products of the β-LS reaction. Acyl-adenylation of CEA is represented by k₃ with the intermediate shown as I. At saturating CEA concentrations, β-lactam formation and the partially rate-determining conformational change are shown as k₄. Product dissociation from the active site is represented as k₅.

SCHEME 3.

Binding of CEA is proposed to be stabilized by Lys-443. After ATP and CEA have bound, the chemical steps of the catalytic cycle begin after ordering of the mobile loop over the active site, squeezing down on the pre-organized substrates as shown from inverse SIE, nonlinear Eyring plots, and viscosity analysis on k_cat/K_m. This pre-organization facilitates in-line attack of the terminal CEA carboxylate onto the α-phosphate of ATP, and protects the high energy adenylated intermediate from solvent. The first chemical transformation, acyl-adenylation, is followed by β-lactam formation, which has a large forward commitment, rendering acyl-adenylation functionally irreversible in wild-type β-LS. On the other hand, the measured forward rate of β-lactam formation is significantly lowered in the K443R mutant and is reflected in the observation of radiochemical PP_i exchange. A modest SIE suggested that the second chemical step, β-lactam formation, involves only partially rate-determining proton transfer(s) in the transition state and that a nonchemical event also contributes to k_cat. Kinetic analysis of K443R points to Lys-443 participation in stabilization of this transition state based on a relatively small change in K_{m, CEA} and significantly large attenuation in k_cat, and the lack of viscosity dependence. DGPC formation is followed by a partially rate-determining conformational change proposed to involve loop relaxation allowing products to dissociate from the active site.

Strain improvement and metabolic engineering, which have led to increased production of clavulanic acid, are appealing avenues for the construction of clavulanic acid derivatives by fermentation technology (68, 69). Structural modifications, for example, on the β-lactam ring of oxapenems have yielded potent activity against not only class A but also class C β-lactamases (8). Identification of the rate-determining steps, recognition of critical catalytic residues, and appreciation of a key protein conformational change presented here afford a clearer understanding of the multifaceted roles of the protein and can guide experiments to engineer the clavulanic acid biosynthetic pathway. β-LS, in particular, provides the platform to produce more effective and broader spectrum β-lactam containing β-lactamase inhibitors.