Metabolic Network Model of a Human Oral Pathogen

Abstract

The microbial community present in the human mouth is engaged in a complex network of diverse metabolic activities. In addition to serving as energy and building-block sources, metabolites are key players in interspecies and host-pathogen interactions. Metabolites are also implicated in triggering the local inflammatory response, which can affect systemic conditions such as atherosclerosis, obesity, and diabetes. While the genome of several oral pathogens has been sequenced, quantitative understanding of the metabolic functions of any oral pathogen at the system level has not been explored yet. Here we pursue the computational construction and analysis of the genome-scale metabolic network of Porphyromonas gingivalis, a gram-negative anaerobe that is endemic in the human population and largely responsible for adult periodontitis. Integrating information from the genome, online databases, and literature screening, we built a stoichiometric model that encompasses 679 metabolic reactions. By using flux balance approaches and automated network visualization, we analyze the growth capacity under amino-acid-rich medium and provide evidence that amino acid preference and cytotoxic by-product secretion rates are suitably reproduced by the model. To provide further insight into the basic metabolic functions of P. gingivalis and suggest potential drug targets, we study systematically how the network responds to any reaction knockout. We focus specifically on the lipopolysaccharide biosynthesis pathway and identify eight putative targets, one of which has been recently verified experimentally. The current model, which is amenable to further experimental testing and refinements, could prove useful in evaluating the oral microbiome dynamics and in the development of novel biomedical applications.

Understanding the role of microbial communities in human health is emerging as a fundamental and fascinating biomedical challenge (42, 46, 94). In the fight against infectious diseases, we are witnessing the discovery of novel connections between infection, inflammation, and systemic human diseases (2-4, 14, 29, 39, 48-50) and a rise in the evolution of antibiotic resistance (12, 15, 17). These threats reinforce the necessity to understand the mechanisms that underlie pathogenicity and the interactions between pathogenic and nonpathogenic microbes coexisting in our body as a means to identify novel drug targets for more aggressive and carefully targeted therapies. Rising technical advancements open new avenues to make progress in this endeavor. Most notably, as sequencing technologies become increasingly approachable, a variety of organisms and community-level metagenomic samples are being sequenced (17, 18, 53). In parallel, the awareness of the importance of quantitative methods and system-level mathematical approaches is gradually percolating through different branches of biology and is going to be a fundamental component of the study of microbial physiology and pathology (24, 63, 64, 76, 77, 92).

These motivations are especially pertinent in the case of the human oral flora, which comprises at least 400 to 700 different bacterial species (42). Oral microorganisms constitute a very complex and dynamical community, responsible for, among others, two oral infectious diseases affecting virtually all humans: carious and periodontal disease. Periodontal disease is the inflammatory process that occurs in the tissues surrounding the teeth in response to the accumulation of bacterial plaque. Chronic and progressive bacterial infection of the gums is responsible for alveolar bone destruction and loss of tissue attachment to the teeth (6, 30, 98). In addition to the local tooth and gum effects, periodontal disease has been shown to influence various systemic disorders and diseases (39, 71, 82, 87). In particular, significant associations between periodontal disease and cardiovascular disease (55), diabetes mellitus (44), preterm low birth weight (45), and osteoporosis (10) have been discovered. Patients diagnosed with periodontal disease may be at higher risk for these diseases also due to a compromised immune system, since infectious and opportunistic microbes responsible for periodontal infection may bring a burden onto the rest of the body (39). Understanding and targeting the pathogenic mechanisms responsible for these diseases is still an open problem.

Among the several factors determining the dynamics and virulence of the oral microbial flora, metabolic processes represent a ubiquitous key component. Many of the interactions between different species are mediated by metabolic processes, such as the competition for common resources, the exchange of nutrients, and the chemical communication involved in quorum sensing and biofilm formation (9, 42, 43, 84, 90). In addition, metabolites are often involved in shaping the relationship between microbes and host cells, from the proinflammatory role of lipopolysaccharides (LPS) present in the bacterial outer membrane (58, 86, 91) to the cytotoxic effect of organic acids secreted as catabolic by-products (72, 90). Therefore, in order to understand the complex interactions in the microbial flora, we need to comprehensively analyze the metabolism of the main individual species involved. The prominent role of metabolism offers the opportunity to undertake quantitative studies, since genome-scale metabolic networks are one of the most well characterized and computationally approachable networks in the cell (7, 19, 28, 67, 75, 79, 88).

Here we start studying the metabolic properties of the oral microbial flora by implementing the first genome-scale stoichiometric model of one of its most prominent pathogenic representatives, the gram-negative anaerobe bacteroides Porphyromonas gingivalis. In particular, we construct and analyze with flux balance methods the metabolic network properties of P. gingivalis strain W83, whose genome sequence was completed in 2003 (61). While research has been performed for several decades exploring the metabolic behavior of P. gingivalis (83), relatively little is known compared to other organisms for which genome-scale stoichiometric models were built. Gaining an understanding into P. gingivalis metabolism is crucial in order to fully dissect host-parasite and intermicrobe interactions in periodontal diseases. Even though P. gingivalis contains functional glucose transporters, the organism's glucose utilization is known to be very poor (83). Under basal medium conditions, the addition of glucose results in negligible increases in the overall cell yield (83). Conversely, sequencing of the P. gingivalis W83 genome identified a large number of putative open reading frames (ORFs) that are parts of amino acid degradation pathways, such as those of arginine, lysine, serine, and glutamate. Through sequencing and homology-based comparisons it was found that as many as 11 amino acids may be substrates for the organism. Amino acids could be used as carbon, as well as nitrogen, sources (61). Interestingly, the growth yield is increased when the organism is grown on mixtures of amino acids and peptides. A preference for peptides is probably a consequence of the organism's gingipain enzymes, known to be highly proteolytic (93). As a result, the organism can take full advantage of the degradation of host tissues by metabolizing the peptide fragments (1). Some by-products of amino acid catabolism, such as isobutyrate, are thought to be mediating the interaction with other species. Another distinctive metabolic property of P. gingivalis is its requirement for heme (65), whose external accumulation is responsible for the black coloration of the cell. It has been suggested that the heme aggregation around the organism constitutes a method of creating an anaerobic microenvironment. The heme on the surface of the cell reacts and binds to oxygen in the surrounding environment. This effectively reduces the ability of oxygen molecules in the environment to come in contact with the cell, mitigating the possible oxidative damage (65). Finally, similarly to other virulent microbes, some P. gingivalis metabolites are known to have powerful effects on the immune system. In particular, LPS activate macrophages to synthesize and secrete a variety of proinflammatory molecules, including the cytokines interleukin-1 and tumor necrosis factor alpha, prostaglandins (especially prostaglandin E₂), and hydrolytic enzymes (13, 47, 99).

Understanding and manipulating complex metabolic networks at or beyond the cellular level requires tractable mathematical formulations and efficient computational approaches. As opposed to traditional differential equations methods, the approach of flux balance analysis (FBA) that we use is exceptionally scalable to (and beyond) cell-level systems and depends minimally on parameters hard to measure in vivo (20, 38, 77). This simplicity, a consequence of the assumptions of steady state and optimality, comes at a price, mainly the fact that predictions are limited to reaction rates (fluxes) and do not include metabolite concentrations. However, since several FBA predictions have proven to accurately reflect experimental data (22, 34, 79, 88), the FBA approach is increasingly used for various applications, most notably the study of how the cell responds to genetic perturbations (e.g., gene deletions), and environmental changes (e.g., carbon source shift). By assembling a first version of the metabolic stoichiometry of P. gingivalis and analyzing it with these flux balance computational techniques, we hope to pave the way for increasingly precise single-species models and for a gradual understanding of the oral community as a whole.

MATERIALS AND METHODS

Genome-scale metabolic network models usually consist of two major components. The first is a “list of parts,” namely, the list of all metabolic reactions (and the corresponding enzyme genes) present in the organism. This is often referred to as metabolic reconstruction and encompasses the stoichiometric coefficients of all known and putative biochemical reactions identified for the desired organism. This stoichiometry, whose assembly usually requires several rounds of trial and error and the screening of large amounts of biochemical literature, can also be seen as a concise description of the topology and atomic balance of the metabolic network and can be represented mathematically as a matrix. The second component is the suite of algorithms that receive as an input the network stoichiometry, together with other parameters, such as the condition-specific definition of available nutrients, and produce as an output predictions of observable quantities, such as reaction rates and growth yield. The use of a steady-state approximation and of optimality criteria make it possible to obtain cell-scale predictions of metabolic fluxes in a fraction of a second.

P. gingivalis model construction.

The FASTA file containing all annotated predicted proteins from the sequenced genome of P. gingivalis strain W83 (36) was downloaded from the Kyoto Encyclopedia of Genes and Genomes (KEGG) (44). These proteins are predicted by an automated algorithm (KAAS) that is part of the KEGG system (56). As part of this process, each metabolic enzyme is associated with an Enzyme Commission (EC) number that characterizes its function. Enzymes associated with reactions that involve tRNAs or generic DNA or protein molecules were not pursued further. For each remaining enzyme (and corresponding EC number) we needed to identify the detailed metabolic reaction stoichiometry. Since FBA models can be quite sensitive to atomic balance errors in the reaction stoichiometry, the safest process was to select, based on the extracted EC numbers, reactions already used in other well-established FBA models. We accessed multiple FBA stoichiometric models through the online BIGG database developed by Bernhard Palsson and collaborators at the University of California at San Diego (51). We first included in the model all reactions associated with P. gingivalis EC numbers found in the Helicobacter pylori, Escherichia coli, or Saccharomyces cerevisiae networks available from the BIGG database. Furthermore, for P. gingivalis enzymes with incomplete EC numbers, we identified and included in our model all H. pylori reactions whose EC numbers matched the available P. gingivalis EC digits. In total, we included 361 reactions based on complete or partial EC numbers matching to reactions available in previous models. Note that ORFs associated with incomplete EC numbers for which we could not find matching EC numbers in H. pylori were not included in the current model. Although predictions of transporters specific to P. gingivalis can be obtained through the transportDB pipeline (65), these predictions usually lack the specificity of substrates. Therefore, upon verifying that transporter classes predicted by transportDB for P. gingivalis matched the ones included in the H. pylori model iIT341, we included all H. pylori transporters in the P. gingivalis model (70 reactions). An additional category of reactions that had to be included in the model is the one of ORFs associated with complete EC numbers which did not match any reaction already present in other microbial models. For the EC numbers in question, we relied on the reaction stoichiometries reported in the corresponding KEGG database entries. KEGG metabolite names were translated into BIGG database names using a “dictionary” available from the BIGG database website (51). This step added to the model 70 reactions. We also included in our P. gingivalis model the 76 reactions that appear in the H. pylori model and that lack an EC number. This step relies on the assumption that H. pylori is metabolically close enough to P. gingivalis to guarantee that fundamental putative metabolic functions ascribed to H. pylori are likely present also in P. gingivalis. Indeed, several steps in our reconstruction make use of information from the already-reconstructed organism that is metabolically closest to P. gingivalis, namely, H. pylori (64). The metabolic similarity between H. pylori and P. gingivalis was established by comparing to each other the enzyme profiles of multiple bacteria for which a stoichiometric model has been published (see below and Fig. 1B). The last step of our reconstruction involved subjecting the list of reactions to a manual screening based on literature searches. This step resulted in the addition of an extra 35 reactions. Overall, despite containing several putative reactions present also in other organisms (especially H. pylori), our P. gingivalis model counts many reactions that make it metabolically unique. A list of all such unique reactions is available in a spreadsheet in the supplemental material. In addition, detailed information for a selected subset of such unique reactions is displayed in Table 1. Note also that a special tag in the spreadsheet's main page (column H) in the supplemental material provides information about the origin of every single reaction in the P. gingivalis reconstruction. This will make it easy to include or exclude whole categories of reactions (e.g., reactions added from KEGG) for the purpose of future troubleshooting and refinement processes.

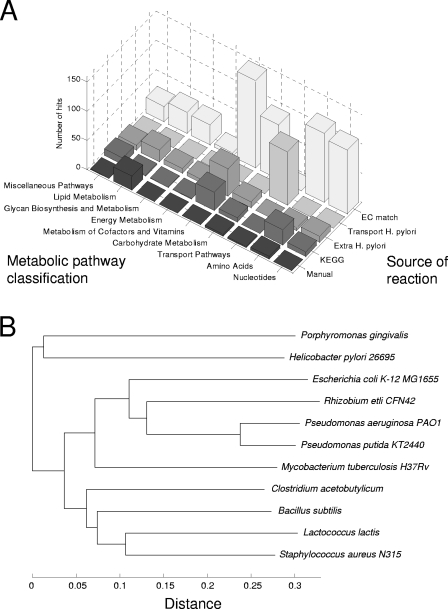
FIG. 1.

(A) Reactions included in the P. gingivalis model can be classified based on two criteria: (i) source of the reaction in the model-building process and (ii) metabolic pathway classification. Some reactions have multiple metabolic pathway annotations. All reactions have only one source. The EC match category represents reactions that have an associated EC number which either matches exactly or closely matches the enzyme classification of a protein gene in the P. gingivalis genome. Transport H. pylori refers to transport reactions that were added based on TransportDB results and on the stoichiometry of transport reactions from the H. pylori model. The extra H. pylori reaction category relates to reactions that had no EC annotation but were added in order to allow the producibility of several biomass components (see Materials and Methods). KEGG reactions were included from the KEGG database on the basis of an exact EC match. Finally, the manual reaction category includes reactions that were introduced and curated manually based on literature searches. The LPS pathway in the model is almost completely putative, as reflected in an increased number of manually added reactions under the lipid metabolism pathways class. KEGG-based reactions contribute greatly to amino acid metabolism and cofactor and vitamin metabolism. This reflects the fact that P. gingivalis is heavily dependent on amino acids from its environment. It is also interesting that, in agreement with the fact that the organism does not rely heavily on carbohydrate metabolism, reactions that are part of the carbohydrate metabolism are relatively under-represented across all reaction sources. (B) Tree of enzyme profile distances between several prokaryotes for which flux balance models are available: P. gingivalis (the present study), H. pylori 26695 (92), E. coli K-12 MG1655 (23), R. etli CFN42 (68), Pseudomonas aeruginosa PAO1 (63), Pseudomonas putida KT2440 (62), Mycobacterium tuberculosis H37Rv (37), Clostridium acetobutylicum (81), Bacillus subtilis (64), Lactococcus lactis (66), and Staphylococcus aureus N315 (8). Using data from the KEGG database, it is possible to calculate the normalized proportion of enzymes that are different between any two organisms (see Materials and Methods). The depicted neighbor-joining tree, based on such a distance metric, provides a map of metabolic similarity between available stoichiometric models. In particular, this shows that the organism metabolically closest to P. gingivalis is H. pylori.

TABLE 1.

Reactions present in the current P. gingivalis model but not in the H. pylori model iIT341

Reaction namea	Enzyme	Reaction details	Pathway(s)	Reference	EC no.	Protein ID	GenBank accession no.	E value	BLAST result (top hit)	BLAST accession no.
R00654	l-Methionine methanethiol-lyase (deaminating)	Methionine + water ↔ methylmercaptan + ammonia + 2-oxobutanoate	Methionine metabolism	100	4.4.1.11	PG0343	NP_904655	3.00E-175	Methionine gamma-lyase (Treponema denticola ATCC 35405)	NP_972801
R00357	l-Aspartic acid:oxygen oxidoreductase (deaminating)	Aspartate + water + oxygen ↔ oxaloacetate + ammonia + hydrogen peroxide	Alanine and aspartate metabolism	11	1.4.3.16	PG1576	NP_905707	7.00E-119	l-Aspartate oxidase (Geobacillus sp. strain Y412MC10)	ZP_03038236
R00764	Pyrophosphate:d-fructose-6-phosphate 1-phosphotransferase	Diphosphate + d-fructose-6-phosphate ↔ phosphate + d-fructose-1,6-bisphosphate	Glycolysis	5	2.7.1.90	PG0163	NP_904504	0	Diphosphate-fructose-6-phosphate 1-phosphotransferase (Parabacteroides distasonis ATCC 8503)	YP_001302896
CTT	Butyryl-CoA oxireductase	Crotonoyl-CoA + menaquinol ↔ butanoyl-CoA + menaquinone	Glutamine metabolism	90	1.3.99.2
4HB2COA	4-Hydroxy butyrate to crotonoyl-CoA	Acetyl-CoA + 4-hydroxybutyrate ↔ acetate + butanoyl-CoA + water	Glutamine metabolism	90

^aR00654 (METase) is a part of the methionine metabolism and is instrumental in methyl-mercaptan production directly from methionine and water. Methyl mercaptan is a toxic volatile sulfur compound known to be a predominant source of oral malodor. In addition, volatile sulfur compounds are able to increase the permeability of the oral mucosa, making them candidate mediators of periodontal disease. This is backed up by the fact that METase mutants have a reduced level of pathogenicity compared with the wild type (100). The reaction R00357 is part of a more generic response to the presence of molecular oxygen. The organism uses an amino acid oxidase to convert molecular oxygen into hydrogen peroxide, which prevents the formation of highly damaging superoxide ions (11). R00764 is a prominent reaction in the glycolytic and gluconeogenic pathway. This reaction is part of a functioning gluconeogenesis pathway that can produce intermediates for pathways such as LPS synthesis (5). Reactions CTT and 4HB2COA are both important reactions required for butyrate production in P. gingivalis. These reactions are extracted directly from the literature (90) and hence do not have associated ORFs or corroborating BLAST evidence. CoA, coenzyme A.

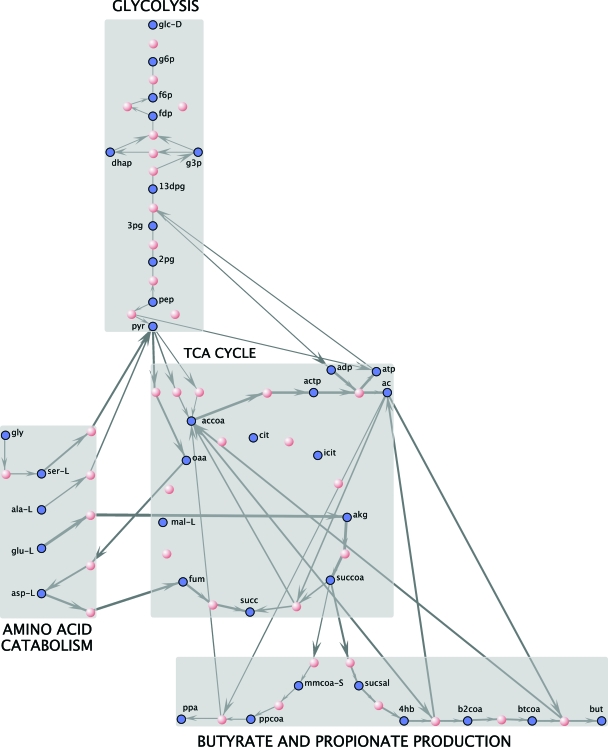
In the manual refinement process we paid special attention to the biosynthesis of P. gingivalis-specific LPS, which is very relevant for their role in triggering host immune response. The LPS pathway (see Fig. 7) was assembled manually based on H. pylori similarity and on P. gingivalis specific details available in the literature (40, 41). The chemical structure of P. gingivalis LPS is unique among other bacterial LPS structures due to the presence of odd-number-chained branched fatty acids that consist mainly of 3-hydroxytetradecanoic acid and are advocated to play an important role in P. gingivalis pathogenesis (69, 70). Our main focus was on the lipid A structure, since this is the section of the LPS that is exposed to the extracellular environment and an organism-specific moiety. A putative pathway was assembled by modifying the H. pylori model's single LPS pathway to incorporate the three different lipid A molecules biosynthesis pathways for P. gingivalis. These pathways use as a precursor the molecule 3-methyl-butrylyl-coenzyme A (CoA), found also in B. subtilis (60, 97). Putative malonyl-CoA-based fatty acid extension reactions (13MMA, PMACP) were then used to produce 13-methyl-myristic acid and 15-methyl-palmitic acid. These molecules, in turn, form the basis of the C₁₅ and C₁₇ terminal branched chains that make up the exposed moieties of the lipidA molecule. Similarly, taking advantage of the detailed study by Takahashi et al. (90), we could refine manually the details of the amino acid fermentation pathways (see below and also Fig. 7).

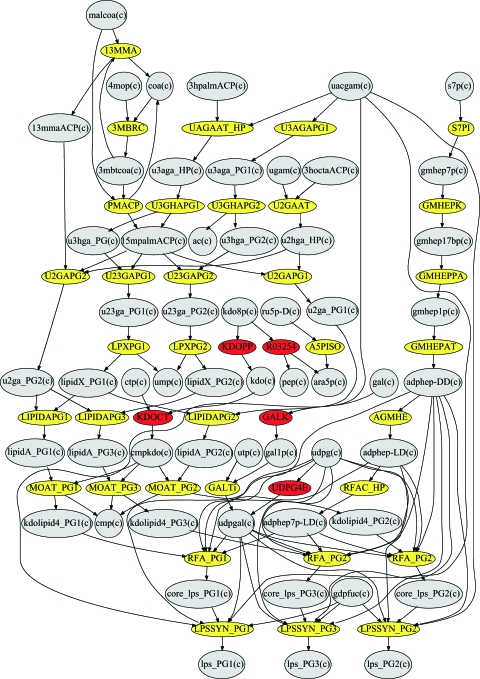
FIG. 7.

Representation of the putative pathways for LPS biosynthesis in the iVM679 P. gingivalis model, with layout automatically generated by using GraphViz (see Materials and Methods). Gray nodes denote metabolites; red and yellow nodes represent reactions. The red nodes denote reactions that have been linked to specific reactions. Yellow nodes represent reactions that are putative and that were manually added in order to make all three specific lipid A molecules. The UDPG4E reaction is linked to the galE gene, producing a UDP-glucose 4-epimerase. The galE mutants are known to have modified lipid A molecules (59). The pathway culminates in the production of lps_PG1, lps_PG2, and lps_PG3 molecules, which refer to the PG1690, PG1450, and PG1435 lipid A structures, respectively.

It must be noted that although our model is based on the genome of the W83 strain, experimental data useful for model validation are mostly available for the ATCC 33277 strain (90). At this point we do not have enough data to make a distinction between the metabolic functions of these two strains. Hence, we assume that the stoichiometric model built for one strain applies equally well to the other strain, especially with respect to amino acid uptake. Reportedly, a large proportion of the differences between the ATCC 33277 and W83 is composed of genome rearrangements and insertions of genetic elements, while the majority of the gene sequence is conserved (95). Future models may gradually allow one to capture potential differences between the two strains.

Visualization of enzyme-based distances for model organisms.

The KEGG database contains EC numbers for annotated enzyme genes in a large number of sequenced organisms. Using this enzymatic information, it is possible to construct a binary vector that captures the overall EC-based functionality of an organism. If i = 1,…,n describes an index that runs over all possible EC numbers, the enzyme content of an organism X can be represented as a binary profile S^(X), whose component S_i^(X) is 1 if the corresponding EC number is present in organism X, or 0 otherwise. We computed the metabolic similarity between any two organisms X and Y for which a stoichiometric model has been published by evaluating the Jaccard distance (36) between S^(X) and S^(Y), defined as follows:

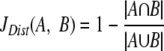In essence, what is calculated is the number of all common EC numbers between the two organisms, normalized by the total amount of EC numbers present in the two organisms. This method provides us with a matrix of distances not unlike those that would be computed for a phylogenetic tree. Using these distances and the neighbor-joining method, we constructed a tree that provides an easy way to compare the metabolomes of multiple organisms (73).

FBA and reaction deletions.

FBA is a constraint-based approach for predicting steady-state reaction rates (fluxes) in a metabolic network and has been described in detail elsewhere (21, 38, 77). The network of reactions is uniquely defined by a stoichiometric matrix S, whose element S_ij represents the stoichiometry of metabolite i in reaction j and is positive if a metabolite is produced and negative if it is consumed. The steady-state constraint is hence formally expressed as S·v = 0, where v is the vector of reaction fluxes. In addition to the steady-state assumption, inequality constraints can be imposed to set upper and lower bounds on individual fluxes. As done before, we use these constraints to impose the irreversibility of specific reactions and to set limits on nutrient uptake rates. In the second step of FBA, linear programming is used to identify among the flux vectors that satisfy the above constraints one that optimizes a given objective function. In the current FBA calculations we used as our objective function the biomass flux (v_growth), corresponding to a requirement of optimal utilization of resources toward maximal growth. The specific proportions of different metabolites composing the v_growth are based on the H. pylori objective function. The only modification is the addition of three LPS molecules present in P. gingivalis and the removal of the single LPS molecule present in the original H. Pylori biomass equation. The linear programming problem solved is therefore:

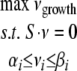It is known that this optimization problem can have multiple solutions (51, 79). In other words, for a given set of constraints, there can be several different sets of fluxes which result in an optimal value for v_growth. To eliminate uncertainty in our calculations, we performed a secondary optimization in which we selected, among all flux vectors that had the maximal value for v_growth, the one which had the minimum sum of absolute values of fluxes. The motivation for this secondary optimization is that an organism may attempt to maximize growth with a minimum investment of resources (32). This criterion has been previously utilized for the study of both wild-type and gene deletion strains (31). Since, by definition, all equivalent optimal solution display the same growth rate v_growth, the use of a secondary optimization is meaningful only when fluxes other than v_growth are analyzed. Hence, a secondary optimization was applied only for the investigation of amino acid uptake rates and by-product secretion rates (see Fig. 3).

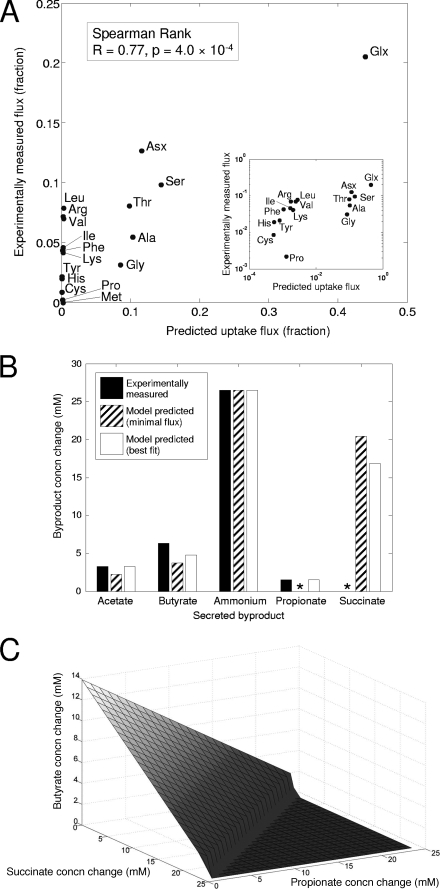
FIG. 3.

A quantitative assessment of model behavior was done by comparing model predictions to experimentally determined amino acid uptake rates and by-product secretion rates reported by Takahashi et al. (90). (A) Experimentally measured fractions of amino acids consumed by P. gingivalis against corresponding flux balance model predictions in linear scale (main plot) and log-log scale (inset) (see Materials and Methods for details). The model correctly predicts glutamate, aspartate, serine, and threonine as the four amino acids with the highest uptake rates. In addition, the model predictions of the relative rates with which less highly utilized amino acids are taken up shows strong correlation with the experiments. On the other hand, model predictions for some amino acids do not match the experiments. For example, the model fails to predict that valine, leucine, and arginine are taken up in significant amounts, although experimental measurements suggest they are utilized nearly as much as serine, threonine, and alanine. Such discrepancies indicate incomplete knowledge of the catabolic route for these amino acids and suggest metabolic pathways where further research can provide novel insights. (B) Experimentally determined by-product secretion rates (▪) were compared to two sets of model predictions. The first (▨) was the set of model-predicted production rates compatible with optimal growth, with the minimal Manhattan distance from the associated experiments. The second (□) was the set of model predicted production rates compatible with optimal growth, which were associated with the flux solution minimizing the overall sum of absolute values of fluxes through the network. Minimizing the sum of flux through the network is a common secondary optimization used to select a particular optimal flux solution. Both sets of predicted fluxes show good agreement with experiments for butyrate, acetate, and ammonium secretion. The predicted rates, which were minimally distant from the experimental values, also accurately capture propionate production. Despite the good agreement with experiments, there is clearly significant flexibility in model-predicted by-product production rates that are compatible with optimal growth. (C) The relationship between model predictions for propionate, succinate, and butyrate production, in the same tryptone media utilized in part A, was assessed by computing all possible values for the three production fluxes, which were consistent with optimal growth. This analysis demonstrated that the model only has constraints on the overall by-product production rate and not on the rates of production of the specific by-products. Succinate and propionate production are metabolically equivalent in the model, with butyrate production differing from the other two by a multiplicative factor. It should be noted that the equivalence between these by-products is only true for the catabolism of particular amino acids. This explains why, despite the symmetry of the surface, butyrate production must be greater than zero for all solutions, whereas succinate and propionate production can be zero. Specifically, butyrate production from glutamate is not equivalent to propionate and succinate production.

The reaction deletions performed (see Fig. 6) were computed by constraining to zero the flux through the deleted reaction and again optimizing for the flux through v_growth. All optimizations were carried out by using the GNU linear programming kit (GLPK) optimization software package (52), through the glpkmex Matlab interface.

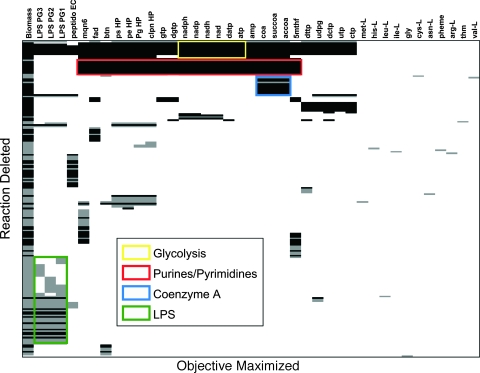
FIG. 6.

Representation of the predicted capacity of the P. gingivalis metabolic network to produce each biomass component upon systematic removal of each reaction in the model. In silico deletion experiments were conducted using an amino-acid-rich medium similar to the one from Takahashi et al. (90) (see Materials and Methods). For each reaction deletion (row), we used the FBA model to check whether each biomass component (column) could be produced. A black or gray bar indicates a case in which the specific biomass component cannot be produced under the chosen reaction deletion. The first column represents the complete biomass, combining all 52 metabolites that are required for cell growth, and corresponding to the objective function most commonly maximized in flux balance models. Biomass components that are not affected by any single deletion would correspond to blank columns and are not shown. Similarly, reaction deletions that do not affect the producibility of any metabolite would correspond to blank rows and were omitted. Black bars refer to reactions that are associated with specific proteins. Gray knockouts denote reactions that currently have no specific protein association. The results are clustered both by biomass component and by reaction deletions, revealing the existence of blocks characterized by similar producibility patterns. The deletions enclosed by the green box relate to the production of all three LPS molecules. The reactions deleted are part of the LPS biosynthetic pathway. The majority of deletions affecting the LPS are related to putative reactions, due to the highly putative nature of the LPS pathway. The yellow box encompasses reactions that are predominantly members of glycolysis and relate to the production of NADPH, NADP, NADH, NAD, dATP, and ATP. Since the cell under the specified nutrient conditions is predominantly catabolizing amino acids, these cofactors, which use glycolytic intermediates as precursors, require an active flux through gluconeogenesis. The deletions enclosed by the red box relate to a large number of biomass components. The corresponding reactions are enriched for purine and pyrimidine biosynthetic pathways. Without purine and pyrimidine biosynthesis, simple cofactors such as ATP and GTP cannot be produced. These cofactors are integral for the production of almost all components of biomass. A version of this table with all gene names is available (see Table S1 in the supplemental material).

Comparison with experimental data on growth on amino acid.

Model behavior was assessed by comparing uptake and/or secretion flux predictions with the corresponding experimentally measured rates reported by Takahashi et al. (90) for in vitro growth of P. gingivalis under different amino acid availability conditions (see Fig. 3, 4, and 5). The set of experimental data in this work details the amount of each amino acid initially available in the medium (C_i for amino acid i), as well as the amounts actually used by the cells throughout the experiment (ΔC_i). If T is the time length of the experiment, and B the total amount of biomass produced, the upper bound to the uptake fluxes to impose in the model should be u_i^(UB) = C_i/(T·B), while the experimental fluxes to which predictions should be compared will be roughly u_i^(Exp) = ΔC_i/(T·B). Hence, since all fluxes are defined up to a factor (T·B, which is experimentally determined and is the same for all amino acids), we may as well solve the FBA problem by imposing rescaled upper bounds w_i^(UB) = C_i and make sure to compare the outcome results to the rescaled fluxes w_i^(Exp) = ΔC_i. In the figures, to make the interpretation easier, we plot the fraction of influx of each amino acid relative to the total amino acid uptake, i.e., the quantities w_i^(Exp)/Σw_i^(Exp) and w_i^(FBA)/Σw_i^(FBA) for the experimental and FBA-predicted fluxes, respectively. The media used by Takahashi et al. provided tryptone as the primary source of amino acids. One may worry about the fact that, in addition to tryptone, the medium used in the experiment contains also yeast extract, whose complex composition cannot be easily mimicked in silico. However, we are primarily concerned in the present study with amino acid availability, whose actual initial concentrations (irrespective of their origin) are measured in the experiment and provided here. Model-predicted amino acid uptake rates were computed with FBA, assuming optimal growth (See details of FBA above, and Fig. 3A). Corresponding experimental amino acid uptake rates were estimated as the concentration changes of amino acids in the medium in the first 240 min of the experiment (Table 2). Currently, the model does not make the distinction between peptides and free amino acids. As a result, the uptake rates were calculated based on the sum of the concentration changes for free amino acids and peptides. In addition to amino acid uptake rates, Takahashi et al. report the experimentally measured production rates of several fermentation products during growth in the tryptone-based medium. For additional validation of the model, we compared these secretion rates with corresponding model predictions (Fig. 3B and C and 4). Assessment of model predictions of by-product secretion rates revealed that there was a wide range of production rates, which were compatible with the optimal growth rate and amino acid uptake rates. For the purpose of comparing model predictions to the experimentally measured production rates, we selected two specific sets of feasible production rates to display, both equally consistent with optimal growth. The first is the set of production rates at minimal Manhattan distance from the experimental measurements. The second is the set of production rates achieved when the sum of the absolute values of fluxes through the entire metabolic network is minimized (see below for the rationale for using this secondary objective) (88).

FIG. 4.

The predicted catabolic routes for glycine, alanine, serine, threonine, aspartate and glutamate relative to the analysis illustrated in Fig. 3 are shown on a metabolic network generated with the VisANT network visualization tool. Red nodes represent reactions, and blue nodes represent metabolites. An edge leading from a metabolite to a reaction indicates that the metabolite is a reactant, while an edge leading from a reaction to a metabolite indicates that the metabolite is a product. Relative reaction flux rates are represented by the thicknesses of the edges between metabolite and reaction nodes. This visualization demonstrates how different amino acids enter central carbon metabolism and allow for production of biosynthetic precursor metabolites and ATP. ATP production is primarily associated with the conversion of acetyl-CoA to acetate, which occurs through reactions catalyzed by phosphotransacetylase and acetate kinase, respectively.

FIG. 5.

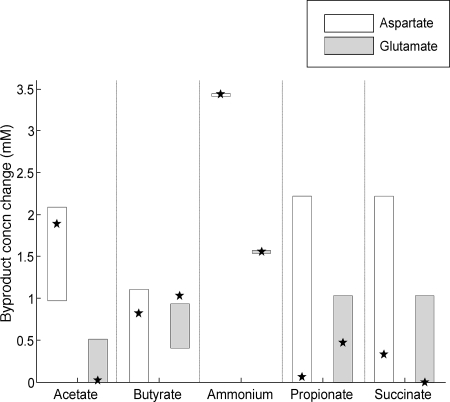
Comparison of predicted and measured by-product secretion rates during growth in a medium with aspartyl-aspartate or glutmayl-glutamate dipeptides as the primary source of amino acids (see Materials and Methods). The vertical boxes indicate the ranges of predicted secretion rates compatible with optimal growth in a medium rich in aspartate (□) or glutamate (░⃞). With the exception of butyrate production in the presence of glutamate, all experimental measurements of by-product secretion fall in the range of model predictions. Furthermore, the model accurately captures the tendency for P. gingivalis to produce less acetate and succinate, but more butyrate, when grown in glutamate-rich medium, relative to what is observed in aspartate-rich medium. On the other hand, the model fails to predict the correct trend for propionate.

TABLE 2.

Amino acid-rich minimal medium^a

Medium component	Concn (mM) in modified amino acid-rich medium
Ala	2.9
Arg	2.35
Asn	0
Asp	3.25
Cys	0.2
Gln	0
Glu	12.4
Gly	2.4
H2O	—b
Heme	10
His	1.35
Ile	2.2
Leu	4.65
Lys	3.15
Met	0.55
Phe	1.9
Phosphate	10
Pimelate	10
Pro	5.55
Ser	4.05
Thiamine	10
Thr	2.75
Trp	1
Tyr	0.9
Val	3.9

^aModified from Takahashi et al. (90). Pimelate and thiamine are not present in the original media but are required for the current model. Pimelate, thiamine, phosphate, and heme are added in excess to make sure that they are not limiting factors.

^b—, Water uptake is not constrained in the model.

In addition to the data presented above for growth in a tryptone-based medium, Takahashi et al. also report a set of by-product secretion rates in media where the primary amino acid source is glutamyl-glutamate or aspartyl-aspartate. In order to compare model predictions to these data (see Fig. 5), we simulated the relevant media by setting the upper bound on the uptake of glutamate (aspartate) to 10 times the one of the other amino acids. The specific upper bounds for amino acids were set so that the model prediction for ammonium secretion would match the corresponding experimental values.

LPS targeted knockouts.

In the knockout map presented in Fig. 6 we sought to determine whether the perturbed cell can produce a specific biomass component, irrespective of whether the capacity to produce all other components was compromised or not. In analyzing in more detail the producibility of LPS molecules (Fig. 7 and Table 3), we wanted to implement a slightly different approach that would mimic the situation of a cell that could still potentially survive but be defective in the capacity to produce LPS. Therefore, we removed the requirement for LPS production from the definition of biomass. A fixed lower bound (10% of wild-type complete biomass growth rate under the same conditions) was then added to the modified objective, forcing the model to produce all other components of the biomass. In the subsequent computation of all reaction knockouts, we used as an objective function a sink reaction that exports each one of the three LPS molecules in turn. Only knockouts of reactions that were associated with one or more specific proteins were selected for further analysis. Knockout strains predicted to be able to grow but not able to produce one of the LPS molecules would provide potential targets for impairing the ability of P. gingivalis to produce LPS.

TABLE 3.

Predicted reaction knockouts that affect the production of LPS without affecting the production of other biomass components^a

Reaction	Protein ID	Gene	Description
GMAND	PG1288	gmd	GDP-d-mannose dehydratase
KDOPP	PG0658		3-Deoxy-manno-octulosonate-8-phosphatase
GFUCS	PG1289	fcl	GDP-l-fucose synthase
PMANM	PG1094, PG2010	pgm	Phosphomannomutase
MAN6PI	PG0468	manA	Mannose-6-phosphate isomerase
MAN1PT2r	PG2215	manC	Mannose-1-phosphate guanylyltransferase (GDP) reversible
UDPG4E	PG0347	galE	UDP-glucose 4-epimerase
KDOCT	PG1815	kdsB	3-Deoxy-manno-octulosonate cytidylyltransferase

^aHere we include only reactions associated with a specific P. gingivalis protein. For each reaction, we list the KEGG protein identification (ID) and gene name, as well as a description of the enzyme function. The entry in boldface is a knockout for which an effect has been reported in the literature (59).

Network visualization.

The central carbon metabolic fluxes in Fig. 4 were displayed by using the freely available VisANT network analysis software package (33). Metabolic networks were displayed as a bipartite graph, with the two classes of nodes representing reactions and metabolites. Edges are directed, such that an edge leading from a metabolite to a reaction indicates that the metabolite is a reactant in the connected reaction, and an edge leading from a reaction to a metabolite indicates that the metabolite is a product of the reaction. Edges were weighted by their relative flux through the network, such that a thicker edge indicates a larger flux. The metabolic chart of Fig. 2, and its LPS biosynthesis subgraph, shown enlarged in Fig. 7, were generated automatically using the network visualization package GraphViz (dot.exe script) through Matlab. Subgraphs, enclosed in boxes, represent individual pathways (based on the pathway annotation available in the spreadsheet in the supplemental material). An interactive, zoomable, and searchable version of the network is available online at http://prelude.bu.edu/pg/.

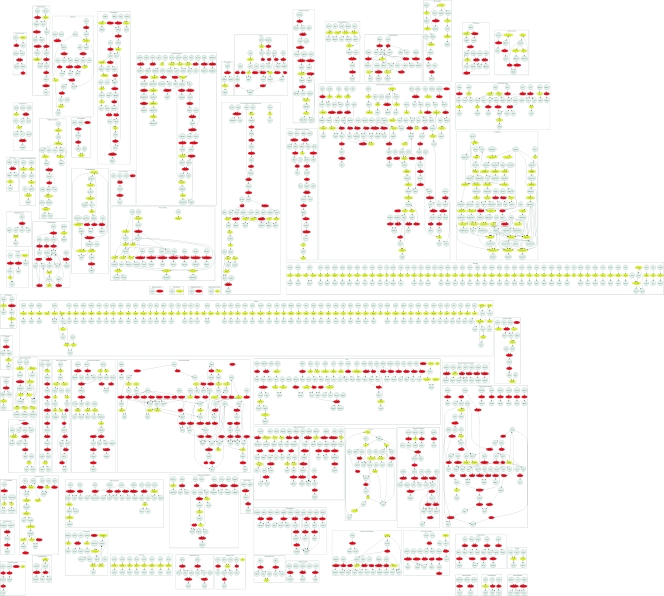
FIG. 2.

Representation of the whole P. gingivalis metabolic network model using the GraphViz package (see Materials and Methods). The reactions are grouped by pathway. Some reactions and metabolites are present in more than one pathway (see spreadsheet in the supplemental material for details). Highly connected metabolites such as ATP and NADH have been removed to simplify the layout. Gray nodes denote metabolites, whereas red and yellow nodes denote specific reactions. Red nodes are reactions that are associated with specific proteins; yellow nodes denote putative reactions.

RESULTS

We assembled the genome-scale metabolic network stoichiometry of P. gingivalis W83 by integrating multiple data sources (Fig. 1A). As with most previous stoichiometric models, the bulk of information utilized was derived from the annotated sequenced genome of the organism (61). In particular, we used sequence-derived annotation of enzyme genes to infer the presence of the corresponding metabolic reactions (see Materials and Methods). A total of 319 reactions were inferred directly from the genome annotation, and the corresponding stoichiometries were derived from online databases (BIGG and KEGG; see Materials and Methods and Fig. 1). As demonstrated in previous genome-scale metabolic network models (24, 63, 64, 92), standard genome annotations are typically not sufficient to produce networks detailed and complete enough to serve as the basis for quantitative modeling. In particular, holes in a pathway, missing transporters, or isolated subnetworks, which are abundantly found in networks generated from such automated annotation, can affect the predictive capacity of the model and must be addressed by additional methods. While some automated methods for pathway completion are available and are subject of active research (26, 74, 80), the most reliable approach for achieving good predictive capacity is currently still to complement genome analyses with manual curation and literature searches. Our manual curation of the model involved (i) adding putative transporters matching the results of a transport prediction tool; (ii) incorporating reactions lacking a gene and EC number, found in the most closely related previously reconstructed stoichiometric model (that of H. pylori; see Fig. 1B); and (iii) refining the list of reactions based on biochemical evidence reported in the literature. The proportions of reactions added based on different criteria, broken by pathway categories, can be seen in Fig. 1A. The reactions added from the KEGG database (and not found in previously reconstructed E. coli, H. pylori, and S. cerevisiae models) are enriched for cofactor and vitamin-related functions, as well as for amino acids metabolism. This last aspect is a preliminary indication of the importance of amino acids catabolism in P. gingivalis relative to other organisms. The abundance of lipid-related reactions in the category of manual curation reflects largely the complexity of the LPS biosynthesis pathways, on which we focused in detail. The complete list of reactions, including references to relevant literature, and the criteria that warranted their inclusion in the model, are available in the in the supplemental material.

The current version of the fully assembled P. gingivalis network includes a total of 679 reactions and 564 metabolites. Following a custom established in previous FBA models, we named our model iVM679. A bird's-eye view of the P. gingivalis metabolic network, zoomable and searchable in the online version, can be seen in Fig. 2. The network, whose layout (subdivided by pathway categories) was generated automatically (see Materials and Methods), includes two types of nodes: metabolites (gray) and reactions (red or yellow). Red reaction nodes correspond to reactions for which a specific gene and protein was identified, and yellow reaction nodes to reactions inferred or putative, lacking a corresponding gene. The overview figure, while not readable in detail, emphasizes the overall distribution of reactions associated with known genes in the network. Uncertainty seems uniformly distributed throughout the network. This implies on one hand that the challenge of producing predictions compatible with experimental observations is greater than in other cases. At the same time, this also means that the potential for discovery is unusually rich.

The lack of comprehensive studies of P. gingivalis metabolism poses challenges not only for model construction but also for model validation. Thorough validation of metabolic models requires quantitative experimental data capturing metabolic behaviors under specific environmental conditions (88). To fulfill the need for quantitative data describing the metabolic behavior of P. gingivalis, we utilized data previously published by Takahashi et al. (90). In their study, Takahashi et al. grew P. gingivalis on a medium containing tryptone as the primary carbon, nitrogen, and energy source and measured amino acid uptake rates, along with by-product secretion rates. This data set is ideal for assessing our metabolic model for two reasons. First, the tryptone-based medium provides a physiologically relevant glimpse into P. gingivalis metabolic behavior, since it is well known that P. gingivalis primarily relies on peptides scavenged from the oral cavity to meet its metabolic needs (101). Second, the fact that both metabolic inputs and outputs were measured over time allowed us to assess the model's nutrient preferences and catabolic pathway utilization.

The tryptone media provided contained all 20 amino acids, in concentrations proportional to the amino acid composition of the protein. An initial observation made by Takahashi et al. was that P. gingivalis showed different preferences for different amino acids, as demonstrated by the variability in their uptake rates. This observation suggested that P. gingivalis prefers certain amino acids as primary carbon sources. As a first assessment of our metabolic model, we sought to determine whether we could reproduce the amino acid usage under the studied condition. To do this, we simulated a condition in which amino acids were available in the proportions reported by Takahashi et al. and computed the amino acid usage, assuming maximum growth rate as the metabolic objective. Imposition of a metabolic objective is necessary with flux balance models in order to select a particular set of fluxes, among all those that are compatible with steady-state and nutrient availability constraints. Maximal growth is often used as a metabolic objective (38, 79, 96), with the underlying assumption being that an organism has evolved to meet metabolic challenges in an optimal manner. Comparisons of experimentally determined and model-predicted amino acid usage are shown in Fig. 3A. Specifically, we compared predicted amino acid uptake rates with experimentally measured changes in amino acid concentrations in the media after 240 min (see Materials and Methods for details). The correlation between predicted and observed amino acid usage is highly significant (Spearman rank; r = 0.77, P = 4.0 × 10⁻⁴), indicating that the model accurately captures the relative efficiencies with which different amino acids can be catabolized. Although the correlation is overall quite strong, it should be noted that some uptake rates are predicted better than others, suggesting that certain catabolic pathways may be incomplete in the model. In addition, while some correlation exists between the imposed upper bounds derived from initial amino acid concentrations and the experimental uptake rates, correlation of predicted uptake rates is stronger with the latter.

Assessment of the model's ability to reproduce amino acid usage evaluates how well the model captures the relative efficiency with which different amino acids are transformed into biomass components. On the other hand, the ability to predict amino acid uptake rates does not guarantee the correctness of the pathways by which the amino acids are predicted to be catabolized. To provide further support for the correctness of model-predicted catabolic routes, we next compared predicted by-product secretion rates to those reported by Takahashi et al. for the same tryptone-based medium composition discussed above (90). The results for this comparison are shown in Fig. 3B, with model predictions again based on an optimal growth assumption. Although imposition of the optimality assumption resulted in unique predictions of amino acid uptake rates, there was a wide distribution of by-product secretion rates that were compatible with the optimality assumption. This is due to the presence of alternative optima, or in other words, to the existence of several routes through the metabolic network which all result in equal growth under the modeled condition (51, 79). The results in Fig. 3B are for two specific alternate optima, one minimally distant from the experimental observation and the other obtained by assuming the minimal overall flux necessary to achieve optimal growth (see Materials and Methods and reference 32).

It can be seen in Fig. 3B that for both of these particular model solutions, predicted by-product secretion rates match experimentally measured values for all products, with the exception of succinate, for which the model predicts more production than was observed experimentally. Despite the concordance between both sets of model predictions and the experimental values, it is clear that there are differences between these two sets of model predictions, despite the fact that both were consistent with the identical growth rate. Specifically, the fluxes predicted based on minimal overall flux did not predict sufficient amounts of butyrate, propionate, or acetate and in turn predicted more succinate to be produced.

The apparent flexibility in amino acid catabolic pathways, as demonstrated by the range of by-product secretion rates compatible with optimal amino acid usage, prompted us to next explore the relationship among the production rates of different by-products. Figure 3C shows the relationship between three major amino acid catabolic by-products: succinate, propionate, and butyrate. These relationships were determined by computing all possible secretion fluxes for these three by-products, which are compatible with the previously determined optimal growth. Figure 3C demonstrates that there is abundant flexibility in the production of these three by-products. In other words, the only constraint seems to be on the total by-product formation and not on the particular by-product that is formed. The implication of this is that the metabolic routes to these by-products are equivalent with respect to redox balancing and energy production. The catabolic routes (and flux intensities) from all amino acids predicted to be utilized as carbon sources to succinate, propionate and butyrate are shown in Fig. 4.

Although the predicted flexibility in by-product secretion by P. gingivalis in tryptone medium has potentially interesting implications for community interactions (see Discussion), it suggests that a clearer insight into specific amino acid degradation processes might be gained from studying growth in simpler media, e.g., rich in a single amino acid at a time. To this end, we utilized additional data provided by Takahashi et al. for by-product production rates in media where the primary amino acid sources were glutamyl-glutamate or aspartyl-aspartate dipeptides, as opposed to tryptone (see Materials and Methods). We specifically wanted to see whether the model could capture the differences in fermentation product secretion rates between the two media, reflecting the different catabolic routes for aspartate and glutamate. Figure 5 shows the predicted ranges for by-product production and the experimentally measured values. With the exception of butyrate production under glutamate availability, all experimental measurements fall within the range of model predictions. In addition, for all by-products except propionate, the rank of the averages of the predicted ranges under the two conditions studied reflects the experimentally measured ranks.

As mentioned above, one of the applications for which the computational efficiency of FBA has been particularly useful is the systematic prediction of the effects of genetic perturbations, especially gene deletions (20, 79). After validating that our model is consistent with experimental measurements of amino acid uptake and organic acid secretion, we therefore performed a systematic analysis of perturbations, both to gain insight into whether our model can capture biologically significant features and to exemplify the potential use of this model for biomedical applications. The analysis presented in Fig. 6 differs slightly from previous systematic gene deletion analyses performed for other organisms. Since, in the case of P. gingivalis, there are often not enough data to establish a specific relationship between genes and reactions, we do the knockout experiment at the level of reactions rather than with respect to genes. This implies, for example, that if we wanted to really block a reaction whose deletion produces a useful phenotype, we would have to independently identify the gene or genes whose enzyme protein product allows that reaction to occur (possibly affecting other reactions as well). Moreover, in addition to looking at whether a certain reaction knockout strain can or cannot produce all biomass components simultaneously and in the correct proportions, we check what single biomass components fail to be produced upon the perturbations. Since we have 596 reactions to delete and 53 objectives to maximize (52 single components and 1 complete biomass), this amounts to 31,588 FBA calculations, which are summarized, after two-dimensional clustering, in Fig. 6. The outcome of this calculation is similar to the producibility analysis performed previously for E. coli (35). Gray or black bars in Fig. 6 indicate that the specific deletion strain cannot produce the selected biomass component. The bar is black for reactions for which a specific P. gingivalis gene was identified and gray otherwise. Colored boxes highlight selected clusters of reactions and biomass components for which one can clearly identify the biology behind the observed patterns. For example, knockouts enclosed in the green box are related to LPS production. Most (but not all) reactions in this cluster are explicitly annotated as being LPS related. Also, most of these reactions have no associated gene and affect all three LPS molecules. Reactions associated with LPS production defects and which have an associated gene are discussed in more detail later. Another significant cluster of biomass components not producible upon several deletions is the one marked in blue. This involves defects in CoA, succinyl-CoA, and acetyl-CoA production. As indicated by the pathway enrichment of the reactions in this block, deletions tend to cause a disruption in CoA production from alanine B. Another cluster of reactions very prominent in Fig. 6 is the one associated with many biomass components (red box). Related knockouts found are enriched for pyrimidine and purine biosynthetic pathways. Since most cofactors such as gtp and atp are connected to this pathway, it would be expected that disruption of purine and pyrimidine synthesis would disrupt cofactor production. Gluconeogenesis (yellow box) is instrumental in the production of a number of cofactors from glycolytic intermediates.

The cluster of knockouts associated with defects in the production of LPS is worth further investigation. P. gingivalis LPS are very important due to their proven role in triggering a strong human immune system response. In order to generate predictions amenable to experimental testing, we repeated the knockout in silico experiments for the production of LPS, while at the same time requiring a minimal rate of production of all other biomass components. In other words, for a specific LPS molecule, we sought to determine what reaction knockout might give rise to a viable cell that lacks only that specific LPS. The pathway for production of LPS is rather complex (Fig. 7 and see Materials and Methods). Some of its genes were identified in the genome of P. gingivalis, but many other are still unknown. The results of the knockout experiment for LPS, restricted to reactions with an associated gene, are summarized in Table 3. Some genes in this table, GMAND and GFUCS, help to produce GDP-l-fucose, which is vital in the final step of LPS assembly. PMANM, MAN6PI, and MAN1PT2r are also involved in alternative carbon metabolism. These reactions process fructose-6-phosphate into GDP-d-mannose, a precursor of GDP-l-fucose. The KDOPP and KDOCT reactions produce CMP-3-deoxy-d-manno-octulosonate, which is a component of bacterial LPS. The UDPG4E mutant stops the production of UDP-galactose from UDP-glucose. UDP-galactose is required in multiple steps within the LPS synthesis pathway. This specific mutant has been documented (59) and is known to have a shortened O-antigen chain as a result but was still viable. In light of this experimental validation of our modeling approach, it will be useful to experimentally test the other potential knockouts listed in Table 3.

DISCUSSION

The stoichiometric model we assembled for the metabolic network of P. gingivalis W83 was obtained largely from genomic information. As opposed to most other previous FBA models, this one is built for an organism whose biochemistry is still poorly understood. This implies, on one hand, that significant uncertainty should be expected in the prediction of growth or flux phenotypes, especially under growth conditions different from the one under which the model was curated and tested. On the other hand, this also implies that the proposed stoichiometry will probably be very useful in the future as a dynamical tool for generating hypotheses that can be tested experimentally. Previous genome-scale stoichiometric models, such as the ones for E. coli and S. cerevisiae, were first published in 2000 and 2003, respectively (20, 25), and have since undergone significant improvement, reaching high levels of agreement with high-throughput experimental data. Given the increasing interest in the metabolic properties of the human oral microbiome, we envisage that a similar refinement process will take place in the coming years also for the P. gingivalis model. Until more iterations of experimental validation and model refinement are performed, the currently proposed P. gingivalis stoichiometry, similarly to several first-round genome scale models, should be regarded more as an exploratory framework than a ready-to-use tool. Improvement of the P. gingivalis model will also have to address the presence in the literature of analyses performed using multiple strains, whose metabolic differences are currently difficult to detect but might become relevant in the future.

Our comparison of model predictions and experimental data for growth on amino acids shows that, despite the current level of uncertainty for several reactions in the stoichiometric model, the FBA approach already constitutes a valuable quantitative framework for the study of P. gingivalis. Upon feeding the FBA algorithm with stoichiometric coefficients, nutrient limitations, and an objective function to be maximized or minimized, one receives back a prediction of all reaction fluxes, including the biomass production flux (growth rate) and the uptake/secretion rates. Since the FBA problem is posed as a linear programming problem in a convex space, it is guaranteed that no multiple local optima will exist. However, the global optimum may not be unique, i.e., there may be multiple (in fact, infinitely many) solutions that are equally optimal for the desired criterion. Although this may be seen as a meaningless mathematical complication, it is possible that the freedom of choice inherent in multiple optima carries important biological meaning (51, 79). In the analysis presented here we found a potentially very relevant case of multiple optima, whose explanation might relate to the interaction of P. gingivalis with other organisms. The surface presented in Fig. 3C demonstrates that, upon amino acid catabolism, the organism is predicted to secrete as fermentation products succinate, propionate, and butyrate. All points on the surface are equally optimal for growth rate, meaning that the cell can, within certain overall constraints, arbitrarily choose what proportion of each to secrete. The model thus tells us that, from the perspective of energetic or reducing power economy, there is no reason to prefer one over the other. However, as seen in Fig. 3B, the cell does choose a certain proportion and specifically produces butyrate and propionate, but no succinate. There could be several explanations for this observation, two of which fit nicely with independently known facts about the physiology of P. gingivalis. The first is that succinate is being produced as a catabolic by-product but can be recycled internally. This would be compatible with the observation that succinate secreted by Capnocytophaga ochracea, Actinomyces viscosus, Prevotella intermedia, or Prevotella nigrescens is known to be used by P. gingivalis to produce ATP (85). Alternatively, the cellular choice of secreting mostly butyrate and propionate might be a deliberate evolved strategy for inducing harm to host cells or for supplying partner organisms with a share of useful nutrients (27, 42, 89). In other words, the metabolic freedom, which the cell might control transcriptionally or posttranscriptionally, might be indicative of a controllable degree of interactions with other organisms and with human host cells.

In addition to relating model predictions to experimental data, we have analyzed the response of the network to systematic perturbations of single reactions. At this stage, the map of Fig. 6 should be seen mostly as a set of guidelines for how to prioritize future experimental testing helpful for model refinement. Although experiments with P. gingivalis gene deletions are possible and have been performed (57), the focus has not been on metabolic enzymes. The results shown here indicate that a lot can be learned from such knockouts, especially when the data can be compared to FBA predictions. The added value of combining FBA models with phenotype measurements across different mutants and conditions has been recently reported for S. cerevisiae (88).

The current P. gingivalis predictions for reaction deletions are particularly promising for the LPS biosynthesis pathway. We identified several genes whose deletion we predict would disrupt the capacity to produce LPS. Some of these deletions are upstream of the actual LPS biosynthesis pathway. This emphasizes the importance of genome-scale analyses, since correlations between functions in apparently unrelated pathways are more common than one might think (78). The reaction deletions for which we can identify specific P. gingivalis genes do not act selectively on different LPS but block the production of all three LPS types simultaneously. Other putative reaction deletions visible in Fig. 6, however, do block selectively specific LPS molecules. It is known that different specific LPS molecular types affect differently the immune system response (16). In particular, it has been shown that an LPS preparation enriched for lipid A species at m/z 1,435 and 1,450 activates human and mouse TLR2, TLR2 plus TLR1, and TLR4 in transiently transfected HEK 293 cells coexpressing membrane-associated CD14 (16). From a therapeutic perspective, selectively blocking the production of specific LPS would be especially valuable to allow control the inflammatory deleterious consequences of LPS production short of eradicating or weakening P. gingivalis, given its potential role in biofilm equilibrium and homeostasis. It is increasingly clear that the microbial consortia that populate the human body serve fundamental beneficial purposes, including protection from much more dangerous bacterial or fungal infections. Hence, in order to contain infectious diseases caused by species constantly present in the human microbial flora, it might be more productive to target specific disease-related pathways than to try and wipe out entire species. In other words, new drugs could target specific microbial biosynthetic pathways without causing major disruption in the global dynamic balance of microbial consortia. While in the present study we focused mostly on LPS as an example of a biomedically relevant pathway to study in depth, other metabolic pathways crucial for the pathogenicity of P. gingivalis could be the focus of future work, such as the pathways related to heme biosynthesis and utilization.

We find it exciting that several molecules known to mediate the interaction of P. gingivalis with host human cells and with the rest of the human microbial flora are already present in the proposed version of the stoichiometric model. Additional molecules, such as quorum-sensing signals, could be incorporated in future versions (54). In the context of microbe-microbe interactions, one of the future tasks of a flux balance model could be to discriminate between molecules that are relevant for growth because they represent building block or electron sources, and molecules that are essential for growth because they represent “green light” signals, reflecting favorable environmental conditions. As the construction of stoichiometric models becomes increasingly more automated and broadly approachable, models of different microbial species will facilitate the study of what differentiates metabolic functions of microbial consortia under normal and disease states. The capacity to approach this problem in a quantitative way, in addition to being useful for biomedical applications, will allow researchers the opportunity to address fundamental questions about microbial consortia dynamics and evolution. For example, since optimization methods are one of the key components of genome-scale metabolic network modeling, it might be possible to determine whether individual species are metabolically optimized for their own survival or rather for striving in the context of the biochemical properties of surrounding organisms.