Abstract
Facile diffusion of globular proteins within a cytoplasm that is dense with biopolymers is essential to normal cellular biochemical activity and growth. Remarkably, Escherichia coli grows in minimal medium over a wide range of external osmolalities (0.03 to 1.8 osmol). The mean cytoplasmic biopolymer volume fraction (〈φ〉) for such adapted cells ranges from 0.16 at 0.10 osmol to 0.36 at 1.45 osmol. For cells grown at 0.28 osmol, a similar 〈φ〉 range is obtained by plasmolysis (sudden osmotic upshift) using NaCl or sucrose as the external osmolyte, after which the only available cellular response is passive loss of cytoplasmic water. Here we measure the effective axial diffusion coefficient of green fluorescent protein (DGFP) in the cytoplasm of E. coli cells as a function of 〈φ〉 for both plasmolyzed and adapted cells. For plasmolyzed cells, the median DGFP (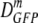 ) decreases by a factor of 70 as 〈φ〉 increases from 0.16 to 0.33. In sharp contrast, for adapted cells,
) decreases by a factor of 70 as 〈φ〉 increases from 0.16 to 0.33. In sharp contrast, for adapted cells, 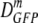 decreases only by a factor of 2.1 as 〈φ〉 increases from 0.16 to 0.36. Clearly, GFP diffusion is not determined by 〈φ〉 alone. By comparison with quantitative models, we show that the data cannot be explained by crowding theory. We suggest possible underlying causes of this surprising effect and further experiments that will help choose among competing hypotheses. Recovery of the ability of proteins to diffuse in the cytoplasm after plasmolysis may well be a key determinant of the time scale of the recovery of growth.
decreases only by a factor of 2.1 as 〈φ〉 increases from 0.16 to 0.36. Clearly, GFP diffusion is not determined by 〈φ〉 alone. By comparison with quantitative models, we show that the data cannot be explained by crowding theory. We suggest possible underlying causes of this surprising effect and further experiments that will help choose among competing hypotheses. Recovery of the ability of proteins to diffuse in the cytoplasm after plasmolysis may well be a key determinant of the time scale of the recovery of growth.
Facile diffusion of globular proteins in the cytoplasm of bacteria is essential for growth and adaptation to stress, but diffusion is hindered by the presence of other biopolymers. For Escherichia coli in the exponential-growth phase in minimal medium at the optimal osmolality of 0.28 osmol, 16% of the cytoplasmic volume is occupied by biopolymers (mean cytoplasmic biopolymer volume fraction [〈φ〉], 0.16). For growth at 1.45 osmol, 〈φ〉 increases to about 0.36, and the growth rate decreases by a factor of 9 (4, 5). However, growth at high osmolalities can be achieved only by gradually transferring cells to growth media of successively higher osmolalities. When cells are plasmolyzed, i.e., abruptly shocked by a high external solute concentration, a substantial fraction of the cytoplasmic water is extracted on a time scale of a few seconds. Plasmolysis is the initial event that triggers subsequent osmoregulation processes: energy-dependent intake of K+, biosynthesis of glutamate anion and neutral osmoprotectants such as trehalose, and, if plasmolysis is not too severe, eventual recovery of growth.
Proteins at high total concentrations may inhibit each other's diffusion by simple crowding (23). In addition, a substantial fraction of the biopolymer mass is part of a branched, time-varying “supermolecule” comprising the nucleoid, associated architectural proteins, RNA polymerase, nascent mRNA chains, attached ribosomes, and nascent polypeptide chains (38). The resulting cross-linked meshwork fragments free space into smaller regions interconnected by passageways that may become sufficiently narrow to hinder further protein diffusion. Such macromolecular crowding and confinement at high 〈φ〉 values also affects the thermodynamics and kinetics of folding (33), assembly (18, 20), and binding (24). Quantitative studies of such biomolecular processes in vivo can shed new light on the remarkable ability of the cell to function over a wide range of 〈φ〉 values (8, 14). They can also inform the kind of modeling necessary to adapt in vitro biochemical results to the living cell (6, 10).
We recently reported strong effects of increasing 〈φ〉 on protein diffusion in vivo (17). Cytoplasmic water was extracted from a B strain of E. coli grown in rich medium at 0.24 osmol by plasmolysis in hyperosmotic medium lacking carbon sources and containing only membrane-impermeant solutes, either NaCl or sucrose. These conditions prohibit active K+ uptake and the usual biochemical adaptation to osmotic stress. In effect, cells are locked into a physical and biochemical condition closely approximating the transient state that would occur immediately after a sudden osmotic upshift but before adaptation can begin. The mean effective axial diffusion coefficient (〈DGFP〉) of green fluorescent protein (GFP) in the cytoplasm on a length scale of ∼0.5 μm decreased by a factor of 430 as the plasmolysis osmolality increased from 0.24 to 0.94 osmol. The recovery of proteins' ability to diffuse in the plasmolyzed cytoplasm may well be a key determinant of the time scale of recovery of growth.
Here we extend the work to GFP diffusion in a K-12 strain grown in minimal medium under conditions for which the amounts of cytoplasmic water, small solutes, and biopolymers are known (4). This enables us to compare GFP diffusion in cells that have the same large value of 〈φ〉, achieved in two very different ways: (i) growth at the optimal 0.28 osmol followed by plasmolysis and (ii) adaptation and growth at a high external osmolality. Remarkably, in cells adapted to growth at the high 〈φ〉 of 0.36, the median GFP diffusion coefficient is only 2.4 times smaller than that for a 〈φ〉 of 0.16 but some 30 times larger than that observed in plasmolyzed cells at a similar 〈φ〉.
For strongly plasmolyzed cells, the distribution of DGFP becomes broad and skewed. Accordingly, throughout this paper we characterize distributions of DGFP by the median value, which we call 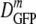 ; by the interquartile range (IQR), the range in which the central 50% of the data lie, which we call δDIQR; and by the total range of values. The compact notation
; by the interquartile range (IQR), the range in which the central 50% of the data lie, which we call δDIQR; and by the total range of values. The compact notation 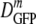 (δDIQR) = xx.x (y.y) μm2·s−1 stands for
(δDIQR) = xx.x (y.y) μm2·s−1 stands for 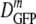 = xx.x μm2·s−1 and δDIQR = y.y μm2·s−1. For skewed distributions, the IQR is not centered on the median value. The more typically used mean and standard deviation are also given in the tables. For reasonably symmetric distributions, such as those for cells adapted to growth at high salt concentrations, the mean and median differ little.
= xx.x μm2·s−1 and δDIQR = y.y μm2·s−1. For skewed distributions, the IQR is not centered on the median value. The more typically used mean and standard deviation are also given in the tables. For reasonably symmetric distributions, such as those for cells adapted to growth at high salt concentrations, the mean and median differ little.
MATERIALS AND METHODS
Bacterial strain and sample preparation.
We studied the E. coli K-12 strain MG1655 expressing GFPmut2 as described in the supplemental material. GFP dimerizes weakly (binding constant [Kb] ≈ 104 M−1 in vitro) and may well exist primarily as a dimer in the cytoplasm (28). The quantitative modeling assumes that GFP dimers are the diffusing entities, but our conclusions are substantially the same if GFP exists as monomers. The GFP diffusion coefficient was measured for cells grown in morpholinopropanesulfonate (MOPS)-buffered glucose minimal medium (MBM) (25) under conditions ranging from 0.10 osmol MBM (low salt) to 1.45 osmol MBM (near the upper limit of viability in MBM). In addition, we studied GFP diffusion in cells grown in 0.28 osmol MBM and plasmolyzed by resuspension in a buffer containing a higher NaCl concentration. The osmolalities of all growth media and resuspension buffers (RBs) was measured to ±0.005 osmol with a Wescor vapor pressure osmometer.
For both adapted and plasmolyzed cells, the RB was the same MBM growth medium but without glucose or K2HPO4 and with NaCl added to obtain the desired final osmolality. The adapted cells were studied in an RB that was isosmotic to the growth medium (whose osmolality was varied), while the plasmolyzed cells were studied in an RB at an osmolality higher than that of the growth medium (0.28 osmol). Such plasmolyzed cells were tested for viability by plating them on agar made from standard MBM growth medium at the osmolality to which they were upshifted, incubating them for 24 h at 37°C, and counting viable colonies. Viability was 100% that of control cells that had not been osmotically stressed.
Fluorescence microscopy and data analysis.
The diffusion measurements were carried out as described previously (17). Seven microliters of cell suspension was placed on a poly-l-lysine-coated slide. A coverslip was added and sealed to prevent evaporation. Cells were grown at 30°C, but diffusion was studied at 25 ± 2°C. Recent experiments using a temperature-controlled microscope stage enabled us to grow cells and study their diffusion at 37°C. The results differ very little from those reported here. Isolated and well-adhered cells of medium brightness were selected for study. Figure 1 shows representative cell images. An uninterrupted, roughly cylindrical segment at least 0.6 μm long was necessary to allow accurate diffusion measurements. Septating cells were omitted. Experiments were limited in time to 45 min after resuspension in order to minimize changes in cell physiology.
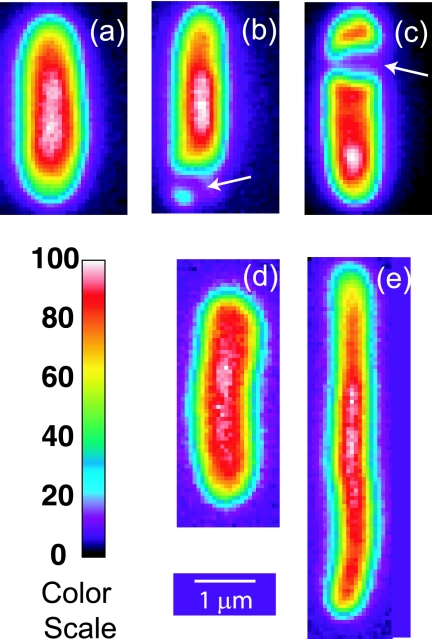
FIG. 1.
Prebleach images of representative cells. A false-color scale is given at the lower left. Cells a, b, and c were grown in 0.28 osmol; cell a was resuspended in isosmotic buffer, while cells b and c, which exhibit visible PSs (arrows), were upshifted from growth at 0.28 osmol to 0.85 osmol. Cells d and e exhibit the normal and thread-like morphologies observed for growth at 1.45 osmol.
The DGFP in live cells was determined by fluorescence recovery after photobleaching (FRAP) as described in detail elsewhere (17). The bleach beam (full width at half-maximal intensity [FWHM], 0.9 μm; duration, 100 to 200 ms; 32 kW/cm2) was positioned at either end of the cylindrical segment of the bacterium. After a single bleach pulse, the weaker probe beam (FWHM, 18 μm; 100 W/cm2) produces a continuous sequence of “snapshots” of the entire cell, recorded on a charge-coupled device camera at 26 ms/frame. For slower diffusion, frames were spaced in time by a variable delay.
The DGFP is obtained by “squashing” the 2-dimensional intensity image onto a line and measuring the single-exponential decay time of the first Fourier mode of the 1-dimensional intensity profile, as described previously (8). The quality of the single-exponential fits is generally good. Recovery of the original shape of the axial GFP spatial distribution is complete under all conditions studied. There is no evidence of an immobile fraction of GFP on the time and length scales of the measurements. The effective length was corrected for the presence of one or two hemispherical endcaps as described previously (17). Multiple measurements on the same cell produced results within ±10% of the mean for that cell. For ellipsoid cells, the absolute accuracy is limited to about ±20% by uncertainty in the length correction. For cells badly distorted by plasmolysis, the analysis becomes more difficult and the absolute uncertainty is larger, typically ±30% but sometimes as large as ±50%. For strong plasmolysis conditions, we deemed it more important to include such high-uncertainty values in the reported data than to bias the results by insisting on uniformly high accuracy. The resulting histograms, then, give an accurate overall sense of the heterogeneity in the diffusion coefficient among cells treated identically. 〈φ〉 was estimated under different conditions from the content data of references 3 and 4 by using approximate density factors as described in the supplemental material.
To test for a possible dependence of the effective GFP diffusion coefficient on the expression level, we varied the duration of the induction time with isopropyl-β-d-thiogalactopyranoside (IPTG) from the usual 45 min to 105 and 165 min. By fixing the imaging laser intensity, we could determine that the mean GFP concentration increased from 100 arbitrary units (the normal value) to 300 and 450 arbitrary units, respectively. At each expression level, we measured DGFP for a substantial number of cells under two conditions: (i) cells adapted to growth at 0.28 osmol and resuspended isosmotically and (ii) cells grown at 0.28 osmol and plasmolyzed to 1.02 osmol. As shown in the supplemental material, there is no obvious dependence of 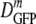 or of δDIQR on the GFP expression level. This result contrasts with an earlier study in rich medium that showed a twofold decrease in the mean GFP diffusion coefficient as the IPTG concentration increased (8). Our usual expression levels may be lower.
or of δDIQR on the GFP expression level. This result contrasts with an earlier study in rich medium that showed a twofold decrease in the mean GFP diffusion coefficient as the IPTG concentration increased (8). Our usual expression levels may be lower.
RESULTS
False-color images of GFP within the E. coli cytoplasm under various osmotic conditions are collected in Fig. 1. Cells adapted to growth in MBM at seven different osmolalities in the range 0.10 to 1.45 osmol were all ellipsoidal (as in Fig. 1a, d, and e); no plasmolysis spaces (PSs) were observed. For growth in 1.45 osmol MBM only, about half of the cells were thread-like (long and narrow) (Fig. 1e). We also investigated GFP diffusion in cells grown in MBM at the osmolality corresponding to the maximum growth rate (0.28 osmol) and plasmolyzed by resuspension in hyperosmotic buffer adjusted with NaCl or sucrose but lacking K+ and glucose. The initial osmoregulatory response to hyperosmotic shock is normally energy-dependent import of K+, which requires a carbon source (39). Cells adapted to growth at high salt concentrations have less water and higher concentrations of K+, glutamate−, and neutral osmoprotectants, primarily trehalose (see Fig. S3 in the supplemental material). Our plasmolysis conditions prevent both K+ import and the biosynthesis of organic osmolytes such as trehalose. Plasmolysis thus removes cytoplasmic water on a time scale of a few seconds without changing the amounts of cytoplasmic solutes or biopolymers (3). When a sufficient volume of water was lost from the cytoplasm, visible PSs are observed (Fig. 1b and c) (16). These may occur at the endcap(s), on the side of the cell (lateral PS or invagination), or both. Such PSs occur in about 70% of cells for an osmotic upshift to 0.61 osmol and in nearly all cells for higher upshifts.
GFP diffusion versus growth osmolality in adapted cells.
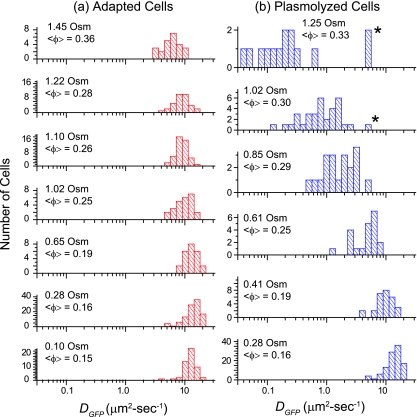
For cytoplasmic GFP, DGFP was measured for 315 cells grown in minimal MBM in the range of 0.10 to 1.45 osmol and resuspended in isosmotic buffer before study. The results are summarized in the histograms of log DGFP in Fig. 2a and in Table 1. At the optimal growth osmolality of 0.28 osmol, 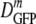 (δDIQR) was 14.1 (4.4) μm2·s−1. At a higher osmolality,
(δDIQR) was 14.1 (4.4) μm2·s−1. At a higher osmolality, 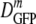 decreased monotonically by a factor of 2.4 from 14.1 μm2·s−1 to 6.0 μm2·s−1 as the growth osmolality increased from 0.28 to 1.45 osmol. Cells grown at 0.10 osmol had a
decreased monotonically by a factor of 2.4 from 14.1 μm2·s−1 to 6.0 μm2·s−1 as the growth osmolality increased from 0.28 to 1.45 osmol. Cells grown at 0.10 osmol had a 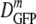 (δDIQR) of 12.3 (3.5) μm2·s−1, slightly lower than that at 0.28 osmol MBM. The diffusion coefficient of GFP in buffer (D0) is 87 μm2·s−1 (32), which exceeded
(δDIQR) of 12.3 (3.5) μm2·s−1, slightly lower than that at 0.28 osmol MBM. The diffusion coefficient of GFP in buffer (D0) is 87 μm2·s−1 (32), which exceeded 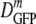 in the cytoplasm of adapted cells by a factor ranging from 6 to 14.5. Among cells grown at 1.45 osmol,
in the cytoplasm of adapted cells by a factor ranging from 6 to 14.5. Among cells grown at 1.45 osmol, 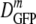 was slightly smaller for the 12 thread-like cells than for the 12 cells with normal aspect ratios.
was slightly smaller for the 12 thread-like cells than for the 12 cells with normal aspect ratios.
FIG. 2.
(a) Histograms of log DGFP, the base 10 logarithm of the effective axial diffusion coefficient of GFP, for cells adapted to growth at different osmolalities as indicated. (b) Histograms of log DGFP for cells grown at 0.28 osmol and plasmolyzed to the total osmolalities shown. In the two upper panels, asterisks mark data for cells that did not exhibit a visible PS. See Tables 1 and 2.
TABLE 1.
GFP diffusion coefficient versus growth osmolality
| Growth osmolality (osmol) | na | 〈φ〉b |
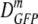 (δDIQR)c (μm2·s−1) (δDIQR)c (μm2·s−1) |
DGFP (μm2·s−1)
|
Growth rate (h−1)e | |
|---|---|---|---|---|---|---|
| Mean ± SDd | Range | |||||
| 0.10 | 54 | 0.15 | 12.3 (3.5) | 12.3 ± 2.8 | 4.2-18.4 | 0.43 ± 0.02 |
| 0.28 | 106 | 0.16 | 14.1 (4.4) | 13.8 ± 3.8 | 4.9-21.6 | 0.55 ± 0.02 |
| 0.65 | 24 | 0.19 | 13.2 (4.4) | 13.3 ± 3.2 | 8.0-19.5 | 0.37 ± 0.02 |
| 1.02 | 25 | 0.25 | 10.3 (4.4) | 9.9 ± 3.1 | 4.8-16.3 | 0.19 ± 0.01 |
| 1.10 | 48 | 0.26 | 8.5 (2.1) | 8.8 ± 2.1 | 4.9-14.5 | 0.12 ± 0.01 |
| 1.22 | 34 | 0.28 | 8.7 (2.1) | 8.9 ± 2.5 | 4.1-15.5 | |
| 1.45 | 24 | 0.36 | 6.0 (3.0)f | 6.2 ± 2.2 | 2.9-10.9 | 0.06 ± 0.01 |
Number of individual cells measured.
Determined as described in the supplemental material.
For definitions, see the text.
For single measurements.
Generations per hour ± 1 standard deviation.
We find two morphologies for cells grown in 1.45 osmol MBM (Fig. 1). One is thread-like (50% of cells), while the other is ellipsoidal (50%), with an aspect ratio similar to those of cells at other growth osmolalities.
For a given growth osmolality, we found no correlation of individual DGFP values with length, volume, integrated cell fluorescence intensity, or the time of the measurement following resuspension under any of the growth or plasmolysis conditions studied. The cell-to-cell variation in DGFP substantially exceeded the ±10% reproducibility of multiple measurements on a single cell. The relative dispersion (δDIQR/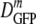 ) varied only modestly, ranging from 0.31 at 0.28 osmol to 0.50 at 1.45 osmol.
) varied only modestly, ranging from 0.31 at 0.28 osmol to 0.50 at 1.45 osmol.
The cell population growth rates versus osmolality (Table 1; see also Fig. S1 in the supplemental material) were consistent with previous measurements (4). At 0.28 osmol MBM, the growth rate was maximal, at 0.55 ± 0.02 generations/h. At higher osmolalities, the growth rate decreased monotonically and roughly linearly to 0.06 ± 0.01 generations/h at 1.45 osmol MBM.
GFP diffusion after plasmolysis (rapid extraction of cytoplasmic water).
DGFP was measured for 223 cells grown at 0.28 osmol and plasmolyzed to various osmolalities prior to study. For cells exhibiting a lateral PS, as in Fig. 1c, DGFP refers to diffusion within a contiguous cylindrical volume at least 0.6 μm long. Such a volume corresponds to one “pool” of GFP in the work of Poolman and coworkers (36). Transport across a lateral PS such as the one in Fig. 1c (i.e., between GFP “pools”) is sometimes observed, but it is typically much slower than the recovery time within a “pool” (17, 36).
The results are shown as a histogram of log DGFP at each osmolality of the RB in Fig. 2b. 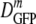 decreased 70-fold as the final osmolality increased from 0.28 to 1.25 osmol. At 0.61 osmol, DGFP was significantly smaller among the 6 cells with PSs than among the 15 cells without PSs. Even at the highest osmotic upshifts, a few cells did not exhibit a PS and had substantially larger DGFP values, a significant source of skew in the distributions. The relative dispersion (δDIQR/
decreased 70-fold as the final osmolality increased from 0.28 to 1.25 osmol. At 0.61 osmol, DGFP was significantly smaller among the 6 cells with PSs than among the 15 cells without PSs. Even at the highest osmotic upshifts, a few cells did not exhibit a PS and had substantially larger DGFP values, a significant source of skew in the distributions. The relative dispersion (δDIQR/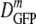 ) increased with increasing final resuspension osmolality, from 0.31 at 0.28 osmol to 1.1 at 1.25 osmol (Table 2). Plasmolyzed cells definitely exhibited significantly greater relative dispersion than adapted cells at comparable total osmolalities. To check that we are observing a purely osmotic effect, we carried out a series of upshift experiments using sucrose instead of NaCl as the external osmotic agent. The results were very similar (see Fig. S2 in the supplemental material).
) increased with increasing final resuspension osmolality, from 0.31 at 0.28 osmol to 1.1 at 1.25 osmol (Table 2). Plasmolyzed cells definitely exhibited significantly greater relative dispersion than adapted cells at comparable total osmolalities. To check that we are observing a purely osmotic effect, we carried out a series of upshift experiments using sucrose instead of NaCl as the external osmotic agent. The results were very similar (see Fig. S2 in the supplemental material).
TABLE 2.
Effects of plasmolysis on the GFP diffusion coefficient for cells grown in 0.28 osmol MBM and osmotically upshifted
| Total osmola | 〈φ〉b | nc |
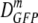 (δDIQR)d (μm2·s−1) (δDIQR)d (μm2·s−1) |
DGFP (μm2·s−1)
|
|
|---|---|---|---|---|---|
| Mean ± SDe | Range | ||||
| 0.28 | 0.16 | 106 | 14.1 (4.4) | 13.8 ± 3.8 | 4.9-21.6 |
| 0.41 | 0.19 | 28 | 10.2 (4.3) | 9.9 ± 3.0 | 3.9-16.0 |
| 0.61 | 0.25 | 21 | 5.0 (3.1) | 5.0 ± 1.9 | 1.4-7.5 |
| 0.85 | 0.29 | 20 | 1.7 (1.7) | 2.0 ± 1.1 | 0.53-4.9 |
| 1.02 | 0.30 | 34 | 0.82 (0.9) | 1.1 ± 0.9 | 0.12-4.7 |
| 1.25 | 0.33 | 14 | 0.20 (0.22) | 0.9 ± 1.8 | 0.04-5.5 |
Total osmolality after plasmolysis with NaCl of cells resuspended from growth in minimal MBM at 0.28 osmol. Uncertainty is ±0.005 osmol due to variations in solution preparation; measurement uncertainty is ±0.003 osmol.
Determined as described in the supplemental material.
Number of individual cells measured.
For definitions, see the text.
For single measurements.
GFP diffusion coefficient versus 〈φ〉.
Cytoplasmic amounts of protein, nucleic acid, K+, glutamate−, and water from earlier work are summarized in Fig. S3 in the supplemental material for four conditions of interest (4, 5). The total amount of nucleic acid can be taken as a proxy for the amount of ribosomes, because some 87% of the nucleic acid is RNA. These amounts plus partial specific volumes of the different biopolymers enable us to calculate 〈φ〉 for each condition in Tables 1 and 2, as detailed in the supplemental material. For a given total osmolality, 〈φ〉 is smaller for cells adapted to growth at high salt concentrations than for cells plasmolyzed to the same external osmolality. The adapted cells import K+ and synthesize osmoprotectants that tend to increase the cytoplasmic water content, but they do not retain as much water as that present under more favorable growth conditions at lower osmolalities (see Fig. S3 in the supplemental material).
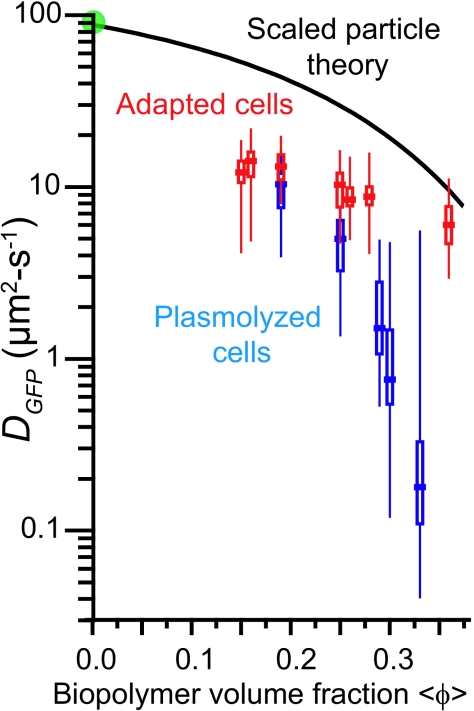
In Fig. 3 we compare 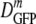 for cells of the same 〈φ〉 obtained either by growth in high-osmolality medium or by plasmolysis to a high osmolality. Remarkably, as 〈φ〉 increased from 0.16 to 0.33 in plasmolyzed cells,
for cells of the same 〈φ〉 obtained either by growth in high-osmolality medium or by plasmolysis to a high osmolality. Remarkably, as 〈φ〉 increased from 0.16 to 0.33 in plasmolyzed cells, 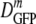 decreased 70-fold. In contrast, as 〈φ〉 increased from 0.16 to 0.36 in growing cells,
decreased 70-fold. In contrast, as 〈φ〉 increased from 0.16 to 0.36 in growing cells, 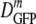 decreased only by a factor of 2.4. Clearly,
decreased only by a factor of 2.4. Clearly,  is not determined by 〈φ〉 alone.
is not determined by 〈φ〉 alone.
FIG. 3.
DGFP versus 〈φ〉 for cells adapted to growth at increasing osmolalities (red symbols) and for cells plasmolyzed to higher osmolalities (blue-gray symbols). For each condition, the horizontal bar represents the median value (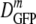 ); the rectangle denotes the δDIQR (the range of the central 50% of values); and the vertical line denotes the complete range of the distribution. See Tables 1 and 2. Green circle, DGFP in buffer. Black curve, SPT prediction for GFP diffusion in a homogeneous cytoplasm of monomeric, hard-sphere crowders of two sizes mimicking small globular proteins and ribosomes, as described in the text. The adjustable parameter Δr/RGFP is chosen as 1.3 based on fits to protein diffusion data in vitro. See the text.
); the rectangle denotes the δDIQR (the range of the central 50% of values); and the vertical line denotes the complete range of the distribution. See Tables 1 and 2. Green circle, DGFP in buffer. Black curve, SPT prediction for GFP diffusion in a homogeneous cytoplasm of monomeric, hard-sphere crowders of two sizes mimicking small globular proteins and ribosomes, as described in the text. The adjustable parameter Δr/RGFP is chosen as 1.3 based on fits to protein diffusion data in vitro. See the text.
DISCUSSION
The cytoplasm hinders GFP diffusion beyond simple crowding effects.
At the optimal growth osmolality of 0.28 osmol in minimal MBM, 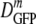 (δDIQR) is 14.1 (4.4) μm2·s−1, smaller by a factor of 6 than D0 (87 μm2·s−1) (32). In three earlier studies of GFP diffusion in the cytoplasm of E. coli grown in rich medium (8, 17, 22), 〈DGFP〉 values were 7.7 ± 2.5 μm2·s−1, 9.0 ± 2.1 μm2·s−1, and 6.1 ± 2.4 μm2·s−1, roughly 10 times smaller than D0. Conditions differ among the studies, but it appears that crowding and confinement effects may be somewhat stronger in cells grown in rich medium.
(δDIQR) is 14.1 (4.4) μm2·s−1, smaller by a factor of 6 than D0 (87 μm2·s−1) (32). In three earlier studies of GFP diffusion in the cytoplasm of E. coli grown in rich medium (8, 17, 22), 〈DGFP〉 values were 7.7 ± 2.5 μm2·s−1, 9.0 ± 2.1 μm2·s−1, and 6.1 ± 2.4 μm2·s−1, roughly 10 times smaller than D0. Conditions differ among the studies, but it appears that crowding and confinement effects may be somewhat stronger in cells grown in rich medium.
For the new data in minimal MBM, the falloff of 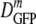 versus 〈φ〉 (Fig. 3) enables us to compare the data with simple models of the effects of crowding on diffusion. The benchmark model for simple crowding is a solution of hard, monodisperse spheres. A good experimental realization of this system is a solution of spherical, monodisperse colloidal particles; these have been well studied both experimentally and theoretically (2, 34). The observed falloff of D/D0 is about a factor of 10 as φ increases from 0 to 0.4, the range of interest in our work. Here D0 is the diffusion coefficient in a dilute solution. Hydrodynamic effects—long-range interparticle forces mediated by the fluid in which the spheres are embedded—are important in crowded solutions. Hard-sphere dynamics simulations that omit hydrodynamic effects, such as Brownian dynamics simulations, capture only about half of the experimental falloff. Theoretical models that properly include hydrodynamic effects reproduce the experimental data well (33).
versus 〈φ〉 (Fig. 3) enables us to compare the data with simple models of the effects of crowding on diffusion. The benchmark model for simple crowding is a solution of hard, monodisperse spheres. A good experimental realization of this system is a solution of spherical, monodisperse colloidal particles; these have been well studied both experimentally and theoretically (2, 34). The observed falloff of D/D0 is about a factor of 10 as φ increases from 0 to 0.4, the range of interest in our work. Here D0 is the diffusion coefficient in a dilute solution. Hydrodynamic effects—long-range interparticle forces mediated by the fluid in which the spheres are embedded—are important in crowded solutions. Hard-sphere dynamics simulations that omit hydrodynamic effects, such as Brownian dynamics simulations, capture only about half of the experimental falloff. Theoretical models that properly include hydrodynamic effects reproduce the experimental data well (33).
Self-diffusion of globular proteins in buffer is often difficult to study above a φ of 0.2, presumably due to aggregation problems. The falloff over the range studied is reminiscent of that of colloidal particles and can, again, be treated by the theory of hard spheres including hydrodynamics (26). In the well-behaved case of myoglobin, the data extend beyond a φ of 0.4 and the theory continues to be accurate. However, to our knowledge, there is no rigorous theory for the diffusion of a tracer hard sphere in a polydisperse sample of crowding hard spheres, the most natural benchmark with which to compare our data. Ellison and coworkers (29) and Elcock and coworkers (6, 19) have carried out molecular-dynamics simulations without hydrodynamic effects for a distribution of crowder sizes that mimics the E. coli cytoplasm in rich growth medium.
A popular model of crowding effects on diffusion that allows for crowders of different sizes is the scaled-particle theory (SPT) (12, 21). Both the diffusing species and the crowders are modeled as hard-sphere monomers. The theory calculates the free energy necessary to open up a pocket within the sea of crowders sufficiently large to enable the diffusing sphere to move a distance, Δr. This leads to an analytical expression for D/D0 versus φ. The theory has one adjustable parameter, the ratio of the step size to the radius of the diffusing protein (Δr/Rprotein). Δr/Rprotein ratios in the range of 0.8 to 2.2 fit a substantial body of in vitro self-diffusion measurements for globular proteins over the φ range of 0.0 to 0.3 or so (1, 11, 15, 23). Such large step sizes are evidently necessary to mimic hydrodynamic effects and protein-protein interactions. We have found that hard-sphere simulations lacking hydrodynamic effects are well approximated by SPT calculations with the much smaller Δr/Rprotein ratio of 0.32. The diffusion of hard spheres including hydrodynamic effects is mimicked by SPT with a Δr/Rprotein ratio of 0.67.
In our SPT calculations, we model the cytoplasm using two crowder sizes: nonribosomal proteins with an average radius (Rprotein) of 2.4 nm, based on the measured protein size distribution (12, 23), and assembled ribosomes with a radius (Rribo) of 11.5 nm. The amount of each type of crowder is based on measurements of the ratio of total protein to total nucleic acid (4, 5). Details are given in Table S1 in the supplemental material. While there are far fewer ribosomes, they account for fully half of the biopolymer volume fraction. All crowders are assumed to be monomeric and distributed homogeneously throughout the entire cytoplasmic volume. Using this mixture of crowders, we carried out SPT calculations versus 〈φ〉 using a Δr/RGFP ratio of 1.3, an average number from successful fits to in vitro protein diffusion data.
The results are shown by the solid black curve in Fig. 3. Simple, homogeneous crowding clearly fails to capture the sixfold decrease in DGFP from the buffer to the cytoplasm. Our assumptions are all intentionally chosen to maximize the possible contribution of crowding to the falloff in the GFP diffusion coefficient. In the real cytoplasm, some proteins surely combine with others to form larger multimers; this would increase the GFP diffusion coefficient for a given value of 〈φ〉. If the same crowders are nonuniformly distributed between two coaxial cylinders but the size distribution of crowders and the concentration of GFP remain uniform, then the effective GFP diffusion coefficient (the mean over the two cylinders) again increases. We discuss the possibility of spatial heterogeneity below. Apparently, GFP diffusion in cells grown at 0.28 osmol is hindered substantially beyond the effects of simple crowding in a homogeneous medium. This might be due to confinement by the branched biopolymer meshwork or to transient binding effects. If binding is important, the unbinding time scale must be less than about 50 ms to be consistent with the observed full recovery of the prebleach GFP intensity distribution in the FRAP experiments.
Striking difference between plasmolyzed cells and cells adapted to growth at high osmolalities.
As shown in Fig. 3, cells adapted to growth at high osmolalities maintain relatively facile GFP diffusion even as 〈φ〉 increases to 0.36, whereas plasmolysis to the same high 〈φ〉 diminishes 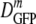 much more sharply. At the highest values of 〈φ〉 studied, the two falloff curves differ by a factor of about 30. We do not understand this observation. Here we suggest several possible underlying causes and indicate experiments and model calculations that can provide important additional information.
much more sharply. At the highest values of 〈φ〉 studied, the two falloff curves differ by a factor of about 30. We do not understand this observation. Here we suggest several possible underlying causes and indicate experiments and model calculations that can provide important additional information.
For cells adapted to growth at high salt concentrations, the slope of the experimental falloff is somewhat less than that obtained with the SPT calculations that assume that all crowders exist as monomers. This suggests the possibility that GFP diffusion in the adapted cells can be understood as a combination of the confinement effects already present in cells grown at 0.28 osmol plus some modest additional hindrance of diffusion due to crowding. The fact that many crowding proteins surely exist as heteromultimers in the cytoplasm may help explain the smaller slope. There is no obvious need to invoke substantial binding of GFP to immobile or slowly diffusing cytoplasmic elements. We plan to test this idea by measuring the time-dependent fluorescence anisotropy [r(t)] of GFP in the cytoplasm of adapted cells. If binding is indeed unimportant, the majority of the GFP population should rotate freely even at a high osmolality of growth. We would expect the rotational correlation time to lengthen as 〈φ〉 increases, due to a gradually increasing hindrance of rotation resulting from crowding by other particles. In addition, it should be possible to build a dimensionally realistic computer simulation of the branched cytoplasmic “supermolecule” comprising DNA, RNA polymerase, RNA chains, ribosomes, and nascent polypeptide chains, plus globular proteins that serve as crowding agents, with the biopolymer volume fraction systematically varied. By studying the diffusion of spheres of various sizes in this complex medium, we can ascertain whether or not the resulting crowding/confinement effects are strong enough to explain both the factor-of-6 decrease in DGFP from the buffer solution to the cytoplasm and the modest falloff at higher growth osmolalities.
The dramatic falloff of 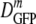 versus 〈φ〉 in the plasmolyzed cells is much more difficult to explain. We might invoke increasingly strong, transient binding of GFP to immobile cytoplasmic elements or oligomerization of GFP itself following plasmolysis. That would be qualitatively consistent with the thermodynamics of crowding (20). However, GFP does not appear to be a particularly sticky protein. It dimerizes only very weakly in solution (Kb ≈ 104 M−1) (28) and lacks large hydrophobic or charged surface patches. Furthermore, this explanation requires the ad hoc assumption that strong binding/oligomerization dominates GFP diffusion after plasmolysis, but little or no binding/oligomerization occurs in cells with the same 〈φ〉 due to growth at high salt concentrations. Again, fluorescence anisotropy measurements may provide important clues to possible differences in local GFP environments under the two conditions.
versus 〈φ〉 in the plasmolyzed cells is much more difficult to explain. We might invoke increasingly strong, transient binding of GFP to immobile cytoplasmic elements or oligomerization of GFP itself following plasmolysis. That would be qualitatively consistent with the thermodynamics of crowding (20). However, GFP does not appear to be a particularly sticky protein. It dimerizes only very weakly in solution (Kb ≈ 104 M−1) (28) and lacks large hydrophobic or charged surface patches. Furthermore, this explanation requires the ad hoc assumption that strong binding/oligomerization dominates GFP diffusion after plasmolysis, but little or no binding/oligomerization occurs in cells with the same 〈φ〉 due to growth at high salt concentrations. Again, fluorescence anisotropy measurements may provide important clues to possible differences in local GFP environments under the two conditions.
An alternative suggestion is that rapid removal of water from the already crowded cytoplasm drives the branched biopolymer meshwork into an entangled, gel-like state that is relatively rigid compared with that of adapted cells. At the same time, the mesh pore size and the size of passageways among pores would decrease. This combination of changes might greatly diminish GFP diffusion. From this perspective, the ability of the adapted cells, which have the same high biopolymer volume fraction, to maintain a flexible meshwork enabling facile GFP diffusion is quite remarkable. Single-cell viscoelastic measurements under both conditions might test the rigidity of the cytoplasmic meshwork (35).
A related possibility is that the nanometer-scale structure of the nucleoid differs between adapted cells and plasmolyzed cells. We know of no good local probe of nucleoid structure on the relevant length scale in live cells. There is evidence from electron microscopy of thin sections of cryo-fixed E. coli cells that plasmolysis compacts the overall size of the nucleoid and alters its branching (31, 37). Perhaps altered nucleoid morphology is the primary determinant of GFP diffusion in plasmolyzed cells. One idea is that the porosity of the nucleoid toward proteins of different sizes may vary with the plasmolyzing osmolality. Suppose, for example, that GFP and other globular proteins of modest size diffuse freely in and out of the nucleoid volume in adapted cells but that in plasmolyzed cells the compaction is so severe that globular proteins are excluded from the nucleoid volume. If many proteins partition sufficiently strongly to the cytoplasmic periphery, the resulting mutual crowding might greatly diminish the effective axial diffusion coefficient of GFP and those of many other proteins as well (27, 41). The same idea might explain why ribosomes, which are very large, cluster outside the nucleoid even under normal osmotic conditions, as observed by electron microscopy and optical imaging (9, 13, 30).
The idea of progressive size exclusion as plasmolysis becomes stronger can be tested by dual-color imaging experiments that monitor the spatial distribution of both GFP and the nucleoid in the same cell, before and after plasmolysis. In addition, single-molecule tracking (7) and small-spot FRAP experiments can test for spatial heterogeneity in the GFP diffusion coefficient by studying motion on smaller length and time scales. Recent results from Poolman and coworkers for E. coli grown in rich medium hint at a possible spatial heterogeneity of GFP diffusion (36). These investigators used a diffraction-limited bleach beam (FWHM, ∼200 nm) to probe diffusion on a much shorter length scale. Even for unstressed cells, the variability in DGFP across cells was much larger than that in our study in rich medium, 0.1 to 24 μm2·s−1 versus 1.2 to 7.8 μm2·s−1 (17). The relative standard deviation of 75% for multiple measurements on the same cell was also quite large. Both results might be due in part to spatial heterogeneity within the cytoplasm.
Conclusion.
Our study demonstrates that at the same high average biopolymer volume fraction, GFP diffusion remains quite facile in cells that have adapted to growth in high salt concentrations but is severely hindered in plasmolyzed cells. Evidently, the cytoplasmic content exists in two very different physical and perhaps biochemical states for adapted and plasmolyzed cells. We do not yet understand the underlying causes. GFP is a relatively small protein; we would expect even stronger effects of plasmolysis on the diffusion of larger proteins.
The ability of adapted cells to maintain facile diffusion under high-salt conditions is surely related to their ability to grow. Plasmolysis in hyperosmotic growth medium causes a lag time before growth resumes, and the lag time lengthens dramatically as the strength of plasmolysis increases (39, 40). The plasmolyzed state studied here should be closely analogous to the transient state of such cells immediately after the sudden osmotic upshift but before they begin the process of adapting to a higher osmolality in order to resume growth. For very high osmotic upshifts, larger than those studied here, the lag time becomes infinite even at osmolalities in which adapted cells can grow. Our results, then, suggest that severely plasmolyzed cells may be trapped in a state in which the diffusion of many key proteins is greatly hindered and normal biochemical activity is impossible. If the diffusion behavior of GFP proves representative of endogenous globular proteins, then we suspect that the lag time before the resumption of growth is strongly related to the restoration of facile protein diffusion within the plasmolyzed cytoplasm.
Supplementary Material
Acknowledgments
This work was supported by the National Science Foundation under grant CHE-0452375 (to J.C.W.) and by the National Institutes of Health under grant NIH GM 47022 (to M.T.R.). B.P.B. has benefited from an NIH traineeship under the UW—Madison Molecular Biophysics Training Program (NIH T32 GM08293-19).
We thank Arun Yethiraj for many useful discussions on the diffusion of hard spheres in complex media.
Footnotes
Published ahead of print on 24 October 2008.
Supplemental material for this article may be found at http://jb.asm.org/.
REFERENCES
- 1.Banks, D. S., and C. Fradin. 2005. Anomalous diffusion of proteins due to molecular crowding. Biophys. J. 892960-2971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brady, J. F. 1994. The long-time self-diffusivity in concentrated colloidal dispersions. J. Fluid Mechanics 272109-134. [Google Scholar]
- 3.Cayley, D. S., H. J. Guttman, and M. T. Record, Jr. 2000. Biophysical characterization of changes in amounts and activity of Escherichia coli cell and compartment water and turgor pressure in response to osmotic stress. Biophys. J. 781748-1764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cayley, S., B. A. Lewis, H. J. Guttman, and M. T. Record, Jr. 1991. Characterization of the cytoplasm of Escherichia coli K-12 as a function of external osmolarity. Implications for protein-DNA interactions in vivo. J. Mol. Biol. 222281-300. [DOI] [PubMed] [Google Scholar]
- 5.Cayley, S., and M. T. Record, Jr. 2003. Roles of cytoplasmic osmolytes, water, and crowding in the response of Escherichia coli to osmotic stress: biophysical basis of osmoprotection by glycine betaine. Biochemistry 4212596-12609. [DOI] [PubMed] [Google Scholar]
- 6.Elcock, A. H. 2004. Molecular simulations of diffusion and association in multimacromolecular systems. Numerical Computer Methods D 383166-198. [DOI] [PubMed] [Google Scholar]
- 7.Elf, J., G. W. Li, and X. S. Xie. 2007. Probing transcription factor dynamics at the single-molecule level in a living cell. Science 3161191-1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Elowitz, M. B., M. G. Surette, P. E. Wolf, J. B. Stock, and S. Leibler. 1999. Protein mobility in the cytoplasm of Escherichia coli. J. Bacteriol. 181197-203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Frenkiel-Krispin, D., and A. Minsky. 2006. Nucleoid organization and the maintenance of DNA integrity in E. coli, B. subtilis and D. radiodurans. J. Struct. Biol. 156311-319. [DOI] [PubMed] [Google Scholar]
- 10.Grigorova, I. L., N. J. Phleger, V. K. Mutalik, and C. A. Gross. 2006. Insights into transcriptional regulation and sigma competition from an equilibrium model of RNA polymerase binding to DNA. Proc. Natl. Acad. Sci. USA 1035332-5337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gros, G. 1978. Concentration-dependence of self-diffusion of human and Lumbricus terrestris hemoglobin. Biophys. J. 22453-468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Han, J., and J. Herzfeld. 1993. Macromolecular diffusion in crowded solutions. Biophys. J. 651155-1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hobot, J. A., W. Villiger, J. Escaig, M. Maeder, A. Ryter, and E. Kellenberger. 1985. Shape and fine structure of nucleoids observed on sections of ultrarapidly frozen and cryosubstituted bacteria. J. Bacteriol. 162960-971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ignatova, Z., and L. M. Gierasch. 2004. Monitoring protein stability and aggregation in vivo by real-time fluorescent labeling. Proc. Natl. Acad. Sci. USA 101523-528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Keller, K. H., E. R. Canales, and S. I. Yum. 1971. Tracer and mutual diffusion coefficients of proteins. J. Phys. Chem. 75379-387. [DOI] [PubMed] [Google Scholar]
- 16.Koch, A. L. 1998. The biophysics of the gram-negative periplasmic space. Crit. Rev. Microbiol. 2423-59. [DOI] [PubMed] [Google Scholar]
- 17.Konopka, M. C., I. A. Shkel, S. Cayley, M. T. Record, and J. C. Weisshaar. 2006. Crowding and confinement effects on protein diffusion in vivo. J. Bacteriol. 1886115-6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kulp, D. T., and J. Herzfeld. 1995. Crowding-induced organization of cytoskeletal elements. III. Spontaneous bundling and sorting of self-assembled filaments with different flexibilities. Biophys. Chem. 5793-102. [DOI] [PubMed] [Google Scholar]
- 19.McGuffee, S. R., and A. H. Elcock. 2006. Atomically detailed simulations of concentrated protein solutions: the effects of salt, pH, point mutations, and protein concentration in simulations of 1000-molecule systems. J. Am. Chem. Soc. 12812098-12110. [DOI] [PubMed] [Google Scholar]
- 20.Minton, A. P. 2005. Influence of macromolecular crowding upon the stability and state of association of proteins: predictions and observations. J. Pharm. Sci. 941668-1675. [DOI] [PubMed] [Google Scholar]
- 21.Minton, A. P. 1989. Lateral diffusion of membrane proteins in protein-rich membranes. A simple hard particle model for concentration dependence of the two-dimensional diffusion coefficient. Biophys. J. 55805-808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mullineaux, C. W., A. Nenninger, N. Ray, and C. Robinson. 2006. Diffusion of green fluorescent protein in three cell environments in Escherichia coli. J. Bacteriol. 1883442-3448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Muramatsu, N., and A. P. Minton. 1988. Tracer diffusion of globular proteins in concentrated protein solutions. Proc. Natl. Acad. Sci. USA 852984-2988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Murphy, L. D., and S. B. Zimmerman. 1994. Macromolecular crowding effects on the interaction of DNA with Escherichia coli DNA-binding proteins: a model for bacterial nucleoid stabilization. Biochim. Biophys. Acta 1219277-284. [DOI] [PubMed] [Google Scholar]
- 25.Neidhardt, F. C., P. L. Bloch, and D. F. Smith. 1974. Culture medium for enterobacteria. J. Bacteriol. 119736-747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nesmelova, I. V., V. D. Skirda, and V. D. Fedotov. 2002. Generalized concentration dependence of globular protein self-diffusion coefficients in aqueous solutions. Biopolymers 63132-140. [DOI] [PubMed] [Google Scholar]
- 27.Odijk, T. 1998. Osmotic compaction of supercoiled DNA into a bacterial nucleoid. Biophys. Chem. 7323-29. [DOI] [PubMed] [Google Scholar]
- 28.Phillips, G. N., Jr. 1997. Structure and dynamics of green fluorescent protein. Curr. Opin. Struct. Biol. 7821-827. [DOI] [PubMed] [Google Scholar]
- 29.Ridgway, D., G. Broderick, A. Lopez-Campistrous, M. Ru'aini, P. Winter, M. Hamilton, P. Boulanger, A. Kovalenko, and M. J. Ellison. 2008. Coarse-grained molecular simulation of diffusion and reaction kinetics in a crowded virtual cytoplasm. Biophys. J. 943748-3759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Robinow, C., and E. Kellenberger. 1994. The bacterial nucleoid revisited. Microbiol. Rev. 58211-232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ryter, A. 1960. Etude au microscope electronique des transformations nucleaires de E. coli K12S (lambda 26) apres irradiation aux rayons ultraviolets et aux rayons x. J. Cell Biol. 8399-412. [Google Scholar]
- 32.Terry, B. R., E. K. Matthews, and J. Haseloff. 1995. Molecular characterisation of recombinant green fluorescent protein by fluorescence correlation microscopy. Biochem. Biophys. Res. Commun. 21721-27. [DOI] [PubMed] [Google Scholar]
- 33.Tokuriki, N., M. Kinjo, S. Negi, M. Hoshino, Y. Goto, I. Urabe, and T. Yomo. 2004. Protein folding by the effects of macromolecular crowding. Protein Sci. 13125-133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tokuyama, M., and I. Oppenheim. 1995. On the theory of concentrated hard-sphere suspensions. Physica A 21685-119. [Google Scholar]
- 35.Vadillo-Rodriguez, V., T. J. Beveridge, and J. R. Dutcher. 2008. Surface viscoelasticity of individual gram-negative bacterial cells measured using atomic force microscopy. J. Bacteriol. 1904225-4232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.van den Bogaart, G., N. Hermans, V. Krasnikov, and B. Poolman. 2007. Protein mobility and diffusive barriers in Escherichia coli: consequences of osmotic stress. Mol. Microbiol. 64858-871. [DOI] [PubMed] [Google Scholar]
- 37.Whitfield, J., and R. Murray. 1956. The effects of the ionic environment on the chromatin structures of bacteria. Can. J. Microbiol. 2245-260. [DOI] [PubMed] [Google Scholar]
- 38.Woldringh, C. L. 2002. The role of co-transcriptional translation and protein translocation (transertion) in bacterial chromosome segregation. Mol. Microbiol. 4517-29. [DOI] [PubMed] [Google Scholar]
- 39.Wood, J. M. 1999. Osmosensing by bacteria: signals and membrane-based sensors. Microbiol. Mol. Biol. Rev. 63230-262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wood, J. M., E. Bremer, L. N. Csonka, R. Kraemer, B. Poolman, T. van der Heide, and L. T. Smith. 2001. Osmosensing and osmoregulatory compatible solute accumulation by bacteria. Comp. Biochem. Physiol. A 130437-460. [DOI] [PubMed] [Google Scholar]
- 41.Zimmerman, S. B. 2006. Cooperative transitions of isolated Escherichia coli nucleoids: implications for the nucleoid as a cellular phase. J. Struct. Biol. 153160-175. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.