A Genomic Distance Based on MUM Indicates Discontinuity between Most Bacterial Species and Genera

Abstract

The fundamental unit of biological diversity is the species. However, a remarkable extent of intraspecies diversity in bacteria was discovered by genome sequencing, and it reveals the need to develop clear criteria to group strains within a species. Two main types of analyses used to quantify intraspecies variation at the genome level are the average nucleotide identity (ANI), which detects the DNA conservation of the core genome, and the DNA content, which calculates the proportion of DNA shared by two genomes. Both estimates are based on BLAST alignments for the definition of DNA sequences common to the genome pair. Interestingly, however, results using these methods on intraspecies pairs are not well correlated. This prompted us to develop a genomic-distance index taking into account both criteria of diversity, which are based on DNA maximal unique matches (MUM) shared by two genomes. The values, called MUMi, for MUM index, correlate better with the ANI than with the DNA content. Moreover, the MUMi groups strains in a way that is congruent with routinely used multilocus sequence-typing trees, as well as with ANI-based trees. We used the MUMi to determine the relatedness of all available genome pairs at the species and genus levels. Our analysis reveals a certain consistency in the current notion of bacterial species, in that the bulk of intraspecies and intragenus values are clearly separable. It also confirms that some species are much more diverse than most. As the MUMi is fast to calculate, it offers the possibility of measuring genome distances on the whole database of available genomes.

Bacteria are so diverse that within a species such as Escherichia coli the proportion of DNA not shared between two strains can be as high as 26 to 27%, e.g., for the MG1655-CFT073 genome pair (5, 10). Diversity is characterized not only by the proportion of unshared sequences, but also by the divergence of the remaining, common DNA. In the case of the MG1655-CFT073 pair, the average percentage of DNA identity is only 96 to 97% (5, 10). Such findings have stimulated the use of whole-genome sequencing on several isolates (or strains), rather than just one, among the numerous species of interest. As of March 2008, there are 68 bacterial species with at least two complete genomes publicly available.

The observations on intraspecies diversity have created the need for new, sensitive tools to evaluate distance between strains, because the 16S RNA-based phylogenies are irrelevant for too closely related strains (27). The most commonly used method is multiple-locus sequence typing (MLST). For this method, sequencing is performed on a few housekeeping genes common to all strains compared within a given species, and phylogenetic studies are derived from the alignments.

However, the availability of ever greater numbers of genomes per species now offers the possibility of developing distance determinations based on whole-genome information. Comparative genomic studies have confirmed the early intuition of Hayashi and coworkers (15) that bacterial species share a pool of common genes, the core genome, while each individual strain within the species has additional, variable segments which together constitute the pangenome (5, 29). Therefore, a first source of variability among genomes originates from slow divergence of the core genome, and a second source of variability is the rapid gain and loss of large DNA segments, especially at the intraspecies level (7). From these notions, two a priori relatively independent ways to assess genomic distances can be derived.

A first approach to estimate genome distances, referred to as the average nucleotide identity (ANI), starts by assessing the list of orthologs and then derives from this information the overall divergence of this core genome by averaging the percentages of identity at the nucleotide level of all orthologs found (22). Recently, the inventors of the ANI proposed the use of a new calculation based on DNA rather than orthologs. Briefly, fixed-length DNA fragments of the first genome are compared, using BlastN, to the second genome, and fragments meeting an identity threshold are kept and used to derive the ANI (10). ANI values are barely affected by this change. Interestingly, the recent study of Goris and collaborators has established that ANI and DNA content values correlate well with the standard DNA-DNA hybridization (DDH) data used to delineate bacterial species (10). In addition, a careful comparison of ANI-based distances with distances derived from the phylogenetic analysis of concatenated genes of the core genome has shown excellent correspondence (21).

A second approach to estimate distances is based on estimating the proportion of common genes (or DNA). The “gene content” (28) and “conserved-gene” (22) methods consist of creating a list of all possible orthologs between two genomes and then estimating the proximity of two strains by the ratio of orthologs to the total number of genes of the smaller or reference genome, respectively. More recently, similar methods, called DNA content and genome BLAST distance phylogeny, make use of DNA rather than genes as the starting point (10, 16). Both categories of genomic methods have the advantage of being general, as they apply to all possible pairs of bacteria, irrespective of their relatedness. However, they both involve a certain amount of calculation and are not readily useable on a new genome pair of interest.

A question immediately arises, namely, how the two kinds of calculation, the one based on gene gain and loss and the one based on divergence among orthologs, are correlated. In the Goris et al. study, which involves a set of both intraspecies and intragenus comparisons, the ANI and DNA content values turned out to be highly correlated (r² = 0.96 for ANI values above 80%) (10). However, when the study was restricted to intraspecies comparisons, the correlation was less (r² = 0.29) (see Results). Indeed, it was reported that among strain pairs having similar ANI values, some also had similar gene content values and some had dissimilar gene content values (20). This lack of correlation calls for a new distance that combines both dimensions of variability at the intraspecies level.

We present here a new calculation for genomic distances that captures in a single value both dimensions of bacterial-genome variability. It is dedicated to and especially sensitive for intraspecies comparisons. This distance is based on the number of maximal unique and exact matches (MUMs) of a given minimal length shared by the two genomes being compared. It is called the MUMi, for MUM index, and varies between 0 for very similar and 1 for very distant genomes. We show that this method of measuring distance correlates well with the ANI (22) and less well with the DNA content distance. Interestingly, the trees derived from MUMi distance matrices for E. coli and Staphylococcus aureus are mostly congruent with MLST trees and perfectly congruent with ANI trees. Because very fast algorithms exist to detect MUMs, calculations are rapid, e.g., MUMi values for a pair of E. coli genomes are calculated in a matter of seconds. We used the MUMi to estimate the level of diversity encountered in the 68 bacterial species and 67 genera for which at least two genomes are available. Despite the considerable span observed, most species encompass relatively homogeneous strains. Moreover, when intraspecies values were systematically compared to intragenus values for a set of 26 species, a significant difference was always found. This seems to indicate that a discontinuity separates species and genus boundaries, at least for the sample of species analyzed. This analysis also confirmed that some species are much more diverse than usual, as reported by others (11). We conclude that the MUMi can help us understand strain grouping within bacterial species and bring some order to the ever-expanding collection of bacterial genomes.

MATERIALS AND METHODS

Calculation of MUMi. (i) Principles.

MUMs are maximal unique exact matches shared by two sequences. Fast algorithms, such as the one implemented in Mummer, allow the calculation in a few seconds of the list of all such matches shared by two genomes, taking into consideration the forward, as well as the reverse, strand of the target genome (23). The calculation in version 3 of Mummer is based on suffix arrays, which are built in linear time and linear space (23). As suggested by others (6), a naïve distance called MUMi can be derived from this MUM list, using the following formula: MUMi = 1 − L_mum/L_av, where L_mum is the sum of the lengths of all nonoverlapping MUMs and L_av is the average length of the two genomes to be compared. Values close to 0 signify very similar sequences, whereas values close to 1 are obtained for distant genomes. An important posttreatment of the MUM list is applied to remove all overlaps between MUMs, so that the distance never becomes negative (see below).

In designing the MUMi formula, we chose to divide L_mum by L_av. Other calculations aiming at estimating global distances between all kinds of bacterial genomes have used the size of the shorter genome of the pair, L_min (16, 28). The use of L_av instead allows a greater sensitivity to variations due to gene loss and gene acquisition (as is necessary between close relatives). L_av has been reported to perform better for tree estimations based on BLAST high-scoring pairs (1). It should be noted that the two kinds of differences between genomes, i.e., originating from vertical evolution or from horizontal transfer, contribute to the MUMi value.

(ii) Generation of the MUM list.

For each genome pair, the list of MUMs was generated using Mummer3 software (http://mummer.sourceforge.net/manual/), with the following options: −mum, −b, −c, and −l19 (unless otherwise stated). Option −b allows the recovery of MUMs present on both strands of the target sequence and hence takes into account DNA inversions. Parameter l is the minimal length of MUM to be detected, called k in this paper (see Results for its choice). We tested the effect of removing the constraint on uniqueness of the MUMs so as to get MEMs (maximal exact matches) by cancelling the option −mum. This did not significantly change the results: an average difference of 0.00069 was measured on 638 pairs of bacterial genomes tested. We therefore chose to do calculations with MUMs.

(iii) Removal of MUM overlaps.

Mummer detects matches that may not be unique, as the uniqueness criterion is examined independently on forward and reverse strands of the target genome being compared to the query sequence. This explains the presence of spurious matches that need to be removed or trimmed. A script was written in Perl to trim overlapping MUMs and to calculate the MUMi value (see the supplemental material). Taking as the entry the Mummer3 output file and the lengths of both genomes (called hereafter g1 and g2), it first trims the MUMs and then calculates the MUMi.

An exact solution for trimming overlapping segments, originally designed for BLAST outputs, is available (13). However, it is time-consuming, and the problem with MUMs is less complex because hits have the same length on the two genomes being compared. We therefore designed an approximate solution with the following steps. (i) Remove MUMs whose coordinates on g1 (or on g2) are completely included in a larger MUM (this is made possible by the fact that in Mummer3, the uniqueness of each MUM is defined according to one strand only). (ii) Remove MUMs whose coordinates on g1 (or on g2) are completely included in two neighboring MUMs. (iii) Treat the remaining MUMs of g1 (or g2) that exhibit partial overlap. To do this, MUMs are ordered according to their beginning positions on g1 (or on g2), and starting from the last element of the list, each MUM is compared to its neighbor. In cases of overlap, the end of the leftward MUM is trimmed, i.e., its end coordinates on both g1 and g2 are shifted so that no overlap exists on g1 (or on g2). This is the part of the script that creates asymmetry, because a different solution is created when g2 is treated before g1. The level of asymmetry was tested on an E. coli genome pair (MG1655 versus CFT073), and the difference was negligible (0.002% difference between the two MUMi values). We then tested two genome pairs suspected to be difficult cases because of abundant repeat sequences (Table 1). A maximal difference in the MUMi estimate was reached with the Shigella flexneri 2a pair. The absolute difference was small (0.0011), but relative to the MUMi value of this pair, which was also small, it resulted in a 2.7% difference between the two MUMi values. We decided that the average of the two MUMi values obtained depending on which genome was treated first was a reasonable way to force symmetry, and the MUMi was therefore calculated by this average. A web interface for calculating MUMi is under construction, and its address will be posted at http://www.jouy.inra.fr/ublo.

TABLE 1.

MUMi variation as a function of genome order treatment

Species	Strain		Accession no.		MUMi		Difference
	1	2	1	2	G1, G2	G2, G1
E. coli	MG1655	CFT 073	U00096	AE014075	0.300798	0.300803	0.000005
N. meningitidis	MC58	Z2491	AE00298	AL157959	0.241190	0.241533	0.000343
S. flexneri	2457T	301	AE014073	AE005674	0.038443	0.039560	0.001117

Source of genomes.

The genomes tested in this study are all publicly available. Fasta files were retrieved starting from the European Bioinformatics Institute list of bacterial genomes (http://www.ebi.ac.uk/genomes/bacteria1.html). Plasmids were excluded from the analysis. We made adjustments in cases where similar strains are designated as different species: Shigella strains were given the additional “species name” E. coli, and Bacillus anthracis, Bacillus thuringensis, and Bacillus weihenstephanensis were placed in the Bacillus cereus group. For species in which the genome is shared between several chromosomes, each chromosome was treated separately (suffixes C1, C2, and C3 indicated whether chromosome 1, 2, or 3 was considered). Independent calculation for each chromosome allowed us to highlight cases where the various chromosomes had different distances, like Burkholderia species. It has been reported that in Vibrio cholerae and Vibrio parahaemolyticus some DNA segments are shuffled between chromosomes (24). In such cases, the distance may decrease when the MUMi is calculated on concatenated chromosomes rather than on each chromosome separately. The MUMi value of concatenated chromosomes was therefore calculated for the two Vibrio species (see Table S4 in the supplemental material) and found not to be inferior to the values calculated on each chromosome. However, the values were very close to 1. The same calculation was repeated at the intraspecies level with V. cholerae (see Table S2 in the supplemental material). Again, the MUMi value was the average of the values obtained on each chromosome.

Comparison of MUMi to MLST and ANI distance matrices.

E. coli MLST distance matrices were determined using the eight genes selected by the Pasteur Institute MLST scheme (http://www.pasteur.fr/recherche/genopole/PF8/mlst/EColi1.html), namely, dinB, icdA, pabB, polB, putP, trpA, trpB, and uidA. The blocks inside the genes were extracted according to the Pasteur scheme, genes were concatenated (9,836 nucleotides), and the product was used for a Muscle alignment (8). In some of the complete genomes, one of the genes was missing, so that only 11 of the 16 genomes were used. Alignments were generated using the Muscle interface (http://www.ebi.ac.uk/muscle/), and gaps were removed by manual inspection. The Seqboot, Dnadist, and Consense programs of the Phylip package were then used to calculate distances (F84 DNA matrix) and the bootstrap values of the consensus trees. Neighbor-joining trees were built with BioNJ (9). The same procedure was applied to calculate the S. aureus MLST distance matrix, starting from the MLST scheme of the centralized MLST database (http://www.mlst.net), which includes the seven genes arcC, aroE, glpF, gmk, pta, tpi, and yqiL (cumulative size, 3,198 nucleotides). Ten of the 14 available genomes in which the MLST primers matched exactly for all seven genes were used. SplitsTrees (18) were calculated directly on the MLST website (http://linux.mlst.net/splits1/index.htm).

To build the ANI distance matrices, new ANI calculations were effected, starting from a homemade script and following exactly the guidelines of Goris et al. (10). BLAST results are different depending on which genome is used as a reference, so the ANI was calculated in both directions, and the average was taken as the ANI value. To convert the ANI into a distance, its complement to 1 was taken.

RESULTS

Designing a distance between closely related complete bacterial genomes based on MUMs.

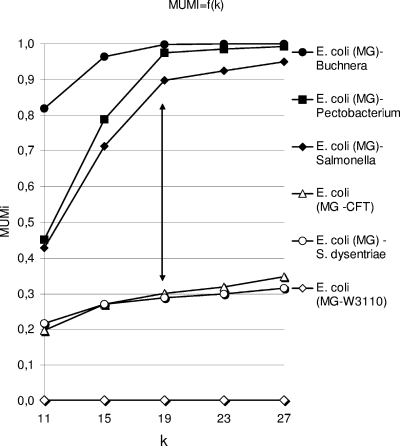
MUMs are maximal unique exact matches of a minimal length k shared by two sequences. A distance derived from these MUMs was calculated by the following formula: MUMi = 1 − L_mum/L_av, where L_mum is the number of nucleotides included in nonoverlapping MUMs and L_av is the average length of the compared genomes (see Materials and Methods). This formula relies on the choice of the value of k, the minimal size of the exact matches to be included in the MUM list. The k value was chosen empirically. As the purpose of this distance was to detect small differences at the intraspecies level in bacteria, a set of three intraspecies pairs was compared to a set of three interspecies pairs, all of which included the E. coli MG1655 genome. The k value was varied from 11 to 27 (Fig. 1). For all intraspecies pairs, MUMi increased slightly with k, but for interspecies pairs, MUMi increased sharply with k. At a k value of 19, the difference between intraspecies and interspecies values was the most pronounced. We therefore set k to 19 for the MUMi. It has been reported that no MUM with a length of >21 is expected by chance when 1.7-Mb random genomes generated under a Bernouilli model (12) are compared. This suggests that the empirical value of 19 allows us to avoid taking into account spurious matches.

FIG. 1.

MUMi values as a function of k (the minimal size of a MUM) for six strain pairs involving E. coli MG1655 (MG) (accession number U00096). This genome was compared to those of E. coli W3110 (AP009048), Shigella dysenteriae (CP000034), E. coli CFT073 (AE014075), S. enterica (strain LT2, AE006468), Pectobacterium atrosepticum (formerly Erwinia carotovora, NC_004547), and B. aphidicola (AE013218). The arrow shows where the points of intraspecies and interspecies MUMi are the most widely separated.

As expected, the MUMi calculation time was short: it took only 18 s to calculate the MUMi between two ∼5-Mb genomes (E. coli K-12 and Sakai genomes) on a Proc Intel Xeon 2.33 GHz dual-core computer with 8 Go RAM (10 s for the Mummer run and 8 s for the trimming posttreatment). For the same pair on the same computer, the ANI calculation took 6 min 9 s.

MUMi correlates well with the ANI.

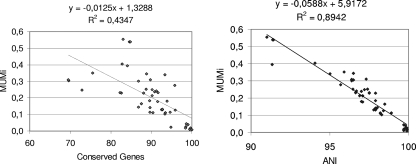
The MUMi distance was first compared to the conserved-gene value, the global ratio of genes common to two genomes. We calculated the MUMi for all intraspecies pairs of strains for which the conserved-gene values were available (Fig. 2, left; the complete list of strain pairs compared with the conserved-gene, MUMi, and ANI values is given in Table S1 in the supplemental material). The coefficient of determination between conserved genes and the MUMi was weak (r² = 0.43), suggesting that the MUMi does not reflect the conserved genes of a genome pair.

FIG. 2.

Correlations of MUMi with other genomic distances. (Left) Correlation between conserved-gene and MUMi values. For the 48 intraspecies pairs used for comparison, the conserved-gene values were available (see the supplemental material) (17), the MUMi was calculated (see the list of pairs in Table S1 in the supplemental material), and both values are reported on the graph. (Right) Correlation between the ANI and MUMi values, with the same pairs as in the left panel.

The MUMi was then compared to the ANI of two genomes, using the same set of intraspecies pairs as above (Fig. 2, right). This time, a better coefficient of determination was found (r² = 0.89), suggesting that the MUMi reflects the same kind of differences as the ANI. An ANI value of 95% ± 0.5% identity corresponds to 70% DDH (10), a value often recommended to delimit species, together with other criteria, such as phenotypic traits (27). The ANI value of 95% ± 0.5% corresponds to a MUMi value of 0.33 ± 0.03.

It should be noted that with the same data set, the determination coefficient between conserved genes and the ANI was 0.2877, a value even lower than those we observed (see Fig. S2 in the supplemental material). This suggests that conserved genes and the ANI indeed analyze different features of intraspecies diversity.

The MUMi groups strains at the intraspecies level similarly to the MLST and the ANI.

We next proceeded to compare MUMi distance matrices with MLST matrices. We built distance matrices from alignments of the set of genes established for MLST schemes of two species, E. coli and S. aureus, choosing, respectively, 10 and 11 sequenced strains per species (see Materials and Methods). Neighbor-joining trees with bootstrapping were produced, and most branches had a 100% bootstrap value (see Fig. S1 in the supplemental material). We next compared these “reference” MLST matrices to the distance matrices calculated with the MUMi. To compare matrices, the Pearson correlation coefficient was used. Coefficients of 0.937 and 0.947 were obtained for E. coli and S. aureus matrices, respectively. We concluded that the MUMi and MLST matrices were highly correlated.

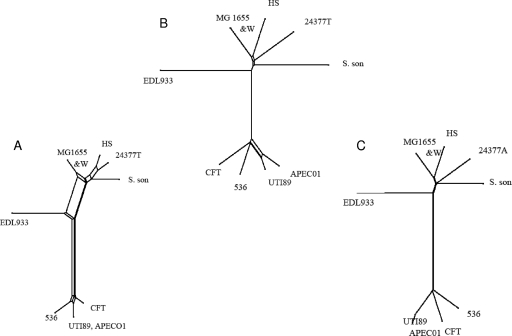
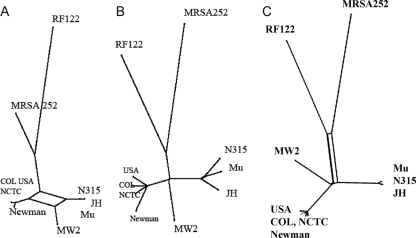
Tree-like representations of the MUMi and MLST distance matrices were then built using SplitsTree, which enables visualization of the ambiguous parts of the tree construction (18). The MLST and MUMi trees for sequenced strains of E. coli (Fig. 3), and S. aureus (Fig. 4) grouped strains essentially in similar ways by the two approaches. In the case of E. coli, greater discrimination was obtained with the MUMi tree for the UTI89 and APEC01 strains. More ambiguities were generally present on the MLST trees. This could be due to the fact that MLST distances are derived from less information than MUMi distances (i.e., seven genes versus the whole genome). In the case of S. aureus, we observed an interesting inversion between MRSA252, a methicillin-resistant clinical isolate, and strain RF122, the only sequenced cattle isolate. While RF122 appears to be the most distant strain by MLST, it is MRSA252 that has this position in the MUMi tree.

FIG. 3.

SplitsTree representations of the MLST (A), MUMi (B), and ANI (C) distance matrices involving 10 E. coli strains, MG1655 (U00096), W3110 (W) (AP009048), HS (CP000802), 24377A (CP000800), Shigella sonnei (S. son) (CP000038), EDL933 (AE005174), CFT073 (CFT) (AE014075), APEC01 (CP000468), UTI89 (CP000243), and 536 (CP000247). Ambiguities are shown as rectangles.

FIG. 4.

SplitsTree representations of the MLST (A), MUMi (B), and ANI (C) distance matrices involving 11 S. aureus strains, Mu50 (Mu) (NC002758), N315 (NC002745), MW2 (NC003923), MRSA (NC002952), RF122 (NC007622), COL (NC002951), JH1 (NC009632), JH9 (NC009487), NCTC8325 (NC007795), USA300 (NC007793), and Newman (NC009641). Ambiguities are shown as rectangles.

Trees based on the same set of strains were also built using the distance derived from the ANI (Fig. 2C and 3C). In each case, the MUMi and ANI trees were congruent and the distance matrices were highly correlated. In the contradictory cases of RF122 and MRSA252, strain MRSA252 also appeared to be the more distant isolate in the ANI tree.

We conclude that MUMi estimates of intraspecies distances are globally satisfactory compared to the generally accepted MLST approach and that the MUMi and the ANI give very similar results.

The MUMi provides an overall view of species diversity.

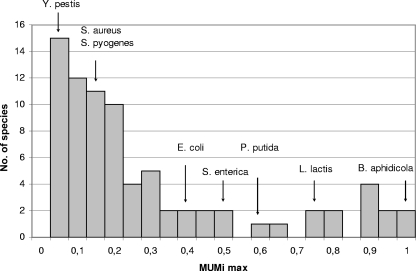
In order to assess global species diversity with the MUMi, all species for which at least two genomes had been sequenced (as of March 2008) were compared with the MUMi. All pair values are given in Table S2 in the supplemental material. Within each species, the minimal, median, and maximal MUMi values were recorded (see Table S3 in the supplemental material). The distribution of intraspecies maximal distances revealed that among 68 species, 77% had a maximal value below 0.5, with most MUMi maximal values in the range 0.05 to 0.2 (Fig. 5).

FIG. 5.

Distribution of all maximal MUMi values per species.

It is well known that some species show considerable strain diversity, as is the case for several Pseudomonas species (Pseudomonas syringae, Pseudomonas putida, and Pseudomonas fluorescens), Rhodopseudomonas palustris, and B. cereus. The maximal MUMi values for these species are in the range of 0.6 to 0.8. The obligate endosymbiont species, e.g., Buchnera aphidicola and Wolbachia, constitute another category of species with high MUMi values. Finally, Lactococcus lactis and Salmonella enterica are two species in which subspecies have been defined. The maximal distance between these subspecies is 0.74 in the case of L. lactis subsp. cremoris versus subsp. lactis and 0.49 for S. enterica subsp. enterica versus subsp. arizonae.

At the opposite extreme are species that exhibit very limited diversity (MUMi below 0.1). These include Yersinia pestis, Chlamydophila pneumoniae, and some strains of Mycobacterium tuberculosis, among many others (see Table S3 in the supplemental material). The fact that some strictly pathogenic species fall into this category may suggest that species definition has been influenced by the clinical need to give a unique species assignment to disease-causing bacteria. In the case of Y. pestis, the ancestor Yersinia pseudotuberculosis from which it derives clonally (3) could in fact be considered to belong to the same species (see Table S3 in the supplemental material).

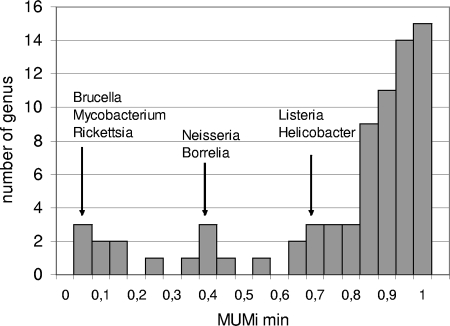
Using the MUMi at the bacterial-genus level reveals closely related species.

MUMi values for numerous genome pairs belonging to the same genus but different species were determined so as to detect extreme cases in which species are particularly close to one another (the values are reported in Table S4 in the supplemental material, and minimal, median, and maximal values for each genus are shown in Table S5 in the supplemental material). The distribution of all intragenus minimal values is plotted in Fig. 6. Among 67 genera analyzed, 64% had a minimal MUMi value above 0.8. Genera that comprise isolates with very low interspecies distances include Brucella, Rickettsia, and some pairs of Mycobacterium with a minimal MUMi below 0.2. More intermediate values of MUMi were observed for Neisseria and Borrelia (range, 0.3 to 0.4) and for Listeria and Helicobacter (mimimal MUMi, 0.7).

FIG. 6.

Distribution of all minimal MUMi values per genus.

A significant gap in MUMi values separates intraspecies from intragenus comparisons.

The MUMi was used to specifically address the question of intra- and interspecies variability. For all species for which at least three genomes are fully sequenced and at least one genome of another species in the genus is available, we calculated two sets of MUMi values: (i) the set of all intraspecies MUMi values and (ii) the set of MUMi values encompassing all pairs composed of a genome of the species and one belonging to another species in the same genus. A nonparametric Mann-Whitney test was then used to test whether the difference between the two sets of values was significant. Table 2 reports the P values obtained for the 26 species for which it was possible to make the analysis. For Y. pestis and M. tuberculosis, an analysis focusing on closely related species only (Y. pseudotuberculosis and Mycobacterium bovis, respectively) was added. In all cases, the P value was lower than 1%, suggesting that a gap exists between the distances within and across species. Looking carefully at all sets of values (see Fig. S3 in the supplemental material), two main situations could be distinguished: a “biphasic” situation in which all intraspecies values are similar and all interspecies values are around 1 (22 cases) and a “polyphasic” situation in which different groups of values are found (3 cases: Burkholderia pseudomallei, B. cereus, and Helicobacter pylori). The last case is Neisseria meningitidis compared to Neisseria gonorrhoeae, where only two sets of values are found, which could be considered biphasic. However, the interspecies values are well below 1, so if another, more distant Neisseria genome was available, a polyphasic situation might be observed. A study based on MLST data indeed suggests that the genus Neisseria contains species with fuzzy borders (14).

TABLE 2.

Statistical test of the difference between intraspecies and intragenus MUMi values

Species	MUMi value				P value
	Intraspecies		Interspecies
	Avg MUMi	No. of genomes	Avg MUMi	No. of genomes
B. cereus	0.481	9	0.993	6	1.1 × 10−18
Burkholderia mallei	0.100	4	0.929	12	3.8 × 10−8
B. pseudomallei	0.069	4	0.796	12	3.8 × 10−8
Campylobacter jejuni	0.240	4	0.983	4	3.3 × 10−8
Chlamydia trachomatis	0.030	4	0.885	1	4.7 × 10−3
C. pneumoniae	0.004	4	0.976	3	5.3 × 10−5
Clostridium botulinum	0.114	4	0.968	12	3.8 × 10−8
Clostridium perfringens	0.235	3	0.972	13	8.7 × 10−5
Ehrlichia ruminantium	0.071	3	0.941	2	1.2 × 10−2
Francisella tularensis	0.108	7	0.877	1	8.4 × 10−7
Haemophilus influenzae	0.212	4	0.973	2	3.3 × 10−4
Helicobacter pylori	0.308	3	0.808	2	1.2 × 10−2
M. tuberculosis/all other mycobacteria	0.010	5	0.788	12	2.5 × 10−7
M. tuberculosis/M. bovis	0.010	5	0.032	2	5.4 × 10−6
Mycoplasma hyopneumoniae	0.106	3	0.988	10	1.8 × 10−4
N. meningitidis	0.222	4	0.380	1	4.7 × 10−3
Pseudomonas aeruginosa	0.308	3	0.923	10	1.8 × 10−4
P. putida	0.493	3	0.913	10	1.8 × 10−4
P. syringae	0.719	3	0.944	10	1.8 × 10−4
Shewanella baltica	0.257	3	0.933	13	8.7 × 10−5
S. aureus	0.105	13	0.950	4	1.5 × 10−24
S. agalactiae	0.151	3	0.959	23	1.8 × 10−3
Streptococcus pneumoniae	0.084	3	0.976	23	1.8 × 10−3
S. pyogenes	0.138	12	0.971	14	6.2 × 10−33
Streptococcus thermophilus	0.106	3	0.976	23	1.8 × 10−3
Xanthomonas campestris	0.091	3	0.792	4	2.2 × 10−3
Y. pestis/all other Yersinia	0.037	7	0.367	3	1.9 × 10−12
Y. pestis/Y. pseudotuberculosis	0.037	7	0.108	2	4.3 × 10−10

DISCUSSION

We developed and validated the MUMi, an index based on MUMs, to rapidly estimate the distance between closely related bacterial genomes. We have shown that the method is accurate in the sense that MUMi distances correlate with those obtained with the ANI estimation (22) and produce distance matrices and trees that are comparable to those obtained by MLST and ANI. We also found a good correlation between MUMi values and DDH values (not shown), which is one of the criteria used by taxonomists to assign strains to a species. This is not surprising, as the ANI itself was reported to correlate with DDH values (10).

The MUMi distance has been designed to be most sensitive in the range of differences between closely related strains (i.e., typically belonging to the same species). The maximum value of 1 is reached when distances at the bacterial-genus level are measured. The MUMi relies on the detection of exact matches and can therefore be viewed as a way to estimate the average distance between two mismatches in the alignment. The strategy used to design the MUMi might also be applicable to comparing more distantly related bacterial genomes by replacing MUMs by inexact matches that can be rapidly identified with an algorithm such as YASS (25). Another interesting approach to determine whole-genome distances has been described, which is based on DNA compression algorithms (4, 26, 31). At the protein level, an approach based on Promer, the amino acid version of Mummer, has also been investigated (2).

Comparative genomic studies often require a decision tool to help select the genomes to compare and in particular which bacterial genomes are close enough to be aligned at the DNA level. A pairwise complete genome alignment routinely takes 2 h; thus, a 20-s MUMi calculation to preselect appropriate genomes should prove to be a convenient tool. A similar preselection strategy is used in large-scale BLAST alignments of proteins or genes and is based on an estimation of word dissimilarity (32, 33). MUMi will also be valuable for fine tuning the parameters of software used for such alignments, e.g., MGA (17), MAUVE (6), or M-GCAT (30). For instance, parameters adapted for E. coli genomes that are never more distant than a MUMi value of 0.4 may have to be changed for the alignment of P. syringae or L. lactis genomes (with MUMi values of around 0.7). Finally, we tested the MUMi on the set of five unfinished and three complete genomes of Streptococcus agalactiae (not shown). It produced a tree comparable to the published tree (29). The MUMi is therefore a versatile, robust, and fast method to obtain a genomic distance between closely related bacterial strains.

Two a priori independent parameters contribute to the MUMi distance value. One is the “vertical” distance due to the accumulation of point mutations during vertical transmission of the ancestral genome. The second parameter is the “horizontal” distance due to the acquisition of new DNA by horizontal transfer and all the differences that can arise due to intrachromosomal-recombination events. Phylogenetic studies intentionally restrict their analysis to the vertical component of the genomes being compared. Therefore, the MUMi was not expected to be relevant, strictly speaking, for phylogenetic studies. However, when tested on the two species E. coli and S. aureus, the MUMi compared well with MLST-based phylogenetic trees. MUMi trees fitted even better with ANI-based trees, which were themselves shown to compare well with reference phylogenetic methods using concatenated core genes (19). This good behavior of MUMi could be explained if the contribution of the horizontal signal was low relative to the vertical signal or if the level of horizontal transfer was proportional to the amount of vertical divergence. The fact that we found, on a set of 48 genome pairs, low correlation between the values of the ANI and conserved genes argues against the last possibility, but more data are clearly needed before any strong conclusion can be reached. For instance, one could test the effect on the MUMi of manipulating in silico, at a given ANI value, the number of shared genes. Also, using large sets of whole-genome alignments, such as those available in the MOSAIC database (5; http://genome.jouy.inra.fr/mosaic), one could systematically compare coverage values (which are related to DNA loss or acquisition) to the divergence of the backbone DNA.

The MUMi provides distances that can be compared from one set of strains to another, something not feasible with MLST data, because different sets of housekeeping genes are used. We used it to determine the maximal distance between all sequenced strains belonging to the same species. Among 68 species tested, we found that in 77% of cases, the maximal value was below 0.5. Among them, some species, such as E. coli, are particularly diverse (maximum MUMi value, 0.38), while most species exhibit a 0.1 to 0.2 intraspecies “diversity,” with the caveat that the sequenced genomes are not necessarily representative of the species. A comparable analysis at the genus level (for 67 genera) revealed that most species within a genus are generally at a MUMi distance of 0.9 to 1 from each other (Fig. 6). A precise analysis of the species-genus boundary has shown that, in the presently available genome sample, there is a significant gap between species and genus. However this result does not necessarily imply that a discontinuity between species and genus exists in nature, as available species are biased by human sampling and the necessity to work with pure cultures. Up to now, however, the pragmatic current species definition fits reasonably well with the genomic data.

The twilight zone of species that contain distant strains (with MUMi distances in the range 0.6 to 0.8), such as B. cereus, several Pseudomonas species, and L. lactis, is interesting for addressing the question of bacterial species boundaries. The case of the genus Burkholderia, in which some species are particularly close to one another, relates to the same question. This question is addressed from many perspectives in the literature. An interesting ecological approach to the question has recently shown that it was possible to delineate ecotypes within three Bacillus species (19). Using a genomic approach, Konstantinidis et al. have proposed making a distinction between species in which all members share high ANI and high conserved-DNA values and those in which despite high ANI values, conserved-DNA values are not as high (20). The first group would correspond to “clear” bacterial species. The second may rather be considered as a group of species, due to the large number of strain-specific genes, some of which may contribute to strain adaptation to a specific environment. Alternatively, it is conceivable that some bona fide species, because of their life styles encompassing survival in harsh environments, such as soil, are just more adept at keeping a reservoir of various genes. Further studies of the distribution of strains within the species, either forming subgroups suggesting subspecies (as assumed for L. lactis or B. cereus) or evenly distant from each other (as may be the case for Pseudomonas species), should help distinguish between these possibilities. Clearly, genomic sequences in progress, and refined tools such as multiple-genome aligners, will be used in the future to address precisely such questions. In the meantime, the MUMi provides a first level of analysis to assess the amount of diversity encountered within, or among, different species.