Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Jan 1.
Published in final edited form as: J Biomech. 2008 Jun 17;41(10):2197–2205. doi: 10.1016/j.jbiomech.2008.04.032

The Apparent Critical Isotherm for Cryoinsult-Induced Osteonecrotic Lesions in Emu Femoral Heads

Jessica E Goetz *,+, Douglas R Pedersen *,+, Duane A Robinson °, Michael G Conzemius °, Thomas E Baer *, Thomas D Brown *,+
PMCID: PMC2612542  NIHMSID: NIHMS63883  PMID: 18561937

Abstract

Cryoinsult-induced osteonecrosis (ON) in the emu femoral head provides a unique opportunity to systematically explore the pathogenesis of ON in an animal model that progresses to human-like femoral head collapse. Among the various characteristics of cryoinsult, the maximally cold temperature attained is one plausible determinant of tissue necrosis. To identify the critical isotherm required to induce development of osteonecrosis in the cancellous bone of the emu femoral head, a thermal finite element (FE) model of intraoperative cryoinsults was developed. Thermal material property values of emu cancellous bone were estimated from FE simulations of cryoinsult to emu cadaver femora, by varying model properties until the FE-generated temperatures matched corresponding thermocouple measurements. The resulting FE model, with emu-bone-specific thermal properties augmented to include blood flow effects, was then used to study intraoperatively performed in vivo cryoinsults. Comparisons of minimum temperatures attained at FE nodes corresponding to the three-dimensional histologically apparent boundary of the region of osteonecrosis were made for six experimental cryoinsults. Series-wide, a critical isotherm of 3.5°C best corresponded to the boundary of the osteonecrotic lesions.

Keywords: cryoinsult, finite element model, emu, osteonecrosis, histology

Introduction

Femoral head osteonecrosis is a debilitating disorder characterized by collapse of the weight-bearing osseous lattice, followed by joint degeneration. Because this condition affects a young patient group (average age 30–40 years), the last-resort treatment option of total hip replacement is often unsatisfactory (Mont et al. 2000). Systematic exploration of candidate joint preservation methods and of new reparative treatment options has been hindered by the lack of an animal model that reliably demonstrates human-like femoral head collapse. While traditional animal models of osteonecrosis such as dogs, rabbits, and rats do develop histologically apparent osteonecrosis, as quadrupeds these species are able to load protect the affected limb and therefore do not progress to frank femoral head collapse (Conzemius and Brown 2001).

By contrast, the emu shows great promise as an animal model of necrotic femoral head collapse because emus, as bipeds, lack the ability to load-protect a study limb. Additionally, their high activity level involves relentless joint loading (Troy et al. 2007). In previous work with this model, osteonecrosis has been induced by liquid nitrogen cryoinsult (Conzemius et al. 2002; Reed et al. 2004). Although not an etiologic factor clinically, there is ample laboratory precedent for using cryoinsult to induce ON in dogs (Dailiana et al. 2001) and in rabbits (Keijser et al. 1999). Moreover, focal osteonecrotic lesions resulting from cryoinsult to the emu femoral head are very consistent with human disease pathophysiology (Goetz et al. 2005).

The (cylindrical) cryoprobe design used in the emu model of ON is 2.5 millimeters in diameter and consists of a closed loop of concentric tubing, in which liquid nitrogen is circulated to an exposed metallic tip. The system includes active electrical heating along the shaft to allow delivery of a cryoinsult emanating nearly point-wise from the probe tip (Reed et al. 2003). Two probe-mounted copper-constantan thermocouples monitor temperature during the cryoinsult, one at the exposed tip and one on the resistance-heated shaft. Through use of specific cryoinsult time/temperature parameter sets, well-prescribed necrotic lesions can be created for controlled study of lesion geometry.

In quantitative analyses of cryosurgery in other applications, freeze rate, coldest temperature, and thaw rate have all been argued to influence particular mechanisms of cell death (direct cellular injury or indirect perfusion interruption) and therefore tissue viability (Gage and Baust 1998; Hoffmann and Bischof 2002; Baust and Gage 2005). While rates of temperature change and duration of cryoinsult are sometimes viewed as independent influence factors, the coldest temperature attained has received the most attention as the dominant parameter for local tissue necrosis during single cryoinsult events (Gage et al. 1985). Indeed, analytical focus on the attainment of a particular extremum tissue temperature has been a very frequent approach, sometimes referred to as the ‘critical isotherm protocol’ (Rewcastle et al. 1998): tissue necrosis due to cryoinsult, all other factors being equal, depends on the coldest temperature achieved locally.

Directly monitoring whole-femoral-head spatial distributions of temperature during intraoperative cryoinsult to emu cancellous bone is not practicable experimentally. Alternatively, transient temperature distributions can be reasonably estimated from numerical models. Various mathematical models of cryoinsult, developed mostly within the context of cryoablative cancer treatment, are frequently used for modeling heat transport through semi-homogenous high-water-content soft tissues such as the prostate gland, kidney, and liver (Rabin and Shitzer 1998; Rewcastle et al. 1998; Wan et al. 2003). Such models usually include the Pennes bioheat equation, which describes heat transfer in blood-perfused tissue, and are implemented numerically with finite difference, finite element, or finite volume techniques.

In the present study, a finite element model was developed to calculate temperature distributions in emu femoral head cancellous bone during intraoperative cryoinsults. These temperature data were then compared to histologically apparent distributions of osteocyte necrosis, in order to estimate the critical temperature associated with local induction of osteonecrosis.

Methods

Finite Element Model

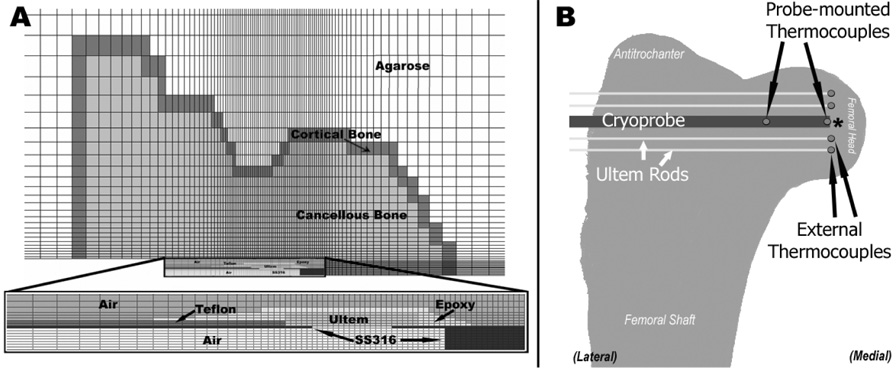
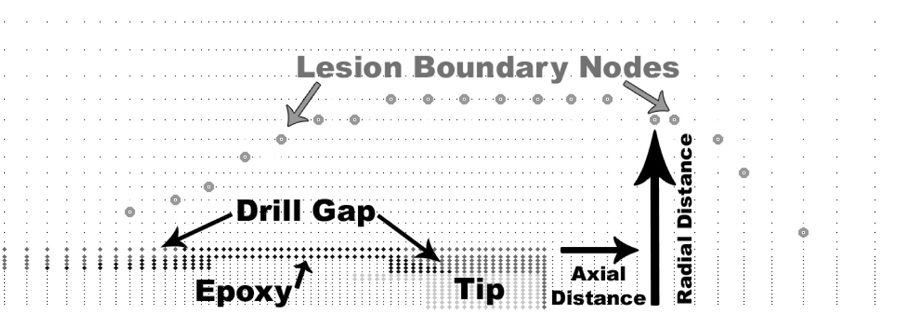
A thermal finite element (FE) model was developed of a cryoprobe embedded in an emu proximal femur (Figure 1A). The FE model was formulated as an axisymmetric (two-dimensional) problem because the cryoprobes used intraoperatively were cylindrical and conducted heat radially 360° around the probe. Using PATRAN software (MSC, Santa Ana, CA) for mesh generation, the probe was modeled as embedded in a region approximating the shape of the emu proximal femur (including the femoral head, neck, and antitrochanter) with a one-element-thick cortical shell around the entire femur. The femur, in turn, was modeled as being inside a semi-infinite matrix representing either in vitro testing conditions (a large reservoir of agarose gel) or in vivo surgical conditions (inside the emu pelvis). The entire model was meshed with four-noded axisymmetric rectangular elements (ABAQUS type DCAX4), with mesh density concentrated around the tip of the cryoprobe. All analyses were run in ABAQUS 6.5.1 (ABAQUS, Inc., Providence, RI).

Figure 1.

Figure 1

Open in a new tab

A.) Two-dimensional (axisymmetric) mesh used for finite element analysis. The geometry of the probe (see inset for detail) reflects the geometry of the outer portion of the cryoprobe used intraoperatively. Ultem is a low-thermal-conductivity polymer used to insulate the stainless steel (SS316) tip from the actively heated shaft. The epoxy and the Teflon tubing seal the cryoprobe. During intraoperative simulations, the area around the probe marked as air was modeled as blood. B.) Schematic of thermocouple arrangement during bench top experimental cryoinsult. Thermocouples glued to Ultem rods were positioned with their junctions near the tip of the cryoprobe. Following testing, the locations of the external thermocouples were measured with respect to the tip of the cryoprobe. The Ultem mounting rods were not represented in the FE model.

Nodes at the outer edge of the cortical shell were constrained to hold the ambient temperature throughout the cryoinsult simulation: 24°C for in vitro bench top testing, and 38°C for intraoperative cryoinsult. To drive the model, temperatures that had been recorded from the tip- and shaft-mounted thermocouples during the experimentally performed cryoinsults were assigned to spatially corresponding FE nodes.

For the cryoprobe materials, agarose, air, and blood, thermal material properties (density ρ, specific heat c, and conductivity k) were straightforwardly assigned from handbook values (Table 1). In the case of the bone, however, experimental data for specific heat and thermal conductivity are available only for mammalian species, and only at or above room temperature. Phylogenic class differences (avian vs. mammalian) of mineralization and trabecular density might plausibly cause the thermal material behavior of emu bone to differ from that of mammals. Therefore, as part of the model development, it was decided to determine apparent material properties of emu cancellous bone during cryoinsult, as described below.

Table 1.

Thermal property values assigned to the model for the materials in the cryoprobe and the surrounding structures. Properties of bone are described in context in Table 2.

Material Density Thermal Conductivity Specific Heat
g/cm3 W/mK J/gK
Stainless Steel 316 7.90 12.97 0.46
Ultem 1.28 0.13 2.00
Teflon 2.15 0.25 1.00
Epoxy 1.29 0.30 1.17
Air 0.0013 0.0243 1.0005
Agarose Gel 1.00 0.59 4.18
Blood 1.06
1.06		 1.60 - Frozen
0.51 - Thawed		 3.89
3.89
Open in a new tab

Thermal Property Determination

Bench top cryoinsults were performed in four cadaver emu femurs stripped of all soft tissue. A 4-millimeter diameter hole was drilled from the lateral side of the proximal femur into the center of the femoral head to accommodate the cryoprobe. Four 1.8-millimeter diameter holes were drilled nominally parallel to and at various distances from the main cryoprobe hole. Copper/constantan thermocouples supported by 1.6-millimeter diameter rods of Ultem polymer (GE Plastics; Pittsfield, MA) were inserted through these smaller drill holes (Figure 1B) until direct contact was made with the bone (or marrow). The femoral head was then embedded in a cylindrical agarose gel block (115 mm diameter, 60 cm long) to provide thermal inertia during the cryoinsult. A single freeze/thaw event was performed with the probe tip temperature held at −45°C for 5 minutes, followed by a passive return to room temperature. Temperature measurements from the four bone-embedded thermocouples and the two probe-mounted thermocouples (tip and shaft) were recorded using LabVIEW software (National Instruments, Austin TX).

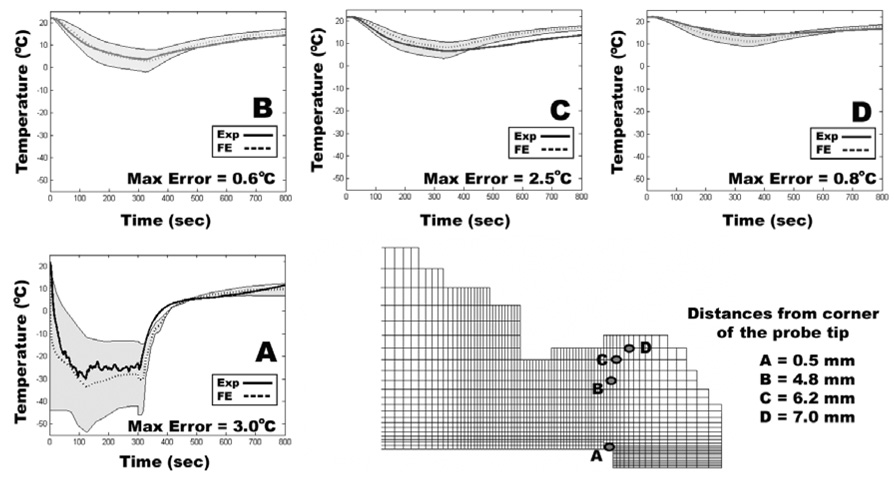
Following the experiment, the femoral head was cut open to measure the radial and axial positions of each thermocouple relative to the probe tip. Nodes in the FE mesh most closely corresponding to these locations were identified for comparison with experimentally measured temperature data. To allow for possible small errors in measurement of thermocouple position, as well as for instances in which the thermocouple locations fell between FE nodes, all nodes within a one-millimeter uncertainty envelope extending in all directions around the node most coincident with the thermocouple were also monitored.

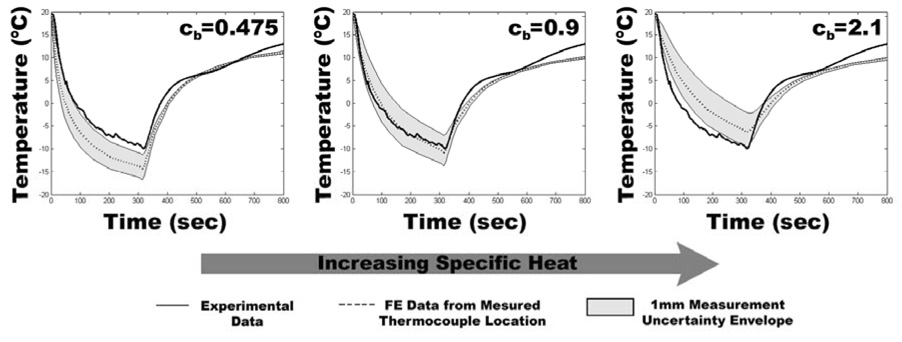
Beginning with provisional values for specific heat and thermal conductivity, assumed equal to those of mammalian bone, temperature histories computed at nodes corresponding to experimental thermocouple locations were compared with temperature recordings made from the cadaver emu femurs. The provisional thermal material properties of the cancellous bone were then iteratively adjusted in subsequent runs of the model so as to bring the computed temperatures at the thermocouple nodes into close consonance with the temperatures recorded during physical testing (Figure 2). Since previous cryoinsult models have indicated that temperature-dependent material properties must be used to obtain accurate thermal histories at the boundary between necrotic and viable tissue (Rabin 2000; Hoffmann and Bischof 2001; He and Bischof 2005), temperature-dependent material properties, based on the temperature dependence of ice (Fukusako 1990), were implemented for bone colder than 0°C. These thermal material properties of emu cadaveric cancellous bone from the FE model of the bench top series were then used in FE models of intraoperative cryoinsults.

Figure 2.

Figure 2

Open in a new tab

Illustrative example (for a single thermocouple channel) of the effects of changing emu bone thermal properties on the agreement between FE generated and experimentally generated temperature information. Because specific heat is treated as a temperature-dependent property in the model, the above values for specific heat of emu cancellous bone (cb) are averages over the range of temperatures defined in the model. The center image shows the best agreement between measured and FE generated temperatures. The right and left images show the effects of a specific heat value that is too low (left) or too high (right).

The FE models for in vivo intraoperative cryoinsults also included the effects of blood perfusion in the cancellous bone, by including a Pennes bioheat generation term Qb in the cancellous bone thermal property definition: Qb = η(Tl)cbρbwb(Tbody−Tl). In this equation, η is a binary switch that precludes heat generation if the tissue is frozen (η=1 if T>0°C → thawed, and η=0 if T<0°C → frozen) (Reed et al. 2003), cb is the specific heat of blood, ρb is the density of blood, wb is the rate of blood flow, estimated as 18.18 mL/min/100gm (Jones et al. 1982), Tbody is the normal emu body temperature (38°C) (Maloney and Dawson 1993), and Tl is the local nodal temperature.

Intraoperative Cryoinsults

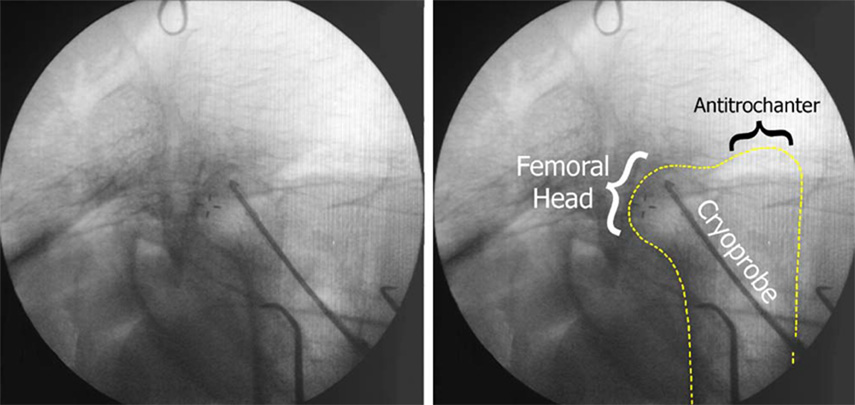
Intraoperative cryoinsults were performed in six anesthetized emus in accordance with an IACUC-approved protocol. During each surgical procedure, a cryoprobe was inserted into the femoral head through a 4-millimeter diameter drill tract made through the lateral femoral cortex, until the probe tip made flush contact with the bone at the end of the tract (Figure 3). Each of the six experimental emus received cyclic cryoinsults consisting of three events of a nine-minute freeze (one bird each to −10°C, −30°C, −40°C, −50°C, and two birds to −20°C), with each freeze being followed by passive thaw back to 30°C (requiring typically 2 – 10 minutes), and then by five minutes of equilibration time. Temperatures at the tip and on the shaft of the cryoprobe were continuously monitored during both the freeze and thaw portions of the cryoinsult. After a one-week period to ensure the histologic manifestation of cryo-induced osteocyte death (Gage et al. 1966; Keijser et al. 1999), the animals were euthanized and their femurs harvested for analysis.

Figure 3.

Figure 3

Open in a new tab

Fluoroscope image of intraoperative cryoprobe positioning (left). The depth of the femoral head within the emu body required imaging through large amounts of soft tissue, thereby degrading image clarity. Because it is difficult to discern the outline of the emu femur, it has been traced on the right.

Histologic Evaluation

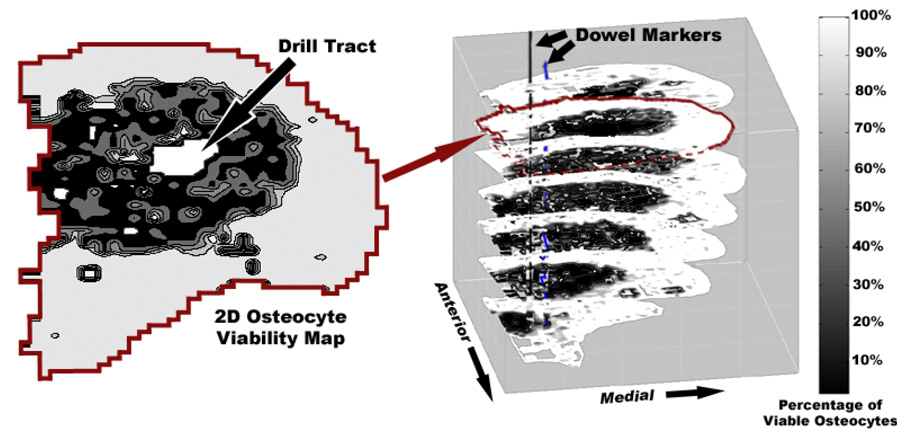
Although non-invasive imaging assessments (x-ray and MRI) are useful clinically, the most definitive assessment of osteonecrosis for quantitative research purposes is documentation of loss of osteocyte viability at the microscopic level. In order to delineate the region of tissue necrosed by the cryoinsult, semi-automated quantitative histologic analysis was applied to the entire femoral head to obtain a three-dimensional mapping of fractional osteocyte viability. Prior to excision of the head from the proximal femur, two parallel fiducial holes 1.6 millimeters in diameter, 10 millimeters apart were drilled through the emu femoral neck in a roughly anterior-to-posterior direction. To prevent these holes from distorting during subsequent processing of the specimen and for later three-dimensional reconstruction of serial section histology, the fiducial holes were filled with cylindrical dowels cut from a partially dehydrated potato. The femoral head was embedded in a paraffin block and serially sectioned through its entire thickness. Five-micron-thick sections were selected at 0.5-millimeter intervals, affixed to microscope slides, and stained with Wiegert’s hematoxylin and eosin.

Stained sections were placed on a stepper-motor-driven microscope stage (StagePro, Prior Scientific, Rockland, MA) and imaged in 8-bit grayscale through the microscope’s 10x objective lens using a digital camera (QICAM, QImaging, Burnaby, BC, Canada). Each whole-head cross-sectional scan involved approximately 2200 high-resolution (1040 × 1392 pixels) images of 0.485 × 0.637 millimeter tissue sub-regions. Each such image was evaluated for percentage of viable osteocytes (viability being defined as the presence of a cell nucleus in a lacuna) using a semi-automated grading program purpose-written in Matlab (Goetz et al. 2005).

Once all sub-images from a given head section were thus evaluated, a 2D osteocyte viability map was generated. A volumetric dataset of osteocyte viability throughout the femoral head was then assembled from the sets of 2D viability maps (corresponding to sets of serial histology sections) by stacking them in 3D, using the dowel-marked fiducial locations for alignment (Figure 4). The osteonecrotic lesion was defined as the region of the femoral head with less than 50% osteocyte viability (Koo et al. 1999). The outer boundary of this region was determined with respect to the axis of the cryoprobe drill tract. Temperature extrema at nodes corresponding to this boundary were extracted from the FE model output file (Figure 5).

Figure 4.

Figure 4

Open in a new tab

Illustration of the 3D viability mapping assembly. Two-dimensional maps of osteocyte viability were stacked in 3D to get a volumetric data set of osteocyte viability. The lesion (shown in dark) edge was determined relative to the drill tract (white space in the center of the necrotic lesion).

Figure 5.

Figure 5

Open in a new tab

Identification of FE nodes corresponding to the edge of a necrotic lesion. Prior to identification of the nodes, the boundary of the necrotic lesion was rotated and translated so as to be aligned with the distal end of the probe tip.

Results

Using FE-derived temperature-dependent values of specific heat and thermal conductivity for emu cancellous bone (Table 2) resulted in FE-generated temperature curves that were able to achieve close concordance with experimentally measured temperatures (series-wide whole-freeze/thaw cycle average error = 0.51°C) (Figure 6).

Table 2.

Representative thermal material properties of mammalian bone reported in literature, versus the present FE-derived material properties of emu cancellous bone. The specific heat of emu cancellous bone was within the range reported in the literature at room temperature, but lower than literature values when below freezing. Thermal conductivity of emu bone increased as temperature decreased. Emu cortical bone was assigned thermal conductivity values according to Davidson et al., and specific heat values according to Lundskog et al. Below freezing, these properties were assigned a similar trend as that seen in the cancellous bone. In the present study, values of material properties were obtained over the entire range of relevant temperatures by linear interpolation (within ABAQUS) between the defined property values.

author species condition tissue type specific heat conductivity
(J/g/°C) (W/m°C)
Biyikli, et al. human
human		 fresh
dried		 cancellous&cortical
cancellous&cortical		 1.50–2.37
1.14–1.64		 0.26–0.34
0.16–0.24
Clattenburg, et al. cow fresh frozen cancellous bone 2.64–3.64 ~0.29
Davidson, et al. cow fresh frozen cortical bone 0.53–0.58
Lundskog, et al. human fresh and dry cortical bone 1.26 3.56
Present Study emu −273°C
−8°C
−1°C
>12°C		 cancellous bone 0.75
1.50
2.10
2.50		 1.30
0.29
0.28
0.26
Present Study emu −273°C
−8°C
>−1°C		 cortical bone 0.50
0.90
1.30		 3.30
0.63
0.55
Open in a new tab

Figure 6.

Figure 6

Open in a new tab

Representative comparisons between four different thermocouple-measured temperatures and the corresponding FE temperatures. While there was very good agreement for the close-to-probe site (A), FE estimated temperatures at other more remote thermocouple locations had some larger disparities (C). Series-wide, the maximum instantaneous error in any one of the channels in any of the FE runs was 4.3°C. Maximum errors in all of the other FE-thermocouple pairs (13 pairs) were always less than 4.3°C, and the instantaneous errors over the freeze and thaw averaged 0.51°C (about 4.5% of the total temperature change).

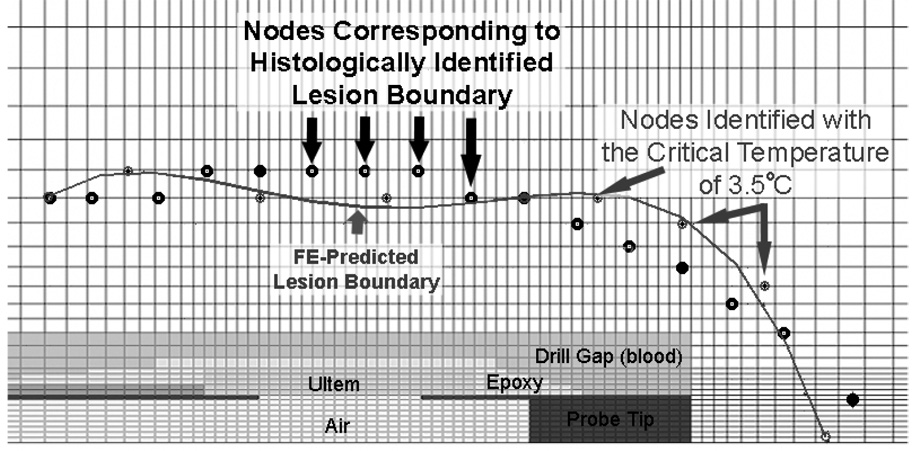
For each intraoperative cryoinsult, the coldest temperatures attained at the nodes closest to the edge of the necrotic lesion were averaged, resulting in six independent estimates of the critical isotherm corresponding to the boundaries of the six respective necrotic lesions (Table 3). Directly averaging these six individual lesion-boundary isotherms in turn yielded a single overall critical isotherm value of 0.9°C. However, the particular experimental trial with the −50°C cryoinsult temperature involved a critical isotherm estimate significantly colder than those for the other five trials. This −50°C trial unfortunately had a malfunction of the shaft-insulating heating element, allowing cryogenic temperatures to develop along much of the length of the cryoprobe shaft. While a seemingly valid FE solution could still be generated for this case, its temporal/spatial pattern of cryoinsult propagation differed appreciably from those of the other five more point-concentrated cryoinsults. By disregarding this single aberrant trial, the variance associated with averaging the trial-specific critical isotherms was substantially decreased, from 7.0°C to 3.4°C, and the value of the apparent critical isotherm was moderated to 3.5°C. Using this latter value of 3.5°C as the preferred critical isotherm, series-wide the lesion boundary was correctly predicted from the FE model (Figure 7) to within a root mean squared error of less than 1.3 millimeters along the full length of the lesion boundary, and the total fractional volume of head necrosis was correctly replicated to within 2% (Table 4).

Table 3.

Critical isotherms determined for each experimental trial. Standard deviations improved with the omission of the critical temperature corresponding to the −50°C trial.

Exp Hold Temperature Average Critical Temperature
−10°C −1.9°C
−20°C 4.8°C
−20°C 5.4°C
−30°C 2.5°C
−40°C 6.7°C
−50°C −11.9°C
Average 0.9°C / 3.5°C**
Standard Deviation 7.0°C / 3.4°C**
Open in a new tab
**

Without outlier at −50°C

Figure 7.

Figure 7

Open in a new tab

Prediction of lesion boundary in the −30°C trial by identification of the critical isotherm at the nodes in the FE model. The nodes most closely corresponding to the histological lesion boundary are circled in black, and the nodes identified by the critical temperature are circled in gray. The lesion boundary is a 4th order polynomial fit to nodes with the critical isotherm.

Table 4.

Predictive ability of the 3.5°C average critical isotherm. Using this critical isotherm value, the FE model was able to accurately predict several key lesion characteristics, including percentage of necrosed femoral head volume and maximum lesion radius. Root mean square errors along the length of the lesion boundary were all less than or equal to 1.3 millimeters.

Exp. Hold Temp. % Head Volume Maximum Radiu (mm) Whole-Boundary RMSE
Histology FE Difference Histology FE Difference
% % % mm mm mm mm
−10°C 3.0 4.9 1.9 3.0 4.1 1.1 1.3
−20°C 5.0 6.4 1.3 3.6 4.1 0.5 1.3
−20°C 8.4 8.1 −0.2 4.9 4.6 −0.3 1.1
−30°C 10.3 12.0 1.7 5.2 5.1 −0.1 1.0
−40°C 14.5 12.8 −1.7 5.7 5.1 −0.6 1.2
Open in a new tab

Discussion

Temperature distributions were determined by means of finite element analysis because the depth of the femoral head within the emu body cavity precluded direct measurement of cancellous bone temperature without extensive, potentially lethal, surgical exposure. Comparisons of the extremum temperatures attained at FE nodes corresponding to histologically defined lesion boundaries allowed estimation of the apparent critical isotherm necessary for inducing osteonecrosis in the emu femoral head.

Intuitively, temperature is the single cryoinsult parameter most significantly influencing tissue survival. Studies in a variety of tissues have determined that the critical isotherm for onset of necrosis in vivo (Table 5) is much warmer than the −40°C to −50°C critical isotherms typically recommended to assure complete ablation of tumor cells (Baust et al. 1997; Gage and Baust 2002). The explanation for the relatively warm critical isotherm presently estimated for necrosis of emu cancellous bone (3.5°C) is in large part that the >50% osteocyte death criterion conventionally used for osteonecrosis (Ficat 1985; Koo et al. 1999) constitutes a very relaxed standard relative to a guaranteed 100% loss of cell viability required for therapeutic tumor cryoablation.

Table 5.

Tissue-specific cryoablative temperatures reported in literature. These temperatures were determined by correlating intraoperative cryoinsult temperature measurements, plus some FE (Hoffmann and Bischof 2001; Schmidlin et al. 2001) and analytically (Rupp et al. 2002) generated temperatures, with histologically apparent complete tissue necrosis and vascular stasis.

Author Year Tissue Investigated Testing Species 100% Ablative Temperature Post-Insult Survival Time
Auge, et al. 2006 Kidney Pig −20°C 4–7 days
Schmidlin. et al. 2001 Kidney Pig −16.1°C 1–2 hours
Rupp,et al. 2002 Kidney Pig −20.3°C 0 hours
−16.9°C 2 hours
−21.9°C 3 days
Cozzi, et al. 1996 Human Prostate Mouse −15°C 2 months
Hoffman & Bischof 2001 Rat Prostate Tumour Rat −19°C 3–7 days
Skin Rat −15°C 3–7 days
Seifert, e al. 2003 Liver Pig −15°C 1 week
Keijser, et al. 1999 Cortical Bone Rabbit −10°C 1 week
Open in a new tab

One important limitation of the present study lies in attributing the extent of the necrotic lesion entirely to the coldest tissue temperature attained, without accounting for other cryoinsult parameters (e.g. rate of temperature change or time spent at cryogenic temperatures) which may also impact tissue viability (Gage et al. 1985). Individual biological variation in response to cryoinsult, slight functional differences in individual cryoprobes, and small histological processing artifacts may also have affected the results. While backing out effective material properties specifically for emu bone did account for the composite nature of the emu bone, these properties were obtained assuming flush contact of the probe tip with the bony bed, a condition that cannot be known for certain during experimental cryoinsults. The computational treatment of heat generation due to blood perfusion in bone was formulated somewhat more simplistically in this work than typically has been necessary in models of cryoinsult to well-hydrated soft tissue (Zhao et al. 2007) owing to the relatively small role that blood perfusion heating has been shown to have in bone (Reed et al. 2003). While the accumulation of tissue damage in cyclic freeze/thaw events can change a tissue’s effective constitutive properties (Gill et al. 1968), the present cryoinsult model used a single heat generation definition (to model blood perfusion) with a single set of temperature-dependent material properties. While necessarily an approximation, this single thermal material property definition was deemed reasonable in this particular cryoinsult environment because information about ‘active’ tissue thermal material property changes immediately following cryoinsult was unavailable.

Despite these several limitations, the present histology-linked FE model of cryoinsult to emu cancellous bone allowed for good replication of lesion geometric characteristics. The 0.9°C critical isotherm value allowed the FE model to estimate maximum lesion radii that were always within 0.7 millimeter of the histologically measured maximum lesion radius, and volumetric head involvement fractions that were always accurate to within 10%. When the −50°C outlier case with the heating element malfunction was excluded, yielding an apparent critical isotherm of 3.5°C, the predictive ability of the model further improved. Using this warmer critical isotherm, the model was able to estimate maximum lesion radius to within 1.1 millimeters of the histologically determined maximum radius, and it was able to estimate the head-fractional volume to within 2%. Root mean squared errors were small, indicating that the critical isotherm paradigm afforded good prediction of the shape of the lesion boundary along the entire length of the lesion.

The use of a histology-linked FE model made it possible to investigate temperatures and temperature changes in a region that could not feasibly be monitored intraoperatively. The use of fully 3D spatial mapping to histologically evaluate osteocyte viability is a novel method for quantifying tissue damage following cryoinsult, allowing for confident delineation of the lesion boundary. Going forward, in the context of the emu model of femoral head osteonecrosis, the utility of having identified a critical isotherm is that it enables credible prediction of lesion patterns resulting from specific cryoinsults. Conversely, and perhaps more importantly, it also allows for identification of the cryoinsult parameters needed to create lesions of a desired size or shape.

Acknowledgements

Financial support was provided by NIH grant #AR 049919. The authors would like to thank Dr. James A. Martin and Ms. Gail Kurriger for histological assistance, and Ms. Marie Frenn and Mr. Erich Stoermer for assistance with digitizing histological sections.

References

  1. Auge BK, Santa-Cruz RW, Polascik TJ. Effect of freeze time during renal cryoablation: a swine model. Journal of Endourology. 2006;20(12):1101–1105. doi: 10.1089/end.2006.20.1101. [DOI] [PubMed] [Google Scholar]
  2. Baust J, Gage AA, Ma H, Zhang CM. Minimally invasive cryosurgery--technological advances. Cryobiology. 1997;34(4):373–384. doi: 10.1006/cryo.1997.2017. [DOI] [PubMed] [Google Scholar]
  3. Baust JG, Gage AA. The molecular basis of cryosurgery. BJU International. 2005;95(9):1187–1191. doi: 10.1111/j.1464-410X.2005.05502.x. [DOI] [PubMed] [Google Scholar]
  4. Biyikli S, Modest MF, Tarr R. Measurements of thermal properties for human femora. Journal of Biomedical Materials Research. 1986;20(9):1335–1345. doi: 10.1002/jbm.820200908. [DOI] [PubMed] [Google Scholar]
  5. Clattenburg R, Cohen J, Conner S, Cook N. Thermal properties of cancellous bone. Journal of Biomedical Materials Research. 1975;9(2):169–182. doi: 10.1002/jbm.820090206. [DOI] [PubMed] [Google Scholar]
  6. Conzemius MG, Brown TD. Animal models in osteonecrosis. Techniques in Orthopaedics. 2001;16(1):90–97. [Google Scholar]
  7. Conzemius MG, Brown TD, Zhang Y, Robinson RA. A new animal model of femoral head osteonecrosis: one that progresses to human-like mechanical failure. Journal of Orthopaedic Research. 2002;20(2):303–309. doi: 10.1016/S0736-0266(01)00108-5. [DOI] [PubMed] [Google Scholar]
  8. Cozzi PJ, Lawson JA, Lynch WJ, Morris DL. Critical temperature for in vivo cryoablation of human prostate cancer in a xenograft model. British Journal of Urology. 1996;77(1):89–92. doi: 10.1046/j.1464-410x.1996.80314.x. [DOI] [PubMed] [Google Scholar]
  9. Dailiana ZH, Fink C, Baust JG, Seaber AV, Urbaniak JR. Femoral head osteonecrosis with the use of cryosurgery - a new canine model; 4th Combined Orthopaedic Research Societies Meeting; 2001. [Google Scholar]
  10. Davidson SR, James DF. Measurement of thermal conductivity of bovine cortical bone. Medical Engineering Physics. 2000;22(10):741–747. doi: 10.1016/s1350-4533(01)00003-0. [DOI] [PubMed] [Google Scholar]
  11. Ficat RP. Idiopathic bone necrosis of the femoral head. Early diagnosis and treatment. Journal of Bone and Joint Surgery. British Volume. 1985;67(1):3–9. doi: 10.1302/0301-620X.67B1.3155745. [DOI] [PubMed] [Google Scholar]
  12. Fukusako S. Thermophysical properties of ice, snow, and sea ice. International Journal of Thermophysics. 1990;11(2):353–372. [Google Scholar]
  13. Gage AA, Baust JG. Mechanisms of tissue injury in cryosurgery. Cryobiology. 1998;37(3):171–186. doi: 10.1006/cryo.1998.2115. [DOI] [PubMed] [Google Scholar]
  14. Gage AA, Baust JG. Cryosurgery - a review of recent advances and current issues. CryoLetters. 2002;23(2):69–78. [PubMed] [Google Scholar]
  15. Gage AA, Greene GW, Jr, Neiders ME, Emmings FG. Freezing bone without excision. An experimental study of bone-cell destruction and manner of regrowth in dogs. Journal of the American Medical Association. 1966;196(9):770–774. doi: 10.1001/jama.196.9.770. [DOI] [PubMed] [Google Scholar]
  16. Gage AA, Guest K, Montes M, Caruana JA, Whalen DA., Jr Effect of varying freezing and thawing rates in experimental cryosurgery. Cryobiology. 1985;22(2):175–182. doi: 10.1016/0011-2240(85)90172-5. [DOI] [PubMed] [Google Scholar]
  17. Gill W, Fraser J, Carter DC. Repeated freeze-thaw cycles in cryosurgery. Nature. 1968;219(5152):410–413. doi: 10.1038/219410a0. [DOI] [PubMed] [Google Scholar]
  18. Goetz JE, Chung YY, Zimmerman DL, Pedersen DR, Robinson DA, Conzemius M, Brown TD. Steroid-induced versus cryoinsult-induced femoral head osteonecrosis: Statistical measurement of histologic abnormality focalization. Journal of Musculoskeletal Research. 2005;9(4):161–172. [Google Scholar]
  19. He X, Bischof JC. Analysis of thermal stress in cryosurgery of kidneys. Journal of Biomechanical Engineering. 2005;127(4):656–661. doi: 10.1115/1.1934021. [DOI] [PubMed] [Google Scholar]
  20. Hoffmann NE, Bischof JC. Cryosurgery of normal and tumor tissue in the dorsal skin flap chamber: Part II--injury response. Journal of Biomechanical Engineering. 2001;123(4):310–316. doi: 10.1115/1.1385839. [DOI] [PubMed] [Google Scholar]
  21. Hoffmann NE, Bischof JC. Cryosurgery of normal and tumor tissue in the dorsal skin flap chamber: Part I--thermal response. Journal of Biomechanical Engineering. 2001;123(4):301–309. doi: 10.1115/1.1385838. [DOI] [PubMed] [Google Scholar]
  22. Hoffmann NE, Bischof JC. The cryobiology of cryosurgical injury. Urology. 2002;60(2 Suppl 1):40–49. doi: 10.1016/s0090-4295(02)01683-7. [DOI] [PubMed] [Google Scholar]
  23. Jones LC, Niv AI, Davis RF, Hungerford DS. Bone blood flow in the femora of anesthetized and conscious dogs in a chronic preparation, using the radioactive tracer microsphere method. Clinical Orthopaedics and Related Research. 1982;(170):286–295. [PubMed] [Google Scholar]
  24. Keijser LC, Schreuder HW, Buma P, Weinans H, Veth RP. Cryosurgery in long bones; an experimental study of necrosis and revitalization in rabbits. Archives of Orthopaedic and Trauma Surgery. 1999;119(7–8):440–444. doi: 10.1007/s004020050017. [DOI] [PubMed] [Google Scholar]
  25. Koo KH, Jeong ST, Jones JP., Jr Borderline necrosis of the femoral head. Clinical Orthopaedics and Related Research. 1999;358:158–165. [PubMed] [Google Scholar]
  26. Lundskog J. Heat and bone tissue. An experimental investigation of the thermal properties of bone and threshold levels for thermal injury. Scandinavian Journal of Plastic and Reconstructive Surgery. 1972;9:1–80. [PubMed] [Google Scholar]
  27. Maloney SK, Dawson TJ. Sexual dimorphism in basal metabolism and body temperature of a large bird, the emu. The Condor. 1993;95(4):1034–1037. [Google Scholar]
  28. Mont MA, Jones LC, Sotereanos DG, Amstutz HC, Hungerford DS. Understanding and treating osteonecrosis of the femoral head. Instructional Course Lectures. 2000;49:169–185. [PubMed] [Google Scholar]
  29. Rabin Y. The effect of temperature-dependent thermal conductivity in heat transfer simulations of frozen biomaterials. CryoLetters. 2000;21(3):163–170. [PubMed] [Google Scholar]
  30. Rabin Y, Shitzer A. Numerical solution of the multidimensional freezing problem during cryosurgery. Journal of Biomechanical Engineering. 1998;120(1):32–37. doi: 10.1115/1.2834304. [DOI] [PubMed] [Google Scholar]
  31. Reed KL, Brown TD, Conzemius MG. Focal cryogen insults for inducing segmental osteonecrosis: Computational and experimental assessments of thermal fields. Journal of Biomechanics. 2003;36(9):1317–1326. doi: 10.1016/s0021-9290(03)00154-4. [DOI] [PubMed] [Google Scholar]
  32. Reed KL, Conzemius MG, Robinson RA, Brown TD. Osteocyte-based image analysis for quantitation of histologically apparent femoral head osteonecrosis: application to an emu model. Computer Methods in Biomechanics and Biomedical Engineering. 2004;7(1):25–32. doi: 10.1080/10255840310001634250. [DOI] [PubMed] [Google Scholar]
  33. Rewcastle JC, Sandison GA, Hahn LJ, Saliken JC, McKinnon JG, Donnelly BJ. A model for the time-dependent thermal distribution within an iceball surrounding a cryoprobe. Physics in Medicine and Biology. 1998;43(12):3519–3534. doi: 10.1088/0031-9155/43/12/010. [DOI] [PubMed] [Google Scholar]
  34. Rupp CC, Hoffmann NE, Schmidlin FR, Swanlund DJ, Bischof JC, Coad JE. Cryosurgical changes in the porcine kidney: histologic analysis with thermal history correlation. Cryobiology. 2002;45(2):167–182. doi: 10.1016/s0011-2240(02)00125-6. [DOI] [PubMed] [Google Scholar]
  35. Schmidlin FR, Rupp CC, Hoffmann NE, Coad JE, Swanlund DJ, Hulbert JC, Bischof JC. Measurement and prediction of thermal behavior and acute assessment of injury in a pig model of renal cryosurgery. Journal of Endourology. 2001;15(2):193–197. doi: 10.1089/089277901750134584. [DOI] [PubMed] [Google Scholar]
  36. Seifert JK, Gerharz CD, Mattes F, Nassir F, Fachinger K, Beil C, Junginger T. A pig model of hepatic cryotherapy. In vivo temperature distribution during freezing and histopathological changes. Cryobiology. 2003;47(3):214–226. doi: 10.1016/j.cryobiol.2003.10.007. [DOI] [PubMed] [Google Scholar]
  37. Troy KL, Lundberg HJ, Conzemius MG, Brown TD. Habitual hip joint activity level of the penned emu (Dromaius novaehollandie) Iowa Orthopaedic Journal. 2007;27:17–23. [PMC free article] [PubMed] [Google Scholar]
  38. Wan R, Liu Z, Muldrew K, Rewcastle J. A finite element model for ice ball evolution in a multi-probe cryosurgery. Computer Methods in Biomechanics and Biomedical Engineering. 2003;6(3):197–208. doi: 10.1080/1025584031000151185. [DOI] [PubMed] [Google Scholar]
  39. Zhao G, Zhang HF, Guo XJ, Luo DW, Gao DY. Effect of blood flow and metabolism on multidimensional heat transfer during cryosurgery. Medical Engineering and Physics. 2007;29(2):205–215. doi: 10.1016/j.medengphy.2006.03.005. [DOI] [PubMed] [Google Scholar]

RESOURCES