Myofiber angle distributions in the ovine left ventricle do not conform to computationally optimized predictions

Abstract

Recent computational models of optimized left ventricular (LV) myofiber geometry that minimize the spatial variance in sarcomere length, stress, and ATP consumption have predicted that a midwall myofiber angle of 20° and transmural myofiber angle gradient of 140° from epicardium to endocardium is a functionally optimal LV myofiber geometry. In order to test the extent to which actual fiber angle distributions conform to this prediction, we measured local myofiber angles at an average of nine transmural depths in each of 32 sites (4 short-axis levels, 8 circumferentially distributed blocks in each level) in five normal ovine LVs. We found: 1) a mean midwall myofiber angle of −7° (SD 9), but with spatial heterogeneity (averaging 0° in the posterolateral and anterolateral wall near the papillary muscles, and −9° in all other regions); and 2) an average transmural gradient of 93° (SD 21), but with spatial heterogeneity (averaging a low of 51° in the basal posterior sector and a high of 130° in the mid-equatorial anterolateral sector). We conclude that midwall myofiber angles and transmural myofiber angle gradients in the ovine heart are regionally non-uniform and differ significantly from the predictions of present-day computationally optimized LV myofiber models. Myofiber geometry in the ovine heart may differ from other species, but model assumptions also underlie the discrepancy between experimental and computational results. To test of the predictive capability of the current computational model would we propose using an ovine specific LV geometry and comparing the computed myofiber orientations to those we report herein.

Introduction

Myocyte arrangement in the mammalian left ventricle is complex, but highly ordered and a thorough understanding of this organization is fundamental to understanding ventricular function. Computational models of cardiac function, which are useful for estimating parameters such as regional wall stress (Bovendeerd et al., 1992), electrical activation patterns (Usyk and McCulloch, 2003), or ATP consumption (Vendelin et al., 2002), all of which cannot be measured directly or non-invasively, depend upon the incorporation of accurate regional myofiber geometry.

The orientation of the myofibers within the epicardial tangent plane relative to the local circumferential direction, termed the myofiber angle (α) changes rapidly from epicardium to endocardium. Arts et al (Arts et al., 2003) used biophyiscal modeling to predict myofiber angle geometry based on an “adaptation hypothesis” (Rijcken et al., 1996; Arts, Bovendeerd et al., 2003) postulating that the heart adapts to minimize the spatial variance of sarcomere lengths, myofiber shortening, wall stress, or ATP consumption.

Most recently, Vendelin et al. (Vendelin, Bovendeerd et al., 2002) provided additional insight regarding the impact of a wide range of myofiber geometries on model predictions of the spatial variance of strain, stress, and ATP consumption. Their results show that computationally optimal myofiber geometries are obtained with a midwall myofiber angle of 20° and a transmural myofiber angle gradient (α_slope, linear estimate of myofiber angle change from epicardium to endocardium) of 140°.

In order to test the extent to which actual fiber angle distributions conform to the predictions of the model of Vendelin et al., we obtained quantitative histologic measurements of the myofiber orientations in five normal ovine left ventricles. We then tested the hypothesis that myofiber geometry in the ovine LV corresponds to the optimal geometry predicted from the computational model of Vendelin and Arts.

Materials and Methods

The experimental procedures were approved by Stanford’s Institutional Animal Care and Use Committee and followed guidelines set forth by the National Institutes of Health. A similar experimental protocol has been described previously, and is briefly summarized below(Harrington et al., 2005).

Surgical preparation

Five adult, Dorsett-hybrid, male sheep 68 kg (SD 4) were intubated, ventilated, and maintained under general anesthesia with inhalational isoflurane (1–2.2%). The heart was exposed, then arrested with an intravenous bolus of potassium chloride (80 mEq). Post-mortem LV pressure was adjusted and held constant to match in vivo LV end-diastolic pressure by venous exsanguination and 300ml of buffered glutaraldehyde (5%) was infused into each coronary artery via balloon catheter to fix the left ventricle. The heart was then excised and stored in 10% formalin.

Tissue preparation

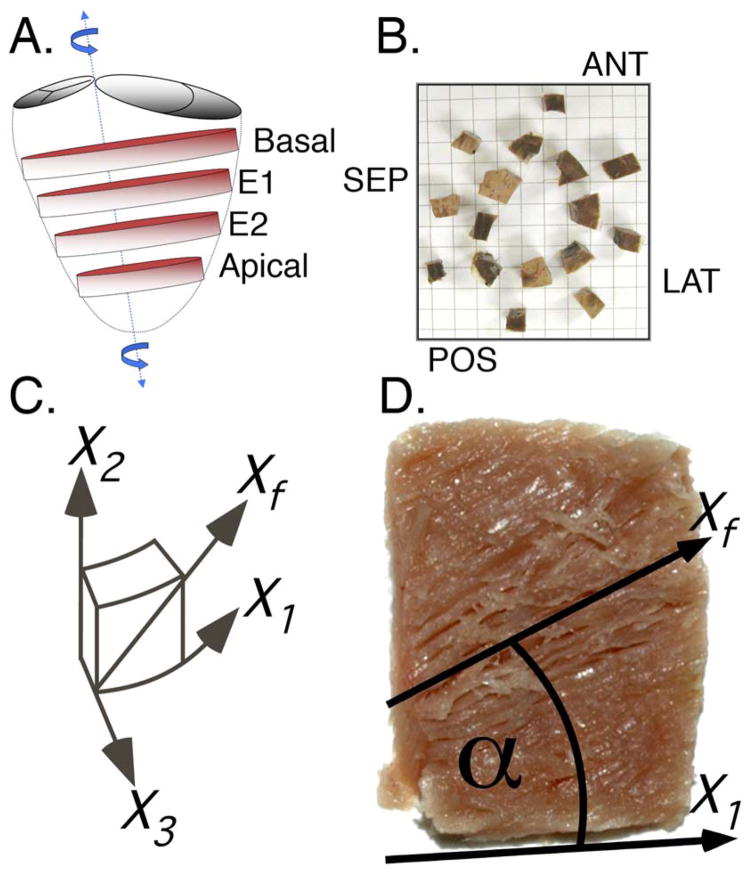
A wooden skewer was placed through the left ventricular apex and the saddle-horn of the mitral valve annulus, near the mitral aspect of the left aortic valve commissure per Streeter (Streeter et al., 1969)(Figure 1A). Eight equally spaced base-to-apex meridians were traced with a permanent marker to aid in sectioning the LV into anterior, anterior-septal, septal, posterior-septal, posterior, posterior-lateral, lateral, and antero-lateral regions. Four transverse (short-axis) slices (~1cm thick) were sectioned as follows: basal slice – first slice below the level of the mitral valve; apical slice – first slice from the apex with a circular lumen; two equatorial slices (E1 and E2) – between the basal and apical slices so that all four slices were evenly spaced. Each block was approximately 1×1×1 cm and contained the full transmural extent of the left ventricular wall. Care was used to avoid using blocks that included papillary muscle tissue. The anterolateral and posterolateral blocks were adjacent to the respective papillary muscles. 32 tissue blocks in each of 5 hearts, for a total of 160 tissue blocks, were available for quantitative assessment (Figure 1B). Each tissue block was then sectioned into 1mm thick transmural layers (parallel to the epicardial tangent plane) from epicardium to endocardium using an arrangement of ganged razor blades. This procedure results in myofiber angle measures in a locally defined polar coordinate system. Defining the endocardial border is complicated by the trabeculae. When sectioning the tissue into 1mm thick layers only sections that remained compact and non-fenestrated were used for measurement. This resulted in an average of 9.4 (SD 2.2) transmural measurements. A total of 1501 transmural tissue layers were used for quantitative analysis.

Figure 1.

Each heart was systematically sectioned for quantitative histologic analysis of the myofiber helix angle. (A) Basal, mid-equatorial (E1 and E2), and apical slices were sliced out of each heart. (B) Each slice was then sectioned into sixteen tissue blocks and eight anatomical sectors (numbered) were used for histologic analysis. Eight chunks of remaining tissue (not numbered) are shown in approximate anatomical location, viewed from base to apex. (C) A “cardiac” coordinate system was defined for each block to enable calculation of the myofiber angle (X₁–circumferential, X₂–longitudinal, X₃–radial). (D) The myofiber angle for each transmural section was measured using computer software and was referenced to the local X₁ axis.

Quantitative Histology

The standardized anatomical reference system described by Streeter et al (Streeter, Spotnitz et al., 1969) was used for all measurements (Figure 1C). Quantitative measurements were then derived from the digital images of freshly fixed tissue at each transmural depth. The myofiber angle (α) was defined as the angle between the predominant myofiber direction, X_f, and the X₁ (circumferential) axis and within the interval of [−90°,+90°] (Figure 1D). Negative α describes a clockwise rotation about the X₃ axis when viewed from epicardium to endocardium. Myofiber angle α was measured at 6.5 (2.4 SD) sites within each of the 1501 acquired digital images using image-processing software. A total of 9828 myofiber orientations were sampled. The mean from multiple measurements within a single image was calculated at each transmural depth.

The normalized transmural depth was calculated for each layer to facilitate the comparison of hearts with slightly different wall thicknesses due to normal anatomic variation (0% – epicardium, 100% – endocardium). The α as a function of normalized wall depth was then fit using linear least squares regression of cubic shifted Legendre polynomials, which were then used to estimate the myofiber angle at 0% (epicardium), 50% wall depth (α_mid), and 100% (endocardium). Linear fits of the α versus wall-depth curves were also used to estimate the linear myofiber angle change from epicardium to endocardium (α_slope).

Results are reported within “walls” (eg base to apex average within the lateral wall), “levels” (eg circumferential average within the basal level), and “sectors” (eg basal lateral sector). To provide a quantitative metric that identifies statistically significant regional heterogeneity of the myofiber geometry, t-tests were performed to compare α_slope and α_mid in each region to the data obtained in all other regions combined. A P<0.05 was considered significant.

Comparison to computational model

The quantitative α measures obtained herein were compared directly to the computationally derived results of Vendelin et al (Vendelin, Bovendeerd et al., 2002) by overlaying our experimental measurements on their computational results. The definition of α_slope reported by Vendelin differs by a factor of −2 because we use a transmural coordinate defined as [0,1] from epicardium to endocardium and they use a coordinate of [+1,−1]. Their results were transformed to our coordinate system to facilitate comparison.

A quantitative statistical comparison between our experimental results and the computational results of Vendelin requires an estimate of the mean and standard deviation (SD) of their optimal solution. The mean value was taken as the model’s optimal values for minimum spatial variance in sarcomere length (α_slope=140°, α_mid=20°). To estimate a suitable α_slope and α_mid SD from their results we assumed a value of half the height (10°) and width (10°) of the contour surrounding the optimal myofiber geometry. A Bonferroni corrected Z-test was performed to compare each of our 32 regional estimates of α_slope and α_mid to their computational optimum.

Comparison to quantitative histology

To compare our quantitative histologic values to previously published results, Figure 4 from Streeter et al (Streeter, Spotnitz et al., 1969), and Figure 3 from Ashikaga et al (Ashikaga et al., 2004), and Figure 16 and 17 from Greenbaum et al (Greenbaum et al., 1981) were digitized. These digitized data were then fit using linear least-squares regression to obtain both α_slope and α_mid.

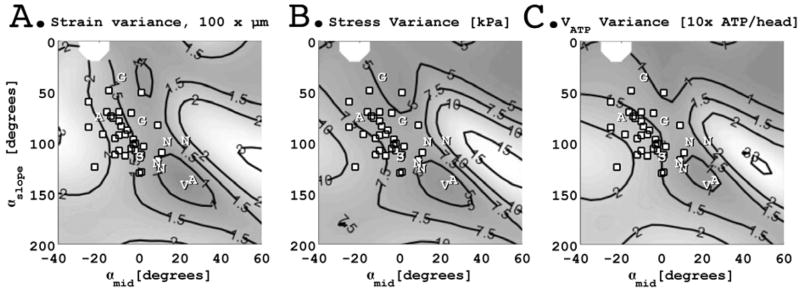
Figure 3.

Direct comparison of myofiber inclination angles obtained in the ovine left ventricle (white dots) and the simulation results of Vendelin et al (Vendelin, Bovendeerd et al., 2002) plotted in the space of myofiber angle transmural slope (α_slope, degrees) and midwall myofiber angle (α_mid, degrees). Vendelin’s approximate optimal myofiber geometry is shown as a ”v”. Results extracted from Streeter (Streeter, Spotnitz et al., 1969)(“S”), Ashikaga (Ashikaga, Omens et al., 2004)(“A”), Greenbaum (Greenbaum, Ho et al., 1981)(”G”), and Nielsen(Nielsen, Le Grice et al., 1991) (“N”) are also shown. Our results from the ovine left ventricle demonstrate a range of myofiber geometries all of which deviate from the optimal results predicted by Vendelin et al. Measured myofiber geometries in the ovine left ventricle, however, do fall within a relatively narrow range of spatial variance in strain, stress, and ATP consumption.

Results

Analysis of Quantitative Histology

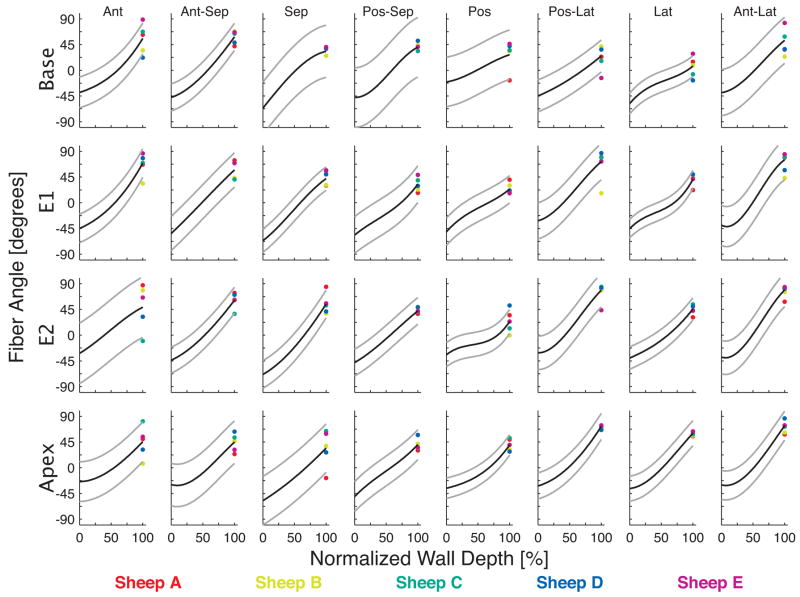
Transmural changes in α were fit using cubic shifted Legendre polynomials with a mean RMS error of 18° (SD 6) (Figure 2). The central tendency of the epicardial, midwall (α_mid), and endocardial α’s are found in Tables 1–3. The mean α of all sectors was −43° (SD 12) in the epicardium and 49° (SD 18) in the endocardium. Epicardial α was most negative in the septal wall (−65°, SD 5) and least negative in the anterior (−35°, SD 9), posterior (−35°, SD 12), and posterolateral wall (−35°, SD 7). Endocardial α was most positive in the anterolateral wall (70°, SD 10) and least positive in the posterior wall (29°, SD 7).

Figure 2.

Transmural myofiber angles in each of the 32 anatomical sectors, color-coded for each heart. The cubic fit is shown in each sector as a black line, with 95% confidence intervals in gray. The anterior papillary muscle was located between the anterior and anterior-lateral sectors and the posterior papillary muscle was located between the posterior and posterior-lateral sectors.

Table 1.

Epicardial myofiber angle (degrees).

	Ant	Ant-Sep	Sep	Pos-Sep	Pos	Pos-Lat	Lat	Ant-Lat	Mean	SD
Basal	−39	−48	−66	−47	−20	−45	−58	−39	−45	14
E1	−45	−54	−66	−57	−51	−31	−45	−39	−49	11
E2	−32	−44	−69	−48	−34	−31	−40	−38	−42	12
Apical	−24	−29	−58	−50	−36	−32	−36	−30	−37	11
Mean	−35	−44	−65	−51	−35	−35	−45	−37
SD	9	10	5	4	12	7	10	4

Table 3.

Endocardial myofiber angle (degrees).

	Ant	Ant-Sep	Sep	Pos-Sep	Pos	Pos-Lat	Lat	Ant-Lat	Mean	SD
Basal	56	58	33	40	27	25	7	52	37	18
E1	69	57	42	33	24	72	41	75	52	19
E2	49	61	54	42	24	78	46	79	54	19
Apical	45	45	34	40	40	72	60	73	51	15
Mean	55	55	41	39	29	62	39	70
SD	11	7	10	4	8	25	22	12

Mean α_mid was −7° (SD 8), but is better characterized by spatial heterogeneity. The posterolateral and anterolateral walls, in close proximity to the anterior and posterior papillary muscles, had an average α_mid of 0° (SD 8). Average α_mid in the remaining walls, including the lateral wall between the papillary muscles, was −9° (SD 7).

The α_slope was estimated in each sector from a linear fit to the transmural α data (Table 4). The α_slope averaged 90° (SD 20) across all sectors. It was lowest in the basal posterior sector (51°) and highest in the mid-equatorial (E1) anterolateral sector (130°). In general, α_slope was highest in the anterolateral wall (116°, SD 16) and lowest in the posterior wall (61°, SD 13). The α measures never exceeded ±90°. As such, phase unwrapping was not needed to condition the linear fit.

Table 4.

Myofiber angle transmural slope (α_slope, degrees).

	Ant	Ant-Sep	Sep	Pos-Sep	Pos	Pos-Lat	Lat	Ant-Lat	Mean	SD
Basal	93†	108†	102†	96†	51*,†	70†	60*,†	97†	84	21
E1	113†	112†	112†	85†	70†	110†	76†	130*	101	21
E2	83†	106†	124*,†	92†	49*,†	117†	84†	129*	98	26
Apical	71†	79†	92†	88†	74†	104†	101†	108†	90	14
Mean	90	101	107	90	61	100	80	116
SD	18	15	14	5	13	21	17	16

Regional heterogeneity quantified by significant deviation from global LV transmural slope indicated by * (P<0.05). Significantly different myofiber geometry compared to computational results of Vendelin indicated by † (P<0.01, Bonferroni corrected).

The t-test for regional heterogeneity demonstrated that α_slope was significantly different from mean LV α_slope in the septal, posterior, and anterolateral walls at the E2 level, in the anterolateral wall at the E2 level, and in the posterior, and lateral walls at the basal levels. Similarly, regional heterogeneity in α_mid (significant difference from mean LV α_mid) was observed in the septal and posterolateral walls at the E2 level, in the posterolateral wall at the E1 level, and in the lateral wall at the basal level. Only the septal wall at the E2 level and the lateral wall at the basal level had significantly different α_slope and α_mid.

Comparison to computational model

Figure 3 compares our quantitative histologic results to the computational modeling results of Vendelin et al (Vendelin, Bovendeerd et al., 2002). The quantitative statistical comparison between the experimental measures and Vendelin’s computational results are indicated in Tables 2 and 4. The experimentally measured α_mid is differs significantly from the computational optima in all regions except the E1/E2/Apical levels in both the posterolateral and anterolateral wall and the E2 level of the anterior wall. The experimentally measured α_slope was significantly different in all regions except the E1 and E2 levels of the anterolateral wall. Thus, only the E1 and E2 levels of the anterolateral wall have a measured myofiber slope and midwall angle that is not significantly different from the computational results of Vendelin et al.

Table 2.

Midwall myofiber angle (α_mid, degrees).

	Ant	Ant-Sep	Sep	Pos-Sep	Pos	Pos-Lat	Lat	Ant-Lat	Mean	SD
Basal	−10†	−10†	−3†	−12†	1†	−16†	−20*,†	−3†	−9	7
E1	−7†	1†	−12†	−20†	−10†	11*	−13†	0	−6	10
E2	9	−4†	−22*,†	−7†	−15†	9*	−9†	1	−5	11
Apical	−4†	−10†	−18†	−6†	−14†	2	−2†	−2	−7	7
Mean	−3	−5	−13	−11	−10	2	−11	−1
SD	9	5	8	6	7	12	8	2

Regional heterogeneity indicated by significant deviation from mean LV α_mid (*, P<0.05). Significantly different myofiber geometry compared to computational results of Vendelin indicated by † (P<0.01, Bonferroni corrected).

Although our measurements fall outside the contour surrounding the computationally optimized result, they still lie within regions of relatively low spatial variance within the space of myofiber geometries studied by Vendelin et al. Figure 3A shows that the spatial variance of the strain for the myofiber geometries we measured falls between strain spatial variance contours of 0.015 and 0.020μm whereas the minimum strain spatial variance of the computational results is near 0.010μm. Figure 3B shows that the stress spatial variance for our measured myofiber geometries falls between contours of 5.0 and 7.5kPa, whereas the minimum stress spatial variance is near 5.0kPa. Figure 3C shows that our myofiber geometry results are near an ATP consumption spatial variance (V_ATP) of 15 to 20 ATP/head and the model’s minimum spatial variance is near 10 ATP/head.

Comparison to quantitative histology

The digitized and fitted data from Figure 4 by Streeter et al (Streeter, Spotnitz et al., 1969) in the basal free-wall of the canine left ventricle resulted in α_slope and the α_mid of 112° (SD 13) and −2° (4 SD), respectively. Digitization and fitting of Figure 3 from Ashikaga et al. (Ashikaga, Omens et al., 2004) resulted in a α_slope of 135° and a α_mid of 24° in the apical anterior wall and 73° and −22° in the basal anterior wall of the dog. Results were also extracted from Figures 16 and 17 in the studies of Greenbaum et al. (Greenbaum, Ho et al., 1981) in human hearts demonstrated a α_slope of 77° and a α_mid of −1° in the posterior equatorial wall and 34° and −11° in the lateral equatorial wall. Lastly, results were extracted from Figure 12A–12D of Nielsen et al in the free wall of canine hearts (12A – α_slope of 124° and a α_mid of 9°; 12B – α_slope of 119° and a α_mid of 7°; 12C – α_slope of 97° and a α_mid of 21°; 12D – α_slope of 98° and a α_mid of 12°).

Discussion

Vendelin’s optimal myofiber geometry parameters represent an extreme relative to the histologic results obtained in the ovine left ventricle – the optimal model geometry exhibits a significantly steeper α_slope (140°) and a more positive α_mid (20°) compared to 25 of 32 regions of the ovine LV. Our experimental results do not fall within the minimum spatial variance iso-contour for myofiber strain, myofiber stress, nor ATP consumption (Figure 3). We conclude that there is a substantial difference between the myofiber geometry of the ovine LV and those predicted by Vendelin’s model of optimized myofiber geometry.

The differences between our experimental results and Vendelin’s computational results suggest that: 1) The ovine heart is not optimized for the minimum spatial variance of myofiber strain, myofiber stress, nor ATP consumption, and/or 2) The assumptions of the model result in an optimal solution that differs from histologic measurements in the left, and/or 3) Systematic histologic measurement errors in the myofiber geometry lead to discrepancies between the histologic and modeling results.

Regarding (1) it is, of course, difficult to know what parameter or parameters the heart optimizes in order to achieve maximum efficiency and function, but the work of Bovendeerd and Vendelin has demonstrated that a principled modeling approach produces reasonable results. We propose, however, that the heart may be optimizing an objective function of several variables, which may include myofiber strain, myofiber stress, and ATP consumption. Furthermore, the incorporation of anatomically accurate myofiber geometry might lead to better insight to the objective function that the heart optimizes to attain maximal functional efficiency. Future experiments (see below) could directly measure the spatial variance of myofiber shortening, but direct measures of regional stress and regional ATP consumption are currently unreported.

Regarding (2) it is possible that regional (base-to-apex or circumferential) non-uniformities in wall thickness, curvature, myofiber geometry, loading conditions, myocardial strain energy function, and cellular physiology contribute to regional differences in the myofiber geometry observed herein and result in deviation from the results obtained by Vendelin which uses axis symmetry, a mathematically uniform myofiber description, linear transmural changes in α, an ad hoc strain energy function, and uniform loading and cellular parameters. Venedelin’s model parameters are likely most representative of the LV free wall.

With regards to (3) it is possible that our histologic measures suffer from a systematic error, which could lead to an under- or overestimate of α at each wall depth. A comparison of α_slope measurements between different studies, however, has the advantage of being insensitive to systematic error so long as the measurement at each wall depth is registered accurately with neighboring tissue samples. If all tissue samples are rotated by α_error degrees, as may occur if the measurement coordinate system is poorly chosen, this will not impact the estimate of the α_slope. A comparison of slopes is also less sensitive to accurate definitions of the wall depth for each observation, which can be confounded by epicardial fat, papillary muscles, and trabeculation. Lastly, if the endocardial border is poorly estimated this may impact measures of α_slope, especially if the local α_slope in the endocardium differs from the average transmural α_slope.

It should be pointed out that the standardized Streeter coordinate system uses a long axis that is biased toward the aortic side. Therefore, α measures in the anterior and posterior walls may have an offset of approximately −9° and +9° respectively compared to a central long axis, which may be more easily defined in a diffusion tensor MRI experiment.

Lastly, quantification of α_mid is more prone to error because of the sensitivity to the accuracy of the wall depth determination and the definition of the endocardial border. If the endocardial border is chosen too near the epicardium then α_mid will be too negative and if chosen closer to the trabeculae then α_mid will be too positive. Furthermore, inaccuracies in defining the circumferential axis (X₁) by α_error degrees will directly offset the α_mid measurements. These effects may, in part, explain differences in α_mid measures from different studies. Reports of α_mid values vary from groups reporting positive values (Streeter, Spotnitz et al., 1969; Nielsen et al., 1991; Chen et al., 2005) and those reporting negative values (Cheng et al., 2005; Harrington, Rodriguez et al., 2005). Costa et al reported positive α_mid in the apex and negative α_mid in the base of canine hearts(Costa et al., 1999). Note that using DTMRI Walker et al have shown ovine hearts have positive and negative α_mid depending upon the wall region(Walker et al., 2005). The α_mid we have characterized may be unique to the ovine heart.

Myofiber geometry

Measurements of α have been previously reported using quantitative histologic techniques in sheep (Cheng, Langer et al., 2005; Harrington, Rodriguez et al., 2005), dog (Streeter, Spotnitz et al., 1969; Nielsen, Le Grice et al., 1991), and man (Streeter, 1979; Greenbaum, Ho et al., 1981). More recently quantitative measurements of α have been made using diffusion tensor magnetic resonance imaging (DTMRI) (Hsu et al., 1998; Scollan et al., 1998; Scollan et al., 2000) and results have been reported in rabbits(Scollan, Holmes et al., 1998), dogs(Helm et al., 2005), goats (Geerts et al., 2002), and sheep (Walker, Guccione et al., 2005).

Our results measured a mean α_slope for all sectors of 90° (SD 20), but the statistical results indicate significant regional heterogeneity of both α_slope and α_mid in the ovine LV. Data extracted from other quantitative histologic studies in dog (Streeter, Spotnitz et al., 1969; Nielsen, Le Grice et al., 1991) and man (Greenbaum, Ho et al., 1981) demonstrate α_slope measures similar or larger than our experimental measures. Some results from Ashikaga (basal anterior) agree with our results, but it should be noted that the histologic results from Ashikaga in the apical anterior wall of the dog match Vendelin’s predictions quite well.

Note that the ovine DTMRI data of Walker et al (Walker, Guccione et al., 2005) demonstrates results for α_slope that are near 90°. In general, ovine studies report quantitative measures of α_slope that are lower than those used by Bovendeerd (Bovendeerd, Arts et al., 1992), the optimal results obtained by Vendelin (Vendelin, Bovendeerd et al., 2002), or results obtained by Geerts et al (Geerts, Bovendeerd et al., 2002) in goats, Chen et al in rats (Chen, Liu et al., 2005), Nielsen or Streeter in dogs ((Streeter, Spotnitz et al., 1969; Nielsen, Le Grice et al., 1991). Our measures of ovine myofiber geometry do not conform to the modeling predictions of Vendelin et al and the results also differ from some previously published histologic results in other species, which indicates that ovine myofiber geometry may be different than other species.

Conclusions

Experimental measurements of the myofiber geometry (α_slope and α_mid) in the ovine LV are significantly different from those resulting from Vendelin’s state-of-the-art computational model of optimized myofiber geometry. Myofiber geometry in the ovine heart may differ from other species, but model assumptions also underlie the discrepancy between experimental and computational results. To test of the predictive capability of the current computational model would we propose using an ovine specific LV geometry and comparing the computed myofiber orientations to those we report herein. The “adaptation hypothesis” proposed by Arts (Rijcken, Arts et al., 1996; Arts, Bovendeerd et al., 2003) is a compelling and useful model for understanding myocardial structure and function and building biophysical models steeped in first principles, but improvements are still needed in order that the results from both experimental measures and computational models better agree.