Neural models and physiological reality

Abstract

Neural models of retinal processing provide an important tool for analyzing retinal signals and their functional significance. However, it is here argued that in biological reality, retinal connectivity is unlikely to be as specific as ideal neural models might suggest. The retina is thought to provide functionally specific signals, but this specificity is unlikely to be anatomically complete. This is illustrated by examples of cone connectivity to macaque ganglion cells. For example, cells of the magnocellular pathway appear to avoid short-wavelength cone input, so that such input is negligible under normal conditions. However, there is anatomical, physiological, and psychophysical evidence that under special conditions, weak input may be revealed. Second, ideal models of how retinal information is centrally utilized have to take into account the biological reality of retinal signals. The stochastic nature of impulse trains modifies signal-to-noise ratio in unexpected ways. Also, non-linearities in cell responses make, for example, multiplexing of luminance and chromatic signals in the parvocellular pathway impracticable. The purpose of this analysis is to show than ideal neural models must confront an often more complex and nuanced physiological reality.

Introduction

Comparing neural activity with psychophysical performance has the goal of identifying the physiological substrates that underlie perceptual tasks. Some early attempts to specify physiological signals underlying, say, detection of a brief flash (Barlow & Levick, 1969), stressed the probability that performance might be based on a few impulses from a few cells. Another viewpoint was that “any statement attempting to relate a response to an individual stimulus would be senseless …. Indeterminacy is a concept of neural activity which is far more likely to be of use” (Burns, 1968). The implication was that large cell assemblies are required to deliver reliable sensory signals. This discussion played out in a context in which cortical connectivity was thought to be mostly, if not entirely, random (Sholl, 1956). Although random connectivity may play a role in the cortex, this extreme viewpoint has now largely been abandoned. Cell responses may be variable, but testing for task or stimulus specific cellular signals has been a more productive approach than seeking more indeterminate substrates; these issues remain much discussed.

Linking psychophysical measurement with a physiological substrate is subject to strict requirements (Brindley, 1960; Teller, 1984); these are easier to meet at a subcortical than at a cortical level, although there have been notable cortical achievements, for example, in MT (Britten et al., 1992). In my laboratory, we have attempted to relate responses of retinal ganglion cells to performance on standard psychophysical tasks (Lee et al., 1988; Kaiser et al., 1990); it is seldom as straightforward as was supposed by pioneer workers in the field (Lee, 1991), but robust linking hypotheses can be developed, especially by parallel exploration of multiple stimulus dimensions in both physiology and psychophysics.

There have been major successes in predicting the properties of physiological entities based on psychophysical measurements. Examples are the presence and spectral sensitivities of the cones (Smith & Pokorny, 1972), and of post receptoral luminance and chromatic channels for detection, both of which now have a firm physiological basis. On the other hand, physiological reality is often more complex than simple neural models. An example would be the way in which at least four retinal adaptation mechanisms (the cone-rod duality, receptor adaptation, inner retinal adaptation, and pigment bleaching), perhaps together with cortical processing, all combine to provide the seamless operation of Weber’s law over a very large range of light intensity (Dunn et al., 2007).

I shall discuss some examples of neural models being betrayed by a messier physiological reality. The first two of these concern retinal connectivity. Chromatic properties of retinal ganglion cells can be modeled through random connections between cones and later neurons; alternatively connectional specificity may be present. It seems most likely that physiological reality falls between these extremes. Second, neural models of the way information can be conducted from the retina to the cortex sometimes fail to consider the signal-to-noise characteristics of physiological signals, which are noisy primarily because of the stochastic nature of the impulse trains, and which are essentially non-linear due to the impossibility of negative firing rates. Retinal signals seem to be designed to optimize information transmission in the face of these constraints.

Random retinal connectivity: Is short-wavelength cone input indiscriminate?

The short-wavelength (S) cone pathway is phylogenetically ancient and present in most mammals (Mollon, 1991). In the primate, S cones make up 5–10% of cones. At least two ganglion cell classes are specifically concerned with transmitting S-cone signals through the koniocellular (KC) layers of the lateral geniculate nucleus (LGN) to visual cortex (Szmajda et al., 2006); one carries excitatory signals of the S cones (Dacey & Lee, 1994), the other inhibitory (Dacey et al., 2002). The other major retinostriate pathways of the primate are the parvocellular (PC) and magnocellular (MC) systems, originating in the midget and parasol ganglion cells, respectively. PC cells in central retina are invariably red-green color opponent, with excitatory input from a single long-wavelength (L) cone and inhibitory input from the middle-wavelength (M) cone, or vice versa (see below); the one-to-one relation between single cones and single midget ganglion cells only begins to break down at ~10° eccentricity, and significant chromatic opponency is present up to much higher eccentricities despite the apparent convergence from midget bipolars to midget ganglion cells (Martin et al., 2001). MC cells have standard ON-or OFF-center receptive field structure, with input from M and L cones to both center and surround.

If these cell classes made random connections to all cones within their receptive fields, they might receive some S-cone input, limited by the low density of this cone class. For a PC cell, the center receives input primarily from a single cone, so that any randomly acquired S-cone input should be consistent in polarity with the surround, as sketched in Fig. 1A, which shows a cone array derived from the literature with hypothetical PC (and MC) cell receptive fields superimposed. Some cells would have surrounds including S cones, and some not. For MC cells, which have larger receptive field centers that dominate the response, some cells would be expected to include S cones within their center and any S cone input would be expected to have a polarity the same as the center.

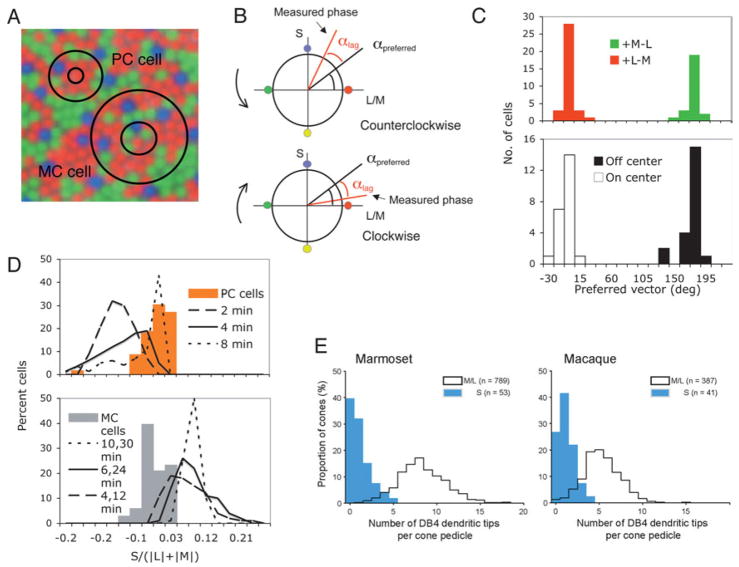
Fig. 1.

(A) Superimposition of hypothetical PC and MC cell receptive fields onto a cone mosaic. PC cells receive a single cone input to the center, so any S-cone input to the cell would be expected to be to the surround. For MC cell, the center is larger and has dominant weighting, so any S-cone input should have center polarity. (B) A sketch of a method of determining cone weights. The equiluminant plane is shown; the stimulus rotates around the circumference of a circle defined by the S- and M/L axes of the plane. Cone weighting can be derived as described in the text. (C) Preferred vectors of PC cells (upper panel) and MC cells (lower panel). Both distributions cluster around 0° and 180°, which indicates little S-cone input. (D) Distributions of S-cone weights for PC and MC cells cluster around zero. The curves show results of a Monte Carlo simulation in which Gaussian receptive field profiles were set on a random cone matrix. For PC cells, the value for each curve represents the surround Gaussian radius used in the simulation. For MC cells, the values refer to simulated center and surround radii with a 3:1 center-surround weighting. The solid curves represent the best physiological estimates. (E) Distribution of pedicle contacts of DB4 bipolar cells to different cone classes in marmoset and macaque. Specificity is present but not complete. Reprinted from Lee and Grünert (2007), with permission.

The psychophysical luminosity function (V_λ) was derived primarily using heterochromatic flicker photometry (HFP), and can be described solely as a sum of M and L cone spectral sensitivities (Smith & Pokorny, 1972, 1975), i.e., with no S-cone input, although S-cones are known to respond to temporal frequencies used in HFP (Baylor et al., 1987; Yeh et al., 1995). MC cells show physiological properties consistent with their being the physiological substrate for HFP, with a spectral sensitivity close to V_λ. Although this implies they have no S-cone input, it has recently been proposed that they receive significant input, in line with random wiring to the underlying cones (Chatterjee & Callaway, 2002). If this were so, it would jeopardize the identification of the MC pathway with a psychophysical luminance channel. For PC cells, physiological measurements show some scatter of null-plane azimuths in the equiluminance plane (see Derrington et al. (1984) and Fig. 5, for details), which might be due to a small degree of S-cone input or to measurement noise. In both cases, it would be a useful test of the specificity of retinal wiring to seek if small S-cone inputs were present.

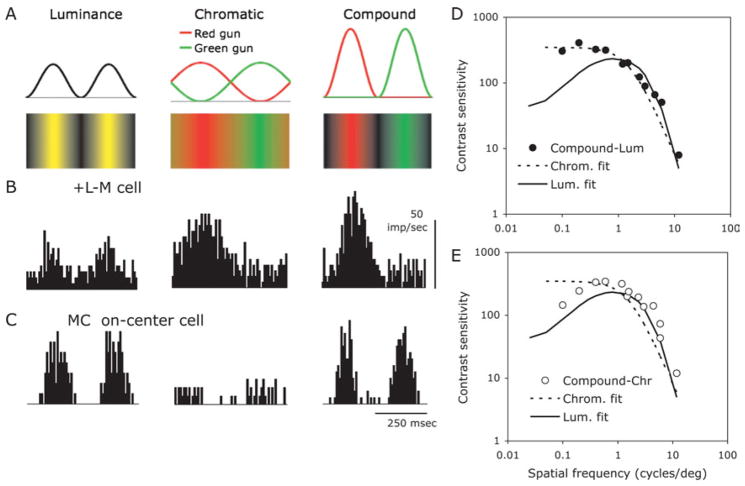
Fig. 5.

(A) Configuration of compound grating stimulus compared to luminance and chromatic gratings. All three gratings have the same mean luminance and chromaticity. The luminance component of the compound grating is at twice the spatial frequency of the chromatic component. (B) Responses of a parafoveal +L-M red ON-center cell to luminance, chromatic and compound gratings. Gratings with a spatial frequency of 0.5 cpd (or 1 cpd for luminance) were drifted at 2 Hz (4 Hz for luminance) across the receptive field. Responses to compound and chromatic gratings are similar. Average of 16 responses, bandwidth 4 ms, 75% contrast. (C) Responses of a MC ON-center cell to the luminance, chromatic and compound gratings. Responses to compound and luminance gratings are similar. (D) Discrimination thresholds (symbols) for one observer between compound and chromatic and compound and luminance gratings. The curves represent fits of detection threshold data for luminance and chromatic gratings. The discrimination data indicate that the gratings can be distinguished at detection threshold.

We have recently developed a sensitive technique for ascertaining the cone weights of visual neurons (Sun et al., 2006a). The principle is sketched in Fig. 1B for a PC cell. An equiluminance plane is shown, with an S-cone axis and an M, L cone opponent axis, as in the cone space used by Derrington et al. (1984). The stimulus rotates around the circumference of this space, either in a clockwise or counter clockwise direction. A cell with input from all three cone types will have a preferred vector determined by the cone weighting (α_preferred). This will be related to the phase of the cell’s response to the stimulus. Response latency will cause a phase lag but by measuring response phase to clockwise and counter clockwise modulation the phase lag will cancel, to give the actual cone weighting. This method proved rapid and accurate, and resistant to such non-linearities as response saturation, which distort weight estimates if response amplitude alone is used as a measure. For MC cells, the appropriate plane to seek S cone input is defined by an S cone axis and a +ML/−ML axis.

Fig. 1C shows preferred vectors of PC and MC cells derived through this technique. PC cell values cluster around values of 0° and 180°, corresponding to +L-M and +M-L cells, and these values suggest little S cone input. MC cell values also cluster around 0° and 180° corresponding to ON- and OFF-center cells, again with little S cone input. This was the case at all temporal frequencies tested (Sun et al., 2006a). These values can be converted to estimated S-cone input to the different cell types from the cone contrasts used, and this is shown in Fig. 1D. Distributions of S cone weights did not differ significantly from zero for either cell class.

How much S-cone input might be anticipated from random connectivity to cones within the receptive field? To ascertain this, we performed a Monte Carlo simulation by setting receptive fields on a random cone matrix as described in Sun et al. (2006b). Briefly, Gaussian receptive field profiles were set on the cone matrix. We used a variety of receptive field parameters, e.g., surround radii, spanning those reported in the literature; the values used are noted in Fig. 1D, where the distributions of S-cone input derived from this simulation are plotted. The thick solid lines in each plot indicate the simulations using the best physiological estimates of receptive field parameters. Actual measurements clearly differ from the random model prediction. For example, for PC cells, any S-cone input is predicted to be negative, i.e., with surround polarity, as expected. The exact shape of the simulated distributions varies with surround radius, but all distributions differ from the actual measurements. These simulations support the hypothesis that MC and PC cells deliberately avoid S cone input.

Should we conclude from this that the ideal model for the lack of input of S cones to the luminosity function has been vindicated? Recent anatomical studies indicate a less straightforward situation. Fig. 1E shows data from Lee and Grünert (2007), in which the number of synaptic contacts of diffuse bipolar cells, which provide input to MC cells, were counted for the various cone types. The histograms shown were for the DB4 cell, but similar data were obtained for other diffuse bipolar types. The histograms show the number of contacts to M and L cones compared to S cones for the marmoset and macaque. Many S cones receive no contacts, but some receive 1–3, fewer than for the other cones.

This partial specificity, together with the low proportion of S cones, is likely to account for the fact that S-cone input to PC and MC cells was undetectable in our experiments, and in most psychophysical measurements of the luminosity function. However, from a functional viewpoint, the retina presumably has no interest in developing absolute specificity; it only does enough to ensure that any S-cone input is functionally insignificant under normal circumstances. It should not surprise us that under certain circumstances some S-cone input might be detectable. Using an elegant in vitro technique for isolating MC-cell responses from individual S cones, it has been shown that some S cones may evoke weak responses in MC cells (E.J. Chichilnisky, personal communication). Psychophysically, with intense yellow backgrounds S cones have been shown to be able to participate in the nulling of flicker, as in HFP (Stockman et al., 1993) although the phase of the S-cone influence may not be consistent with the model in Fig. 1.

Thus biological reality may be less clear-cut than ideal models. The reason why PC and MC cells seem to go to some trouble to avoid S cone input when in the cortex cone signals of all types are combined (Lennie et al., 1990) remains unresolved.

Random retinal connectivity; the surrounds of PC cells

Almost all PC cells in central retina show color-opponent responses, with the opponent M and L cones showing a cone balance close to 1:1 (Derrington et al., 1984; Lee et al., 1987). The means by which this opponency is brought about has been the subject of much debate. Early workers revealed cone mechanisms in opponency by differential adaptation (de Monasterio & Gouras, 1975), which led to the implicit assumption that the center and surround were cone specific. Paulus and Kröger-Paulus (1983) were the first to suggest that color opponency was automatically conferred on PC cells by the presence of a single cone in the center as a consequence of midget morphology. The implication is that surrounds draw their input randomly from the local cone population, either through H1 horizontal cells or by other means. More sophisticated modeling lent a firm basis to this suggestion (Lennie et al., 1991). Direct experimental test of this suggestion is difficult because it requires spatial measurements at a very fine scale due to the small size of PC cell receptive fields, but information that is available is not in favor of the random wiring hypothesis (Reid & Shapley, 1992, 2002; Lee et al., 1998). However, it has not been possible to find any evidence for cone-specific lateral connections among midget cell in primate inner retina (Calkins & Sterling, 1996). The two hypotheses—random wiring versus complete specificity—are ideal neural models, and partial specificity is seldom considered as a possibility (but see Buzas et al. (2006)). I shall argue that some degree of specificity would improve the chromatic signal-to-noise ratio, whereas complete specificity would confer little additional advantage.

The evolution of the red-green opponent system in primates required a point mutation of the opsin gene to provide pigments with different spectral sensitivities and second a gene duplication on the X chromosome to provide the tandem gene array found in Old-World primates (Mollon, 1991). Given the presence of two opsins, the neural machinery to elaborate the cone opponent signal must have derived from an existing ganglion cell class, a precursor of the midget system. The imposition of M, L cone opponency on a previously existing cell class is probably the reason for an unique feature of the midget system. Almost all retinal neurons form a regular mosaic distributed across the retina, each neuron having similar physiological properties. The midget system has two arrays of ganglion cells, ON- and OFF-center, within each of which there is a mix of cell types with diametrically opposite chromatic properties, i.e., red and green ON-center, and red and green OFF-center cells. This unusual feature must be a consequence of the superimposition of red-green opponency on an existing cell system. Wässle and Boycott (1991) proposed that a PC cell precursor designed for spatial vision with a single cone center would automatically inherit cone opponency. The only difficulty with this hypothesis is how it evolved from a ganglion cell class with greater cone convergence. We have calculated that a ganglion cell center which is 5–6 cones across (i.e., 25–30 cones total) is effectively circular with a Gaussian profile, but a center with 2–6 cones is spatially anisotropic and liable to aliased signals with patterns finer than the cone grain. Consider the extreme case of a receptive field center with only two cones. Neglecting blurring caused by the point spread function of the eye, such a field will be anisotropic, i.e. orientation specific. Second, the amplitude and phase of response at high spatial frequencies will be irregular, with a secondary peak at a spatial frequency corresponding to the cone separation. Both of these factors might be considered disadvantageous for reliable representation of fine patterns. Such effects have been noted in PC cells in the fovea with interference gratings (McMahon et al., 2000), although the origin of this effect near the fovea is unclear. In any event, a gradual evolution from multiple cone centers to single cones might pose functional difficulties. A possible way around this would be evolution of the system through a cell class designed for mesopic operation in which rods compensated for sampling problems and anisotropy. In any event, evolution of red-green cone opponency in the way proposed by Wässle and Boycott (1991) is a most plausible scenario.

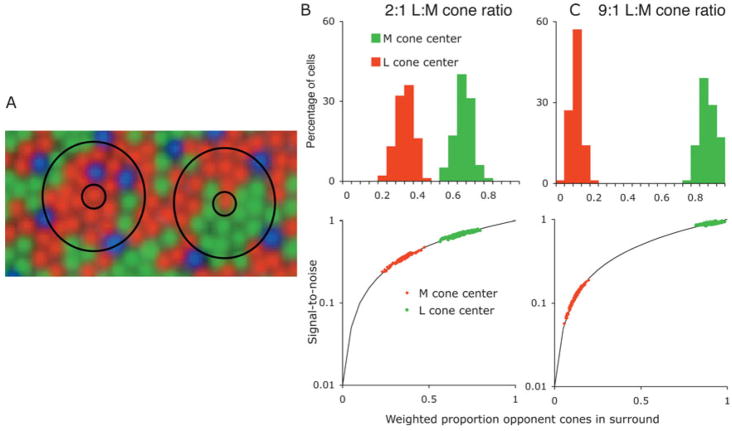
On evolution of the red-green system, the operation of random wiring had to have been effective in providing an opponent signal. What possible advantage could later development of cone specificity in the surround confer? One possibility is an improvement in chromatic sensitivity, assuming that receptor noise limits ganglion cell signal-to-noise ratio (Vorobyev & Osorio, 1998). We consider an L-cone center cell in a retina with a 2:1 L:M cone ratio, cones randomly distributed within the array. In the case of cone-specific surrounds, to achieve a 1:1 L:M cone balance each cone will contribute equal signals; there will be two units of cone signal (1M,1L)and two units of noise. For random surrounds, most of the L-cone center input will be antagonized by the L-cone input to the surround. To achieve a 1:1 L:M net balance, this would require a 3L:(1M + 2L) center-surround weighting. The opponent signal may still be made similar (i.e., 1L,1M), but now it will be three times noisier (5L + 1M) since most of the L-cone center signal is attenuated by the L cones in the surround. This is made more explicit in Fig. 2. Fig. 2A shows a cone array with a 2:1 L:M ratio with two superimposed PC cell receptive fields. In each case, there is a L cone providing input to the center. The surround encompasses a mix of cones. The proportion of L:M cones is, by chance, different in the two examples. We estimated the M:L cone weighting in PC cell surrounds, assuming S cones provide no input, using surround diameters from the literature (Croner & Kaplan, 1995; Lee et al., 1998) and assuming a Gaussian profile for weighting the cone inputs. Distributions for a 2:1 L:M ratio are shown for L- and M-cone center cells in Fig. 2B. One may then predict the signal-to-noise ratio of the chromatic signal, with unity being the value expected from a cone-specific surround. Variability in overall M:L cone weighting for L and M on-center cells was incorporated from earlier results (Lee et al., 1987). Predicted signal-to-noise ratio differs for M- and L-cone center cells. An interesting case is posed by individuals with extreme cone ratios (Hofer et al., 2005). We applied the same approach for such a distribution. For such individuals, the difference in chromatic sensitivity between L- and M-cone center cells would be expected to be extreme, as sketched in Fig. 2C.

Fig. 2.

(A). Receptive fields of PC cells with L-cone centers superimposed on a random cone mosaic with a 2:1 L:M ratio. Some receptive fields would be expected to have few M cones in the surround; others would have a higher proportion. (B) Upper panel: expected proportion of opponent cones in the surround of L and M-cone center cells in parafovea with a random mosaic. Random cone inputs were weighted with a Gaussian profile. Proportion of opponent cones in the surround differs for M and L-cone centers. (C) Signal-to-noise ratio expected for chromatic responses, assuming that this is determined at the receptor level, or at least before the opponent site. Normalized to unity for a cone specific surround. (D) With extreme L:M cone ratios, the difference in signal-to-noise ratio would be expected to be more marked. Even a moderate degree of specificity would substantially improve signal-to-noise ratio.

In our recordings from PC cells of the macaque, there has been no indication of any imbalance in the chromatic sensitivities of Land M-cone center cells, although the L:M cone ratio in these animals was unknown. There is no evidence for any asymmetry in sensitivity to red versus green perturbations in human observers in central retina (Stromeyer et al., 1992). Also, chromatic sensitivity and color vision in observers with highly skewed cone ratios is similar to that in observers with more typical cone ratios. It seems inherently unlikely that there is a wide difference in chromatic sensitivity of M- and L-cone center cells.

Some degree of cone specificity in the surround would improve the chromatic signal. However, such specificity need not be absolute. A moderate degree of specificity would shift the distributions up the solid curves to bring sensitivity of M- and L-cone center cells into a similar range. This would improve chromatic signal strength but once, say, 70–80% specificity were achieved, further specificity would provide only minor additional improvement in the chromatic signal; the retina might develop connectivity just specific enough to attain a reasonable signal-to-noise ratio, without going to the expense of striving for complete specificity.

In our modeling of PC cell receptive field structure (Lee et al., 1998), we concluded that measurements were inconsistent with random wiring, but could not rule out partial specificity. Partial specificity might also explain why it has been difficult to find an anatomical substrate. In any event, this is another instance in which biological reality is likely to be less well defined than simple neural models. However, a critical assumption in this analysis is that receptor noise plays a critical role in ganglion cell and psychophysical sensitivity. This is a common hypothesis in the psychophysical literature (Vorobyev & Osorio, 1998) but physiological confirmation at the ganglion cell level is absent. How much noise is introduced into retinal signals by the spike generating mechanism of the ganglion cell remains uncertain; the relative roles of noise from this source and that originating in the receptors (or at other sites prior to spike generation) is unknown. This may be another case in which biological reality is more complex than a simple model.

Impulse trains and information in physiological responses—transient cells can be sustained

The ganglion cell transforms analog signals from bipolar cells into impulse trains. Although the stochastic nature of neural responses is well recognized, models of retinal signals have often assumed that transmission of neural signals is linear and noise-free. However, the stochastic nature of impulse trains leads to some unexpected effects in retinal coding. Also, retinal ganglion cells may display approximately linear behavior, but one fundamental non-linearity is rectification due to the impossibility of negative firing rates. I give here two examples of how these factors effect coding of visual signals.

MC cells deliver transient responses. It is often assumed that, as a consequence, MC cells are specialized for fast movement or fast modulation. It turns out that this is incorrect, for MC cells can give very precise information about slow movement. A starting point for this study was the finding that Vernier acuity is largely independent of the speed of a moving target, up to about 4°/s in the fovea (Westheimer & McKee, 1975). Is this remarkable result inherent in the retinal signal of one cell class, or does it require integration over more classes and retinal regions?

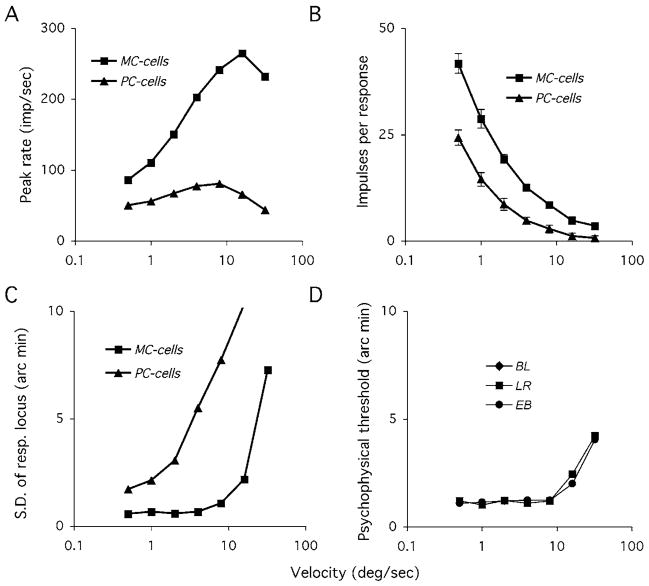
It turns out that MC cells deliver an accurate spatial signal over a wide range of stimulus velocities (Rüttiger et al., 2002). Fig. 3 summarizes this result. We measured responses to high-contrast moving bar targets. Peak rate of MC cell responses increased rapidly with stimulus velocity, as expected of a transient neuron, whereas PC cell responses showed much less increase (Fig. 3A). However, although peak rate of MC cells is low with slow targets, there are many impulses per response. As velocity increases, the number of impulses per response decreases. The positional information contained in the response would be expected to be dependent on both peak rate and the number of impulses present. We performed a neurometric analysis to ascertain the positional uncertainty in the response as a function of stimulus velocity. Briefly, a response template was generated by smoothing the response histogram, and individual responses were correlated with this template; the location of maximum correlation provided for each a response locus. The spatial variation of these loci was expressed in terms of their standard deviation from trial to trial. As seen in Fig. 3B, the positional accuracy of the MC signal remains constant over a range of target speeds, while that of PC cell decreases rapidly as speed increases. These data were acquired from parafoveal retina, and so we repeated the psychophysical measurements of Westheimer and McKee (1975) at 5° eccentricity, measuring Vernier thresholds to pairs of line targets as used in the physiology. Vernier thresholds are stable over the same velocity range as the cell responses, with a similar level of precision.

Fig. 3.

An example of how transient MC cells can yield positionally accurate signals at low velocities. (A) Standard deviation of response locus of MC and PC cells to high-contrast moving bar targets. Response locus was determined using a template matching technique (see Rüttiger et al. (2002)) Data represent means of 10–15 cells per class. At low speeds, for MC cells firing rates are low but there are many impulses. As velocity increases, so does peak firing rate, but the number of impulses decreases. These cells seem well adapted to yield a positionally accurate signal independent of velocity. (B) Psychophysical performance with a parafoveal vernier task with similar stimuli. Vernier thresholds are independent of target velocity over a similar range.

This approach can also be applied to moving grating targets (Sun et al., 2004) and as a function of contrast and other spatial parameters (Lee et al., 2005). This extends earlier studies which suggested that MC cells form the physiological substrate for the hyperacuities (Lee et al., 1993, 1995; Sun et al., 2003; Sun & Lee, 2004). Their vigorous responses to achromatic targets deliver a much more precise positional signal than the weaker responses of PC cells. As pointed out by Shapley and Perry (1986), since signal-to-noise ratio of the signal of a given pathway is expected to increase with the square root of the number of cells available, the five- to ten-fold difference in achromatic responsiveness between PC and MC cells would require a 25–100 fold difference in numerosity to compensate, but the difference in numerosity of PC and MC cells is only a factor of 6–8.

This example shows that the stochastic structure of impulse trains can yield unexpected consequences. A simple neural model that just (in this case) considered firing rates would not predict this result. Transient neurons can give accurate information about slow moving targets or slow changes. Indeed, the properties of MC cells seem well adapted to provide accurate positional information at any speed, provided appropriate readout mechanisms exist at the cortical level.

Is multiplexing of retinal signals physiologically realistic?

It has been proposed that transmission of information through the optic nerve is optimized by segregating luminance and chromatic information in separate channels (Buchsbaum & Gottschalk, 1983; van der Twer & MacLeod, 2001), corresponding to additive or subtractive combinations of cone signals. The high degree of correlation of M and L cone signals means that a segregation of this sort optimizes information transmission in a system of limited bandwidth, assuming that noise in individual ganglion cell signals limits transmission (MacLeod & van der Twer, 2003). On the other hand, it has also been suggested that both luminance and red-green chromatic information can be multiplexed within the PC pathway (Ingling & Martinez-Uriegas, 1983; Lennie & D’Zmura, 1988).

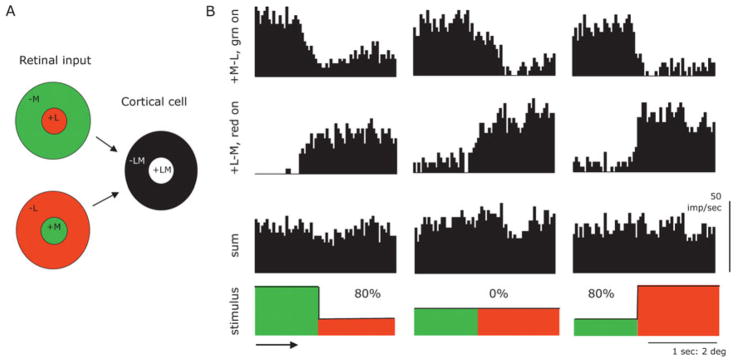
The type of scheme proposed is illustrated in Fig. 4A. Two PC cells, a red ON-center and a green ON-center cell, combine at a cortical level to yield an achromatic receptive field with M and L cones in the center and in the surround. Such a scheme is superficially plausible but does not take into account the fact that ganglion cell signals rectify (firing rates cannot be negative) and saturate, which makes an achromatic signal difficult to retrieve from such a combination as in Fig. 1A. This conclusion is also implicit in the split range coding arrangement suggested by MacLeod and van der Twer (2003).

Fig. 4.

(A) An ideal neural model of how a luminance signal might be derived by combing an L-cone and an M-cone center cell at a cortical level. (B) This model is superficially plausible but rectifying and saturating non-linearities make a luminance signal difficult to extract from combined inputs. Responses of a red and a green ON-center cell to red-green moving contour are shown, at equiluminance and for two different directions of luminance contrast (Michelson contrast 80%). Adding the two responses together does not provide a signal related to the luminance contrast (sketched as thick line in stimulus plot). Edges were moved at 2°/s across the receptive field. Bandwidth 16 ms, average of 20 responses.

Fig. 4B shows an example of how this scheme does not work well in practice with stimuli that contain both luminance and chromatic contrast. Responses of a +M-L green ON-center and a +L-M red ON-center cell to moving red-green borders are shown; this analysis is more extensively described elsewhere (Valberg et al., 1992). Briefly, red-green borders of various luminance ratios were drifted across the receptive field. The luminances of the two sides of the border were set equal (center histograms) or unequal, as indicated. The individual histograms show vigorous responses of the +M-L cell to the green side of the border, and vigorous responses of the +L-M cell to the red side of the border. The cells were selected to be about equally responsive. One can add the responses of the two cells to approximate the operation of such a model as in Fig. 4A. At equal luminance, the sum shows little response, which is as required for an achromatic channel. However, if a substantial luminance imbalance is present, it was very difficult to construct in the summed signal a modulation corresponding to a luminance signal, which is indicated by the solid line in the stimulus sketches. Response distortions associated with response rectification and saturation make the operation of the model unreliable. Similar results were obtained with other combinations of cells. Other combinations to that in Fig. 4A would be possible (such as a combination of an ON-center from one cone and a surround from OFF-center cells with the other cone type) but these are likely to suffer from similar difficulties.

A more general approach to segregation of chromatic and luminance signals can be achieved using another stimulus configuration which we call a compound grating stimulus. Fig. 5A shows luminance, chromatic and compound gratings, together with the gun waveforms that produce them. The compound grating consists of red and green raised cosine waveforms. The chromatic component has the same spatial frequency as the chromatic grating in the center panel, but its luminance component is at twice the spatial frequency of the chromatic component. Contrast of the compound grating can be adjusted in the normal way. All gratings have the same mean luminance and chromaticity. In Fig. 5B are responses of a +L-M red on center PC cell to the three grating types; details of spatial and temporal frequency and contrast can be found in the figure legend. There is a weak response to the luminance grating, and strong and very similar responses to the chromatic and compound gratings. With MC cells (Fig. 5C), there is little response to the chromatic grating but vigorous and very similar responses to the luminance and compound gratings. These differences were robust over spatial and temporal frequency and contrast. We conducted an analysis of individual responses and found that on a neurometric basis differences between chromatic and compound for PC cells, and between luminance and compound for MC cells were not significant, at least at low contrasts.

The three grating types are clearly distinguishable perceptually. A neurometric analysis (not shown) demonstrated that the Fourier spectra of PC cell responses to chromatic and compound gratings were very similar and became indistinguishable at low contrast. A similar result held for MC cell responses and luminance and compound gratings. We therefore tested if it was possible to distinguish the grating types close to detection threshold. We first measured detection thresholds for standard luminance and chromatic gratings. For each observer, the data were fitted with sets of filters. These are indicated by the curves in Figs. 5D, 5E. They had the expected shapes; the luminance curve is bandpass, the chromatic curve low pass, with a lower high spatial frequency cut-off. Note that the curve for the luminance grating has been shifted leftward by an octave to take the difference in spatial frequency between luminance and chromatic components of a compound grating into account. We also measured detection thresholds for the compound grating. These approximated the envelope of the luminance and compound grating detection curves (not shown). We then measured ability to discriminate between compound and luminance and compound and chromatic gratings, and results for one observer are shown in Figs. 5D, 5E. For the discrimination of compound versus luminance grating, thresholds follow the chromatic detection curve, for the discrimination of compound versus chromatic grating; thresholds follow the luminance detection curve. These data strongly support the hypothesis that separable luminance and chromatic afferent channels both participate in the discrimination. Since individual PC cells cannot distinguish between chromatic and compound gratings, a multiplexed signal from the ideal neural model in Fig. 4B is incompatible with our results. Similar results were found with blue-yellow gratings and cells with excitatory S-cone input.

These results are strongly in favor of a strict segregation of luminance and chromatic retinal signals, as suggested by MacLeod and van der Twer (2003) and suggest that information about the chromatic and luminance structure of visual scenes requires sophisticated comparison of PC, MC, and KC pathway signals at a cortical level, and that a more nuanced approach to cortical analysis than a simple additive combination of signals is required.

In any event, this example show that it is important to consider physiological reality when constructing models of cortical function; neurons are noisy and non-linear transmitters of information, and cortical schemes have to take this into account. One argument for sparse coding approaches in cortical processing is that they are more noise resistant (Barlow, 1994).

Discussion

In the first part of this review, I have tried to illustrate that physiological reality may not be as specific as ideal neural models may suggest. The retina functions as any other biological system; it is as specific as functionally necessary, but does not expend resources to process signals with a specificity not required by the natural environment. As well as S-cone input to MC and PC cells, and mixed or specific input to PC cell surrounds, there are other instances in primate retina where retinal wiring is more specific than might be expected on a random basis, but this specificity is incomplete. For example, in mid-peripheral retina (20–40°), where there is substantial convergence from cones onto midget ganglion cells at the bipolar level, there is much more chromatic sensitivity than may be expected from random convergence. However, some PC cells appear to have lost chromatic specificity (Martin et al., 2001; Solomon et al., 2005). Some form of connectional specificity must exist, but at higher eccentricities even this seems to be lost (Dacey, 1999).

In the second half of this review, I have tried to show that ideal neural models must consider the structure of impulse trains in retinal coding. This leads to the unexpected result that transient MC cells can provide accurate information about slow movement, provided appropriate cortical readout mechanisms are present. Second, ideal neural models such as the multiplexing scheme in Fig. 4A may be feasible for a highly linear and noise-free transmission system, but they are unrealistic in the face of the distortions and noise inherent in biological signals.

It could be argued that the MC pathway does not have the visual resolution to permit discrimination of compound and luminance gratings at high spatial frequencies. It is commonly held that MC cells have much larger receptive fields and lower resolution than PC cells, but experimental data do not support this suggestion. The strongest argument is from anatomy, in which PC cells of the midget system have centers derived from a single cone (Polyak, 1941). However, physiological measurements indicate center size or visual resolution of individual cells is similar for PC and MC cells of similar eccentricity (Derrington & Lennie, 1984; Crook et al., 1988). This is probably due to enlargement of PC cells beyond the diameter of a single cone by the point-spread function of the eye (Lee, 2003). In the most extensive data set available (Derrington & Lennie, 1984), plots of receptive field center size against eccentricity extrapolate to a Gaussian center radius of 2–3 min of arc in the fovea for both PC and MC cells. One Gaussian radius corresponds approximately to the period of the highest spatial frequency resolved by a ganglion cell (Peichl & Wassle, 1979) which would correspond to 20–30 cycles/degree, and this is about the resolution limit of the macaque (Cavonius & Robbins, 1973). A second argument is that the sampling density of MC cells is too low to permit high resolution, especially in the fovea (Drasdo, 1989). It now appears that the proportion of MC cells decreases little, if at all, in the fovea (Grünert et al., 1993). Also, the patch-wise analysis of different orientations in cortical columns might be a good way to avoid sampling restrictions; in each orientation column, the two-dimensional cell matrix will collapse into a one-dimensional array of higher density.

To distinguish between the grating types in Fig. 5, a comparison of MC and PC is required at some central site. This point to a more nuanced view of combination of PC and MC signals in the cortex than just simple summation. For example, Kingdom (2003) demonstrated how subtle interaction of luminance and chromatic signals generate a perception of depth. Lesion experiments often assume a quasi-linear partition of function between the pathways (Merigan et al., 1991), but interference with a complex system seems unlikely to lead to such a simple result. Combination of MC- and PC-pathway signals begin in area 17 (Johnson et al., 2004) but a detailed model by which central cells, or networks of cells, extract spatiochromatic information from visual patterns is lacking. The reason for the apparently haphazard mixture of afferent signals in V1 while different cone inputs are so carefully segregated in subcortical structures remains one of the most intriguing questions in visual neurobiology.

The picture shows a howler monkey Alouatta caraya from the Centro Nacional de Primatas in Ananindeua, State of Pará, Brazil (photograph by Francisco Assis Fonseca and José Augusto Pereira Carneiro Muniz).