The state of h index research. Is the h index the ideal way to measure research performance?

How does one measure the quality of science? The question is not rhetorical; it is extremely relevant to promotion committees, funding agencies, national academies and politicians, all of whom need a means by which to recognize and reward good research and good researchers. Identifying high-quality science is necessary for science to progress, but measuring quality becomes even more important in a time when individual scientists and entire research fields increasingly compete for limited amounts of money. The most obvious measure available is the bibliographic record of a scientist or research institute—that is, the number and impact of their publications.

Identifying high-quality science is necessary for science to progress...

Currently, the tool most widely used to determine the quality of scientific publications is the journal impact factor (IF), which is calculated by the scientific division of Thomson Reuters (New York, NY, USA) and is published annually in the Journal Citation Reports (JCR). The IF itself was developed in the 1960s by Eugene Garfield and Irving H. Sher, who were concerned that simply counting the number of articles a journal published in any given year would miss out small but influential journals in their Science Citation Index (Garfield, 2006). The IF is the average number of times articles from the journal published in the past two years have been cited in the JCR year and is calculated by dividing the number of citations in the JCR year—for example, 2007—by the total number of articles published in the two previous years—2005 and 2006.

Owing to the availability and utility of the IF, promotion committees, funding agencies and scientists have taken to using it as a shorthand assessment of the quality of scientists or institutions, rather than only journals. As Garfield has noted, this use of the IF is often necessary, owing to time constraints, but not ideal (Garfield, 2006). Nature has, for example, shown “how a high journal impact factor can be the skewed result of many citations of a few papers rather than the average level of the majority, reducing its value as an objective measure of an individual paper” (Campbell, 2008).

Needless to say, the widespread use of the IF and the way in which it is calculated have attracted much criticism and even ridicule (Petsko, 2008). Many commentators have argued that it wrongly equates the importance of a paper with the IF of the journal in which it was published (Notkins, 2008), and that some scientists are now more concerned about publishing in high-IF journals than they are about their research, which negatively affects the peer-review and scientific publication process. “Scientists ... submit their papers to journals at the top of the impact factor ladder, circulating progressively through journals further down the rungs when they are rejected” (Simons, 2008); this is a waste of time for both editors and reviewers. Moreover, Thomson Reuters itself has been criticized for a lack of transparency and for the fact that journals can negotiate what to include in the denominator and are thus able to influence their IF (Anon, 2006).

In August 2005, Jorge Hirsch—a physicist at the University of California, San Diego, USA—introduced a new indicator for quantifying the research output of scientists (Bornmann & Daniel, 2007a; Hirsch, 2005). Hirsch's so-called h index was proposed as an alternative to other bibliometric indicators—such as the number of publications, the average number of citations and the sum of all citations (Hirsch, 2007)—and is defined as follows: “A scientist has index h if h of his or her N_p papers have at least h citations each and the other (N_p − h) papers have ≤ h citations each” (Hirsch, 2005). All papers by a scientist that have at least h citations are called the “Hirsch core” (Rousseau, 2006). An h index of 5 means that a scientist has published five papers that each have at least five citations. An h index of 0 does not inevitably indicate that a scientist has been completely inactive: he or she might have already published a number of papers, but if none of the papers was cited at least once, the h index is 0.

...the widespread use of the IF and the way in which it is calculated have attracted much criticism and even ridicule...

Shortly after Hirsch submitted his 2005 paper on the h index to the electronic archive arXiv.org as a preprint, both Nature (Ball, 2005) and Science (Anon, 2005) reported on it. At the initiative of Manuel Cardona, Emeritus Professor at the Max Planck Institute for Solid State Research in Stuttgart, Germany, and a member of the US National Academy of Sciences (Washington, DC, USA), the preprint was published a few weeks later in a revised form in the Proceedings of the National Academy of Sciences. Until late 2008, the paper has been cited about 200 times, which shows that Hirsch's proposal to represent the research achievements of a scientist as a single number is fascinating to many people, not only to science news editors. However, the combination of publications and citation frequencies into one value has been criticized by some scientists as making little sense: “The problem is that Hirsch assumes an equality between incommensurable quantities. An author's papers are listed in order of decreasing citations with paper i having C(i) citations. Hirsch's index is determined by the equality, h = C(h), which posits an equality between two quantities with no evident logical connection” (Lehmann et al, 2008).

The h index can now be calculated automatically for any publication set in the Web of Science (WoS; provided by Thomson Reuters) and is already regarded as the counterpart to the IF (Gracza & Somoskovi, 2007). WoS is not the only literature database that allows a user to calculate the h index; any database that includes the references cited in the publication will do, such as Chemical Abstracts provided by Chemical Abstracts Services (Columbus, OH, USA), Google Scholar, or Scopus provided by Elsevier (Amsterdam, The Netherlands; Jacso, 2008). Depending on what publications a database covers and analyses, however, the calculation of the h index will produce different results. Using Google Scholar, for example, can lead to different results from using databases that require subscription fees, such as Chemical Abstracts, Scopus and WoS (Bornmann et al, 2008a).

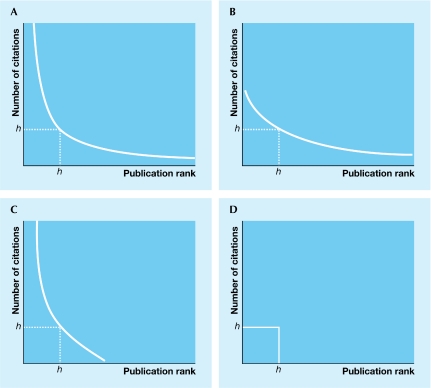
In any case, the main debate surrounding the h index concerns how meaningful it is as a measure of a scientist's performance. Fig 1 shows a range of distributions of citation frequencies for a given publication set and the corresponding h index. As a rule, the distribution of citation frequencies for a larger number of publications is skewed to the right according to a power law (Joint Committee on Quantitative Assessment of Research, 2008). A scientist's publication record usually contains a few highly cited papers and many rarely cited papers. As Fig 1A shows, the h index captures only a part of the publication and citation data if the distribution is right-skewed, as it fails to represent highly and rarely cited or non-cited papers. Scientists with very different citation frequencies can therefore have the same h index (Table 1; Fig 1B, C): “Think of two scientists, each with 10 papers with 10 citations, but one with an additional 90 papers with 9 citations each; or suppose one has exactly 10 papers of 10 citations and the other exactly 10 papers of 100 each. Would anyone think them equivalent”? (Joint Committee on Quantitative Assessment of Research, 2008).

Figure 1.

The h index for distributions of citation frequencies (the publications are sorted in graphs A–D by number of citations).

Table 1.

Example of h indices for different publication records

Paper	Citations
	Scientist A	Scientist B
1	51	6
2	34	5
3	29	4
4	22	4
5	3	3
6	1	3
7	0	2
8	–	2
9	–	1
10	–	0
11	–	0
h	4	4

Two scientists with the same h index: scientist A with few, highly cited papers and scientist B with many rarely cited papers.

An h index that completely captures the distribution of citation frequencies is shown in Fig 1D: a scientist has published h papers, of which each has received h citations; however, such ‘constant performers' are very rare. The h index therefore provides an incomplete picture for most scientists, whose publication and citation data have a right-skewed distribution. Evidence Ltd, a company in Leeds, UK, that analyses research performance, considers the h index to be an indicator with low information content that is not applicable to the general body of researchers (Evidence Ltd, 2007). Nonetheless, h-index values are already being used in various disciplines—for example, in chemistry, information sciences, medicine, physics and economics—to produce ranking lists of scientists.

The h index is no longer being used only as a measure of scientific achievement for individual researchers, but also to measure the scientific output of research groups (van Raan, 2006), scientific facilities and even countries. The ranking list for the research of individual nations in biology and biochemistry for the period 1996–2006, for example, shows that the USA, the UK and Germany have h indices of 400, 219 and 206 respectively (Csajbók et al, 2007). The indices at such aggregated levels—group, research facility or country—are calculated analogously to those of individual researchers. In addition, it is also possible to calculate successive h indices at higher aggregate levels (Prathap, 2006): “The institute has an index h₂ if h₂ of its N researchers have an h₁-index of at least h₂ each, and the other (N − h₂) researchers have h₁-indices lower than h₂ each. The succession can then be continued, for example, for networks of institutions or countries or other higher levels of aggregation” (Schubert, 2007).

The h index [...] is already regarded as the counterpart to the IF...

Braun et al (2005) also recommend using the h index as an alternative to the IF to qualify journals: “Retrieving all source items of a given journal from a given year and sorting them by the number of times cited, it is easy to find the highest rank number which is still lower than the corresponding times cited value. This is exactly the h-index of the journal for the given year.” As the h index for a journal cannot be higher than the number of papers that are published in a certain period, journals that publish only a few highly cited papers should therefore not be included in a ranking list that is based on the h index—this concerns mainly journals that predominantly publish reviews. For example, the Annual Review of Biochemistry published only 28 papers in 2005, which were cited on average about 100 times up until mid-2008. Other authors have proposed an hb index to assess research in selected areas (Banks, 2006; Egghe & Ravichandra, 2008).

Any new bibliometric indicator to measure scientific performance should be carefully checked for its validity and its ability to represent scientific quality correctly. In a series of investigations (Bornmann & Daniel, 2007b; Bornmann et al, 2008b), we have shown that, for individual scientists, the h index correlates well with both the number of their publications and the number of citations these publications have attracted—which is hardly surprising given that the h index was proposed to do exactly that. More importantly, however, are studies that have examined the relationship between the h index and peer judgements of research performance (Moed, 2005), of which there are only four available so far. Bornmann & Daniel (2005) and Bornmann et al (2008b) have shown that the average h-index values of accepted and rejected applicants for biomedicine research fellowships differ statistically significantly, while van Raan (2006) found that the h index “relates in a quite comparable way with peer judgments” for 147 Dutch research groups in chemistry. Finally, Lovegrove & Johnson (2008) have reported similar findings for the relationship between the h index and peer judgements in the context of grant applicants to the National Research Foundation of South Africa (Pretoria, South Africa). Although these studies provide confirmation of the h index's validity, it will require more time and research before it can be used in practice to assess scientific work.

Several disadvantages to the h index have also been pointed out (Bornmann & Daniel, 2007a; Jin et al, 2007). For example, “like most pure citation measures it is field-dependent, and may be influenced by self-citations ...; [t]he number of co-authors may influence the number of citations received ...; [t]he h-index, in its original setting, puts newcomers at a disadvantage since both publication output and observed citation rates will be relatively low ...; [t]he h-index lacks sensitivity to performance changes: it can never decrease and is only weakly sensitive to the number of citations received” (Rousseau, 2008).

This has led to the development of numerous variants of the h index (Sidebar A). The m quotient, for example, is computed by dividing the h index by the number of years that the scientist has been active since the first published paper (Hirsch, 2005). Unlike the h index, the m quotient avoids a bias towards more senior scientists with longer careers and more publications. The h_I index is “a complementary index h_I = h² / N_a^(T)), with N_a^(T)) being the total number of authors in the considered h papers” (Batista et al, 2006). It is meant to reduce the bias towards scientists that publish frequently as co-authors. The h_c index excludes self-citations to avoid a bias towards scientists who disproportionately often cite their own work (Schreiber, 2007).

To measure the quality of scientific output, it would therefore be sufficient to use just two indices: one that measures productivity and one that measures impact...

The a index indicates the average number of citations of publications in the Hirsch core (Jin, 2006), whereas the g index is defined as follows: “[a] set of papers has a g-index g if g is the highest rank such that the top g papers have, together, at least g² citations” (Egghe, 2006). In contrast to the h index, which corresponds to the number of citations for the publication with the fewest citations in the Hirsch core, the a index and the g index are meant to give more weight to highly cited papers. The ar index is defined as the square root of the sum of the average number of citations per year of articles included in the h-core (Jin, 2007) and is meant to avoid favouring scientists who have stopped publishing because the h index can never decrease over time; even if a scientist is no longer active, his or her h index remains constant in the worst case. Of the various indices that have been proposed in recent years, the g index by Egghe (2006) has received most attention, whereas many other derivatives of the h index have had little response.

All empirical studies that have tested the various indices for scientists or journals have reported high correlation coefficients. Apparently, this indicates a redundancy among the various indices to measure achievement. The results of two studies by Bornmann et al (2008c, d) state more precisely that the h index and its variants are, in effect, two types of index. “The one type of indices [...] describe the most productive core of the output of a scientist and tell us the number of papers in the core. The other indices [...] depict the impact of the papers in the core” (Bornmann et al, 2008c). To measure the quality of scientific output, it would therefore be sufficient to use just two indices: one that measures productivity and one that measures impact—for example, the h index and the a index.

As described above, only four studies have examined the validity of the h index by testing the relationship between a scientist's h-index value and peer assessments of his or her achievements. Although the results of the studies mentioned are positive, we need further studies that use extensive data sets to examine the h index and possibly to select variants for use in various fields of application. Future research on the h index should no longer be aimed at developing new variants, but should instead test the validity of the existing ones. Only once such studies have confirmed the fundamental validity of the h index and certain variants should it be used to assess scientific work.

As a basic principle, it is always prudent to use several indicators to measure research performance (Glänzel, 2006a; van Raan, 2006). The publication set of a scientist, journal, research group or scientific facility should always be described using many indicators such as the number of publications with zero citations, the number of highly cited papers and the number of papers for which the scientist is first or last author. As publication and citation conventions differ considerably across disciplines, it is also important to use additional bibliometric indicators that measure the “relative, internationally field-normalized impact” of publications (van Raan, 2005)—for example, the indicators developed by the Centre for Science and Technology Studies (CWTS; Leiden, The Netherlands) or the Institute for Research Policy Studies of the Hungarian Academy of Sciences (Budapest, Hungary; Glänzel, 2006b, 2008). In addition to bibliometric indicators, every evaluation study should also provide a measure of concentration, such as the Gini coefficient or the Herfindahl index, to assess the distribution of the citations among a scientist's publications (Bornmann et al, 2008e; Evans, 2008).

As a basic principle, it is always prudent to use several indicators to measure research performance...

If the h index is used for the evaluation of research performance, it should always be taken into account that, similar to other bibliometric measures, it is dependent on the length of an academic career and the field of study in which the papers are published and cited. For this reason, the index should only be used to compare researchers of a similar age and within the same field of study. At the end of the day, all measurements of research quality should be taken with a grain of salt; it is certainly not possible to describe a scientist's contributions to a given research field with mere numerical values. As Albert Einstein (1879–1955) famously noted: “[n]ot everything that counts is countable, and not everything that's countable counts.”

Sidebar A | Definition of the h index and its variants.

Index Definition

h index “A scientist has index h if h of his or her N_p papers have at least h citations each and the other (N_p − h) papers have fewer than ≤ h citations each” (Hirsch, 2005, p 16569)

m quotient 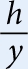where h is h index, y is number of years since publishing the first paper

g index “The g-index g is the largest rank (where papers are arranged in decreasing order of the number of citations they received) such that the first g papers have (together) at least g² citations” (Egghe, 2006, p 144)

a index 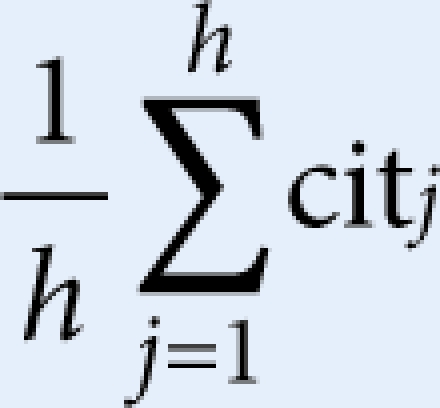where h is h index, cit is citation counts

ar index 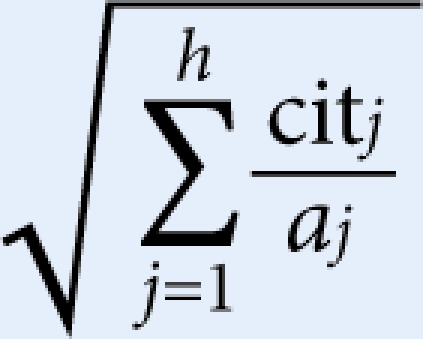where h is h index, cit is citation counts, a is number of years since publishing

Lutz Bornmann

Hans-Dieter Daniel