Categorical Data Analysis: Away from ANOVAs (transformation or not) and towards Logit Mixed Models

Abstract

This paper identifies several serious problems with the widespread use of ANOVAs for the analysis of categorical outcome variables such as forced-choice variables, question-answer accuracy, choice in production (e.g. in syntactic priming research), et cetera. I show that even after applying the arcsine-square-root transformation to proportional data, ANOVA can yield spurious results. I discuss conceptual issues underlying these problems and alternatives provided by modern statistics. Specifically, I introduce ordinary logit models (i.e. logistic regression), which are well-suited to analyze categorical data and offer many advantages over ANOVA. Unfortunately, ordinary logit models do not include random effect modeling. To address this issue, I describe mixed logit models (Generalized Linear Mixed Models for binomially distributed outcomes, Breslow & Clayton, 1993), which combine the advantages of ordinary logit models with the ability to account for random subject and item effects in one step of analysis. Throughout the paper, I use a psycholinguistic data set to compare the different statistical methods.

In the psychological sciences, training in the statistical analysis of continuous outcomes (i.e. responses or independent variables) is a fundamental part of our education. The same cannot be said about categorical data analysis (Agresti, 2002; henceforth CDA), the analysis of outcomes that are either inherently categorical (e.g. the response to a yes/no question) or measured in a way that results in categorical grouping (e.g. grouping neurons into different bins based on their firing rates). CDA is common in all behavioral sciences. For example, much research on language production has investigated influences on speakers’ choice between two or more possible structures (see e.g. research on syntactic persistence, Bock, 1986; Pickering and Branigan, 1998; among many others; or in research on speech errors). For language comprehension, examples of research on categorical outcomes include eye-tracking experiments (first fixations), picture identification tasks to test semantic understanding, and, of course, comprehension questions. More generally, any kind of forced-choice task, such as multiple-choice questions, and any count data constitute categorical data.

Despite this preponderance of categorical data, the use of statistical analyses that have long been known to be questionable for CDA (such as analysis of variance, ANOVA) is still commonplace in our field. While there are powerful modern methods designed for CDA (e.g. ordinary and mixed logit models; see below), they are considered too complicated or simply unnecessary. There is a widely-held belief that categorical outcomes can safely be analyzed using ANOVA, if the arcsine-square-root transformation (Cochran, 1940; Rao, 1960; Winer et al., 1971) is applied. This belief is misleading: even ANOVAs over arcsine-square-root transformed proportions of categorical outcomes (see below) can lead to spurious null results and spurious significances. These spurious results go beyond the normal chance of Type I and Type II errors. The arcsine-square-root and other transformations (e.g. by using the empirical logit transformation, Haldane, 1955; Cox, 1970) are simply approximations that were primarily intended to reduce costly computation time. In an age of cheap computing at everyone’s fingertips, we can abandon ANOVA for CDA. Modern statistics provide us with alternatives that are in many ways superior.

This paper provides an informal introduction to one such method: generalized linear mixed models with a logit link function, henceforth mixed logit models(Bates & DebRoy, 2004; Bates & Sarkar, 2007; Breslow & Clayton, 1993; see also conditional logistic regression, Dixon, this issue; for an overview of other methods, see Agresti, 2002). Mixed logit models are a generalization of logistic regression. Like ordinary logistic regression (Cox, 1958, 1970; Dyke & Patterson, 1952; henceforth ordinary logit models), they are well-suited for the analysis of categorical outcomes. Going beyond ordinary logit models, however, mixed logit models include random effects, such as subject and item effects. I introduce both ordinary and mixed logit models and compare them to ANOVA over untransformed and arcsine-square-root transformed proportions using data from a psycholinguistics study (Arnon, 2006, submitted). All analyses were performed using the statistics software package R (R Development Core Team, 2006). The R code is available from the author.

The inadequacy of ANOVA over categorical outcomes

Issues with ANOVAs and, more generally, linear models over categorical data have been known for a long time (e.g. Cochran, 1940; Rao, 1960; Winer et al., 1971; for summaries, see Agresti, 2002: 120; Hogg & Craig, 1995). I discuss problems with the interpretability of ANOVAs over categorical data and then show that these problems stem from conceptual issues.

Interpretability of ANOVA over categorical outcomes

ANOVA compares the means of different experimental conditions and determines whether to reject the hypothesis that the conditions have the same population means given the observed sample variances within and between the conditions. For continuous outcomes, the means, variances, and the confidence intervals have straightforward interpretations. But what happens if the outcome is categorical? For example, we may be interested in whether subjects answer a question correctly depending on the experimental condition. So, we may observe that of the 10 elicited answers, 8 are correct and 2 are incorrect. What is the mean and variance of 8 correct answers and 2 incorrect answers? We can code one of the outcomes, e.g. correct answers, as 1 and the other outcome, e.g. wrong answers, as 0. In that case, we can calculate a mean (here 0.8) and variance (here 0.18). The mean is apparently straightforwardly interpreted as the mean proportion of correct answers (or percentages of correct answers if multiplied by 100).

The current standard for CDA in psychology follows the aforementioned logic. Categorical outcomes are analyzed using subject and item ANOVAs (F1 and F2) over proportions or percentages. The approach is seemingly intuitive and, by now, so widespread that it is hard to imagine that there is any problem with it. Unfortunately, that is not the case. ANOVAs over proportions can lead to hard-to-interpret results because confidence intervals can extend beyond the interpretable values between 0 and 1. For the above example, a 95% confidence interval would range from 0.52 to 1.08 (= 0.8 +/− 0.275), rendering an interpretation of the outcome variable as a proportion of correct answers impossible (proportions above 1 are not defined). One way to think about the problem of interpretability is that ANOVAs attribute probability mass to events that can never occur, thereby likely underestimating the probability mass over events that actually can occur. This intuition points at the most crucial problem with ANOVAs over proportions of categorical outcomes. ANOVA over proportions easily leads to spurious results.

Categorical outcomes violate ANOVA’s assumption

The inappropriateness of ANOVAs over categorical data can be derived on theoretical grounds. Assume a binary outcome (e.g. correct or incorrect answers to yes/no-questions) that is binomially distributed; that is, for every trial there is a probability p that the answer will be correct. Then the probability of k correct answers in n trials is given by the following function:

$$f(k,n,p)=\left(\begin{array}{c}n\\ k\end{array}\right)p^k{(1-p)}^{n-k}=\frac{n!}{k!(n-k)!}{p}^k{(1-p)}^{n-k}$$ (1)

The population mean and variance of a binomially distributed variable X are given in (2) and (3).

$${\mu }_X=n\left[1p+0(p-1)\right]=np$$ (2)

$${\sigma }_X^2=n\left[{(1-p)}^{2}p+{(0-p)}^2(1-p)\right]=np(1-p)$$ (3)

The expected sample proportion P over n trials is given by dividing μ_X by the number of trials n, and hence is p. Similarly, the variance of the sample proportion is a function of p:

$${\sigma }_P^2=\frac{p(1-p)}{n}$$ (4)

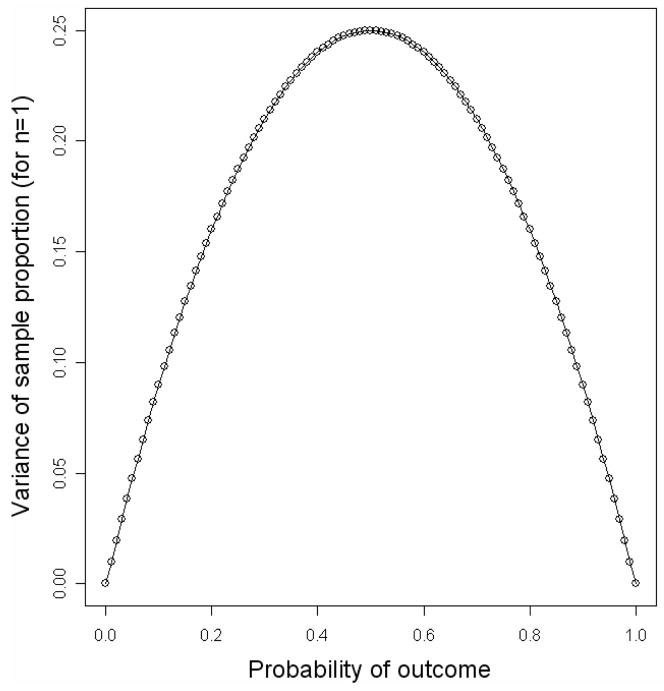
From (4) it follows that the variance of the sample proportions will be highest for p= 0.5 (the product of n numbers x that add up to 1 is highest if x₁ = … = x_n) and will decrease symmetrically as we approach 0 or 1. This is illustrated in Figure 1. Note that the shape of the curve and the location of its maximum are determined by p alone.

Figure 1.

Variance of sample proportion depending on p (for n= 1)

Now assume that we have two samples elicited under different conditions. In one condition, the probability that a trial will yield a correct answer is p₁, in the other condition it is p₂. For example, if p₁ = 0.45 and p₂ = 0.8, then:

$${\sigma }_P^2(p_1)=\frac{p_1(1-p_1)}{n}=\frac{0.2475}{n}>\frac{0.16}{n}=\frac{p_2(1-p_2)}{n}={\sigma }_P^2(p_2)$$ (5)

In other words, if the probability of a binomially distributed outcome differs between two conditions, the variances will only be identical if p₁ and p₂ are equally distant from 0.5 (e.g. p₁ = 0.4 and p₂ = 0.6). The bigger the difference in distance from 0.5 between the conditions, the less similar the variances will be. Also, as can be see in Figure 1, differences close to 0.5 will matter less than differences closer to 0 or 1. Even if p₁ and p₂ are unequally distant from 0.5, as long as they are close to 0.5, the variances of the sample proportions will be similar. Sample proportions between 0.3 and 0.7 are considered close enough to 0.5 to assume homogeneous variances (e.g. Agresti, 2002: 120). Within this interval, p(1 – p) ranges from 0.21 for p= 0.3 or 0.7 to 0.25 for p= 0.5. Unfortunately, we usually cannot determine a priori the range of sample proportions in our experiment (see also Dixon, this issue). Also, in general, variances in two binomially distributed conditions will not be homogeneous – contrary to the assumption of ANOVA.

The inappropriateness of ANOVA for CDA was recognized as early as Cochran (1940, referred to in Agresti, 2002: 596). Before I discuss the most commonly used method for CDA using ANOVA over transformed proportions, I introduce logistic regression, which is an alternative to ANOVA that was designed for the analysis of binomially distributed categorical data.

An alternative: Ordinary logit models (logistic regression)

Logistic regression, also called ordinary logit models, was first used by Dyke and Patterson (1952), but was most widely introduced by Cox (1958, 1970; see Agresti, 2002: Ch. 16). For extensive formal introductions to logistic regression, I refer to Agresti (2002: Ch. 5), Chatterjee and colleagues (2000: Ch. 12), and Harrell (2001). For a concise formal introduction written for language researchers, I recommend Manning (2003: Ch. 5.7).

Logit models can be seen to be a specific instance of a generalization of ANOVA. To see this link between logit models and ANOVA, it helps to know that ANOVA can be understood as linear regression (cf. Chatterjee, 2000: Ch. 5). Linear regression describes outcome y as a linear combination of the independent variables x₁ … x_n (also called predictors) plus some random error ε (and optionally an intercept β₀). Equation (6) provides two common descriptions of linear models. The first equation describes the value of y. The second equation describes the expected value of y. Note that categorical predictors have to be recoded into numerical values for (6) to make sense (treatment-coding being a common coding in the regression literature).

$$y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_n{x}_n+\epsilon \iff E(y)={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_n{x}_n$$ (6)

We can further abbreviate (6) using vector notation E(y) = x′β (boldface for vectors), where x′ is a transposed vector consisting of 1 for the intercept, and all predictor values x₁ … x_n, and β is a vector of coefficients β₀ … β_n. The coefficients β₀ … β_n have to be estimated. This is done in such a way that the resulting model fits the data ‘optimally’. Usually, the model is considered optimal if it is the model for which the actually observed data are most likely to be observed (the maximum likelihood model; for an informal introduction, see Baayen et al., this issue).

Now imagine that we want to fit a linear regression to proportions of a categorical outcome variable y. So, we could define the following model of expected proportions:

$$E(y)=p={\mathit{x}}^{\prime }\mathit{\beta }$$ (7)

Such a linear model, also called linear probability model (Agresti, 2002: 120; not to be confused with a probit model), has many of the problems mentioned above for ANOVAs over proportions. But, what if we transformed proportions into a space that is not bounded by 0 and 1 and that captures the fact that, in real binomially distributed data, a change in proportions around 0.5 usually corresponds to a smaller change in the predictors than the same change in proportions close to 0 or 1 (i.e. the relation between the predictors and proportions is nonlinear; cf. Agresti, 2002: 122)? Consider odds. They are easily derived from probabilities (and vice versa):

$$\mathit{odds}(p)=\frac{p}{1-p}\text{and}p(\mathit{odds})=\frac{\mathit{odds}}{1+\mathit{odds}}$$ (8)

Thus, odds increase with increasing probabilities, with odds ranging from 0 to positive infinity and odds of 1 corresponding to a proportion of 0.5. Differences in odds are usually described multiplicatively (i.e. in terms of x-fold increases or decreases). For example, the odds of being on a plane with a drunken pilot are reported to be “1 to 117” (http://www.funny2.com/). In the notation used here, this corresponds to odds of 1 / 117 ≈ 0.0086. Unfortunately, these odds are 860 times higher than the odds of dating a supermodel (≈ 0.00001). Thus, we can describe the odds of an outcome as a product of coefficients raised to the respective predictor values (assuming treatment-coding, predictor values are either 0 or 1):

$$\frac{p}{1-p}={\beta }_0\ast {{\beta }_1}^{x_1}\ast \cdots \ast {{\beta }_n}^{x_n}$$ (9)

By simply taking the natural logarithm of odds instead of plain odds, we can turn the model back into a linear combination, which has many desirable properties:

$$ln\frac{p}{1-p}=ln\left({\beta }_0\ast {{\beta }_1}^{x_1}\ast \cdots \ast {{\beta }_n}^{x_n}\right)=ln({\beta }_0)+ln({\beta }_1)x_1+\cdots +ln({\beta }_n)x_n$$ (10)

The natural logarithm of odds is called the logit (or log-odds). The logit is centered around 0 (i.e. logit( p) = −logit(1 – p) ), corresponding to a probability of 0.5, and ranges from negative to positive infinity. The ln β₀ … ln β_n in (10) are constants, so we can substitute β… β_n for them (or any other arbitrary variable name). This yields (11):

$$ln\frac{p}{1-p}=\text{logit}p={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_n{x}_n={\mathit{x}}^{\prime }\mathit{\beta }$$ (11)

In other words, we can think of ordinary logit models as linear regression in log-odds space! The logit function defines a transformation that maps points in probability space into points in log-odds space. In probability space, the linear relationship that we see in logit space is gone. This is apparent in (12), describing the same model as in (11), but transformed into probability space:

$$p=\frac{e^{{\mathit{x}}^{\prime }\mathit{\beta }}}{1+e^{{\mathit{x}}^{\prime }\mathit{\beta }}}=\frac{1}{1+e^{-{\mathit{x}}^{\prime }\mathit{\beta }}}=\text{E}[y]$$ (12)

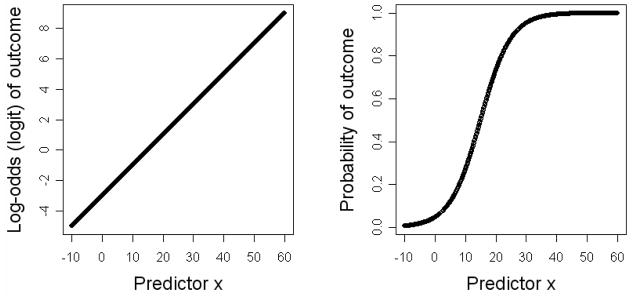
Logit models capture the fact that differences in probabilities around p= 0.5 matter less than the same changes close to 0 or 1. This is illustrated in Figure 2, where the left panel shows a hypothetical linear effect of a predictor x in logit space ( y= −3+0.2x ), and the right panel shows the same effect in probability space. As can be seen in the right panel, small changes on the x-axis around p= 0.5 (i.e. x= 15 since 0= −3+0.2*15 = logit(0.5) ) lead to large decreases or increases in probabilities compared to the same change on the x-axis closer to 0 or 1.

Figure 2.

Example effect of predictor x on categorical outcome y. The left panel displays the effect in logit space with $ln\frac{1}{1-p(x)}=-3+0.2x$. The right panel displays the same effect in probability space with $p(x)=\frac{1}{1+e^{3-0.2x}}$

Thus logit models, unlike ANOVA, are well-suited for the analysis of binomially distributed categorical outcomes (i.e. any event that occurs with the same probability at each trial). Logit models have additional advantages over ANOVA. Logit models scale to categorical dependent variables with more than two outcomes (in which case we call the model a multinomial model; for an introduction, see Agresti, 2002). Among other things, this can help avoid confounds due to data exclusion. For example, in priming studies where researchers are interested in speakers’ choice between two structures, subject sometimes produce neither of those two. If non-randomly distributed, such “errors” can confound the analysis because what appears to be an effect on the choice between two outcomes may, in reality, be an effect on the chance of an error. Consider a scenario in which, for condition X, participants produce 50% outcome 1, 45% outcome 2, and 5% errors, but, for condition Y, they produce 50% outcome 1, 30% outcome 2, and 20% errors. If an analysis was conducted after errors are excluded, we may conclude, given small enough standard errors, that there is a main effect of condition (in condition X, the proportion of outcome 1 would be 50/95 = 0.53; in condition Y, 50/80 = 0.63). This conclusion would be misleading, since what really happens is that there is an effect on the probability of an error. We would find a spurious main effect on outcome 1 vs. 2. The problem is not only limited to errors. It also includes any case in which “other” categories are excluded from the analysis (e.g. when speakers in a production experiment produce structures that we are not interested in). Multinomial models make such exclusion unnecessary and allow us to test which of all possible outcomes a given predictor affects. For the above example, we could test whether the condition affects the probability of outcome 1 or outcome 2, or the probability of an error.

Logit models also inherit a variety of advantages from regression analyses. They provide researchers with more information on the directionality and size of an effect than the standard ANOVA output (this will become apparent below). They can deal with imbalanced data, thereby freeing researchers from all too restrictive designs that affect the naturalness of the object of their study (see Jaeger, 2006 for more details). Like other regressions, ordinary logit models also force us to be explicit in the specification of assumed model structure. At the same time, regression models make it easier to add and remove additional post-hoc control in the analysis, thereby giving researchers more flexibility and better post-hoc control. Another nice feature that logit models inherit from regressions is that they can include continuous predictors. Modern implementations of logit models come with a variety of tools to investigate linearity assumptions for continuous predictors (e.g. rcs for restricted cubic splines in R’s Designlibrary; Harrell, 2005). Ordinary logit models do, however, have a major drawback compared to ANOVA: they do not model random subject and item effects. Later I describe how mixed logit models overcome this problem. First I present a case study that exemplifies the problems of ANOVA over proportions using a real psycholinguistic data set. The case study illustrates that these problems persist even if arcsine-square-root transformed proportions are used in the ANOVA.

A case study: Spurious significance in ANOVA over proportions

Arnon (2006, submitted) investigated the source of children’s difficulty with object relative clauses in production and comprehension. Arnon presents evidence that children are sensitive to the same factors that affect adult language processing. I consider only parts of the comprehension results of Arnon’s Study 2. In this 2 x 2 experiment, twenty-four Hebrew-speaking children listened to Hebrew relative clauses (RCs). RCs were either subject or object extracted. The noun phrase in the RC (the object for subject extracted RCs and the subject for object extracted RCs) was either a first person pronoun or a lexical noun phrase (NP). An example item in all four conditions is given in Table 1 (taken from Arnon, 2006), where the manipulated NP is underlined.

Table 1.

Materials from Study 2 in Arnon (2006; Comprehension experiment)

Subject RC, Lexical NP	Eize tzeva ha-naalaim shel ha-yalda she metzayeret et ha-axot?
	Which color the-shoes of the-girl that draws the nurse-ACC
	What color are the shoes of the girl that is drawing the nurse?
Object RC, Lexical NP	Eize tzeva ha-naalaim shel ha-yalda she ha-axot metzayeret?
	Which color the-shoes of the-girl that the nurse draws?
	What color are the shoes of the girl that the nurse is drawing?
Subject RC, Pronoun	Eize tzeva ha-naalaim shel ha-axot she metzayeret oti?
	Which color the-shoes of the-nurse that draws me-ACC?
	What color are the shoes of the nurse that is drawing me?
Object RC, Pronoun	Eize tzeva ha-naalaim shel ha-axot she ani metzayeret?
	Which color the-shoes of the-nurse that I-NOM draw?
	What color are the shoes of the nurse that I am drawing?

Arnon hypothesized that, like adults (Warren & Gibson, 2003), children perform better on RCs with pronoun NPs than on RCs with lexical NPs, and that they perform better on subject RCs than on object RCs. Table 2 summarizes the mean question-answer accuracy (i.e. the proportion of correct answers) and standard errors across the four conditions.

Table 2.

Percentage of correct answers and standard errors by condition

	Lexical NP	Pronoun NP
Subject RC	89.7% (.02)	95.7% (.02)
Object RC	68.9% (.04)	84.3% (.03)

Arnon (submitted) used mixed logit models to analyze her data which yielded two main effects and no interaction. For the sake of argument, I demonstrate that using ANOVAs would have resulted in a spurious interaction.

Note that, contrary to the assumption of the homogeneity of variances, but as expected for binomially distributed outcomes, the standard errors (and hence the variances) are bigger the closer the mean proportion of correct answers is to 50%. The results in Table 2 also suggest that an ANOVA will find main effects of RC type and NP type as well as an interaction. Question-answer accuracy is higher for subject RCs than for object RCs (92.7% vs. 76.6%) and higher for pronoun NPs than for lexical NPs (90.0% vs. 79.3%). Furthermore, the effect of NP type on the percentage of correct answers seems to be bigger for object RCs (68.9% vs. 84.3%) than for subject RCs (89.7% vs. 95.7%), suggesting that an ANOVA will find an interaction.

ANOVA over untransformed proportions

Indeed, subject and item ANOVAs over the average percentages of correct answers return significance for both main effects and the interaction.

As expected the interaction comes out as highly significant in the ANOVA. Now, are these effects spurious or not? In the previous section, I discussed several theoretical issues with ANOVAs over proportions. But do those issues affect the validity of these ANOVA results? As I show next, the answer is yes, they do.

Ordinary logit model

Ordinary logit models are implemented in most modern statistics program. I use the function lrm in R’s Designlibrary (Harrell, 2005). The model formula for the R function lrm is given in (13).

$$\text{Correct}\sim 1+\text{RCtype}+\text{NPtype}+\text{RCtype}:\text{NPtype}$$ (13)

The “1” specifies that an intercept should be included in the model (the default). Further shortening the formula, I could have written Correct ~ RCtype*NPtype,which in R implies inclusion of all combinations of the terms connected by “*” (I will use this notation below).

For the ordinary logit model, the analyzed outcomes are the correct or incorrect answers. Thus, all cases are entered into the regression (instead of averaging across subjects or items). Significance of predictors in the fitted model is tested with likelihood ratio tests (Agresti, 2002: 12). Likelihood ratio tests compare the data likelihood of a subset model with the data likelihood of a superset model that contains all of the subset model’s predictors and some more. A model’s data likelihood is a measure of its quality or fit, describing the likelihood of the sample given the model. The −2 * logarithm of the ratio between the likelihoods of the models is asymptotically χ²-distributed with the difference in degrees of freedoms between the two models. Thus a predictor’s significance in a model is tested by comparing that model against a model without the predictor using a χ²-test.

Here I use the function anova.Design from R’s Designlibrary (Harrell, 2005). The function automatically compares a model against all its subset models that are derived by removing exactly one predictor. For Arnon’s data, we find that a model without RC type has considerably lower data likelihood (χ²(1)= 28.8, p< 0.001), as does a model without NP type (χ²(1)= 12.2, p< 0.001). Thus RC and NP type contribute significant information to the model. The interaction, however, does not (χ²(1)= 0.01, p> 0.9). The summary of the full model in Table 4 confirms this.

Table 4.

Summary of the ordinary logit model (N= 696; model Nagelkerke r²= 0.126)

Predictor	Coefficient	SE	Wald Z	P
Intercept	0.80	(0.167)	4.72	<0.001
RC type=subject RC	1.35	(0.295)	4.58	<0.001
NP type=pronoun	0.89	(0.272)	3.26	<0.001
Interaction=subject RC & pronoun	0.05	(0.511)	0.10	>0.9

Note that the standard summary of a regression model provides information about the size and directionality of effects (an ANOVA would require planned contrasts for this information). The first column of Table 4 lists all the predictors entered into the regression. The second column gives the estimate of the coefficient associated with the effect. The coefficients have an intuitive geometrical interpretation: they describe the slope associated with an effect in log-odds (or logit) space. For categorical predictors, the precise interpretation depends on what numerical coding is used. Treatment-coding compares each level of a categorical predictor against all other levels. This contrasts with effect-coding, which compares two levels against each other. Here I have used treatment-coding, because it is the most common coding scheme in the regression literature. For example, for the current data set, subject RCs are coded as 1 and compared against object RCs (which are taken as the baseline and coded as 0). So, the coefficient associated with RC type tells us that the log-odds of a correct answer for subject RCs are 1.35 log-odds higher than for object RCs. But what does this mean? Recall that log-odds are simply the log of odds. So, the odds of a correct answer for subject RCs are e^1.35 ≈ 3.9 times higher than the odds for object RCs. Following the same logic, the odds for RCs with pronouns are estimated to be e^0.89 ≈ 2.4 times higher than the odds for RCs with lexical NPs.

The third column in Table 4 gives the estimate of the coefficients’ standard errors. The standard errors are used to calculate Wald’s z-score (henceforth Wald’s Z, Wald, 1943) in the fourth column by dividing the coefficient estimate by the estimate for its standard error. The absolute value of Wald’s Z describes how distant the coefficient estimate is from zero in terms of its standard error. The test returns significance if this standardized distance from zero is large enough. Coefficients that are significantly smaller than zero decrease the log-odds (and hence odds) of the outcome (here: a correct answer). Coefficients significantly larger than zero increase the log-odds of the outcome. Unlike the likelihood ratio test, however, Wald’s z-test is not robust in the presence of collinearity (Agresti, 2002: 12). Collinearity leads to inflated estimates of the standard errors and changes coefficient estimates (although in an unbiased way). The model presented here contains only very limited collinearity because all predictors were centered (VIFs < 1.5).¹ This makes it possible to use the coefficients to interpret the direction and size of the effects in the model.

The main effects of RC type and NP type are highly significant. We can also interpret the significant intercept. It means that, if the RC type is not ‘subject RC’ and the NP type is not ‘pronoun’, the chance of a correct answer in Arnon’s sample is significantly higher than 50%. The odds are estimated at e^0.8 ≈ 2.2, which means that the chance of a correct answer for object RCs with a lexical NP is estimated as $p=\frac{2.2}{1+2.2}\approx 0.69$. Indeed, this is what we have seen in Table 2. Similarly the predicted probability of a correct answer for subject RC with a pronoun is calculated by adding all relevant log-odds, 0.8+1.35+0.89=3.04, which gives $p=\frac{e^{3.04}}{1+e^{3.04}}\approx 0.95$ (compared to 95.7% given in Table 2).

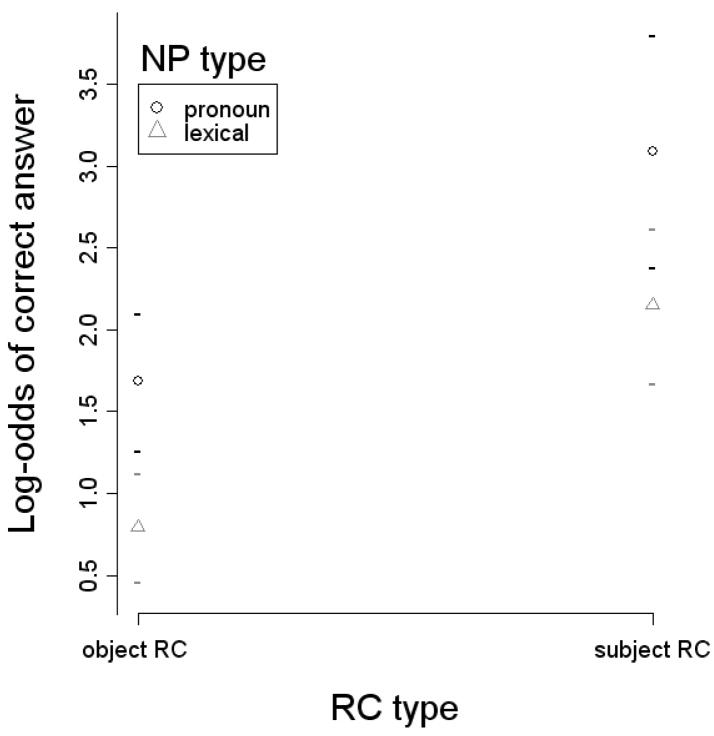
The numbers do not quite match because we did not include the coefficient for the interaction. However, notice that they almost match. This is the case because the interaction does not add significant information to the model (Wald’s Z= 0.01, P> 0.9). The effects are illustrated in Figure 3, showing the predicted means and confidence intervals for all combinations of RC and NP type (the plot uses plot.Design from R’s Design library, Harrell, 2005 ):

Figure 3.

Estimated effects of RC type and NP type on the log-odds of a correct answer.

In sum, there is no significant interaction because the effect of NP type for different levels of RC type does not differ in odds (and hence neither does it differ in log-odds). Indeed, both the change from 68.9% to 84.3% associated with NP type for object RCs and the change from 89.7% to 95.7% associated with NP type for subject RCs correspond to an approximate 2.5-fold odds increase. So, unlike ANOVA, logistic regression returns a result that respects the nature of the outcome variable.

The spurious interaction in the ANOVA should be of no further surprise given the before-mentioned conceptual problems. Readers familiar with transformations for proportional data may find the argument against ANOVA a straw man because they believe that ANOVAs will correctly recognize the interaction as insignificant once the data is adequately transformed. Next I describe why this assumption is wrong for at least the most commonly used transformation.

The arcsine-square-root transformation and its failure

There are several problems with the reliance on transformation for ANOVA over proportional data. To begin with there is also reason to doubt that transformations are applied correctly. The most popular transformation, the arcsine-square-root transformation ( $t(x)=arcsin\left(\sqrt{x}\right)$; e.g. Rao, 1960; Winer et al., 1971; henceforth arcsine transformation) requires further modifications for small numbers of observations or proportions close to 0 or 1 (e.g. Bartlett, 1937: 168; for an overview, see Hogg & Craig, 1995). In practice these modifications are rarely applied (Victor Ferreira, p.c.), although sample proportions close to 0 or 1 are common (e.g. in research on speech errors or when analyzing comprehension accuracies). Even more worrisome is the lack of any theoretical justification for the use of transformed proportions (cf. Cochran, 1940: 346). Most importantly, however, even ANOVA over transformed proportions can lead to spurious results. I use Arnon’s data to illustrate this point.

Spurious significance persists even after arcsine-square-root transformation

I focus on the subject analysis, where the insufficiency of the arcsine transformation is most apparent. The two main effects are correctly recognized as significant (RC type: F1(1,23)= 28.5, P< 0.01; NP type: F1(1,23)= 17.3, P< 0.01). However, the interaction is still incorrectly considered significant (F1(1,23)= 8.5; P< 0.01). This is the case because several children in Arnon’s experiment performed close to ceiling (the proportions of correct answers are 1 or close to 1). For such data, ANOVAs over arcsine transformed data are unreliable.

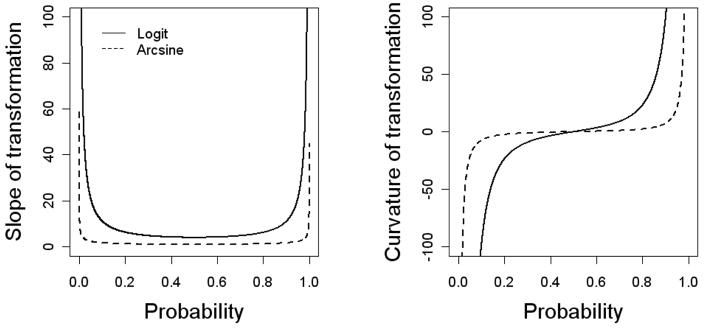
One reason why the arcsine transformation is unreliable for such data becomes apparent once we compare the plots of logit and arcsine transformed proportions. Figure 4 shows the slope (1^st derivative) and curvature (2^nd derivative) of the two transformations. Both transformations have a saddle point at p= 0.5, but for all p ≠ 0.5 the slope of the logit is always higher than the slope of the arcsine-square-root. The absolute curvature (the change in the slope) is also larger. In other words, as one moves away from p= 0.5, a change in probability p₁ to p₂ corresponds to more of a change in log-odds than to a change in arcsine transformed probabilities. This means that, compared to the logit, the arcsine transformation underestimates changes in probability more the closer they are to 0 or 1.

Figure 4.

Slope and curvature of the logit and arcsine-square-root transformation

In other words, while the arcsine transformation makes for proportional data more similar to logit transformed data, for proportions close to 0 or 1, even ANOVA over arcsine transformed data can return spurious results. As mentioned earlier, this problem is not limited to spurious significances. Imagine that in Arnon’s data the effect of NP type would be identical in proportions for subject and object RCs (e.g. imagine Arnon’s data but with 74.9% correct answers for object RCs with pronouns): in proportions there would seem to be no interaction, but in logit space there would be one (granted sufficiently small standard errors).

At this point, one may ask whether there are any better transformations that would allow us to continue to use ANOVA for CDA. Several such transformations have been proposed, the most well-known being the empirical logit (first proposed by Haldane, 1955, but often attributed to Cox, 1970). The idea behind such transformations is to stay as close as possible to the actual logit transformation while avoiding its negative and positive infinity values for proportions of 0 and 1, respectively (for an empirical comparison of different logit estimates, see Gart and Zweifel, 1967). Indeed, appropriate transformations combined with appropriate weighing of cases mostly avoid the problems of ANOVA described above (for weighted linear regression that deals with heterogeneous variances, see McCullagh and Nelder, 1989). However, it is important to note that even these transformations are still ad-hoc in nature (which transformation works best depends on the actual sample the researcher is investigating, Gart & Zweifel, 1967). Transformations for categorical data were originally developed because they provided a computationally cheap approximation of the more adequate logistic regression –approximations that are no longer necessary.

This leaves one potential argument for the use of ANOVA (with transformations) for CDA: the fact that ordinary logit models provide no direct way to model random subject and item effects. The lack of random effect modeling is problematic as repeated measures on the subject or item in our sample constitute violations of the assumption that all observations in our data set are independent of one another. Data from the same subject or item is often referred to as a cluster. Analyses that ignore clusters produce invalid standard errors and therefore lead to unreliable results. Next I show that mixedlogit models address this problem (other methods include separate logistic regressions for each subject/item, see Lorch and Meyers, 1990, or bootstrap sampling with random cluster replacement, see Feng et al., 1996).

Mixed logit models

Mixed logit models are a type of Generalized Linear Mixed Model (Breslow & Clayton, 1993; Lindstrom & Bates, 1990; for a formal introduction, see Agresti, 2002). Mixed Models with different link functions have been developed for a variety of underlying distributions. Mixed logit models are designed for binomially distributed outcomes.

Generalized Linear Mixed Models (Breslow & Clayton, 1993; for an introduction, see Agresti, 2002: Chapter 12) describe an outcome as the linear combination of fixed effects (described by x′β below) and conditional random effects associated with e.g. subjects and items (described by z′b). Just as x′ contains the values of the explanatory variables for the fixed effects (the predictors), z′ contains the values of the explanatory variables for the random effects (e.g. the subject and item IDs). The random effect vector b can be thought of as the coefficients for the random effects. It is characterized by a multivariate normal distribution, centered around 0 and with the variance-covariance matrix Σ (for details, see Agresti, 2002: 492). A mixed logit model then has the form (for linear mixed models, cf. Baayen et al., this issue):

$$\text{logit}(p)={\mathit{x}}^{\prime }\mathit{\beta }+{\mathit{z}}^{\prime }\mathit{b},\mathit{b}\sim N(0,{\sigma }^2\mathit{\sum })$$ (14)

Just as for ordinary logit models, the parameters of mixed logit models are fit to the data in such a way that the resulting model describes the data optimally. However, unlike for mixed linear models, there are no known analytic solutions for the exact optimization of mixed logit models’ data likelihood (Hausman & Harding, 2006:2; Bates, 2007: 29). Instead, either numerical simulations, such as Monte Carlo simulations, or analytic optimization of approximations of the true log likelihood, so called quasi-log-likelihoods, are used to find the optimal parameters. For larger data sets, Monte Carlo simulations are computationally unfeasible even for models with parameters. Optimization of quasi-log-likelihood is a computationally efficient alternative (see Agresti, 2002: 523–524). R’s lmer function (lme4 library, Bates & Sakar, 2007) uses Laplace approximation to maximize quasi-log-likelihood (Bates, 2007: 29). Laplace approximation “performs extremely well, both in terms of numerical accuracy and computational time” (Hausman & Harding, 2006: 19).

A case study using mixed logit models

The model formula is specified in (15), where the term in parentheses describes the random subject effects for the intercept, the effects of RC and NP type, and their interaction. Random effects are assumed to be normally distributed (in log-odds space) around a mean of zero. The only parameter the model fits for the random effects is their variance (see also Baayen et al., this issue; for details on the implementation, see Bates & Sakar, 2007). The random intercept captures potential differences in children’s base performance. The other random effects capture potential differences between children in terms of how they are affected by the manipulations.

$$\text{Correct}\sim 1+\text{RCtype}\ast \text{NPtype}+(1+\text{RCtype}\ast \text{NPtype}\mid \text{child})$$ (15)

The estimated fixed effects are summarized in Table 5. The number of observations and the quasi-log-likelihood of the model are given in the table’s caption. The estimated variances of the random effects are summarized in Table 6.

Table 5.

Summary of the fixed effects in the mixed logit model (N= 696; log-likelihood= −256.2)

Predictor	Coefficient	SE	Wald Z	P
Intercept	0.84	(0.203)	4.17	<0.001
RC type=subject RC	1.82	(0.365)	4.97	<0.001
NP type=pronoun	1.05	(0.288)	3.66	<0.001
Interaction=subject RC & pronoun	0.59	(0.580)	1.02	>0.3

Table 6.

Summary of random subject effects and correlations in the mixed logit model

		Correlation with random effect for
Random subject effect	s2	Intercept	RC type	NP type
Intercept	0.283
RC type=subject RC	0.645	0.625
NP type=pronoun	0.010	0.800	0.459
Interaction=subject RC & pronoun	0.221	0.800	0.459	1.000

In sum, a mixed logit model analysis of the data from Arnon (submitted) confirms the results from the ordinary logit model presented above. Even after controlling for random subject effects, the interaction between RC type and NP type is not significant. Note that the total correlation between the random interaction and effect of NP type for subjects in Table 6 suggests that the model has been overparameterized (cf. Baayen et al., this issue) – one of the two random effects is redundant. I get back to this shortly, when I show that we can further simplify the model.

Additional advantages of mixed logit models

Mixed logit models combine all the advantages of ordinary logit models with the ability to model random effects, but that’s not all. Mixed logit models do not make the frequently unjustified assumption of the homogeneity of variances. Also, the R implementation of mixed logit models used here (lmer) actually maximizes penalized quasi-log-likelihood (Bates, 2007: 29). Fitting a model that is optimal in terms of penalized likelihood rather than absolute likelihoods reduces the chance that the model will be overfitted to the sample. Overfitting is a potential problem for any statistical model (including ANOVA), because it makes a model less likely to generalize to the entire population (Agresti, 2002: 524). Penalization is thus a welcome feature of mixed logit models.

Another crucial advantage of mixed logit models over ANOVA for CDA is their greater power. That is, mixed logit models are more likely to detect true effects. Simulations show that lmer’s quasi-likelihood optimization outperforms ANOVA in terms of accurately estimating effect sizes and standard errors (Dixon, this issue). The greater power of mixed logit models may in part depend on the method used to approximate quasi-likelihood (Dixon’s results are based on Laplace approximation, implemented in lmer; even better approximations are under development, Bates & Sakar, 2007).

Another advantage of mixed models is that they allow us to test rather than to stipulate whether a hypothesized random effect should be included in the model. The question of whether or to what extent random subject and items effects (especially the latter) are actually necessary has been the target of an ongoing debate (Clark, 1974; Raaijmakers et al., 1999, a.o.). As Baayen et al. (this issue) demonstrate, mixed models can be used to test a hypothesized random effect. The test follows the same logic that was used above to test fixed effects: we simply compare the likelihood of the model with and the model without the random effect. Before I illustrate this for the mixed logit model from Table 5 and 6, a word of caution is in order. Comparisons of models via quasi-log-likelihood can be problematic, since quasi-likelihood are approximations (see above). This problem is likely to become less of an issue as the employed approximations become better (for discussion, see Bates & Sakar, 2007). In any case, we can use quasi-log-likelihood comparisons between models to get an idea of how much evidence there is for a hypothesized random effect.

As mentioned above, the correlation between the random subject effects in Table 6 shows that some of the random effects are redundant. Indeed, model comparisons suggest that neither the random effect for the interaction nor the random effect for NP type is justified. The quasi-log-likelihood decreases only minimally (from −256.8 to −258.5) when these two random effects are removed. A revised mixed logit model without random effects for NP type and the interaction is specified in (16). Table 7 and Table 8 give the updated results.

Table 7.

Summary of the fixed effects in the mixed logit model (N= 696; log-likelihood= −256.8)

Predictor	Coefficient	SE	Wald Z	P
Intercept	0.86	(0.212)	3.99	<0.001
RC type=subject RC	1.90	(0.380)	5.01	<0.001
NP type=pronoun	0.96	(0.278)	3.44	<0.001
Interaction=subject RC & pronoun	0.10	(0.544)	0.18	>0.8

Table 8.

Summary of random subject effects and correlations in the mixed logit model

		Correlation with random effect for
Random subject effect	s2	Intercept	RC type	NP type
Intercept	0.399
RC type=subject RC	0.744	0.629

$$\text{Correct}\sim 1+\text{RCtype}\ast \text{NPtype}+(1+\text{RCtype}\mid \text{child})$$ (16)

Note that most fixed effect coefficients have not changed much – neither compared to the full mixed logit model in (15), nor compared to the ordinary logit model in (13). In all models the main effects are significant but the interaction is not. Only the coefficient of RC type differs between the current mixed logit model and the ordinary logit model: it is quite a bit larger in the current model, but note that the standard error has also gone up. Wald’s Z for RC type does not differ much between the two models. In summary, if there are random subject effects associated with NP type or the interaction of RC and NP type (e.g. if children in the sample differ in terms of how they react to NP type), they would seem to be subtle.

Finally, mixed logit models inherit yet another advantage from the fact that they are a type of generalized linear mixed model. They allow us to conduct one combined analysis for many independent random effects. For example, we could include random intercepts for both subjects and items in the model:

$$\text{Correct}\sim 1+\text{RCtype}\ast \text{NPtype}+(1+\text{RCtype}\mid \text{child})+(1\mid \text{item)}$$ (17)

If a fixed effect is significant in such a model, this means it is significant after the variance associated with subject and items is simultaneously controlled for. In other words, mixed logit models can combine F1 and F2 analysis (for more detail and further examples for linear mixed models, see Baayen et al., this issue). Here only a random intercept (rather than random slopes for RC type, etc.) is included for items, because all further random effects are highly correlated with the random intercept (rs > 0.8) and hence unnecessary. The resulting model is summarized in Table 9 and Table 10. The minimal change in the quasi-log-likelihood, and the small estimates for the item variance, suggest that item differences do not account for much of the variance. Note that despite the fact that two items had missing cells and had to be excluded from the ANOVA, the current model uses all 8 items and 24 subjects in Arnon’s data.

Table 9.

Summary of the fixed effects in the mixed logit model (N= 696; log-likelihood= −256.0)

Predictor	Coefficient	SE	Wald Z	P
Intercept	0.85	(0.244)	3.49	<0.001
RC type=subject RC	1.97	(0.385)	5.11	<0.001
NP type=pronoun	0.99	(0.283)	3.49	<0.001
Interaction=subject RC & pronoun	0.07	(0.550)	0.13	>0.8

Table 10.

Summary of random subject and item effects and correlations in the mixed logit model

		Correlation with random effect for
Random effect	s2	Intercept	RC type	NP type
Subject intercept	0.420
Subject RC type=subject RC	0.770	0.620
Item intercept	0.086

Combining subject and item analyses into one unified model is efficient and conceptually desirable (cf. Clark, 1973). Note that, in principle, mixed models are even compatible with random effects beyond subject and item effects (e.g. if the children spoke different dialects and we hypothesized that this matters, we could include a random effect for dialect).

Conclusions

I have summarized arguments against the use of ANOVA over proportions of categorical outcomes. Such an analysis – regardless of whether the proportional data are arcsine-square-root transformed – can lead to spurious results. With the advent of mixed logit models, the last remaining valid excuse for ANOVA over categorical data (the inability of ordinary logit models to model random effects) no longer applies. Mixed logit models combine the strengths of logistic regression with random effects, while inheriting a variety of advantages from regression models. Most crucially, mixed models avoid spurious effects and have more power (Dixon, this issue). Finally, they form part of the generalized linear mixed model framework that provides a common language for analysis of many different types of outcomes.

Table 3.

Summary of the ANOVA results over untransformed data

	Subject analysis		Item analysis		Combined
	F1(1,23)	P	F2(1,5)	P	minF(1,10)	P
RC type	24.2	<0.01	10.2	<0.03	7.2	<0.03
NP type	16.1	<0.01	19.7	<0.01	8.9	<0.01
Interaction	9.7	<0.01	12.6	<0.02	5.5	<0.04