Causal Effect Models for Realistic Individualized Treatment and Intention to Treat Rules

Abstract

Marginal structural models (MSM) are an important class of models in causal inference. Given a longitudinal data structure observed on a sample of n independent and identically distributed experimental units, MSM model the counterfactual outcome distribution corresponding with a static treatment intervention, conditional on user-supplied baseline covariates. Identification of a static treatment regimen-specific outcome distribution based on observational data requires, beyond the standard sequential randomization assumption, the assumption that each experimental unit has positive probability of following the static treatment regimen. The latter assumption is called the experimental treatment assignment (ETA) assumption, and is parameter-specific. In many studies the ETA is violated because some of the static treatment interventions to be compared cannot be followed by all experimental units, due either to baseline characteristics or to the occurrence of certain events over time. For example, the development of adverse effects or contraindications can force a subject to stop an assigned treatment regimen.

In this article we propose causal effect models for a user-supplied set of realistic individualized treatment rules. Realistic individualized treatment rules are defined as treatment rules which always map into the set of possible treatment options. Thus, causal effect models for realistic treatment rules do not rely on the ETA assumption and are fully identifiable from the data. Further, these models can be chosen to generalize marginal structural models for static treatment interventions. The estimating function methodology of Robins and Rotnitzky (1992) (analogue to its application in Murphy, et. al. (2001) for a single treatment rule) provides us with the corresponding locally efficient double robust inverse probability of treatment weighted estimator.

In addition, we define causal effect models for “intention-to-treat” regimens. The proposed intention-to-treat interventions enforce a static intervention until the time point at which the next treatment does not belong to the set of possible treatment options, at which point the intervention is stopped. We provide locally efficient estimators of such intention-to-treat causal effects.

1 Introduction

A wide range of statistical tools are available to estimate the causal effects of static treatment interventions. The identifiability of such effects relies on the assumption that treatment assignment in the observed data is not based deterministically on a subject's past (the assumption of experimental treatment assignment, or ETA). However, in practical applications the full set of treatment options is often not available to all individuals. Moreover, when the treatment of interest is assigned longitudinally over time, subjects for whom a given treatment regimen was initially possible may develop conditions that reduce their set of future treatment options. Common occurrences such as these result in violation of the ETA assumption, potentially causing considerable bias in estimators of the causal treatment effect.

In this article we introduce two new classes of causal models that address this pressing challenge to practical data analysis. These classes of causal models are indexed by the following two types of intervention: 1) realistic treatment rules; and 2) intention-to-treat interventions. By definition, both types of intervention assign treatment at each time point only from among those treatments which are possible given a subject's past. We further introduce two types of causal models indexed by realistic individualized treatment rules. The first type estimates the causal effects of a user-supplied set of individualized treatment rules (or dynamic treatment regimes), and can thus be used to identify the optimal rule from among this user-supplied set. The second type estimates the causal effects of realistic rules indexed by static treatment regimens; the parameter estimated is the causal effect of remaining on a static treatment regimen for only as long as such a static regimen is possible. Similarly, causal models for intention-to-treat interventions estimate the effect of remaining on a static treatment regimen only to the extent possible given a subject's covariates. As we explain below, the difference between intention-to-treat and realistic rules lies in the type of intervention that is assigned after the initial static regimen becomes impossible.

By defining a specific type of treatment intervention, the causal parameters indexed by both realistic treatment rules and intention-to-treat interventions avoid violation of the ETA assumption. As a result, the causal effects discussed in this article are fully identifiable based on the data. The article provides a detailed interpretation of the causal effects indexed these different types of interventions, using both the formal counterfactual framework and an example drawn from the treatment of HIV. The article further develops inverse probability weighted, likelihood-based, and double robust estimators of these causal effects. The estimation of causal effects indexed by a user-supplied set of realistic treatment rules is illustrated using a data analysis based on the HIV example.

This introduction begins by defining the data structure that underlies the causal parameters and corresponding estimators developed in the article. The causal effect of a static treatment and its relation to the ETA assumption is then reviewed. Next, we introduce our first class of causal models, indexed by realistic treatment rules. We then introduce the intention-to-treat intervention and corresponding causal effect. These three types of causal effect (ie. indexed by a static intervention, realistic rule, and intention-to-treat intervention) are compared using the HIV example. We provide a general road map to the rest of the article, and review the relevant literature.

1.1 Data structure

Consider a data generating experiment in which the experimental unit results in the following time-ordered sequential data structure

$$O=\left(L\left(0\right),A\left(0\right),L\left(1\right),A\left(1\right),\dots ,L\left(T\right),A\left(T\right),L\left(T+1\right)\right),$$

where A(j) denotes a treatment assignment at time j, L(j) denotes all variables measured on the experimental unit after A(j−1) and before A(j), and T+1 is a fixed or random end-point such as a survival time. We assume that T+1 ≤ τ+1 with probability 1 for a fixed τ. Suppose we observe n independently and identically distributed copies O₁, …, O_n of O. For simplicity, throughout this article, we will treat all random variables as discrete, but all formulas have natural continuous analogues.

We let R(t) ≡ I(T ≤ t) be a component of L(t), and we truncate the A and L process at T so that A(t) = A(min(t, T)), L(t) = L(min(t, T + 1)). In this manner, we can now also represent the observed longitudinal data structure O on the experimental unit as a vector of fixed length,

$$O=\left(L\left(0\right),A\left(0\right),L\left(1\right),A\left(1\right),\dots ,L\left(\tau \right),A\left(\tau \right),L\left(\tau +1\right)\right),$$

where we remind the reader that after time T + 1 the data structure becomes degenerate in the sense that A(T + j) = A(T), and L(T + 1 + j) = L(T + 1) for j = 1, 2, ….

Let Y be a real-valued function of L, which will denote the outcome of interest. For example, Y = T + 1 might be the survival time T + 1, or it might be an outcome Y(τ + 1) of a time-dependent process Y(·) measured at a fixed time τ + 1. We use the notation L̄(t) ≡ (L(0), …, L(t)), but the complete covariate/outcome and treatment process are also denoted with L = L̄(τ + 1) and A = Ā(τ).

The time-dependent treatment options process

Let (t) be the support of the marginal random variable Ā(t) ≡ (A(0), …, A(t)), t = 0, …, τ. Let (t) represent a set of possible treatment options for A(t), given an experimental unit with history Ā(t − 1), L̄(t), in the sense that

$$g_0\left(a\left(t\right)|\overline{L}\left(t\right),\overline{A}\left(t-1\right)\right)\equiv Pr\left(A\left(t\right)=a\left(t\right)|\overline{L}\left(t\right),\overline{A}\left(t-1\right)\right)>0\text{for}a\left(t\right)\in \mathcal{D}\left(t\right).$$

It is assumed that (t) is a function of L(t): e.g., (t) could be one of the components of L(t).

1.2 The causal effect of a static treatment intervention

The current literature on causal inference provides models and corresponding methods for the estimation of static treatment effects. Typically, the data of interest are based on sampling subjects from a particular population and recording the treatment assignments, co-variables, and outcomes of interest for these subjects over time. Marginal structural models (MSM), introduced by Robins (e.g., Robins (1999), Robins (2000)), provide a powerful tool for causal inference in the context of such longitudinal data structures, and address many of the limitations of the traditional regression approach. MSM model the dependence of the distribution of treatment regimen-specific counterfactual outcomes (or outcome processes) on the treatment regimen. In other words, MSM model the population distribution of the outcome process that would be observed if all members of the population were to follow a particular static treatment regimen. The causal effect of a change in treatment is estimated as the difference in the population distribution of the outcome under the two treatment regimens being compared. For example, marginal structural models model as a function of ā(t) the mean outcome under an intervention setting Ā(t) = ā(t) with probability 1, possibly conditional on user-supplied baseline covariates. Inverse Probability of Treatment Weighted (IPTW) estimators, locally efficient double robust IPTW (DR-IPTW) estimators, and likelihood-based estimators have been proposed by Robins and co-authors for the unknown causal parameters in the marginal structural model. van der Laan and Robins (2003) provide a comprehensive overview of the development of these methods, together with a review of the relevant literature.

Identification of the causal effects of static treatment interventions based on observational data relies on the standard sequential randomization assumption (SRA) on the treatment mechanism, otherwise known as the assumption that there are no unmeasured confounders. In addition, because these methods aim to produce the results of a trial in which static treatment interventions are randomly assigned and each subject is forced to fully comply with the assigned intervention, they further require that treatment in the observed data not be deterministically assigned at any time point based on a subject's observed past; this latter assumption is called the experimental treatment assignment (ETA) assumption. In most studies all static treatment interventions cannot be followed by all sampled subjects, due either to baseline characteristics or to the occurrence of certain events over time. For example, clinical progression may force a clinician to initiate treatment before an assigned time, or the development of serious adverse effects or a contraindication, such as pregnancy, may force a clinician to stop an assigned treatment regimen. In practice, the ETA assumption can be somewhat weakened, to say that treatment cannot be deterministically assigned in response to that subset of a subject's observed past which is sufficient for the SRA to hold; thus the development of a condition that forces a subject to stop an assigned therapy need not lead to an ETA violation if it is causally unrelated to the outcome of interest.

Violation of the ETA assumption, whether theoretical (i.e. due to the occurrence of events which make a given treatment impossible) or practical (i.e. due to finite sample size), is known to result in potentially extreme bias in the IPTW estimators of marginal structural model parameters. Further, when ETA is violated, both likelihood-based estimators and DR-IPTW estimators rely fully on model assumptions (beyond the SRA) which cannot be tested from the data (Neugebauer and van der Laan (2005b)). The use of stabilizing weights (Robins (1999)) can somewhat mitigate the problem of ETA violations, by weakening the assumption from the requirement that

$$\underset{\overline{a}\in \mathcal{A}}{\text{inf}}{g}_0\left(a\left(t\right)|\overline{A}\left(t-1\right),\overline{L}\left(t\right)\right)>0,t=0,\dots ,\tau$$

to the requirement that

$$\underset{\overline{a}\in \mathcal{A}}{\text{sup}}\frac{g\left(a\left(t\right)|V\right)}{g\left(a\left(t\right)|\overline{A}\left(t-1\right),\overline{L}\left(t\right)\right)}<\infty ,t=0,\dots ,\tau ,$$

where g₀(a(t)|Ā(t − 1), L̄) = P(A(t) = a(t)|Ā(t − 1), L̄(t)) is the true treatment mechanism, and V denotes any baseline covariates of interest included in the marginal structural model. In many applications, however, violation of the ETA assumption remains a significant problem.

In addition to the potentially serious bias in effect estimates caused by ETA violations, the fact that models for static treatment interventions and their corresponding estimates aim to reproduce the results of typically unrealistic randomized trials has been a source of philosophical criticism. Finally, even in settings where ETA violations of static treatment interventions do not occur, it is frequently of interest to estimate the causal effect of a dynamic rather than static treatment regimen. In other words, the researcher may be interested in the difference in mean outcome that would be observed between individuals randomized to receive different treatment strategies (or individualized treatment rules, in which treatment is changed in response to patient evolution), rather than different static regimens. In this article we propose a set of causal models and corresponding estimators that address these challenges.

1.3 Realistic individualized treatment rules

Lack of identifiability of the counterfactual distribution of the data under a static treatment intervention results from a non-zero probability of sampling an experimental unit for which the static intervention cannot occur. In this article we define realistic individualized treatment rules as rules which always assign treatments (in response to observed history) that fall in the set of possible treatment options. Causal effects comparing realistic individualized treatment rules are now identifiable from the observed data distribution.

Such a class of realistic individualized treatment rules can be user-defined. This approach is comparable to designing a randomized trial to compare realistic individualized treatment rules of interest. For example, the researcher may specify a priori a set of interesting rules which assign treatment over time by responding to patient covariates in a clinically realistic way, thus avoiding violations of the ETA assumption. Modeling the mean outcome for such a user-supplied class of realistic individualized treatment rules also yields a model for the optimal rule among the user-supplied class (i.e. by selecting the rule which maximizes or minimizes the mean outcome). The causal models for realistic treatment rules presented in this paper thus provide an alternative method for modelling and estimation of optimal dynamic treatment regimes from among a user-supplied set, based on a generalization of structural nested models (Robins (1989),Robins (1998), Robins (1999), Robins (1994)), as developed in (Murphy (2003), Robins (2003)).

It may not always be straightforward to propose such an interesting set of realistic individualized treatment rules. For example, the set of possible treatment options, given a subject's covariates ( (t)) may not be known or collected as part of the study. In such a case, then we propose to define the set of possible treatment rules by employing a stabilized version of the treatment mechanism:

$$\mathcal{D}\left(t\right)\equiv \{a\left(t\right):\frac{g_0\left(a\left(t\right)|V\right)}{g_0\left(a\left(t\right)|\overline{A}\left(t-1\right),\overline{L}\left(t\right)\right)}<\alpha <\text{inf}\},t=0,\dots ,\tau$$

for some α, and if the treatment mechanism g₀ is unknown, then one estimates this set by substitution of an estimator g_n of g₀.

In addition, it may be the case that the researcher is in fact interested in the effect of a static (rather than dynamic) treatment regimen, to the extent that subjects are realistically able to follow it. One option is to map a static treatment intervention into a corresponding realistic individualized treatment rule, in which the subject follows the assigned static treatment intervention for only as long as the assigned intervention remains possible. When the assigned regimen no longer falls within the set of possible treatment options for the subject (as a result of the subject's covariate history), then the subject is assigned a particular alternative treatment in the set of remaining treatment options (e.g., the one “closest” to the treatment assigned by the static intervention). Again, this new static regimen is applied until the subject is forced to switch again, and so on. In this manner, these individualized treatment rules are indexed by static treatment regimens, and provide natural realistic approximations of the intended static treatment intervention. Such rules correspond to randomized controlled trials that incorporate explicit rules for altering patients' randomized static treatment assignment in order, for example, to protect patient health.

Note that if the ETA assumption holds, so that the set of possible treatment options at time t can be chosen to be equal to the set of all marginally possible treatments at time t, then the realistic individualized treatment rules indexed by static interventions reduce to the class of static treatment interventions, and thus the causal model for such realistic rules reduces to a standard marginal structural model for static treatments. As a consequence, the realistic causal models introduced in this article generalize causal effect models for static treatment interventions (MSM's) that rely on the ETA assumption to causal effect models for individualized treatment rules, indexed by static interventions, that also apply when the ETA assumption is violated.

1.4 Intention-to-treat interventions

The previous section introduced a new class of causal models for realistic individualized treatment rules. These rules assign a treatment at each time point, based on a subject's current covariates, that always falls within the set of possible treatment options for that subject; the rules may be, but are not necessarily, indexed by static treatment regimens. In this section we introduce a related class of causal models that estimate the effects of “intention-to-treat” interventions indexed by static treatment regimens. As with realistic treatment rules indexed by static regimens, intention-to-treat interventions enforce the assigned static intervention up till the time point t at which the next prescribed treatment does not fall in the set of possible treatment options (t + 1). If a realistic treatment rule were being applied, at this point a pre-specified alternative regimen would be assigned. In contrast, in an intention-to-treat intervention, when the assigned regimen is no longer possible then all intervention on that subject is stopped.

The name “intention-to-treat” is based on the loose association of this type of intervention with the practice of analyzing the results of randomized controlled trials based on treatment assignment, rather than on the treatment that subjects were observed to follow. In other words, even though in practice some individuals may find it impossible to follow the treatment arm to which they are randomly assigned, conventional clinical trial analysis treats these individuals as if they had followed their assigned treatment. A key difference between this classic definition of “intention-to-treat” and the intention-to-treat parameter described in this paper is that the latter assumes that the set of possible treatment options for a subject is fully determined given a subject's past, whereas in the context of a controlled trial, failure to adhere to assigned treatment may occur even in the absence of conditions which make the assigned treatment impossible.

The causal effects of these intention-to-treat interventions indexed by static treatment regimens are now fully identifiable from the data. As a consequence, as with realistic treatment rules, we can develop locally efficient estimators of these causal effects without the need to assume the often unrealistic ETA assumption. As with realistic treatment rules, this model for intention-to-treat interventions indexed by static treatments generalizes marginal structural models for static interventions, which depend on the ETA assumption, to causal models for corresponding intention-to-treat interventions that reduce to marginal structural models if the ETA assumption holds.

1.5 Example

Suppose that we sample subjects from an HIV-infected population receiving antiretroviral therapy, who at time 0 experience a persistent rebound in plasma HIV RNA level as a result of viral resistance to their prescribed drug regimens. Suppose that Y (8) is the CD4 T cell count measured 8 months after rebound and that the measurements L(t), t = 0, …, 8 include plasma HIV RNA level (viral load), CD4 T cell count, and other time-dependent characteristics of interest. Let (A(t), t = 0, …, 7) be the indicator process which equals 1 up till the time point at which a subject modifies his or her antiretroviral regimen, and then jumps to 0. One might now be interested in estimation of the causal effect of time until treatment modification on CD4 T cell count at 8 months, based on this sample of patients experiencing a rebound of the virus at time 0. Specifically, we refer to Petersen et al. (2005) for a description of the SCOPE cohort of HIV-infected patients, and of the interest and relevance of the “when to switch?” question in the HIV-AIDS research community, with relevant references. In particular, it has been observed that a drug can still have a significant beneficial effect on a resistant virus by making it less lethal and/or fit, so that an increase in viral load does not necessarily imply a decrease in CD4 T cell count.

Consideration of hypothetical randomized trials can be used to illustrate how the three types of causal parameters described in this article compare with the effect of a static treatment regimen as typically estimated using marginal structural models.

Estimating the effect of a static modification time

First, consider a trial in which each subject is randomly assigned a time at which to modify treatment. Note that this is a randomized trial of a static intervention, in that subjects are assigned a modification time at baseline and this time is not altered in response to the condition of the patient or virus. In order to estimate the mean outcome in the trial arm assigned to modify treatment at time t, one would need that every subject in this group (or at least a representative subgroup of these subjects) is able to fully comply with the assigned modification time t. However, suppose that some subjects in the population develop an opportunistic infection or adverse drug effects before time t, and as a result are unable to remain on their baseline regimen. Such patients cannot comply with the assigned modification time. Assuming that the measurement of such deterministic events is necessary to ensure sequential randomization, or put another way, assuming that individuals who are unable to comply with their assigned modification time t are not representative of all subjects assigned to modify at time t with respect to their counterfactual outcome, the causal effect of time until treatment modification is not identifiable from the data. As a consequence, any of the candidate estimators of a marginal structural model modeling the causal effect of time until treatment modification on mean CD4 T cell count at 8 months suffer from potentially serious bias. Further, one might argue that such a causal effect is not in fact of primary interest, as it corresponds with an intervention that would never be employed in practice.

Estimating the effect of a realistic rule/intention-to-treat intervention indexed by a static modification time

Alternatively, consider a trial in which each subject is assigned a realistic treatment rule indexed by a random modification time t. A subject in such a trial remains on his or her original therapy until the minimum of time t and the first time point at which an event occurs which forces him or her to modify therapy. Under ETA (i.e. the absence of deterministic events that force treatment modification), these realistic treatment rules are identical to the static modification regimens described in the prior example. However, unlike the effects of the static modification regimens, the causal effects of the realistic rules are still interpretable and identifiable if ETA is violated. In this case, the realistic treatment rule indexed by the static modification time t is identical to the “intention-to-modify at time t” intervention, due to the fact that the treatment process A(t) is binary.

Estimating the effect of a user-supplied set of realistic rules for modifying therapy

The prior example describes estimation of the effect of realistic treatment rules indexed by static modification times. In clinical practice, however, the effects of a set of dynamic strategies, which assign a patient a rule for when to modify therapy based on (e.g.) the evolution of CD4 T cell count over time, are likely to be of greater clinical interest than the effects of set modification times assigned at baseline (even if such static modification times are allowed to be changed if they become impossible). With this motivation, consider a third clinical trial, in which subjects are assigned to modify treatment only when their CD4 T cell count falls below a certain randomly assigned threshold θ. Again, such a user-supplied set of treatment rules should be realistic. This implies that either any patient characteristics that make the assigned threshold impossible to comply with must not be required for the SRA to hold, or such covariates should be incorporated into the treatment rules considered. For example, we could now define the following user-supplied set of realistic individualized treatment rules indexed by a threshold θ: “modify therapy if CD4 T cell count drops below θ or if an event occurs that forces modification”.

1.6 Organization

This article introduces causal models for realistic individualized treatment rules and intention-to-treat interventions, and develops corresponding estimators. In Section 2 the causal model for realistic (and thereby identifiable) individualized treatment rules is presented, and the corresponding locally efficient double robust inverse probability of treatment weighted estimator is derived. This model and methodology for the special (but common) case in which the treatment is assigned at a single point in time in response to baseline covariates is provided in Appendix A. In Section 3 we present a data analysis, based on the example presented above, that illustrates this model and methodology. In the analysis we estimate the causal effect of a user-supplied set of realistic rules for modifying antiretroviral therapy, based on a subject's current and baseline CD4 T cell counts.

The remainder of the article focuses on causal effect models for intention-to-treat regimens. Specifically, in Section 4 we define a causal inference framework which allows us to define the causal effects of a range of interventions on the data generating distribution of the data structure O, and, in particular, allows us to define our wished non-parametric identifiable intention-to-treat causal effect parameter. This framework represents a set of assumptions which do not put any restrictions on the data generating distribution, but are essential for the definition and identification of the wished causal effect of an intention-to-treat regimen from the data generating distribution. Given the causal inference framework, we define the intention-to-treat counterfactual processes, and corresponding models for the conditional mean of the intention-to-treat counterfactual outcome.

In Section 5 we present the intention-to-treat causal effect model for the point treatment data structure (W = L(0), A, Y). We further present the corresponding efficient Double Robust Inverse Probability of Treatment Weighted (DR-IPTW) estimating function and the locally efficient double robust estimator. The latter estimator (derived in Appendix B) is locally efficient in the sense that its consistency (and asymptotic linearity) relies on either correct specification of the treatment mechanism P(A = a | W) or the regression E(Y | A, W), and it is efficient if both are correctly specified. We also present the likelihood-based estimator and the simpler IPTW estimator, which is a special case of the DR-IPTW estimator. The presentation of the estimating function-based estimators of the intention-to-treat causal parameter for the general longitudinal data structure is deferred to Appendices C-D, since this work happens to be quite involved.

Section 6 is devoted to a discussion.

1.7 Some immediately relevant literature

Based on personal communication we became aware of completely independent unpublished work on individualized treatment rules by Andrea Rotnitzky, who presented similar/overlapping ideas in a November 2005 NIH grant proposal titled “Methods for Analysis with Missing and/or Censored Data and for Causal Inference”. Specifically, in the aforementioned grant, Rotnitzky proposed the consideration of parametric and semiparametric models for the marginal means of counterfactual variables under a class of dynamic treatment regimes as a device for estimating the optimal treatment regime in the class. She also indicated how doubly-robust locally efficient Inverse Probability Weighted estimators of the model parameters can be constructed. These estimators essentially agree with those derived at the end of Section 2 of the present paper. Finally, she also noted that an important application of the methodology was to estimate the optimal CD4 T cell count level at which to either start or switch antiretroviral therapies, much along the lines of the example presented in Section 3 here. We were not aware of this work, but certainly wish to acknowledge her independent and overlapping original work in this area of research.

The method of inverse probability of treatment weighting in order to compare dynamic treatment regimens and their corresponding double robust estimators was presented in Murphy et al. (2001), and Hernan et al. (2006), and, as a method, goes back to the general Inverse Probability of Censoring Weighting as presented in Robins and Rotnitzky (1992) and Robins (1993). Murphy et al. (2001) proposes a model for a single dynamic treatment regimen conditional on baseline covariates, while the current article generalizes that to a model for a user-supplied class of dynamic treatment regimens. The introduction of dynamic treatment regimens, and the notion and idea of (what we call) realistic individualized treatment rules goes back to Robins (1986) who discusses such regimens in the context of a study aiming to estimate the effects of exposure of chemicals on employees, noting that static regimens cannot be identified since the subjects can only be exposed if at work. Finally, we also wish to point out the relation between the statistical framework/assumptions as we presented for defining and identifying the causal effects of the intention-to-treat regimens and the work in Robins (1986) (specifically, pages 1422-1423 in Robins (1986)).

2 Causal effect models for realistic individualized treatment rules

In this section we present a causal effect model for realistic individualized treatment interventions, and present the corresponding locally efficient double robust inverse probability of treatment weighted estimator following the general estimating function methodology of Robins and Rotnitzky (1992) and van der Laan and Robins (2003).

2.1 The counterfactual framework for realistic individualized treatment rules

We use the statistical framework of counterfactuals on which marginal structural models are based. This framework was introduced in Neyman (1990), extended to causal effects of time-independent treatments by Rubin (1978), and further extended to a formal theory of causal inference for direct and indirect effects of time-varying treatments from experimental and observational longitudinal studies by Robins (1986, 1987). This causal framework for treatment interventions ā assumes the existence of counterfactuals indexed by static treatment interventions ā, the corresponding link between the observed data and these counterfactuals (i.e., consistency assumption), and the sequential randomization assumption (SRA). By applying the result in (Gill and Robins (2001), Yu and van der Laan (2002)), it follows that, by construction, assuming the consistency and randomization assumptions puts no restriction on the data generating distribution. These assumptions do, however, allow us to define the causal parameter of interest as a parameter of the data generating distribution.

As defined in Robins (1986), an individualized treatment rule d is a function (d(0), …, d(τ)), where the j-th function, (Ā(j − 1), L̄(j)) → d(j)(Ā(j − 1), L̄(j)), maps the history at time j into a treatment choice for A(j), j = 0, …, τ.

Consistency assumption

We define the full data as the collection X = (L_ā : ā ∈ ) of counterfactual processes L_ā indexed by static treatment interventions varying over the support of the marginal distribution of Ā = (A(0), …, A(τ)). We also assume the temporal ordering assumption, L_ā(j) = L_{ā(j − 1)}(j), and the consistency assumption stating that O = (Ā, L_Ā) or, as a chronological data structure:

$$O=(L\left(0\right),A\left(0\right),L_{A(0)}\left(1\right),A\left(1\right),\dots ,L_{\overline{A}(\tau -1)}\left(\tau \right),A\left(\tau \right),L_{\overline{A}(\tau )}\left(\tau +1\right).$$

Dynamic treatment counterfactuals

Given this standard consistency assumption, for any rule d, the counterfactual L_d indexed by a dynamic treatment d can be defined as L_ā with ā = ā(X, d) defined as the following function of X and the rule d: a(0) = d(0)(L(0)), a(1) = d(1)(a(0), L̄_a(0)(1)), and, in general, a(j) = d(j)(ā(j − 1), L̄_{ā(j − 1)}(j)), j = 0, …, τ. Thus, given the existence of the random variable X defined as the collection of static treatment-specific counterfactuals, one can also define the dynamic treatment regimen-specific counterfactuals L_d ≡ L_ā(X,d) as a measurable function of X and the rule d. We recall that the treatment options process t → (t) is included in the t → L(t) process, so that _d denotes the d-specific treatment options process for the experimental unit.

It is also of interest to note that, for each experimental unit, the rule d maps into a unique treatment regimen ā(d, X). However, a static treatment intervention ā can correspond with various individualized treatment rules d: e.g. L_ā = L_d1 = L_d2 for two different rules d₁ and d₂ in a set of dynamic regimens *. If an experimental unit follows rule d starting at time 0, then it follows that d_j is, in fact, only a function of L̄_d(j). For the sake of notational convenience, in that case we will use the notation L̄_d(j) → d(j) L̄_d(j)).

Sequential randomization assumption

We will assume the (strong) sequential randomization assumption: i.e., for each j = 0, …, τ, A(j) is independent of X, given L̄(j), Ā(j − 1). The data generating distribution of O will be denoted with P₀ = P_FX0,g0, and is indexed by the distribution F_X0 of X and the conditional probability distribution, g₀(· | X), of Ā, given X.

Realistic dynamic treatment assumption

Let * be a set of dynamic treatment regimens so that for any d ∈ * we have

$$P(d\left(j\right)({\overline{L}}_d\left(j\right))\in {\mathcal{D}}_d\left(j\right),j=0,\dots ,\tau )=1.$$ (1)

That is, for each possible history at time j under a dynamic treatment regimen d ∈ *, the next treatment assigned by this individualized treatment rule d at time j + 1 is an element of the set _d(j + 1) of possible treatment options. This condition on the rule d guarantees that the distribution of L_d is identifiable by the G-computation formula (Robins (1999), Gill and Robins (2001), Yu and van der Laan (2002)):

$$P\left(L_d=l\right)=\prod _{j=0}^{\tau +1}P\left(L\left(j\right)=l\left(j\right)|\overline{A}\left(j-1\right)=\overline{d}\left(j\right)\left(l\right),\overline{L}\left(j-1\right)=\overline{l}\left(j-1\right)\right).$$

where we defined d̄(j)(l) ≡ (d(1)(l(0)), …, d(j − 1)(l̄(j − 1)).

Realistic individualized treatment rules indexed by static treatment regimens

Let C_ā be the counterfactual stopping time defined as

$$C_{\overline{a}}\equiv \text{min}\left\{t\in \left\{-1,0,\dots ,\tau \right\}:a\left(t+1\right)\notin {\mathcal{D}}_{\overline{a}}\left(t+1\right)\text{or}t=\tau \right\}.$$

Given a static treatment regimen ā, one can define a dynamic treatment regimen as one which follows the static treatment regimen ā until time point t = C_ā at which a(t + 1) ∉ (t + 1) or t = τ, and subsequently one proceeds assigning treatments in the set of treatment options according to a particular user-supplied rule.

For example, the following construction describes such a set of dynamic treatment regimens indexed by static treatment interventions ā. Suppose that the maximal set of treatment options is in the sense that (j) ⊂ for all j = 0, …, τ, with probability 1. In addition, define a dissimilarity measure between any pair of elements in so that for each s ∈ , we can identify the element in (j) closest to s. We could now define the following individualized treatment rule indexed by a static treatment regimen ā: 1) follow static treatment regimen ā until time point t = C_ā at which a(t + 1) ∉ (t + 1) or t = τ; 2) if t < τ (that is, it was not possible to fully comply with the static regimen ā), then set the next treatment equal to the element in (t + 1) closest to a(t + 1); 3) keep this treatment constant until the time point at which the treatment is not an element of the set of treatment options so that a switch of treatment is required, or until the endpoint τ; 4) if the treatment needs to be switched before τ, then switch again to the element in the set of treatment options closest to the current treatment; 4) continue in this manner until one reaches the end point τ. Notice that this defines an individualized treatment rule as a deterministic function of a static intervention ā. Therefore, we can denote this set of dynamic treatment rules with d_ā, ā ∈ .

2.2 Causal effects of realistic individualized treatment rules

The above standard causal inference assumptions put no restrictions on the data generating distribution and thereby cannot be tested based on the data. In particular, the model for the distribution of the data implied by the above assumptions is still unspecified/nonparametric.

We define the parameter of interest on this nonparametric model as the conditional mean of Y_d, given a subset V of the baseline covariates L(0), for all d ∈ *. In order to deal with the curse of dimensionality, one can choose between two approaches. Firstly, one can assume a model

$$E_0(Y_d|V)=m(d,V|{\beta }_0)$$ (2)

for some parametrization (d, V) → m(d, V | β) indexed by a finite dimensional Euclidean parameter β. In this model β(F_X) is the parameter of interest, and β₀ = β(F_X0) is the true value of this parameter. For example, if d = d_ā is a deterministic function of a static treatment intervention, as in our example above, then we would have

$$E_0(Y_{d_{\overline{a}}}|V)=m(\overline{a},V|{\beta }_0).$$

Alternatively, if one believes that the model assumed on E(Y_d | V) is not realistic, then it might be sensible to define the parameter of interest as

$${\beta }_h(F_X)\equiv \text{arg}\underset{\beta }{\text{min}}\sum _{d,V}(E_{F_X}(Y_d|V)-m(d,V|\beta ){)}^{2}h(d,V).$$

If model (2) holds, then β_0h = β₀ for all h. One can map β(F_X0) into a corresponding optimal individualized treatment rule within each strata V:

$$d(F_{X0})\left(V\right)=\text{arg}\underset{d\in \mathcal{A}\ast }{\text{max}}m(d,V|{\beta }_0).$$

Note that the parameters β(F_X) and β_h(F_X) are parameters of F_X. As a consequence, we can apply the general estimating function methodology of Robins and Rotnitzky (1992) and van der Laan and Robins (2003), to obtain the class of all estimating functions, including the optimal DR-IPTW estimating function, which equals the efficient influence curve when evaluated at the true parameter values. This general estimating function methodology involves three steps: 1) identify the class of all full data estimating functions (formally, the space spanned by the gradients of the path-wise derivative of the parameter of interest, also called the orthogonal complement of the nuisance tangent space); 2) construct an inverse probability of treatment weighted class of estimating functions which are such that the conditional expectation, given X, maps into the class of full data estimating functions; and, 3) map this class of IPTW estimating functions into the double robust IPTW estimating functions by subtracting the projection on the tangent space spanned by all scores of the treatment mechanism under the sole model assumption SRA. For details, we refer to the original paper Robins and Rotnitzky (1992) which laid out this general approach for censored data models and to Chapters 1 and 2 of van der Laan and Robins (2003).

Firstly, we need to determine the class of full data estimating functions one would obtain in the full data model for X. It follows that this class of full data estimating functions is given by:

$$\left\{\sum _{d\in \mathcal{A}\ast }h(d,V)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_d-m(d,V|{\beta }_0)):h\right\}.$$

In the case that one defines the parameter of interest as

$${\beta }_h(F_X)\equiv \text{arg}\underset{\beta }{\text{min}}{\sum _{d,V}(E_{F_X}(Y_d|V)-m(d,V|\beta ))}^{2}h(d,V),$$

then the only full data estimating function is

$$\sum _{d\in \mathcal{A}\ast }h(d,V)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_d-m(d,V|{\beta }_0)).$$

We now need to find an IPTW estimating function which has the property that its conditional expectation, given X, maps into the class of full data estimating functions. As established in the following result, we can use

$$\begin{array}{l}{D}_{h,\text{IPTW}}(O|g_0,{\beta }_0)\\ =\sum _{d\in \mathcal{A}\ast }\frac{I\left(\overline{A}=d\left(\overline{L}\right)\right)}{g\left(\overline{A}|X\right)}h\left(d,V\right)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y-m(d,V|{\beta }_0)),\end{array}$$

where ā = d(L̄) is defined as

$$(a\left(0\right)=d_0\left(L\left(0\right)\right),a\left(1\right)=d\left(1\right)\left(a\left(0\right),\overline{L}\left(1\right)\right),\dots ,a\left(\tau \right)=\left(\overline{a}\left(\tau -1\right),\overline{L}\left(\tau \right)\right)).$$

Result 1 Assume that for all individualized treatment rules d ∈ *, we have

$$Pr\left(g\left(\overline{a}\left(X,d\right)|X\right)>0\right)=1,$$

where ā(X, d) is the treatment regimen followed by the experimental unit with full data counterfactuals X if the experimental unit follows rule d: a(0) = d(0)(L(0)), a(1) = d(1)(L̄_a(0)(1)), and, in general, a(j) = d(j)(L̄_{ā(j − 1)}(j)), j = 0, …, τ.

We have for all h

$$E(D_{h,\text{IPTW}}(O|g_0,{\beta }_0)|X)=\sum _{d\in \mathcal{A}\ast }h(d,V)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_d-m(d,V|{\beta }_0)).$$

As a consequence, if E(Y_d | V) = m(d, V | β₀), then

$$E_0{D}_{h,\text{IPTW}}(O|g_0,{\beta }_0)=0\text{for}\text{all}h,$$

and, we always have for all h

$$E_0{D}_{h,\text{IPTW}}(O|g_0,{\beta }_{h0})=0.$$

Proof. Because g(ā(d, X) | X) > 0, the conditional expectation E(D_h,IPTW(g₀, β₀) | X) equals

$$\begin{array}{l}{\sum }_{\overline{a}\in \mathcal{A}}{\sum }_{d\in \mathcal{A}\ast }I(\overline{a}=d({\overline{L}}_{\overline{a}}))h(d,V)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_{\overline{a}}-m(d,V|{\beta }_0))\hfill \\ ={\sum }_{d\in \mathcal{A}\ast }{\sum }_{\overline{a}\in \mathcal{A}}I(\overline{a}=d({\overline{L}}_{\overline{a}}))h(d,V)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_d-m(d,V|{\beta }_0)).\hfill \end{array}$$

Now, we note that ā = d(L̄_ā) is equivalent with the unique solution a(0) = d(L(0)), a(j) = d(L̄_ā(j−1)(j))(j), j = 1, …, τ. Thus, the inner Σ_ā∈A reduces to the single term h(d, V)d/dβ₀m(d, V | β₀)(Y_d − m(d, V | β₀)), so that the conditional expectation reduces to

$$\sum _{d\in \mathcal{A}\ast }h(d,V)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_d-m(d,V|{\beta }_0)),$$

which completes the proof.

Finally, we map this IPTW estimating function for β_h into the efficient estimating function by subtracting its projection on the tangent space of the treatment mechanism under SRA. The following result describes this double robust IPTW estimating function, and thereby the efficient influence curve. The proof of this result is a direct consequence of Theorem 1.3 and Theorem 1.6 in van der Laan and Robins (2003).

Result 2 The efficient influence curve of β_h in the (nonparametric) model for the data generating distribution P₀ at P₀ is given by −c(β_h0)⁻¹ D_h,DR(O | g₀, Q₀, β_h0), where

$$\begin{array}{r}\hfill D_{h,DR}(O|g_0,Q_0,{\beta }_{h0})=D_{h,\text{IPTW}}(O|g_0,{\beta }_0)-\sum _{t=0}^{\tau }\\ \hfill \left\{E_{g_0,Q_0}(D_{h,\text{IPTW}}(g_0,{\beta }_0)|\overline{A}(t),\overline{L}(t))-E_{g_0,Q_0}(D_{h,\text{IPTW}}(g_0,{\beta }_0)|\overline{A}(t-1),\overline{L}(t))\right\}\end{array}$$

and $c(\beta )\equiv \frac{d}{d\beta }{E}_0{D}_{h,DR}(O|g_0,Q_0,\beta )$. If E₀(Y_d | V) = m(d, V | β₀), then for all h

$$E_0{D}_{h,DR}(O|g,Q,{\beta }_0)=0\text{if}g=g_0\text{or}Q=Q_0.$$

In general, for all h,

$$E_0{D}_{h,DR}(O|g,Q,{\beta }_{h0})=0\text{if}g=g_0\text{or}Q=Q_0.$$

Inverse probability of treatment weighted and double robust locally efficient estimators

Given an estimator g_n of the treatment mechanism g₀, and a possibly data dependent index h_n, we define the IPTW estimator as the solution β_hn,IPTW of

$$0=\sum _{i=1}^n{D}_{h_n,\text{IPTW}}(O_i|g_n,\beta ).$$

Similarly, given an estimator (g_n, Q_n) of the nuisance parameter (g₀, Q₀), and a possibly data dependent index h_n, we define the double robust locally efficient estimator as the solution β_hn,DR of

$$0=\sum _{i=1}^n{D}_{h_n,DR}(O_i|g_n,Q_n,\beta ).$$

Under regularity conditions, the estimator β_hn,DR is consistent and asymptotically linear if either g_n converges to g₀ or Q_n converges to Q₀, and, if both nuisance parameters are consistently estimated, then β_hn,DR is an asymptotically efficient estimator of β_h0. Therefore we call such an estimator β_hn,DR locally efficient. In contrast, the consistency of β_hn,IPTW requires that g_n converges to g₀. For the formal statement for the asymptotics of the double robust estimator with the required regularity conditions, we refer to Theorem 2.4 and 2.5 in van der Laan and Robins (2003).

In order to avoid technicalities, for statistical inference we propose the bootstrap method which is known to be asymptotically valid under the same conditions required to establish the asymptotic linearity of the estimators β_hn,IPTW and β_hn,DR.

3 Data example: Realistic individualized rules for treatment modification in HIV-infected patients experiencing viral rebound

In this section we present the results of a data analysis based on the example described in subsection (1.5). Specifically, data drawn from the Study of the Consequences of the Protease Inhibitor Era (SCOPE) were used to estimate counterfactual mean CD4 T cell count 8 months after confirmed virologic rebound on an antiretroviral treatment regimen, under a set of user-supplied realistic treatment rules. Specifically, we considered rules indexed by a range of CD4 T cell count thresholds θ. Thus, we aimed to replicate the results of a clinical trial in which subjects were assigned to modify their initial failing regimen only when CD4 T cell count reached a randomly assigned threshold.

Recall that Ā in this example is an indicator process that jumps only once, when a subject modifies therapy for the first time; thus, treatment decisions are made only for those individuals who have not yet modified their original antiretroviral regimen. We defined the following set of realistic individualized treatment rules d_θ, indexed by threshold CD4 T cell count θ:

$$\begin{array}{l}{d}_{\theta }\left(t\right)\equiv I\left(CD4\left(t\right)\le \theta \right)\\ d_{\theta }\left(t\right)=1:\text{Modify therapy at time t}\\ d_{\theta }\left(t\right)=0:\text{Do not modify therapy at time t}\text{.}\end{array}$$

This set of treatment rules uses a subject's current CD4 T cell count (CD4(t)) to assign a treatment decision d_θ(t) (modify treatment or not) at each time point t from baseline until a subject modifies therapy. Note that for a given subject, d_θ applied from baseline onwards deterministically implies a static treatment regimen ā.

By calling this set of rules d_θ “realistic”, we imply that, given the subset of a subject's covariates necessary for the SRA to hold, the rule d_θ does not assign, at any time point, a treatment action that is impossible for that subject. Below, we discuss whether this realistic dynamic treatment assumption is reasonable for the set of user-supplied rules considered in the current data example.

We estimated the following parameter by assuming a model on the counterfactual mean future CD4 T cell count under a realistic treatment rule indexed by d_θ:

$$E(Y_{d_{\theta }})=m(\theta |\beta ).$$

Thus β was our parameter of interest, providing a summary of how the counterfactual outcome varied depending on the threshold CD4 T cell count at which a subject modified his or her virologically failing therapy. In particular, estimation of β implied estimation of an optimal threshold θ at which to modify the failing antiretroviral regimen (i.e. the optimal threshold was defined as the θ which maximized the expected counterfactual CD4 T cell count 8 months later).

We further modelled this counterfactual dynamic mean conditional on baseline CD4 T cell count. In other words, we estimated the following causal parameter:

$$E(Y_{d_{\theta }}|V)=m(\theta ,V|\beta ).$$

where V ≡ CD4(0) denotes CD4 T cell count at time of confirmed virologic failure (baseline). Estimation of this parameter allowed us to address the question of whether the optimal threshold at which to modify therapy varied depending on a subject's baseline CD4 T cell count.

In defining θ and V, CD4 T cell count was categorized using 23 discrete levels (corresponding to cell counts of 0-50 cells, 51-100 cells, etc…).

3.1 IPTW estimation

We assumed the following models on the causal parameter of interest.

$$m\left(\theta |\beta \right)={\beta }_0+{\beta }_1\theta +{\beta }_2{\theta }^2,$$

and

$$m\left(\theta ,V|\beta \right)={\beta }_0+{\beta }_1\theta +{\beta }_2{\theta }^2+{\beta }_3\theta \times V+{\beta }_4{\theta }^2\times V+{\beta }_{5}V.$$

As noted above, if one is uncomfortable with assuming these models, the causal parameter of interest could alternatively be viewed as the projection of the true causal parameters onto working models m(θ|β) and m(θ, V|β).

The parameter β was estimated using the IPTW estimating function

$$\begin{array}{l}{D}_{h,\text{IPTW}}(O|g_0,{\beta }_0)\hfill \\ =\sum _{d_{\theta }}\frac{I(\overline{A}=d_{\theta }(C\overline{D}4))}{g_0(\overline{A}|X)}h(d_{\theta },V)\frac{d}{d{\beta }_0}m(\theta ,V|{\beta }_0)(Y-m(\theta ,V|{\beta }_0)),\hfill \end{array}$$

where we used h(d_θ, V) ≡ 1. Under this estimating function, β was estimated using weighted least squares regression, with each subject contributing one line of data for each threshold θ consistent with the subject's observed treatment history, and using the following weights:

$$\text{weight}=\frac{I(\overline{A}=d_{\theta }(C\overline{D}4))}{g(\overline{A}|X)}.$$

Estimation of β thus required, for each possible threshold θ, determination of whether each subject complied with the treatment rule implied by that threshold (I (Ā = d_θ(CD̄4)). This determination was made according to the following algorithm:

• Among subjects who modified therapy at some time M before 8 months, we evaluated whether CD4(t) > CD4(M) for t = 0, …, M − 1. If yes, the subject was considered to have followed a treatment rule corresponding to θ = CD4(M). If no, the subject failed to follow a rule for treatment modification based on any CD4 T cell count threshold, and was assigned no value for θ.

• Subjects who did not modify therapy prior to measurement of the outcome were considered to have followed multiple treatment rules, corresponding to each threshold CD4 T cell category below the minimum CD4 T cell count category observed over the course of follow-up.

In implementing the IPTW estimator, the treatment mechanism g(Ā|X) was estimated using logistic regression of the probability of switching therapy at each time point given a subject's observed past. The regression fits were estimated data-adaptively using the Deletion/Substitution/Addition algorithm of Sinisi and van der Laan (2004), and 5-fold cross validation. Potentially informative censoring was addressed by modeling the censoring mechanism and employing inverse probability of censoring weights (as outlined in van der Laan and Robins (2003)). Standard errors were estimated based on 100 bootstrap samples.

3.2 Results

One hundred thirty three subjects experienced 167 episodes of confirmed virologic failure during SCOPE follow-up; of these, 33 subjects were censored before the outcome at 8 months was obtained. For a full description of this sample, and the covariates measured on each subject over time, see (Petersen et al. (2005)). Of the 100 subjects who failed an antiretroviral therapy regimen and were not censored prior to measurement of the outcome, 56 subjects (57 episodes of failure) had observed treatment histories that corresponding with following the rule d_θ (as defined above) for at least one threshold θ.

The estimated treatment mechanism is reported in Table (1). The resulting weights ranged from 1.01 to 53; in order to reduce variability, weights were truncated at 10, which resulted in truncation for 8 of the subjects. Under the assumption that the treatment mechanism was consistently estimated (as required for the consistency of the IPTW estimator), we further considered the assumption that the rules d_θ considered are in fact realistic. As a means of partially examining the assumption that modification is not deterministically assigned given time-dependent covariates, we assessed the stabilizing weights that would have been employed in a standard marginal structural model estimating the effect of a static switch time; we estimated $sup\frac{g\left(a\left(t\right)=1|\overline{A}\left(t-1\right)=1,V\right)}{g\left(a\left(t\right)=1|\overline{A}\left(t-1\right)=1,X\right)}=1.2$ and $sup\frac{g\left(a\left(t\right)=0|\overline{A}\left(t-1\right)=1,V\right)}{g\left(a\left(t\right)=0|\overline{A}\left(t-1\right)=1,X\right)}=7.1$. Given that a subject can only switch regimens once, ${sup}_{\overline{a}\in \overline{A}}\frac{g\left(\overline{a}|V\right)}{g\left(\overline{a}|X\right)}$ was estimated as less than or equal to 1.2⁷ × 7.1 = 25.4 ≪ ∞, suggesting the absence of extreme ETA violations for static modification rules (i.e. those assigning modification at a fixed time). We note, however, that this does not necessarily imply that the dynamic rules d_θ are realistic. Further investigation of possible ETA violations under these rules (for example, by applying a bootstrap simulation as described in Wang et al. (2006) for the point treatment setting) seems sensible and necessary, but is not performed here.

Table 1.

Odds ratios for switching treatment based on data-adaptive fit of treatment mechanism

Covariate	Odds Ratio
Current diagnosis with an opportunistic disease	1.21
Number of protease inhibitor drugs experienced	1.11
Most recent HIV RNA level undetectable	0.44
Percent average adherence (per 10%)	0.92
Most recent CD4 T cell count (per 100 CD4 T cells)	0.92
Nadir CD4 T cell count (per 100 CD4 T cells)	1.06
Most recent HIV RNA level more than one month prior	0.90
Age (per 5 years)	0.80

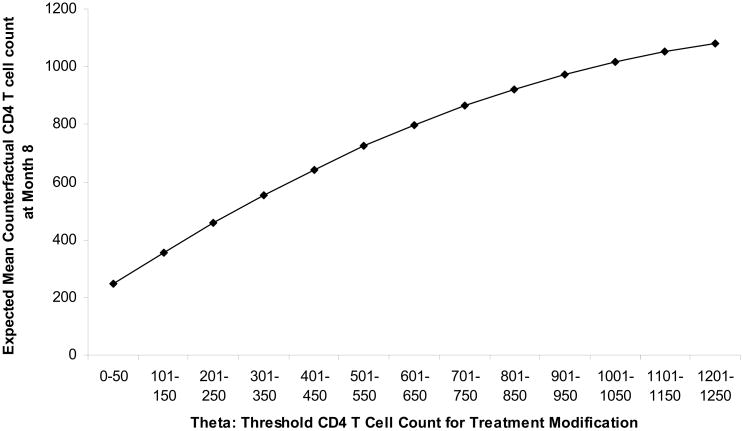
Tables 2 and 3 show estimates of β for the models m(θ|β) and m(θ, V|β), respectively. Based on the results in Table (2), Figure (1) illustrates how estimated mean counterfactual CD4 T cell count varies as a function of modification threshold θ. The estimate β_n of m(θ|β) suggests that the optimal threshold for modification is a CD4 T cell count category higher than the maximum CD4 T cell count category observed at baseline (θ_opt = 31.7, corresponding to > 1500 cells), suggesting that, on average, all subjects would benefit from modifying therapy immediately following loss of suppression.

Table 2.

Estimated mean counterfactual CD4 T cell count 8 months after virologic failure under treatment modification at CD4 threshold θ, based on model m(θ|β) = β₀ + β₁θ + β₂θ²

Term	Point Estimate	95% CI
β0	188.2	117.4, 258.9
β1	58.9	22.7, 95.2
β2	-0.9	-4.2, 2.3

Table 3.

Estimated mean counterfactual CD4 T cell count 8 months after virologic failure under treatment modification at CD4 threshold θ, given baseline CD4 T cell count, based on model m(θ, V|β) = β₀ + β₁θ + β₂θ² + β₃θ × V + β₄θ² × V + β₅V

Term	Point Estimate	95% CI
β0	-40.8	-113.3, 31.7
β1	-1.1	-55.5, 53.4
β2	4.4	-1.8, 10.7
β3	-0.9	-6.1, 4.3
β4	-0.2	-0.7, 0.4
β5	50.1	41.0, 59.2

Figure 1.

Mean counterfactual outcome under individualized rule where treatment modified at CD4 T cell count threshold=θ

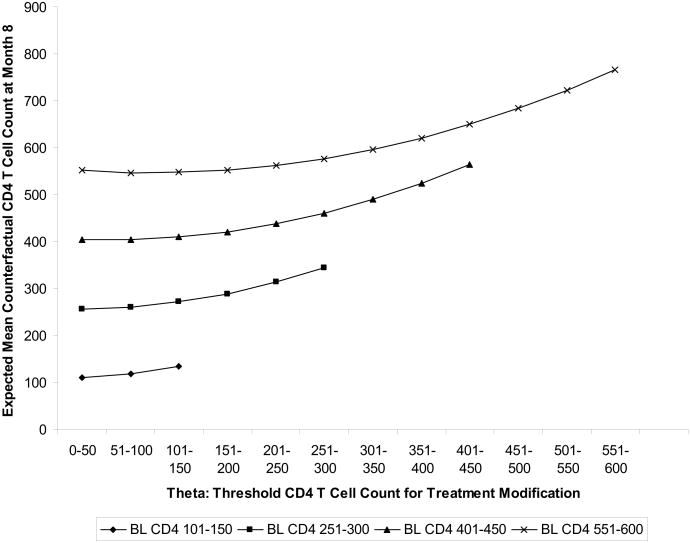
Figure (2) uses the estimated β_n of m(θ, V|β₀), reported in Table 3, to plot how the mean counterfactual outcome varies as a function of modification threshold θ and baseline CD4 T cell count, The results of Table 3, and Figure 2 suggest that, regardless of a subject's baseline CD4 T cell count, the highest expected counterfactual CD4 T cell count 8 months later is achieved by switching therapy immediately (i.e. at a threshold corresponding to the subject's baseline CD4 T cell count).

Figure 2.

Mean counterfactual outcome under individualized rule where treatment modified at CD4 T cell count threshold=θ, given baseline CD4 T cell count

While suggestive, it should be emphasized that these findings are preliminary, and are intended as an example of the proposed methodology, rather than as a meaningful guide to clinical practice. Significant limitations of the current data example include small sample size, and the definition of treatment modification employed. Given small sample size, modification here was defined broadly as interruption or addition of at least 1 drug to the patient's failing antiretroviral regimen. Thus treatment simplification and interruption were included in the definition of modification, while the real clinical question of interest focuses on when the patient should be switched to a new combination regimen with the goal of re-suppressing the virus. Analyses using several large HIV cohorts based on a refined definition of treatment modification and consideration of alternative outcomes are currently underway, with the goal of providing more clinically relevant results.

4 Causal effect models for intention-to-treat interventions

4.1 The counterfactual framework for intention-to-treat causal models

The counterfactual causal inference framework for treatment interventions ā(t) up till time t assumes the existence of counterfactuals indexed by static treatment interventions ā(t), the corresponding link between the observed data and these counterfactuals (i.e., consistency assumption), and the sequential randomization assumption (SRA). Our framework below simply assumes the consistency and sequential randomization assumptions for all t. By applying the result of Gill and Robins (2001) and Yu and van der Laan (2002) for all t, it follows that, by construction, assuming these consistency and randomization assumptions for all t puts no restrictions on the data generating distribution. However, these assumptions do allow us to define the intention-to-treat causal parameter of interest as a parameter of the data generating distribution.

Existence of t-specific static treatment counterfactuals

For each t and each possible ā(t) ∈ (t), we define

$$O_{\overline{a}\left(t\right)}\equiv (L_{\overline{a}\left(t\right)},A_{\overline{a}\left(t\right)})$$

as the data one would have observed on the experimental unit if it would have been assigned Ā(t) = ā(t). Thus the first t + 1 components of A_ā(t) are set at ā(t), but the subsequent treatment actions are random: A_ā(t)(0) = a(0), …, A_ā(t)(t) = a(t). It is assumed that for all t and ā(t) ∈ (t), we have

$$L_{\overline{a}\left(t\right)}=L_{A_{\overline{a}\left(t\right)}}.$$

We define X(t) ≡ (L_ā(t), A_ā(t)) : ā(t) ∈ (t)) as the collection of treatment-specific processes corresponding with setting the first t + 1 treatment actions, t = 0, …, τ. Thus, X(τ) = (L_ā : ā) denotes the collection of counterfactual processes L_ā indexed by fully set static treatment regimens ā = (a(0), …, a(τ)).

t-specific temporal ordering assumption

For each time point t, we assume the usual temporal ordering assumption:

$$O_{\overline{a}\left(t\right)}\left(j\right)=O_{\overline{a}\left(\text{min}\left(j-1,t\right)\right)}\left(j\right).$$

This states that the counterfactual data at time j is only affected by past interventions.

t-specific consistency assumption

It is assumed that for all t = 0, …, τ

$$\left(A,L\right)=(\overline{A}\left(t\right),O_{\overline{A}\left(t\right)})=(A_{\overline{A}\left(t\right)},L_{\overline{A}\left(t\right)}).$$

That is, we can represent O as a missing data structure on the full data structure X(t) = {O_ā(t) : ā(t) ∈ (t)}, where the missingness variable is Ā(t), t = 0, …, τ. In particular, for t = τ, this presents our observed longitudinal data structure as a missing data structure on a collection of treatment regimen-specific processes X(τ):

$$O=(A=\overline{A}(\tau ),L=L_A).$$

t-specific sequential randomization assumption

For each t, we assume the sequential randomization assumption: for all j = 0, …, t

$$A\left(j\right)\perp X\left(t\right)|\overline{A}\left(j-1\right),\overline{L}\left(j\right).$$ (3)

We will refer to this as the strong sequential randomization assumption (SSRA). This implies, in particular, the typical sequential randomization assumption (SRA): for all j = 0, …, τ

$$A\left(j\right)\perp X\left(\tau \right)|\overline{A}\left(j-1\right),\overline{L}\left(j\right).$$ (4)

That is, at each time-point, conditional on the observed past, the treatment at this time-point is conditionally independent of the full data X(τ). The latter sequential randomization assumption implies (and is, in essence, equivalent with) the coarsening at random (CAR) assumption on G_Ā|X(τ) for the observed data O w.r.t. full data structure X(τ). In censored data structures, one frequently assumes coarsening at random (CAR) (Heitjan and Rubin (1991), Jacobsen and Keiding (1995), Gill et al. (1997), in increasing generality).

Taking the τ-specific missing data representation of the observed data structure, it follows that the data generating distribution P_FX(τ)0,G0 of O is indexed by a distribution of X(τ) = (L_ā : ā), and the conditional probability distribution G₀(· | X(τ)) of Ā, given X(τ). We will refer to the latter as the treatment mechanism, and we denote its probability density with g₀(· | X(τ)). By the chronological ordering, and our conventions above, the τ-specific missing data structure assumption is equivalent with

$$O=(L(0),A(0),L_{A(0)}(1),A(1),\dots ,L_{\overline{A}(T_A-1)}(T_A),A(T_A),L_{\overline{A}(T_A)}(T_A+1)).$$

By our missing data representations for all t, we have A = A_Ā, but also A = A_ā(t) for any ā(t) = Ā(t), and, as a consequence, L_Ā = L_ā(t) for any ā(t) = Ā(t).

Identifiability results for static treatment interventions under the experimental treatment assignment (ETA) assumption

Under the SRA and the experimental treatment assignment assumption (ETA), it is possible to identify the treatment-specific counterfactual distributions from the observed data partial likelihood, through the G-computation formula (Robins (1999), Gill and Robins (2001), Yu and van der Laan (2002)). That is, under the assumption that g(ā | X(τ)) > 0, the SRA allows us to identify the marginal distribution of L_ā, while the SSRA allows us to also identify the marginal distribution of O_ā(t) = (A_ā(t), L_ā(t)) for any t = 0, …, τ. Specifically, for each t, we have the following t-specific factorization of the likelihood of O:

$$d{P}_{F_{X\left(t\right)},g_{\overline{A}\left(t\right)|X\left(t\right)}}\left(O\right)=Q_{X\left(t\right),t}\left(O\right)g_{\overline{A}\left(t\right)|X\left(t\right)}\left(\overline{A}\left(t\right)|X\left(t\right)\right),$$

where

$$\begin{array}{r}\hfill Q_{X(t),t}\left(\overline{L},\overline{A}\left(t\right),\underset{\_}{A}\left(t+1\right)\right)=\\ \hfill \prod _{j=0}^{t+1}P\left(L\left(j\right)|\overline{L}\left(j-1\right),\overline{A}\left(j-1\right)\right)P\left(\underset{\_}{A}\left(t+1\right),\underset{\_}{L}\left(t+2\right)|\overline{L}\left(t+1\right),\overline{A}\left(t\right)\right),\end{array}$$

and

$$g_{\overline{A}\left(t\right)|X\left(t\right)}\left(\overline{A}\left(t\right)|X\left(t\right)\right)=\prod _{j=0}^{t}g\left(A\left(t\right)|\overline{A}\left(t-1\right),\overline{L}\left(t\right)\right).$$

For t < τ, we define A̱(t) = (A(t), …, A(τ)) and Ḻ(t) = (L(t), …, L(τ + 1)). In addition,

$$\begin{array}{r}P\left(\underset{\_}{A}\left(t+1\right),\underset{\_}{L}\left(t+2\right)|\overline{L}\left(t+1\right),\overline{A}\left(t\right)\right)\equiv \\ \prod _{t+1}^{\tau }g\left(A\left(t\right)|\overline{A}\left(t-1\right),\overline{L}\left(t\right)\right)\prod _{t+2}^{\tau +1}P\left(L\left(t\right)|\overline{L}\left(t-1\right),\overline{A}\left(t-1\right)\right).\end{array}$$

If we assume SSRA, and the ETA assumption g₀(ā(t) | X(t)) > 0 a.e., then we have that the probability distribution of O_ā(t) is given by the following likelihood-based formula (G-computation formula)

$$P_{O_{\overline{a}\left(t\right)}}\left(\overline{l},\underset{\_}{a}\left(t+1\right)\right)=Q_{0X\left(t\right),t}\left(\overline{l},\overline{a}\left(t\right),\underset{\_}{a}\left(t+1\right)\right).$$

In other words, by setting Ā(t) = ā(t) in the likelihood factor Q_0X(t),t, one obtains the density of O_ā(t). In many applications, as discussed in the introduction, this ā(t)-specific experimental treatment assignment assumption Pr(g₀(ā(t) | X(t)) > 0) = 1 does not hold for lots of static treatment regimens ā(t). The intention-to-treat parameter developed here is identifiable without the need to assume these typically unrealistic ETA-assumptions.

The observed data model implied by the causal inference assumptions

The model for the observed data structure implied by the above consistency assumptions and the strong SRA is nonparametric. As a consequence, the strong SRA and the consistency assumptions cannot be tested, but these assumptions provide us with a set of assumptions which provide the wished causal interpretation of our target parameters, defined below, of the data generating distribution. Possible data generating distributions are the elements of the nonparametric structural equation model corresponding with the causal graph implied by the time-ordering: i.e., let L(j) = g_j(L̄(j − 1), Ā(j − 1), U), A(j) = f_j(Ā(j − 1), L̄(j), e(j)) for arbitrary deterministic functions f_j, g_j, an arbitrary random variable U, and an exogenous random vector e. This nonparametric structural equation model is indeed a saturated model, and, for all t ∈ {0, 1 …, τ}, it satisfies the consistency assumption and the SRA w.r.t. to the counterfactuals X(t) implied by this structural equation model (see Pearl (2001), Gill and Robins (2001), Yu and van der Laan (2002)).

4.2 The intention-to-treat causal parameter

This section formally defines “intention-to-treat” counterfactuals, indexed by static treatment regimens. Specifically, for every ā ∈ , we define the individualized stopped treatment-specific process

$$X_{d(\overline{a})}=(L_{d(\overline{a})},A_{d(\overline{a})})\equiv (L_{\overline{a}(C_{\overline{a}})},A_{\overline{a}(C_a)}),$$

where C_ā is a counterfactual stopping time defined as

$$C_{\overline{a}}\equiv \text{min}\{t\in \{-1,0,\dots ,\tau \}:a(t+1)\notin {\mathcal{D}}_{\overline{a}}(t+1)\text{or}t=\tau \}.$$

That is, X_d(ā) is the process we would have observed on the subject if the subject had followed the static treatment ā till the end τ, or till time C_ā at which ā for the next time point corresponds with a treatment outside the set of options _a(C + 1). After the stopping time C_ā, the experimental unit is subjected to the data generating process applicable in the counterfactual world in which one has followed ā up till time C_ā; that is, it follows its counterfactual treatment process A_ā(t) with t = C_ā. In particular, Y_d(ā) denotes the treatment-specific outcome of interest. For example, Y_d(ā) = T_d(ā) + 1 might be the survival time under treatment regimen d(ā), or it might be the counterfactual outcome Y_d(ā)(τ + 1) of a time-dependent process Y_d(ā)(·) measured at a fixed time τ + 1.

Missing data structure on intention-to-treat treatment-specific counterfactuals

It is of interest to understand the information the observed data provide about these intention-to-treat counterfactuals. For any ā, we define the observed

$$C\left(\overline{a}\right)\equiv \text{min}\left\{t:A\left(t+1\right)\ne a\left(t+1\right)\text{or}a\left(t+1\right)\notin \mathcal{D}\left(t+1\right)\text{or}t=\tau \right\}.$$

Thus C(ā) is the amount of time the experimental unit has followed d(ā) (if it did not even follow a(0), then it equals -1), where C(ā) ∈ {−1, 0, 1, …, τ}. Consider the indicator

$$\Delta \left(\overline{a}\right)=I\left(A\left(C\left(\overline{a}\right)+1\right)\notin \mathcal{D}\left(C\left(\overline{a}\right)+1\right)\text{or}C\left(\overline{a}\right)=\tau \right).$$ (5)

We note that, if Δ(ā) = 1, then the experimental unit has followed the intention-to-treat treatment regimen d(ā). Formally, we have the following link between the observed data structure and the intention-to-treat treatment-specific counterfactuals:

$$(A,L)=(A_{d(\overline{a})},L_{d(\overline{a})})\text{if}\Delta (\overline{a})=1.$$

Thus, one could represent the observed data structure O also as

$$O=(\Delta (\overline{a}),\Delta (\overline{a})(A_{d(\overline{a})},L_{d(\overline{a})}):\overline{a}\in \mathcal{A}).$$

That is, for each static treatment regimen ā, we observe if the experimental unit followed the individualized stopped treatment regimen d(ā), and if it did, then we observe its corresponding intention-to-treat counterfactual process.

Intention-to-treat causal effect parameter

Let V ⊂ L(0) be a user-supplied set of baseline co-variables. Consider the model

$$E_0(Y_{d\left(\overline{a}\right)}|V)=m(\overline{a},V|{\beta }_0),$$ (6)

for some parametrization β → m(· | β) and parameter value β₀. Let β(P_FX(τ),G) be the parameter of interest defined on the model for the observed data structure O defined by the assumptions above and the model (6), so that β₀ = β(P_FX(τ)0,G0) denotes the true parameter value corresponding with the true data generating distribution P₀.

We prefer not to assume the model m(· | β), but rather to use it as a working model to define a smooth version of E₀(Y_d(ā) | V) (see Neugebauer and van der Laan (2005a)). Specifically, following Neugebauer and van der Laan (2005a), we define our parameter of interest nonparametrically as

$${\beta }_h\left(P\right)\equiv \text{arg}\underset{\beta }{\text{min}}\sum _{\overline{a},V}{(m\left(\overline{a},V|\beta \right)-E_P(Y_{d\left(\overline{a}\right)}|V))}^{2}h\left(\overline{a},V\right),$$

where the weight function h is user-supplied. Thus in this case, our model is still nonparametric, but our parameter is defined by a working model m(· | β) and a weight function h. Note that, if (6) holds at P, then β_h(P) = β(P) for all h. It is also of interest to note that β_h is a parameter of both the full data distribution of X(τ) = (L_ā : ā ∈ ) and the treatment mechanism G_Ā|X.

Identifiability of intention-to-treat-specific distribution

We have the following identifiability result providing the mapping from the likelihood of O to the distribution of the intention-to-treat counterfactual data structure O_d(ā) = (A_d(ā), L_d(ā)).

Result 3 We have the following identifiability result:

$$\begin{array}{l}{P}_{O_{d(\overline{a})}}(a^{\ast },l)=I({\overline{a}}^{\ast }(c_a(l))=\overline{a}(c_a(1)))\times \\ \prod _{t=0}^{\tau +1}{P}_{L(t)|\overline{L}(t-1,\overline{A}(t-1)}(l(t)|\overline{l}(t-1),{\overline{a}}^{\ast }(t-1))\\ \prod _{t=c(l)+1}^{\tau }{g}_0(a^{\ast }(t)|{\overline{a}}^{\ast }(t-1),\overline{l}(t))\end{array}$$ (7)

where c_a(l) ≡ min {t ∈ {−1, …, τ} : a(t + 1) ∉ (l)(t + 1) or t = τ} is the realization of the stopping time for treatment ā as identified by L = l and ā.

The above identifiability result can be used to define a likelihood-based estimator. The consistency of this estimator will rely on correct estimation of the complete data generating mechanism: i.e., both the treatment mechanism g₀ and the Q₀-factor of the density of O need to be consistently estimated. Alternatively, estimating function-based estimators can be derived that only rely on correct estimation of the treatment mechanism g₀, or that are possibly double robust w.r.t misspecification of g₀, Q₀. The inverse probability of treatment weighted and (possibly) double robust estimating functions, and corresponding estimators, are presented for the longitudinal data setting in Appendices C-D. Specifically, the efficient influence curve of β_h at P₀ is derived for the general longitudinal data structure, and the corresponding locally efficient estimating function and estimator are presented.

For pedagogical purposes, in the section that follows we provide a comprehensive analysis of our intention-to-treat causal effect model for the much simpler point treatment data structure, and present the corresponding likelihood-based, IPTW and DR-IPTW estimators of β_h0 for a given h. The corresponding class of IPTW and locally efficient estimators of β₀ under the assumption that m(· | β) is a correctly specified model is obtained by letting h be arbitrary.

5 Intention-to-treat effects for point treatment

We observe the chronological data structure O = (W, A, Y), where W are baseline co-variables, A is treatment, and Y is a final outcome. We assume the usual consistency assumption which states that X = (W, (Y_a : a ∈ )), and O = (W, A, Y_A) is a missing data structure on X. In addition, we assume the randomization assumption which states that A is independent of X, given W: g₀(a | X) ≡ Pr(A = a | X) = g₀(a | W) = Pr(A = a | W). Let ⊂ W be a set of possible treatment options in the sense that g₀(a | W) > 0 for a ∈ .

Intention to Treat Causal Effect

Let V ⊂ W be a user-supplied set of baseline co-variables. Let Y_d(a) ≡ YI(a ∉ ) + Y_aI(a ∈ ) and A_d(a) ≡ aI(a ∈ ) + AI(a ∉ ). Let (W, A_d(a), Y_d(a)) denote the data we would observe on the experimental unit if it followed the intention-to-treat treatment d(a). The parameter of interest is ψ₀(a, V) = Ψ(P₀)(a, V) ≡ E_P0(Y_d(a) | V). Note that this parameter corresponds with the mean outcome one would observe if one only intervenes (by setting A = a) on the experimental units for which a is a possible treatment option in the sense that a ∈ . In order to deal with the curse of dimensionality, we consider a working model {m(a, V | β) : β} for ψ₀(a, V), indexed by a Euclidean parameter β. For a user-supplied function h, let

$${\beta }_h\left(P\right)\equiv \text{arg}\underset{\beta }{\text{min}}{E}_P\sum _a{\left(\Psi \left(P\right)\left(a,V\right)-m\left(a,V|\beta \right)\right)}^{2}h\left(a,V\right)$$ (8)

Let β_h0 = β_h(P_FX0,G0) be the true parameter value corresponding with the true data generating distribution P₀ = P_FX0,G0. Note that β_h is a parameter of both the full data distribution of X = (W, (Y_a : a ∈ )) and the treatment mechanism G_A|X. We note that, if one is willing to assume that the model m(· | β) is correctly specified, then β_h(P) = β(P) does not depend on h, and each estimator we present for β_h in this section is a valid estimator for β.

For any a ∈ , consider the indicator

$$\Delta \left(a\right)=I\left(A=a\text{or}a\notin \mathcal{D}\right)).$$ (9)

We note that, if Δ(a) = 1, then the experimental unit has followed treatment d(a). It is also possible that A = a and a ∉ , except if = {a : g₀(a | W) > 0}. Formally, we have the following representation of the observed data in terms of the intention-to-treat counterfactuals (W, A_d(a), Y_d(a)):

$$O=(W,(\Delta (a),\Delta (a)(A_{d(a)},Y_{d(a)}):a\in \mathcal{A})).$$

Thus, the observation O = (W, A, Y) is equivalent with 1) observing the baseline co-variables W, and 2) for each a, observing if the experimental unit followed d(a), and if it did, then observing (A_d(a), Y_d(a)).

The model for the distribution of O is still nonparametric under the above assumptions. As a consequence, in this model all regular asymptotically linear estimators of β_h0 at P₀ are efficient. In the next three subsections we present three estimators of β_h: likelihood-based estimator, inverse probability of treatment weighted estimator, and the estimator based on the efficient influence curve which we refer to as the double robust IPTW estimator, which is also locally efficient.

5.1 Likelihood-based estimation

The parameter E(Y_d(a) | V) is identifiable from the observed data distribution under the above stated consistency assumption and randomization assumption. This is shown by the following result.

Result 4 Consider a joint random variable (X, A) with X = (W, (Y_a : a ∈ )), and assume that g₀(A | X) = g₀(a | W). Let ⊂ W be such that P(min_a∈ g₀(a | W) > 0) = 1. Let (W, A, Y) = (W, A, Y_A). Define the random variable Y_d(a) ≡ Y_AI(a ∉ ) + Y(a)I(a ∈ ). For any V ⊂ W, we have

$$E_0(Y_{d\left(a\right)}|V)=E_0(E_0\left(Y|A=a,W\right)I\left(a\in \mathcal{D}\right)+E\left(Y|A,W\right)I\left(a\notin \mathcal{D}\right)|V)$$

In general, we have that the probability distribution of (W, A_d(a), Y_d(a)) at w, a*, y is given by

$$\begin{array}{c}{P}_{d\left(a\right)}\left(w,a^{\ast },y\right)=P_W\left(w\right){\left\{I\left(a=a^{\ast }\right)P_{Y|A,W}\left(y|a,W\right)\right\}}^{I\left(a\in \mathcal{D}\left(w\right)\right)}\\ \times {\left\{g_0\left(a^{\ast }|w\right)P_{Y|A,W}\left(y|a^{\ast },w\right)\right\}}^{I(a\notin \mathcal{D}\left(w\right)}.\end{array}$$

One can generate the intention-to-treat counterfactuals (W, A_d(a), Y_d(a)) straightforwardly. Given the marginal distribution of W, the conditional distribution of A given W, and the conditional distribution of Y given (A, W), one generates W, A_d(a), Y_d(a) as follows: 1) generate W from P_W; 2) if a ∉ , then generate A from P_A|W and set A_d(a) = A, else set A = A_d(a) = a; 3) generate Y from P_{Y|W, A}(· | W, A) and set Y_d(a) = Y.

By applying this data generating experiment to an estimate of the data generating distribution, one obtains a large sample (Ŵ_b, Â_d(a),b, Ŷ_d(a),b), b = 1, …, B for all a ∈ , which yields a simulation-based estimate of the distribution of (W, A_d(a), Y_d(a)). Such an estimate could now also be mapped into an estimate of β_h0 by regressing the simulated Ŷ_d(a),b on a, V̂_b according to the regression model {m(· | β) : β} using weights h(a, V̂_b), a ∈ , b = 1,…, B.

If one is only concerned with estimation of the conditional mean E(Y_d(a) | V), then it suffices to directly estimate Q₀(a, W) = E₀(Y | A = a, W) with an estimator Q_n, and regress

$$Q_{n,d\left(a\right)}\left(a,W\right)\equiv Q_n\left(a,W\right)I\left(a\in \mathcal{D}\right)+Q_n\left(A,W\right)I\left(a\notin \mathcal{D}\right)$$

on a, V according to the model m(· | β). That is, the likelihood-based estimator of β_h0 can be defined as

$${\beta }_n(Q_n)=\text{arg}\underset{\beta }{\text{min}}\sum _{i=1}^n\sum _a{\left(Q_{n,d\left(a\right)}(a,W_i)-m(a,V_i|\beta )\right)}^{2}h(a,V_i).$$

5.2 Inverse probability of treatment weighted estimation

The proposed inverse probability of treatment weighted estimator of β_h0 is based on the following result.

Result 5 Let Δ(a) = I(A = a or a ∉ ). We have

$$\begin{array}{l}{E}_0\left(\Delta \left(a\right)|X\right)=I\left(a\notin \mathcal{D}\right)+I\left(a\in \mathcal{D}\right)g_0\left(a|X\right)\\ =g_0{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}.\end{array}$$

We also have for any set of baseline co-variables V ⊂ W

$$E_0(Y_{d\left(a\right)}|V)=E_0\left(\frac{Y\Delta \left(a\right)}{g_0{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}}|V\right).$$

Proof: The first statement is trivial. Regarding the second statement we note that $\frac{Y\Delta \left(a\right)}{g{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}}$ equals

$$I\left(a\notin \mathcal{D}\right)Y_A+I\left(a\in \mathcal{D}\right)\frac{I\left(A=a\right)}{g\left(a|X\right)}{Y}_a.$$

The conditional expectation of the second term, given X, equals I(a ∈ ) Y_a. Thus, the conditional expectation, given W, of Y Δ(a)/g(a | X)^{I(a ∈ )} equals the conditional expectation of I(a ∉ )Y_A + I(a ∈ )Y_d(a), given W, which proves the second statement of the result.

IPTW loss-based learning of intention-to-treat causal effect

We note that ψ₀(a, V) ≡ E₀(Y_d(a) | V) can be estimated nonparametrically by using available machine learning/data adaptive regression algorithms. The above result shows

$$\begin{array}{l}{E}_0(Y_{d\left(a\right)}|V)=E_0\left(\frac{Y\Delta \left(a\right)}{g_0{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}}|V\right)\\ \equiv E_0(Y_g(a)|V).\end{array}$$

Thus, for any user-supplied function h, we have

$${\psi }_0=\text{arg}\underset{\psi }{\text{min}}{E}_0{L}_h(O,\psi |g_0),$$

where the loss function is defined as

$$L_h\left(O,\psi |g\right)\equiv \sum _{a\in \mathcal{A}}{(Y_g\left(a\right)-\psi \left(a,V\right))}^{2}h\left(a,V\right).$$

As a consequence, we can estimate ψ₀ with the unified loss-based estimation methodology of van der Laan and Dudoit (2003) with the loss function given by L_h(O, ψ | g) for any choice h. For example, given an estimator g_n of g₀, one can estimate ψ₀ by data-adaptively regressing Y_gn,i(a) on a, V_i, with weights h(a, V_i), a ∈ , i = 1, …, n, using a machine learning algorithm such as the cross-validated deletion/substitution/addition (CV-DSA) algorithm of Sinisi and van der Laan (2004).

Similarly, we can apply the unified loss function-based learning approach to the inverse probability of treatment weighted loss function

$$L_h\left(O,\psi |g\right)\equiv \sum _{a\in \mathcal{A}}\frac{\Delta \left(a\right)}{g{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}}{\left(Y-\psi \left(a,V\right)\right)}^{2}h\left(a,V\right).$$

For example, given an estimator g_n of g₀, one can estimate ψ₀ by data adaptively regressing Y_i on a, V_i, with weights h(a, V_i)Δ_i(a)/g_n(a | X_i)^{I(a∈ _i)}, a ∈ , i = 1, …, n, using a machine learning algorithm.

IPTW estimation of the intention-to-treat causal effect

The above first loss function implies the following estimator of β_h0:

$${\beta }_n=\text{arg}\underset{\beta }{\text{min}}\sum _{i=1}^n\sum _a{(Y_{g_n,i}(a)-m(a,V_i|\beta ))}^{2}h(a,V_i),$$

which is a standard weighted least squares regression of (Y_gn,i(a) : a) on V_i for a repeated (over a) measures type data set, where the weights are given by (h(a, V_i) : a). The second loss function implies the following estimator of β_0h:

$${\beta }_n=\text{arg}\underset{\beta }{\text{min}}\sum _{i=1}^n\sum _a{(Y_i-m(a,V_i|\beta ))}^{2}h(a,V_i)\frac{{\Delta }_i(a)}{g_n{(a|X_i)}^{I(a\in \mathcal{D})}}.$$

This is now a standard weighted least squares regression of Y_i on a, V_i for a repeated (across a ∈ ) measures type data set, where the weights are given by h(a, V_i)Δ_i(a)/g_n(a | X_i)^{I(a∈ _i)}.

The latter weighted least squares regression estimator corresponds with the following IPTW estimating function

$$\begin{array}{l}{D}_h\left(O|\beta ,g\right)\equiv \sum _{a\in \mathcal{A}}h\left(a,V\right)\frac{d}{d\beta }m\left(a,V|\beta \right)\left(Y-m\left(a,V|\beta \right)\right)\frac{\Delta \left(a\right)}{g{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}}\\ =I\left(A\in \mathcal{D}\right)\frac{h\left(A,V\right)}{g\left(A|X\right)}\frac{d}{d\beta }m\left(A,V|\beta \right)\left(Y-m\left(A,V|\beta \right)\right)\\ +\sum _{a\notin \mathcal{D}}h\left(a,V\right)\frac{d}{d\beta }m\left(a,V|\beta \right)\left(Y-m\left(a,V|\beta \right)\right)\end{array}$$

By Result 5 we have that this IPTW estimating function is unbiased for β_h0:

$$E_0{D}_h(O|{\beta }_0,g_0)=0.$$

Relation to IPTW estimating function for marginal structural model

We note that in the special case that = with probability 1, we have that

$$D_h\left(O|\beta ,g\right)=\frac{h\left(A,V\right)}{g\left(A|X\right)}\frac{d}{d\beta }m\left(A,V|\beta \right)\left(Y-m\left(A,V|\beta \right)\right)$$

reduces to the standard IPTW estimating function for a marginal structural model E(Y_a | V) = m(a, V | β), which is known to be unbiased if indeed the ETA assumption, inf_{a∈ g}(a | W) > 0, or its stabilized version, ${\text{sup}}_{a\in \mathcal{A}}\frac{h\left(a,V\right)}{g\left(a|W\right)}<\infty$, holds.

5.3 Locally efficient double robust estimation

The following result provides the optimal estimating function based on the efficient influence curve of β_h at P₀. The proof and derivation of the corresponding influence curve is provided in Appendix B.

Result 6 Consider the following estimating function:

$$\begin{array}{l}{D}_{h,DR}({\beta }_0,g_0,Q_0)\\ =\sum _a\frac{\Delta \left(a\right)}{g_0{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}}h\left(a,V\right)\frac{d}{d\beta }m(a,V|{\beta }_0)(Y-m(a,V|{\beta }_0))\\ -\sum _{a\in \mathcal{D}}(I\left(A=a\right)-g_0\left(a|W\right))\frac{h\left(a,V\right)\frac{d}{d{\beta }_0}m(a,V|{\beta }_0)}{g_0\left(a|W\right)}(Q_0\left(a,W\right)-m(a,V|{\beta }_0)).\end{array}$$

If E(Y_d(a) | V) = m(a, V | β₀), then for all functions h

$$E_0{D}_{h,DR}({\beta }_0,g,Q)=0\text{if}g=g_0\text{or}Q=Q_0.$$

If β_h0 = arg min_β E₀Σ_a(E₀(Y_d(a) | V) − m(a, V | β))²h(a, V), then

$$E_0{D}_{h,DR}({\beta }_{h0},g,Q)=0\text{if}g=g_0\text{or}Q=Q_0.$$

The efficient influence curve of β_h at P₀ is given by −c(β_h0)⁻¹ D_h,DR(β_h0, g₀, Q₀).

If P₀ is such that E₀(Y_d(a) | V) = m(a, V | β₀), then β₀ does not depend on h so that D_h,DR yields an estimating function for all functions h.

Locally efficient double robust IPTW estimator

Given an estimator g_n, Q_n of g₀, Q₀, we can define the estimator β_h,n,DR as the solution of the estimating equation

$$0=\sum _{i=1}^n{D}_{h_n,DR}(O_i|\beta ,g_n,Q_n).$$

If m(· | β) is linear in β, then this estimating equation is linear in β so that its solution exists in closed form. This estimator is locally efficient under regularity conditions, in the sense that it is consistent, asymptotically linear and efficient if both g_n and Q_n are consistent, and it remains consistent and asymptotically linear if only one of these two nuisance parameters is incorrectly estimated. In order to avoid technicalities, we propose the bootstrap method to obtain an estimate of the sampling distribution of β_hn,DR and to construct corresponding confidence intervals.

6 Discussion

Violations of the ETA assumption have the potential to severely bias IPTW estimates of static treatment effects. In particular, both data applications and simulation studies, such as Neugebauer and van der Laan (2005b), have exposed the importance of “practical” violations in the ETA assumption, which arise due to finite sample size. In recognition of the importance of this issue, we developed a diagnostic tool, based on bootstrap simulation, that can be applied to provide an estimate of ETA bias, in essence quantifying the lack of finite sample identifiability for the causal effect of interest (Wang et al. (2006)).

Unfortunately, in many data sets the ETA bias of the IPTW estimator is a serious concern, and having diagnosed the impact of ETA bias, one is left with the question of how to address it. In the case that the parameter of interest is a causal effect of a treatment at a single point in time, then the experimental units causing the ETA bias can be identified by their baseline covariates. Therefore, it might seem a reasonable approach to only estimate the causal effect conditional on the experimental unit having baseline covariates for which all treatments have positive probability (e.g., larger than a user-supplied δ > 0). However, this seemingly sensible and natural approach forces one to restrict to a sub-distribution which may not be the sub-distribution of interest. In addition, it will require throwing away the observations not drawn from this sub-distribution. Due to the resulting forced reduction in sample size, it does not necessarily follow that the finite sample ETA bias shrinks. So, even in the point-treatment case, there does not seem to be a simple manner to deal with the ETA bias.

If the treatment is time-dependent then such a sub-sampling approach fails to be valid because the experimental units causing ETA bias are not known at baseline t = 0. Instead, the experimental units causing the ETA bias make themselves known during the course of the study by developing time-dependent covariates which change their set of treatment options. As a consequence, if the parameter of interest is the causal effect of a static longitudinal treatment intervention, then deleting the experimental units causing ETA bias corresponds with adjusting for variables on the pathway between the treatment and outcome of interest, an approach that is known to result in non-interpretable parameters.

To summarize, static treatment interventions are typically not realistic, and, as a consequence, are typically either non-identifiable or extremely hard to estimate based on finite samples. It is this issue which motivated the current article proposing two classes of causal effect models which do not rely on the ETA assumption, but restrict attention to interventions for which the data carries information.

In this article, we have introduced causal effect models for intention-to-treat interventions and realistic treatment rules indexed by static treatment interventions. By choosing the realistic individualized treatment rules appropriately, the proposed causal effects of realistic individualized treatment rules generalize causal effects of static treatment interventions, are always identifiable from the data while remaining interpretable, and are easier to learn based on finite samples. Intention-to-treat interventions have similar advantages to realistic treatment rules indexed by static treatments; however, in contrast to causal parameters indexed by realistic treatment rules, the intention-to-treat causal parameter is a function of the treatment mechanism. As a result, a change in the way that treatment is assigned can change the causal effect being estimated. Thus, in applications for which the treatment mechanism followed in the observed cohort is considered a nuisance, causal effect models for realistic individualized treatment rules are the preferred approach.

In addition, we have introduced models for realistic individualized treatment rules that allow the user to supply his or her own set of realistic individualized treatment rules to be compared. As illustrated in the data example, such models for realistic individualized treatment rules identify the optimal individualized treatment rule among the user-supplied set of realistic individualized treatment rules.

Both of our proposed causal effect models force the user to identify for each experimental unit at each point in time a set of possible treatment options. We believe that this is actually a nice feature since it forces the researcher to ask the very questions which are needed to be able to obtain a collection of identifiable and realistic treatment regimens from data. Consultation with subject matter experts must clearly play a central role in answering these questions. For example, the researcher might need to determine which events correspond with a reduction of treatment options for the patient. If such knowledge is not available, then we propose to learn the treatment mechanism from the data and map the fitted treatment mechanism in a time-dependent set of possible treatment options for each experimental unit.

Appendix A: Causal effect models for realistic point treatment rules

In order to illustrate causal effect models for realistic treatment rules we walk through the special and simple case that treatment is assigned at a single point in time.

The observed data structure is O = (W, A, Y), where W is a vector of baseline covariates, A is a subsequent treatment, and Y is a final outcome of interest.

Consistency assumption

We define the full data as the collection X = (W, (Y(a), a ∈ )) of counterfactual outcomes Y(a) indexed by static treatment interventions varying over the support of the marginal distribution of A. The consistency assumption states that O = (W, A, Y = Y(A)).

Dynamic treatment counterfactuals

Given this standard consistency assumption, for any rule d, Y_d can be defined as Y_a with a = d(W). Thus, given the existence of the random variable X defined as the collection of static treatment-specific counterfactuals, one can also define the dynamic treatment regimen-specific counterfactuals Y_d ≡ Y_d(W) as a measurable function of X and the rule d.

Randomization assumption (RA)

We will assume the randomization assumption stating that A is independent of X, given W. The data generating distribution of O will be denoted with P₀ = P_FX0,g0, and is indexed by the distribution F_X0 of X and the conditional probability distribution, g₀(· | X), of A, given X, where g₀(A | X) = g₀(A | W).

Realistic dynamic treatment assumption

Let * be a set of dynamic treatment regimens so that for any d ∈ * we have

$$P\left(d\left(W\right)\in \mathcal{D}\right)=1.$$ (10)

That is, for each possible baseline covariate W, the treatment assigned by this treatment rule d is an element of the set of possible treatment options. This condition on the rule d guarantees that the distribution of (W, Y_d) is identifiable by the G-computation formula (Robins (1999), Gill and Robins (2001), Yu and van der Laan (2002)):

$$P\left(W=w,Y_d=y\right)=P\left(W=w\right)P\left(Y=y|A=d\left(w\right),W=w\right).$$

Realistic individualized treatment rules indexed by static treatment regimens

Given a static treatment a, one can define a dynamic treatment regimen as one which follows the static treatment a if a ∈ , and if a ∉ , then one assigns treatment in the set of treatment options according to a particular user-supplied rule. For example, the following construction describes such a set of dynamic treatment regimens indexed by static treatment interventions a. Suppose that the maximal set of treatment options is in the sense that ⊂ for all subjects with probability 1. 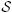In addition, define a dissimilarity measure between any pair of elements in so that for each s ∈ 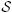we can identify the element in closest to s. We could now define the following individualized treatment rule indexed by a static treatment a: If a ∈ , then set A = a, else set A equal to the element in closest to a. Notice that this defines an individualized treatment rule as a deterministic function of a static intervention A = a. Therefore, we can denote this set of treatment options with d_a, a ∈ .

Causal effect model for realistic individualized treatment rules

The above standard causal inference assumptions put no restrictions on the data generating distribution and thereby cannot be tested based on the data. In particular, the model for the distribution of the data implied by the above assumptions is still unspecified/nonparametric.

We define the parameter of interest on this nonparametric model as the conditional mean of Y_d, given a subset V of the baseline covariates W, for all d ∈ *. In order to deal with the curse of dimensionality, one can follow two types of approaches. Firstly, one could assume a model

$$E_0(Y_d|V)=m(d,V|{\beta }_0)$$ (11)

for some parametrization (d, V) → m(d, V | β) indexed by a finite dimensional Euclidean parameter β. In this model β(F_X) is the parameter of interest, and β₀ = β(F_X0) is the true value of this parameter. For example, if d = d_a is a deterministic function of a static treatment intervention, as in our example above, then we would have

$$E_0(Y_{d\left(a\right)}|V)=m(a,V|{\beta }_0).$$

Alternatively, if one believes such a model is not realistic, then it might be sensible to define the parameter of interest as

$${\beta }_h(F_X)\equiv \text{arg}\underset{\beta }{\text{min}}\sum _{d,V}{(E_{F_X}(Y_d|V)-m\left(d,V|\beta \right))}^{2}h\left(d,V\right).$$

If model (11) holds, then β_0h = β₀ for all h. One can map β(F_X0) into a corresponding optimal individualized treatment rule within each strata V:

$$d(F_{X0})\left(V\right)=\text{arg}\underset{d\in \mathcal{A}\ast }{\text{max}}m(d,V|{\beta }_0).$$

Note that the parameters β(F_X) and β_h(F_X) are parameters of F_X. As a consequence, we can apply the general estimating function methodology as presented in van der Laan and Robins (2003) to obtain the class of all estimating functions, including the optimal double robust inverse probability of treatment weighted estimating function, which equals the efficient influence curve when evaluated at the true parameter values. The general methodology involves three steps: 1) identify the class of all full data estimating functions (formally, the space spanned by the gradients of the path-wise derivative of the parameter of interest, also called the orthogonal complement of the nuisance tangent space), 2) construct an inverse probability of treatment weighted class of estimating functions which are such that the conditional expectation, given X, maps into the class of full data estimating functions, 3) map this class of IPTW estimating functions in the so-called double robust IPTW estimating functions by subtracting the projection on tangent space spanned by all scores of the treatment mechanism under the sole model assumption RA. For details, we refer to the original paper Robins and Rotnitzky (1992) which laid out this general approach for censored data models or to Chapter 1 and 2 of van der Laan and Robins (2003).

Firstly, we need to determine the class of full data estimating functions one would obtain in the full data model for X. It follows that this class of full data estimating functions is given by:

$$\left\{\sum _{d\in \mathcal{A}\ast }h\left(d,V\right)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_d-m(d,V|{\beta }_0)):h\right\}.$$

In the case that one defines the parameter of interest as

$${\beta }_h(F_X)\equiv \text{arg}\underset{\beta }{\text{min}}{\sum _{d,V}(E_{F_X}(Y_d|V)-m\left(d,V|\beta \right))}^{2}h\left(d,V\right),$$

then the only full data estimating function is

$$\sum _{d\in \mathcal{A}\ast }h\left(d,V\right)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_d-m(d,V|{\beta }_0)).$$

We now need to find an IPTW-estimating function which has the property that its conditional expectation, given X, maps into the class of full data estimating functions. We can use

$$\begin{array}{l}{D}_{h,\text{IPTW}}(O|g_0,{\beta }_0)\\ =\sum _{d\in \mathcal{A}\ast }\frac{I\left(A=d\left(W\right)\right)}{g\left(A|X\right)}h\left(d,V\right)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y-m(d,V|{\beta }_0)).\end{array}$$

The following result establishes the wished result.

Result 7 Assume that for all individualized treatment rules d ∈ * we have

$$Pr\left(g\left(d\left(W\right)|X\right)>0\right)=1.$$

We have for all h

$$\begin{array}{l}E(D_{h,\text{IPTW}}(O|g_0,{\beta }_0)|X)\\ =\sum _{d\in \mathcal{A}\ast }h\left(d,V\right)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Y_d-m(d,V|{\beta }_0)).\end{array}$$

As a consequence, if E(Y_d | V) = m(d, V | β₀), then

$$E_0{D}_{h,\text{IPTW}}(O|g_0,{\beta }_0)=0\text{for all}h,$$

and, we always have for all h

$$E_0{D}_{h,\text{IPTW}}(O|g_0,{\beta }_{h0})=0.$$

Finally, we map this IPTW estimating function for β_h into the efficient estimating function by subtracting its projection on the tangent space of the treatment mechanism under RA. The following result describes this double robust IPTW estimating function, and thereby the efficient influence curve. The proof of this result is a direct consequence of Theorem 1.3 and Theorem 1.6 in van der Laan and Robins (2003).

Result 8 Let

$$\begin{array}{l}{D}_{h,RA}(O|g_0,Q_0)=\\ \sum _{d\in \mathcal{A}\ast }\frac{I\left(A=d\left(W\right)\right)}{g\left(A|X\right)}h\left(d,V\right)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Q_0(A,W)-\\ m(d,V|{\beta }_0))-\sum _{d\in \mathcal{A}\ast }h\left(d,V\right)\frac{d}{d{\beta }_0}m(d,V|{\beta }_0)(Q_0\left(d\left(W\right),W\right)-m(d,V|{\beta }_0)),\end{array}$$

where Q₀(A, W) = E₀(Y | A, W) and β₀ = β(Q₀). The efficient influence curve of β_h in the (nonparametric) model for the data generating distribution P₀ at P₀ is given by −c(β_h0)⁻¹D_h,DR(O | g₀, Q₀, β_h0), where

$$D_{h,DR}(O|g_0,Q_0,{\beta }_{h0})=D_{h,\text{IPTW}}(O|g_0,{\beta }_0)-D_{h,RA}(O|g_0,Q_0).$$

and $c\left(\beta \right)\equiv \frac{d}{d\beta }{E}_0{D}_{h,DR}(O|g_0,Q_0,\beta )$. If E₀(Y_d | V) = m(d, V | β₀), then for all h

$$E_0{D}_{h,DR}(O|g,Q,{\beta }_0)=0\text{if}g=g_0\text{or}Q=Q_0.$$

In general, for all h,

$$E_0{D}_{h,DR}(O|g,Q,{\beta }_{h0})=0\text{if}g=g_0\text{or}Q=Q_0.$$

Double robust locally efficient estimator

Given an estimator (g_n, Q_n) of the nuisance parameter (g₀, Q₀), and a possibly data-dependent index h_n, we define the double robust locally efficient estimator as the solution β_hn of

$$0=\sum _{i=1}^n{D}_{h_n,DR}(O_i|g_n,Q_n,\beta ).$$

Under regularity conditions, the estimator β_hn is consistent and asymptotically linear if either g_n converges to g₀ or Q_n converges to Q₀, and, if both nuisance parameters are consistently estimated, then β_hn is an asymptotically efficient estimator of β_h0. Therefore we call such an estimator β_hn locally efficient. For the formal statement for the asymptotics of this double robust estimator with the required regularity conditions, we refer to Theorem 2.4 and 2.5 in van der Laan and Robins (2003). In order to avoid technicalities, for statistical inference we propose the bootstrap method which is known to be asymptotically valid under the same conditions required to establish the asymptotic linearity of the double robust estimator β_hn,DR.

Appendix B: Proofs and derivations for point treatment intention-to-treat causal effects

Proof of Result 6. We will first show the double robustness result for D_h,DR. Firstly, if g = g₀, then the first term has mean zero, and the second term has trivially mean zero. Consider now the case that Q = Q₀. Write the first terms as a sum of two terms Σ_a Δ(a)/g₀ | W)^{I(a∈ )}S(O) = Σ_a∈ I(A = a)/g₀S(O) + Σ_a∉D S(O) for some S, and write the second term as a difference of two terms as well. This gives:

$$\begin{array}{l}{\sum }_a\frac{I\left(A=a,a\in \mathcal{D}\right)}{g\left(a|X\right)}{h}^{\ast }\left(Y-m\right)+{\sum }_{a}I\left(a\notin \mathcal{D}\right)h^{\ast }\left(Y-m\right)\\ -{\sum }_{a\in \mathcal{D}}\frac{I\left(A=a\right)}{g}{h}^{\ast }(Q_0-m)+{\sum }_{a\in \mathcal{D}}{h}^{\ast }(Q_0\left(a,W\right)-m).\end{array}$$

The expectation of the sum of the first and the third term equals zero. The second and fourth term can be written as (use that Q₀(a, W) = E(Y_a | W))

$$\begin{array}{r}\sum _a{h}^{\ast }\left(a,V\right)(YI\left(a\notin \mathcal{D}\right)+Y_{a}I\left(a\in \mathcal{D}\right)-m(a,V|{\beta }_0))=\\ \sum _a{h}^{\ast }\left(a,V\right)(Y_{d\left(a\right)}-m(a,V|{\beta }_0))\end{array}$$

which has mean zero. This proves that E₀D_h,DR(β₀, g, Q₀) = 0.

It remains to derive the efficient influence curve of the nonparametric parameter β_h(P) and show that it is indeed given by −c(β₀)⁻¹D_h,DR(β₀, g₀, Q₀). Since our model for the observed data structure O is non-parametric, we can use the following equivalent formulation of the model and parameter of interest in terms of the distribution of the observed data. We observe (W, A, Y) ∼ P₀. Consider a working model {m(a, V | β) : β} for ψ₀(a, V) = Ψ(P₀) ≡ E_P0 (E_P0(Y | A = a, W)I(a ∈ ) + E_P0(Y | A, W)I(a ∉ ) | V), indexed by a Euclidean parameter β. Let

$${\beta }_h\left(P\right)\equiv \text{arg}\underset{\beta }{\text{min}}{E}_P{\sum _a\left(\Psi \left(P\right)\left(a,V\right)-m\left(a,V|\beta \right)\right)}^{2}h\left(a,V\right)$$

be the parameter of interest, and let the model for P₀ be nonparametric. We have that β_h is exactly the same parameter (of the data generating distribution) as defined above in terms of intention-to-treat counterfactuals. Therefore, the efficient influence curve of β_h at P₀ in this nonparametric model is also the efficient influence curve in the model in which we assume the additional non-identifiable non-testable consistency and randomization assumptions. Let β_h0 = β_h(P₀) denote the true parameter value.

Consider the estimator

$${\beta }_n=\text{arg}\underset{\beta }{\text{min}}\sum _{i=1}^n\sum _a{(Y_i-m(a,V_i|\beta ))}^{2}h(a,V_i)\frac{{\Delta }_i(a)}{g_n{(a|X_i)}^{I(a\in {\mathcal{D}}_i)}}.$$

We will derive the influence curve of this estimator in the case that g_n is a nonparametric estimator. Because the influence curve of a regular asymptotically linear estimator in a saturated model equals the efficient influence curve, this exercise will result in the wished efficient influence curve.

Derivation of influence curve of nonparametric estimator

Firstly, we note that β_n is the solution of

$$0=P_n{D}_h(\beta ,g_n)\equiv \frac{1}{n}\sum _{i=1}^n{D}_h(O_i|\beta ,g_n),$$

where

$$D_h(O|\beta ,g_n)=\sum _a\frac{\Delta \left(a\right)}{g_n{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}}h\left(a,V\right)\frac{d}{d\beta }m\left(a,V|\beta \right)\left(Y-m\left(a,V|\beta \right)\right),$$

where we use the notation Pf ≡ ∫ f(o)dP(0). A standard M-estimator analysis shows that, in first order, we have

$${\beta }_n-{\beta }_0\approx -c{({\beta }_0)}^{-1}\{(P_n-P_0)D_h({\beta }_0,g_0)+P_0\{D_h({\beta }_0,g_n)-D_h({\beta }_0,g_0)\}\},$$

where $c({\beta }_0)=\frac{d}{d{\beta }_0}{P}_0{D}_h({\beta }_0,g_0)$. So, it remains to determine the influence curve D₁(P₀) of the latter term P₀{D_h(β₀, g_n) − D_h(β₀, g₀)}. Then, the influence curve of β_n is given by:

$$IC(P_0)=-c{({\beta }_0)}^{-1}\{D_h({\beta }_0,g_0)+D_1(P_0)\}.$$

Derivation of the influence curve D₁(P₀)

We note that

$$\begin{array}{l}\frac{\Delta \left(a\right)}{g_n^{I\left(a\in \mathcal{D}\right)}}-\frac{\Delta \left(a\right)}{g_0^{I\left(a\in \mathcal{D}\right)}}=I\left(a\in \mathcal{D},A=a\right)\left(\frac{1}{g_n}-\frac{1}{g_0}\right)\\ \approx -I\left(a\in \mathcal{D},A=a\right)\frac{g_n-g_0}{g_0^2}.\end{array}$$

Thus,

$$\begin{array}{l}{P}_0(D_h({\beta }_0,g_n)-D_h({\beta }_0,g_0))=\\ -{\sum }_a{P}_{0}I\left(A=a,a\in \mathcal{D}\right)\frac{(g_n-g_0)\left(a|W\right)}{g_0^2\left(a|W\right)}{h}^{\ast }\left(a,V\right)\left(Y-m\left(a,V|\beta \right)\right),\end{array}$$

where we denote h* = hd/dβm. This can be written as:

$$-P_{W0}\sum _{a\in \mathcal{D}}\frac{(g_n-g_0)\left(a|W\right)}{g_0\left(a|W\right)}{h}^{\ast }\left(a,V\right)(Q_0\left(a,W\right)-m(a,V|{\beta }_0)).$$

We have

$$\begin{array}{l}{g}_n\left(a|w\right)-g_0\left(a|w\right)=\frac{(p_n-p_0)\left(a,w\right)}{p_0\left(w\right)}-\frac{p_0\left(a,w\right)}{p_0^2\left(w\right)}(p_n-P_0)\left(w\right)\\ =\frac{p_n\left(a,w\right)}{p_0\left(w\right)}-\frac{p_0\left(a,w\right)}{p_0^2\left(w\right)}{p}_n\left(w\right)\\ =\frac{p_n\left(a,w\right)}{p_0\left(w\right)}-\frac{g_0\left(a|w\right)}{p_0\left(w\right)}{p}_n\left(w\right),\end{array}$$

where $p_n\left(w\right)=\frac{1}{n}{\sum }_{i}I\left(W_i=w\right)$, p₀(w) = Pr(W = w), $p_n\left(a,w\right)=\frac{1}{n}{\sum }_{i}I\left(A_i=a,W_i=w\right)$, and p₀(a, w) = Pr(A = a, W = w). So − D_1i is given by

$$P_{W0}{\sum }_{a\in \mathcal{D}\left(W\right)}\left(\frac{I\left(A_i=a,W_i=w\right)}{p_0\left(W\right)}-\frac{g_0\left(a|W\right)}{p_0\left(W\right)}I\left(W_i=W\right)\right)h^{\ast }\left(a,V\right)\left(Q_0\left(a,W\right)-\frac{m_0\left(a,V\right)}{g_0\left(a|W\right)}\right).$$

Now, note that for a given function f P_W0I(W_i = W)f(W)/p₀(W) = Σ_w I(W_i = w)f(w) = f(W_i). Thus,

$$-D_{1i}=\sum _{a\in {\mathcal{D}}_i}(I(A_i=a)-g_0(a|W_i))\frac{h^{\ast }(a,V_i)}{g_0(a|W_i)}(Q_0(a,W_i)-m(a,V_i|{\beta }_0)).$$

We conclude that the efficient influence curve IC*(P₀) of β(P) at P₀ is given by:

$$\begin{array}{l}-c({\beta }_0)I{C}^{\ast }(P_0)=D_h({\beta }_0,g_0,Q_0)\\ \equiv D_h({\beta }_0,g_0)-D_{1h}({\beta }_0,g_0,Q_0)\\ \equiv \sum _a\frac{\Delta \left(a\right)}{g_0{\left(a|X\right)}^{I\left(a\in \mathcal{D}\right)}}h\left(a,V\right)\frac{d}{d\beta }m(a,V|{\beta }_0)(Y-m(a,V|{\beta }_0))\\ -\sum _{a\in \mathcal{D}}(I\left(A=a\right)-g_0\left(a|W\right))\frac{h^{\ast }\left(a,V\right)}{g_0\left(a|W\right)}(Q_0\left(a,W\right)-m(a,V|{\beta }_0)).\end{array}$$

This completes the proof of Result 6.

Appendix C: Inverse probability of treatment weighted estimation of intention-to-treat causal effects of time-dependent treatments

The IPTW estimation methodology is based on the following identifiability result for the intention-to-treat treatment-specific distributions.

Result 9 For any ā, we define the observed

$$C\left(\overline{a}\right)\equiv \text{min}\left\{t:A\left(t+1\right)\ne a\left(t+1\right)\text{or}a\left(t+1\right)\notin \mathcal{D}\left(t+1\right)\text{or}t=\tau \right\}.$$

Consider the indicator

$$\Delta \left(\overline{a}\right)=I\left(A\left(C\left(\overline{a}\right)+1\right)\notin \mathcal{D}\left(C\left(\overline{a}\right)+1\right)\text{or}C\left(\overline{a}\right)=\tau \right).$$ (12)

We have

$$\begin{array}{l}{E}_0\left(\Delta \left(\overline{a}\right)|X\left(\tau \right)\right)=g_0\left(\overline{a}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)\\ =\prod _{t=0}^{C\left(\overline{a}\right)}P\left(A\left(t\right)=a\left(t\right)|\overline{A}\left(t-1\right)=\overline{a}\left(t-1\right),\overline{L}\left(t\right)\right),\end{array}$$

where the latter product is defined as 1 if C(ā) = −1. We also have that, for any set of baseline co-variables V ⊂ L(0),

$$E_0\left(\frac{Y\Delta \left(\overline{a}\right)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}|V\right)=E_0\left(T_{d\left(\overline{a}\right)}|V\right).$$

Proof: Firstly, we note that

$$\Delta \left(\overline{a}\right)=\sum _{c=-1}^{\tau }I(\overline{A}\left(c\right)=\overline{a}\left(c\right),a\left(c+1\right)\notin {\mathcal{D}}_A\left(c+1\right)={\mathcal{D}}_{\overline{a}}\left(C+1\right),c\le C_{\overline{a}}\left(\overline{a}\right)),$$

where, for simplicity, we define I(a(τ + 1) ∉ (τ + 1) =1. Here we noted that _A(c + 1) = _ā(c)(c + 1), and I(c ≤ C_Ā(ā)) = I(c ≤ C_ā(c)(ā)). In addition, we noted that at most one of the indicators in the sum can be equal to 1. Now, take the conditional expectation, given X(τ), which gives

$$\sum _{c=-1}^{\tau }{g}_0\left(\overline{a}\left(c\right)|X\left(\tau \right)\right)I(a\left(c+1\right)\notin {\mathcal{D}}_{\overline{a}}\left(c+1\right),c\le C_{\overline{a}}\left(\overline{a}\right)).$$

We have that for c < C_ā(ā), a(c + 1) ∈ _ā(c + 1), and for c > C_ā(ā) the indicator is 0. Thus, the latter sum equals

$$g_0(\overline{a}(C_{\overline{a}}\left(\overline{a}\right))|X\left(\tau \right)).$$

This proves the first statement in the result.

Regarding the second statement, firstly, we note that $Y\frac{\Delta \left(\overline{a}\right)}{g_0\left(\overline{a}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}$ equals

$$\sum _{c=-1}^{\tau }\frac{Y_{\overline{a}\left(c\right)}}{g_0\left(\overline{a}\left(c\right)|X\left(c\right)\right)}I(\overline{A}\left(c\right)=\overline{a}\left(c\right),a\left(c+1\right)\notin {\mathcal{D}}_a\left(c+1\right),c\le C_{\overline{a}}\left(\overline{a}\right)),$$

where g₀(ā(c) | X(c)) is defined as 1 at c = −1. We also used that g₀(· | X(c)) = g₀(· | X(τ)). For c = −1, the term equals Y_d(ā)I(a(0) ∉ _a(0), c ≤ C_ā(ā)), and we will now show that for the terms with c ≥ 0 the conditional expectation, given X(c), equals Y_d(ā)I(a(c + 1) ∉ _ā(c + 1), c ≤ C_ā(ā)). Consider the c-specific term for c ≥ 0. We take the conditional expectation, given X(c) (so that Y_ā(c) and g₀(ā(c) | X(c)) is fixed), which yields

$$\begin{array}{l}\frac{g_0\left(\overline{a}\left(c\right)|X\left(c\right)\right)}{g_0\left(\overline{a}\left(c\right)|X\left(c\right)\right)}{Y}_{\overline{a}\left(c\right)}I(a\left(c+1\right)\notin {\mathcal{D}}_{\overline{a}}\left(c+1\right),c\le C_{\overline{a}}\left(\overline{a}\right))\\ =Y_{\overline{a}\left(c\right)}I(a\left(c+1\right)\notin {\mathcal{D}}_{\overline{a}}\left(c+1\right),c\le C_{\overline{a}}\left(\overline{a}\right)).\end{array}$$

We have that for c < C_ā(ā), a(c+1) ∈ _ā (c+1) and for c > C_ā(ā) the indicator is 0. Thus, the sum over c ∈ {−1, …, τ} of the conditional expectations of the c-specific term, given X(c), reduces to a single term corresponding with c = C_ā given by

$$Y_{\overline{a}(C_{\overline{a}}\left(\overline{a}\right))}=Y_{d\left(\overline{a}\right)}.$$

Finally, note that V ⊂ X(c) for all c ≥ 0. This proves the second statement of the result.

IPTW-estimating function for β_h

We can estimate β₀ with the following IPTW estimator

$${\beta }_n=\text{arg}\underset{\beta }{\text{min}}\sum _{i=1}^n\sum _{\overline{a}}{(Y_i-m(\overline{a},V_i|\beta ))}^{2}h(\overline{a},V_i)\frac{{\Delta }_i\left(\overline{a}\right)}{g_n({\overline{A}}_i(C_i\left(\overline{a}\right))|X_i\left(\tau \right))}.$$

This estimator is now a standard weighted least squares regression of (Y_i : ā) on V_i for a repeated measures type data set, where the weights are given by h(ā, V_i)Δ_i(ā)/g_n(Ā_i(C_i(ā)) | X_i(τ)), i = 1, …, n.

The latter weighted least squares regression corresponds with the following h-specific IPTW estimating function:

$$\begin{array}{l}{D}_h\left(O|\beta ,g\right)\equiv \\ \sum _{\overline{a}\in \mathcal{A}}h\left(\overline{a},V\right)\frac{d}{d\beta }m\left(\overline{a},V|\beta \right)\left(Y-m\left(\overline{a},V|\beta \right)\right)\frac{\Delta \left(\overline{a}\right)}{g\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}.\end{array}$$

By Result 9 we have that this estimating function is unbiased for β₀ = β_h0:

$$E_0{D}_h(O|{\beta }_0,g_0)=0.$$

In order to implement the above mentioned IPTW estimators of β_h0, or, ψ₀ itself, one needs to know the set {ā : Δ(ā) = 1} and the corresponding stopping times C(ā) for each observed O.

Algorithm for generating followed intention to treat treatments

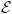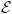Let ¹ denote the set of treatment left over during the algorithm, and let denote the wished set of treatments with corresponding stopping times. We initiate ¹ = , and initiate at the empty set.

Given L(0), set 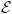= 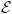∪ {(ā, −1) : a(0) ∉ (0)}: (thus, we add all ā ∈ ¹ with a(0) ∉ (0), and we set C(ā) = −1.

¹ = ¹/{ā ∈ ₁ : a(0) ∉ (0)}: that is, we delete the selected treatments from ₁.

Given L(0), A(0), L(1), set 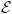= 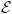∪ {(ā, 0) : ā ∈ ¹, a(0) = A(0), a(1) ∉ (1)}.

¹ = ¹/{ā ∈ ¹ : a(0) = A(0), a(1) ∉ (1)}.

In general, for j = 0, …, given L(0), A(0), …, A(j − 1), L(j), set = ∪ {(ā, j − 1) : ā, j − 1) : ā ∈ ¹, ā(j − 1) = Ā(j − 1), a(j) ∉ (j)}.

¹ = ¹/{ā ∈ ₁ : ā(j − 1), = Ā(j − 1), a(j) ∉ (j)}. Proceed till j = τ or ¹ is empty.

Appendix D: The optimal estimating function and corresponding locally efficient estimator for intention-to-treat causal effects of time-dependent treatments

The following result presents the efficient influence curve for β_h at P₀, and its corresponding optimal estimating function.

Result 10 Given a working model {m(ā, V | β) : β} for ψ₀(ā, V) = Ψ(P₀)(ā, V) ≡ E_P0(Y_d(ā) | V) indexed by a Euclidean parameter β, our parameter of interest is defined on the nonparametric model for P₀ as

$${\beta }_h\left(P\right)\equiv \text{arg}\underset{\beta }{\text{min}}{E}_P\sum _{\overline{a}}{\left(\Psi \left(P\right)\left(\overline{a},V\right)-m\left(\overline{a},V|\beta \right)\right)}^{2}h\left(\overline{a},V\right).$$

Let β_h0 = β_h(P₀) denote the true parameter value. Consider the following class of estimating functions:

$$D_{h,DR}({\beta }_0,g_0,Q_0)\equiv D_h({\beta }_0,g_0)-D_h({\beta }_0,g_0,Q_0),$$

where

$$\begin{array}{l}{D}_h(O|{\beta }_0,g_0)=\sum _{\overline{a}}\frac{\Delta \left(\overline{a}\right)h\left(\overline{a},V\right)\frac{d}{d{\beta }_0}m(\overline{a},V|{\beta }_0)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}(Y-m(\overline{a},V|{\beta }_0))\\ D_{h,t}^{\ast }({\beta }_0,g_0)\\ =\sum _{\overline{a}}I\left(C\left(\overline{a}\right)\ge t\right)\frac{\Delta \left(\overline{a}\right)h\left(\overline{a},V\right)\frac{d}{d\beta }m\left(\overline{a},V|\beta \right)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}(Y-m(\overline{a},V|{\beta }_0))\\ t=0,\dots ,\tau \\ D_h({\beta }_0,Q_0,g_0)=\\ \sum _{t=0}^{\tau }{E}_{g_0,Q_0}(D_{h,t}^{\ast }({\beta }_0,g_0)|\overline{A}\left(t\right),\overline{L}\left(t\right))-E_{g_0,Q_0}(D_{h,t}^{\ast }({\beta }_0,g_0)|\overline{A}\left(t-1\right),\overline{L}\left(t\right)).\end{array}$$

Here $g_0\left(\overline{A}\left(\tau \right)|X\left(\tau \right)\right)={\prod }_{t=0}^{\tau }{g}_0\left(A\left(t\right)|\overline{A}\left(t-1\right),\overline{L}\left(t\right)\right)$ and $Q_0\left(O\right)={\prod }_{t=0}^{\tau +1}Q\left(L\left(t\right)|\overline{L}\left(t-1\right),\overline{A}\left(t-1\right)\right)$.

We have that the efficient influence curve of β_h at P₀ is given by

$$I{C}^{\ast }\left(O\right)=-c{({\beta }_{h0})}^{-1}{D}_{h,DR}({\beta }_{h0},g_0,Q_0).$$

If E(Y_d(ā) | V) = m(ā, V | β₀), then for all functions h

$$E_0{D}_{h,DR}({\beta }_0,g_0,Q)=0\text{for all}Q.$$

If β_h0 = arg min_β E₀Σ_a(E₀(Y_d(ā) | V) − m(ā, V | β))²h(ā, V), then

$$E_0{D}_{h,DR}({\beta }_{h0},g_0,Q)=0\text{for all}Q.$$

For the point treatment data structure O = (L(0), A(0), Y), we have the following double robustness result:

$$E_0{D}_{h,DR}({\beta }_0,g,Q)=0\text{if either}g=g_0\text{or}Q=Q_0.$$

We have not been able to establish the double robustness of D_h,DR for time-dependent treatment processes, and suggest that the double robustness as stated for the point treatment data structure might only hold for point treatment. However, a particular type of generalized double robustness might be achievable, as defined in Robins and Rotnitzky (2001), but this remains to be established in future work.

Given an estimator g_n, Q_n of g₀, Q₀, we can define the estimator β_hn,DR as the solution of the estimating equation

$$0=\sum _{i=1}^n{D}_{h,DR}(O_i|\beta ,g_n,Q_n).$$

If m(· | β) is linear in β, then this estimating equation is linear in β so that its solution exists in closed form. This estimator is locally efficient under regularity conditions, in the sense that it is consistent, asymptotically linear and efficient if both g_n and Q_n are consistent, and it remains consistent and asymptotically linear if g₀ is consistently estimated. In order to avoid technicalities, we propose the bootstrap method to obtain an estimate of the sampling distribution of β_hn,DR and to construct corresponding confidence intervals.

Proof of result 10. We will first show the robustness of the unbiasedness of the estimating function w.r.t. miss-specification of Q: E₀D_h,DR(β₀, g₀, Q) = 0 for all Q. Firstly, we have E₀D_h(β₀, g₀) = 0. In addition, we have D_h(β₀, g₀, Q) = Σ_t r_t(Ā(t), L̄(t)) − E_g0(r_t | Ā(t − 1), L̄(t)) for $r_t=E_{Q,g_0}(D_{h,t}^{\ast }\left(Q,g\right)|\overline{A}\left(t\right),\overline{L}\left(t\right))$ so that each t-specific term has conditional mean zero, given Ā(t), L̄(t) (for all functions r). This shows that E₀D_h,DR(β₀, g₀, Q) = 0 for all Q.

Derivation of influence curve of nonparametric estimator

Consider the estimator

$${\beta }_n=\text{arg}\underset{\beta }{\text{min}}\sum _{i=1}^n\sum _{\overline{a}}{(Y_i-m(\overline{a},V_i|\beta ))}^{2}h(\overline{a},V_i)\frac{{\Delta }_i\left(\overline{a}\right)}{g_n({\overline{A}}_i(C_i\left(\overline{a}\right))|X_i\left(\tau \right))}$$

We will derive the influence curve of this estimator in the case that g_n is a nonparametric estimator. Because the influence curve of a regular asymptotically linear estimator in a saturated model equals the efficient influence curve, this exercise will result in the wished efficient influence curve. In the sequel, we will use the notation ≈ to indicate a first order approximation: since all our random variables are discrete and finite, the claimed asymptotic linearity of the estimator with corresponding influence curve can be fully formalized. Firstly, we note that β_n is the solution of

$$0=P_n{D}_h(\beta ,g_n)=0,$$

where

$$D_h(O|\beta ,g_n)=\sum _{\overline{a}}\frac{\Delta \left(\overline{a}\right)}{g_n\left(C\left(\overline{a}\right)|X\left(\tau \right)\right)}h\left(\overline{a},V\right)\frac{d}{d\beta }m\left(\overline{a},V|\beta \right)\left(Y-m\left(\overline{a},V|\beta \right)\right).$$

In first order we have

$${\beta }_n-{\beta }_0=-c{({\beta }_0)}^{-1}\{(P_n-P_0)D_h({\beta }_0,g_0)+P_0\{D_h({\beta }_0,g_n)-D_h({\beta }_0,g_0)\}\},$$

where $c({\beta }_0)=\frac{d}{d{\beta }_0}{P}_0{D}_h({\beta }_0,g_0)$. So, we need to determine the influence curve D₁(P₀) of the latter term P₀(D_h(β₀, g_n) − D_h(β₀, g₀)). Then, the influence curve of β_n is given by:

$$IC(P_0)=-c{({\beta }_0)}^{-1}\{D_h({\beta }_0,g_0)+D_1(P_0)\}.$$

We note that

$$\frac{\Delta \left(\overline{a}\right)}{g_n\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}-\frac{\Delta \left(\overline{a}\right)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}\approx -\Delta \left(\overline{a}\right)\frac{(g_n-g_0)\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}{g_0^2\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)},$$

where we remind the reader that this term equals zero if C(ā) = −1, even when Δ(ā) = 1, since in that case Δ(ā)/g(C(ā) | X(τ)) ≡ 1 for both g = g_n and g = g₀.

Thus,

$$\begin{array}{l}{P}_0(D_h({\beta }_0,g_n)-D_h({\beta }_0,g_0))\approx \\ -{\sum }_{\overline{a}}{P}_0\frac{\Delta \left(\overline{a}\right)}{g_0^2\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}(g_n-g_0)\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)h^{\ast }\left(\overline{a},V\right)\left(Y-m\left(\overline{a},V|\beta \right)\right),\end{array}$$

where we denote h* = hd/dβm. Let

$$B\left(\overline{a},O\right)\equiv \frac{\Delta \left(\overline{a}\right)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}{h}^{\ast }\left(\overline{a},V\right)\left(Y-m\left(\overline{a},V|\beta \right)\right).$$

Then the latter expectation w.r.t. P₀ can be rewritten as follows:

$$-{\sum }_{\overline{a}}{P}_0\frac{B\left(\overline{a},O\right)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}(g_n-g_0)\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right).$$

Define $g_n\left(\underset{\_}{a}\left(l+1,c\right)|X\left(\tau \right)\right)\equiv {\prod }_{j=l+1}^c{g}_0\left(a\left(j\right)|\overline{a}\left(j-1\right),X\left(\tau \right)\right)$. Now, we note that

$$\begin{array}{l}(g_n-g_0)\left(\overline{a}\left(c\right)|X\left(\tau \right)\right)\\ =\prod _{j=0}^c{g}_n\left(a\left(j\right)|\overline{a}\left(j-1\right),X\left(\tau \right)\right)-\prod _{j=0}^c{g}_0\left(a\left(j\right)|\overline{a}\left(j-1\right),X\left(\tau \right)\right)\\ =\sum _{l=0}^c{g}_n\left(\overline{a}\left(l-1\right)|X\left(\tau \right)\right)(g_n-g_0)\left(a\left(l\right)|\overline{a}\left(l-1\right),X\left(\tau \right)\right)g_0\left(\underset{\_}{a}\left(l+1,c\right)|X\left(\tau \right)\right)\\ \approx \sum _{l=0}^c\frac{g_0\left(\overline{a}\left(c\right)|X\left(\tau \right)\right)}{g_0\left(a\left(l\right)|\overline{a}\left(l-1\right),X\left(\tau \right)\right)}(g_n-g_0)\left(a\left(l\right)|\overline{a}\left(l-1\right),X\left(\tau \right)\right).\end{array}$$

Substitution of this latter expression with c = C(ā) gives us now:

$$-{\sum }_{\overline{a}}{P}_{0}B\left(\overline{a},O\right)\left({\sum }_{l=0}^{C\left(\overline{a}\right)}\frac{(g_n-g_0)\left(A\left(l\right)|\overline{A}\left(l-1\right),X\left(\tau \right)\right)}{g_0\left(A\left(l\right)|\overline{A}\left(l-1\right),X\left(\tau \right)\right)}\right).$$

Let W(l) = (Ā(l − 1), L̄(l)). We have

$$\begin{array}{l}{g}_n\left(a\left(l\right)|w\left(l\right)\right)-g_0\left(a\left(l\right)|w\left(l\right)\right)\\ =\frac{(p_n-p_0)\left(a\left(l\right),w\left(l\right)\right)}{p_0\left(w\left(l\right)\right)}-\frac{p_0\left(a\left(l\right),w\left(l\right)\right)}{p_0^2\left(w\left(l\right)\right)}(p_n-p_0)\left(w\left(l\right)\right)\\ =\frac{p_n\left(a\left(l\right),w\left(l\right)\right)}{p_0\left(w\left(l\right)\right)}-\frac{p_0\left(a\left(l\right),w\left(l\right)\right)}{p_0^2\left(w\left(l\right)\right)}{p}_n\left(w\left(l\right)\right)\\ =\frac{p_n\left(a\left(l\right),w\left(l\right)\right)}{p_0\left(w\left(l\right)\right)}-g_0\left(a\left(l\right)|w\left(l\right)\right)\frac{p_n\left(w\left(l\right)\right)}{p_0\left(w\left(l\right)\right)},\end{array}$$

Where

$$\begin{array}{c}{p}_n\left(w\left(l\right)\right)=\frac{1}{n}\sum _{i}I(W_i\left(l\right)=w\left(l\right)),\\ p_n\left(a\left(l\right),w\left(l\right)\right)=\frac{1}{n}\sum _{i}I(A_i\left(l\right)=a\left(l\right),W_i\left(l\right)=w\left(l\right)),\\ p_0\left(w\left(l\right)\right)=P\left(W\left(l\right)=w\left(l\right)\right),\end{array}$$

and

$$p_0\left(a\left(l\right),w\left(l\right)\right)=P\left(A\left(l\right)=a\left(l\right),W\left(l\right)=w\left(l\right)\right).$$

So we obtain

$$\begin{array}{l}-{\sum }_{\overline{a}}{P}_{0}B\left(\overline{a},O\right){\sum }_{l=0}^{C\left(\overline{a}\right)}\frac{p_n\left(A\left(l\right),W\left(l\right)\right)-g_0\left(A\left(l\right)|W\left(l\right)\right)p_n(W\left(l\right)}{g_0\left(A\left(l\right)|W\left(l\right)\right)p_0\left(W\left(l\right)\right)}\\ =-\frac{1}{n}{\sum }_{i=1}^n{\sum }_{\overline{a}}{P}_{0}B\left(\overline{a},O\right)\\ \left({\sum }_{l=0}^{C\left(\overline{a}\right)}\frac{I(W_i\left(l\right)=W\left(l\right))}{g_0\left(A\left(l\right)|W\left(l\right)\right)p_0\left(W\left(l\right)\right)}(I(A_i\left(l\right)=A\left(l\right))-g_0\left(A\left(l\right)|W\left(l\right)\right))\right)\\ =-\frac{1}{n}{\sum }_{i=1}^n{\sum }_{\overline{a}}{\sum }_{l=0}^{\tau }{P}_{0}B\left(\overline{a},O\right)I\left(l\le C\left(\overline{a}\right)\right)\\ \left(\frac{I(W_i\left(l\right)=W\left(l\right))}{g_0\left(A\left(l\right)|W\left(l\right)\right)p_0\left(W\left(l\right)\right)}(I(A_i\left(l\right)=A\left(l\right))-g_0\left(A\left(l\right)|W\left(l\right)\right))\right)\\ =-\frac{1}{n}{\sum }_{i=1}^n{\sum }_{\overline{a}}{\sum }_{l=0}^{\tau }{P}_{0,A\left(l\right),W\left(l\right)}{E}_0\left(I\left(l\le C\left(\overline{a}\right)\right)B\left(\overline{a},O\right)|A\left(l\right),W\left(l\right)\right)\\ \frac{I(A_i\left(l\right)=A\left(l\right),W_i\left(l\right)=W\left(l\right))-g_0\left(A\left(l\right)|W\left(l\right)\right)I(W_i\left(l\right)=W\left(l\right)}{g_0\left(A\left(l\right)|W\left(l\right)\right)p_0\left(W\left(l\right)\right)}\\ =-\frac{1}{n}{\sum }_{i=1}^n{\sum }_{\overline{a}}{\sum }_{l=0}^{\tau }{\sum }_{a^{\ast }\left(l\right)}\\ E_0(I\left(l\le C\left(\overline{a}\right)\right)B\left(\overline{a},O\right)|A\left(l\right)=a^{\ast }\left(l\right),W_i\left(l\right))(I(A_i\left(l\right)=a^{\ast }\left(l\right))-g_0(a^{\ast }\left(l\right)|W_i\left(l\right)))\\ =-\frac{1}{n}{\sum }_{i=1}^n{\sum }_{\overline{a}}{\sum }_{l=0}^{\tau }\\ E_0(I\left(l\le C\left(\overline{a}\right)\right)B\left(\overline{a},O\right)|A\left(l\right)=A_i\left(l\right),W_i\left(l\right))-E_0(I\left(l\le C\left(\overline{a}\right)\right)B\left(\overline{a},O\right)|W_i\left(l\right))\end{array}$$

Thus we can represent −D₁(O) as:

$$\begin{array}{l}{\sum }_{\overline{a}}{\sum }_{l=0}^{\tau }{E}_0\left(I\left(C\left(\overline{a}\right)\ge l\right)B\left(\overline{a},O\right)|A\left(l\right),W\left(l\right)\right)-E_0\left(I\left(C\left(\overline{a}\right)\ge l\right)B\left(\overline{a},O\right)|W\left(l\right)\right)\\ ={\sum }_{l=0}^{\tau }(E_0\left({\sum }_{\overline{a}}I\left(C\left(\overline{a}\right)\ge l\right)\frac{\Delta \left(\overline{a}\right)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}{h}^{\ast }\left(\overline{a},V\right)\left(Y-m\left(\overline{a},V|\beta \right)\right)|A\left(l\right),W\left(l\right)\right)-\\ E_0\left({\sum }_{\overline{a}}I\left(C\left(\overline{a}\right)\ge l\right)\frac{\Delta \left(\overline{a}\right)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}{h}^{\ast }\left(\overline{a},V\right)\left(Y-m\left(\overline{a},V|\beta \right)\right)|W\left(l\right)\right).\end{array}$$

So,

$$-D_1\left(O\right)=\sum _{l=0}^{\tau }{E}_0(D_{h,l}^{\ast }(g_0,\beta )|A\left(l\right),W\left(l\right))-E_0(D_{h,l}^{\ast }(g_0,{\beta }_0)|W\left(l\right)),$$

Where

$$D_{h,l}^{\ast }(O|{\beta }_0,g_0)\equiv \sum _{\overline{a}}I\left(C\left(\overline{a}\right)\ge l\right)\frac{\Delta \left(\overline{a}\right)}{g_0\left(\overline{A}\left(C\left(\overline{a}\right)\right)|X\left(\tau \right)\right)}{h}^{\ast }\left(\overline{a},V\right)\left(Y-m\left(\overline{a},V|\beta \right)\right).$$

We conclude that the efficient influence curve IC*(P₀) of β(P) at P₀ is given by:

$$\begin{array}{l}-c({\beta }_0)I{C}^{\ast }(P_0)=D_h({\beta }_0,g_0,Q_0)\\ =D_h({\beta }_0,g_0)-D_h({\beta }_0,g_0,Q_0)\\ \equiv D_h({\beta }_0,g_0)-\sum _{t=0}^{\tau }{E}_0(D_{h,t}^{\ast }({\beta }_0,g_0)|\overline{A}\left(t\right),\overline{L}\left(t\right))\\ +\sum _{t=0}^{\tau }{E}_0(D_{h,t}^{\ast }({\beta }_0,g_0)|\overline{A}\left(t-1\right),\overline{L}\left(t\right)).\end{array}$$

This completes the proof of Result 10.