BETTER STATISTICS FOR BETTER DECISIONS: REJECTING NULL HYPOTHESES STATISTICAL TESTS IN FAVOR OF REPLICATION STATISTICS

Abstract

Despite being under challenge for the past 50 years, null hypothesis significance testing (NHST) remains dominant in the scientific field for want of viable alternatives. NHST, along with its significance level p, is inadequate for most of the uses to which it is put, a flaw that is of particular interest to educational practitioners who too often must use it to sanctify their research. In this article, we review the failure of NHST and propose p_rep, the probability of replicating an effect, as a more useful statistic for evaluating research and aiding practical decision making.

Statistics can address three different types of questions (Royall, 1997):

1. What should I believe?

2. How should I evaluate this evidence?

3. What should I do?

The first two are of great importance to scientists: Finding the answers to these questions defines their praxis. The last question, on which we focus here, is of greater relevance to practitioners who must deal with decisions that have practical consequences. In its simplest form, a decision is a choice between two alternative courses of action. All other things being equal, optimal decisions favor courses of action that are expected to yield higher returns (e.g., better indices of class attendance) and are less costly to implement over those that are expected to yield lower returns and cost more. Choices with dominant alternatives are trivial; it is when costs and expected returns covary in the same direction that practical choices may become dilemmas, invoking the aid of decision committees and statisticians. Costly actions must be justified by their returns exceeding some minimum standard of expected improvement. Once that minimum improvement is defined, researchers produce data from which statisticians, in turn, are expected to determine whether the minimum improvement is real or not. Null hypothesis significance tests (NHST) are the conventional tool for making these evaluations. The privileged status of NHST is most clearly reflected in its prevalence as a diagnostic tool in the psychological and educational literature and in its entrenchment in the statistical training of education and psychology professionals. We will illustrate its use by applying the NHST routine to the solution of a practical binary-choice situation and demonstrate its inadequacy in informing a decision in that scenario. We argue that the probability of obtaining a minimum cost-effective return is more informative than arbitrary decisions about statistical significance and provide the rationale and algorithm for its estimation.

The Null Hypothesis Significance Testing Routine

Imagine that you are asked to evaluate a method for teaching English as a second language (ESL). How would you decide whether this new method for teaching ESL is better than the traditional one? First, you would collect data from two groups of students being taught ESL, matched as closely as possible on all potentially relevant variables, one using the old teaching method (Group OLD), and the other the new method (Group NEW). At the end of the course, you would obtain a validated measure of ESL performance (e.g., CBT-TOEFL) from each student; this score, or the student’s change score, is the measure of the return yielded by each teaching method. These results are then entered as two columns of numbers in an SPSS spreadsheet; what to do with them depends on the research question. With certain assumptions, a specific NHST procedure such as a one- or two-tailed t test would allow a researcher to determine the probability p that the difference in mean TOEFL scores between Group OLD and Group NEW would be obtained, given that those scores are sampled from the same population distribution—that is, given that the intervention did not separate the groups into two subpopulations with different labels such as “speaks English better.” This difference is often normalized and reported as effect size, measured as

$$d^{\prime }=(M_{\text{NEW}}-M_{\text{OLD}})/s_{\text{POOLED}},$$ (1)

where s_POOLED is the pooled standard deviation of performances. The null hypothesis, which assumes that scores in both groups are samples of the same population distribution, is H₀: μ_NEW = μ_OLD. A p value indicates the probability of d′ given H₀, or p (d′|H₀).

We specified a simple binary choice and followed the traditional NHST steps to reach a decision—but instead we obtained a p value. What decision should be made based on a particular p value? If the p value is below a criterion α, say .01, we would conclude that the difference between groups is “significant,” and would probably decide to adopt the new method for teaching ESL, other things being equal. This decision procedure, however, presents two problems.

Problem 1: Confidence

If other things are truly equal, a significance test is unnecessary. Regardless of the p value obtained, the method that yields higher mean TOEFL scores should be adopted, given that there is no differential cost in implementing one or the other. Although the population means may be predicted with more or less accuracy by the sample means, a predicted improvement should be pursued, assuming there is no cost for changing techniques. The triviality of this choice vanishes when other things are not equal. In the ESL example, the better teaching method must have expected returns that are high enough to offset the cost of its implementation (i.e., retraining, acquisition of new material). How should this minimum difference be factored into a decision, given p and a d′ values? The usual strategy is to focus on the effect size d′: If d′ is greater than a minimum criterion (e.g., d′ > 0.3) the better alternative is adopted, regardless of cost—otherwise it is not. However, d′ is an estimate of the difference between groups: How certain can one be of that estimate? More generally, what is the certainty that, given an obtained difference d′ = 0.3, further tests would demonstrate any difference in the same direction (i.e., d′ > 0)?

One conventional solution is to obtain a confidence interval (CI) of the difference of treatment means. A CI provides a range of treatment differences within which the population difference is expected 100(1 > α)% of the time. That is, if 1000 comparisons between ESL teaching methods were made, and if in each comparison a 95% CI was drawn around each mean difference (i.e.,α = .05), we would expect approximately 950 of those intervals to include the population difference between ESL methods. Unfortunately, a single CI is frequently misinterpreted as the range within which 950 of the next 1000 mean differences would fall. The difference between these two interpretations is illustrated in Figure 1. Data points are d′ values obtained from hypothetical replications of TOEFL scores comparisons. When 95% CIs are drawn around each d′ value (shown as bars in Figure 1), 95% of them include the parameter δ (horizontal line). However, many fewer than 95% of the d′ values fall within the first CI (projected as broken lines). This is because there are two sources of sampling error: the error realized in the obtained measure and all the future errors in the hypothetical replications. It requires considerable conceptual effort to avoid this misconception when using CIs. A discussion of CIs and their proper interpretation may be found both in Estes (1997) and Thompson (2002), and in the excellent reviews by Cumming and associates—in this issue, in other journals, (e.g., Cumming & Finch, 2001) and on his Web site (http://www.latrobe.edu.au/psy/staff/cumming.html).

Figure 1.

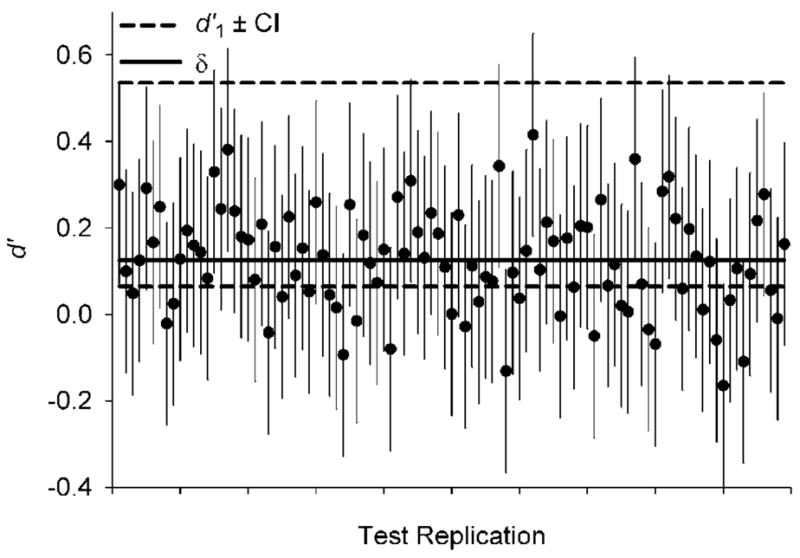
Hypothetical results of 100 replications of a comparison between two group means. Each data point was sampled from a normal distribution, its mean (δ) represented by the solid horizontal line. Confidence intervals around each data point were calculated using the standard deviation of the data. The dashed horizontal lines are projections of a confidence interval centered on the first data point.

Problem 2: Power

What if d′ > 0, but p = .05 or .07 or even .25? Should the old method be preserved because there was no real difference? Recall that p indicates the probability that a difference ≥d′ would be obtained by chance, which is not the same as the expected magnitude of that difference. A high p value does not necessarily mean that the new method is not an improvement over the old; rather, there exists the possibility that the statistical test was not powerful enough to render a real difference significant. The conventional solution to this problem is to choose the size of each treatment group based on the results of a power analysis conducted prior to the comparison of teaching methods. The inputs to a power analysis are the hypostasized population effect size (δ*) and the probability α of rejecting the null given that d′ = δ*. In a choice situation, δ^* could take on the value of the minimum effect size that would justify adoption of the more costly alternative; if no difference is detected, the less costly alternative would be chosen, decision makers knowing that there is a probability β of having made the wrong choice (Type II error). Thus, two criteria must be established: a minimum d′ value that would justify the adoption of the new method and the probability, or willingness, of missing a significant effect (β ≈ 20% is conventional). As an example, suppose that the power analysis says that at least 1000 students should be recruited for each ESL teaching method group. If these group sizes are not physically or financially possible, the probability of making a Type II error would increase. But even if it were possible to recruit 1000 students for each group, we may be back close to where we started, obtaining an “insignificant” p value of .07 regardless! Thus, conducting a power analysis does not guarantee that NHST will guide us to a resolute decision.

An Alternative to NHST: Probability of Replication

The NHST routine provides a probability (p) associated with a statistic (d′), given a null hypothesis (H₀). When factoring in decision-relevant variables such as the difficulty of switching teaching methods, the statistics d′ and p, by themselves, are inadequate. Confidence intervals appear to show the probability of a minimum and maximum mean difference in future comparisons, but they do not. Even with power analysis, marginal significance is always possible, confounding any decision. To solve these problems, we suggest the adoption of a statistic that provides what confidence intervals do not and abandons the discontinuous acceptance criteria on which the issue of marginal significance hinges. That statistic is the estimated probability of replication (p_rep). While in this article we cover the basic rationale of p_rep, further reading can provide a tutorial (Killeen, 2005c, in press), a more detailed discussion (Killeen, 2005a, 2005b), and an alternate decision-theoretic approach (Killeen, 2006).

Consider the information provided by the p value in a NHST. The null hypothesis (H₀) is represented in Figure 2A by a distribution of effects centered on zero; the shaded area represents the probability of sampling an effect $d_2^{\prime }$ larger than the one obtained ( $d_1^{\prime }$) if the null hypothesis were true, that is, $p(d_2^{\prime }>d_1^{\prime }\mid H_0)$. This is the conventional “level of significance.” A particular level of significance connotes the likelihood of the null hypothesis, $p(H_0\mid d_1^{\prime })$, by pointing at the unlikelihood of an obtained effect. Note, however, that level of significance p and likelihood of H₀ are not the same; even if they were, the probability of effects sampled from H₀ in future comparisons does not translate into an expectation of the size of future effects on which to base a decision. A decision would be better informed by knowing the probability of obtaining another positive effect in replication, one that exceeds some minimum effect size $d_s^{\prime }:PR=p(d^{\prime }>d_s^{\prime }\mid \delta )$, where d′ is any effect size greater than the minimum effect size that would support a positive decision (e.g., adopt new method), $d_s^{\prime }$, and δ is the true mean of the distribution of the effects. In the example of ESL teaching methods, this is the probability that a minimum acceptable improvement in ESL performance would be obtained, if the new method were adopted. If this probability is satisfactory, the new method should be adopted; otherwise, it should be rejected.

Figure 2.

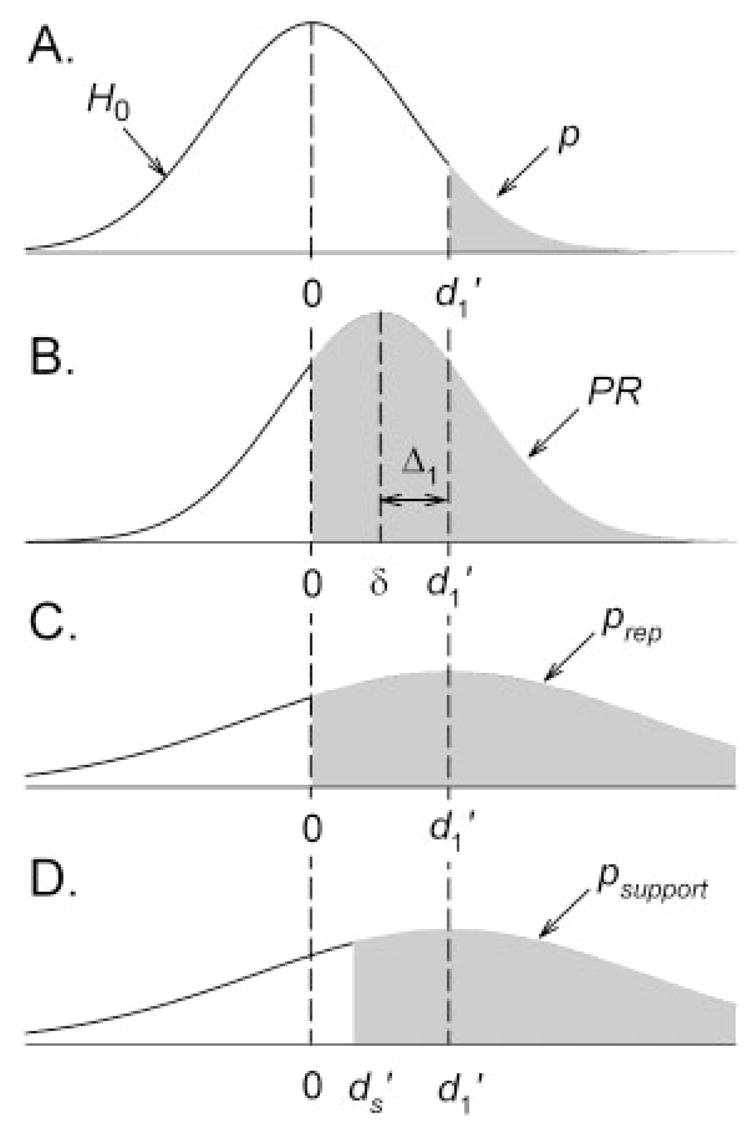
The shaded areas in these panels show the following: (A) probability (p) of obtaining an effect larger than $d_1^{\prime }$ under a null distribution. (B) Probability of obtaining an effect larger than zero (the probability of replication, or PR) under the true normal distribution of effects with mean $\delta ;d_1^{\prime }$ is a sample from this distribution, with sampling error Δ₁. (C) Estimate of PR (p_rep) under the distribution of effects estimated from $d_1^{\prime }$. (D) Estimate of the probability of a replication having an effect size greater than criterion $d_s^{\prime }$.

Figure 2B illustrates this approach graphically, where the true distribution of effects is represented as a normal distribution (Hedges & Olkin, 1985), centered on the true (but unknown) population effect size δ; sampling error for a measurement $d_1^{\prime }$ is represented by

$${\mathrm{\Delta }}_1=d_1^{\prime }-\delta .$$ (2)

For the moment, the minimum difference criterion, $d_s^{\prime }$, has been set to zero for simplicity (i.e., any improvement supports a positive decision). The shaded area to the right of $d_s^{\prime }=0$ in Figure 2B represents PR. Note that (a) in the calculation of PR, the null hypothesis H₀ may be disregarded, but (b) without δ, PR cannot be calculated. Because δ is unknown, we must estimate PR based solely on $d_1^{\prime }$.

Effect sizes are approximately normally distributed, with a standard error approximately equal to the square root of

$${\sigma }_{d^{\prime }}^2\approx \frac{n^2}{n_1{n}_2(n-4)},$$ (3)

where n₁ and n₂ are the sample sizes of each treatment, n + n₁ + n₂, and $-1<d_1^{\prime }<1$ (Hedges & Olkin, 1985; Killeen, 2005a). When n₁ = n₂, this further simplifies to

$${\sigma }_{d^{\prime }}^2\approx 4/(n-4).$$ (4)

With these estimates of effect size ( $d_1^{\prime }$) and its variance ( ${\sigma }_{d^{\prime }}^2$), an estimate of PR may be calculated. We call this estimate p_rep.

Calculating p_rep

The path leading to this statistic is somewhat technical (Appendix A), but an intuitive understanding may be gained from Figure 2. The variance of the sampling distribution for the original effect size is ${\sigma }_{d^{\prime }}^2$. This error is incurred twice: once in the original estimate (shown as the sampling error Δ₁) and again as the sampling error of the replication Δ₂. The expected value of the squares of these errors corresponds to the variance of the sampling distributions. Because they are incurred twice, these variances summate. Therefore, the variance of the replication distribution, shown in the bottom of Figure 2, is

$${\sigma }_R^2=2{\sigma }_{d^{\prime }}^2,$$ (5)

and the probability distribution for replications is

$$p(d_2^{\prime }\mid d_1^{\prime })\sim N(d_1^{\prime },{\sigma }_R).$$ (6)

The estimated probability of a replication, $p(d_2^{\prime }>0\mid d_1^{\prime })$ or p_rep, is the area of the distribution for which $d_1^{\prime }$ is greater than 0, shaded in Figure 2C. This is equivalent to the cumulative probability in a normal distribution up to

$$z=d_1^{\prime }/{\sigma }_R.$$ (7)

In a spreadsheet program such as Microsoft Excel, simply input the obtained z value in a NORMS-DIST() function to obtain p_rep. Appendix B summarizes the steps to obtain p_rep from group means and standard deviations.

Let us illustrate the calculation of p_rep with a hypothetical example. Suppose that the two methods of teaching ESL were tested in two groups of 127 students (n_OLD = n_NEW = 127; n = 254). Both groups are matched on all relevant variables (e.g., baseline TOEFL scores, age, gender, educational background, etc.). After a semester of exposure to their group’s teaching method, each student is tested using CBT-TOEFL, which has a range of possible scores between 40 (worst) and 300 (best). The mean TOEFL score obtained by Group OLD was 206.1, whereas the mean score of Group NEW was 240. Pooled standard deviation s_POOLED = 169.3; thus

$$\text{From}\text{Equation}1:d_1^{\prime }=(240-206.1)/169.3=0.2;$$

$$\text{From}\text{Equation}4:{\sigma }_{d^{\prime }}^2=4/(254-4)=0.016;$$

$$\text{From}\text{Equation}5:{\sigma }_R^2=2·0.016=0.032;$$

$$\text{From}\text{Equation}7:d_1^{\prime }/{\sigma }_R=0.2/\sqrt{0.032}=1.12;$$

finally,

$$p_{\mathit{rep}}=\text{NORMSDIST}(1.12)=\mathrm{.87.}$$

These results indicate that, on average, almost nine out of every ten groups of 127 students may be expected to obtain higher average TOEFL scores when exposed to the new method rather than the old.

Incorporating a Minimum Difference Criterion ( $d_s^{\prime }$)

So far we have considered the situation where the minimum difference criterion $d_s^{\prime }=0$, that is, where any positive difference in scores justifies the adoption of the more costly alternative. It is more realistic, however, to work under the assumption that very small positive differences, however certain, may not justify the cost of the better option. In that case, the first step is to calculate the difference in costs between the two alternatives and define the minimum effect size $d_s^{\prime }$ that would justify the cost differential. The function that relates cost differentials and minimum difference criteria could take any shape; it may be continuous, as in the case where performance is evaluated by the average TOEFL score obtained, or it may be discontinuous, as in the case where foreign teaching assistants must obtain a minimum TOEFL score to become certified. For illustration purposes and simplicity, let us assume the latter. Suppose that the old ESL teaching method yielded an average TOEFL score of 206.1, but students need at least a 223 to qualify for teaching assistantships. This would represent a minimum difference between passing and failing of 16.9 points. For generality’s sake, we specify the minimum difference as an effect size, which is the difference divided by the pooled standard deviation (s_POOLED). An estimate of s_POOLED, in this case, can be obtained from prior TOEFLs. Using the values from the examples above (M_NEW = 240, M_OLD = 206.1, s_POOLED = 169.3), if the required minimum improvement in TOEFL scores is 16.9 points, and, as in the above example, M_NEW − M_OLD = 33.9, then $d_s^{\prime }=16.9/169.3=\mathrm{0.1.}$ Thus, 0.1 is the minimum effect required from the new method.

Just as p_rep is an estimate of the probability of obtaining a second effect greater than zero, p_support is an estimate of the probability of obtaining a second effect greater than $d_s^{\prime }$. This probability is the area of the distribution for which d′ is greater than $d_s^{\prime }$, shaded in Figure 2D and equivalent to the cumulative probability in a normal distribution up to

$$z=(d_1^{\prime }-d_s^{\prime })/{\sigma }_R.$$ (8)

This z value may be input into a table of normal deviates, or a spreadsheet, to obtain p_support. From Equation 8:

$$\begin{array}{l}(d_1^{\prime }-d_s^{\prime })/{\sigma }_R=(0.2-0.1)/0.18=0.56;\\ p_{\mathit{support}}=\text{NORMSDIST}(0.56)=\mathrm{.71.}\end{array}$$

This means that we expect about seven of every ten groups of 127 students to increase their average TOEFL score by at least 16.9 points, and therefore qualify for a teaching assistantship, when exposed to the new method rather than the old.

From p to p_rep and p_support: Two Examples from Psychology in the Schools

In a study of mathematics proficiency and frustration response, Scime and Norvilitis (2006) asked 64 children with and without attention deficit hyperactivity disorder (ADHD) to complete a complex puzzle task and arithmetic problems of increasing difficulty. They compared the ADHD and non-ADHD groups across 17 ratings of task performance, reaction to frustration, emotional competence, and proficiency in mathematics. Individual t tests established the significance of between-group differences on each rating category. Because of the large number of t tests, the researchers applied a Bonferroni correction to minimize Type I errors, elevating the significance criterion to α = .003. Given the high criterion level, only three significant differences were detected.

Even when informing an intervention decision is not strictly the intent of a comparison, remaining agnostic about nonsignificant differences may prove difficult. In comparing the mathematics proficiency of ADHD and non-ADHD children, Scime and Norvilitis (2006) found a significant difference in overall completion rates, but not in overall accuracy. Based on these results, Scime and Norvilitis concluded that “children with ADHD did not complete as many items but were equally accurate on those that they did complete” (p. 383, italics added). This conclusion, however, is not supported by the data, as shown in Table 1: Children without ADHD were more accurate in their problem solving than those with ADHD, although the difference was not statistically significant (p > .003). In fact, p_rep for this comparison suggests that in 65% of similar comparisons, the children without ADHD would outperform the children with ADHD. This percentage is, undoubtedly, much smaller than the proportion of tests in which ADHD is predicted to be associated with lower completion rates (99%). However, the fact that accuracy is more similar across groups than completion rates does not translate into equal performance. Whether 65% is a meaningful failure rate or not is a theoretical and practical consideration, not a statistical one.

Table 1.

Statistical Analysis of Selected Tests From Two Studies

Study	Variable	n	M1 (s1)	M2 (s2)	d′	p	prep
Scime & Norvilitis (2006)	Mathematics-Accuracy	64	83.81 (15.44)	86.44 (18.71)	0.15	.285	.649
	Mathematics-Completion	64	26.88 (22.14)	44.52 (15.69)	0.98	.002	.994
	TMMS-C Emotional Attention	64	3.30 (0.43)	3.65 (0.56)	0.67	.028	.958
	TMMS-C Emotional Clarity	64	3.63 (0.69)	3.85 (0.64)	0.34	.085	.806
Linares et al. (2005)	Reading (UMSP)	94	2.63 (0.91)	2.81 (0.79)	0.21	.163	.753
	Reading (Comparison)	102	2.54 (1.02)	2.73 (0.89)	0.20	.169	.748
	Math (UMSP)	94	2.41 (0.98)	2.75 (0.85)	0.36	.044	.884
	Math (Comparison)	102	2.78 (1.02)	2.67 (0.95)	−0.11	n.a.	.353

Note. Scime and Norvilitis (2006): Group 1 = ADHD, Group 2 = No-ADHD; Mathematics scores were based on total number of problems completed and number of problems completed correctly; TMMS-C = Trait Meta-Mood Scale for Children. Linares et al. (2005): Group 1 = Grades at baseline, Group 2 = Grades at Year 2; reading and math grades are on a range of 1 (unsatisfactory) to 4 (excellent). All p values were estimated from published data using one-tailed t tests for independent samples.

The high significance criterion imposed by Scime and Norvilitis (2006) did yield some differences marginally significant. For example, in the Emotional Attention variable of the Trait Meta-Mood Scale for Children (TMMS-C), we may expect children without ADHD to score higher than children with ADHD in 96% of similar tests. Despite such a high percentage, Scime and Norvilitis report the difference as not significant. Contradictions such as this one may be attributed to the stringent familywise error correction established by the researchers, although other seemingly replicable results would have been reported as not significant even under more lenient criteria (e.g., Emotional Clarity: p = .085; p_rep = 81%). Like p, p_rep is not immune to familywise errors. As the number of comparisons increase, so too does the likelihood that an extreme p_rep value will be obtained due to sampling error; yet the best estimate of any given PR is its corresponding p_rep. When retesting is not possible, any decision based on multiple comparisons should be tempered by these considerations.

In a treatment comparison study, Linares et al. (2005) analyzed 14 outcome measures in fourth-graders, comparing students in a school that adopted the Unique Minds School Program (UMSP) with one that did not, over a 2-year period. Two of the outcome measures were academic grades in reading and in mathematics. Linares et al. reported no significant differences in reading grades, but a Time × School interaction in mathematics. This interaction suggests that students in the UMSP school showed larger improvement in mathematics grades than students in the comparison school (see Table 1). The p_rep statistic allows us to look at this interaction in a way that informs the UMSP adoption decision. A comparison of students’ grades at baseline versus Year 2 indicates that, over the course of 2 years, we can expect 75% and 88% of fourth-graders exposed to UMSP to improve their reading and math grades, respectively. To control for student maturation, we compare these improvement percentages with those expected from a non-UMSP school: Results indicate that 75% of students improve in reading and only 35% in math. Subtracting the expected improvement percentage in non-UMSP from UMSP shows that slightly more than half of the students would obtain better math grades after 2 years if exposed to the UMSP; no effect is expected in reading grades.

Despite the strong effects obtained, the difference in baseline grades across schools undermines an unequivocal interpretation of the Time × School interaction obtained by Linares et al. (2005). The implementation of the UMSP is confounded with undetermined variables responsible for baseline differences. Rescaling the grades to equalize both groups at baseline may solve this problem. Another way to assess Linares et al.’s results is by determining the expected percentage of UMSP students that will increase their math and reading grades at least to the level of the comparison school in their second year (sixth grade). The minimum grade improvements (0.10 in reading, 0.26 in mathematics) were divided by the corresponding s_POOLED for UMSP grades to obtain $d_s^{\prime }$ for reading and math (Table 2). The obtained values of p_support suggest that three out of every five groups of UMSP students will obtain higher grades in both math and reading in the sixth grade than non-UMSP sixth-graders.

Table 2.

Computation of p_support for Two Tests in Linares et al. (2005)

Study	Variable	d′	$d_s^{\prime }$	psupport
Linares et al. (2005)	Reading (UMSP)	0.21	0.12	.619
	Math (UMSP)	0.36	0.28	.611

Note. Values of $d_s^{\prime }$ were based on mean performance of comparison school at Year 2. See text for explanation.

The Loss of False Certainty Is a Gain

Something seems to be lost in using p_rep and p_support in place of p. Even though nonsignificant differences may leave us in a limbo of indecision, significant differences appear to inform researchers about some true effect, embodied in the low probability that such differences could be obtained by chance. Who would doubt the reality of an effect when, for instance, p < .001? This false sense of certainty is derived from the rather unlikely assumption that, for any comparison, there is only one real and detectable effect, instead of a distribution of obtainable effects with a hypothetical mean and dispersion. Only the assumption of an underlying binary status of effects (real vs. not real) would support a routine that allows for only two possible outcomes: Either the reality of a tested effect is detected (i.e., it is “significant”) and we can safely assume its existence or it is not detected (i.e., it is “not significant”) and nothing can be said about its existence. Under NHST, researchers are asked to operate as if an effect was a single value of which we may only know its sign. It is for this reason that Fisher (1959) suggested null hypothesis testing as a method to detect unlikely events that deserve further examination—not as a substitute for that examination.

The difference between two delimited populations (e.g., senior high school students in the state of Louisiana vs. Texas in 2004) over an attribute (e.g., mean grade point average) may be reasonably represented as a single value. This is, however, a rare case. Generally, researchers are interested in differences between populations that may change from test to test. In our example of ESL teaching methods, a retest would certainly involve different students that may respond differently to each teaching method. Which of the two tests would yield results closer to the real difference between teaching methods? This would be a moot question if effects were thought of as normally distributed real differences, rather than estimates of a single real difference, that is, if we admit that a teaching method may be beneficial most of the time but not necessarily all of the time. The uncertainty inherent in a probability distribution may undermine the resoluteness that is expected to guide practical action; however, resolute and statistically sophisticated decisions based on false assumptions are but esoteric routes to failure. We argued for and described a simple way to reduce such discomfiture by estimating the probability distribution of replication, based on $d_1^{\prime }$ and σ_R. The closure provided by a p value is misleading. In contrast, p_rep provides the basis for a cautious, fully informed decision, one open to graded assent and recalibration against minimal standards such as p_support. Most importantly, perhaps, p_rep provides a clearer level of communication to all participants regarding the complicated decisions that the educational community faces today.

Appendix A: Justification

To calculate the probability of a successful replication, we must be able to calculate the probability of any particular value of a replicate effect $d_2^{\prime }$, given the population mean effect δ. But δ is unknown. The probability of δ having any particular value can only be estimated from prior information and from current information such as $d_1^{\prime }$. Attempts to leapfrog over the nuisance parameter δ and directly determine the probability that $d_2^{\prime }$ will take any particular value $d_2^{\ast }$ given $d_1^{\prime }$ have not clearly succeeded (Macdonald, 2005; Seidenfeld, 1979), unless they invoke Bayesian updating of prior information. This is because the value of $d_2^{\prime }$ is not independent of the value of $d_1^{\prime }$. So instead we must go by the indirect route of estimating $p(d_2^{\prime }\mid d_1^{\prime })$ in terms of $p(d_2^{\prime }\mid \delta )$ and $p(\delta \mid d_1^{\prime })$. The latter is derived from $p(d_1^{\prime }\mid \delta )$ and p(δ) using Bayes Theorem. The problem with such updating is that (a) it commits us to agree that parameters can themselves have distributions and (b) it requires knowledge of p(δ)—and in determining that we eventually regress to conditions about which we are ignorant. Justifying how to formulate that ignorance has been the bane of progress. Unlike frequentists, Bayesians are willing to bite both these bullets. One way of engaging “ignorance” priors is with an appropriate (conjugate) distribution with an arbitrarily large variance, which entails that any prior value for a parameter such as δ is equally likely (Doros & Geier, 2005; O’Hagan & Forster, 2004, pp. 89–91).

The advantage of this approach is that it can naturally take advantage of available prior information, enhancing the accuracy of our predictions. Alternatively, as argued here and by Maurer (2004, p. 17), the engagement of informative priors “can obfuscate formal tests [of the data under inspection] by including information not specifically contained within the experiment itself”; for primary credentialing of results, ignorance priors and the calculations of p_rep given in text and below, are ideal.

Appendix B: Calculation

To calculate p_rep for the difference of two group means:

1. Divide the difference of the two group means by the pooled standard deviation to compute the effect size $d_1^{\prime }=(M_1-M_2)/s_{\text{POOLED}}$.

2. If the only dispersion data available are the standard deviation of each group, compute

   $$s_{\mathit{POOLED}}=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$$ (B1)

   where n_i and s_i are the number of subjects and the standard deviation of group i, respectively.

3. Obtain the estimated standard error of the replication (from Equations 3 and 5):

   $${\sigma }_R=(n_1+n_2)\sqrt{\frac{2}{n_1{n}_2(n_1+n_2-4)}}$$ (B2)

4. Using Microsoft Excel, input in a cell the command NORMSDIST ( $d_1^{\prime }/{\sigma }_R$). This is equivalent to consulting a normal probability table for the cumulative probability up to $z=d_1^{\prime }/{\sigma }_R$.

If the data are from regression analyses, the standard t value is (Rosenthal, 1994; Rosnow & Rosenthal, 2003)

$$t=\frac{r}{\sqrt{1-r^2}}\sqrt{df};$$ (B3)

this may be converted to p_rep by evaluating $1-F(t\sqrt{2})$, where F(x) returns the tail probability of the t distribution. In a spreadsheet such as Excel this can be computed with $p_{\mathit{rep}}=1-\text{TDIST}(t/\sqrt{2},\text{df},1)$. Other useful conversions are d′= 2r(1 − r²)^−1/2 (Rosenthal, 1994), and d′=t[1/n₁ + 1/n₂]^1/2 for the simple two independent group case, and d′= t_r[(1 − r)/n₁ (1 − r)/n₂]^1/2 for a repeated measures t, where r is the correlation between the measures (Cortina & Nouri, 2000).