A HAUSDORFF-BASED NOE ASSIGNMENT ALGORITHM USING PROTEIN BACKBONE DETERMINED FROM RESIDUAL DIPOLAR COUPLINGS AND ROTAMER PATTERNS

Abstract

High-throughput structure determination based on solution Nuclear Magnetic Resonance (NMR) spectroscopy plays an important role in structural genomics. One of the main bottlenecks in NMR structure determination is the interpretation of NMR data to obtain a sufficient number of accurate distance restraints by assigning nuclear Overhauser effect (NOE) spectral peaks to pairs of protons. The difficulty in automated NOE assignment mainly lies in the ambiguities arising both from the resonance degeneracy of chemical shifts and from the uncertainty due to experimental errors in NOE peak positions. In this paper we present a novel NOE assignment algorithm, called HAusdorff-based NOE Assignment (HANA), that starts with a high-resolution protein backbone computed using only two residual dipolar couplings (RDCs) per residue^{37, 39}, employs a Hausdorff-based pattern matching technique to deduce similarity between experimental and back-computed NOE spectra for each rotamer from a statistically diverse library, and drives the selection of optimal position-specific rotamers for filtering ambiguous NOE assignments. Our algorithm runs in time O(tn³ +tn log t), where t is the maximum number of rotamers per residue and n is the size of the protein. Application of our algorithm on biological NMR data for three proteins, namely, human ubiquitin, the zinc finger domain of the human DNA Y-polymerase Eta (pol η) and the human Set2-Rpb1 interacting domain (hSRI) demonstrates that our algorithm overcomes spectral noise to achieve more than 90% assignment accuracy. Additionally, the final structures calculated using our automated NOE assignments have backbone RMSD < 1.7 Å and all-heavy-atom RMSD < 2.5 Å from reference structures that were determined either by X-ray crystallography or traditional NMR approaches. These results show that our NOE assignment algorithm can be successfully applied to protein NMR spectra to obtain high-quality structures.

1. INTRODUCTION

High-throughput structure determination based on X-ray crystallography and Nuclear Magnetic Resonance (NMR^a) spectroscopy are key steps towards the era of structural genomics. Unfortunately, structure determination by either approach is generally time-consuming. In X-ray crystallography, growing a good quality crystal is in general a difficult task, while in NMR structure determination, the bottleneck lies in the processing and analysis of NMR data, and in interpreting a sufficient number of accurate distance restraints from experimental Nuclear Over-hauser Enhancement Spectroscopy (NOESY) spectra, which exploit the dipolar interaction of nuclear spins, called nuclear Overhauser effect (NOE), for through-space correlation of protons. The intensity (or volume) of an NOE peak in a NOESY spectrum is converted into a distance restraint by calibrating the intensity (or volume) vs. distance curve or classifying all NOESY peaks into different bins.^{12, 16, 38} Traditional NMR structure determination approaches use NOE distance restraints as the main source of information to compute the structure of a protein, a problem known to be strongly NP-hard,³⁰ essentially due to the local nature of the restraints. Rigorous approaches to solve this problem using NOE data, such as the distance geometry method,¹⁰ require exponential time in the worst-case (see discussion in Ref. 39). While substantial progress has been made to design practical algorithms for structure determination,^{3, 12–14, 24, 28, 31} most algorithms still rely on heuristic techniques such as molecular dynamics (MD) and simulated annealing (SA), which use NOE data plus other NMR data to compute a protein structure. The NOE distances used by these distance-based structure determination protocols must be obtained by assigning NOE data, i.e., for every NOE, we must determine the associated pair of interacting protons in the primary sequence. This is called the NOE assignment problem.

While much progress has been made in automated NOE assignment,^{12, 14, 16, 21, 24, 27, 28} most NOE assignment algorithms have a SA/MD-based or a distance geometry-based structure determination protocol sitting in a tight inner loop, which is invoked many times to filter ambiguous assignments. Since distance geometry methods have exponential worst-case time complexity, and SA/MD-based structure determination protocols lack combinatorial precision and have no guarantees on solution quality or running time, these NOE assignment algorithms suffer from the same drawbacks, in addition to the inherent difficulties in the interpretation of NOESY spectra. Therefore, it is natural to ask if there exists a provably polynomial-time algorithm for the NOE assignment problem, which can guarantee solution quality—this will pave new ways for better understanding and interpretation of experimental data, and for developing robust protocols with both theoretical guarantees and good practical performance.

In Ref. 39, a new linear time algorithm was developed, based on Refs. ³⁷ and ³⁶, to determine protein backbone structure accurately using a minimum amount of residual dipolar coupling (RDC) data. RDCs provide global orientational restraints on internuclear vectors, for example, backbone NH and CH bond vectors with respect to a global frame of reference. The algorithm in Refs. ^{37, 36}, and ³⁹ computes the backbone conformation by solving, in closed form, systems of low-degree polynomial equations formulated using the RDC restraints. The algorithm is combinatorially-precise and employs a systematic search strategy to compute the backbone structure in polynomial time. The accurately-computed backbone conformations enable us to propose a new strategy for NOE assignment. In Ref. 38, for example, an NOE assignment algorithm was proposed to filter ambiguous NOE assignments based on an ensemble of distance intervals computed using intra-residue vectors mined from a rotamer database, and inter-residue vectors from the backbone structure determined from Refs. ^{37, 36}, and ³⁹. The algorithm in Ref. 38 uses a triangle-like inequality between the intra-residue and inter-residue vectors to prune incorrect assignment for side-chain NOEs. However, the algorithm in Ref. 38 has the following deficiencies: (a) it does not exploit the diversity of the rotamers in the library, (b) uncertainty in NOE peak position, and other inherent difficulties in interpreting NOESY spectra suggest a probabilistic model with provable properties which Ref. 38 does not capture, and (c) it does not exploit rotamer pattern structure in NOESY spectra.

To address the shortcomings in Ref. 38 and other previous work, our algorithm, HAusdorff-based NOE Assignment (HANA), uses a novel pattern-directed framework for NOE assignment, that combines a combinatorially-precise, algebraic geometry-based approach for computing high-resolution protein backbones from residual dipolar coupling data, with a framework that uses a statistically diverse library of rotamers and the Hausdorff distance to measure similarity between experimental and back-computed NOE spectra, and drives the selection of optimal position-specific rotamers to prune ambiguous NOE assignments. Our Hausdorff-based framework views the NOE assignment problem as a pattern-recognition problem, where the objective is to establish a match by choosing the correct rotamers between the experimental NOESY spectrum and the back-computed NOE pattern. By explicitly modeling the uncertainty in NOE peak positions and the probability of mismatches between NOE patterns, we provide a rigorous means of analyzing and evaluating the algorithmic benefits and the quality of assignments.

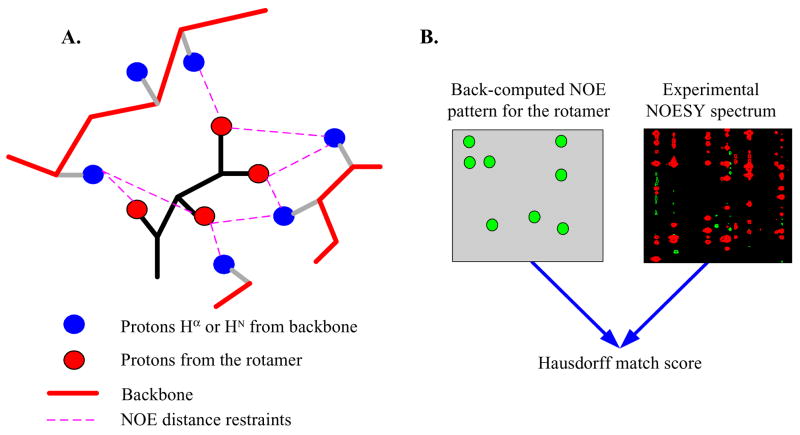
We first compute a high-resolution protein backbone from RDC data using the algorithms in Refs. ^{37, 36}, and ³⁹. Using this backbone structure, an assigned resonance list, and a library of rotamers²⁵, the NOE pattern for each rotamer can be back-computed (Figure 1B). By measuring the match of the back-computed NOE patterns with experimental NOESY spectrum, we choose an ensemble of top rotamers according to the match scores for each residue. Then, we construct an initial low-resolution protein structure by combining the high-resolution backbone and the chosen approximate rotamers together. The low-resolution structure is then used to filter ambiguous NOE assignments. Finally, our NOE assignments are fed to a structure calculation program, e.g., XPLOR/CNS ³ which outputs the final ensemble of structures. The experimental results, based on our NMR data for three proteins, viz., human ubiquitin, the zinc finger domain of the human DNA Y-polymerase Eta (pol η) and the human Set2-Rpb1 interacting domain (hSRI) show that HANA achieves an assignment accuracy of more than 90%. In summary, our main contributions in this paper are:

Fig. 1.

Schematic illustration of the NOE assignment approach.

1. Development of a novel framework that combines a combinatorially-precise, algebraic geometry-based linear time algorithm for high-resolution backbone structure determination with the Hausdorff distance measure, and exploits the statistical diversity of a rotamer library to infer accurate NOE assignments for both backbone and side-chain NOEs from 2D and 3D NOESY spectra.

2. Introduction of Hausdorff distance-based pattern matching technique to measure the similarity between experimental NOE spectra and back-computed NOE spectra, and modeling uncertainties arising both from false random matches and from experimental deviations in NOE peak positions.

3. A fully-automated O(tn³ + tn log t) time NOE assignment algorithm, where t is the maximum number of rotamers in a residue and n is the number of residues in the protein.

4. Derivation of provable properties, viz. soundness in rotamer selection.

5. Application of our algorithm on three real biological NMR data sets to demonstrate high assignment accuracy (> 90%), and fast running times (< 2 minutes).

2. PRELIMINARIES AND PROBLEM DEFINITION

In NMR spectra, each proton or atom is identified by its chemical shift (or resonance), which is obtained by mapping atom names in the known primary sequence of the protein to the corresponding frequencies from triple-resonance or other NMR spectra; this process is referred to as resonance assignment. Substantial progress has been made in designing efficient algorithms^{1, 20, 22, 26} for automatic resonance assignment. Given the chemical shift of each proton, the NOE assignment problem in two dimensions^b is to assign each NOESY peak to each pair of protons that are correlated through a dipole-dipole NOE interaction.

Formally, let {a₁,…, a_q} denote the set of proton names (e.g., H^α of Arg56), where q = Θ (n) is the total number of protons and n is the number of residues in a protein. Let ω(a_i) denote the chemical shift for proton a_i determined from resonance assignment, 1 ≤ i ≤ q. An NOE peak (a.k.a. cross-peak) with respective frequencies x and y for a pair of protons, is denoted by the point (x, y) on the plane of NOESY spectrum. Given a set of known chemical shifts L = {ω (a_i),…, ω (a_q)} for all protons {a₁,…, a_q} and a list of NOESY peaks (i.e., a set of points on the plane of NOESY spectrum), the NOE assignment problem is to map each NOE cross-peak (x, y) to an interacting proton pair (a_i, a_j) such that ||ω (a_i) − x|| ≤ δ_x and ||ω (a_j) − y|| ≤ δ_y, where δ_x and δ_y encode the uncertainty in the peak position due to experimental errors.

In a hypothetical ideal case without any experimental error and noise, this would be an easy problem. However, for most proteins, two pairs of interacting protons can produce overlapping NOE peaks in a NOESY spectrum. The chemical shift differences of different protons are often too small to resolve experimentally, a phenomenon often referred to as chemical shift degeneracy. Also, due to experimental noise, artifact NOE peaks might occur from either manual or automated peak picking. These factors lead to more than one possible NOE assignment for a 2D NOESY spectrum which are called ambiguous NOE assignments.^{12, 21} Hence, one or more additional dimensions are generally introduced to relieve the congestion of NOE peaks. In a 3D NMR experiment, for example, each NOE peak is labeled with chemical shifts of a triple of atoms, viz., dipole-dipole interacting protons plus the heavy atom nucleus such as ¹⁵N or ¹³C bonded to the second proton. Even for 3D spectra, the interpretation and assignment of NOESY cross-peaks still remains hard, and poses a difficult computational challenge to obtain a unique NOE assignment. Manual assignment of NOESY peaks take months of time on average, requires significant expertise, and is prone to human errors. In structure determination, even a few incorrect NOE assignments can result in incorrect structures.⁵ Hence, it is critical to develop highly efficient and fully automated NOE assignment algorithms to aid high-throughput NMR structure determination.

3. PREVIOUS WORK

Protein structure determination using NOE distance restraints is strongly NP-hard,³⁰ essentially due to sparsity of the experimental data and local nature of the constraints. While rigorous approaches to solve this problem using distance intervals from NOE data, such as the distance geometry method,¹⁰ require exponential time in the worst-case; heuristic approaches such as SA/MD, while providing practical ways of solving this problem, lack combinatorial precision, and have no guarantees on running time or solution quality. Previous approaches for NOE assignment^{12, 14, 16, 21, 24, 27, 28} follow an iterative strategy, in which an initial set of relatively unambiguous NOEs is used to generate an ensemble of structures, which are then used to filter ambiguous and inconsistent NOE assignments. This iterative assignment process is repeated until no further improvements in NOE assignments or structures can be obtained. What makes such approaches loose guarantees on the running time and assignment accuracy is their tight coupling with a heuristic structure determination protocol, which sits in a tight inner-loop of the assignment algorithm.

NOAH,^{27, 12} for example, uses the structure determination package DYANA,¹⁴ and follows the previously mentioned iterative strategy starting with an initial set of NOE assignments with supposedly one or two possible assignments. ARIA ^{28, 24} and CANDID¹⁴ improved on NOAH by incorporating better modeling of ambiguous distance constraints. In AUTO-STRUCTURE¹⁶ more experimental data such as dihedral angle restraints from TALOS ⁸ and slow H-D exchange data are used to improve assignment accuracy. In PASD ²¹ several strategies were proposed to reduce the chance of invoking the structure calculation into a biased path due to the incorrect initial global fold. Since all these iterative NOE assignment programs invoke SA/MD-based structure determination protocols such as XPLOR/CNS³, they may converge to a local, but not a global minimum to obtain a best-fit of the data; therefore, the NOE assignments might not be correct.

An alternative approach for automated NOE assignment proposed by Wang and Donald in Ref. 38, based on Refs. ^{37, 36}, and ³⁹, uses a rotamer ensemble and residual dipolar couplings, and is the first polynomial-time algorithm for automated NOE assignment. However, Ref. 38 does not exploit the pattern structure of NOESY spectrum to model the uncertainty in peak positions probabilistically using a library of rotamers; therefore, assignment accuracy is reduced while processing NOESY spectra with many noisy peaks.

Our algorithm HANA retains the paradigm of Ref. 38, and develops a novel framework using the algebraic geometry-based linear time algorithm developed in Ref. 39 to compute high-resolution protein backbones from residual dipolar couplings, and then uses this backbone and a library of rotamers to do NOE assignments. Viewing the NOE assignment problem as a pattern-recognition problem, our algorithm uses an extended Hausdorff distance-based probabilistic framework to model the uncertainties in NOE peak positions and the probability of mismatches between NOE patterns. In contrast to previous heuristic algorithms^{12, 14, 16, 21, 24, 27, 28} for NOE assignment, HANA has the advantages of being combinatorially precise with a running time of O(tn³ + tn log t), where t is the maximum number of rotamers per residue and n is the size of the protein, and runs extremely fast in practice to compute high quality NOE assignments (> 90% assignment accuracy).

4. NOE ASSIGNMENT BASED ON ROTAMER PATTERNS

4.1. Overview of our approach

Our goal is to assign pairs of proton names^c to cross-peaks in NOESY data. Figure 1 illustrates the basic idea of our algorithm. The NOE assignment process can be divided into three phases, viz. initial NOE assignment (phase 1), rotamer selection (phase 2), and filtration of ambiguous NOE assignments (phase 3). The initial NOE assignment (phase 1) is done by considering all pairs of ambiguous NOEs assigned to a NOESY cross peak if the resonances of corresponding atoms fall within a tolerance window around the NOE peak. In the rotamer selection phase, we first compute the backbone structure from RDCs (see Section 4.2), and then place all the rotamers at each residue into backbone and compute all expected NOEs within the upper-bound limit of NOE distance (Figure 1A). Based on the set of all expected NOEs and the resonance assignment list, we back-compute the expected NOE peak pattern for each rotamer (Figure 1B). By matching the back-computed NOE pattern with the experimental NOESY spectrum using an extended model of the Hausdorff distance,^{17, 19} we measure how well a rotamer fits the real side-chain conformation when interpreted in terms of the NOESY data. We then select the top k rotamers with highest fitness scores at each residue, and obtain a “low-resolution” structure,^d by combining the high-resolution backbone structure and the approximate ensemble of side-chain conformations at each residue. The low-resolution structure is then used (in phase 3) to filter ambiguous NOE assignments. The details of filtering ambiguous NOE assignments using the low-resolution structure are provided in Supplementary Material (SM) Section 4 available online in Ref. 40.

4.2. Protein backbone structure determination from residual dipolar couplings

Residual dipolar coupling^{33, 34} data provide global orientational restraints on the internuclear bond vectors, such as, backbone NH and CH bond vectors with respect to a global coordinate frame. In solution NMR, RDCs can be recorded with high precision, and assigned much faster than NOEs. In Refs. ³⁹ and ³⁷, the authors proposed the first polynomial-time de novo algorithm, which we henceforth refer to as RDC-EXACT, to compute high-resolution protein backbone structures from RDC data. RDC-EXACT takes as input (a) two RDCs per residue (e.g., assigned NH RDCs in two media or NH and CH RDCs in a single medium), (b) delimited α-helices and β-sheets with known hydrogen bond information between paired strands, and a few unambiguous NOEs (used to pack the helices and strands). Note that, these sparse set of NOEs used by RDC-EXACT can usually be assigned using chemical shift information alone^{37, 39} without requiring any sophisticated NOE assignment algorithm. Our algorithm HANA uses the high-resolution backbones computed by RDC-EXACT. Loops with missing RDCs are computed using an enhanced version of robotics-based cyclic coordinate descent (CCD) algorithm.^{4, 32} The details of RDC-EXACT and modeling of loops (in case of missing RDCs) are provided in SM⁴⁰ Section 1.

4.3. NOE pattern matching based on the Hausdorff distance measure

Given two finite sets of points B = {b₁,…, b_m} and Y = {y₁,…, y_n} in Euclidean space, the Hausdorff distance between B and Y is defined as H(B, Y) = max{h(B, Y), h(Y, B)}, where h(B, Y) = max_b∈B min_{y∈ Y} ||b − y||, and ||b − y|| measures the normed distance (e.g., L₂-norm) between points b and y. Intuitively, the Hausdorff distance H(B, Y ) finds the point in one set that is farthest from any point in the other set, and thus measures the degree of mismatch between the two point sets B and Y. The Hausdorff distance has been widely used in the image processing and computer vision problems, such as visual correspondence,¹⁷ pattern recognition,¹⁹ and shape matching,¹⁸ etc. Unlike many other pattern-recognition algorithms, Hausdorff-based algorithms are combinatorially precise, and provide a robust method for measuring the similarity between two point sets or image patterns^{18, 19} in the presence of noise and positional uncertainties.

In the NOE assignment problem, let B denote a back-computed NOE pattern, i.e., the set of back-computed NOE peaks, and let Y denote the set of experimental NOESY peaks. Generally, the size of a back-computed NOE pattern is much smaller than the total number of experimental NOESY peaks. Therefore, we only consider the directed Hausdorff distance from B to Y, namely, h(B, Y ) = max_b∈B min_y∈Y ||b − y||. We apply an extended model of Hausdorff distance^{18, 19, 17} to measure the match between the back-computed NOE pattern and experimental NOESY spectrum. Below, we assume 3D NOESY spectra without loss of generality.

Given the back-computed NOE pattern B with m peaks, and the set of NOESY peaks Y with w peaks, the τ-th Hausdorff distance from B to Y is defined as

$$h_{\tau }(B,Y)=\underset{b\in B}{\tau \text{th}}\underset{y\in Y}{min}\mid \mid b-y\mid \mid ,$$

where τth is the τ-th largest of m values. We call f = τ/m the similarity score between the back-computed NOE pattern B and the experimental peak set Y, after fixing the Hausdorff distance h_τ(B, Y ) = δ, which is the error tolerance in the NOESY spectra. The similarity score for a rotamer given δ can be computed using a scheme similar to Ref. 17:

$$s=\frac{\mid B\cap Y_{\delta }\mid }{\mid B\mid },$$ (1)

where Y_δ denotes the union of all balls obtained by replacing each point in Y with a ball of radius δ, B ∩Y_δ denotes the intersection of sets B and Y_δ, and |·| denotes the size of a set.

We incorporate two types of uncertainty in the calculation of the similarity score in Equation (1) for the match between the back-computed NOE pattern and experimental NOESY spectrum: (a) possibility of a false random match¹⁷ in the NOESY spectra; (b) uncertainty of NOE peak positions due to experimental noise.

(a) Possibility of a false random match ¹⁷

A false random match between the back-computed NOE pattern and the experimental NOESY spectrum is defined as a match when h_τ (B, Y ) ≤ δ occurs at random. We calculate the probability of a false random match and use it as a weighting factor for the similarity score in Equation (1). Let p be the probability for a back-computed NOE peak to randomly match to an experimental peak in Y_δ. Let θ be the probability of a false random match, which can be estimated using the following asymptotic approximation from Ref. 17:

$$\theta \approx \frac{1}{2}(\mathrm{\Phi }(\frac{(1-p)m}{\rho })-\mathrm{\Phi }(\frac{(s-p)m}{\rho })),$$

where $\rho =\sqrt{2mp(1-p)}$, and Φ(·) is the Gauss error function.

(b) Uncertainty from the NOE peak positions

Let b_i = (ω (a₁), ω (a₂), ω (a₃)) denote the back-computed NOE peak for an NOE (a₁, a₂, a₃) in a 3D NOESY spectrum. The likelihood for a back-computed peak b_i = (ω (a₁), ω (a₂), ω (a₃)) in the NOE pattern B to match an experimental NOESY peak within the distance δ in Y_δ can be defined as

$${\mathcal{N}}_i(b_i)=\prod _{j=1}^3\mathcal{N}(\mid \omega (a_j)-p_j\mid ,{\sigma }_j),$$

where (p₁, p₂, p₃) is the experimental NOESY peak matched to (ω (a₁), ω (a₂), ω (a₃)) according to the Hausdorff distance measure, and (|x − μ|, σ) is the probability of observing the difference |x − μ| in a normal distribution with mean μ and standard deviation σ. Here we assume that the noise distribution of peak positions at each dimension is independent of each other. We note that the normal distribution and other similar distribution families have been widely and efficiently used to approximate the noise in the NMR data, e.g., see Refs. ²⁹ and ²².

Then the expected number of peaks in B∩Y_δ can be bounded by $\mid B\cap Y_{\delta }\mid ={\sum }_{i=1}^m{\mathcal{N}}_i(b_i)$. Thus, we have the following equation for the similarity score:

$$s=\frac{1}{m}\sum _{i=1}^m{\mathcal{N}}_i(b_i).$$ (2)

After considering both possibility from a false random match and uncertainty from the NOE peak positions, we obtain the following fitness score for a rotamer

$$s^{\prime }=(1-\theta )s=\frac{1-\theta }{m}\sum _{i=1}^m{\mathcal{N}}_j(b_i).$$ (3)

For each rotamer, the computation of its similarity score s′ can be computed in O(mw) time, where m is the number of back-computed NOE peaks, and w is the total number of cross peaks in the experimental NOESY spectrum. The detailed pseudocodes for computing the similarity score and for HANA are provided in SM Sections 3–4 available in Ref. 40.

5. ANALYSIS

5.1. Analysis of rotamer selection based on NOE patterns

Given a back-computed NOE peak b_i = (ω_i1, ω_i2, ω_i3) in the NOE pattern of a rotamer, suppose that it finds a matched experimental peak in Y^δ with probability g(ω_i1, ω_i2, ω_i3, Y^δ). Finding such a matched experimental NOESY peak for b_i can be regarded as a Poisson trial with success probability g(ω_i1, ω_i2, ω_i3, Y^δ). We present the following result about the expected number of matched peaks for the back-computed NOE pattern of a rotamer.

Lemma 5.1

Let X_i be an indicator random variable which is equal to 1 if the back-computed NOE peak b_i of a rotamer r finds a matched experimental peak; 0 otherwise. Let $X={\sum }_{i=1}^m{X}_i$, where m is the total number of back-computed NOE cross-peaks for the rotamer r. Then the expected number of back-computed NOE peaks that find matched experimental peaks is given by

$$E(X)=\sum _{i=1}^{m}E(X_i)=\sum _{i=1}^{m}g({\omega }_{i1},{\omega }_{i2},{\omega }_{i3},Y^{\delta }).$$

Let r_t denote the rotamer closest to the real side-chain conformation for a residue, and let r_f denote another rotamer in the library for the same residue. We call r_t the true rotamer, and r_f the false rotamer. Let X_i and Y_i be indicator random variables as defined in Lemma 5.1 for each back-computed NOE peak in the true rotamer r_t and the false configuration r_f respectively. Let m_t and m_f denote the numbers of back-computed NOE peaks for the true rotamer r_t and the false rotamer r_f. Let $X={\sum }_{i=1}^{m_t}{X}_i$ and $Y={\sum }_{i=1}^{m_f}{Y}_i$ denote the number of back-computed NOE peaks that find matched experiment peaks for rotamers r_t and r_f respectively. Let μ_t = E(X) and μ_f = E(Y ) denote the expectations of X and Y. For simplicity of our theoretical analysis, we use Equation (1) to measure the fitness between the back-computed NOE pattern of a rotamer and the experimental spectrum in our theoretical model.

To measure the accuracy of the rotamer chosen based on our scoring function, we calculate the probability that the algorithm chooses the wrong rotamer r_f rather than the true rotamer r_t, and show how it is bounded by certain threshold. The following theorem formally states this result. The proof of this theorem can be found in SM⁴⁰ Section 5.

Theorem 5.1

Suppose that $m_f{\mu }_t-m_t{\mu }_f\ge max(m_f,\sqrt{m_f{m}_t})·4\sqrt{{\mu }_{t}ln{m}_t}$. Then with probability at least $1-m_t^{-1}$, our algorithm chooses the true rotamer r_t rather than the false rotamer r_f.

Theorem 5.1 indicates that if the difference between the expected numbers of matched NOE peaks for two roatmers is larger than certain threshold, we are able to distinguish these two roamters based on the Hausdorff distance measure with certain probability bound. By Theorem 5.1, we have the following result on the bound of the probability of picking the correct rotamer from the library based on the Hausdorff distance measure, if we select top k rotamers with highest similarity scores.

Theorem 5.2

Let t denote the maximum number of rotamers for a residue. Suppose that $m_f{\mu }_t-m_t{\mu }_f\ge 4max(m_f,\sqrt{m_f{m}_t})·\sqrt{{\mu }_{t}ln{m}_t}$ and m_t > t − k hold for the true rotamer r_t and every false rotamer r_f. Then with probability at least $1-\frac{t-k}{m_t}$, our algorithm chooses the correct rotamer.

Proof

Since the total number of rotamers in a residue is t, by Theorem 5.1 the probability that the similarity score of the true rotamer is larger than that of at least t − k rotamers is at least ${(1-\frac{1}{m_t})}^{t-k}$. According to the fact (1 + x)^a ≥ 1 + ax for x > −1 and a ≥ 1, we have ${(1-\frac{1}{m_t})}^{t-k}\ge 1-\frac{t-k}{m_t}$. Thus, the probability for the algorithm to choose the right rotamer is at least $1-\frac{t-k}{m_t}$.

Theorem 5.2 shows that if the discrepancy of the expected number of matched NOE peaks between the true rotamer and every other rotamer, and the number of back-computed NOE peaks are sufficiently large, the ensemble of top k rotamers with highest similarity scores will contain the true rotamer.

5.2. Time complexity analysis

The following theorem states that HANA runs in polynomial time.

Theorem 5.3

HANA runs in O(tn³ +tn log t) time, where t is the maximum number of rotamers at a residue and n is the total number of residues in the protein sequence.

The detailed derivation of the time complexity can be found in SM⁴⁰ Section 6. We note that in practice, our NOE assignment algorithm HANA runs in 1–2 minutes on a 3 GHz single-processor Linux workstation.

6. RESULTS

HANA takes as input (a) protein sequence, (b) 3D NOESY-HSQC or 2D NOESY peak list, (c) assigned resonance list, (d) backbone computed by using the rdc-exact algorithm^{37, 39} (Section 4.2), and (e) Xtalview rotamer library.²⁵ HANA was tested on experimental NMR data for human ubiquitin,^{35, 9} zinc finger domain of the human DNA Y-polymerase Eta (pol η)² and human Set2-Rpb1 interacting domain (hSRI).²³ The high-resolution structures of these three proteins have been solved either by X-ray crystallography³⁵ or by traditional NMR approaches using both distance restraints from NOE data and orientational restraints from scalar and dipolar couplings.^{9, 2, 23} We used these solved structures, which are also in the Protein Data Bank (PDB), as the reference structures to compare and check the quality of NMR structures determined from our NOE assignment tables. The NMR data for hSRI and pol η were recorded using Varian 600 and 800 MHz spectrometers at Duke University. Ubiquitin NMR data was obtained from Ref. 15 and from the PDB (ID: 1D3Z).

6.1. Robustness of Hausdorff distance and NOE assignment accuracy

To check the robustness of the Hausdorff distance measure for NOE pattern matching, we first computed a low-resolution structure of ubiquitin by combining the backbone determined from RDC-EXACT,^{37, 36, 39} and rotamers selected based on the Hausdorff distance measure using patterns for backbone-sidechain NOEs. This low-resolution NMR structure is not the final structure, but is used to filter ambiguous NOE assignments (including backbone-backbone, backbone-sidechain and sidechain-sidechain NOE assignments). Our result shows that the low-resolution structure of ubiquitin obtained from our algorithm has a backbone RMSD 1.58 A and an all-heavy-atom RMSD 2.85 Å from the corresponding X-ray structure (PDB ID: 1UBQ). Using this low-resolution structure, HANA was able to resolve the NOE assignment ambiguity caused from the chemical shift degeneracy, and prune a sufficient number of ambiguous NOE assignments, as we will discuss next.

To measure the assignment accuracy of HANA, we define a compatible NOE assignment as one in which the distance between the assigned pair of NOE protons in the reference structure is within NOE distance bound of 6.0 Å. Otherwise, we call it an incompatible NOE assignment. The number of compatible NOE assignments can be larger than the number of total NOESY peaks, since it is possible that multiple compatible NOEs can be assigned to a single NOESY cross peak. Next, the assignment accuracy is defined as the fraction of compatible assignments in the final assignment table output by HANA.

As summarized in Table 1, our NOE assignment algorithm achieved above 90% assignment accuracy for all three proteins. We note that the fraction of assigned peaks of hSRI is less than the other two proteins. This is because we only used backbones in the secondary structure regions (residues 15–34, 51–72, 82–97) for pruning ambiguous NOE assignments for hSRI. Presently we are developing new algorithms to solve long loops. We believe that with more accurate loop backbone structures, we will be able to improve the accuracy of our NOE assignment algorithm, while assigning more NOE peaks. We note that the ubiquitin ¹³C NOESY data from Ref. 15 are quite degenerate, thus we carefully picked a subset of NOESY peaks for assigning NOEs. Presently we are re-collecting a completely new set of ubiquitin NMR data including four-dimensional NOESY spectra for further testing of our algorithm.

Table 1.

NOE assignment results for ubiquitin, pol η and hSRI.

Proteins	# of residues	# of NOESY peaks§	# of compatible assignments†	# of incompatible assignments†	Assignment accuracy
ubiquitin*	76	1580	901	93	90.6%
pol η**	39	1386	590	65	90.1%
hSRI***	112	5916	1429	119	92.3%

^*The ubiquitin backbone calculated from the RDC data using RDC-EXACT has RMSD 1.58 Å from the X-ray reference structure (PDB ID: 1UBQ) (residues 2–71).

^**The pol η backbone calculated from the RDC data using RDC-EXACT has RMSD 1.28 Å for the secondary structure regions and RMSD 2.71 Å for both secondary structure and loop regions (residues 8–36) from the NMR reference structure (PDB ID: 2I5O).

^***The hSRI backbone calculated from the RDC data using RDC-EXACT has RMSD 1.62 Å from the NMR reference structure (PDB ID: 2A7O) for the secondary structure regions (residues 15–34, 51–72, 82–97).

^§The NOESY peak list contains diagonal and symmetric cross peaks.

^†Redundant symmetric NOE restraints have been removed from the final NOE assignment table.

Since the long-range NOEs, in which the spin-interacting protons are at least four residues away, play an important role in the structure determination, we also checked the fraction of incompatible long-range NOE assignments from our algorithm. We found that less than 3% of total assignments were from incompatible long-range NOEs in our computed assignments. As we will discuss next, such a small fraction of incompatible long-range NOE assignments can be easily resolved after one iteration of structure calculation.

6.2. Evaluation of structures from our NOE assignment tables

To test the quality of our NOE assignment results for structure determination, we fed the NOE assignment tables into the standard structure calculation program XPLOR.³ The input files for the structure calculation include protein sequence, NOE assignment table, and dihedral restraints. Compared with Refs. ² and ²³, in which RDCs are incorporated along with NOE restraints into the final structure calculation, here we only used RDCs to compute the initial backbone fold. From an algorithmic point of view, our structure determination using only NOEs can be considered as a good “control” test of the quality of our NOE assignment. The structure calculation was performed in two rounds. After the first round of structure calculation, the NOE violations larger than 0.5 Å among top 10 structures with lowest energies were removed from the NOE assignment table. Then the refined NOE table was fed into the XPLOR program for the second-round structure calculation.

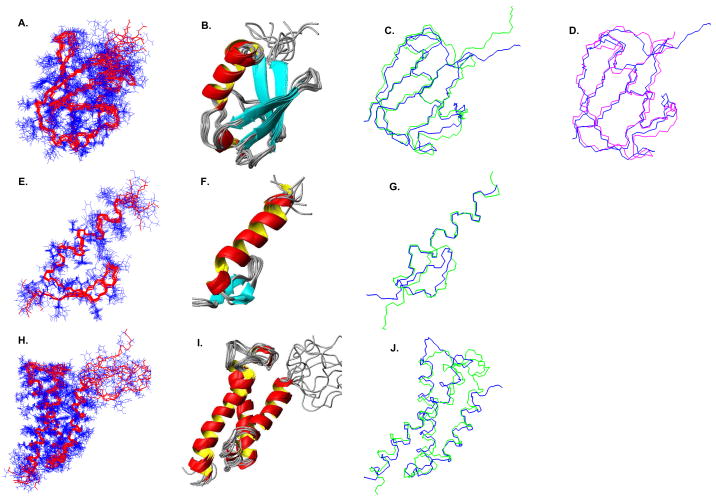
Figures 2 illustrates final NMR structures of ubiquitin, pol η and hSRI calculated from XPLOR using our NOE restraint tables. For all three proteins, only a small number 18–60 (which is 1–4% of the total number of NOE assignments) of NOE violations larger than 0.5 Å occurred after the first round of structure calculation. All final structures converged to an ensemble of low-energy structures with small RMSDs from the reference structure solved either by the X-ray crystallography or by traditional NMR approaches. For all three test cases, the mean structure of final top 10 structures with lowest energies had a backbone RMSD less than 1.7 Å and an all-heavy-atom RMSD less than 2.5 Å from the reference structure. This implies that our NOE assignment algorithm has provided a sufficient number of accurate distance restraints for protein structure determination. In particular, we examined the structure quality in secondary structure and loop regions. We found that the secondary structure regions have better RMSD from the reference structure than the loop regions. After the final structure calculated by XPLOR using our NOE assignment table output by HANA, the RMSD of secondary structure regions in pol η is 0.81 Å for backbone atoms and 1.74 Å for all heavy atoms, and the RMSD of secondary structure regions in ubiquitin is 0.93 Å for backbone atoms and 1.59 Å for all heavy atoms. These results show that the initial fold of secondary structure regions solved using the RDC-EXACT algorithm is accurate enough to combine with chosen rotamers from NOE patterns to resolve the NOE assignment ambiguities. In addition, we also found that the short loop regions of final structures can achieve about the same RMSD from the reference structure as the secondary structure regions. This indicates that the CCD algorithm with filtering of loops based on RDC fit can provide accurate short loops for our NOE assignment algorithm.

Fig. 2.

The NMR structures of ubiquitin, pol η and hSRI computed from our automatically-assigned NOEs. Panels A, B, C and D in first row show the structures of ubiquitin, Panels E, F and G in the middle row show the structures of pol η, and Panels H, I and J in the bottom row show the structures of hSRI. Panels A, E and H show the ensemble of 10 best NMR structures with minimum energies. The backbones are shown in red while the side-chains are shown in blue. Panels B, F and I show the ribbon view of the ensemble of structures. Panel D shows the backbone overlay of the mean structures (in blue color) of ubiquitin with its X-ray reference structures³⁵ (in magenta color). The RMSD between the mean structure and the x-ray structure of ubiquitin is 1.23 Å for backbone atoms and 2.01 Å for all heavy atoms. Panels C, G and J show the backbone overlay of the mean structures (in blue color) with corresponding NMR reference structures (in green color) that have been deposited into the Protein Data Bank (PDB ID of ubiquitin⁹: 1D3Z; PDB ID of pol η²: 2I5O; PDB ID of hSRI²³: 2A7O). The backbone RMSDs between the mean structures and the reference structures are 1.20 Å for ubiquitin, 1.38 Å for pol η, and 1.71 Å for hSRI. The all-heavy-atom RMSDs between the mean structures and the reference structures are 1.92 A for ubiquitin, 2.39 Å for pol η, and 2.43 Å for hSRI.

Our structure calculation protocol only requires one iteration, while other traditional NMR approaches in general take 7–10 iterations between NOE assignment and structure calculation. In addition, our NOE assignment algorithm only takes 1–2 minutes, versus hours to weeks for other methods. This efficiency is consistent with the proofs of correctness and time complexity of our algorithm. Therefore, the structure calculation framework based on our NOE assignment algorithm is more efficient than all other previous approaches in both theory and practice.

7. CONCLUSION

We have described a novel automated NOE assignment algorithm, HANA, that is combinatorially precise, and runs in polynomial time. To our knowledge, HANA is the first NOE assignment algorithm that simultaneously exploits the accurate algebraic geometry-based high-resolution backbone computation from RDC data,^{37, 39} the statistical diversity of rotamers from a rotamer library,²⁵ and the robust Hausdorff measure^{17, 19} for comparing the back-computed NOE patterns with the experimental NOE spectra and choosing accurate rotamers, to finally compute the NOE assignments with high accuracy. Owing to its simplicity, HANA runs extremely fast in practice. Furthermore, when applied to real biological NMR spectra for three proteins, our algorithm yields high assignment accuracy (> 90%) in each case suggesting its ability to play a role in high-throughput structure determination.

Although our current implementation of HANA uses 2D and 3D NOESY spectra, HANA is general and can be easily extended to use higher-dimensional (e.g., 4D) NOESY data.^{6, 7} In addition, it would be interesting to extend the current version of HANA for NOE assignment with missing resonances. In general, acquisition of complete resonance assignment can require selective labeling of proteins, and is time-consuming. On the other hand, selection of correct rotamers can help the resonance assignment for side-chains. In principle, HANA can be extended to accommodate the NOE assignment with a partially assigned resonance list, as long as the back-computed NOE patterns with missing peaks are sufficient to identify accurate rotamers. Finally, it would be interesting to explore the use of side-chain rotamer packing algorithms¹¹ to choose rotamers that fit the data.