Statistical considerations for use of composite health-related quality-of-life scores in randomized trials

Abstract

Background

Quality of life instruments are frequently used as outcomes in randomized trials. Instruments that consist of several subscales present researchers with a choice of whether to combine some or all scales into a single composite score. There may be several clinically and scientifically reasonable alternative combinations of subscales for the primary outcome measure.

Major findings

The statistical efficiency of different combinations of subscales depends on the relative effect size of the intervention on each subscale and the correlation between the subscales. Simple equations can be derived for determining the relative statistical efficiency of each clinically reasonable combination of subscales. Hypothetical scenarios show that the number of patients needed in a clinical trial can be twice as great for some combinations of subscales as for others.

Conclusions

There are often compelling clinical or scientific reasons to use a particular subscale or composite in a randomized trial. In the case where a number of different alternatives would be reasonable, statistical efficiency can help guide the choice of endpoint.

Introduction

There are numerous instruments for the quantitative measurement of health related quality-of-life. These commonly consist of a number of different questions that are grouped into different domains or health concepts. The numerical scores given in answer to these questions are summed separately and reported as subscales. Subscales can be summed and reported as composite scores.

For example, the general Functional Assessment of Cancer Therapy scale (FACT-G) includes 33 statements. Each statement - “I have a lack of energy” is typical - is rated on a five point scale ranging from “not at all” to “very much”, scored numerically from 0 to 4. The scores from each question are added to one of four subscales: Physical; Functional; Social; Emotional. The subscales can then be added to give a total score (1). Similarly, the Profile of Mood States (POMS) consists of 65 mood adjectives grouped in six sub-scales: Tension – anxiety; Depression – dejection; Anger – hostility; Vigor; Fatigue; Confusion- bewilderment. These can be summed to give a “Total mood disturbance” score(2).

In this paper, I will examine the statistical implications of reporting either subscales (e.g. FACT-G physical scale) or composite scores (e.g. FACT-G total score) in randomized trials. It is common in such trials to choose a primary outcome on which to base sample size calculations(3). Furthermore, comparisons between groups become problematic if multiple endpoints, such as eight different subscales, are independently tested(4). The general question I will attempt to answer is: what are the implications for statistical efficiency of combining two or more subscales into a composite score for the primary outcome in a randomized trial? In this paper, “statistical efficiency” will be interpreted in terms of sample size: the more efficient a trial design, the fewer the number of patients required to complete a study.

The research scenario

A research team wishes to assess the effect of an intervention on quality-of-life and is designing a randomized trial. The researchers have chosen a measurement instrument that consists of several subscales. These can be combined into a single composite score. They now need to decide on the primary outcome on which to base sample size calculations for their trial. Their choices are:

1. To choose a single subscale (e.g. FACT-G physical)

2. To choose the composite score (e.g. POMS total mood disturbance)

3. To chose a clinically reasonable combination of several, but not all, subscales (e.g. the sum of POMS tension-anxiety and depression-dejection)

In some cases, there will be compelling reasons for one or another of these choices. For example, a group therapy method for patients with metastatic breast cancer was developed to reduce overall mood disturbance in this highly symptomatic population. The researchers therefore chose the composite POMS scale (“total mood disturbance”)(5). In a trial of acupuncture for chronic low back pain, conversely, the primary interest of the trial was whether treatment could relieve pain. Though the researchers administered the SF36 quality-of-life scale, the single SF36 subscale “bodily pain” was chosen as the primary outcome measure(6). Researchers might also choose the primary endpoint on the basis of comparative data. For example, if a previous trial on a similar population and intervention had been conducted, a research group might choose the same endpoint in order to compare the relative effects of the two interventions.

Where there are several reasonable alternatives, the choice of primary outcome can also be informed by statistical considerations. In particular, researchers will want to reduce sample size by maximizing the comparative effect size. Effect size can be defined as the hypothesized difference between groups divided by the pooled standard deviation(4). Sample size requirements decrease as effect size increases. If researchers are able to predict which combination of subscales maximizes effect size, they will be able to complete a trial with less time, effort, money and disruption to patients. A choice of subscale that maximizes predicted effect size can therefore be termed “statistically efficient”. In the following section, I show how simple equations can be used to determine the relative effect size of different combinations of subscales and thus guide the choice of primary outcome measure in a randomized trial. It is important to note that this process is one that takes place during trial planning; data-driven composites created post hoc to maximize effect sizes clearly introduce bias.

Effect size of composite scores

Quality of life instruments may measure aspects of quality of life that are not strongly affected by a particular intervention. For example, one of the questions on the FACT-G social well-being scale concerns “support from friends and neighbors”. Patients who received an intervention that reduced symptoms such as pain and dyspnea might not answer this question any differently from control patients, despite experiencing improved quality of life. Use of the composite FACT-G scale as the principal endpoint of a randomized trial may therefore dilute the apparent effects of the intervention on quality of life.

It is often possible to predict the principal effect of an intervention. For example, a cancer support group is likely to have the greatest effect on social and emotional domains; improvements in physical well-being and functioning are quite possible, but are unlikely to be of a similar extent. Conversely, a newly developed chemotherapy regime is most likely to lead to improved physical well-being compared to an established agent of high toxicity. An increase in emotional well-being might well result, but the improvement will probably be less pronounced.

I propose that these estimates can be combined with simple equations to predict the statistical efficiency of different combinations of subscales. The effect size for the sum of two subscales a and b, can be calculated from the effect size of each (d_a, d_b) and their correlation (ρ_ab). The formula (which is derived in the appendix) is given below:

$$d_{a+b}=\frac{d_a+d_b}{\sqrt{2+2{\rho }_{ab}}}$$

This formula can be used to derive a decision rule about whether it is statistically efficient to combine two subscales.

$$d_b>\sqrt{2+2\rho }-1$$

This equation gives the relative effect size of an intervention on a second subscale (d_b) below which combining subscales would reduce statistical power. For example, if ρ, the correlation between subscales, is 0.5, the right side of the equation is approximately 0.73. If the effect size of the intervention on the second subscale is less than three-quarters as great as for the single subscale alone, using the combined scale would decrease efficiency. Some sample effect sizes and correlations are given in table 1.

Table 1.

Relative effectiveness of a second subscale below which combination with a primary subscale would reduce statistical power

Correlation between subscales	Effect size
0	41%
0.2	55%
0.35	64%
0.5	73%
0.65	82%
0.8	90%
1	100%

Further formulae are given in the appendix for the effect size when three or more subscales are combined. These formulae can be used to develop three general rules-of-thumb:

1. Use of a single subscale will only have greatest efficiency if the predicted effect size on the scale is considerably larger than that of any other subscale. Correlations between subscales are typically about 0.3 – 0.6. Looking at table 1, it can be seen that effect size on a single subscale will have to be about 50% greater as all other subscales to make it inefficient to combine scales.

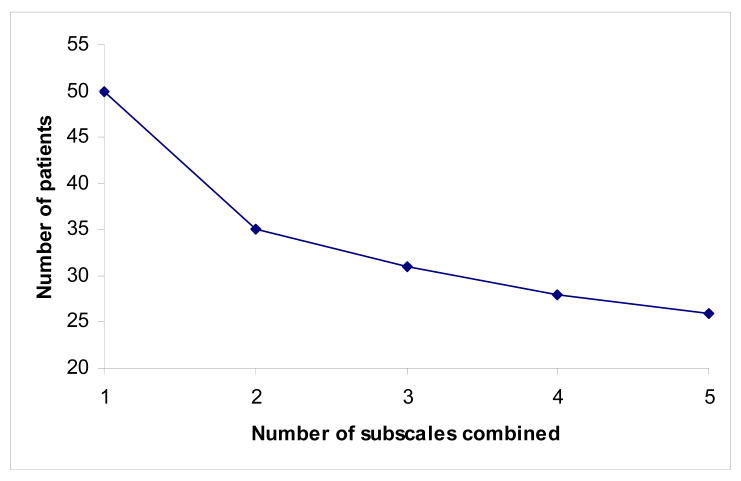
2. A composite of all scales will only have greatest efficiency if the predicted effect sizes are similar. This is most likely to be the case if researchers are unsure which aspects of an instrument are most affected by an intervention (that is, the predicted relative effect size of each subscale is one.) As shown in figure 1, effect size of the composite scale always increases with addition of more subscales.

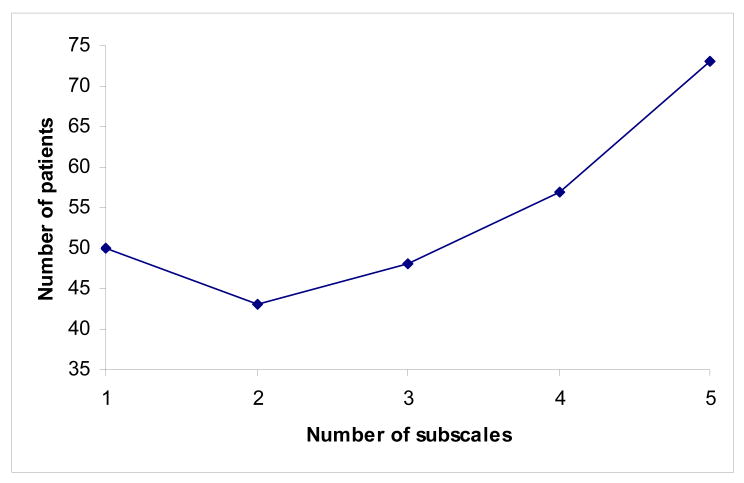
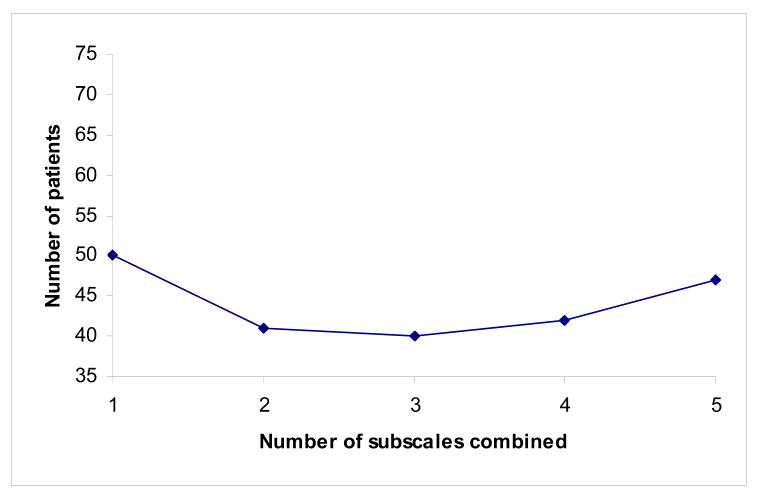
3. It will therefore often be the case that a combination of some but not all subscales will have greatest statistical efficiency (see figures 2 and 3).

Figure 1.

Number of patients needed per group for a clinical trial where the primary outcome measure is a composite of up to five subscales and the intervention is thought to affect each subscale equally. For the purposes of illustration, correlation between subscales is set at 0.4, and the required sample size if only one subscale used is set at 50. Number of patients needed continues to fall as the number of subscales combined increases.

Figure 2.

Number of patients needed per group for a clinical trial where the primary outcome measure is a composite of up to five subscales. Relative effect size on each subscale is 1, 0.8, 0.6, 0.4 and 0.2. For the purposes of illustration, correlation between subscales is set at 0.4, and the required sample size if only one subscale used is set at 50.

Figure 3.

Number of patients needed per group for a clinical trial where the primary outcome measure is a composite of up to five subscales. Even if relative effect size is quite similar between different scales (in this case 1, 0.85, 0.75, 0.65 and 0.5), the most statistically efficient combination of subscales is neither the single subscale or the composite of all five.

Illustrative examples

Correlations (table 2) between FACT-G subscales and standard deviations of each scale were calculated using raw data provided by the authors of the scale. The data come from 806 patients in the NIH funded “Quality of Life Evaluation in Oncology” project, approximately evenly divided between breast cancer, colorectal cancer, head and neck cancer, HIV/AIDS, lung cancer, lymphoma, prostate, and other cancers. Though FACT-G is used as an example, the same principles apply regardless of the instrument used.

Table 2.

Correlations between FACT-G subscales

	Physical	Social	Emotional
Physical	-	-	-
Social	0.15	-	-
Emotional	0.46	0.34	-
Functional	0.65	0.33	0.50

Hypothetical chemotherapy trial

Take the case of a research team who wish to study whether a newly developed chemotherapy regime improves quality of life (measured using FACT-G) compared to an established regime of high toxicity. Preliminary evidence suggests that there is unlikely to be an important difference in survival between groups and therefore the quality of life outcome figures importantly in the sample size calculation. The researchers predict that the largest effect of the new regime will be on the physical well-being subscale (e.g. “I feel sick”) and on the functional well-being subscale (e.g. “I am enjoying my usual leisure pursuits”). They feel that there will be less effect on emotional well-being (e.g. “I am proud of how I'm coping with my illness”) and little, if any, impact on social functioning (e.g. “I get emotional support from my family”). The researchers feel that using the FACT-G total score might dilute any difference between groups. They want to know the statistical implications of their different options for combining subscales.

The first step is to try to put some numbers on the researchers' predictions. They estimate the greatest effects will be on the physical scale. The predicted effects on the other scales relative to the physical scale are given in the second column of table 3. These estimates need to be converted into effect sizes using relative standard deviation: to obtain the relative effect size for the functional scale, for example, the standard deviation for the physical scale (5.9) is divided by the standard deviation for the functional scale (6.9) and multiplied by the predicted relative effect (80%) on the functional scale compared to the physical scale.

Table 3.

Predicted effect sizes for the chemotherapy trial

Subscale	Predicted relative effect	SD	Relative effect size
Physical	100%	5.9	100%
Functional	80%	6.9	68%
Emotional	40%	3.6	66%
Social	25%	5.6	26%

Given that the researchers are most interested in physical and functional well-being, an immediate question is whether there are any reasons not to combine these scales. The correlation between the subscales is 0.65 (see table 2) corresponding to a required relative effect size of 0.82 (table 1). The means that the effect size of the functional scale would have to be at least 80% as large as the effect size on the physical scale to make it statistically efficient to combine the two scales. In fact, the relative effect size is closer to 70%, suggesting that a randomized trial with a combined physical and functional scale as the primary endpoint would probably require more patients than the physical scale alone. The team decides to use the physical subscale as the primary endpoint for their randomized trial. The functional and other FACT-G subscales, as well as total FACT-G, would be reported as secondary outcomes.

However, researchers at a collaborating site disagree: they say that physical and functional well-being will be affected equally and that the primary endpoint should be a combination of these scales. They point out that this composite is similar to the FACT Trial Outcomes Index(7). If the difference between groups is the same for both physical and functional well-being, the effect size of the functional scale relative to the physical scale is 0.86 (this is because it has a larger standard deviation). Although this means that the combination of physical and functional subscales meets the formal criterion for statistical efficiency, it is not greatly more efficient than using the physical scale alone. The principal investigator feels that a single subscale is probably easier to interpret and decides to retain physical well-being as the primary outcome.

Hypothetical support group trial

As a second example, a research team wishes to study whether a support group for newly diagnosed cancer patients is of benefit. The support group deals with issues such as communication, family problems and coping strategies. The researchers are very confident about their intervention and say that it will help all aspects of quality of life. Though they want to use a FACT-G total score, a colleague suggests that it may be better to concentrate on the one or two scales most likely to be affected by the support group. To understand the statistical implications of their various options, the researchers give some estimates as shown in table 4. This table shows the effect size of combining subscales using the equations given in the appendix.

Table 4.

Predicted effect sizes for the support group trial

Subscale	Predicted relative effect	SD	Relative effect size
Social	100%	5.6	100%
Emotional	90%	3.6	147%*
Functional	50%	6.9	n/a+
Physical	25%	5.9	102%-

^*Effect size for a composite of the social and emotional scales

⁺The researchers want to know the relative effect size of combining social and emotional scales, or the total FACT-G, compared to just the social scale. The combination of social, emotional and functional scales is not of interest.

^-Compositive of all scales, equivalent to the overall FACT-G score.

The largest effect size is for the combination of emotional and social scales and the principal investigator decides to use this as the primary outcome. The study question could be phrased as: “Does a cancer support group improve social and emotional well-being in newly diagnosed cancer patients?” One of the researchers is suspicious of this decision and suggests that “the cart is pushing the horse”. The researcher asks: “why should we let statistics tell us what to measure?” and states that as the intervention is “holistic”, all domains of quality of life should be included in the outcome measure. The researchers think this is a good point and want to know what would result if they decided to combine all scales.

The implications can be expressed in terms of sample size. Sample size is proportional to the reciprocal of effect size squared. Using the effect sizes of 1.02 and 1.47 from table 4, the number of patients required for a trial with the total FACT-G score as the main outcome measure is about twice that for a trial with the primary outcome measure as the combination of emotional and social scales. The researchers therefore have to decide whether the time and trouble involved in accruing twice as many patients is worth the benefit of using the total quality of life scale. Changes on other subscales of the FACT-G or the total score could of course be reported as secondary outcome measures.

The role of pilot data

It might be argued that the choice of subscale or combinations of subscales should be decided by pilot data. In this line of reasoning, researchers should undertake a small pilot – advisable in any case for ironing out practical issues – analyze the results using a variety of different combinations of scales and chose the analysis which shows the largest difference between groups. The problem with such an argument is sample sizes in pilot studies are small and so estimates are associated with wide confidence intervals. For example, I established a simulation of a pilot randomized trial with 20 patients where outcome is measured on a quality of life instrument with three subscales (physical, emotional and social functioning). The 95% confidence intervals for the effect size for using one, two or all three subscales were 0.6 – 2.5, 0.4 – 3.3 and 0.2 – 4.3 respectively. It would be very difficult to make a sensible choice of primary endpoint on the basis of these data. It is therefore preferable to use sensible estimates of effect size based on clinical judgment, and calculate predicted effect sizes accordingly, than to use empirical estimates prone to large statistical indeterminacy.

Conclusions

Quality of life instruments are frequently, and increasingly, used as outcomes in randomized trials. Instruments which consist of several subscales present researchers with a choice of whether to combine some or all scales into a single composite score. This choice can be informed by statistical considerations. If researchers are able to make reasonable estimates of the relative effect size of the intervention on different subscales, these can be combined with published data on subscale correlations and standard deviations to predict the relative effect size of a set of clinically reasonable combinations of scales. Such predictions will have only moderate precision: correlations between subscales may be different in the study and the normative sample; they may also be affected by randomization. There is also likely to be imprecision in clinicians' estimates of treatment effects. Nonetheless, calculating quantitative estimates of effect size for different clinically reasonable combination of subscales seems likely to lead to trials with greater statistical power than mere guesswork.

It is assumed that scale validity, reliability and internal consistency are transitive. For example, if patients give good test-retest reliability for a physical and an emotional subscale separately, then it seems reasonable that the combined physical and emotional subscales will have acceptable reliability. However, in determining whether a certain combination of subscales is meaningful, researchers will want to consider any threats to the validity, reliability and internal consistency arising when scales are combined.

As should be clear from the examples, this paper should not be taken as an argument for the statistical determination of endpoint selection in quality-of-life trials. It is not difficult to think of subscale combinations that, despite being statistically efficient, are clinically meaningless. Conversely, in many trials, there may be overriding clinical reasons to chose a particular subscale or composite. However, researchers will often have a choice between several reasonable alternatives for the primary outcome measure. In such cases, considerations of statistical efficiency can provide important information to guide design choices.