Abstract
As local drug delivery continues to emerge as a clinical force, so does understanding of its potentially narrow therapeutic window. Classic molecular transport studies are of value but do not typically account for the local nature of drug transport or the regional dynamic function in target tissues like muscle that may undergo cyclical and variable mechanical motion and loading. We examine the impact of dynamic architecture on intramuscular drug distribution. We designed a tissue mounting technique and mechanical loading system that uniquely enables pharmacokinetics investigations in association with control of muscle biomechanics while preserving physiologic tissue architecture. The system was validated and used to elucidate the influence of architecture and controlled cyclic strain on intramuscular drug distribution. Rat soleus muscles underwent controlled deformations within a drug delivery chamber that preserved in vivo physiology. Penetration of 1 mM 20 kDa FITC-dextran at planar surfaces of the soleus increased significantly from 0.52 ± 0.09 mm under 80 min of static (0%) strain to 0.81 ± 0.09 mm under cyclic (3 Hz, 0–20% peak-to-peak) strain, demonstrating the driving effect of cyclic loading on transport. Penetration at curved margins was 1.57- and 2.53-fold greater than at planar surfaces under static and cyclic strain, respectively, and was enhanced 1.6-fold more by cyclic strain, revealing architecturally dictated spatial heterogeneity in transport and modulation of motion dynamics. Architectural geometry and dynamics modulate the impact of mechanical loading on local drug penetration and intramuscular distribution. Future work will use the biomechanical test system to investigate mechanisms underlying transport effects of specific loading regimens. It is hoped that this work will initiate a broader understanding of intramuscular pharmacokinetics and guide local drug delivery strategies.
Keywords: Mechanical, Strain, Muscle, Delivery, Transport
1. Introduction
Muscle tissue presents an exclusive drug transport environment in which dynamic mechanical motion and loading may be a predominant influence on the pharmacokinetics of locally delivered agents. These motions and loads, which are shaped by both structure and function of the muscle, can present significant and variable physical influences on aqueous drug transport by means of their effect on modulating extracellular space or fluid distribution (Sreter, 1963b).
The effects of mechanical loading on transport of local agents have been investigated in a variety of load-bearing tissues. Studies have examined the effects of tension-compression on solute and dextran transport in cartilage (Huang and Gu, 2007, Quinn et al., 2001), static tensile loading on diffusion of water in Achilles tendon (Han et al., 2000, Helmer et al., 2006), and stretch on transmural transport of albumin, LDL, and Evans Blue in the arterial wall (Fry et al., 1981, Meyer et al., 1996). Similar studies in skeletal muscle have investigated the impact of contraction on total uptake of glucose (Ihlemann et al., 2001, Ihlemann et al., 2000). However, no studies have investigated the interrelated effects of architecture and mechanical loading on the regional distribution – not just volumetric uptake – of local agents in skeletal muscle. With the advent of local drug delivery to contractile tissues, and the present clinically motivated need for effective strategies to locally deliver therapeutic angiogenic growth factors to ischemic muscles (Epstein et al., 2001), a quantitative knowledge of the pharmacokinetics in muscle is critically important. Thus, the goal of this study is to elucidate the combined influences of architecture and dynamic mechanical loading on the regional distribution of aqueous drug in skeletal muscle.
A tissue mounting technique and biomechanical loading system were designed to investigate intramuscular distribution of locally delivered drugs in association with control of muscle biomechanics. The preparation uniquely enables muscles to be secured in a natural, physiologic configuration and undergo in vitro mechanical testing while incubated in drug under functionally viable conditions to preserve accurate drug transport.
2. Tissue Handling and Mechanical Loading System
Surgical Isolation Protocol
Experiments were conducted within the animal welfare regulations and guidelines of Massachusetts. Male Sprague-Dawley rats (450–470 g) were administered 1000 U of Heparin via intraperitoneal injection 5 min prior to euthanasia with inhaled CO2. Thoracotomy was performed immediately after euthanasia, and 60 ml of Krebs-Henseleit-Butanedione Monoxime (KH-BDM) (118.1 mM NaCl, 4.7 mM KCl, 2.5 mM CaCl2, 1.2 mM MgSO4, 1.2 mM KH2PO4, 25 mM NaHCO3, 11.1 mM Glucose, supplemented with 1 mM Sodium Pyruvate, 1 mM Isoleucine, 1 mM Leucine, 1 mM Valine, and 5 mM BDM, pH 7.4) oxygenated with 95% O2-5% CO2 was infused down the aorta to relax and preserve the lower extremities.
The soleus was surgically exposed in one of the distal hindlimbs. The tendons of overlying muscles at the tuber calcanei and fibular head were dissociated from the tendons of the soleus. The in situ length of the soleus was measured using a Mitutoyo Digimatic caliper with ± 0.01 mm precision between the proximal and distal myotendinous junctions while flexing the knee and ankle at 90°. This in situ length is referred to as nominal length. Because rats were selected in a narrow weight range, all soleus muscles were of uniform size and measured 28 mm in nominal length. The soleus was isolated from surrounding fascial connections and tissues, and resected with its tendons and segments of the calcaneus and fibula still intact.
During isolation, the soleus was regularly superfused with KH-BDM to prevent drying. Surgical isolation was repeated for the contralateral soleus while the excised soleus was held at nominal length in KH without BDM that was oxygenated and chilled on ice. After excision, soleus samples equilibrated in KH for at least 15 min before mechanical loading.
Mounting Configuration
A mounting technique and associated mechanical loading system were invented to investigate accurate intramuscular drug transport under mechanical loading. The excised whole muscle is secured onto specially-designed mounting blocks by inserting its intact bone segments into angled slots in the blocks (Fig. 1). The slots secure the bone segments by mechanical fit and leverage to hold them at an acute angle to the muscle axis without using additional fastening mechanisms that physically disrupt the soft tissues and could result in drug transport artifacts. The innovation of the blocks and mounting configuration is that they hold a muscle sample in an in situ configuration via its own physiologic attachments, and allow forces to be transmitted from the bones through the muscle in a physiologic manner to preserve the natural physical dimensions of the muscle. The mechanical loading system consists of two major components: mounting blocks and a dynamic loading system.
Fig. 1. Mounting configuration and blocks.
(A) Mounting configuration of an isolated soleus muscle and its natural bone attachments in the mounting blocks. The angled slots are sized specifically for either the calcaneus or fibula to secure the respective bone segments without using traditional mounting techniques such as sutures, hooks, clamps, pins, or other fixtures, which lead to tissue distortion, disruption of anatomic integrity and natural force transmission, and development of non-physiologic mechanical properties that could result in drug transport artifacts. (B) Solidworks design and rendering of the mounting blocks. (C) Cross-sectional view of the mounting blocks showing the internal course of the angled slots through the blocks (arrows). The two Lexan blocks of equal size each have two primary through-holes that run at a 10° angle from the top surface of the block to serve as mounting holes for bone segments.
Mounting Blocks
The conjugate mounting blocks can be secured in a static mounting assembly as a standalone device to impose static tensile strain on a pair of mounted muscle samples (Fig. 2). The assembly enables samples to be stretched while incubated in drug solution. The blocks can be disengaged from the static assembly and individually attached onto the dynamic loading system to serve as mounting fixtures that hold samples in a physiologic configuration for dynamic tensile loading.
Fig. 2. Static mounting assembly.
(A) In the static mounting assembly, a lead screw adjusts the separation distance between the conjugate blocks. Set screws lock each block at a user-defined fixed position along the guide-rails. (B) Static tensile strain can be applied to a pair of mounted soleus muscles while they incubate in oxygenated drug source. (C) The simple mounting method allows muscles to incubate in a minimal volume of solution to conserve drug source and avoid the use of excessive, suprapharmacologic doses in transport studies.
Dynamic Loading System
The dynamic loading system enables automated, oscillatory, linear strains to be imposed on mounted samples while they incubate in drug solution (Fig. 3). Mechanical loading is driven directly by a LinMot® P01-37x240/60x260 linear servo motor that can achieve a peak force, velocity, and acceleration of 72 N, 0.45 m/s, and 8.5 m/s2, respectively. Motor position is tracked by an internal sensor with 20 µm resolution and controlled by proportional-integral-derivative (PID) logic that enables execution of a 0.7 mm peak-to-peak displacement with ± 60 µm positional error. Total mechanical compliance of the series combination of motor, rack and pinion assembly, and mounting blocks is less than 0.0057 ± 0.002 mm/N and linear over a 75 N force range. This enables more precise force transmission than other systems developed to apply high frequency vibrations concurrent with larger amplitude elongations, which have 2.5- to 116-fold greater compliance (Ettema, 1997, Ettema et al., 1998, Loeffler and Sagawa, 1975, Templeton et al., 1973). All static and dynamic strains in our experiments were applied using the static and dynamic loading assembly, respectively.
Fig. 3. Dynamic loading system.
(A) A PID-controlled linear servo motor actuates dynamic loading. (B) The dynamic mounting assembly incorporates a rack and pinion arrangement that enables the symmetric and simultaneous displacement of the ends of mounted tissue samples to impose strain. (C) A connecting block offsets the mounting block from the dynamic assembly to enable mounted samples to be submerged in solution during cyclic mechanical loading. (D) The dynamic mounting assembly with mounting blocks attached. (E) Mounted soleus muscles. (F) In the experimental setup, mounted samples are stretched either statically or dynamically while incubated in well-mixed and oxygenated drug solution at room temperature under architecturally physiologic and functionally viable conditions.
3. Methods
Force-Length Relationships
Using a reconfigured static assembly (Fig. 4), individual muscles (n = 7) were pre-strained to 0%, 5%, 10%, 15%, and 20%, and stimulated to produce isometric twitch contractions using a biphasic stimulus (15 V, 50 ms pulse) applied to opposite tendons using stainless steel electrodes. Passive and total tensions were measured. Active twitch force was calculated by subtracting passive from total tension. Between recordings, samples incubated in oxygenated KH. Assessment of in vitro viability demonstrated samples maintained a minimum isometric twitch force of 0.19 N for at least 2 h and contractile activity at 3 Hz for at least 1 h.
Fig. 4. The static assembly reconfigured for force measurement.
A thin-beam load cell (Omega Engineering, Inc., LCL-227G, 0-227 g) secured to one of the guide-rails was attached to the fibula mounting block, which was allowed to slide freely on the rails. The calcaneus block was fixed to the guide-rails. Electric stimulus was generated and force measurements were recorded using a National Instruments DAQPAD-6062E data acquisition board controlled by LabView 7.0.
Drug Transport
Soleus muscles (n = 5) were continuously, cyclically stretched between 0% and 20% strains at 3 Hz. Controls (n = 5) were held fixed at 0%. Samples were loaded for 80 min while incubated in 16 ml of 1 mM 20 kDa FITC-dextran (Sigma-Aldrich) in KH. Drug source was kept well-mixed by magnetic stir bar and oxygenated at room temperature, which is optimal for maintaining physiologic stability and functional performance of muscles in vitro (Blomstrand et al., 1985, Petrofsky and Lind, 1981, Segal and Faulkner, 1985) without inhibition of drug binding or transport properties. Fluorescence intensity of the bulk source, sampled before and after an 80-min incubation using fluorometry, remained constant. Therefore, drug source concentration remained constant throughout incubations.
Preliminary histologic assessment of tissue porosity (ratio of extracellular space area to total tissue area) demonstrated that permanent tissue degradation and injury was only a function of time and independent of mechanical loading conditions. Thus baseline architecture was consistent among all samples incubated for the same duration, and differences in extracellular transport (Osman et al., 1971, Rutili and Arfors, 1976) of soluble dextran can be attributed to the dynamic influences of mechanical loading on architecture.
Preliminary transport studies validated the bulk uptake (Elmquist et al., 1992) and non-binding properties (Rutili and Arfors, 1976) of FITC-dextran in soleus tissue. Fractional volume of distribution, which defines an effective transport space reflecting the effects of both steric interaction and charged partitioning on soluble (not bound) drug distribution, was determined by the slope of the empiric relationship between equilibrium drug concentration in tissue versus the corresponding bulk source concentration. The fractional volume of distribution (ε), defined as the ratio of the equilibrium tissue concentration of soluble drug (cs) per unit total tissue volume (VT) to bulk phase concentration (cbulk): ε = cs/cbulk, reflects the partition coefficient, κtissue/bulk=ctot/cbulk (where ctot is the tissue concentration of soluble and bound drug in the accessible tissue volume), scaled by the ratio of the tissue volume accessible for drug distribution (Va) to VT (which represents sterical effects): ε = κtissue/bulk·Va/VT (Lovich and Edelman, 1996). Equilibrium incubation studies demonstrated a fractional volume relationship that was linear over 0.1 µM–1 mM bulk concentrations with a slope of 84%, indicating bulk uptake of dextran. A fractional volume approximating 100% suggests minimal reduction of source concentration by charged partitioning or steric hindrance of dextran to freely diffuse throughout the muscle. Using an equilibrium distribution analysis (Lovich and Edelman, 1996) of the fractional volume relationship, bound fraction of dextran was calculated by subtracting cs from the empiric tissue concentration. This demonstrated a spread about zero across the range of source concentrations, indicating that binding site density for dextran in the soleus was lower than the scatter in the data, and therefore insignificant. These transport characteristics and the in vitro stability of FITC-dextran (Mehvar, 2000, Schroder et al., 1976) enable investigation of transport that is unaffected by drug-tissue interactions and accurate demonstration of the isolated transport effects of tissue structure and mechanical loading.
Tissue Processing and Drug Measurement
After loading, samples were rinsed twice in 15 ml of fresh KH and snap-frozen at nominal length in −145°C Isopentane. 8 µm axial cross-sections from the midpoint of the samples were cut using a Leica CM1850 cryotome. FITC-dextran was imaged using epifluorescence microscopy (Leica DMRA2, 50× magnification, Hamamatsu ORCA 286, Metamorph 6.3, ex: 450–490 nm bandpass/ em: 515 nm longpass). An exposure rate was chosen that eliminated tissue autofluorescence and avoided intensity saturation of the system by the drug source. Images were analyzed using Matlab. A preliminary calibration confirmed the linear relationship between image fluorescence intensities and tissue drug concentrations for 0.01 mM–1 mM bulk source concentrations of 20 kDa FITC-dextran. Drug distribution and unidirectional penetration were quantified in the muscle cross-section. Intramuscular penetration depth was defined as the perpendicular distance from the muscle surface at which fluorescence intensity decreased to 5% of the surface intensity.
Statistical Analysis
Student’s t-Test and Two-Factor Analysis of Variance (ANOVA) with Replication were applied to assess significance in force-length relationship and drug penetration data, respectively.
4. Results
Force-Length Relationships
The classic exponential curve characterizing the passive extensibility of skeletal muscle was observed (Fig. 5). Active twitch tension demonstrated a classic parabolic increase, by 1.5-fold, to a maximum at 10% strain and fell off thereafter. Nominal length corresponds to initial length and 10% strain the optimal length of the soleus. Peak twitch tension (0.35 ± 0.06 N) agrees with values measured by previous in vitro (0.35 ± 0.02 N) and in situ (0.30 ± 0.10 N) studies using rats of similar size (Rankin et al., 1988, Ryall et al., 2002). Passive force (0.12 ± 0.06 N) at the optimal length (10%) also agrees with previous findings (0.15 N) (Rankin et al., 1988).
Fig. 5. Force-length relationships of the soleus.
(A) Total, active, and passive tensions of a single soleus muscle (n = 7). 0% strain is the nominal length, 5% strain is elongation to 105% of the nominal length, etc. Active twitch tension increases from 0.24 ± 0.06 N at 0% strain, to a maximum of 0.35 ± 0.06 N at 10%, and decreases to 0.19 ± 0.06 N at 20%. Twitch tensions measured at each strain in both the increasing and decreasing halves of the parabolic force-length relationship are statistically significantly different (T-test, p<0.05). Because the nominal in situ length, or 0% strain, is the length at which the first passive resistance to stretch occurs, it is equivalent to the initial length of the muscle. Maximal active force is developed at 10% strain, defining it as the optimal or resting length, L0, of the muscle. (B) Isometric twitch tension of 7 different single soleus samples, showing reproducibility of force measurements and consistency of muscle preservation in our drug delivery preparation.
Drug Transport Under Mechanical Loading
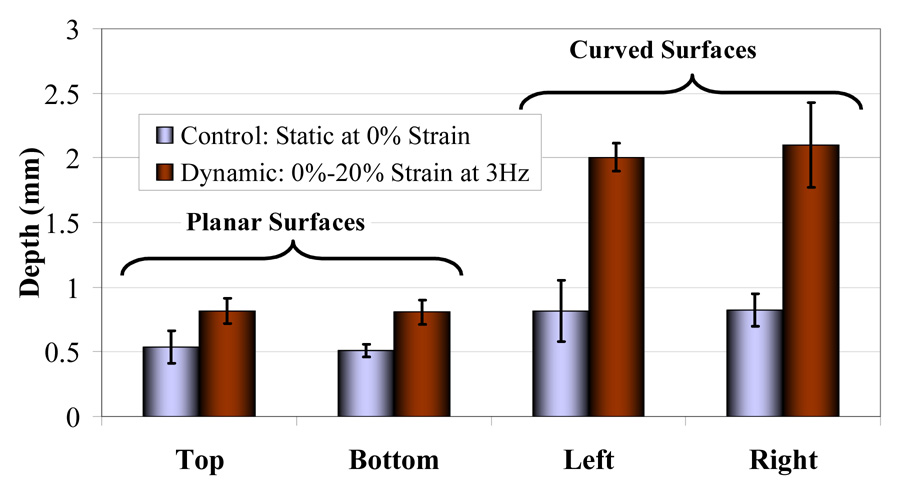
Drug distribution and penetration was quantified at the planar and curved surfaces of the muscle cross-section (Fig. 6). Two-Factor ANOVA revealed that while penetration (Fig. 7) was equivalent at opposing surfaces with similar geometry (p>0.05), it was significantly impacted by differences in regional tissue geometry and architecture (penetration was 1.57- to 2.53-fold greater at curved than planar surfaces, p<0.05, under static and cyclic strain, respectively), as well as enhanced by cyclic strain (p<0.05). Dynamic loading interacted with regional architecture to enhance penetration at curved margins by 1.6-fold more than at planar surfaces (p<0.05).
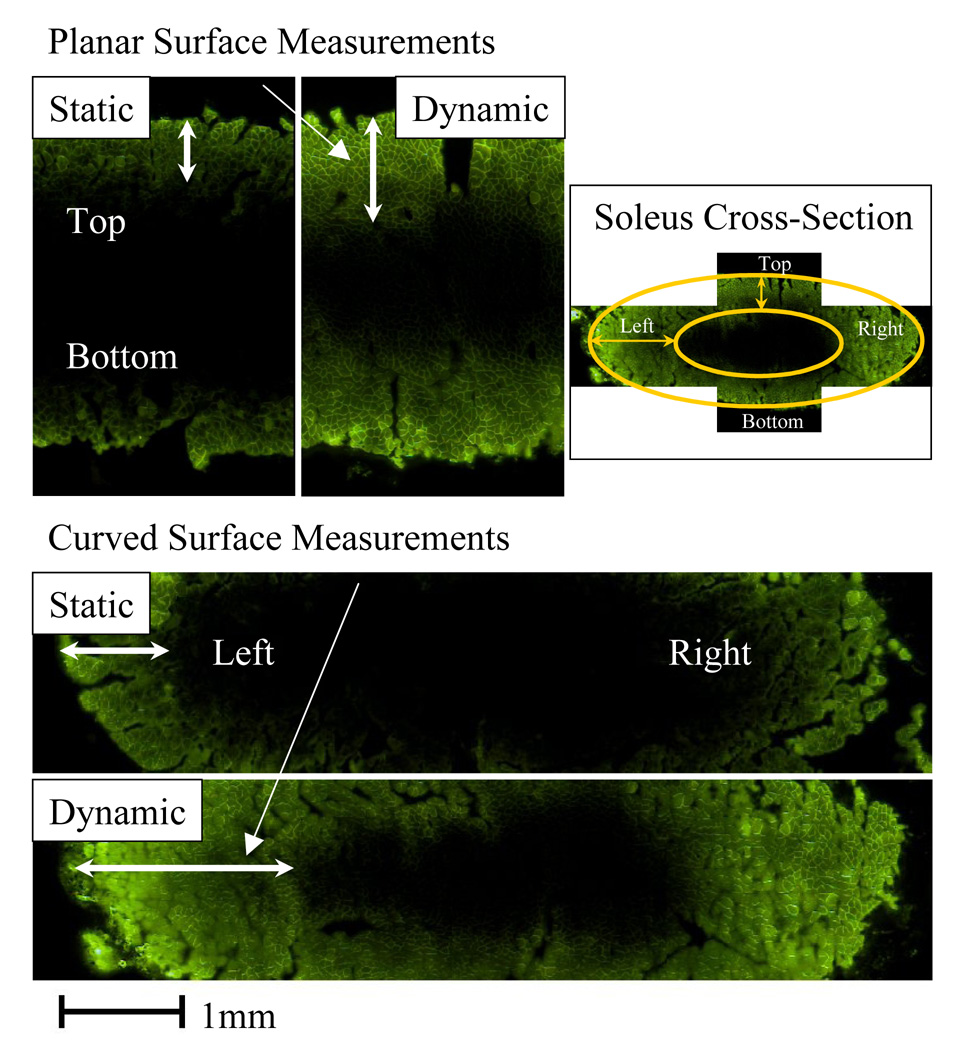
Fig. 6. Quantification of fluorescent drug transport in statically and dynamically strained soleus.
Fluorescence intensity values in images of the elliptical soleus cross-section were quantified using Matlab. Drug distribution was visualized and penetration depth was measured at the planar (Top, Bottom) and curved (Left, Right) surfaces. Planar surfaces are the dorsal and ventral surfaces, and curved surfaces are the medial and lateral margins of the muscle. Surfaces are referred to as top, bottom, left, and right based on their location in the images. Drug distribution is influenced by the regional geometry of the muscle surface. The impact of dynamic strain on drug distribution is modulated by local tissue geometry and architecture.
Fig. 7. Impact of regional architecture and mechanical loading on drug transport.
Penetration was equivalent at opposing planar surfaces for each loading condition, averaging 0.52 ± 0.09 mm under static strain and 0.81 ± 0.09 mm under dynamic strain. Similarly, penetration was equivalent at opposing curved surfaces, averaging 0.82 ± 0.19 mm under static strain and 2.1 ± 0.24 mm under dynamic strain. Penetration was significantly greater at curved than planar surfaces by 1.57- and 2.53-fold under static and dynamic strain, respectively. Penetration at both groups of surfaces was significantly enhanced by dynamic strain. Dynamic strain enhanced penetration at curved surfaces more than at planar surfaces by a factor of 1.6 – penetration increased by 1.56- and 2.51- fold at planar and curved surfaces, respectively.
5. Discussion
A quantitative knowledge of the impact of architecture and structural dynamics on local drug transport is critical to a complete understanding of intramuscular pharmacokinetics and pharmacodynamics. To date much work on intramuscular transport has focused on measuring volumetric changes in interstitial space or total tissue volume induced by strain or contraction using tritiated water (Cappelli et al., 1981); molecular markers like inulin (Cappelli et al., 1981, Creese et al., 1955); albumin (Baker and Davis, 1974, Ward et al., 1996); or solutes like EDTA (Ward et al., 1996), sodium, and potassium (Sreter, 1963a, 1963b). Studies have measured contraction-induced diffusion of water (Trombitas et al., 1993) or myoglobin (Papadopoulos et al., 2000), but only intracellularly in single myofibers. While studies have investigated how strain or contraction in whole muscles affects total uptake of glucose (Aslesen et al., 2001, Constable et al., 1988, Holloszy and Narahara, 1965, Ihlemann et al., 2001, Ihlemann et al., 1999, 2000), lactate (McDermott and Bonen, 1994), phosphate (Abraham and Terjung, 2004), calcium (Armstrong et al., 1993, Gissel and Clausen, 1999), and sodium (Gissel and Clausen, 2000), they focused only on the pharmacokinetic influence of activity-dependent metabolism on substrate uptake. Using and validating a robust mechanical loading preparation designed for local drug delivery in association with accurate biomechanical testing in vitro, this investigation visually quantified structural and mechanical loading effects on regional intramuscular drug distribution. The mounting preparation uniquely eliminated disruptive tissue handling artifacts and preserved physiologic architecture and force transmission to enable accurate drug transport while muscle samples underwent mechanical loading in vitro.
Transport Environment
As tendons exhibit minimal length extensibility within a physiologic strain range (Hawkins and Bey, 1997), the length range from 0% to 20% strain reflects the physiologic range of muscle function and viscoelastic extensibility. Drug transport within this range reflects the pharmacokinetic environment dictated by physiologic architectural configurations.
Intramuscular Pharmacokinetics
Regional Drug Distribution
Equivalent penetration at both sets of opposing surfaces suggests homogeneity of morphology for transport with respect to both the dorsal-ventral and medial-lateral orientation. Assuming an isotropic transport environment based on histology, greater penetration at curved margins than at planar surfaces may result from both geometry of the curved surface and the edge effect on drug distribution occurring at the margins of a nearly flat muscle cross-section. Curvature of the margin results in a semi-circumferential exposure to drug, which increases the surface area and directionality for drug entry into a fixed tissue space. Furthermore, drug transporting from the margins readily encounters drug penetrating at planar surfaces due to the elliptical geometry of the cross-section. Thus, penetration at planar surfaces can contribute significantly to drug distribution at the margins, especially when penetration is enhanced at all surfaces by dynamic loading.
Impact of Dynamic Loading
In the absence of an external convective force driving bulk fluid flow into the muscle, and particularly as drug penetration proceeds against an increasing intramuscular pressure gradient (Wisnes and Kirkebo, 1976) and decreased muscle volume (Baskin and Paolini, 1966) during stretch, enhancement of drug penetration by oscillatory loading is unlikely due to bulk convection. Cyclic strain may modify intramuscular accessible space, interstitial permeability, and transport kinetics. Dynamic loading between 0% and 20% strain may cyclically expose drug to strain-dependent architectural configurations with larger accessible volumes than that at nominal length. This may result from myofiber deformation, displacement, and thinning due to conservation of volume during elongation that increase tissue porosity. Cyclic increase in accessible space may create spatially and temporally heterogeneous concentration gradients that increase diffusional driving force. Interstitial permeability may increase due to alignment of collagen fibers in their dense interstitial networks that form the endomysium and perimysium during stretch (Purslow, 1989, Purslow and Trotter, 1994), which reduces their screening effect on soluble drug (Gauthier and Slater, 2002). Such changes may result in a greater time-averaged porosity and permeability that increases penetration.
The dynamics of oscillatory loading may impact transport kinetics by creating dispersive influences on soluble drug that increase transport beyond molecular diffusion alone (McCarthy et al., 1984). Cyclic displacement and deformation of myofibers compress and expand extracellular space and impose normal and shear forces on interstitial fluid, resulting in pulsatile agitation of soluble drug in the absence of bulk convective fluid flow. Such pulsatile agitation can disperse or spread drug in a rate-dependent manner over a greater extracellular volume and thereby drive greater penetration.
Interaction Between Loading and Architecture
Greater enhancement of penetration at curved margins than at planar surfaces by dynamic loading may be attributed to spatially heterogeneous strain dynamics and heterogeneous extracellular space changes during stretch that are likely shaped by muscle structure and local geometry.
The uni-pinnated, parallel-fibered soleus has an elliptical cross-section that flattens and widens during muscle stretch. Studies of uni-pinnated muscle have revealed that they experience geometry changes during isometric contractions at various initial muscle lengths that consist of spatially heterogeneous changes in aponeurosis length, angle of pinnation of myofibers, and fiber length (Zuurbier and Huijing, 1993). One study observed transverse (perpendicular to muscle surface) strains in superficial myofibers during isometric contraction and aponeurosis surface area decreases with increasing initial muscle length (van Donkelaar et al., 1999). It can be extrapolated from these studies, which assessed strains and geometry changes only from the muscle surface, that flattening and widening of the soleus resulting from conservation of muscle volume during elongation translate into heterogeneous internal fiber rearrangements and intramuscular forces that can alter local drug distribution space and dynamic dispersion effects. While superficial myofibers at planar surfaces tighten with muscle flattening, those at the curved margins of the soleus may experience increased outward transverse strains with widening. Furthermore, because superficial fibers at the margins occur more peripheral to the center of the muscle, they have more obtuse angles of insertion relative to the muscle axis compared to fibers at planar surfaces, which are located towards the midline. These differences in local muscle geometry, fiber arrangement, and angle of insertion likely dictate heterogeneous local strain dynamics and changes in extracellular space during stretch or contraction. These architectural and dynamic heterogeneities may result in greater porosity or dispersive effects at curved margins that significantly impact the heterogeneous drug distribution observed under dynamic stretch.
Conclusions
Dynamic loading increases drug penetration and impacts drug distribution based on the dictates of muscle structure and geometry. These findings yield broad implications for pharmacokinetics investigations and clinical drug delivery strategies to mechanically active target tissues, which should now consider the intimate interplay between tissue architecture and functional dynamics that underlies tissue pharmacokinetics. Modulation of mechanical activity in muscle tissues may possibly serve as a physiological means for controlled drug delivery. A robust biomechanical testing preparation designed for drug transport studies was validated. Further pharmacokinetics studies using this system intend to investigate the mechanisms underlying transport effects of different mechanical loading regimens.
Acknowledgements
These studies were supported in part by graduate fellowships from the Department of Defense and the Whitaker Foundation for Biomedical Engineering to Peter I. Wu, and a research grant from the National Institutes of Health (NIH/NIGMS R01/HL049039) to Elazer R. Edelman. Special thanks to Gerry Wentworth and Mark Belanger of the M.I.T. Laboratory of Manufacturing and Productivity for technical advice on the manufacturing process of the mechanical loading system.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Peter I-Kung Wu, 1. Biomedical Engineering Center, Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, E25-442, Cambridge, Massachusetts 02139, USA.
Elazer R. Edelman, 1. Biomedical Engineering Center, Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, E25-438, Cambridge, Massachusetts 02139, USA 2. Cardiovascular Division, Department of Medicine, Brigham and Women's Hospital, Harvard Medical School, Boston, Massachusetts 02115, USA.
References
- Abraham KA, Terjung RL. Phosphate uptake in rat skeletal muscle is reduced during isometric contractions. Journal of Applied Physiology. 2004;97(1):57–62. doi: 10.1152/japplphysiol.01294.2003. [DOI] [PubMed] [Google Scholar]
- Armstrong RB, Duan C, Delp MD, Hayes DA, Glenn GM, Allen GD. Elevations in rat soleus muscle [ca2+] with passive stretch. Journal of Applied Physiology. 1993;74(6):2990–2997. doi: 10.1152/jappl.1993.74.6.2990. [DOI] [PubMed] [Google Scholar]
- Aslesen R, Engebretsen EM, Franch J, Jensen J. Glucose uptake and metabolic stress in rat muscles stimulated electrically with different protocols. Journal of Applied Physiology. 2001;91(3):1237–1244. doi: 10.1152/jappl.2001.91.3.1237. [DOI] [PubMed] [Google Scholar]
- Baker CH, Davis DL. Isolated skeletal muscle blood flow and volume changes during contractile activity. Blood Vessels. 1974;11(1–2):32–44. doi: 10.1159/000157997. [DOI] [PubMed] [Google Scholar]
- Baskin RJ, Paolini PJ. Muscle volume changes. Journal of General Physiology. 1966;49(3):387–404. doi: 10.1085/jgp.49.3.387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blomstrand E, Larsson L, Edstrom L. Contractile properties, fatiguability and glycolytic metabolism in fast- and slow-twitch rat skeletal muscles of various temperatures. Acta Physiologica Scandinavica. 1985;125(2):235–243. doi: 10.1111/j.1748-1716.1985.tb07712.x. [DOI] [PubMed] [Google Scholar]
- Cappelli V, Poggesi C, Ricciardi L, Reggiani C. Tritiated water (hto) and inulin spaces in isolated skeletal and cardiac muscles: Influence of contractile activity. Experientia. 1981;37(8):849–850. doi: 10.1007/BF01985674. [DOI] [PubMed] [Google Scholar]
- Constable SH, Favier RJ, Cartee GD, Young DA, Holloszy JO. Muscle glucose transport: Interactions of in vitro contractions, insulin, and exercise. Journal of Applied Physiology. 1988;64(6):2329–2332. doi: 10.1152/jappl.1988.64.6.2329. [DOI] [PubMed] [Google Scholar]
- Creese R, D'Silva JL, Hashish SE. Inulin space and fibre size of stimulated rat muscle. Journal of Physiology. 1955;127(3):525–532. doi: 10.1113/jphysiol.1955.sp005274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elmquist S, Libelius R, Lawoko G, Tagerud S. Dextrans as markers for endocytosis in innervated and denervated skeletal muscle. Muscle and Nerve. 1992;15(8):876–884. doi: 10.1002/mus.880150803. [DOI] [PubMed] [Google Scholar]
- Epstein SE, Fuchs S, Zhou YF, Baffour R, Kornowski R. Therapeutic interventions for enhancing collateral development by administration of growth factors: Basic principles, early results and potential hazards. Cardiovascular Research. 2001;49(3):532–542. doi: 10.1016/s0008-6363(00)00217-0. [DOI] [PubMed] [Google Scholar]
- Ettema GJ. Mechanical behaviour of rat skeletal muscle during fatiguing stretch-shortening cycles. Experimental Physiology. 1997;82(1):107–119. doi: 10.1113/expphysiol.1997.sp004001. [DOI] [PubMed] [Google Scholar]
- Ettema GJ, Goh JT, Forwood MR. A new method to measure elastic properties of plastic-viscoelastic connective tissue. Medical Engineering and Physics. 1998;20(4):308–314. doi: 10.1016/s1350-4533(98)00026-5. [DOI] [PubMed] [Google Scholar]
- Fry DL, Mahley RW, Oh SY. Effect of arterial stretch on transmural albumin and evan's blue dye transport. American Journal of Physiology: Heart and Circulatory Physiology. 1981;240(4):H645–H649. doi: 10.1152/ajpheart.1981.240.4.H645. [DOI] [PubMed] [Google Scholar]
- Gauthier MG, Slater GW. Exactly solvable ogston model of gel electrophoresis. Ix. Generalizing the lattic model to treat high field intensities. Journal of Chemical physics. 2002;117(14):6745–6756. [Google Scholar]
- Gissel V, Clausen T. Excitation-induced ca2+ uptake in rat skeletal muscle. American Journal of Physiology: Regulatory, Integrative and Comparative Physiology. 1999;276(2 Pt 2):R331–R339. doi: 10.1152/ajpregu.1999.276.2.R331. [DOI] [PubMed] [Google Scholar]
- Gissel H, Clausen T. Excitation-induced ca(2+) influx in rat soleus and edl muscle: Mechanisms and effects on cellular integrity. American Journal of Physiology: Regulatory, Integrative and Comparative Physiology. 2000;279(3):R917–R924. doi: 10.1152/ajpregu.2000.279.3.R917. [DOI] [PubMed] [Google Scholar]
- Han S, Gemmell SJ, Helmer KG, Grigg P, Wellen JW, Hoffman AH, Sotak CH. Changes in adc caused by tensile loading of rabbit achilles tendon: Evidence for water transport. Journal of Magnetic Resonance. 2000;144(2):217–227. doi: 10.1006/jmre.2000.2075. [DOI] [PubMed] [Google Scholar]
- Hawkins D, Bey M. Muscle and tendon force-length properties and their interactions in vivo. Journal of Biomechanics. 1997;30(1):63–70. doi: 10.1016/s0021-9290(96)00094-2. [DOI] [PubMed] [Google Scholar]
- Helmer KG, Nair G, Cannella M, Grigg P. Water movement in tendon in response to a repeated static tensile load using one-dimensional magnetic resonance imaging. Journal of Biomechanical Engineering. 2006;128(5):733–741. doi: 10.1115/1.2244573. [DOI] [PubMed] [Google Scholar]
- Holloszy JO, Narahara HT. Studies of tissue permeability. X. Changes in permeability to 3-methylglucose associated with contraction of isolated frog muscle. Journal of Biological Chemistry. 1965;240(9):3493–3500. [PubMed] [Google Scholar]
- Huang CY, Gu WY. Effects of tension-compression nonlinearity on solute transport in charged hydrated fibrous tissues under dynamic unconfined compression. Journal of Biomechanical Engineering. 2007;129(3):423–429. doi: 10.1115/1.2720920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ihlemann J, Ploug T, Galbo H. Effect of force development on contraction induced glucose transport in fast twitch rat muscle. Acta Physiologica Scandinavica. 2001;171(4):439–444. doi: 10.1046/j.1365-201X.2001.00807.x. [DOI] [PubMed] [Google Scholar]
- Ihlemann J, Ploug T, Hellsten Y, Galbo H. Effect of tension on contraction-induced glucose transport in rat skeletal muscle. American Journal of Physiology: Endocrinology and Metabolism. 1999;277(2 Pt 1):E208–E214. doi: 10.1152/ajpendo.1999.277.2.E208. [DOI] [PubMed] [Google Scholar]
- Ihlemann J, Ploug T, Hellsten Y, Galbo H. Effect of stimulation frequency on contraction-induced glucose transport in rat skeletal muscle. American Journal of Physiology: Endocrinology and Metabolism. 2000;279(4):E862–E867. doi: 10.1152/ajpendo.2000.279.4.E862. [DOI] [PubMed] [Google Scholar]
- Loeffler L, 3rd, Sagawa K. A one-dimensional viscoelastic model of cat heart muscle studied by small length perturbations during isometric contraction. Circulation Research. 1975;36(4):498–512. doi: 10.1161/01.res.36.4.498. [DOI] [PubMed] [Google Scholar]
- Lovich MA, Edelman ER. Tissue average binding and equilibrium distribution: An example with heparin in arterial tissues. Biophysical Journal. 1996;70(3):1553–1559. doi: 10.1016/S0006-3495(96)79719-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy MJ, Soong DS, Edelman ER. Control of drug release from polymer matrices impregnated with magnetic beads - a proposed mechanism and model for enhanced release. Journal of Controlled Release. 1984;1:143–147. [Google Scholar]
- McDermott JC, Bonen A. Lactate transport in rat sarcolemmal vesicles and intact skeletal muscle, and after muscle contraction. Acta Physiologica Scandinavica. 1994;151(1):17–28. doi: 10.1111/j.1748-1716.1994.tb09717.x. [DOI] [PubMed] [Google Scholar]
- Mehvar R. Dextrans for targeted and sustained delivery of therapeutic and imaging agents. Journal of Controlled Release. 2000;69(1):1–25. doi: 10.1016/s0168-3659(00)00302-3. [DOI] [PubMed] [Google Scholar]
- Meyer G, Merval R, Tedgui A. Effects of pressure-induced stretch and convection on low-density lipoprotein and albumin uptake in the rabbit aortic wall. Circulation Research. 1996;79(3):532–540. doi: 10.1161/01.res.79.3.532. [DOI] [PubMed] [Google Scholar]
- Osman FH, Munson JL, Paton DM. Estimation of extracellular space in rabbit detrusor muscle. Comparative Biochemistry and Physiology. A, Comparative Physiology. 1971;40(1):45–54. doi: 10.1016/0300-9629(71)90145-9. [DOI] [PubMed] [Google Scholar]
- Papadopoulos S, Jurgens KD, Gros G. Protein diffusion in living skeletal muscle fibers: Dependence on protein size, fiber type, and contraction. Biophysical Journal. 2000;79(4):2084–2094. doi: 10.1016/S0006-3495(00)76456-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrofsky JS, Lind AR. The influence of temperature on the isometric characteristics of fast and slow muscle in the cat. Pflügers Archiv: European Journal of Physiology. 1981;389(2):149–154. doi: 10.1007/BF00582106. [DOI] [PubMed] [Google Scholar]
- Purslow PP. Strain-induced reorientation of an intramuscular connective tissue network: Implications for passive muscle elasticity. Journal of Biomechanics. 1989;22(1):21–31. doi: 10.1016/0021-9290(89)90181-4. [DOI] [PubMed] [Google Scholar]
- Purslow PP, Trotter JA. The morphology and mechanical properties of endomysium in series-fibred muscles: Variations with muscle length. Journal of Muscle Research and Cell Motility. 1994;15(3):299–308. doi: 10.1007/BF00123482. [DOI] [PubMed] [Google Scholar]
- Quinn TM, Morel V, Meister JJ. Static compression of articular cartilage can reduce solute diffusivity and partitioning: Implications for the chondrocyte biological response. Journal of Biomechanics. 2001;34(11):1463–1469. doi: 10.1016/s0021-9290(01)00112-9. [DOI] [PubMed] [Google Scholar]
- Rankin LL, Enoka RM, Volz KA, Stuart DG. Coexistence of twitch potentiation and tetanic force decline in rat hindlimb muscle. Journal of Applied Physiology. 1988;65(6):2687–2695. doi: 10.1152/jappl.1988.65.6.2687. [DOI] [PubMed] [Google Scholar]
- Rutili G, Arfors KE. Fluorescein-labelled dextran measurement in interstitial fluid in studies of macromolecular permeability. Microvascular Research. 1976;12(2):221–230. doi: 10.1016/0026-2862(76)90019-4. [DOI] [PubMed] [Google Scholar]
- Ryall JG, Gregorevic P, Plant DR, Sillence MN, Lynch GS. Beta 2-agonist fenoterol has greater effects on contractile function of rat skeletal muscles than clenbuterol. American Journal of Physiology: Regulatory, Integrative and Comparative Physiology. 2002;283(6):R1386–R1394. doi: 10.1152/ajpregu.00324.2002. [DOI] [PubMed] [Google Scholar]
- Schroder U, Arfors KE, Tangen O. Stability of fluorescein labeled dextrans in vivo and in vitro. Microvascular Research. 1976;11(1):57–66. [PubMed] [Google Scholar]
- Segal SS, Faulkner JA. Temperature-dependent physiological stability of rat skeletal muscle in vitro. American Journal of Physiology: Cell Physiology. 1985;248(3 Pt 1):C265–C270. doi: 10.1152/ajpcell.1985.248.3.C265. [DOI] [PubMed] [Google Scholar]
- Sreter FA. Cell water, sodium, and potassium in stimulated red and white mammalian muscles. American Journal of Physiology. 1963a;205:1295–1298. doi: 10.1152/ajplegacy.1963.205.6.1295. [DOI] [PubMed] [Google Scholar]
- Sreter FA. Distribution of water, sodium, and potassium in resting and stimulated mammalian muscle. Canadian Journal of Biochemistry and Physiology. 1963b;41:1035–1045. [PubMed] [Google Scholar]
- Templeton GH, Donald TC, 3rd, Mitchell JH, Hefner LL. Dynamic stiffness of papillary muscle during contraction and relaxation. American Journal of Physiology. 1973;224(3):692–698. doi: 10.1152/ajplegacy.1973.224.3.692. [DOI] [PubMed] [Google Scholar]
- Trombitas K, Baatsen P, Schreuder J, Pollack GH. Contraction-induced movements of water in single fibres of frog skeletal muscle. Journal of Muscle Research and Cell Motility. 1993;14(6):573–584. doi: 10.1007/BF00141554. [DOI] [PubMed] [Google Scholar]
- van Donkelaar CC, Willems PJ, Muijtjens AM, Drost MR. Skeletal muscle transverse strain during isometric contraction at different lengths. Journal of Biomechanics. 1999;32(8):755–762. doi: 10.1016/s0021-9290(99)00073-1. [DOI] [PubMed] [Google Scholar]
- Ward DS, Hamilton MT, Watson PD. Measurement of tissue volume during non-steady state high-intensity muscle contraction. American Journal of Physiology: Regulatory, Integrative and Comparative Physiology. 1996;271(6 Pt 2):R1682–R1690. doi: 10.1152/ajpregu.1996.271.6.R1682. [DOI] [PubMed] [Google Scholar]
- Wisnes A, Kirkebo A. Regional distribution of blood flow in calf muscles of rat during passive stretch and sustained contraction. Acta Physiologica Scandinavica. 1976;96(2):256–266. doi: 10.1111/j.1748-1716.1976.tb10194.x. [DOI] [PubMed] [Google Scholar]
- Zuurbier CJ, Huijing V. Changes in geometry of actively shortening unipennate rat gastrocnemius muscle. Journal of Morphology. 1993;218(2):167–180. doi: 10.1002/jmor.1052180206. [DOI] [PubMed] [Google Scholar]